高中数学选修2-2与选修2-3知识点(反复修改)
高中数学 选修2-3知识点(完整知识点梳理及经典例题答案详解)

高中数学选修2-3知识点总结第一章 计数原理知识点:1、分类加法计数原理:做一件事情,完成它有N 类办法,在第一类办法中有M 1种不同的方法,在第二类办法中有M 2种不同的方法,……,在第N 类办法中有M N 种不同的方法,那么完成这件事情共有M 1+M 2+……+M N 种不同的方法。
2、分步乘法计数原理:做一件事,完成它需要分成N 个步骤,做第一 步有m1种不同的方法,做第二步有M 2不同的方法,……,做第N 步有M N 不同的方法.那么完成这件事共有 N=M 1M 2...M N 种不同的方法。
3、排列:从n 个不同的元素中任取m(m ≤n )个元素,按照一定顺序......排成一列,叫做从n 个不同元素中取出m 个元素的一个排列4、排列数: ),,()!(!)1()1(N m n n m m n n m n n n A m∈≤-=+--= 规定:0!1=5、组合:从n 个不同的元素中任取m (m ≤n )个元素并成一组,叫做从n 个不同元素中取出m 个元素的一个组合。
6、组合数:)!(!!!)1()1(m n m n C m m n n n A A C m nm mm n mn-=+--== )!(!!!)1()1(m n m n C m m n n n A A C m n m m m n m n -=+--==;mn n m n C C -= mn m n m n C C C 11+-=+7、解排列、组合题的基本策略 (1)两种思路:①直接法;②间接法:对有限制条件的问题,先从总体考虑,再把不符合条件的所有情况去掉。
这是解决排列组合应用题时一种常用的解题方法。
(2)分类处理:当问题总体不好解决时,常分成若干类,再由分类计数原理得出结论。
注意:分类不重复不遗漏。
即:每两类的交集为空集,所有各类的并集为全集。
(3在处理排列组合问题时,常常既要分类,又要分步。
其原则是先分类,后分步。
(4)两种途径:①元素分析法;②位置分析法。
高中数学选修2-2,2-3知识点、考点、典型例题

高中数学选修2-2,2-3知识点、考点、典型例题高中数学选修2-2,2-3知识点、考点、典型例题一、2-2数列的概念、数列的通项公式及递推公式1. 数列的概念数列是按照一定规律排列的一系列数,一般用字母 an 表示第n 个数。
2. 数列的通项公式数列的通项公式是指通过数列的位置 n,直接求出该位置上的数 an 的公式。
通项公式可以是一个数学式子,也可以是一个算法。
3. 数列的递推公式数列的递推公式是指通过数列前一项或前几项的值,推导出数列下一项的公式。
递推公式是数列中相邻两项之间的关系式。
4. 常见数列的通项公式和递推公式- 等差数列:an = a1 + (n-1)d (通项公式),an = an-1 + d (递推公式)- 等比数列:an = a1 * q^(n-1) (通项公式),an = an-1 * q (递推公式)- 斐波那契数列:an = an-1 + an-2 (递推公式)二、2-3数列的求和、数列的性质及应用1. 数列的求和- 等差数列的前 n 项和:Sn = (a1 + an) * n / 2- 等比数列的前 n 项和(q ≠ 1):Sn = a1 * (1 - q^n) / (1 - q) - 斐波那契数列的前 n 项和:Sn = Fn+2 - 12. 数列的性质- 常数列:数列中的每一项都是一个常数。
- 奇数列:数列中的每一项都是奇数。
- 偶数列:数列中的每一项都是偶数。
- 单调递增数列:数列中的每一项都比前一项大。
- 单调递减数列:数列中的每一项都比前一项小。
- 正项数列:数列中的每一项都是正数。
- 负项数列:数列中的每一项都是负数。
3. 数列的应用- 利用数列的递推关系,求解实际问题中的特定数值。
- 利用数列的性质,进行数学推理和证明。
- 利用数列的规律,设计算法解决问题。
典型例题:1. 已知等差数列的前三项分别为 1,5,9,求数列的通项公式和第 n 项的值。
解:设数列的首项为 a,公差为 d,则有以下等差数列的递推公式:a2 = a1 + d = 1 + da3 = a2 + d = (1 + d) + d = 1 + 2d将 a1,a2,a3 分别代入等差数列的通项公式,可得:a1 = a = 1a2 = a + d = 1 + d = 5 --> d = 4a3 = a1 + 2d = 1 + 2(4) = 9所以该等差数列的通项公式为 an = a + (n-1)d = 1 + 4(n-1) = 4n - 3第 n 项的值为:an = 4n - 32. 求等差数列 3,6,9,...,101 的前 n 项和。
高中数学选修2-3知识点

高中数学选修2-3知识点高中数学选修2-3知识点第一章:计数原理1.分类加法计数原理:完成一件事情,有N类方法,第一类方法有M1种不同的方法,第二类方法有M2种不同的方法,以此类推,第N类方法有MN种不同的方法。
那么完成这件事情共有M1+M2+。
+MN种不同的方法。
2.分步乘法计数原理:完成一件事情需要分成N个步骤,第一步有m1种不同的方法,第二步有M2种不同的方法,以此类推,第N步有MN种不同的方法。
那么完成这件事情共有XXX种不同的方法。
3.排列:从n个不同的元素中任取m(m≤n)个元素,按照一定顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
4.排列数:从n个不同元素中取出m(m≤n)个元素排成一列,称为从n个不同元素中取出m个元素的m个排列。
从n个不同元素中取出m个元素的一个排列数,用符号An表示。
An=m!/(n-m)!(m≤n,n,m∈N)。
5.公式:A(n+m)=An+Am*m!(m≤n,n,m∈N);An=m*(m-1)*。
*(n-m+1)=n!/(n-m)。
6.组合:从n个不同的元素中任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合。
7.公式:C(m,n)=C(n,n-m)=m!/[(n-m)!*m!];C(m,n)=C(n-1,m-1)+C(n-1,m);C(n,m)=C(n-1,m-1)*(n-m+1)/m。
8.二项式定理:(a+b)^n=C(n,0)*a^n*b^0+C(n,1)*a^(n-1)*b^1+。
+C(n,n)*a^0*b^n。
9.二项式通项公式展开式的通项公式:T=C(n,r)*a^(n-r)*b^r (r=0,1.n),其中C(n,r)为二项式系数。
10.二项式系数Cn:C(n,r)=C(n,n-r)=n!/(r!(n-r)!),其中r为从n个元素中取出的元素个数。
11.杨辉三角:杨辉三角是一种数学图形,由二项式系数构成,XXX的数为C(n,0),C(n,1)。
高二数学选修2-1--2-2--2-3-知识点(全面)

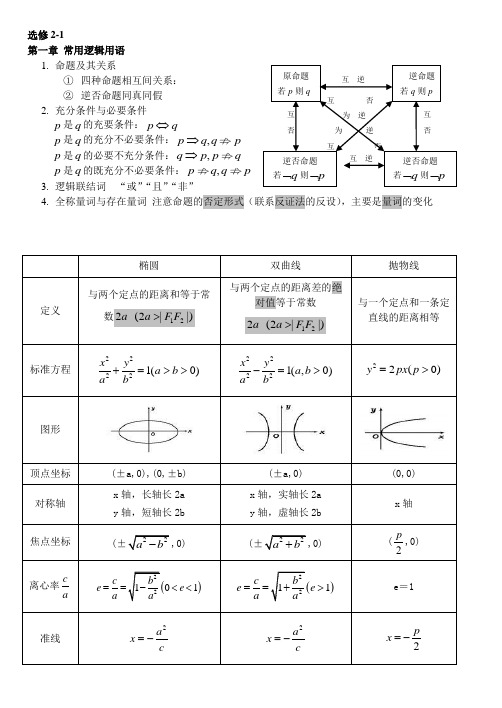
选修2-1、2-2. 2-3知识点选修2-1第一章 常用逻辑用语 1. 命题及其关系① 四种命题相互间关系: ② 逆否命题同真同假 2. 充分条件与必要条件p 是q 的充要条件:p q ⇔p 是q 的充分不必要条件:,p q q p ⇒ p 是q 的必要不充分条件:,q p p q ⇒ p 是q 的既充分不必要条件:,p q q p3. 逻辑联结词 “或”“且”“非”4. 全称量词与存在量词 注意命题的否定形式(联系反证法的反设),主要是量词的变化. 例:“a=1”是“0,21ax x x∀>+≥”的( ) A .充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 第二章 圆锥曲线与方程 1.三种圆锥曲线的性质(以焦点在x 轴为例)椭圆双曲线抛物线定义与两个定点的距离和等于常数122 (2||)a a F F >与两个定点的距离差的绝对值等于常数122 (2||)a a F F >与一个定点和一条定直线的距离相等标准方程22221(0)x y a b a b +=>> 22221(,0)x y a b a b -=> 22(0)y px p =>图形顶点坐标 (±a,0),(0,±b) (±a,0) (0,0) 对称轴x 轴,长轴长2a y 轴,短轴长2b x 轴,实轴长2a y 轴,虚轴长2b x 轴焦点坐标 (±22a b -,0)(±22a b +,0)(2p,0) 离心率c a()22101c b e e a a ==-<<()2211c b e e a a==+>e =1互 否为 逆 为 逆 互 否互否互否互 逆原命题 若p 则q互 逆 逆命题 若q 则p逆否命题 若q ⌝则p ⌝逆否命题 若q ⌝则p ⌝2.“回归定义”是一种重要的解题策略。
如:(1)在求轨迹时,若所求的轨迹符合某种圆锥曲线的定义,则根据圆锥曲线的方程,写出所求的轨迹方程;(2)涉及椭圆、双曲线上的点与两个焦点构成的焦点三角形问题时,常用定义结合解三角形(一般是余弦定理)的知识来解决;(3)在求有关抛物线的最值问题时,常利用定义把到焦点的距离转化为到准线的距离,结合几何图形利用几何意义去解决。
高中数学选修2-2知识点总结(最全版)

高中数学选修2-2知识点总结第一章、导数1.函数的平均变化率为=∆∆=∆∆xfx y x x f x x f x x x f x f ∆-∆+=--)()()()(111212 注1:其中x ∆是自变量的改变量,平均变化率 可正,可负,可零。
注2:函数的平均变化率可以看作是物体运动的平均速度。
2、导函数的概念:函数)(x f y =在0x x =处的瞬时变化率是xx f x x f x yx x ∆-∆+=∆∆→∆→∆)()(lim lim 0000,则称函数)(x f y =在点0x 处可导,并把这个极限叫做)(x f y =在0x 处的导数,记作)(0'x f 或|'x x y =,即)(0'x f =xx f x x f x yx x ∆-∆+=∆∆→∆→∆)()(lim lim 0000.3.函数的平均变化率的几何意义是割线的斜率; 函数的导数的几何意义是切线的斜率。
4导数的背景(1)切线的斜率;(2)瞬时速度;5、常见的函数导数 函数 导函数 (1)y c ='y =0 (2)n y x =()*n N ∈ 1'n y nx -= (3)x y a =()0,1a a >≠ 'ln x y a a =(4)x y e ='x y e =(5)log a y x =()0,1,0a a x >≠> 1'ln y x a =(6)ln y x = 1'y x=(7)sin y x = 'cos y x =(8)cos y x = 'sin y x =-6、常见的导数和定积分运算公式:若()f x ,()g x 均可导(可积),则有: 和差的导数运算[]'''()()()()f x g x f x g x ±=± 积的导数运算[]'''()()()()()()f x g x f x g x f x g x ⋅=±特别地:()()''Cf x Cf x =⎡⎤⎣⎦商的导数运算[]'''2()()()()()(()0)()()f x f x g x f x g x g x g x g x ⎡⎤-=≠⎢⎥⎣⎦ 特别地:()()21'()'g x g x g x ⎡⎤-=⎢⎥⎣⎦复合函数的导数x u x y y u '''=⋅微积分基本定理()baf x dx =⎰F(a)--F(b)(其中()()'F x f x =)和差的积分运算1212[()()]()()b bbaaaf x f x dx f x dx f x dx±=±⎰⎰⎰ 特别地:()()()bb aakf x dx k f x dx k =⎰⎰为常数积分的区间可加性()()()()bcbaacf x dx f x dx f x dx a c b =+<<⎰⎰⎰其中.用导数求函数单调区间的步骤: ①求函数f (x )的导数'()f x②令'()f x >0,解不等式,得x 的范围就是递增区间. ③令'()f x <0,解不等式,得x 的范围,就是递减区间; [注]:求单调区间之前一定要先看原函数的定义域。
高二第二学期理科数学总结(选修2-2_2-3知识点)

选修2-2、2-3单元总结一、导数1、导数定义:f(x)在点x0处的导数记作x x f x x f x f y x x x ∆-∆+='='→∆=)()(lim)(00000;2、几何意义:切线斜率;物理意义:瞬时速度;3、常见函数的导数公式:①'C 0=;②1')(-=n n nx x ;③x x cos )(sin '=;④x x sin )(cos '-=;⑤a a a x x ln )('=; ⑥x x e e =')(;⑦a x x a ln 1)(log '=;⑧x x 1)(ln '= 。
⑨211x x -='⎪⎭⎫ ⎝⎛;⑩()xx 21='4、导数的四则运算法则:;)(;)(;)(2v v u v u v u v u v u uv v u v u '-'=''+'=''±'='±5、复合函数的导数:;x u x u y y '⋅'='6、导数的应用: (1)利用导数求切线:)(0x f k '=;利用点斜式()(00x x k y y -=-)求得切线方程。
注意ⅰ)所给点是切点吗?ⅱ)所求的是“在”还是“过”该点的切线?(2)利用导数判断函数单调性:①)(0)(x f x f ⇒>'是增函数;②)(0)(x f x f ⇒<'为减函数;③)(x f 是增函数⇒0)(≥'x f ;④)(x f 是减函数⇒0)(≤'x f(3)利用导数求极值:ⅰ)求导数)(x f ';ⅱ)求方程0)(='x f 的根;ⅲ)列表得极值。
(4)利用导数最大值与最小值:ⅰ)求得极值;ⅱ)求区间端点值(如果有);ⅲ得最值。
(5)求解实际优化问题: ①设未知数x 和y ,并由题意找出两者的函数关系式,同时给出x 的范围;②求导,令其为0,解得x 值。
选修数学2-3知识点总结

选修数学2-3知识点总结本文将对选修数学2-3中的几个重要知识点进行总结和介绍。
选修数学2-3是高中数学课程中的一部分,主要涉及到高中数学中的几个重要概念和方法。
在本文中,我将按照以下顺序进行介绍:函数的定义和性质、指数函数和对数函数、三角函数。
一、函数的定义和性质在选修数学2-3中,我们首先学习了函数的定义和性质。
函数是一种关系,它将一个集合中的每个元素映射到另一个集合中的唯一元素。
函数可以用图像、表格或公式来表示。
函数的性质包括定义域、值域、单调性、奇偶性等。
我们学会了如何通过观察图像和计算来分析函数的性质,并解决与函数相关的问题。
二、指数函数和对数函数在选修数学2-3中,我们还学习了指数函数和对数函数。
指数函数是形如y=a^x的函数,其中a是一个正实数。
对数函数是指数函数的逆运算,由y=loga(x)表示,其中a是一个大于1且不等于1的实数。
我们学习了指数函数和对数函数的基本性质,如指数函数的增长特性和对数函数的性质。
这些函数在实际问题中有广泛的应用,如利息计算和指数增长问题等。
三、三角函数在选修数学2-3中,我们还学习了三角函数。
三角函数是以圆上的点坐标为基础定义的函数。
我们学习了正弦函数、余弦函数和正切函数的定义和性质。
我们了解了三角函数的周期性、奇偶性、对称性等性质,并学会了通过图像和计算来分析三角函数的特性。
三角函数在物理、工程和计算机图形学等领域有广泛的应用。
以上就是选修数学2-3中的几个重要知识点的总结和介绍。
通过学习这些知识点,我们可以更好地理解数学的基本概念和方法,并在实际问题中应用数学知识解决问题。
希望本文对你在学习选修数学2-3时有所帮助。
高中数学选修2-1、2-2、2-3知识总结
mn1C
m n
C
m n1
8、二项式定理: ( a b ) n C 0 n a n C 1 n a n 1 b C 2 n a n 2 b 2 … C n r a n r b r … C n n b n
二 项 9展 、开 二式 项的 式通 通项 项公 公式 式: T r 1 C n r a n r b r ( r 0 , 1 … … n )
② 解不等式 f '(x) 0或f '(x) 0 ;
③ 确定并指出函数的单调区间(区间形式,不要写范围形式),区间之间用“,”★隔开,不能 用“ ”连结。
8. 极值与最值
对于可导函数 f (x) ,在 x a 处取得极值,则 f '(a) 0 .
最值定理:连续函数在闭区间上一定有最大最小值.
若 f (x) 在开区间 (a, b) 有唯一的极值点,则是最值点。
求极值步骤:
① 确定函数 y f (x) 的定义域(不可或缺,否则易致错);
② 解不等式 f '(x)=0 ;
③ 检验 f '(x)=0 的根的两侧的 f '(x) 符号(一般通过列表)
求最值时,步骤在求极值的基础上,将各极值与端点处的函数值进行比较大小,切忌直接说某某 就是最大或者最小。
4、排列数:从 n 个不同元素中取出 m(m≤n)个元素排成一列,称为从 n 个不同元素中取出 m 个元素的
一个排列. 从 n 个不同元素中取出 m 个元素的一个排列数,用符号 Anm 表示。
Am n(n 1)(n m 1) n! (m n, n, m N) (n m)!
5、公式 Anm nAnm11
(答:(1)a=-3,b=4;(2) c (, 1) (9, ) )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学选修2-2第一章导数及其应用知识点必记1、函数的平均变化率:=∆∆=∆∆x fx y xx f x x f x x x f x f ∆-∆+=--)()()()(111212 注1:其中x ∆是自变量的改变量,可正,可负,可零。
注2:函数的平均变化率可以看作是物体运动的平均速度。
2、导函数的概念:函数)(x f y =在0x x =处的瞬时变化率是xx f x x f x yx x ∆-∆+=∆∆→∆→∆)()(limlim0000,则称函数)(x f y =在点0x 处可导,并把这个极限叫做)(x f y =在0x 处的导数,记作)(0'x f 或0|'x x y =,即)(0'x f =xx f x x f x yx x ∆-∆+=∆∆→∆→∆)()(limlim0000. 3、平均变化率和导数的几何意义是什么?答:函数的平均变化率的几何意义是割线的斜率;函数的导数的几何意义是切线的斜率。
4、导数的背景:切线的斜率;(2)瞬时速度;(3)边际成本。
5、常见的函数导数和积分公式有哪些?6、常见的导数和定积分运算公式有哪些? 答:若()f x ,()g x 均可导(可积),则有:7、用导数求函数单调区间的步骤: (注:求单调区间之前一定要先看原函数的定义域)。
①求函数f (x )的导数'()f x ②令'()f x >0,解不等式,得x 的范围就是递增区间. ③令'()f x <0,解不等式,得x 的范围就是递减区间; 8、利用单调性求参数的取值(转化为恒成立问题)(1)()f x 在该区间内单调递增⇒'()0f x ≥在该区间内恒成立; (2)()f x 在该区间内单调递减⇒'()0f x ≤在该区间内恒成立; 9、求可导函数f (x )的极值的步骤(1)确定函数的定义域。
(2) 求函数f (x )的导数'()f x (3)求方程'()f x =0的根(4) 用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格,检查/()f x 在方程根左右的值的符号,如果左正右负,那么f (x )在这个根处取得极大值; 如果左负右正,那么f (x )在这个根处取得极小值; 如果左右不改变符号,那么f (x )在这个根处无极值。
10、利用导数求函数的最值的步骤求)(x f 在[]b a ,上的最大值与最小值的步骤如下:⑴求)(x f 在[]b a ,上的极值;⑵将)(x f 的各极值与(),()f a f b 比较,其中最大的一个是最大值,最小的一个是最小值。
注:实际问题的开区间唯一极值点就是所求的最值点;数学选修2-2 第二章 推理与证明知识点必记11、归纳推理的定义:从个别事实....中推演出一般..性.的结论,像这样的推理通常称为归纳推理。
归纳推理是由部分到整体..,由个别到一般..的推理。
12、归纳推理的思维过程大致如图:13、归纳推理的特点:①归纳推理的前提是几个已知的特殊现象,归纳所得的结论是尚属未知的一般现象。
②由归纳推理得到的结论具有猜测的性质,结论是否真实,还需经过逻辑证明和实验检验,因此,它不能作为数学证明的工具。
③归纳推理是一种具有创造性的推理,通过归纳推理的猜想,可以作为进一步研究的起点,帮助人们发现问题和提出问题。
14、类比推理的定义:根据两个(或两类)对象之间在某些方面的相似或相同,推演出它们在其他方面也相似或相同,这样的推理称为类比推理。
类比推理是由特殊..到特殊..的推理。
15、类比推理的思维过程:16、演绎推理的定义:演绎推理是根据已有的事实和正确的结论(包括定义、公理、定理等)按照严格的逻辑法则得到新结论的推理过程。
演绎推理是由一般..到特殊..的推理。
17、演绎推理的主要形式:三段论 18、“三段论”可以表示为什么?答: ①大前题:M 是P ②小前提:S 是M ③结论:S 是P 。
其中①是大前提,它提供了一个一般性的原理;②是小前提,它指出了一个特殊对象;③是结论,它是根据一般性原理,对特殊情况做出的判断。
19、直接证明定义:从命题的条件或结论出发,根据已知的定义、公理、定理,直接推证结论的真实性。
直接证明包括综合法和分析法。
20、综合法定义:综合法就是“由因导果”,从已知条件出发,不断用必要条件代替前面的条件,直至推出要证的结论。
21、分析法定义:分析法就是从所要证明的结论出发,不断地用充分条件替换前面的条件或者一定成立的式子,可称为“由果索因”。
要注意叙述的形式:要证A ,只要证B ,B 应是A 成立的充分条件. 分析法和综合法常结合使用,不要将它们割裂开。
22、什么是间接证明?答:即反证法:是指从否定的结论出发,经过逻辑推理,导出矛盾,证实结论的否定是错误的,从而肯定原结论是正确的证明方法。
23、反证法的一般步骤:(1)假设命题结论不成立,即假设结论的反面成立;(2)从假设出发,经过推理论证,得出矛盾;(3)从矛盾判定假设不正确...,即所求证命题正确。
24、常见的“结论词”与“反义词”有哪些?25、反证法的思维方法是正难则反....26、如何归缪矛盾?答:(1)与已知条件....矛盾;(2)与已有..公理、定理、定义........矛盾;(3)自相..矛盾.27、数学归纳法(只能证明与正整数...有关的数学命题)的步骤是什么?答:(1)证明:当n取第一个值....() 00n n N*∈时命题成立;(2)假设当n=k (k∈N*,且k≥n0)时命题成立,证明当n=k+1.....时命题也成立.由(1),(2)可知,命题对于从n0开始的所有正整数n都正确注:常用于证明不完全归纳法推测所得命题的正确性的证明。
第三章数系的扩充和复数的概念知识点必记28、复数的概念:形如a+bi....的数叫做复数,其中i叫虚数单位,a叫实部,b叫虚部,数集{}|,C a bi a b R=+∈叫做复数集。
规定:a bi c di+=+⇔a=c...且.b=d...,强调:两复数不能比较大小,只有相等或不相等。
29、数集的关系有哪些?答:bZ aba=⎧⎪≠⎧⎨⎪≠⎨⎪=⎪⎩⎩实数 ()复数一般虚数()虚数 ()纯虚数()30、复数的几何意义:复数与平面内的点或有序实数对一一对应。
31、什么是复平面?答:根据复数相等的定义,任何一个复数bi a z +=,都可以由一个有序实数对),(b a 唯一确定。
由于有序实数对),(b a 与平面直角坐标系中的点一一对应,因此复数集与平面直角坐标系中的点集之间可以建立一一对应。
这个建立了直角坐标系来表示复数的平面叫做复平面,x 轴叫做实轴,y 轴叫做虚轴。
实轴上的点都表示实数,除了原点外,虚轴上的点都表示纯虚数。
32、求复数的模:与复数z 对应的向量OZ 的模r 叫做复数bi a z +=的模(也叫绝对值)记作bi a z +或。
由模的定义可知:22b a bi a z +=+= 33、复数的运算法则及几何意义①复数的加、减法法则:12z a bi c di =+=+与z ,则12()z z a c b d i ±=±+±。
注:复数的加、减法运算也可以按向量..的加、减法来进行。
②复数的乘法法则:()()()()a bi c di ac bd ad bc i ++=-++。
③复数的除法法则:2222()()()()a bi a bi c di ac bd bc adi c di c di c di c d c d ++-+-==+++-++ 其中c di -叫做实数化因子34、共轭复数:两复数a bi a bi +-与互为共轭复数,当0b ≠时,它们叫做共轭虚数。
第一章 计数原理知识点必记1. 分类加法计数原理:做一件事情,完成它有n 类办法,在第一类办法中有1m 种不同的方法,在第二类办法中有2m 种不同的方法…在第n 类办法中有n m 种不同的方法。
那么完成这件事情共有n m m m N +++= 21种不同的方法。
2. 分步乘法计数原理:做一件事情,完成它需要n 个步骤,做第一个步骤有1m 种不同的方法,做第二个步骤有2m 种不同的方法……做第n 个步骤有n m 种不同的方法。
那么完成这件事情共有n m m m N ⨯⨯⨯= 21种不同的方法。
3. 排列的定义:一般地,从n 个不同的元素中任取()n m m ≤个元素,按照一定的顺序排成一列,叫做从n 个不同的元素中任取m 个元素的一个排列。
4. 组合的定义:一般地,从n 个不同的元素中任取()n m m ≤个元素并成一组,叫做从n 个不同的元素中任取m 个元素的一个组合。
5. 排列数:从n 个不同的元素中任取()n m m ≤个元素的所有排列的个数,叫做从n 个不同的元素中任取m 个元素的排列数,记作mn A 。
6. 组合数:从n 个不同的元素中任取()n m m ≤个元素的所有组合的个数,叫做从n 个不同的元素中任取m 个元素的组合数,记作m n C 。
7.排列数公式:(1)()()()121+---=m n n n n A m n 或()!m n n A m n-=!; (2)!n A nn =,规定1!0=。
8.组合数公式:(1)()()()!121m m n n n n C m n+---= 或()!!m n m n C mn -=!; (2)m n nm n C C -=,规定10=n C 。
9.排列与组合的区别是:排列有顺序,组合无顺序。
10.排列与组合的联系是:mm m n m n A C A ⋅=,即排列就是先组合再全排列。
11.排列与组合性质公式:(1)排列的性质公式:11-++=m nm n m n mA A A (2)组合的性质公式:mn n m n C C -=;11-++=m nm n m n C C C 12.二项式定理:()()+---∈++++++=+N n b C b a C b a C b a C a C b a nn n r r n r n n n n n n n n222110。
13二项展开式的通项:()+-+∈∈≤≤=N n N r n r b a C T r r n r n r ,,01。
14.()nx +1的展开式:()0221101x C x C x C x C x n n n n n n n n n++++=+-- ,若令1=x ,则有()nnn n n n nC C C C ++++==+ 210211。
第二章 随机变量及其分布知识点必记15.随机变量:在某试验中,可能出现的结果可以用一个变量X 来表示,并且X 是随着试验的结果的不同而变化的,我们把这样的变量X 叫做一个随机变量。
