模型视图矩阵和投影矩阵:webgl笔记
three.js中的矩阵变换(模型视图投影变换)

three.js中的矩阵变换(模型视图投影变换)⽬录1. 概述我在这篇博⽂⾥详细讲解了OpenGL\WebGL关于绘制场景的图形变换过程,并推导了相应的模型变换矩阵、视图变换矩阵以及投影变换矩阵。
这⾥我就通过three.js这个图形引擎,验证⼀下其推导是否正确,顺便学习下three.js是如何进⾏图形变换的。
2. 基本变换2.1. 矩阵运算three.js已经提供了向量类和矩阵类,定义并且查看⼀个4阶矩阵类:var m = new THREE.Matrix4();m.set(11, 12, 13, 14,21, 22, 23, 24,31, 32, 33, 34,41, 42, 43, 44);console.log(m);输出结果:说明THREE.Matrix4内部是列主序存储的,⽽我们理论描述的矩阵都为⾏主序。
2.2. 模型变换矩阵在场景中新建⼀个平⾯:// create the ground planevar planeGeometry = new THREE.PlaneGeometry(60, 20);var planeMaterial = new THREE.MeshBasicMaterial({color: 0xAAAAAA});var plane = new THREE.Mesh(planeGeometry, planeMaterial);// add the plane to the scenescene.add(plane);three.js中场景节点的基类都是Object3D,Object3D包含了3种矩阵对象:1. Object3D.matrix: 相对于其⽗对象的局部模型变换矩阵。
2. Object3D.matrixWorld: 对象的全局模型变换矩阵。
如果对象没有⽗对象,则与Object3D.matrix相同。
3. Object3D.modelViewMatrix: 表⽰对象相对于相机坐标系的变换。
webgl矩阵乘法

webgl矩阵乘法摘要:1.WebGL 简介2.矩阵乘法的概念和原理3.WebGL 中的矩阵乘法实现4.矩阵乘法的应用案例5.总结正文:【1.WebGL 简介】WebGL(Web Graphics Library)是一种3D 图形编程接口,它允许在支持HTML5 Canvas 元素的网页上渲染3D 图形。
WebGL 提供了与本地图形硬件的直接访问,使得在浏览器中进行高性能的3D 渲染成为可能。
在WebGL 中,开发者可以利用矩阵乘法实现各种3D 变换,如旋转、平移、缩放等。
【2.矩阵乘法的概念和原理】矩阵乘法在计算机图形学中具有重要意义。
矩阵是一个数学对象,用于表示线性变换。
在WebGL 中,矩阵主要用于实现3D 场景中的坐标变换。
矩阵乘法的基本原理是:将一个向量表示为矩阵的列向量,通过矩阵乘法得到一个新的列向量,这个新的列向量表示的是原向量经过矩阵变换后的结果。
矩阵乘法可以用于实现各种复合变换,如平移、旋转、缩放等。
【3.WebGL 中的矩阵乘法实现】在WebGL 中,矩阵乘法主要通过gl.matrixMultiply() 函数实现。
这个函数接收两个矩阵参数,并返回一个新的矩阵,表示的是两个矩阵相乘的结果。
在实际应用中,开发者需要自己实现矩阵的初始化、存储和更新。
常用的做法是将矩阵存储在数组中,然后通过gl.matrixMultiply() 函数进行计算。
【4.矩阵乘法的应用案例】矩阵乘法在WebGL 中有广泛的应用,下面举一个简单的例子来说明矩阵乘法的应用:假设有一个3D 场景,其中有一个物体需要进行旋转、平移和缩放等变换。
首先,我们需要创建一个表示变换的矩阵,然后通过矩阵乘法将这个变换应用到物体的顶点坐标上。
具体步骤如下:1.创建一个表示变换的矩阵,例如:```const matrix = [1, 0, 0, 0,0, 1, 0, 0,0, 0, 1, 0,0, 0, 0, 1];```2.通过矩阵乘法将变换应用到物体的顶点坐标上:```javascriptgl.matrixMultiply(matrix, modelViewMatrix);```3.将变换后的顶点坐标上传到GPU:```javascriptgl.vertexAttribPointer(顶点坐标属性,3, GL_FLOAT, GL_FALSE, 3 * 4, 顶点坐标偏移);```【5.总结】WebGL 中的矩阵乘法是实现3D 图形变换的重要手段。
WEBGL教程

尝试WebGL的第一步就是让浏览器支持它。
现在,这意味着你必须使用特殊的预览发布版本,因为它甚至还不是测试版。
幸运的是,这非常容易!WebGL 不能运行在我所知道的任何版本的Internet Explorer上,但对于其他三大主流浏览器,情况如下:∙Firefox:WebGL工作在Windows、Mac OS X和Linux中每日构建(Nightly Build,也叫Daily Build),是将一个软件项目的所有最新代码取出,从头开始编译,链接,运行测试软件包对代码进行单元测试并对主要功能进行测试,发现错误并报告错误的完整过程。
——译者注)的Firefox开发版上。
点击此处了解如何安装支持WebGL的Firefox。
如果你使用PC机,建议用Firefox。
∙Safari:Safari的WebKit核心支持WebGL,但只针对Mac电脑的雪豹操作系统(即OS X 10.6)(它曾工作在版本10.5——又名豹操作系统——上,但遗憾的是现在不再被支持了)。
如果你在使用雪豹操作系统,我建议你选择Safari;如果你仍旧使用豹操作系统,我建议你使用Chromium 或Minefield。
点击此处了解如何安装支持WebGL的Safari。
∙Chrome:在Chrome上尝试WebGL的最佳方式是使用每日构建的多个Chromium浏览器版本之一,Chromium开源项目是Chrome的基础。
点击此处了解如何获取可在Chromium上运行的WebGL。
Firefox“不稳定的”Firefox开发版叫做Minefield。
它每天更新,实际上现在相当稳定:在设置上有一个小调整,最近我还没有看见它崩溃(我使用它做一切事情)。
同时也可以安装一个普通版本的Firefox。
因此,如果你不想用它或者只是想切换回普通版本一段时间,你不必去卸载。
获取Minefield:∙登陆到每日构建网页上去获取与你电脑匹配的版本。
∙安装它(当你安装时,你需要退出所有正在运行的Firefox实例)。
《WebGL 3D开发实战详解 第2版 》读书笔记思维导图

9.5 简单镜像 9.6 非真实感绘制
9.7 描边效果的实现 9.8 本章小结
第10章 渲染出更加酷炫的3D场 景——几...
10.1 剪裁测试 10.2 模板测试
10.3 任意剪裁平面 10.4 本章小结
第11章 Three.js引擎基础
0 1
11.1 Three.js 概述
0 2
11.2 初识 Three.js 应用
0 5
12.5 杂项
第13章 Babylon.js引擎
0 1
13.1 Babylon. js概述
0 2
13.2 初识 Babylon. js应用
0 4
13.4 模型 加载
0 6
13.6 粒子 系统
0 3
13.3 Babylon. js基本组件
0 5
13.5 纹理 贴图
13.8 渲染到纹理
13.7 物理引擎
资源与支持
第1章 HTML5开发基础——进入 Web...
1.1 HTML的发展简 史
1.2 HTML5简介
1.3 初识HTML5 1.4 初识CSS
1.6 HTML5 Canvas简介
1.5 初识JavaScript
1.7 本章小结
第2章 初识WebGL 2.0
2.1 WebGL 2.0概 述
2.2 初识WebGL 2.0应用
2.3 着色器与渲染管 线
2.4 本章小结
第3章 着色语言
3.1 着色语言概述 3.2 着色语言基础
3.3 特殊的内建变量
3.4 着色语言的内置 函数
3.6 预处理器
3.5 用invariant修 饰符避免值...
3.7 本章小结
webgl考试题及答案

webgl考试题及答案**WebGL考试题及答案**一、选择题(每题5分,共30分)1. WebGL的全称是什么?A. Web Graphics LibraryB. Web Graphics LanguageC. Web Graphics LayerD. Web Graphics Library答案:A2. 以下哪个是WebGL中用于创建顶点着色器的函数?A. gl.createProgram()B. gl.createShader(gl.VERTEX_SHADER)C. pileShader()D. gl.attachShader()答案:B3. 在WebGL中,以下哪个函数用于清除画布?A. gl.clear()B. gl.clearColor()C. gl.clearDepth()D. gl.viewport()答案:A4. WebGL中,以下哪个函数用于将纹理应用到物体上?A. gl.bindTexture()B. gl.texImage2D()C. gl.texParameteri()D. gl.generateMipmap()答案:A5. 在WebGL中,以下哪个函数用于设置视图矩阵?A. gl.uniformMatrix4fv()B. gl.uniformMatrix3fv()C. gl.uniformMatrix2fv()D. gl.uniform1i()答案:A6. 以下哪个是WebGL中用于创建帧缓冲对象的函数?A. gl.createFramebuffer()B. gl.bindFramebuffer()C. gl.framebufferTexture2D()D. gl.deleteFramebuffer()答案:A二、填空题(每题5分,共30分)1. WebGL的渲染循环通常包括三个步骤:________、________和________。
答案:清空画布、绘制场景、交换缓冲区2. 在WebGL中,顶点着色器的主要任务是处理________和________。
前端进阶webgl中数学知识

前端进阶webgl中数学知识
在WebGL中,主要涉及的数学知识有坐标系转换、向量和矩阵。
1. 坐标系转换:在WebGL中,物体(模型)坐标系、世界坐标系、观察坐标系、裁剪坐标系、规范化设备坐标系和屏幕坐标系之间需要进行一系列的转换。
这些转换涉及到平移、旋转和缩放等操作,需要使用到矩阵和向量的知识。
2. 向量:向量是既有大小,又有方向的量,在物理中又称为矢量。
向量一般用一个上方带箭头的字母表示,高中数学知识告诉我们,矢量在坐标系中即可以表示一个向量,也可以表示一个顶点坐标。
在WebGL中,如果一个vec4类型向量(x,y,z,w)中的w分量不为0,那么它代表的必然是一个点坐标。
3. 矩阵:矩阵是线性代数中的基本工具,用于表示和操作变换。
在WebGL 中,矩阵主要用于坐标系的转换,例如平移、旋转和缩放等操作。
4×4的矩阵可以表示一个3D物体在空间中的位置和方向,以及它在不同坐标系之间的转换。
以上是WebGL中涉及到的部分数学知识,建议咨询数学领域专业人士或查阅相关书籍获取更多信息。
HTML5之WebGL3D概述(上)—WebGL原生开发开启网页3D渲染新时代

HTML5之WebGL3D概述(上)—WebGL原⽣开发开启⽹页3D渲染新时代WebGL开启了⽹页3D渲染的新时代,它允许在canvas中直接渲染3D的内容,⽽不借助任何插件。
WebGL同canvas 2D的API ⼀样,都是通过脚本操纵对象,所以步骤也是基本相似:准备⼯作上下⽂,准备数据,在canvas中绘制对象并渲染。
与2D不同的就是3D涉及的知识更多了,例如世界、光线、纹理、相机、矩阵等专业知识。
WebGL有⼀个很好的中⽂教程,就是下⾯使⽤参考中的第⼀个链接,所以这⾥不再班门弄斧,后⾯的内容只是简单的总结⼀下学习的内容。
在正常安装以上浏览器之后还是不能运⾏WebGL,那你可以强制开启WebGL⽀持试⼀试。
开启⽅法如下:Chrome浏览器我们需要为Chrome加⼊⼀些启动参数,以下具体操作步骤以Windows操作系统为例:找到Chrome浏览器的快捷⽅式,右键点击快捷⽅式,选择属性;在⽬标框内,chrome.exe后⾯的引号后⾯,加⼊以下内容:--enable-webgl--ignore-gpu-blacklist--allow-file-access-from-files点击确定后关闭Chrome,然后⽤此快捷⽅式启动Chrome浏览器。
⼏个参数的含义如下:--enable-webgl的意思是开启WebGL⽀持;--ignore-gpu-blacklist的意思是忽略GPU⿊名单,也就是说有⼀些显卡GPU因为过于陈旧等原因,不建议运⾏WebGL,这个参数可以让浏览器忽略这个⿊名单,强制运⾏WebGL;--allow-file-access-from-files的意思是允许从本地载⼊资源,如果你不是WebGL的开发者,不需要开发调试WebGL,只是想要看⼀下WebGL的Demo,那你可以不添加这个参数。
Firefox浏览器Firefox的⽤户请在浏览器的地址栏输⼊“about:config”,回车,然后在过滤器(filter)中搜索“webgl”,将webgl.force-enabled 设置为true;将webgl.disabled设置为false;在过滤器(filter)中搜索“security.fileuri.strict_origin_policy”,将security.fileuri.strict_origin_policy设置为false;然后关闭⽬前开启的所有Firefox窗⼝,重新启动Firefox。
WebGL简易教程(五):图形变换(模型、视图、投影变换)
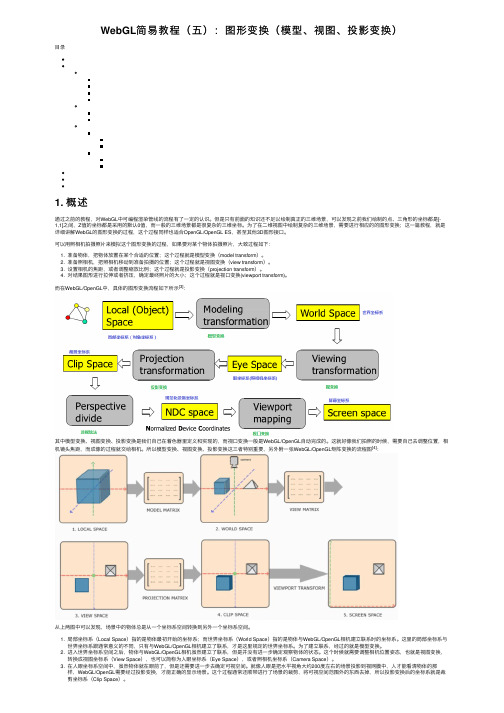
WebGL简易教程(五):图形变换(模型、视图、投影变换)⽬录1. 概述通过之前的教程,对WebGL中可编程渲染管线的流程有了⼀定的认识。
但是只有前⾯的知识还不⾜以绘制真正的三维场景,可以发现之前我们绘制的点、三⾓形的坐标都是[-1,1]之间,Z值的坐标都是采⽤的默认0值,⽽⼀般的三维场景都是很复杂的三维坐标。
为了在⼆维视图中绘制复杂的三维场景,需要进⾏相应的的图形变换;这⼀篇教程,就是详细讲解WebGL的图形变换的过程,这个过程同样也适合OpenGL/OpenGL ES,甚⾄其他3D图形接⼝。
可以⽤照相机拍摄照⽚来模拟这个图形变换的过程,如果要对某个物体拍摄照⽚,⼤致过程如下:1. 准备物体,把物体放置在某个合适的位置;这个过程就是模型变换(model transform)。
2. 准备照相机,把照相机移动到准备拍摄的位置;这个过程就是视图变换(view transform)。
3. 设置相机的焦距,或者调整缩放⽐例;这个过程就是投影变换(projection transform)。
4. 对结果图形进⾏拉伸或者挤压,确定最终照⽚的⼤⼩;这个过程就是视⼝变换(viewport transform)。
⽽在WebGL/OpenGL中,具体的图形变换流程如下所⽰[3]:其中模型变换、视图变换、投影变换是我们⾃⼰在着⾊器⾥定义和实现的,⽽视⼝变换⼀般是WebGL/OpenGL⾃动完成的。
这就好像我们拍照的时候,需要⾃⼰去调整位置,相机镜头焦距,⽽成像的过程就交给相机。
所以模型变换、视图变换、投影变换这三者特别重要,另外附⼀张WebGL/OpenGL矩阵变换的流程图[4]:从上两图中可以发现,场景中的物体总是从⼀个坐标系空间转换到另外⼀个坐标系空间。
1. 局部坐标系(Local Space)指的是物体最初开始的坐标系;⽽世界坐标系(World Space)指的是物体与WebGL/OpenGL相机建⽴联系时的坐标系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最近在学习WebGL技术的过程中,我补充了一些原本了解甚少的计算机图形学知识。
如果有同学和我一样,没有系统学过计算机图形学就接触了3D图形编程,而对不少略为艰深的概念有困惑,希望这些笔记能够帮助你。
模型矩阵我们必须考虑,当空间中点的位置会发生变化的时候,其坐标如何变化。
考虑三种基本的变换:平移、旋转和缩放。
“变换”的含义就是,将点的初始位置的坐标P映射到平移、旋转、缩放后的位置坐标P’,即:平移变换是最简单的变换:旋转变换有一些复杂,先看在二维平面上的旋转变换:很容易得到:矩阵形式的表达更加简洁,后面大多使用这种形式:推广到三维空间中:点绕z轴旋转:点绕x轴旋转:点绕y轴旋转:绕指定的任意轴旋转变换是由几个绕坐标轴旋转变换和平移变换效果叠加而成的,后文会有详细叙述。
缩放变换也比较简单:总结一下:平移变换,变换后点坐标等于初始位置点坐标加上一个平移向量;而旋转变换和缩放变换,http://fei 变换后点坐标等于初始位置点坐标乘以一个变换矩阵。
齐次坐标这天才的发明,允许平移变换也表示成初始位置点坐标左乘一个变换矩阵的形式。
齐次坐标使用4个分量来表示三维空间中的点,前三个分量和普通坐标一样,第四个分量为1。
平移变换巧妙地表示为:旋转变换(以绕z轴旋转为例)和缩放变换相应为:综上,在齐次坐标下三种基本变换实现了形式上的统一,这种形式的统一意义重大。
矩阵有一个性质:考虑一个点,先进行了一次平移变换,又进行了一次旋转变换,结合上面矩阵的性质,可知变换后的点P’为:旋转矩阵和平移矩阵的乘积R·T也是一个4×4的矩阵,这个矩阵代表了一次平移变换和一次旋转变换效果的叠加;如果这个点还要进行变换,只要将新的变换矩阵按照顺序左乘这个矩阵,得到的新矩阵能够表示之前所有变换效果的叠加,将最初的点坐标左乘这个矩阵就能得到一系列变换后最终的点坐标,这个矩阵称为“模型矩阵”。
一个模型矩阵乘以另一个模型矩阵得到的还是一个模型矩阵,表示先进行右侧模型矩阵代表的变换,再进行左侧模型矩阵代表的变换这一过程的效果之和,因此模型矩阵的乘法又可以认为是闭合的。
模型矩阵之所以称之为“模型矩阵”,是因为该矩阵与点的位置没有关系,仅仅包含了一系列变换的信息。
而在三维世界中,一个模型里所有的顶点往往共享同一个变换,对应同一个模型矩阵,比如抛在空中的一个木块,运转机器的一个齿轮。
之前说到,考虑一个物体绕指定轴旋转,如以下这个变换:绕着过顶点(x,y,z)方向为(a,b,c)的轴旋转角度θ,利用多个变换的叠加构建绕任意轴旋转的变换矩阵。
首先将顶点(x,y,z)平移到原点,绕x轴旋转角度p使指定的旋转轴在x-z平面上,绕y轴旋转角度q使指定的旋转轴与z轴重合,绕指定旋转轴(也就是z轴)旋转角度θ,绕y轴旋转角度-q,绕x轴旋转角度-p,将顶点平移到向量(x,y,z),p和q 的值由方向(a,b,c)决定。
综上,变换矩阵为:因此在处理围绕非坐标轴旋转的模型时,根据指定的旋转参数可以直接按照上述公式生成按照指定轴旋转的旋转矩阵,参加模型矩阵的构建。
齐次坐标还有一个优点,能够区分点和向量:在普通坐标里,点和向量都是由三个分量组成的,表示位置的点坐标(2,3,4)和表示方向的向量(2,3,4)没有区别。
而在齐次坐标中,第四个分量可以区分它们,点坐标的第四个分量为1,而向量坐标第四个分量为0。
比如,平移一个点是有意义的,能够得到平移后的点坐标;而平移一个向量是没有意义的,方向不会因为平移而改变。
以上,我们已经了解到模型矩阵可以存储一个模型空间位置变化的信息,在生成三维动画每一帧的过程中,我们首先计算每个模型的模型矩阵,然后将最初的模型的每一顶点坐标都左乘该模型矩阵,得到这一帧表示的时刻(模型已经经过多次变换)该模型每一顶点的坐标。
上面说的“帧”并不狭义地指屏幕的两次刷新时间的短暂间隔中屏幕上呈现的图像,而是指在这幅图像所描绘的整个三维空间的这个瞬间的所有顶点的位置。
来看个具体的例子:一个绕z轴匀速螺旋匀速上升的立方体,在某一帧中(即在这一帧对应的时刻t下),其向z轴正方向平移的长度和绕z轴旋转的角度分别为:则模型矩阵(注意上文齐次坐标下的基本变换矩阵)为:产生这一帧时,只需要计算一次模型矩阵,再将立方体中8个顶点坐标分别左乘该矩阵,就可以得到经过变换后8个顶点的坐标。
当一个模型顶点数量增加到上百甚至上千个,模型变换的步骤数也增加到几十步时,模型矩阵的作用就很明显了:如果没有齐次坐标(也当然没有模型矩阵),对每个顶点都需要一步一步地变换:平移的时候加上一个向量,旋转的时候左乘一个矩阵,才能得到变换后的顶点坐标;而模型变换只需要计算一次模型矩阵(当然也是一步一步的),然后每个顶点左乘模型矩阵就可以直接得到变换后的坐标了。
视图矩阵在模型矩阵中,我们关心的是空间中的点在经历变换后在世界坐标系下的位置。
事实上,我们更加关心空间中的点相对于观察者的位置。
最简单的方案是将观察者置于原点处,面向z轴(或x轴、y轴)正半轴,那么空间中的点在世界坐标系下的位置就是其相对于观察者的位置。
观察者的位置和方向会变化,看上去就好像整个世界的位置和方向发生变化了一样,所以解决的方案很简单,将世界里的所有模型看作一个大模型,在所有模型矩阵的左侧再乘以一个表示整个世界变换的模型矩阵,就可以了。
这个表示整个世界变换的矩阵又称为“视图矩阵”,因为他们经常一起工作,所以将视图矩阵乘以模型矩阵得到的矩阵称为“模型视图矩阵”。
模型视图矩阵的作用是:乘以一个点坐标,获得一个新的点坐标,获得的点坐标表示点在世界里变换,观察者也变换后,点相对于观察者的位置。
视图矩阵同样也可以分为平移、旋转和缩放,视图矩阵是将观察者视为一个模型,获得的观察者在世界中变换的模型矩阵的逆矩阵。
观察者平移了(tx,ty,tz),视图矩阵如下,可以看出如果将视图矩阵看作整个世界的模型矩阵,相当于整个世界平移了(-tx,-ty,-tz)。
观察者绕z轴旋转了角度θ,视图矩阵如下,相当于整个世界绕z轴旋转了-θ度。
观察者在三个方向等比例缩小了s倍,视图矩阵如下,相当于整个世界放大了s倍。
观察者缩小的情形可能会引起困惑:如果人和猫咪的眼睛在同一个位置,人看到的世界和一只猫咪看到的世界应当是一样尺寸的,这和上述视图矩阵的情形矛盾;但是直觉告诉我,如果你喝了缩小药水,你应该会觉得整个世界在膨胀,就像视图矩阵所表现的那样。
解答是这样:如果在计算机上模拟观察者喝了缩小药水的情形,在屏幕上看到整个世界是膨胀的,因为在那个虚拟的三维空间中,计算机屏幕这个“窗口”也随你(观察者)缩小。
视图矩阵实际上就是整个世界的模型矩阵,这给我一点启发:一个模型可能由多个较小的子模型组成,模型自身有其模型矩阵,而子模型也有自己的局部模型矩阵。
考虑一辆行驶中的汽车的轮胎,其模型视图矩阵是局部模型矩阵(描述轮胎的旋转)左乘汽车的模型矩阵(描述汽车的行驶)再左乘视图矩阵得到的。
投影矩阵模型视图矩阵的作用是确定某一帧中,空间里每个顶点的坐标,而投影矩阵则将这些顶点坐标映射到二维的屏幕上,即:最主要的有两种投影方式,正射投影和透视投影。
前者用于精确制图,如工业零件侧视图或建筑物顶视图,从屏幕上就可以量测平行于屏幕的线段长度;后者用于模拟视觉,远处的物体看上去较小。
下图中,空间中的同一个矩形,正射投影后仍然是矩形,而透视投影后则变成了梯形。
正射投影(投影面和相机空间):透视投影(投影面和相机空间):三维世界的显示中,屏幕模拟了一个窗口,你透过这个窗口观察“外面”的世界。
你的屏幕是有边缘的(除非你有一个球形的房间,内壁全是屏幕),因此你仅仅能观察到那个世界的一部分,即“相机空间”。
相机空间的左、右、上、下边界是受限于屏幕的边缘,同时也设定前、后边界,因为你很难看清太近或太远的东西。
在正射投影中,相机空间是一个规则的立方体,而在透视投影中则是一个方台体。
三维模型可能在不同的显示器上展现,因此投影的过程中不该将显示器参数加入进来,而是将空间中的点投影到一个规范的显示器中。
另外,透视投影中的z值并不是毫无用处,它可以用来表示顶点的“深度”:如果三维空间中的两个不同顶点投影到平面上时重合了,那么将显示深度较浅的顶点。
定义一个规范的视窗区域(CCV),为x,y,z都处在区间[-1,1]之间的边长为2的立方体。
x和y坐标值用来线形拉伸到到实际屏幕上,而z值存储了“深度”。
而投影的过程就是将三维空间中的点从相机空间映射到CCV中。
正射投影非常简单,直接将矩形的相机空间线形压缩到CCV中即可。
采取顶视图,相机空间的左右边界为:简单的线形成比例关系:推广到y轴和z轴:相机空间中的点经过正射投影矩阵左乘后得到的点都在CCV之中:透视投影相对较为复杂,同样用顶视图考虑x坐标的情况:转化为齐次的方式:推广到y轴:透视投影矩阵的第三行不是我们关心的内容,只要保证不同顶点投影前后的点坐标的第三个分量z和z’的大小关系不变就可以。
透视投影矩阵尾行是(0,0,1,0),这样就将计算得到的坐标的第四个分量赋值为z而不是1。
将相机空间左乘投影矩阵后的结果不是一个CCV空间,如果你将这个空间画出来,会发现其仍然是一个方台形。
这时进行“透视除法”,将上一步得到的点坐标化为第四个分量为1的标准齐次坐标:然后我们直接取齐次坐标中的x’和y’值,并将其线形映射到屏幕上,比如点(0,0)出现在屏幕中央,点(-1,1)出现在屏幕左上角。
WebGLWebGL中对于模型视图矩阵和投影矩阵的操作依赖于第三方库,比如Oak3D或glMatrix,WebGL本身不支持(或者说不限制)任何对模型视图矩阵和投影矩阵的操作。
WebGL是在浏览器端运行的,所以使用JavaScript编程。
下面的代码来自翻译的的WebGL教程。
以glMatrix库为例:// 新建空模型视图矩阵var mvMatrix = mat4.create();// 将矩阵设置为单位阵mat4.identity(mvMatrix);// 平移和旋转mat4.translate(mvMatrix, [-1.5, 0.0, -8.0]);mat4.rotate(mvMatrix, degToRad(45), [0, 1, 0]);将矩阵设置为单位阵相当于说:“这个矩阵表示什么都还没做(平移、旋转、缩放)呢”,事实上,任意点坐标乘以单位矩阵都只能得到自己,正说明“什么都没做”。
平移矩阵的函数mat4.translate()做的仅仅是将mvMatrix左乘一个平移矩阵而已。
旋转矩阵的函数mat4.rotate()也许比较复杂,它做的是上面我们讨论过的“围绕任意轴旋转”的问题,这个函数默认使用“本地轴”,即过所有平移效果累加后的那一点的轴,参数向量[0,1,0]是轴的指向,因此上面的函数调用处理了一个围绕本地y轴的旋转。
