工程力学习题答案第十三章王永跃
智慧树知到《工程力学(吉林联盟)》章节测试答案

智慧树知到《工程力学(吉林联盟)》章节测试答案智慧树知到《工程力学(吉林联盟)》章节测试答案绪论1、力学是研究物体宏观机械运动的学科。
()A:对B:错正确答案:对2、构件是组成结构的元件。
()A:对B:错正确答案:对3、构件在外力作用下丧失正常功能的现象称为失效,简称破环。
()A:对B:错正确答案:对4、工程力学的失效分为()。
A:强度失效B:刚度失效C:稳定性失效D:偶然失效正确答案:强度失效,刚度失效,稳定性失效5、工程力学求解问题的方法有理论解析法、模型实验法、数值模拟法。
()A:对B:错正确答案:对第一章1、力的可传性公理只适用于刚体。
A:对B:错正确答案:对2、物体受到汇交于一点的三个力作用,则此物体处于平衡状态。
A:对B:错正确答案:错3、关于二力构件,下述说法正确的是()。
A:只受两个力作用的构件是二力构件B:只在两点受力作用且平衡的构件是二力构件C:除受重力外,还受两个力作用且平衡的构件是二力构件D:二力构件只能是直杆正确答案:只在两点受力作用且平衡的构件是二力构件4、三力平衡汇交定理是()。
A:共面不平行的三个力若平衡必汇交于一点B:共面三力若平衡,必汇交于一点C:三力汇交于一点,则这三个力必互相平衡。
正确答案:共面不平行的三个力若平衡必汇交于一点5、加减平衡力系公理适用于()。
A:刚体B:变形体C:刚体和变形体正确答案:刚体第二章1、下列说法中,哪个说法正确()。
A:力越大,则力的投影越大B:力作用点离矩心越远,则该力的力矩越大C:力偶由力组成,可以与一个力等效D:力偶矩与矩心位置无关正确答案:力偶矩与矩心位置无关2、关于力对点之矩的说法,( )是错误的。
A:力对点之矩与力的大小有关,而与力的方向无关B:力对点之矩不会因为力矢沿其作用线移动而改变C:力的数值为零、或力的作用线通过矩心时,力矩均为零D:互相平衡的两个力,对同一点之矩的代数和等于零正确答案:力对点之矩与力的大小有关,而与力的方向无关3、已知某平面一般力系与一平面力偶系等效,则此平面一般力系向平面内任一点简化的结果应是一个力偶。
《工程力学》课后习题解答

4日1-1试画出以下各题中圆柱或圆盘的受力争.与其它物体接触处的摩擦力均略去.12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N =⨯+-==⨯--=∴==∑∑AC 与BC 两杆均受拉.2-3 程度力F 感化在刚架的B 点,如图所示.如不计刚架重量,试求支座A 和D 处的束缚力.解:(1) 取整体(2) 22D A F2-4 在简支梁AB 的中点C 感化一个竖直45o 的力F,力的大小等于20KN,如图所示.若梁的自重不计,试求两支座的束缚力.解:(1) 研讨AB ,(2)类似关系:B A F F FCDE cde CD CE ED ∆≈∆∴==几何尺寸:11 222CE BD CD ED =====FFF AF D求出束缚反力:12010 22010.4 45arctan 18.4B A o oCE F F kNCDED F F kNCDCECD α=⨯=⨯==⨯===-= 2-6 如图所示构造由两弯杆ABC 和DE 构成.构件重量不计,图中的长度单位为cm.已知F =200N,试求支座A 和E 的束缚力.解:(1)取 (2) 取3-1已知梁,支座A和B解:(a) A B M F F l∴==(b) 受力剖析,画受力争;A.B 处的束缚力构成一个力偶;0 0 B B A B M M Fl M F lM F F l=⨯-==∴==∑(c)受力剖析,画受力争;A.B 处的束缚力构成一个力偶;列均衡方程:cos cos A B MM l M F F l θθ==∴==∑3-3 齿轮箱的两个轴上感化的力偶如题图所示,它们的力偶矩的大小分离为M 1=500Nm,M 2=125Nm.求两螺栓处的铅垂束缚力.图中长度单位为cm.解:(1);(2) 500125750 50750 A B M N F F N-===∴==∑3-5 四连杆机构在图示地位均衡.已知OA=60cm,BC=40cm,感化BC 上的力偶的力偶矩大小为M 2=1N.m,试求感化在OA 上力偶的力偶矩大小M 1和AB 所受的力F AB .各杆重量不计.解:(1) 研讨BC 杆,列均衡方程:22015 0.4sin 30sin 30BB o oM M F N BC ====⨯BF F B(2) 研讨AB (二力杆),受力如图:可知:'' 5 A B B F F F N===(3) 研讨OA 杆,受力剖析,画受力争:列均衡方程:113 M M M Nm==∴=∑4-1 试求题4-1图所示各梁支座的束缚力.设力的单位为kN,力偶矩的单位为kN ⋅m,长度单位为m,散布载荷集度为kN/m.(提醒:盘算非均布载荷的投影和与力矩和时需应用积分). 解:(b):(1) 整体受力剖析,(2) 选坐标系Axy ,(20AB B MF +⨯=∑0B =(c):(1) 研讨AB 杆,受力剖析,画出受力争(平面随意率性力系); (2) 选坐标系Axy ,0A B AF (e)F x F20: 2cos3004.24 kNo y Ay B B F F dx F F =-⨯+==∑⎰0: sin 3002.12 kNo xAx B Ax FF F F =-==∑束缚力的偏向如图所示.(e):(1) 研讨C ABD 杆,受力剖析,画出受力争(平面随意率性力系);(2) 选坐标系Axy ,(021 kNAB B MF F ==∑0.80: 2020015 kNyAy B Ay Fdx F F F =-⨯++-==∑⎰束缚力的偏向如图所示.4-13 运动梯子置于滑腻程度面上,并在铅垂面内,梯子两部分AC 和A B 各重为Q ,重心在A 点,彼此用搭钮A 和绳索DE 衔接.一人重为P 立于F 处,试求绳索DE 的拉力和B .C 两点的束缚力.解:(1):研讨整体,受力剖析,(2) 选坐标系Bxy ,)()0: -2cos 2cos 0B C C M F Q l a F l F αα=-+⨯=∑0: 202yB C B FF F Q P a F Q P l=+--==+∑(3) 研讨AB ,受力剖析,画出受力争(平面随意率性力系);xq x(4) 选A 点为矩心,()0:0A D M F F h α=+⨯=∑4-16 由AC 和CD 4-16图所示.已知均布载荷集度q =10 kN/m,力偶M =40 kN ⋅m,a =2 m,不计梁重,试求支座A .B .D 的束缚力和搭钮C 所受的力.解:(1) 研讨CD 杆,(2) 选坐标系Cxy ,20D a ⨯=∑0: 025 kNy C D C F F q dx F F =-⨯-==∑⎰(3) 研讨ABC 杆,受力剖析,画出受力争(平面平行力系);(4) 选坐标系Bxy ,'()0B C M F x F a -⨯=∑'080 kNyB C B FF F =-==∑束缚力的偏向如图所示.4-17 刚架ABC 和刚架CD 经由过程搭钮C 衔接,并与地面经由过程搭钮A .B .D 衔接,如题4-17图所示,载荷如图,试求刚架的支座束缚力(尺寸单位为m,力的单位为 kN,载荷集度单x(a):(1) 研讨CD 杆,它是二力杆,又依据D 点的束缚性质,可知:F C =F D =0;(2) 研讨整体,受力剖析,画出受力争(平面随意率性力系);(3) 选坐标系Axy ,60B F ⨯=∑180 kNy Ay B Ay F ==束缚力的偏向如图所示.(b):(1) 研讨CD 杆,受力剖析,画出受力争(平面随意率性力系);(2) 选C 点为矩心,3015 kN D q dx x F ⨯⨯+⨯=(3) 研讨整体,);(4) 选坐标系35030AyM⨯+⨯=∑300: 010 kNyAy B D B FF q dx F F F =-⨯-+==∑⎰束缚力的偏向如图所示.=50x5-5 感化于半径为120 mm 的齿轮上的啮合力F 推进皮带绕程度轴AB 作匀速迁移转变.已知皮带紧边拉力为200 N,松边拉力为100 N,尺寸如题5-5图所示.试求力F 的大小以及轴承A .B 的束缚力.(尺寸单位mm).解: (1) 研讨整体,8-2 试画出8-1解:(a) (b)(c) (d) 8-14 图示桁架,杆与d 2=20mm,两杆材料雷同,F =80kN 感化,试校解:(1) 对节点A(2) 列均衡方程0 sin 0 cos30x AB yAB FF FF =-=∑∑解得:41.4 58.6AC AB F kN F kN ====(2)分离对两杆进行强度盘算;[][]1282.9131.8ABAB ACAC F MPa A F MPa A σσσσ====所以桁架的强度足够.8-15 图示桁架,杆1为圆截面钢杆,杆2为方截面木杆,在节点A 处推却铅直偏向的载荷F 感化,试肯定钢杆的直径d 与木杆截面的边宽b .已知载荷F =50kN,钢的许用应力[σS ] =160MPa,木的许用应力[σW ] =10MPa.解:(1) 对节点A;50AB F kN ==(2) []322 20.070.71010 84.1ABAC ACW d mm F MPa b mm A b σσσ≥⨯==≤=≥所以可以肯定钢杆的直径为20mm,木杆的边宽为84mm. 8-16 题8-14所述桁架,试定载荷F 的许用值[F ].解:(1) 由8-14得到AB.AC 两杆所受的力与载荷F 的关系;AC AB F F ==(2) 应用强度前提,分离对两杆进行强度盘算;[]211160 154.54ABAB F MPa F kN A d σσπ==≤=≤[]222160 97.14ACAC F MPa F kN A d σσπ==≤=≤取[F ]=97.1kN.8-18图示阶梯形杆AC ,F =10kN,l 1= l 2=400mm,A 1=2A 2=100mm 2,E =200GPa,试盘算杆AC 的轴FFF ABF AC向变形△l .解:(1)(2) 分段盘算个杆的轴向变形;33112212331210104001010400200101002001050 02 N N F l F l l l l EA EA .mm⨯⨯⨯⨯∆=∆+∆=+=-⨯⨯⨯⨯=-AC 杆缩短.8-26 图示两头固定等截面直杆,横截面的面积为A ,推却轴向载荷F 感化,试盘算杆内横截面上的最大拉应力与最大压应力.解:(1)xA B(2) 用截面法求出AB .BC .CD 段的轴力;123 N A N A N BF F F F F F F =-=-+=-(3) 用变形调和前提,列出补充方程;AB BC CD l l l ∆+∆+∆=代入胡克定律;231 /3()/3/3 0N BC N CDN ABAB BC CD A A B F l F l F l l l l EA EA EA F l F F l F l EA EA EA ∆=∆=∆=-+-+-=求出束缚反力:/3A B F F F ==FACB(b)(4) 最大拉应力和最大压应力;21,max ,max 2 33N N l y F F F FA A A A σσ====-8-27 图示构造,梁BD 为刚体,杆1与杆2用统一种材料制成,横截面面积均为A =300mm 2,许用应力[σ]=160MPa,载荷F =50kN,试校核杆的强度.解:(1) 对BD=(2) 由变形调和关系,代之胡克定理,可得;21212 2N N N N F l F lF F EA EA ==解联立方程得:122455N N F F F F ==(3) 强度盘算;[][]3113222501066.7 160 530045010133.3 160 5300N N F MPa MPaA F MPa MPaA σσσσ⨯⨯====⨯⨯⨯====⨯所以杆的强度足够.8-33 图示接头,推却轴向载荷F 感化,试校核接头的强度.已知:载荷F =80kN,板宽b =80mm,板厚δ=10mm,铆钉直径d =16mm,许用应力[σ]=160MPa,许用切应力[τ] =120MPa,许用挤压应力[σbs ] =340MPa.板件与铆钉的材料相等.解:(1)[]21499.5 120 14QSF F MPa MPaA d ττπ===≤=(2) 校核铆钉的挤压强度;[]14125 340 b bs bs b FF MPa MPaA d σσδ===≤=(3) 斟酌板件的拉伸强度; 对板件受力剖析,画板件的轴力争;校核1-1160 MPa校核2-2] 160 MPa =所以,接头的强度足够.10-2. 解:(c)(1) (2) 11111 (0/2) (0/2)S F F x l M Fx x l =-=-≤≤ ()21221 (/2) (/2)S F F l x l M F l x l x l ==--≤≤(3) 画剪力争与弯矩图 F xq(d)(1) )S F l 21 (0)42M x x x l =-≤(2) 画剪力争与弯矩图10-5(b)(1) 求束缚力;(2) 画剪力争和弯矩图 (c)(1) 求束缚力; q AxF xM A xF S(2) 画剪力争和弯矩图; (d)(1) 求束缚力;(2) 画剪力争和弯矩图;(e)(1) 求束缚力;(2) 画剪力争和弯矩图 (f)(1) 求束缚力;(2) 11-6图示悬臂梁,折正应力,解:(1)(2) (3) 盘算应力: 最大应力:F SM xFzK 点的应力:11-7图示梁,由No22槽钢制成,弯矩M =80N.m,并位于纵向对称面(即x-y 平面)内.试求梁内的最大曲折拉应力与最大曲折压应力.解:(1)79 b mm =(2) 最大曲折拉应力(产生鄙人边缘点处)()30max880(7920.3)10 2.67 17610x M b y MPaI σ-+-⋅-⨯-⨯===⨯(3) 最大曲折压应力(产生在上边缘点处)30max88020.3100.92 17610x M y MPa I σ---⋅⨯⨯===⨯6max max max227.510176 408066ZM M MPabh W σ⨯====⨯6max max 337.51030132 ********K ZM y M y MPa bh I σ⋅⋅⨯⨯====⨯MMz。
工程力学材料力学(北京科大东北大学版)第4版13章习题答案

第一章参考答案1-1: 解:(a):N 1=0,N 2=N 3=P (b):N 1=N 2=2kN (c):N 1=P,N 2=2P,N 3= -P (d):N 1=-2P,N 2=P (e):N 1= -50N,N 2= -90N (f):N 1=0.896P,N 2=-0.732P 注(轴向拉伸为正,压缩为负)1-2: 解: σ1= 2118504P kN S d π==35.3Mpa σ2=2228504P kNS d π==30.4MPa∴σmax =35.3Mpa 1-3:解:下端螺孔截面:σ1=19020.065*0.045P S ==15.4Mpa上端单螺孔截面:σ2=2PS =8.72MPa上端双螺孔截面:σ3= 3PS =9.15Mpa∴σmax =15.4Mpa 1-4:解: 受力分析得: F 1*sin15=F 2*sin45 F 1*cos15=P+F 2*sin45∴σAB = 11F S =-47.7MPa σBC =22F S =103.5 MPa1-5:解: F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2FS =38.1MPa1-6:解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm (2) ∴AB l ∆=-0.02mm 1-7:解:AC AC AC LNL EA EA σε===1.59*104, CB CB CB LNL EA EA σε===6.36*1041-8:解: 1-9:解: 1-10:解:[][]max 59.5MPa σσ=<1-11:解:(1)当45oα=,[]11.2σσ=>强度不够(2)当60oα=,[]9.17σσ=< 强度够1-12:解:1-13:解:[]max 200213MPa MPa σ=< 1-14:解: 1.78, 1.26d cm d cm==拉杆链环1-15 解:22BC F Q ==70.7 kN查表得: 45*45*3 1-16解:(1)[]2401601.5ssn σσ===MPa(2)1-17 解:(1)'61544014.521542390F n F ===≈1-18 解:P=119kN 1-19 解:所以最大载荷 84kN 1-20 解: P=33.3 kN 1-21 解: 1-22 解: 1-23 解:第二章习题2-1 一螺栓连接如图所示,已知P=200 kN , =2 cm ,螺栓材料的许用切应力[τ]=80Mpa ,试求螺栓的直径。
工程力学第13章答案

习题13-1图(a)第13章 弹性杆件位移分析与刚度设计13-1 直径d = 36mm 的钢杆ABC 与铜杆CD 在C 处连接,杆受力如图所示。
若不考虑杆的自重,试:1.求C 、D 二截面的铅垂位移;2.令F P1 = 0,设AC 段长度为l 1,杆全长为l ,杆的总伸长EA lF l 2P =∆,写出E 的表达式。
解:(1)4π)(4π)(2sN 2sN d E l F d E l F u u BC BC ABAB A C ++=947.236π41020030001010020001015002333=⨯⨯⨯⨯⨯+⨯⨯+=mm286.536π101054250010100947.24π)(2332cN =⨯⨯⨯⨯⨯⨯+=+=d E l F u u CD CD C D mm(2)A E l l F A E l F l l l EAl F C D AC c 12P s 12P 2P )(-+=∆+∆=∆=, 令l l 1=ηc s 11E E E ηη-+=s c sc )1(E E E E E ηη-+=13-2长为 1.2m 、横截面面积为31010.1-⨯m 2的铝制筒放置在固定刚块上,直径为15.0mm 的钢杆BC 悬挂在铝筒顶端的刚性板上,若二者轴线重合、载荷作用线与轴线一致,且已知钢和铝的弹性模量分别为E s = 200GPa ,E a = 70GPa ,F P = 60kN 。
试求钢杆上C 处位移。
习题13-2图m(a)A E kN kNx l l l l解:铝筒:a a P A E l F u u ABB A -=-(其中u A= 0)935.0101010.11070102.1106063333=⨯⨯⨯⨯⨯⨯⨯=-B u mm钢杆:50.4154π10200101.21060935.02333s s P =⨯⨯⨯⨯⨯⨯+=+=A E l F u u BC B C mm13-3 对于图a 、b 、c 、d 所示的坐标系,小挠度微分方程可写成EI M x w /d /d 22-=形式有以下四种。
工程力学习题答案

球的尺寸忽略不计。
TA
TB
A
ϕ1 ϕ2
B
FNA
FNB 2N
1N
习题 1-12 图
解:
∩
AB
=
0.2m
, ϕ1
+ϕ2
=
2×
360° 2π
= 114°35′
图(a):A 平衡: ∑ Fy = 0 , TA = 1⋅ sin ϕ1
AG = 2CD (图(a)) 在图(a)中: 设 OF = d,则
d = 4 cot θ (d + 3sin θ ) = AG = 2CD
(1)
CD = CE sin θ = (4.5 − d )sin θ 2
(2)
即 (d + 3)sin θ = 2(4.5 − d )sin θ 2
d +3=9−d
1 一 5 试画出图示结构中各杆的受力图。
习 题 1-5 图
B FB
FC
C
C
FC'
FD'
D
FAx
A
FAy
(a-1)
D FD
F
E
FE'
(a-2)
FE
E
(a-3)
T
FCx C FCy
W
(b-1)
FAx
A
C FC' x
FAy
FC' y
(b-3)
FE E
B
FB
(b-2)
FB'
B
FB'
FC'
工程力学 13章、14章习题
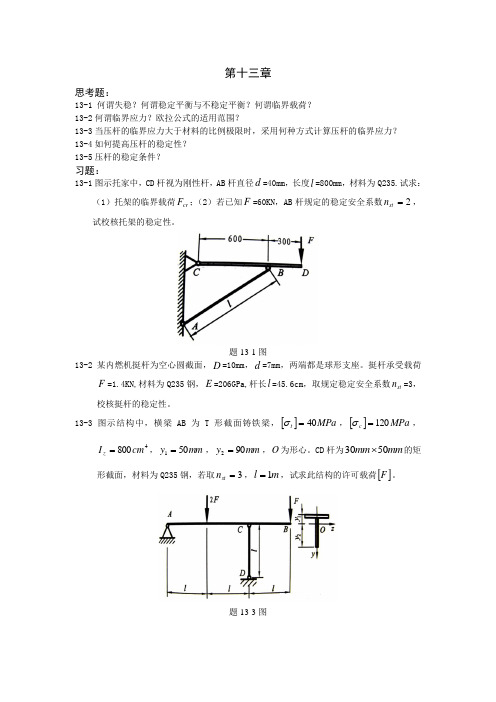
第十三章思考题:13-1 何谓失稳?何谓稳定平衡与不稳定平衡?何谓临界载荷?13-2何谓临界应力?欧拉公式的适用范围?13-3当压杆的临界应力大于材料的比例极限时,采用何种方式计算压杆的临界应力? 13-4如何提高压杆的稳定性?13-5压杆的稳定条件?习题:13-1图示托家中,CD 杆视为刚性杆,AB 杆直径d =40mm ,长度l =800mm ,材料为Q235.试求:(1)托架的临界载荷cr F ;(2)若已知F =60KN ,AB 杆规定的稳定安全系数2=st n ,试校核托架的稳定性。
题13-1图13-2某内燃机挺杆为空心圆截面,D =10mm ,d =7mm ,两端都是球形支座。
挺杆承受载荷F =1.4KN,材料为Q235钢,E =206GPa,杆长l =45.6cm ,取规定稳定安全系数st n =3,校核挺杆的稳定性。
13-3图示结构中,横梁AB 为T 形截面铸铁梁,[]MPa t 40=σ,[]MPa c 120=σ,4800cm I z =,mm y 501=,mm y 902=,O 为形心。
CD 杆为mm mm 5030⨯的矩 形截面,材料为Q235钢,若取3=st n ,m l 1=,试求此结构的许可载荷[]F 。
题13-3图13-4图示工字钢立柱,A 端自由、B 端固定,顶部轴向载荷F=200KN ,材料为 Q235钢,[]M P a 160=σ,在立柱中点处开有直径d =70mm 的圆孔,试选择工字钢的型号。
题13-4图13-5图示结构中,AB 为b =40mm, h =60mm 的矩形截面梁,AC 及CD 为d =40mm 的圆形截面杆,l =1m ,材料均为Q235钢,若取强度安全系数n =1.5,规定稳定安全系数st n =4,试求许可载荷[]F 。
题13-5图第十三章答案13-1 (1)KN F cr 109=(2)不满足稳定条件13-2 358.2〈=n 不满足稳定条件13-3 []KN F 4.6=13-4 25a 工字钢13-5 []KN F 5.7=第十四章思考题:14-1 何为交变应力?试举工程实例说明?14-2交变应力时材料发生破坏的原因是什么?疲劳断口有什么特点?14-3何为循环特征?在一次应力循环中的σm、σa、σmax、σmin之间有何关系?14-4何为材料的持久极限?简述通过实验方法测定材料的疲劳极限的过程?14-5每一种材料是否只有一个疲劳极限?由此得到什么体会?14-6影响构件疲劳极限的主要因素有哪些?如何提高构件的疲劳极限?14-7在对称交变循环应力、非对称交变循环应力及弯扭组合交变应力作用下,如何进行构件的疲劳强度计算?14-8线性累积损伤理论的基本假设是什么?复习题:14-1 试分别计算下图所示各交变应力的平均应力,应力幅度和循环特征r。
《工程力学》习题答案解析

第1章静力学基础思考题1-1 说明下面两个式子的意义。
(1)F1=F2(2)F1=F2解:(1)式中F表示力矢量;因此F1=F2表示力F1和F2的大小相等,方向相同。
(2)式中F表示力的大小;因此F1=F2表示力F1和F2的大小相等。
1-2 能否说合力一定比分力大,为什么?解:不一定。
例如,大小相等、方向相反,且作用在同一直线上的两个力的合力为零。
1-3 二力平衡原理与作用和反作用定律有何异同?解:二力平衡原理是指:作用在刚体上的两个力,使刚体保持平衡的充要条件是:这两个力的大小相等,方向相反,且作用在同一直线上。
作用和反作用定律是指:任何两个物体间的作用,总是大小相等、方向相反、沿同一作用线分别作用在两个物体上。
可以看出,二力平衡原理描述的是,两个不同的力作用在同一个物体上的情况;作用和反作用定律描述的是两个不同物体之间相互作用的情况。
但它们有一个相同点,即上述两种情况下的一对力均满足大小相等、方向相反。
1-4 约束反力的方向和主动力的方向有无关系?解:约束反力的方向总是与约束限制物体位移的方向相反。
对于有些约束类型,如具有光滑接触表面的约束,其约束反力必然作用在接触点处,作用线沿着接触面的公法线方向,且指向被约束物体。
又如绳索类柔性约束,其约束反力只能是沿柔性体的轴线而背离被约束物体的拉力。
而对于圆柱铰链约束等,其约束反力的作用点位置(即接触点位置)、方向和大小由构件所受主动力确定。
因此,约束反力的方向是否和主动力的方向有......专业资料...仅供学习.参考.分享关,取决于约束类型。
1-5 什么叫二力构件?分析二力构件受力时与构件的形状有无关系?解:所谓二力构件,是指只有两点受力而处于平衡状态的构件,如下图所示。
二力构件受力时,二力大小相等、方向相反,且都沿两作用点的连线方向;与构件的形状无关。
1-6 图1-18所示物体的受力图是否正确?如有错误如何改正?(a)(b)图1-18解:图1-18(b)所示受力图错误,正确的受力图所图1-18(c)所示。
《工程力学》课后习题与答案全集

工程力学习题答案第一章静力学基础知识思考题:1. X ;2. V ;3. V ;4. V ;5. K 6. K 7. V ;8. V习题一1•根据三力汇交定理,画出下面各图中A 点的约束反力方向。
解:(a )杆AB 在 A B 、C 三处受力作用。
u由于力p和uuv R B 的作用线交于点Q 如图(a )所示,根据三力平衡汇交定理, 可以判断支座A 点的约束反力必沿 通过A 0两点的连线。
uP 3uvB 处受绳索作用的拉力uuv R B (b )同上。
由于力交于0点,根据三力平衡汇交定理, 可判断A 点的约束反力方向如 下图(b )所示。
的作用线 2.不计杆重,画出下列各图中 AB 杆的受力图。
uP 解:(a )取杆AB 和E 两处还受光滑接触面约束。
约束力UJVN E uuvuuN A 和 N E,在A的方向分别沿其接触表面的公法线, 外,在 并指向杆。
其中力uuvN A 与杆垂直,通过半圆槽的圆心 Q力 AB 杆受力图见下图(a )。
和C 对它作用的约束力 NBo------- r -------- —y —uuv N C铰销此两力的作用线必须通过(b )由于不计杆重,曲杆 BC 只在两端受 故曲杆BC 是二力构件或二力体,和 B 、C 两点的连线,且B O两点的连线。
见图(d).第二章力系的简化与平衡思考题:1. V ;2.>;3. X ;4. K 5. V ;6.$7.>;8. x ;9. V .1.平面力系由三个力和两个力偶组成, 它们的大小和作用位置如图示,长度单位为cm 求此力系向O 点简化的结果,并确定其合力位置。
uvR R 解:设该力系主矢为 R ,其在两坐标轴上的投影分别为Rx、y。
由合力投影定理有:。
4.梁AB 的支承和荷载如图, 小为多少?解:梁受力如图所示:2. 位置:d M o /R 25000.232 火箭沿与水平面成F ,100 0.6100 80 2000 0.5 580m 23.2cm,位于O 点的右侧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程力学习题答案第十三章王永跃-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII第十三章习 题 解 答13−1 木制构件中的单元体应力状态如图所示,其中所示的角度为木纹方向与铅垂线的夹角。
试求:(l )平行于木纹方向的切应力; (2)垂直于木纹方向的正应力。
解: 由图a 可知MPa 0MPa,6.1,MPa 2.0=-=-=x y x τσσ(1)平行于木纹方向的切应力:则由公式可直接得到该斜截面上的应力MPa1.0)]15(2sin[26.12MPa 97.1)]15(2cos[26.1226.121515=-⨯+-=-=-⨯+-+--=--τσ (2)垂直于木纹方向的正应力MPa1.0)752sin(26.12MPa 527.1]752cos[26.1226.127575-=⨯+-=-=⨯+-+--=τσ 由图b 可知MPa 25.1,0,0-===x y x τσσ(1)平行于木纹方向的切应力:则由公式可直接得到该斜截面上的应力MPa08.1)]15(2cos[25.12cos MPa625.0)15(2sin 25.12sin 1515-=-⨯⨯-==-=-⨯=-=--αττατσx x(2)垂直于木纹方向的正应力MPa08.1)752cos(25.12cos MPa625.0)752sin(25.12sin 7575=⨯⨯-===⨯⨯=-=αττατσx x13−2 已知应力状态如图一所示(应力单位为MPa ),试用解析法计算图中指定截面的正应力与切应力解:(a )已知 MPa 20MPa,10,0MPa 3-===x y x τσσ则由公式可直接得到该斜截面上的应力习题13−1图(a)(b)MPa10)42cos(20)42sin(210302cos 2sin 2MPa40)42sin(20)42cos(21030210302sin 2cos 22=⨯⨯-⨯⨯-=+-==⨯⨯+⨯⨯-++=--++=ππατασστππατασσσσσααx y x x yx yx(b )已知 MPa20MPa,10,0MPa 3===x y x τσσ则:MPa21.21)5.222cos(20)5.222sin(210302cos 2sin 2MPa93.12)5.222sin(20)5.222cos(21030210302sin 2cos 22=⨯⨯+⨯⨯-=+-==⨯⨯-⨯⨯-++=--++=ατασστατασσσσσααx y x x yx y x (c )已知60MPa15MPa,20,MPa 10-====ατσσx y x则:60(2cos[15)]60(2sin[220102cos 2sin 2MPa49.30)]60(2sin[15)]60(2cos[22010220102sin 2cos 22-⨯⨯+-⨯⨯-=+-==-⨯⨯--⨯⨯-++=--++=ατασστατασσσσσααx yx x yx yx 13−3 已知应力状态如图所示(应力单位为MPa ),试用图解法(应力圆)计算图中指定截面的正应力与切应力。
13−4 已知应力状态如习题13−2图所示(应力单位为MPa ),计算图示应力状态中的主应力及方位。
习题13−2图(c)(b)(a)(d)习题13−3图(a)(b)解:(a )已知 MPa 20MPa,10,0MPa 3-===x y x τσσ则由公式可直接得到该单元体的主应力主应力为:因为,主应力对应的方位角为。
13−5 试确定图示应力状态中的主应力及方位、最大切应力(按三向应力状态考虑)。
图中应力的单位为MPa 。
解:(a )已知 MPa 20MPa,20,0MPa 4===x y x τσσ则由公式可直接得到该单元体的主应力主应力为:因为,主应力对应的方位角为。
(b )已知 MPa 40MPa,20,0MPa 4-=-==x y x τσσ则由公式可直接得到该单元体的主应力(a)202040习题13−5图204040 302020 (b) (c)主应力为:因为,主应力对应的方位角为。
(c )已知 MPa 20MPa,03,20MPa ==-=x y x τσσ则由公式可直接得到该单元体的主应力主应力为:因为,主应力对应的方位角为。
13−6已知应力状态如图所示(应力单位为MPa ),试画三向应力圆,求最大切应力。
解:图a 为单向应力状态,图b 为纯剪切应力状态,图c 为平面应力状态,其应力圆如图。
最大切应力分别为:(a) 习题13−6图τ(b) (c)στσ13−7已知应力状态如图所示,试画三向应力圆,并求主应力、最大切应力(应力单位为MPa )。
解:图a 为三向主应力状态,,应力圆如图(a )。
图b 一方向为主应力,另两方向为纯剪切应力状态,则根据公式可直接得出另两主应力。
于是有其应力圆如图(b )。
13−8图示悬臂梁,承受荷载F = 10KN 作用,试求固定端截面上A 、B 、C 三点最大切应力值及作用面的方位。
解:固定端截面的弯矩,剪力。
截面a 点的应力:,其应力状态为单向应力状态,即习题13−7图40(a)56720 (b4习题13−8图2m A160 80BC F 图图图τOσ1 σ2 σ1τOσσ3σ1στO图76σ τ 5图4τO 20-40, 最大切应力作用面的方位为。
截面b点的应力:,其应力状态为平面应力状态,即主应力:。
求最大切应力作用面的方位先求主应力的方位,即截面c点的应力:,其应力状态为纯剪切应力状态,则, 最大切应力作用面的方位为13−9 空心圆杆受力如图所示。
已知F=20kN,D=120mm,d =80mm,在圆轴表面A点处测得与轴线成30°方向的线应变ε30°= ×10-5,弹性模量E=210GPa, 试求泊松比ν。
解:1、A点对应的横截面上只有正应力,即2、取A点的单元体3、由斜截面应力计算公式有3、根据广义胡克定律有Aσ习题13−9图30AF则13−10 在其本身平面内承受荷载的铝平扳,巳知在板平面内的主应变为ε1 = ×10-4,ε3 = ×10-4 其方向如图13−10 所示。
铝的E =70 GPa ,ν=,试求应力分量σx 、σy 及τx 。
解:由题意可知该应力状态为平面应力状态,根据广义胡克定律有代入得利用斜截面应力公式及 得13−11 已知各向同性材料的一主应力单元体的σ1 = 30MPa ,σ2 = 15MPa ,σ3 =-5MPa ,材料的弹性模量E = 200GPa ,泊松比250.ν=。
试求该点得主应变。
解:直接应用广义胡克定律即可求出。
5-35-24-31108.125- 104.375 101.375)((1⨯=⨯=⨯=+=εεε;;)σσ-νσE2113−12 图示矩形板,承受正应力σx 与σy 作用,试求板厚的改变量Δδ与板件的体积改变ΔV 。
已知板件厚度δ=10mm ,宽度b = 800mm ,高度h = 600mm ,正应力σx = 80MPa ,σy = -40MPa ,材料为铝,弹性模量E =70GPa ,泊松比ν = 。
解:由广义胡克定律即可求出43y 10886.1)4080(33.010701-)]([1-⨯=-⨯⨯=+=σσ-νσE x z z ε则 mm z 3410886.11010886.1--⨯=⨯⨯==∆δεδ体应变习题13−12图h b σxσy 60ºx zy 13习题13−10图4310943.1)4080(107033.021)(2-1-⨯=-⨯⨯-=+=y x E σσνθ 板件的体积改变量3457.9321060080010943.1mm V V =⨯⨯⨯⨯==∆-θ13−13 如图所示,边长为20cm 均质材料的立方体,放入刚性凹座内。
顶部受轴向力F = 400kN 作用。
已知材料的E =×104MPa ,ν = 。
试求下列两种情况下立方体中产生的应力。
(1)凹座的宽度正好是20cm ; (2)凹座的宽度均为20.001cm 。
解:(1)根据题意立方体两水平方向的变形为零,即0==y x εε为变形条件,由广义胡克定律得)]([10)]([1x y =+==+=σσ-νσEσσ-νσEz y y z x x εε上式解出 z y x σννσσ-==1。
式中 MPa A Fz 100.20.2104003=⨯⨯==σ。
代入数据,得 MPa y x 195.2100.1810.18=⨯-==σσ(2)根据题意立方体两水平方向的变形为0.001cm ,应变5-105.0200.001⨯===y x εε,由广义胡克定律得5-x 5-y 105.0)]([1105.0)]([1⨯=+=⨯=+=σσ-νσEσσ-νσEz y y z x x εε式中 MPa A Fz 100.20.2104003=⨯⨯==σ。
上式解出 E z y x σννσσ-⨯⨯==-1100.55。
代入数据,得MPay x 854.2106.2100.1810.18100.545=⨯⨯⨯-⨯⨯==-σσ13−14 已知如图所示受力圆轴的直径d =20mm ,若测得圆轴表面A 点处与轴线45°方向习题13−1320c m 20.001c m的线应变ε45°= ×10-4,材料的弹性模量E = 200GPa ,泊松比ν = 。
试求外力偶矩M e 。
解:A 点应力状态为纯剪切状态,故45°方向为主应力方向,且有-0 321τσστσ===,,。
由43111020.5)1(1)(1-⨯=+=-=τννσσεEE 得MPa 80=τ。
对于扭转是A 点的切应力PeM W =τ,则m kN D M e ⋅=⨯⨯==6.125161080W 36P πτ13−15 一直径为25mm 的实心钢球承受静水压力,压强为14MPa 。
设钢球的E=210GPa ,ν=。
试问其体积减少多少 解:根据题意有MPa -14321===σσσ体应变53321100.-8143100213.021-)(2-1-⨯=⨯⨯⨯⨯-=++=σσσνθE 体积改变量3350.654176100.8V mm d V =⨯⨯==∆-πθ13−16 试对图示三个单元体写出第一、二、三、四强度理论的相当应力值,设ν =。
解:(a) 由题图可知MPa MPa MPa 30,10,20321-===σσσ则习题13−16(a)(b) (c)MPa MPa MPa MPa 83.45])()()[(21;503020;26)3010(3.020)(;20213232221r431r3321r21r1=-+-+-==+=-==--=+-===σσσσσσσσσσσσνσσσσ(b)已知MPa01τ0MPa,2σ,30MPa σx y x =-==MPa MPa MPa 93.21,0,93.31321-===σσσ则MPa MPa MPa MPa 91.46])()()[(21;86.5393.2193.31;51.38)93.210(3.093.31)(;93.31213232221r431r3321r21r1=-+-+-==+=-==--=+-===σσσσσσσσσσσσνσσσσ (c )由题图可知MPa MPa MPa x 20,0,51xy y z -====τσσσ则MPa MPa MPa 20,51,20321-===σσσMPa MPa MPa MPa 75.37])()()[(21;402020;5.21)2015(3.020)(;20213232221r431r3321r21r1=-+-+-==+=-==--=+-===σσσσσσσσσσσσνσσσσ则由公式可直接得到该单元体的主应力13−17 有一铸铁制成的零件。
