09工程力学答案第13章一点的运动分析
工程力学之点的运动学

简谐振动
点在平衡位置附近作周期性往 复运动,加速度与位移成正比 、方向相反。
抛体运动
点在重力作用下沿抛物线轨迹 的运动,如平抛、斜抛等。
一般平面曲线运动
点在平面内沿任意曲线轨迹的 运动,加速度和速度方向可任
意变化。
05
工程应用实例分析
机械手臂的运动控制
运动学建模
01
通过D-H参数法或旋量理论建立机械手臂的运动学模型,描述
在航空航天工程中,点的运动学可用于分 析飞行器的飞行轨迹和姿态控制,为航空 航天技术的发展提供理论支持。
土木工程
生物医学工程
在土木工程中,点的运动学可用于研究结 构的动力响应和稳定性问题,为工程结构 的设计和施工提供科学依据。
在生物医学工程中,点的运动学可用于分 析人体运动系统的生物力学特性,为医疗 器械的设计和康复治疗提供理论指导。
曲线运动的合成与分解
运动的合成
将点的运动分解为沿不同坐标轴的分运动,通过矢量合成得到点 的实际运动。
运动的分解
根据实际需要,将点的曲线运动分解为多个简单的直线或圆周运动, 便于分析和计算。
运动的叠加原理
多个独立的分运动可以线性叠加,形成复杂的曲线运动。
曲线运动的特殊形式
匀速圆周运动
点绕固定中心以恒定速率作圆 周运动,加速度始终指向圆心
速直线运动。
特点
速度大小随时间均匀变化,加速度 大小和方向保持不变。
公式
s = v0t + 1/2at^2,其中s为位移, v0为初速度,a为加
已知分运动求合运动,其位移、速度、加速度遵 循平行四边形定则。
分解
已知合运动求分运动,可将合运动分解为两个简 单的分运动进行处理。
大学《工程力学》课后习题解答-精品
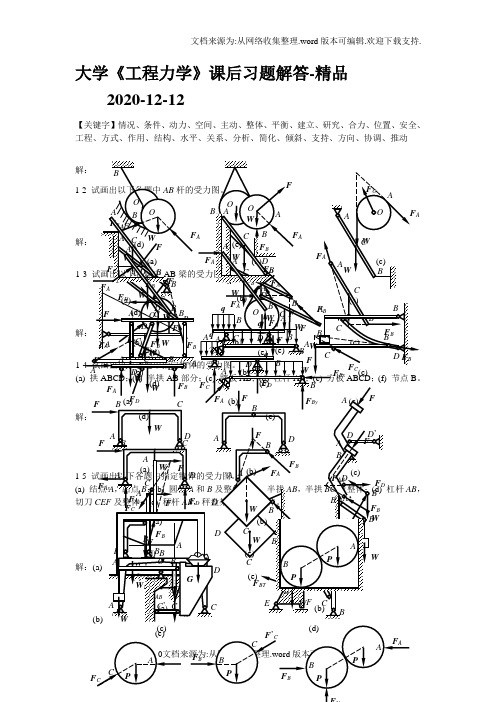
大学《工程力学》课后习题解答-精品2020-12-12【关键字】情况、条件、动力、空间、主动、整体、平衡、建立、研究、合力、位置、安全、工程、方式、作用、结构、水平、关系、分析、简化、倾斜、支持、方向、协调、推动(e)(c)(d)(e)’CD2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点(2) AC 与BC 2-3 水平力F A 和D 处的约束力。
解:(1) 取整体(2) 2-4 在简支梁,力的大小等于20KN ,如图所示。
若解:(1)(2)求出约束反力:2-6 如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计,图中的长度单位为cm 。
已知F =200 N ,试求支座A 和E 的约束力。
解:(1) 取DE (2) 取ABC2-7 在四连杆机构ABCD 试求平衡时力F 1和F 2解:(1)取铰链B (2) 取铰链C 由前二式可得:F FF ADF2-9 三根不计重量的杆AB,AC,AD在A点用铰链连接,各杆与水平面的夹角分别为450,,450和600,如图所示。
试求在与O D平行的力F作用下,各杆所受的力。
已知F=0.6 kN。
解:(1)间汇交力系;(2)解得:AB、AC3-1 已知梁AB 上作用一力偶,力偶矩为M ,梁长为l ,梁重不计。
求在图a ,b ,c 三种情况下,支座A 和B 的约束力解:(a) (b) (c) 3-2 M ,试求A 和C解:(1) 取 (2) 取 3-3 Nm ,M 2解:(1)(2) 3-5 大小为AB 。
各杆 解:(1)(2)可知:(3) 研究OA 杆,受力分析,画受力图:列平衡方程:AB A3-7 O1和O2圆盘与水平轴AB固连,O1盘垂直z轴,O2盘垂直x轴,盘面上分别作用力偶(F1,F’1),(F2,F’2)如题图所示。
工程力学(第二版)习题册答案

一、填空题
1. 相 对 滑 动 相 对 滑 动 趋 势 接触面的切线 相反 2. 10N 20N 30N 30N 30N 3. 100N 竖直向上 平衡 4. 平稳无冲击 自锁
阻碍物体相对滑动
相对滑动趋势
二、选择题
1. A
三、简答题
1. ①问题中含有可能发生相对滑动的摩擦面,因此,存在摩擦力; ②受力图中要画出摩擦力,摩擦力总是沿着接触面的切线方向并与物体相对滑
7.
8.
9.
第二章 平面力系
第一节 共线力系的合成与平衡
一、填空题
1. 在同一条直线上
2. FR Fi FR 0
二、计算题
设向右为正方向。 则 FR=120+40-80-200=-120N 方向:水平向左
第二节 平面汇交力系的合成
一、填空题
1. 作用于同一平面内且各力作用线相交于一点的力系 共线力系 力的作用点 2. -F 或 F 0 0 -F 或 F 3. 合力在任一坐标轴上的投影 各分力在同一轴上投影的代数和 4. F4 F3 5. 自行封闭 6. 所有各力在 x 轴上投影的代数和为零 所有各力在 y 轴上投影的代数和为零 Fx 0 Fy 0
3. 后轮:摩擦力向前 前轮:摩擦力向后
4. 不下滑,处于自锁状态
四、计算题
FT 60 18 3N
五、应用题
1. (提示)从摩擦力与 F 对 B 点的力矩大小的比较进行考虑
第三章 空间力系 第一节 力在空间坐标轴上的投影与合成
一、填空题
1. 力的作用线不都在同一平面内呈空间分布的力系 2. 一次投影法 二次投影法
二、选择题
1. A 2.B
它所限制物体
三、简答题
1.柔性体约束只能承受拉力,不能承受压力。 2.被约束物体可以沿约束的水平方向自由滑动,也可以向离开约束的方向运动, 但不能向垂直指向约束的方向运动。 3.剪刀的两半部分可以绕销钉轴线相对转动,但不能在垂直销钉轴线的平面内沿 任意方向做相对移动。 4.木条不能沿圆柱销半径方向移动,但可以绕销轴做相对转动。 5.固定端约束既限制物体在约束处沿任何方向的移动,也限制物体在约束处的转 动。
(完整版)工程力学课后详细答案
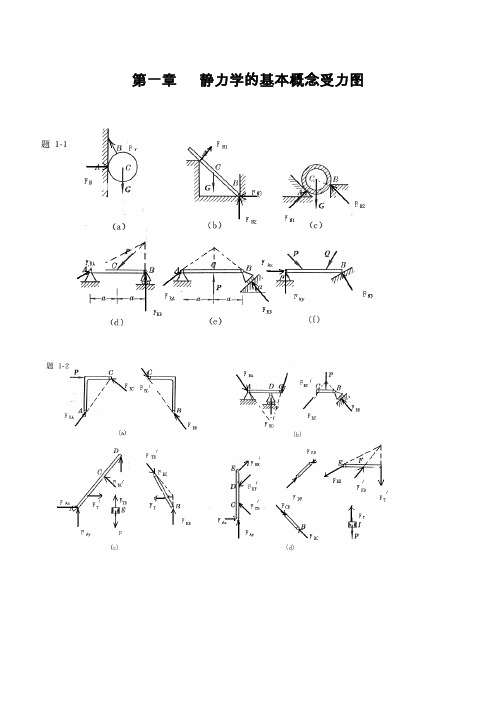
第一章静力学的基本概念受力图第二章 平面汇交力系2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故: 223R RX RY F F F KN=+= 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解:(a )受力分析如图所示:由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以:5RA F KN= (压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得: 5RD F Q =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得: 22RA F Q =2RB F Q P=+(3)取BCE 部分。
《工程力学》课后习题解答

z
A
F
B 45o
FAB
60o FAD
O
D
y
45o
C
FAC
x
解:(1) 取整体为研究对象,受力分析,AB、AB、AD 均为二力杆,画受力图,得到一个空 间汇交力系;
(2) 列平衡方程:
Fx 0 FAC cos 45o FAB cos 45o 0 Fy 0 F FAD cos 60o 0 Fz 0 FAD sin 60o FAC sin 45o FAB sin 45o 0
FA
FB
M l
FB
M l
(c) 受力分析,画受力图;A、B 处的约束力组成一个力偶;
FA A
M
l/2 l
B
θ
FB
9
《工程力学》习题选解
列平衡方程:
M 0 FB l cos M 0
FA
FB
l
M cos
FB
l
M cos
3-2 在题图所示结构中二曲杆自重不计,曲杆 AB 上作用有主动力偶,其力偶矩为 M,试求 A 和 C 点处的约束力。
解得:
FAD 2F 1.2 kN AB、AC 杆受拉,AD 杆受压。
FAC FAB
6 4
FAD
0.735
kN
8
《工程力学》习题选解
3-1 已知梁 AB 上作用一力偶,力偶矩为 M,梁长为 l,梁重不计。求在图 a,b,c 三种情 况下,支座 A 和 B 的约束力
M
l/2
A
B
l
(a)
M
l/3
A
30o
B
C
M2
M1
O
解:(1) 研究 BC 杆,受力分析,画受力图:
(完整版)工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 3 1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础 5 (b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7 (f)(g)8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如第二章 平面力系 9图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
《工程力学》课后习题与答案全集
工程力学习题答案第一章静力学基础知识思考题:1. X ;2. V ;3. V ;4. V ;5. K 6. K 7. V ;8. V习题一1•根据三力汇交定理,画出下面各图中A 点的约束反力方向。
解:(a )杆AB 在 A B 、C 三处受力作用。
u由于力p和uuv R B 的作用线交于点Q 如图(a )所示,根据三力平衡汇交定理, 可以判断支座A 点的约束反力必沿 通过A 0两点的连线。
uP 3uvB 处受绳索作用的拉力uuv R B (b )同上。
由于力交于0点,根据三力平衡汇交定理, 可判断A 点的约束反力方向如 下图(b )所示。
的作用线 2.不计杆重,画出下列各图中 AB 杆的受力图。
uP 解:(a )取杆AB 和E 两处还受光滑接触面约束。
约束力UJVN E uuvuuN A 和 N E,在A的方向分别沿其接触表面的公法线, 外,在 并指向杆。
其中力uuvN A 与杆垂直,通过半圆槽的圆心 Q力 AB 杆受力图见下图(a )。
和C 对它作用的约束力 NBo------- r -------- —y —uuv N C铰销此两力的作用线必须通过(b )由于不计杆重,曲杆 BC 只在两端受 故曲杆BC 是二力构件或二力体,和 B 、C 两点的连线,且B O两点的连线。
见图(d).第二章力系的简化与平衡思考题:1. V ;2.>;3. X ;4. K 5. V ;6.$7.>;8. x ;9. V .1.平面力系由三个力和两个力偶组成, 它们的大小和作用位置如图示,长度单位为cm 求此力系向O 点简化的结果,并确定其合力位置。
uvR R 解:设该力系主矢为 R ,其在两坐标轴上的投影分别为Rx、y。
由合力投影定理有:。
4.梁AB 的支承和荷载如图, 小为多少?解:梁受力如图所示:2. 位置:d M o /R 25000.232 火箭沿与水平面成F ,100 0.6100 80 2000 0.5 580m 23.2cm,位于O 点的右侧。
建筑力学 第十三章答案
C1mABD441ADCP i=11B1(a)(b)习题13-2图13-2解:(1)建立支座移动的实状态(a ),和虚设单位力状态(b )。
(2)由∑-=∆C R iiC 公式求三种情况时的D 点的水平位移:1)当只有支座A 发生向左10mm 的位移时)(1001.0)01.01(←-=-=⨯-=-=∆=∆∑mm m m C R i iC H D (负号表示D 点的水平位移与所设的向右的单位力方向相反,向左。
)2)当只有支座A 只发生向下10mm 的位移时)(5.20025.0)01.041(←-=-=⨯-=-=∆=∆∑mm m m C R i iCH D 3)当只有支座B 只发生向下10mm 的位移时)(5.20025.0)01.041(→==⨯--=-=∆=∆∑mm m m C R i iCH D (正号表示D 点的水平位移与所设的向右的单位力方向相同,向右。
)CBqAaM=qa 2aqa 223qax x2a2a1A1B2aM i=1A11aB22xx aP i=1a 1) a 2) a 3)习题13-5a)图13-5a 解:(1) 荷载作用的实状态如图13-5 a 1)。
其弯矩方程如a 1)式)]2,0[212a a x qx qa M P ∈=21-x(2) 选虚拟状态如图13-5 a 2)、a 3)。
其弯矩方程分别如a 2)、a 3)式)]2,0[2121a a x aM ∈-=x)]2,[21)(21],0[2132a a a x a x a x x a x M ⎪⎪⎩⎪⎪⎨⎧∈+-=--∈=x(3)由求位移公式知:1)积分实状态a 1) 和虚拟状态a 2)的弯矩表达式求B ϕ。
EIqa dx qx qa x a EI ds EI M M a P B 3)2)(21(132021-=-==∑⎰∑⎰21-x ϕ()2)积分实状态a 1) 和虚拟状态a 3)的弯矩表达式求VC ∆。
∑⎰=∆ds EIM M PV C 2)(24)2)(21()2)(21(1422022202↑-=⎥⎦⎤⎢⎣⎡+-+=+=⎰⎰⎰⎰EIqa dx qx qa a x dx qx qa x EI dx EIM M dx EI M M a a a a a PaP 21-x 21-x 右左C B 5m10mA xxP i=1xxCB A xxB ACP i=1CAB xxM i=1a 1) a 2) a 3) a 4)13-6a)13-6a) 解:(1) 荷载作用的实状态如图a 1)。
(完整版)工程力学课后详细答案
(完整版)⼯程⼒学课后详细答案第⼀章静⼒学的基本概念受⼒图第⼆章平⾯汇交⼒系2-1解:由解析法,23cos 80RX F X P P N θ==+=∑12sin 140RY F Y P P N θ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos 2944RYR RF F P F '∠==o v v2-2解:即求此⼒系的合⼒,沿OB 建⽴x 坐标,由解析法,有123cos45cos453RX F X P P P KN ==++=∑o o13sin 45sin 450RY F Y P P ==-=∑o o故:223R RX RY F F F KN=+= ⽅向沿OB 。
2-3 解:所有杆件均为⼆⼒杆件,受⼒沿直杆轴线。
(a )由平衡⽅程有:0X =∑sin 300AC AB F F -=o0Y =∑cos300AC F W -=o0.577AB F W=(拉⼒)1.155AC F W=(压⼒)(b )由平衡⽅程有:0X =∑ cos 700AC AB F F -=o0Y =∑sin 700AB F W -=o1.064AB F W=(拉⼒)0.364AC F W=(压⼒)(c )由平衡⽅程有:0X =∑cos 60cos300AC AB F F -=o o0Y =∑sin 30sin 600AB AC F F W +-=o o 0.5AB F W= (拉⼒)0.866AC F W=(压⼒)(d )由平衡⽅程有:0X =∑sin 30sin 300AB AC F F -=o o0Y =∑cos30cos300AB AC F F W +-=o o0.577AB F W= (拉⼒)0.577AC F W= (拉⼒)2-4 解:(a )受⼒分析如图所⽰:由x =∑ 22cos 45042RA F P -=+o15.8RA F KN∴=由0Y =∑22sin 45042RA RB F F P +-=+o7.1RB F KN∴=(b)解:受⼒分析如图所⽰:由x =∑cos 45cos 45010RA RB F F P ? --=o o0Y =∑sin 45sin 45010RA RB F F P ?+-=o o联⽴上⼆式,得:22.410RA RB F KN F KN==2-5解:⼏何法:系统受⼒如图所⽰三⼒汇交于点D ,其封闭的⼒三⾓形如图⽰所以:5RA F KN= (压⼒)5RB F KN=(与X 轴正向夹150度)2-6解:受⼒如图所⽰:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-?=--2-7解:受⼒分析如图所⽰,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=o o0Y =∑sin 45sin 450CBRA F F '-=o o联⽴后,解得:0.707RA F P=0.707RB F P=由⼆⼒平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为⼆⼒杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ?--=o o0Y =∑sin 30sin 600AB AC F F W +-=o o联⽴上⼆式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反⼒全为拉⼒,以D ,B 点分别列平衡⽅程(1)取D 点,列平衡⽅程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡⽅程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联⽴上⼆式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα=+取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '=Q 故有:22cos 1cos 2sin cos 2sin NH P P F ααααα??=+= ?2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=o o0Y =∑cos 75cos 750AB AD F F P +-=o o联⽴后可得: 2cos 75AD AB PF F ==o取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=o ocos5cos80NDAD F F '=?oo由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND ADP F F F KN '∴===?=o o o o o2-12解:整体受⼒交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=o0Y =∑sin sin 300RA F P α-=o联⽴上⼆式得:2.92RA F KN=1.33DC F KN=(压⼒)列C 点平衡x =∑405DC AC F F -?=0Y =∑ 305BC AC F F +?=联⽴上⼆式得: 1.67AC F KN=(拉⼒)1.0BC F KN=-(压⼒)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联⽴⽅程后解得: 5RD F Q =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=o0Y =∑sin 450RB RA F F P --=o且RE REF F '=联⽴上⾯各式得: 22RA FQ =2RB F Q P=+(3)取BCE 部分。
第13章动能定理习题答案
第13章 动能定理13-1 圆盘的半径r = 0.5 m ,可绕水平轴O 转动。
在绕过圆盘的绳上吊有两物块A 、B ,质量分别为m A = 3 kg ,m B = 2 kg 。
绳与盘之间无相对滑动。
在圆盘上作用一力偶,力偶矩按ϕ4=M 的规律变化(M 以m N ⋅计,ϕ以rad 计)。
试求由π20==ϕϕ到时,力偶M 与物块A 、B 重力所作的功之总和。
解:作功力M ,m A g ,m B gJ1105.0π28.91π8π2)(π8π2)(d 40π222=⨯⨯⨯+=⋅-+=⋅-+=⎰rg m m r g m m W B A B A ϕϕ13-3 图示坦克的履带质量为m ,两个车轮的质量均为m 1。
车轮被看成均质圆盘,半径为R ,两车轮间的距离为R π。
设坦克前进速度为v ,试计算此质点系的动能。
解:系统的动能为履带动能和车轮动能之和。
将履带分为四部分,如图所示。
履带动能: IV III II I 221T T T T v m T i i +++=∑=履由于v v v 2,0IV 1==,且由于每部分履带长度均为R π,因此222IV IV IV 2I I I IV III II I 2)2(421210214v m v m v m T v m T m m m m m =⨯======== II 、III 段可合并看作一滚环,其质量为2m ,转动惯量为22R m J =,质心速度为v ,角速度为Rv=ω则2222222222III II 2202221421221mv v mv m T vm R v R m mv J v m T T =++==⋅⋅+=+⋅=+履ω 轮动能 21222121123221222v m R v R m v m T T =⎥⎦⎤⎢⎣⎡⋅⋅+==轮轮 则系统动能 21223v m mv T T T +=+=轮履13-5 自动弹射器如图放置,弹簧在未受力时的长度为200 mm ,恰好等于筒长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13-5 如图摇杆结构的滑杆AB 以u 的速度匀速向上运动,试建立摇杆的OC 上点的运动方程;并求此C 点在4
π
ϕ=时的速度大小,假定初始瞬时0ϕ=。
摇杆长OC=a ,距离OD=b 。
解:方法一(直角坐标法): (1)建立C 点的运动方程: 由图示几何关系可知:
tan arctan cos(arctan )cos sin sin(arctan )
ut l
ut l ut x a x a l y a ut y a l ϕϕϕϕ==⎧
=⎪=⎧⎪−−−−→⎨⎨=⎩⎪=⎪⎩
(2)求C 点速度方程
将运动方程对时间求一阶导数,即可求C 的速度在x 、y 轴上的投影。
2
2
sin(arctan )1()cos(arctan )1()x y u l ut x
a ut l l u l ut y a ut l l ⎫==-⎪+⎪
⎬
⎪==⎪+⎭ v v
于是速度的大小为:
21()u l a ut l ==+v = 速度与杆垂直。
(3)求C 点在4
π
ϕ=时的速度大小
当4
πϕ=时tan 1ut l ϕ==,2112u l au
a l
==+v
方法二:(弧坐标法)
(1)以C 点的初始位置为弧坐标原点,建立运动方程为:
tan arctan
arctan
ut
l ut
l ut s a s a l
ϕϕϕϕ=
==−−−−→= (2)求C 点速度方程
2
()arctan()1()ds d a d d ut l u l a a a dt dt dt dt ut l ϕϕ=
===→=+v v
当4
πϕ=时tan 1ut
l
ϕ== 2112u l au
a
l
==+v
13-7 已知刚体的角速度ω与角加速度α如图所示,求A 、M 两点的速度、切向加速度和法向加速度的大小,并图示其方向。
v b
解:(a )因杆的角速度与角角速度的转向相反,OAM 绕O 匀减速定轴转动,其上任意点绕O 作匀减速圆周运动。
2
2
222A M n A
A OA a OM OA a OA a τ
ωωωωω
αα
=⋅==⋅==⋅==⋅=v v a a
速度、加速度方向如图所示。
(b )因杆的角速度与角角速度的转向相反,AB 作曲线平动, A 点绕O 作匀减速圆周运动,AB 杆上任意点与A 的轨迹、速度、加速度完全相同。
22A M
n n n
M A
M A OA r OA r OA r τωωωωαα
=⋅====⋅===⋅=v v a a a a
速度、加速度方向如图所示。
13-8 物体做定轴转动的运动方程为2
43t t ϕ=-(φ为rad 计,t 以s 计),试求该物体
内,转动半径r=0.5m 的一点,在t 0=0s,t 1=1s 的速度和加速度的大小,并求物体在哪一瞬时改变方向。
解:(1)求该物体的角速度和角速度
对转动方程求一阶导数得角速度方程:46t ω=- 再求一次导数得角加速度:6α=-
(2)转动半径r=0.5m 点的速度方程、加速度方程
20.5(46)23n t t
a a a τωωα=⨯-=-==−−→===v =r r r 当t 0=0
时:2328.54t a -====2
m /s v =m /s; 当t 1=1s 时:
231 3.61t a -=-===2m /s v =m /s;
13-12 在题图(a )、(b )所示的两种机构,已知12120cm,3OO a ω===rad /s ,求图示位置时,杆O 2A 的角速度。
(b )
A
a
y '
O 1
30ω
y O 2
'
a
O 1
O 2
30ω1
ω30
(a )图:(1)三选:取曲柄
O 1A 的端点A (即滑块A )常接触点
为动点。
机座上固连定系O 2xy ,摆杆O 2A 上固连动系O 2x ’y ’。
(2)运动分析:滑块A 的绝对运动是以O 1为圆心,a 为半径的圆周运动:动点的相对运动为沿O 2A 的直线运动;牵连运动为摆杆的定轴转动(绕O 2)即牵连点随动系的转动
(3)速度分析:作速度平行四边形,e v 为动系上的牵连点的速度
ωθωθωωθωθ=→⋅=→=
==2211
21cos cos cos 1.5/2cos 2
e a O A O A a v v O A a rad s a (↺)
a v e
r
v x '
x
A
30
O 2
1
30
ω1
v
(b )图:(1)三选:取曲柄
O 2A 的端点A (即滑块A )常接触点
为动点。
机座上固连定系O 2xy ,摆杆O 1A 上固连动系O 1x ’y ’。
(2)运动分析:滑块A 的绝对运动是以O 2为圆心,θ2cos a 为半径的圆周运动:动点的相对运动为沿O 1A 的直线运动;牵连运动为摆杆的定轴转动(绕O 1)即牵连点随动系的转动
(3)速度分析:作速度平行四边形,e v 为动系上的牵连点的速度
ωωωωωθθθθθ
=
→⋅=→===22111
222/cos cos cos 2cos 2cos e a O A O A v a a v O A rad s a (↺) 13-13 杆OA 长l ,由推杆推动而在图示平面内绕O 转动,假定推杆的速度为v ,其弯头高为a ,求杆端A 点的速度大小(表示为x 的函数)。
(1)三选:取推杆MBCD 的端点M 常接触点为动点。
机座上
固连定系xy,摇杆OA上固连动系x’y’。
(2)运动分析:M点的绝对运动是以v向左的直线运动,动点M的相对运动为沿OA的直线运动,牵连运动为摆杆OA的定轴转动(牵连点随动系绕O作匀速圆周运动)
(3)速度分析:作速度平行四边形,
e
v
为动系上的牵连点的速度。
ϕϕωω
====⋅=→=
+
22
sin sin
e a
av
v v v OM
a x
故:ω
==
+
22
A
alv
v l
a x
13-14 图所示曲柄滑杆机构中,滑杆上有一圆弧滑道,其半径R=100mm,圆心O1在导杆BC上,曲柄长OA=100mm,以等角速度4
ω=rad/s绕O点转动。
求导杆BC的运动规律,以及曲柄与水平线间的交角30
ϕ= 时,求导杆BC的速度和加速度。
(1)导杆BC作直线平动,可以归结为点的运动,其运动方程
为:
1
2cos0.2cos4
O
x R t t
ω
==
(2)三选:取曲柄OA的端点A常接触点(即滑块A)为动点,
(3)运动分析:A 点的绝对运动是绕O 的匀速圆周运动,动点A 的相对运动为沿滑道的圆弧运动,牵连运动为推杆的以v 向左的直线运动平动(牵连点随动系作直线运动)
(4)速度分析:作速度平行四边形,e v 为平动动系上的牵连点的速度。
由图可知:===e a r v v v v
(5)加速度分析:作加速度矢量图,则:n a e r r τ=++a a a a 。
建立ξ轴如图示,将加速度矢量式向ξ轴投影得:
2
2222cos60cos60cos60cos60cos30 2.771/()cos30cos30cos30
r n n r a a e r e R R R R rad s ωωω+++-=-+→====←
v a a a a a a
13-17图所示曲柄滑杆机构中,曲柄长OA =10cm ,并绕O 转动,在某瞬时,其角速度1ω=rad /s ,角加速度21α=rad /s ,30AOB ∠= ,求导杆上点C 的加速度和滑块A 在滑道上的相对加速度。
(1)三选:取曲柄OA 的端点A 常接触点(即滑块A )为动点,
(2)运动分析:A 点的绝对运动是绕O 的匀加速圆周运动,动点A 的相对运动为沿滑道的直线运动,牵连运动为导杆的竖直直线平动(牵连点随动系作直线运动)
(3)加速度分析:作加速度矢量图,则:n
a a e r τ+=+a a a a 。
建立η、ξ轴如图示,将加速度矢量式向η、ξ轴投影得:
22cos30cos600sin 30sin 600cos30cos60cos30cos6013.66()sin 30sin 60sin 30sin 60 3.66()n a a e n a a r
n e a a n r a a r r r r ττττξηωαωα⎧+=+⎪⎨+=-⎪⎩⎧=+=+=↑⎪⇒⎨===-→⎪⎩
2
2
cm /s cm /s :a a a :
-a a a a a a a a -a -。
