江苏省苏州高新区第二中学九年级数学下册 7.2 正弦 余弦导学案2(无答案)(新版)苏科版
新苏科版九年级数学下册《7章锐角三角函数7.2正弦、余弦》教案_19
4、余弦的定义
如图,在 Rt△ ABC中,∠ C=90° , 我们把锐角∠ A 的邻边 b 与
斜边 c 的比叫做∠ A 的 ______,记作 =_________,即: cosA=______=_____。
(你能写出∠ B 的正弦、余弦的表达式吗?)试试看 ____________________.
7.2 正弦、余弦 (1)
【教学目标】
授课日期:
月
1、 认识锐角的正弦、余弦的概念及锐角三角函数的概念。
2、 会求一个锐角的正弦、余弦值。
3. 经历操作观察思考求解等过程,感受数形结合的数学思想方法。
【重点难点】
1. 锐角的正弦、余弦的概念 【教学过程】
一、【自主探学】
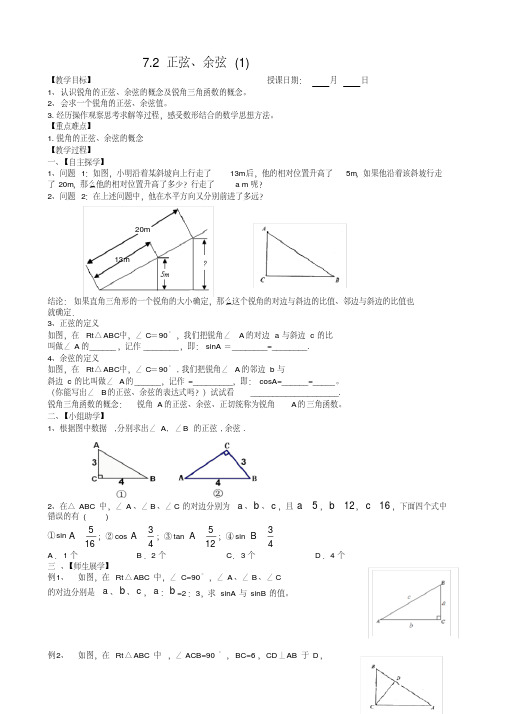
1、问题 1:如图,小明沿着某斜坡向上行走了 13m后,他的相对位置升高了
3
;④ sin B
16
4
12
4
A.1 个
B.2 个
C. 3 个
三 、【师生展学】
例 1、 如图,在 Rt △ ABC 中,∠ C=90°,∠ A 、∠ B 、∠ C
的对边分别是 a 、 b 、 c , a : b =2 :3,求 sinA 与 sinB 的值。
5 , b 12, c
D.4 个
16 ,下面四个式中
则 sin =
, cos =
.
3、如图△ ABC 中,∠ C=90°, sinA= 3 ,则 BC :AC=( ) 5
A . 3:4
B . 4: 3
C. 3: 5
D. 4: 5
(第 2 题 )
4、在 Rt△ABC 中,∠ C=90 °, AC=4 ,BC=3 ,则 cosB=( )
九年级数学下册 第7章 锐角三角函数 7.2 正弦、余弦(一)导学案(无答案) 苏科版

当锐角α越来越大时,它的正弦值是怎样变化的?余弦值又是怎样变化的?
例题分析:
例:已知:如图,∠ACB=90°,CD⊥AB,垂足为D.
(1)
(2)
(3)
(4)
展示交流:
1.根据如图中条件,分别求出下列直角三角形中锐角的正弦、余弦值。
2.如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,则sinA=_____,
当
堂
达
标
1.在Rt△ABC中,∠C=90°,AC= ,BC=1,则sinA=_____,cosB=_______,cosA=________,sinB=_______.
2.在Rt△ABC中,如果各边长度都扩大3倍,则锐角A的各个三角函数值( )
A.不变化B.扩大3倍C.缩小 D.缩小3倍
3.若0°<α<90°,则下列说法不正确的是( )
(你能写出∠B的正弦、余弦的表达式吗?)试试看________________.
4.怎样计算任意一个锐角的正弦值和余弦值呢?
(1)如书P42图7—8,当小明沿着15°的斜坡行走了1个单位长度到P点时,他的位置在竖直方向升高了约0.26个单位长度,在水平方向前进了约0.97个单位长度。
根据正弦、余弦的定义,可以知道:sin15°=0.26,cos15°=0.97
(2)你能根据图形求出sin30°、cos30°吗?sin75°、cos75°呢?
sin30°=_____,cos30°=_____.sin75°=_____,cos75°=_____.
(3)利用计算器我们可以更快、更精确地求得各个锐角的正弦值和余弦值。
(4)观察与思考:
九年级数学下册第7章锐角三角函数72正弦余弦一导学案无答案苏科版

(你能写出∠B的正弦、余弦的表达式吗?)试试看________________.
4.怎样计算任意一个锐角的正弦值和余弦值呢?
(1)如书P42图7—8,当小明沿着15°的斜坡行走了1个单位长度到P点时,他的位置在竖直方向升高了约0.26个单位长度,在水平方向前进了约0.97个单位长度。
根据正弦、余弦的定义,可以知道:sin15°=0.26,cos15°=0.97
(2)你能根据图形求ຫໍສະໝຸດ sin30°、cos30°吗?sin75°、cos75°呢?
sin30°=_____,cos30°=_____.sin75°=_____,cos75°=_____.
(3)利用计算器我们可以更快、更精确地求得各个锐角的正弦值和余弦值。
7.2正弦、余弦(一)
课题
7.2正弦、余弦(一)
自主
空间
学习目标
知识与技能:理解并掌握正弦、余弦的含义,会在直角三角形中求出某个锐角的正弦和余弦值。
过程与方法:能用函数的观点理解正弦、余弦和正切。
情感、态度与价值观:通过对正弦、余弦概念的学习感受数学知识的系统性。
学习重点
理解并掌握正弦、余弦的含义,会在直角三角形中求出某个锐角的正弦和余弦值。
(根据是______________________________。)
2.正弦的定义
如图,在Rt△ABC中,∠C=90°,
我们把锐角∠A的对边a与斜边c的比
叫做∠A的______,记作________,即:sinA=________=________.
3.余弦的定义
如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的邻边b与
新苏科版九年级数学下册《7章锐角三角函数7.2正弦、余弦》教案_18

课时( 67 ):7.2正弦余弦(1)学习目标1.认识锐角的正弦、余弦的概念;学习重点认识锐角的正弦、余弦的概念;会求一个锐角的正弦值、余弦值.学习难点认识锐角的正弦、余弦的概念;会求一个锐角的正弦值、余弦值.自主探究任意画Rt △ABC ,使得∠C =90°,∠A =30°,测量BC,AB 边的长度,计算AB BC的值,如果∠A 是45°时呢?∠A 是60°时呢?正弦、余弦的概念1.正弦的定义.如图,在Rt △ABC 中,∠C =90°,我们把锐角∠A的与的比叫做∠A 的正弦,记作________.即:sinA =_________=_________.2.余弦的定义如图,在Rt △ABC 中,∠C =90°,我们把锐角∠A 的与的比叫做∠A 的余弦,记作=_________.即:cosA =__________=_________.3.你能写出∠B 的正弦、余弦的表达式吗?试试看.例1 .根据图中数据,分别求出∠A 、∠B 的正弦和余弦.例题学习135例2 如图,在等边△ABC 中,AD ⊥BC,垂足为D.求sin ∠BAD.思考:由例2知道,sin30°= 12,如何求cos30°?你会求60°角的正弦、余弦吗?比较大小:sin40° sin80°;cos40° cos80°拓展延伸例3:.如图,⊙0是△ABC 的外接圆,AD 是⊙O 的直径,若⊙O 的半径为5,AC=6,则cosB 的值是1.如图,直角三角形ABC 中,斜边AB 的长为m ,∠B=40°,则直角边BC 的长是()A .msin40°B .mcos40°C .mtan40°D .2、如图,△ABO 的顶点都是小正方形组成的网格中的格点,则cos ∠OAB 等于()效果检测班级学号姓名等第1.在Rt △ABC 中,∠C =90°,BC =3,sinA =0.6,则AC =_ _,AB =___, tanB =_ __.2.在Rt △ABC 中,锐角A 的对边和邻边同时扩大100倍,sinA 的值()A .扩大100倍B .缩小100倍C .不变D .不能确定3.已知∠A,∠B 为锐角(1)若∠A =∠B ,则sinA sinB ;(2)若∠A<∠B ,则sinA sinB ;cosA cosB ;tanA tanB4.在Rt △ABC 中,∠C =90°, cosA =35,BC =12,求斜边AB 上的中线CD 长.tan 40m o C A B D B。
九年级数学下册 7.2 正弦、余弦导学案2(无答案)(新版)

7.2正弦、余弦 一、学习目标 1.能够根据直角三角形的边角关系进行计算; 2. 能用三角函数的知识根据三角形中已知的边和角求出未知的边和角.二、追本塑源:1.在Rt△ABC 中,∠C =90°,分别写出∠A 的三角函数关系式:sin A =___ __,cos A =____ _,tan A =___ __.∠B 的三角函数关系式_ ___________.2.基础训练①在Rt△ABC 中,∠C =90°,BC =6,AC =8,则sin A =_____,cos A =_____,tan A =_____.②在Rt△ABC 中,∠C =90°,BC =2,AC =4,则sin B =_____,cos B =_____,tan B =_____.③在Rt△ABC 中,∠C =90°,AB =10,sin A =35,则BC =_____.④在Rt△ABC 中,∠C =90°,AB =10,sin B =45,则AC =_____.⑤在Rt△ABC 中,∠B =90°,AC =15,sin C =35,则AB =_____.⑥在Rt△ABC 中,∠B =90°,AC =2BC ,求sin C⑦在Rt△ABC 中,∠C =90°,cos A =23,AC =12,求AB 、BC三、数学源于生活:小明正在放风筝,风筝线与水平线成35°角时,小明的手离地面1m ,若把放出的风筝线看成一条线段,长95m ,求风筝此时的高度.(精确到1m )(参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002)四、拓展与提高: 通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化。
类似的,可以在等腰三角形中建立边角之间的联系。
苏科版数学九年级下册7.2《正弦、余弦》(第2课时)讲教学设计

苏科版数学九年级下册7.2《正弦、余弦》(第2课时)讲教学设计一. 教材分析苏科版数学九年级下册7.2《正弦、余弦》(第2课时)的内容主要包括正弦函数和余弦函数的定义、性质及其应用。
这部分内容是学生学习三角函数的基础,对于培养学生的数学思维能力和解决实际问题的能力具有重要意义。
在学习本节课时,学生需要掌握正弦函数和余弦函数的定义,了解它们的基本性质,并能运用它们解决一些实际问题。
二. 学情分析在学习本节课之前,学生已经学习了初中阶段的函数知识,对函数的概念和性质有一定的了解。
同时,学生通过之前的学习,已经掌握了锐角三角函数的定义和性质。
然而,对于正弦函数和余弦函数的定义和性质,学生可能还存在一定的困惑。
因此,在教学过程中,教师需要结合学生的实际情况,采用适当的教学方法,引导学生理解和掌握正弦函数和余弦函数的知识。
三. 教学目标1.知识与技能目标:使学生理解正弦函数和余弦函数的定义,掌握它们的基本性质,并能运用它们解决一些实际问题。
2.过程与方法目标:通过自主学习、合作交流等方法,培养学生探究和解决问题的能力。
3.情感态度与价值观目标:激发学生学习三角函数的兴趣,培养学生的数学思维能力和创新意识。
四. 教学重难点1.重点:正弦函数和余弦函数的定义、性质及其应用。
2.难点:正弦函数和余弦函数的性质的理解和运用。
五. 教学方法1.情境教学法:通过设置一些实际问题,激发学生的学习兴趣,引导学生主动探究。
2.自主学习法:鼓励学生自主学习,培养学生的独立思考能力。
3.合作交流法:学生进行小组讨论,促进学生之间的相互学习。
4.案例分析法:通过分析一些典型案例,使学生更好地理解和掌握正弦函数和余弦函数的知识。
六. 教学准备1.教学课件:制作精美的教学课件,辅助教学。
2.教学案例:收集一些与正弦函数和余弦函数相关的实际问题,用于教学实践。
3.学习资料:为学生提供一些学习资料,帮助学生巩固所学知识。
七. 教学过程1.导入(5分钟)教师通过设置一些实际问题,引导学生回顾已学的函数知识,为新课的学习做好铺垫。
苏教版九年级数学下册第7章锐角三角函数7.2正弦余弦二导学案无答案
堂
达
标
1.在△ABC中,∠C=90°,cosB= ,AC=10,求△ABC的周长和斜边AB边上的高。
2.一把梯子靠在一堵墙上,若梯子与地面的夹角是68°,而梯子底部离墙脚1.5m,求梯子的长度(精确到0.1m)
(参考数据:sin68°≈0.9272,cos68°≈0.3746,tan68°≈2.475)
7.2正弦、余弦
课题
7.2正弦、余弦(二)
自主
空间
学习目标
知识与技能:能够根据直角三角形的边角关系进行计算;
过程与方法:能用三角函数的知识根据三角形中已知的边和角求出未知的边和角
情感、态度与价值观:在学习中体会数学与生活的联系,培养应用意识。
学习重点
能根据直角三角形的边角关系进行计算;用函数的观点理解正切,正弦、余弦值。
例题分析:
小明正在放风筝,风筝线与水平线成35°角时,小明的手离地面1m,若把放出的风筝线看成一条线段,长95m,求风筝此时的高度。(精确到1m)
(参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002)
三、展示交流:
1.为了测量河的宽度,在河的一边选定点C,使它正对着(视线与河岸垂直)河对岸的一棵树B,沿着点C所在的河岸行走100m,到达A处,测得∠CAB=35°,求河的宽度BC(精确到0.1m)(参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002)
学习难点
用函数的观点理解正切,正弦、余弦值。ABC中,∠C=90°,BC=2,AC=4,
则sinB=_____,cosB=_____,tanB=_____。
如图,在Rt△ABC中,∠C=90°,AB=10,
九年级数学下册正弦余弦学案苏科版
§7.2 正弦、余弦(1)学习目标:1.认识锐角的正弦、余弦的概念;2.会利用计算器求一个锐角的正弦、余弦;3.了解锐角的正弦值随锐角的增大而增大,余弦值随锐角的增大而减小,初步学会利用计算器进行计算的方法.学习重点:会求一个锐角的正弦值、余弦值.学习难点:会求一个锐角的正弦值、余弦值.学习过程:一.【情景创设】问题1:如图,小明沿着某斜坡向上行走了13m后,他的相对位置升高了5m,如果他沿着该斜坡行走了20m,那么他的相对位置升高了_________m,行走了_________m。
问题2:在上述问题中,他在水平方向又分别前进了_________m,_________m。
二.【问题探究】问题1:1、思考:从上面的两个问题可以看出:当直角三角形的一个锐角的大小已确定时,它的对边与斜边的比值__________;它的邻边与斜边的比值___________。
(根据是______________________________________。
)2、正弦的定义:如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的对边a与斜边c的比叫做∠A的______,记作_______。
即:sin A=________=________.3、余弦的定义如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的邻边b与斜边c的比叫做∠A的______,记作=_________。
即:cosA=______=_____。
(你能写出∠B的正弦、余弦的表达式吗?)试试看.________________________________________________.问题2:思考与探索怎样计算任意一个锐角的正弦值和余弦值呢?(1)如图,当小明沿着15°的斜坡行走了1个单位长度到P点时,他的位置在竖直方向升高了约______个单位长度,在水平方向前进了约______个单位长度。
根据正弦、余弦的定义,可以知道:sin15°=0.26,cos15°=0.97(2)你能根据图形求出sin30°、cos30°吗?sin75°、cos75°呢?sin30°=_____,cos30°=_____.sin75°=_____,cos75°=_____.(3)利用计算器我们可以更快、更精确地求得各个锐角的正弦值和余弦值。
苏科初中数学九下《72正弦余弦》word教案2
正弦余弦课堂教学教案教材第七章第二节第 2 课时总 3 课时课题 7.2正弦、余弦(2)备课人课型新授课:展现标点讲解重点突破难点巩固疑点教学目标(认知技能情感)【知识与技能】1、能够根据直角三角形的边角关系进行计算;2、能用三角函数的知识根据三角形中已知的边和角求出未知的边和角。
【过程与方法】经历观察、比较、概括直角三角形的边角关系;通过探究直角三角形的边角关系的条件和结果,达成知识目标【情感态度与价值观】培养学生观察、猜想、探究、归纳的习惯和能力,体验数学发现的乐趣教学重难点重点:能够根据直角三角形的边角关系进行计算;用函数的观点理解正切,正弦、余弦值。
难点:能够根据直角三角形的边角关系进行计算;用函数的观点理解正切,正弦、余弦值。
教具与课件多媒体与三角尺板书设计7.2正弦、余弦(2)如图,在Rt△ABC中, ∠C=90º, AC=12, BC=5.求: sinA、cosA、sinB、cosB的值. 你发现sinA与cosB 、 cosA与sinB的值有什么关系吗?教学环节学生自学共研的内容方法(按环节设计自学、讨论、训练、探索、创新等内容)教师施教提要(启发、精讲、活动等)再次优化一、创设情境二、探究活动【课前复习】:【新课导入】:如图,在Rt△ABC中, ∠C=90º, AC=12, BC=5.求: sinA、cosA、sinB、cosB的值. 结论:你发现sinA与cosB 、 cosA与sinB的值有什么关系吗?【典型例题】:1.比较大小以提问的形式进行。
可将这两个台阶抽象地看成两个三角形BC与AC长度的比与台阶的倾斜程度有何关系?如图,一般地,如果锐角A的大小已90A B∠+∠=︒若sinA=cosBcosA=sinB90A B∠+∠=︒若sinA=cosBcosA=sinB三、例题教学四、小结五、(1)巩固练习2.已知α为锐角:(1) sin α= ,则cosα=______,tanα=______,(2) cosα= ,则sinα=______,tanα=______,(3)tanα= ,则sinα=______,cosα=______,3.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CD=8,AC=10 (1)求锐角A、B的正弦、余弦: (2)求AB、BD4.如图, ∠C=90º,D是BC中点,且∠ADC=45º,AD=2,求tanB【知识要点】:在Rt△ABC中,若∠A+∠B=90゜,则sinA=cosB, cosA=sinB【基础演练】:1.在Rt△ABC中,如果各边长度都扩大3倍,则锐角A的各个三角函数值 ( )A.不变化B.扩大3倍C.缩小13D.缩小3倍2.在Rt△ABC中,∠C=90º,且锐角∠A满足sinA=cosA,则∠A的度数是 ( ) A.30º B.45º C.60º D.90º3.在Rt△ABC中,∠C=90º,sinA=12,则BC:AC:AB等于( )A. 1:2:5B. 1:3:5C. 1:3:2D. 1:2:34. 如图,在Rt△ABC中,CD是斜边AB上的高,则下列线段的比中不等于sinA的是( )A.CDACB.DBCBC.CBABD.CDCB5.如图,P是∠α的边OA上一点, 且P点坐标为(3,4),则αsin=_____,αcos=_____.6. 在Rt△ABC中,∠B=90º,AC=15,sinC=35,则BC=_______7.比较大小:(用>,<或=表示)①sin40゜ cos40゜②sin80゜ cos30゜③sin45゜ cos45゜8.菱形的两条对角线长分别是8和6,较短的一条对角线与菱形的一边的夹角为α,则sinα=__,cosα=___,tanα=__9.已知α为锐角,确定,我们可以作出无数个相似的RtAB1C1,RtAB2C2,RtAB3C3……,那么有:Rt△AB1C1∽________∽________……如图,在Rt△ABC中,∠C=90°,a、b分别是∠A的对边和邻边。
苏教版九年级下册数学教学课件:7.2《正弦、余弦(2)》
B
5
2.sinA=____,cosA=____;
A
C
3.sinB=____,cosB=____;
12
4.tanA=____,tanB=____.
3
7.2 正弦、余弦(2)
通过计算,你 有何发现?
1
sinA=cosB,cosA=sinB,tanA= .
tanB
A 12
B
5
C
4
7.2 正弦、余弦(2)
6
7.2 正弦、余弦(2)
一把梯子靠在一堵墙上,若梯子与地面的 夹角是68°,而梯子底部离墙脚1.5 m,求梯子 的长度(精确到0.1 m)(参考数据:sin68°≈ 0.9272, cos68°≈ 0.3746,tan68°≈ 2.475) .
7
7.2 正弦、余弦(2)
畅所欲言
1.对于一个角的正弦、余弦,你有了什么新 的认识?和你的同伴交流一下!
初中数学 九年级(下册)
7.2 正弦、余弦(2)
1
7.2 正弦、余弦(2)
正弦
sinA=∠A斜的边对边
=
a c
三
角 函
余弦
cosA=∠A斜的边邻边
=
b c
数
正切
tanA=∠ ∠AA的 的对 邻边 边
=
a b
2
7.2 正弦、余弦(2)
如图,在Rt△ABC 中,∠C=90°,AC=12,BC=5.
1.AB=______;
2.你还有什么收获或困惑吗?
8
9
小明在放风筝时,他的手离地面的距离AD= 1m.假设风筝线AB是一条直线段,当AB=95 m时, 测得风筝线与水平线所成角为35°,求此时风筝的高 度(精确到1m)(参考数据:sin35°≈0.5736, cos35°≈0.8192,tan35°≈0.7002).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.2正弦、余弦
课前准备:1 默写∠A 的正弦、余弦、正切
2.练习:
在Rt △ABC 中,∠B=90°,AC=2BC,则sinC=_____。
如图,在Rt △ABC 中,∠C=90°,AB=10,sinA=53,则BC=_____。
在Rt △ABC 中,∠C=90°,AB=10,sinB=5
4,则AC=_____。
如图,在Rt △ABC 中,∠B=90°,AC=15,sinC=5
3,则AB=___。
探究新知
1.例1 如图,在Rt ⊿ABC 中,∠C=90°,AC=12,BC=5.
求 sinA 、cosA 、sinB 、cosB ,的值。
思考:通过例1,你能发现在Rt ⊿ABC (∠C=90°)中,sinA 与cosB 、cosA 与sinB 的值有什么关系吗?这种关系在直角三角形中总成立吗?
结论:__________________ ______。
比较tanA 与tanB 的表达式,你有什么发现?_______________________________。
知识运用
例题1如图,在Rt △ABC 中,∠ACB=90°,CD ⊥AB,垂足为D,CD=8,AC=10
(1)求锐角A 、B 的正弦、余弦:
(2)求AB 、BD 的长
例题2 小明正在放风筝,风筝线与水平线成35°角时,小明的手离地面1m ,若把放出的风筝线看成一条线段,长95m ,求风筝此时的高度。
(精确到1m )
(参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002)
当堂反馈 1、
2.已知α为锐角: (1) sin α=
,则cos α=______,tan α=______, (2) cos α= ,则sin α=______,tan α=______, (3)tan α= ,则sin α=______,cos α=______, A B C
5 12 121212
α3.如图,在△ABC 中, ∠C=90º,D 是BC 的中点,且∠ADC=45º,AD=2,求tanB 的值.
4.小明从8m 长的笔直滑梯自上而下滑至地面,已知滑梯的倾斜角为40°,求滑梯的高度。
(精确到0.1m )(参考数据:sin40°≈0.6428,cos 40°≈0.7660,tan40°≈0.8391)
1.如图,两条宽度都是1的纸条交叉叠在一起,且它们
的夹角为α,则它们重叠部分(图中阴影部分)的面积是( )
A 、αsin 1
B 、αcos 1
C 、αsin
D 、1
2.已知:在Rt△ABC 中,∠ACB =90°,CD⊥AB,垂足为D ,CD =8cm ,AC =10cm ,求AB ,BD 的长。
3.在Rt△A BC 中,∠C=90°,已知cosA =
1312,请你求出sinA 、co sB 、tanA 、tanB 的值。
4.在△ABC 中,∠C=90°,cosB=13
12,AC =10,求△ABC 的周长和斜边AB 边上的高。
5.一把梯子靠在一堵墙上,若梯子与地面的夹角是68°,而梯子底部离墙脚1.5m ,求梯子的长度(精确到0.1m )(参考数据:sin68°≈0.9272,cos68°≈0.3746,tan68°≈2.475)
-。
