年广西普通高中学业水平数学测试卷及其答案
广西高中学业水平测试数学模拟试卷(包含答案)

高中学业水平测试数学试卷一、选择题(本大题共30个小题,每小题2分,共60分)每小题给出的四个选项中,只有一个是符合题目要求的.请将正确答案的代号填在表格中。
1.设集合A ={0,1,2,4,5,7},集合B ={1,3,6,8,9},集合C={3,7,9},则集合 (A ∩B )∪C 等于A .{0,1,2,6,9}B .{3,7,9}C .{1,3,7,9}D .{3,6,7,9} 2.下列各组函数中,表示相同函数的是 A .xx y =与1=y B .x y =与2)(x y = C .2+=x y 与242--=x x y D .||x y =与2x y =3.已知几何体的三视图如右图,则该几何体为( )A.正三棱柱B.三棱锥C.长方体D.三棱台4.已知函数y =x 2,那么它的反函数为( )A. y=x 2log (x>0)B. yx 2= C. y=2log x D. y x 2= 5.已知53cos =α,则α2cos 等于 A .257 B .257- C .2516 D .2516- 6.函数x y 2sin 4=是 A .周期为2π的奇函数 B .周期为2π的偶函数 C .周期为π的奇函数 D .周期为π的偶函数 7.抛物线y x 62=的准线方程为( )23.-=y A 3.-=y B 23.=x C 3.=x D8.在空间下列命题中正确的是A .同平行于同一个平面的两条直线平行B .垂直于同一直线的两条直线平行A B 1C 正视图侧视图俯视图C. 平行于同一直线的两条直线平行 D .与同一个平面成等角的两条直线平行 9.“两条直线a 、b 为异面直线”是“直线a 、b 不相交”的 A. 充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 10.将x y sin =的图象上所有点向左平移3π个单位长度,再把所得图象上个点的横坐标扩大到原来的2倍,则得到的图象解析式为 A .)32sin(π+=x y B .)32sin(π-=x y C .)62sin(π-=x y D .)32sin(π+=x y 11.如果直线ax+2y+1=0与直线x+y-2=0互相垂直,那么a 的值等于 A .1 B .31- C .32-D .-2 12.复数ii z 1+=(i 为虚数单位)的共轭复数是( ) A.-1-i B.-1+i C.1-i D.1+i13.在△ABC 中,已知a=4,A=45°B=60°则b 等于 A .364 B .22 C .32 D .62 14.直线043=+y x 与圆9)4()3(22=-++y x 的位置关系是 A .相切 B .相离C .相交但不过圆心D .相交且通过圆心 15.等轴双曲线122=-y x 的渐近线方程为( )x y A ±=. x y B =.xy C 21.±= x y D -=.16.已知向量a=(1,2),b=(-4,x ),且a ⊥b ,则x 的值是 A .-8 B .-2 C .2 D .817.已知正四棱锥的侧棱与底面边长相等,则侧棱与底面所成的角等于 A .30° B .45°C .60°D .70° 18.cos3000的值等于 A .21 B .-21 C .23 D .-2319.设a=0.7-0.1b=0.7-0.2 c=log 30.7则下列结果正确的是A .c <b <aB .c <a <bC .a <b <cD . b <a <c20.若偶函数)(x f y =在]1,(--∞上是增函数,则下列各式成立的是 A .)2()2(->f f B .)3()2(f f >- C .)()3(πf f < D .)3()2(f f <- 21. 当输入的值为3时,输出的结果为( ) A.8 B.20 C.2 D. 622.十进制数119化为六进制数是( ) A.315 B.513 C.35 D. 1123.已知{a n }为等差数列7,22583==+a a a 则6a =( ) A.15 B.11 C.29 D.2024.不等式的01832<++-x x 解是( ) A.x<-3或x>6 B.-3<x<6 C.x<-3 D.x>625.x,y满足约束条件 ⎪⎩⎪⎨⎧-≥≤+≤11y y x xy ,则目标函数z=2x+y 的最大值为( )A.3B.1.5C.-3D.026.从装有2个红球和2个白球的口袋内任取2个球,那么互斥的两个事件是().?A.至少有1个白球与都是白球B.至少有1个白球与至少有1个红球C.恰有1个红球与恰有1白球D.至少有1个白球与都是红球 27.若直线倾斜角是 45,且过点)2,1(,则其方程为( ) A. 01=+-y x B. 01=--y x C. 01=-+y x D.03=--y x28.某校有老师200人,男生1200人,女生1000人,现用分层抽样的方法从所有师生中抽取一个容量为n 的样本;已知从女生中抽取的人数为80人,则n=( ) A.192 B.200 C.33 D.24029.关于命题“矩形的对角线相等”的逆命题,否命题,逆否命题,下列说法正确的是( ) A.逆命题真 B.否命题真 C.逆否命题假 D.逆否命题真30.在正方体ABCD —A 1B 1C 1D 1中,直线A 1C 与平面ABCD 所成的角的正弦值为( ) A.23 B.21C.22D.33二、填空题(本大题共6个小题,每题2分,共12分)请将答案填在题中横线上 31.45与80的等比中项是32.已知一个球的半径R=3cm ,那么它的体积是 cm 333.过点P (-2,2) 和Q (-2,4)的直线的倾斜角为 34.函数)34(log 5.0-=x y 的定义域是35.已知双曲线 12222=-b y a x 离心率 45=e ,实半轴长为4,则双曲线方程为36.已知→a =4,→b =3,且→→⊥b a ,则⎪⎭⎫⎝⎛-∙⎪⎭⎫ ⎝⎛+→→→→b a b a 2=三、解答题(本大题共4个小题,共28分) 37.(本小题满分6分)已知等差数列{n a }中, 3a =9, 9a =3,求⑴1a 和公差d ;⑵前15项的和S 15。
2022年广西普通高中学业水平合格性考试数学学科试卷结构及参考样卷

附件22022年广西普通高中学业水平合格性考试 数学学科试卷结构及参考样卷一、试卷结构(一)题型结构。
题型选择题填空题解答题和证明题单项选择题多项选择题题量约26小题约2小题约4小题约3小题分值52分6分12分30分(二)试卷难度分布及比例。
难度比例容易约70%中等约20%较难约10%(第1题图)二、参考样卷广西普通高中学业水平合格性考试数 学(全卷满分100分,考试时间90分钟)注意事项:1.答题前,考生务必将姓名、座位号、考籍号填写在试卷和答题卡上。
2.考生作答时,请在答题卡上作答(答题注意事项见答题卡),在本试卷上作答无效。
一、单项选择题(本大题共26小题,每小题2分,共52分。
在每小题所列的4个备选项中,只有1个符合题目要求,错选、多选或未选均不得分。
温馨提示:请在答题卡上作答,在本试卷上作答无效。
) 1.已知集合,,则图中阴影部分所表示的集合为A .B .C .D .2.2015年以来,我国的年度GDP 数据如下表:时间(年度) 2015 2016 2017 2018 2019 2020 2021 GDP(万亿元)68.550674.4127 82.712191.928199.0865 101.5986 114.3670设时间为n ,与其对应的年度GDP 为,那么A .82.7121B .91.9281C .99.0865D .101.59863.设命题p :,,则为A .200,1x R x ∃∈+≤0 B .2,1x R x ∀∈+≤0C .200,10x R x ∃∈+<D .200,10x R x ∃∈+>4.欧拉(L.Euler ,1707—1783)是明确提出弧度制思想的瑞士数学家,他提出一个圆周角等于2π弧度.由此可知,π弧度等于 A .B .C .D .5.(5i)+(12i)+−= A .78i +B .6i −C .9D .4i6.若,则A .B .C .D .7.已知向量()12=,a ,()30=,b ,则+a b =A .()40,B .()02,C .()42,D .()32,8.某学校有高中学生2000人,其中高一年级、高二年级、高三年级的人数分别为700,660,640. 为调查学生参加“社区志愿服务”的意向,现采用分层抽样的方法按比例从中抽取一个容量为100的样本,那么应抽取高二年级学生的人数为 A .32 B .33C .64D .669.下列函数中,在上为增函数的是 A .2log y x =B .12log y x =C .2x y =D .12xy=10.边长为2的正方形以一边所在直线为轴旋转一周,所得到的几何体的体积为 A .B .C .D .11.=A .0B .1C .2D .312.若,则下列不等式正确的是A .B .C .D .13. =A .B . 1C .D .(第14题图)14. 如图,已知有向线段表示向量,则图中能表示向量的有向线段是A .B .C .D .15.函数()1()23f x x x=≤≤的最大值等于A .12B .14C .15D .1816.已知正数,x y 满足4x y +=,则xy 的最大值为A . 2B .4C . 6D .817.命题“1x =”是命题“210x −=”的 A .充分非必要条件 B .必要非充分条件C .充要条件D .既非充分也非必要条件18.2sin 30cos30°°的值为A .2B .12CD19.用二分法研究函数()321f x x x =+−的零点时,第一次计算,得()00f <,()0.50f >,第二次应计算()1f x ,则1x 等于A .1−B .0.25C .0.75D .120.高二(1)班7人宿舍中每个同学的身高(单位cm )分别为170,168,172,172,175,176,180,则这7人的第40百分位数为A .168B .170C .171D .17221.为了保护水资源,提倡节约用水,某城市对居民实行“阶梯水价”,计费方法如下表:每户每月用水量 水价 不超过的部分3元/ 超过但不超过的部分6元/ 超过的部分9元/若某户居民某月的用水量为,则此户居民本月交纳的水费(单位:元)为A .50B .54C .56D .58第26题图PABCDOM22.关于正弦函数,下列说法正确的是A .最小正周期为B .值域为C .在区间内单调递减D .在区间内单调递增23.如果幂函数=y x α的图象经过点1(2,)4,那么α等于A .2−B .2C .12−D .1224.cos52.5cos 7.5sin 52.5sin 7.5°°°°−=A.BCD .1225.已知4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为A.13B.12C.23D.3426.如图所示,P 为矩形ABCD 所在平面外一点,矩形对角线的交点为O , M 为PB 的中点,给出以下结论,其中正确的是( ) A .OM ∥平面PBC B .OM ∥平面P ACC .OM ∥平面PDAD .OM ∥平面PBA二、多项选择题(本大题共2小题,每小题满分3分,共6分。
广西壮族自治区南宁市第二中学2023届高一上数学期末学业水平测试试题含解析

(1)
, ,即
(2)
,
21、(1) ,
(2)把仓库建在距离车站4千米处才能使两项费用之和最小,最小费用是7.2万元
【解析】(1)设出 与 以及 与x的解析式,将x=9的费用代入,求得答案;
(2)列出两项费用之和的表达式,利用基本不等式求得其最小值,可得答案.
【小问1详解】
设 , ,其中 ,
11、①④
【解析】①由 ,解得 .可得函数 单调增区间;
②函数 在定义域内不具有单调性;
③由 ,即可得出函数 的最小正周期;
④利用诱导公式可得函数 ,即可得出奇偶性
【详解】解:①由 ,解得 .可知:函数 的单调增区间是 , , ,故①正确;
②函数 在定义域内不具有单调性,故②不正确;
③ ,因此函数 的最小正周期是 ,故③不正确;
16、
【解析】利用同角三角函数的基本关系,化简函数的解析式,配方利用二次函数的性质,求得y的最小值
【详解】y=sin2x﹣2cosx+2=3﹣cos2x﹣2cosx=﹣(cosx+1)2+4,
故当cosx=1时,y有最小值等于0,
故答案为0
【点睛】本题考查同角三角函数的基本关系的应用,二次函数的图象与性质,把函数配方是解题的关键
(2)由对任意 ,存在 ,使得 ,可得 ,
设 ,因为 ,所以 ,
同理可得 ,
所以
,
所以 ,可得 ,
即 ,所以 在R上单调递增,所以 ,
则 ,即 恒成立,
因为 ,所以 恒成立,
当 时, 恒成立,
因为 ,当且仅当 时等号成立,所以 ,
所以 ,解得 ,所以 ;
当 时,显然成立;
当 时, 恒成立, 没有最大值,不合题意,
2023年12月广西普通高中学业水平合格性考试数学含答案

2023年12月广西普通高中学业水平合格性考试数学(全卷满分100分,考试时间90分钟)一、单项选择题(本大题共26小题,每小题2分,共52分,在每小题所列的4个备选项中,只有1个符合题目要求,错选、多选或来选均不得分。
)1.图中阴影区域所表示的集合为A.{2}B.{1}C.{5,6}D.{1,2}2.若复数z满足z=(1+i)i(i是虚数单位),则在复平面内z对应的点在A.第二象限B.第一象限C.第四象限D.第三象限3.已知函数f(x)=1,则f(4)=xA.13B.14C.1D.124.某学校高一年级女生定制校服规格的数据如图所示,则这组数据的众数为A.160B.55C.170D.1654=5.√24A.13B.0C.2D.16.如图、以矩形ABCD的边AB所在直线为轴,其余三边旋转一周形成的面所围成的几何体是A.圆台B.圆锥C.球D.圆柱7.函数y=x(1≤x≤5)的最大值为A.3B.2C.5D.48.若实数a,b满足,则A.2a<2bB.2a>2bC.a-b<0D.a+1<b+1弧度化为角度是9.将π3A.60°B.45°C.90°D.75°10.若sinα=1,则sin(-α)=2A.-13B .-12C .1D .1511.一支羽毛球队有男运动员20人,女运动员15人,按性别进行分层.用分层随机抽样的方法从全体运动员中抽出一个容量为7的样本.如果样本按比例分配,那么女运动员应抽取的人数为A .3B .2C .6D .512.log 33=A .2B .3C .13D .113.如图,在正方形ABCD 中,AB ⃗⃗⃗⃗⃗ 与AD ⃗⃗⃗⃗⃗ 的夹角为A .90°B .30°C .180°D .120°14.已知圆柱的底面积为1,高为2,则该圆柱的体积为A .2B .1C .6D .4。
广西普通高中2021-2022学年高二6月学业水平考试数学试题 (2)

一、单选题二、多选题1.已知扇形的圆心角为,半径长为2,则该扇形的弧长为( )A.B.C .πD .2π2. 根据如下样本数据,得到回归直线方程,则( )345678-3.0-2.00.5-0.52.5 4.0A .,B .,C .,D .,3. 若,是第三象限的角,则=( )A .2B.C .﹣2D.4. 朱载堉是明太祖朱元璋的九世孙,虽然贵为藩王世子,却自幼俭朴敦本,聪颖好学,遂成为明代著名的律学家,历学家、音乐家.朱载堉对文艺的最大贡献是他创建下十二平均律,亦称“十二等程律”.十二平均律是将八度的音程按频率比例分成十二等份,也就是说,半单比例应该是,如果12音阶中第一个音的频率是,那么第二个音的频率就是,第三个单的频率就是,第四个音的频率是,……,第十二个音的频率是,第十三个音的频率是,就是.在该问题中,从第二个音到第十三个音,这十二个音的频率之和为( ).A.B.C.D.5.已知函数,将函数的图像上所有点的横坐标伸长为原来的倍,纵坐标不变,再将所得函数图像向右平移个单位,得到函数的图像,则函数的一个单调递增区间为A.B.C.D.6. 已知抛物线的焦点为为该抛物线上一点,且(点为坐标原点),则( )A .2B .3C .4D .87. 已知集合,,,则A.B.C.D.8. 已知双曲线的一条渐近线方程为,则C 的离心率为( )A.B.C.D.9. 已知函数且,则( )A .当时,恒成立B.当时,有且仅有1个零点C .当时,没有零点D .存在,使得存在三个极值点10. 在长方体中,,E 是棱的中点,过点B ,E ,的平面交棱AD 于点F ,点P 为线段上广西普通高中2021-2022学年高二6月学业水平考试数学试题 (2)广西普通高中2021-2022学年高二6月学业水平考试数学试题 (2)三、填空题四、解答题一动点,则( )A.三棱锥的体积为定值B .存在点P,使得C .直线PE与平面所成角的正切值的最大值为D.三棱锥外接球表面积的取值范围是11. 已知是圆上的两点,则下列结论中正确的是( )A.若点到直线的距离为,则B.若,则C .若,则的最大值为6D.的最小值为12. 某学生社团有男生32名,女生24名,从中随机抽取一个容量为7的样本,某次抽样结果为:抽到3名男生和4名女生,则下列说法正确的是( )A .这次抽样可能采用的是抽签法B .这次抽样不可能是按性别分层随机抽样C .这次抽样中,每个男生被抽到的概率一定小于每个女生被抽到的概率D .这次抽样中,每个男生被抽到的概率不可能等于每个女生被抽到的概率13.如图,在正四棱柱中,P 是侧棱上一点,且.设三棱锥的体积为,正四棱柱的体积为V ,则的值为________.14. 已知关于,的一组数据:根据表中这五组数据得到的线性回归直线方程为,则的值为___________.15. 如图,正方体的棱长为1,,分别是棱,的中点,过直线的平面分别与棱,交于,.设,,给出以下四个结论:①平面平面;②当且仅当时,四边形的面积最小; ③四边形的周长,是单调函数;④四棱锥的体积在上先减后增.其中正确命题的序号是__________.16. 在平面四边形中,对角线平分,,,,,且.(1)求;(2)求△的面积.17. 记的内角的对边分别为,已知,是边上的点,且满足,.(1)求;(2)若,求的外接圆的直径.18. 甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为,乙投篮命中的概率为.(1)求甲至多命中2个且乙至少命中2个的概率;(2)若规定每投篮一次命中得3分,未命中得分,求乙所得分数的概率分布和数学期望.19. 已知椭圆的焦距为,该椭圆的焦点与双曲线的焦点重合,圆与椭圆有且仅有两个公共点.(1)求椭圆的标准方程及离心率;(2)已知动直线过椭圆的左焦点,且与椭圆分别交于,两点,点的坐标为,判断是否为定值,若是,求出这个值;若不是,请说明理由.20. 某电子元件厂对一批新产品的使用寿命进行检验,并且厂家规定使用寿命在为合格品,使用寿命超过500小时为优质品,质检科抽取了一部分产品做样本,经检测统计后,绘制出了该产品使用寿命的频率分布直方图(如图):(1)根据频率分布直方图估计该厂产品为合格品或优质品的概率,并估计该批产品的平均使用寿命;(2)从这批产品中,采取随机抽样的方法每次抽取一件产品,抽取4次,若以上述频率作为概率,记随机变量为抽出的优质品的个数,列出的分布列,并求出其数学期望.21. 如图,在底面是直角梯形的四棱锥中,面.(1)求四棱锥的体积;(2)求面与面所成的二面角的正切值.。
广西壮族自治区普通高中2020—2021学年高二7月学业水平考试数学试题
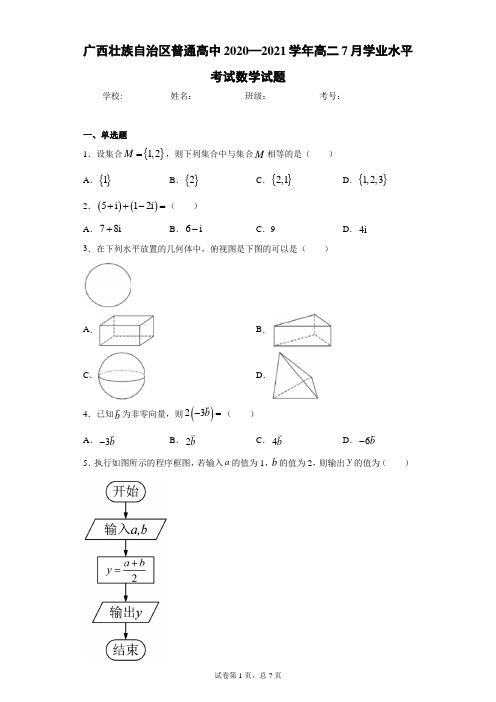
因为幂函数 在 上单调递增,所以 在 上单调递增,因此 ,
故选:A.
20.B
【分析】
直接利用诱导公式即可求解.
【详解】
解: .
故选:B.
21.D
【分析】
根据茎叶图读出相应的数据,然后根据平均数的计算公式即可求解.
【详解】
由茎叶图可知7天的销售量分别为:6,7,10,12,13,15,21,
所以国庆期间的日平均销售量是 ,
(1)求证: ;
(2)若 , ,求三棱锥 的体积.
(参考公式:锥体体积公式 ,其中 为底面面积, 为高.)
38.已知 .
(1)当 时,求 的单调区间;
(2)讨论函数 的零点的个数情况.
参考答案
1.C
【分析】
根据集合相等的定义判断选项.
【详解】
两个集合的元素相同,两个集合相等,集合 中有2个元素,分别是1和2,所以与集合 相等的集合是 .
解: .
故选:C.
12.C
【分析】
由向量的坐标运算可直接求出结果.
【详解】
因为 ,所以 ,
故选:C.
13.C
【分析】
根据圆心坐标和半径直接写出圆的标准方程.
【详解】
解:因为圆的圆心在原点半径为3,
所以圆的方程是 .
故选:C.
14.A
【分析】
直角根据向量数量积的定义计算即可.
【详解】
由题意知, .
故选:A
故选:C
2.B
【分析】
直接利用复数的加法运算即可求解.
【详解】
解: .
故选:B.
3.C
【分析】
根据选项中几何体的特征逐项分析即可求出结果.
广西壮族自治区普通高中2018-2019学年高二6月学业水平考试数学试题(含答案解析)
广西壮族自治区普通高中2018-2019学年高二6月学业水平考试数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知集合{1,2},{2,3}A B ==,则图中阴影部分所表示的集合为( ).A .{2}B .{0}C .{1,2}D .{2,3}2.已知i 是虚数单位,则(1i)(22i)+++=( ). A .1i +B .22i +C .33i +D .56i +3.如图是一个几何体的三视图,则该几何体是( ).A .长方体B .圆锥C .棱台D .棱锥4.设,a b 为非零向量,则3(2)a b +=( ). A .63a b +B .6aC .3bD .43a b +5.执行如图所示的程序框图,当输入x 的值为1时,则输出y 的值为( )6.欧拉(L.Euler,17071783)-是明确提出弧度制思想的瑞土数学家,他提出一个圆周角等于2π弧度.由此可知,π弧度等于( ).A .360B .180C .60D .307.已知向量()()1,2,3,0a b ==,则a b +=( ). A .(4,0)B .(0,2)C .(4,2)D .(3,2)8.椭圆22221(0)x y a b a b+=>>的左焦点1F 的坐标为(1,0)-,则右焦点2F 的坐标是( ).A .(1,2)B .(2,1)-C .(2,0)-D .(1,0)9.某校为了解高二年级教学情况,用系统抽样法从编号为000,001,…,499的500名学生中抽取一个容量为50的样本.已知编号004,014,024在样本中,则下列编号在样本中的是( ). A .010B .020C .034D .04310.体操中有“后空翻转体720度”的动作,其中“转体720度”是转体( ). A .1周B .2周C .3周D .4周11.在平面直角坐标系中,抛物线24y x =的大致图象是( ).A .B .C .D .12.已知圆柱1OO 及其侧面展开图如图所示,则该圆柱的侧面积为( ).A .6πB .7πC .8πD .9π13.2sin30cos30的值为( ).A .2B C D .1214.2log 8=( ). A .0B .1C .2D .315.偶函数的图象关于y 轴对称,下列图象中,可以表示偶函数的是( ).A .B .C .D .16.如图,在长方体1111ABCD A BC D -中,下列结论正确的是( ).A .11//AA CCB .1 AA 与1 CC 异面C .1//AA BCD .1 AA 与1CC 相交17.已知直线y ax =与直线23y x =+平行,则a 的值为( ). A .-2B .12C .1D .218=( ). A .1B .2C .4D .819.已知函数()1[]226f x x x ∈-=(,),则f (x )的最大值为( ).A .13B .12C .1D .220.书架上有4本数学书,3本物理书和1本英语书,从中任取1本,则取到的是物理书的概率为( ). A .78B .58C .38D .1221.如图,在三棱锥A BCD -中,,E F 分别是,AB AD 的中点,则下列结论正确的是( ).A . EF ⊥平面BCDB .//EF 平面BCDC .//EF 平面ACDD . EF ⊂平面BCD22.函数sin ,y x x =∈R 的最大值为( ). A .-3 B .0C .1D .323.若1sin 3α=,则sin()α-=( ). A .-1B .13-C .0D .124.已知直线12:0,:20l x y l x y -=+-=,则1 l 与2l 的交点坐标是( ). A .(1,1)B .(1,3)C .(2,6)D .(2,2)-25.不等式2430x x -+<的解集是( ).A .{13}x x <<∣B .{0}x x <∣C .{5}x x <∣D .{7}xx >∣ 26. 3x =“”是||3x =“”的( ).A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件27.在ABC 中,角,,A B C 的对边分别为,,a b c ,若11,2,cos 2a c B ===,则b =( ).A .B .C .2D 28.已知向量(2,1),(3,0)a b =-=,则⋅=a b ( ). A .4B .5C .6D .729.假设一个蜂巢里只有1只蜜蜂,第1天它飞出去找回了2个伙伴:第2天,3只蜜蜂飞出去,各自找回了2个伙伴……如果这个找伙伴的过程继续下去,则到第4天所有蜜蜂都归巢后,蜂巢中全部蜜蜂的只数是( ).A .1B .3C .9D .8130.函数2()3f x x x =-的零点个数为( ). A .0 B .1C .2D .3二、填空题31.已知正整数按如图的规律排列,则位于第1行第5列的数是______________.32.已知函数()3xf x =,则()1f =__________.33.已知实数,x y 满足0,0,1x y x y ⎧⎪⎨⎪+⎩则z x y =+的最大值是_______________.34.已知直线1x y +=与圆224x y +=相交于A,B 两点,则弦AB 的长为________.三、解答题35.为了庆祝建国70周年,某市计划国庆期间在市民广场用不同颜色的鮮花摆放一个“塔状”花坛.花坛的每一层呈圆环形,最上面一层摆20盆鲜花,由上往下,从第二层起每一层都比上一层多摆20盆,共摆放7层.问:摆放一个这样的花坛共需要多少盆鲜花?36.为了促进教育均衡发展,让每一个孩子享受公平教育,教育行政部门鼓励优秀教师到教育资源薄弱学校支教.已知甲、乙两所学校报名支教的教师情况如下表:现从甲、乙两校报名支教的教师中各任选1名教师,求选取的2名教师性别相同的概率. 37.如图,AB 是O 的直径,E 是圆周上异于,A B 的动点,矩形ABCD 的边CB 垂直于⊙O 所在的平面,已知2,1AB AD ==.(1)求证:AE ⊥平面EBC ;(2)求几何体ABCDE 的体积的最大值.(参考公式:锥体体积公式13V Sh =,其中S 为底面面积,h 为高.)38.已知函数2()ln 2f x x x a x =+--(1)若曲线()y f x =在点()2,(2)f 处的切线与直线y x =-垂直,求该切线的方程; (2)若1x >时,()0f x >恒成立,求实数a 的取值范围.参考答案1.A【分析】根据图形可得,阴影部分表示的集合为A B,求出即可.【详解】根据图形可得,阴影部分表示的集合为A B,A B==,{}2{1,2},{2,3}∴=.A B故选:A.2.B【分析】直接利用复数加法的运算法则求解.【详解】+++=+.(1i)(22i)33i故选:B.3.A【分析】正视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【详解】由于正视图和左视图为长方形可得此几何体为柱体,由俯视图为长方形可得为长方体.故选:A.4.A【分析】利用平面向量的数乘运算即可求出结果.【详解】+=+a b a b3(2)63故答案为:A.5.B【分析】根据程序框图计算即可求出结果. 【详解】输入1x =,12y x =+=,输出2y =, 故选:B. 6.B 【分析】由2=360π︒推导即可. 【详解】 由题意知, 2=360π︒,所以=180π︒. 故选:B 7.C 【分析】结合向量加法的坐标表示即可. 【详解】 由题意知,(12)(30)a b ==,,,, 所以(42)a b +=,, 故选:C 8.D 【分析】根据椭圆的几何性质可得答案. 【详解】因为椭圆22221(0)x y a b a b+=>>的左焦点1F 的坐标为(1,0)-,所以右焦点2F 的坐标是(1,0),故选:D. 9.C 【分析】根据系统抽样的抽样间隔,逐项分析即可.【详解】由题意知抽样间隔为5001050=,所以样本中的编号相差为10的倍数,结合选项可知只有C 符合, 故选:C. 10.B 【分析】根据转体动作名称的实际意义得解. 【详解】在现实中,“转体720度”是转体2周, 故选:B. 11.A 【分析】根据各函数的图形特征判断即可得出结论. 【详解】选项A 为抛物线的图像,为正确答案.选项B 表示圆心在原点的圆的图像,选项B 错误; 选项C 表示直线,故选项C 错误;选项D 表示平行于x 轴的一条直线,选项D 错误 故选:A 12.C 【分析】根据圆柱的侧面展开图的形状和矩形的面积公式计算可得选项. 【详解】由图可知圆柱的侧面展开图是一个矩形,所以该圆柱的侧面积为248ππ⨯=, 故选:C. 13.B 【分析】由正弦的二倍角公式可得选项. 【详解】32sin 30cos30sin 602==, 故选:B. 14.D 【分析】根据对数的运算性质可得选项. 【详解】因为322log 8log 23==,所以2log 83=,故选:D. 15.A 【分析】根据图像是否关于y 轴对称判断. 【详解】A 的图像关于y 轴对称,故A 符合题意.BCD 的图像都不关于y 轴对称,故BCD 均不符合题意. 故选:A. 16.A 【分析】依据长方体中各棱的空间位置关系,逐个验证得出答案即可. 【详解】根据长方体中各直线的位置关系可知:11//AA CC ,AA 1和 BC 为异面直线 所以选项B ,C ,D 错误,选项A 正确. 故选:A 17.D 【分析】直接根据斜率相等,即可求得. 【详解】因为直线y ax =与直线23y x =+平行, 所以斜率相等,即a 的值为2. 故选:D18.B【分析】结合根式与指数形式的互化即可直接得到结果.【详解】2=,故选:B.19.D【分析】先判断()21f x x -=在[]2,6上的单调性,即可求出最大值. 【详解】 因为2y x=在()0+∞,上单减,所以21y x -=在()1+∞,上单减, 即21y x -=在[]2,6上单减, 所以f (x )的最大值为()22=221f -=. 故选:D20.C【分析】 直接算出总事件数和取到一本物理书的事件数,即可得出结果.【详解】由题意知,总的事件数为8,3本物理书取到1本的事件为13=3C , 所以任取一本,取到物理书的概率为38故选:C21.B【分析】根据线面平行的判定可得选项.【详解】因为,E F 分别是,AB AD 的中点,所以//EF BD ,又EF ⊄平面BCD ,BD ⊂平面BCD ,所以//EF 平面BCD ,故选:B.22.C【分析】结合三角函数sin y x =的值域即可.【详解】由题意知,sin [11]y x =∈-,, 所以sin y x =的最大值为1.故选:C23.B【分析】根据诱导公式可得选项.【详解】 因为1sin 3α=,所以1sin()sin 3αα-=-=-, 故选:B.24.A【分析】联立两直线方程,解方程即可得出交点的坐标.【详解】由题意知, 01201x y x x y y -==⎧⎧⇒⎨⎨+-==⎩⎩, 所以两直线的交点为(11),, 故选:A25.A【分析】结合一元二次不等式(不含参)的解法即可【详解】2430(1)(3)0x x x x -+<⇒--< 所以原不等式的解集为{}13x x <<,故选:A26.A【分析】根据充分条件,必要条件的定义即可解出.【详解】因为3x =⇒3x =,但是33x x =⇒=±,所以“3x =”是“3x =”的充分不必要条件. 故选:A .27.D【分析】结合余弦定理计算即可.【详解】由余弦定理,可得2222cos 1423b a c ac B =+-=+-=,又0b >,所以b 故选:D28.C【分析】由向量的数量积的坐标运算可得选项.【详解】因为向量(2,1),(3,0)a b =-=,所以()23+106a b ⋅=⨯-⨯=,故选:C.29.D【分析】先由前几天结束时,蜂巢中的蜜蜂数量观察出其组成了首项为3,公比为3的等比数列,求出通项公式,把4直接代入即可.由题意知,第一天所有蜜蜂归巢后,蜂巢中一共有1+2=3只蜜蜂,第二天所有蜜蜂归巢后,蜂巢中一共有339⨯=只蜜蜂,第三天所有蜜蜂归巢后,蜂巢中一共有39=27⨯只蜜蜂,第n 天所有蜜蜂归巢后,蜂巢中一共有133=3n n -⨯只蜜蜂,所以归巢后的蜜蜂数列组成了首项为3,公比为3的等比数列,所以其通项公式为:3n ,所以,第四天共有4381=只蜜蜂.故选:D30.C【分析】令()0f x =,解方程230x x -=,求得方程根的个数即为零点的个数.【详解】令()0f x =,则230x x -=,解得0x =或3,所以函数2()3f x x x =-有两个零点,故选:C.31.17【分析】根据所给图形找到规律即可求出结果.【详解】由图可知第一列的数是行数的平方,所以第五行的第一个数是2525=,然后沿行向右逐次减1,到第n 行第n 列的的位置沿列向上逐次减1,直到第1行结束,所以第5行5列的数是21,进而可得第1行第5列的数为17,故答案为:17.32.3【分析】根据指数幂的运算,代入即可求解.【详解】由题意,函数()3x f x =,可得()1133f ==.故答案为:3.33.1【分析】根据约束条件,画出可行域,根据目标函数的几何意义,利用数形结合的方法,即可得出结果.【详解】由约束条件0,0,1x y x y ⎧⎪⎨⎪+⎩画出对应的平面区域如下,因为目标函数z x y =+可化为+y x z =-,所以z 表示直线+y x z =-在y 轴截距,由图象可得,当直线+y x z =-与直线+1y x =-重合时,z 最大,因此max 1z =.故答案为:1.34【分析】 表示出圆的圆心与半径,然后求出圆心到直线的距离,进而根据2222AB d r ⎛⎫+= ⎪⎝⎭,即可求出结果.【详解】圆224x y +=的圆心为()0,0,半径2r, 则圆心()0,0到直线的距离d =因为2222AB d r ⎛⎫+= ⎪⎝⎭,所以2AB =35.560【分析】由题得每一层的花盆数组成一个首项为20,公差为20的等差数列,利用等差数列的求和公式即得解.【详解】由题得每一层的花盆数组成一个首项为20,公差为20的等差数列,由于该数列共有7个数, 所以摆放一个这样的花坛所需的鲜花盆数为76720+20=5602⨯⨯⨯. 所以摆放一个这样的花坛共需要560盆鲜花.36.12 【分析】先求出都是男性、都是女性的概率,把两个概率加起来即可.【详解】由题意知,P (都是男性)=211=323⨯, P (都是女性)=111=326⨯, 所以P (性别相同)=P (都是男性)+P (都是女性)=111=362+. 37.(1)证明见解析;(2)23【分析】(1)由题意可证得AE BE ⊥和CB AE ⊥,结合BE BC B BE =⊂,平面EBC 即可;(2) 当点E 到平面ABCD 的距离最大时,多面体ABCDE 的体积最大,利用三棱锥的体积公式计算即可.【详解】(1)因为AB 是直径,E 是圆上一点,所以AE BE ⊥,因为CB ⊥平面ABE ,所以CB AE ⊥,又BEBC B BE =⊂,平面EBC ,所以AE ⊥平面EBC .(2)当点E 到平面ABCD 的距离最大时,多面体ABCDE 的体积最大,点E 到平面ABCD 的距离max 1d r ==,因为CB ⊥平面ABE ,BC ⊂平面ABCD ,所以平面ABCD ⊥平面ABE , 所以max max 112121333ABCD V d S ==⨯⨯⨯=矩形. 38.(1)28ln 20x y -+-=;(2)(],3-∞.【分析】(1)根据导数的几何意义已知两直线垂直斜率的关系得到(2)22112a f '=⨯+-=,求得8a =,进而得到2(2)228ln 2248ln 2f =+--=-,然后根据点斜式即可写出切线方程;(2)研究函数2()ln 2f x x x a x =+--的单调性,使得1x >时,函数()y f x =的最小值恒大于0即可求出结果.【详解】(1)因为2()ln 2f x x x a x =+--,所以()()210a f x x x x'=+-> 因为曲线()y f x =在点()2,(2)f 处的切线与直线y x =-垂直。
2020年广西高中数学学业水平考试模拟试卷(二)附答案
广西普通高中业水平考试模拟卷(二)数 学(全卷满分100分,考试时间120分钟)一、单项选择题:本大题共30小题,每小题2分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}25A x x =≤<,{}3782B x x x =-≥-,则()R C A B U ( )A.∅B.{}2x x <C.{}5x x ≥D.{}25x x ≤< 2.若复数()()211z x x i =-+-为实数,则实数x 的值为( )A.1-B.0C.1D.1-或1 3.在x 轴上的截距为2.倾斜角为135︒的直线方程为( )A.2y x =-+B.2y x =--C.2y x =+D. 2y x =-4.已向量()1,0a =r,12b ⎛=- ⎝⎭r ,a r 与b r 的夹角为( )A.30︒B.60︒C.120︒D.150︒ 5.若函数()()21x a f x a R x +=∈+是奇函数,则a 的值为( ) A.1 B.0C.1-D.1± 6.有一个几何体的三视图如下图所示,这个几何体是一个( )A.棱台B.棱锥C.棱柱D.圆柱7.某城市有大型、中型与小型超市共1500个,它们的个数之比为1:5:9.为调查超市每日的零销售额情况,需通过分层抽样抽取30个超市进行调查,那么抽取的小型超市个数为( )A.5B.9C.18D.208.某程序框阳如图所示,若分别输入下四个函数:()1f x x=,()2f x x =,()x f x e =,()sin f x x =,可以输出的函数是( )A.()2f x x =B.()1f x x =C.()x f x e =D.()sin f x x = 9.13tan 3π的值是( )A. B.10.函数y = )A.B. C. D.11.已知直线l 点)P,圆C :224x y +=,则直线l 圆C 的位置关系是( ) A.相交 B.相切 C.相交或相切 D.相离 12.要得到余弦曲线cos y x =,只需将正弦曲线sin y x =向左平移( ) A.2π个单位 B.3π个单位 C.4π单位 D. 6π单位 13.若2510a b ==,则11a b +=( ) A.a b + B.1- C.1 D.214.现有下列四个命题:①若直线11y k x b =+与直线22y k x b =+垂直,则121k k =-;②若向量a ,b 满足0a b ⋅=r r ,则0a =或0b =;③若实数a 、b 、c 满足2b ac =,则a 、b 、 c 成等比数列.其中真命题的个数是( )A.0B.1C.2D.315.若等差数列{}n a 的第一项为1,公差为2,则第四项为( )A.1B.3C.5D.716.下列函数是奇函数的是( )A.2log y x =B.2x y =C.cos y x =D.1y x -=17.已知平面向量()1,a x =r ,(),1b y =r .若a b ⊥r r ,则实数x ,y 一定满足( )A.10xy -=B.10xy +=C.0x y -=D.0x y +=18.在ABC △中,若()()3a b c b c a bc +++-=,则A =( )A.30︒B.60°C.135°D.150︒19焦点在x 轴上、焦距等于4,离心率等于2的椭圆的标准方程是( ) A.2211612x y += B.2211216x y += C.22148x y += D.22184x y +=20.函数y = )A.()0,+∞B.[)0,+∞C.()1,+∞D.[)1,+∞21.设点M 是Z 轴上一点,且点M 到A ()1,0,2与点B ()1,3,1-的距离相等,则点M 的坐标是() A.()3,3,0-- B.()0,0,3- C.()0,3,3-- D.()0,0,322.抽查10件产品,设事件A :至少有两件次品,则A 的对立事件为( )A.至多两件次品B.至多一件次品C.至多两件正品D.至少两件正品23.直线3y x =+在y 轴上的截距是( )A.3B.3-C.1D.1-24.不等式组1110x y x y ≤⎧⎪≤⎨⎪+-≥⎩表示的平面区域面积是( ) A 12 B.14 C.1 D.225.已知一等比数列的前三项依次为x ,22x +,33x +,那么1132-是此数列的第几项( )A.2B.4C.6D.826.计算:sin 225︒的值为( )A.2B.2-C.2-D.12- 27.已知0a >,0b >满足1a b +=,则19a b +的最小值为( ) A.12B.16C.20D.25 28.已知()32f x x x =+,则()()f a f a +-的值是( )A.0B.1-C.1D.229.下列命题中正确的是( )A.若直线//m 平面α,直线n α⊂,则//m nB.若直线m ⊥平面α,直线n α⊂,则m n ⊥C.若平面//α平面β,直线m α⊂,直线n β⊂,则//m nD.若平面α⊥平面β,直线m α⊂,则m β⊥30.下列函效中,既是奇函数又在()0,+∞上单调递减的函数是( ) A.1y x = B.cos y x = C.23y x =-+ D.xy e = 二、填空题:本大題共6小题,每小题2分,共12分.31.设函数[]243,1,4y x x x =-+∈-,则()f x 的最小值________. 32.等比数列{}n a 前n 项的和为21n -,则数列{}2n a 前n 项的和为_______________. 33命题p :0x R ∃∈,200220x x --=,则命题p 的否定是_____________. 34.若向量a r 、b r 满足1a =r ,2b =r 且a r 与b r 的夹角为3π,则()a ab ⋅+=r r r __________. 三、解答题:本大题共4小题,共28分,解答应写出文字说明、证明过程或演算步驟.35.(本小题满分6分)已知函数()f x 是定义在R 上的偶函数,且在区间[)0,+∞单调递增.若实数a 满足()212log log ,2(1)f a f a f ⎛⎫+≤ ⎪⎝⎭,求a 的取值范围.36.(本小题满分6分)如图,已知正方体1111ABCD A B C D -的棱长为1,求四棱锥11A BB D D -的体积.37.(本小题满分8分) 设2()sin cos cos 4f x x x x π⎛⎫=-+⎪⎝⎭ (Ⅰ)求()f x 的单调区间;(Ⅱ)在锐角ABC △中,角A ,B ,C ,的对边分别为a ,b ,c ,若02A f ⎛⎫=⎪⎝⎭,a =1,求ABC △面积的最大值.38.(本小满分8分)某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r 米,高为h 米,体积为V 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000π元(π为圆周率).(Ⅰ)将V 表示成r 的函数()V r ,并求该函数的定义域;(Ⅱ)讨论函数()V r 的单调性,并确定r 和h 为何值时该蓄水池的体积最大.广西普通高中学业水平考试数学模拟卷(二)参考答案一、1.C 2.C 3.A 4.C 5.B 6.B 7.C 8.D 9.D 10.A11.C 12.A 13.C 14.B l5.D 16.D 17.D 18.B 19.D 20.B21.B 22.B 23.A 24.A 25.B 26.B 27.B 28.A 29.B 30.A二、31. 1- 32.413n - 33.x R ∀∈,2220x x --≠ 34. 2三、35.解:因为函数()f x 是定义在R 上的偶函数,且122log log a a =-,所以,()()()()()222122log log log log 2log 21f a f a f a f a f a f ⎛⎫+=+-=≤ ⎪⎝⎭,因为函数在区间[)0,+∞单调递增,所以()()2log 1f a f ≤,即2log 1a ≤,所以21log 1a -≤≤,解得122a ≤≤,即a 的取值范围是1,22⎡⎤⎢⎥⎣⎦. 36.解:连接11A C ,交11B D 于点E ,则111A E B D ⊥,11A E BB ⊥,则1A E ⊥平面11BB D D ,所以1A E 为四棱锥11A BB D D -的高,且12A E =,矩形11BB D D1,故11111323A BB D D V -=⨯=. 37.解(Ⅰ)由题意()1cos 2111112sin 2sin 2sin 2sin 2222222x f x x x x x π⎛⎫++ ⎪⎝⎭=-=-+=-.由()22222k x k k Z ππππ-+≤≤+∈, 可得()44k x k k Z ππππ-+≤≤+∈; 由()322222k x k k Z ππππ+≤≤+∈,得()344k x k k Z ππππ+≤≤+∈; 所以()f x 的单调递增区间是(),44k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦;单调递减区间是()3,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦. (Ⅱ)∵1sin 022A f A ⎛⎫=-= ⎪⎝⎭,∴1sin 2A =,由题意A是锐角,所以cos 2A =.由余弦定理:2222cos a b c bc A =+-,可得2212b c bc +=+≥,∴2bc ≤=b c =时成立.2sin 4bc A ≤.∴ABC △面积最大值为24+. 38.解(Ⅰ)因为蓄水池侧面积的总成本为1002200rh rh ππ⋅=元,底面的总成本为2160r π元,所以蓄水池的总成本为()2200160rh r ππ+元.又题意据220016012000rh r πππ+=,所以()2130045h r r =-,从而()()2330045V r r h r r ππ==-.因0r >,又由0h >可得r <()V r 的定义域为(.。
年广西普通高中学业水平数学测试卷及其答案
广西普通高中学业水平测试数学卷(5)一、单项选择题:本大题共30小题,每小题2分,共60分。
在每小题给出的四个选项中,有且只有一项是符合题目要求的。
1.已知, B=,则下列关系中正确的是( A )A .AB .BC .A D.B2.李明离开家不久,发现自已的作业本忘记在家里了,于是返回家里找到作业本后再上学。
下面的图形中与这件事吻合得最好的是( D )离开家的距离离开家的距离离开家的距离离开家的距离A B C D3.函数的单调递增区间是( C )A.R B. C .(0, D.(-1,1)4.下列算式正确的是( C )A .2B . 2 C. 2 D.25.函数的定义域是( A )A.(2,+ B .(-2,+ C . D.6 .函数在区间上的最大值是( D )A -1B 0C 1D 37 .已知棱长为1,各面均为等边三角形的三棱锥A-BCD,则它的表面积为( C )A B C D8 .空间四边形ABCD中, E、F、G、H分别是AB、BC、CD、DA的中点,若AC=BD,则四边形EFGH一定是(D )A 正方形B 矩形C 梯形 D菱形9. 已知是i虚数单位,复数z=1+2i , z=3+4i , 那么z+z=(B )A 5+5iB 4+6iC 10iD 1010.已知直线经过点P(0,0) 、Q(-1,,则它的倾斜角是( C )A 60B 90C 120 D15011.右图是一个几何体的三视图,它对应的几何体的名称是( B )A 球B 圆柱C 圆锥 D圆台12. 已知点A(a , 0)与B(0 , 4)间的距离是5, 则a的值为( C )A 2B -2C 3或-3D 1或-113 .直线在轴上的截距是( A )A 1B -1C D14.已知直线和圆,则直线和圆的位置关系为( A )A 相交B 相切C 相离 D不能确定15. 运行如右程序框图,若输入,则输出的结果是(C )A 3B 0C -3D -616. 高中某班有男生同学36人,女同学24人,用分层抽样的方法从全班同学中抽取一个容量为10的样本,则应从女同学中抽取的人数为( A )A 4B 6C 8 D1017 .已知角的终边经过点P(3 ,-4) , 那么(B )A B C D18 .( D )A B C D19.函数的最小正周期是( C )A B C 4 D.620.已知向量、(O、A、B三点不共线),若2=,则点M 是(A )A .AB的中点 B.AC的中点 C.BC的中点 D.的重心21.已知向量=(3 ,2),,1),则的坐标是(B )A (7 , 5)B (11 ,5)C (7 , 7) D(11,7)22.由三角形数组成的数列1,3,6,10,中第7项是( B )A .21B 28C 36 D5623.已知向量,,若与平行,则实数等于( A )A B C -2 D 224.已知点在第三象限,则角的终边落在( B )A 第一象限B 第二象限C 第三象限 D第四象限25.在等差数列中,公差,那么( C )A. 15B. 17 C 19 D.2126.命题“若都是偶数,则是偶数”的逆否命题是( D )A 若都不是偶数,则不是偶数B 若不都是偶数,则不是偶数C若不是偶数,则都不是偶数 D若不是偶数,则不都是偶数27.如图,在底面ABCD是正方形的四棱锥P-ABCD中,面PAB面ABCD,PAB 为等边三角形,那么PC与平面ABCD所成的角的正切值为( B )A B C D28.如右茎叶图记录了某学习小组全部10名学生在一次数学测验中的成绩(单位:分),则该学习小组在这次数学测验中的平均分是( C )A 84B 84.4C 85 D85.429.双曲线的焦点坐标是( D )A (0 ,,(0,B ,C (5,0),(-5,0)D (0, 5), (0,-5)30.已知函数在上具有单调性,则的取值范围是( C )A . B. C. D.二、填空题:本大题共6小题,每小题2分,共12分。
广西普通高中2021-2022学年高二6月学业水平考试数学试题(1)
一、单选题二、多选题1. 已知命题p :,,则为( )A .,B .,C .,D .,2. 已知复数满足(为虚数单位),则( )A.B.C.D.3. 某校高三(1)班(45人)和高三(2)班(30人)进行比赛,按照分层抽样的方法从两个班共抽取10名同学,相关统计情况如下:高三(1)班答对题目的平均数为,方差为;高三(2)班答对题目的平均数为,方差为,则这10人答对题目的方差为( )A.B.C.D.4. 已知关于的方程有三个不等的实数根,则实数的取值范围是( )A.B.C.D.5. 垃圾分类是指按一定规定或标准将垃圾分类储存、投放和搬运,从而转变成公共资源的一系列活动,做好垃圾分类是每一位公民应尽的义务.已知某种垃圾的分解率与时间(月)近似地满足关系(其中a ,b ,为正常数),经过6个月,这种垃圾的分解率为,经过12个月,这种垃圾的分解率为,那么这种垃圾完全分解大约需要经过( )个月(参考数据:)A .20B .28C .32D .406. 如图,在正方体ABCD -A 1B 1C 1D 1中,直线BD 1与直线AC 所成的角是()A .30°B .45°C .60°D .90°7. 设为正项等比数列的前项和,若,则的最小值为( )A .2B .3C .4D .68. 设,则( )A.B.C.D.9.已知四面体中,,,,直线AB 与CD 所成角为,则下列说法正确的是( )A .AD的取值可能为B .AD 与BC所成角余弦值一定为C .四面体ABCD体积一定为D .四面体ABCD的外接球的半径可能为10.已知函数的部分图像如图所示,则()广西普通高中2021-2022学年高二6月学业水平考试数学试题(1)广西普通高中2021-2022学年高二6月学业水平考试数学试题(1)三、填空题四、解答题A.B.C .在上单调递增D .若为偶函数,则11. 已知分别为双曲线的左、右焦点,过的直线交于,(点在点的上方)两点,且,则的离心率可能为( )A.B.C.D.12.透明塑料制成的正方体密闭容器的体积为注入体积为的液体.如图,将容器下底面的顶点置于地面上,再将容器倾斜.随着倾斜度的不同,则下列说法正确的是()A .液面始终与地面平行B.时,液面始终是平行四边形C .当时,有液体的部分可呈正三棱锥D .当液面与正方体的对角线垂直时,液面面积最大值为13. 设是实数,且是实数,则_______.14. 盒中有四张形状与大小均相同的卡片,分别写着数字1,2,3,4.每次不放回地从盒中随机取出一张卡片,直到取出的所有卡片上数字之积大于10为止.设此时取出的所有卡片上数字之和为,则______,______.15. 正方体的棱长为2.动点P在对角线上.过点P 作垂直于的平面.记平面截正方体得到的截面多边形(含三角形)的周长为y =f (x ),设BP =x ,.下列说法中,正确的编号为 _____.①截面多边形可能为四边形;②函数f (x )的图象关于x =对称;③当x=时,三棱锥P ﹣ABC 的外接球的表面积为9π.16.已知抛物线的焦点为,点在抛物线上,点的纵坐标为8,且.(1)求抛物线的方程;(2)若点是抛物线准线上的任意一点,过点作直线与抛物线相切于点,证明:.17. 如图,为圆柱的母线,是底面圆的直径,分别是的中点,面.(1)证明:面;(2)求四棱锥与圆柱的体积比.18. 设等比数列的前项和为,且,.(1)求的通项公式;(2)若,求数列的前项和.19. 设函数,(e为自然对数的底数)(1)若函数有两个极值点,求a的取值范围;(2)设函数,其中为的导函数,求证:的极小值不大于1.20. 在中,角A,B,C的对边分别为a,b,c,已知,,的面积为24.(1)求sin B;(2)求a的长;(3)求的值.21. 如图,在三棱锥中,,,,.(Ⅰ)求证:;(Ⅱ)求二面角的大小.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广西普通高中学业水平测试数学卷(5)
一、单项选择题:本大题共30小题,每小题2分,共60分。
在每小题
给出的四个选项中,有且只有一项是符合题目要求的。
1.已知, B=,则下列关系中正确的是( A )
A .A
B .B
C .A D.B
2.李明离开家不久,发现自已的作业本忘记在家里了,于是返回家里找到作业本后再上学。
下面的图形中与这件事吻合得最好的是( D ) 离开家的距离离开家的距离离开家的距离离开家的距离
A B C D
3.函数的单调递增区间是( C )
A.R B. C .(0, D.(-1,1)
4.下列算式正确的是( C )
A .2
B . 2 C. 2 D.2
5.函数的定义域是( A )
A.(2,+ B .(-2,+ C . D.
6 .函数在区间上的最大值是( D )
A -1
B 0
C 1
D 3
7 .已知棱长为1,各面均为等边三角形的三棱锥A-BCD,则它的表面积为( C )
A B C D
8 .空间四边形ABCD中, E、F、G、H分别是AB、BC、CD、DA的中点,若AC=BD,则四边形EFGH一定是(D )
A 正方形
B 矩形
C 梯形D菱形
9. 已知是i虚数单位,复数z=1+2i , z=3+4i , 那么z+z=(B )
A 5+5i
B 4+6i
C 10i
D 10
10.已知直线经过点P(0,0) 、Q(-1,,则它的倾斜角是( C )
A 60
B 90
C 120D150
11.右图是一个几何体的三视图,它对应的几何体的名称是( B )
A 球
B 圆柱
C 圆锥D圆台
12. 已知点A(a , 0)与B(0 , 4)间的距离是5, 则a的值为( C )
A 2
B -2
C 3或-3
D 1或-1
13 .直线在轴上的截距是( A )
A 1
B -1
C D
14.已知直线和圆,则直线和圆的位置关系为( A )
A 相交
B 相切
C 相离D不能确定
15. 运行如右程序框图,若输入,则输出的结果是(C )
A 3
B 0
C -3
D -6
16. 高中某班有男生同学36人,女同学24人,用分层抽样的方法从
全班同学中抽取一个容量为10的样本,则应从女同学中抽取的人数为( A )
A 4
B 6
C 8 D10
17 .已知角的终边经过点P(3 ,-4) , 那么(B )
A B C D
18 .( D )
A B C D
19.函数的最小正周期是( C )
A B C 4 D.6
20.已知向量、(O、A、B三点不共线),若2=,则点M是(A )
A .AB的中点 B.AC的中点 C.BC的中点 D.的重心21.已知向量=(3 ,2),,1),则的坐标是(
B )
A (7 , 5)
B (11 ,5)
C (7 , 7)D(11,7)22.由三角形数组成的数列1,3,6,10,中第7项是( B )
A .21
B 28
C 36 D56
23.已知向量,,若与平行,则实数等于
( A )
A B C -2 D 2
24.已知点在第三象限,则角的终边落在( B )
A 第一象限
B 第二象限
C 第三象限D第四象限25.在等差数列中,公差,那么( C )
A. 15
B. 17 C 19 D.21
26.命题“若都是偶数,则是偶数”的逆否命题是( D )
A 若都不是偶数,则不是偶数
B 若不都是偶数,则不是偶数
C若不是偶数,则都不是偶数D若不是偶数,则不都是偶数
27.如图,在底面ABCD是正方形的四棱锥P-ABCD中,面PAB面ABCD,PAB为等边三角形,那么PC与平面ABCD所成的角的正切值为( B )
A B C D
28.如右茎叶图记录了某学习小组全部10名学生在一次数学
测验中的成绩(单位:分),则该学习小组在这次数学测验中
的平均分是( C )
A 84
B 84.4
C 85 D85.4
29.双曲线的焦点坐标是( D )
A (0 ,,(0,
B ,
C (5,0),(-5,0)
D (0, 5), (0,-5)
30.已知函数在上具有单调性,则的取值范围是( C )
A . B. C. D.
二、填空题:本大题共6小题,每小题2分,共12分。
31.若向如图所示正方形区域内随机撒一粒黄豆,则它落到阴影部分的概率为_____________
32. 等于_____1/2__________
33.函数在点(1,0)处的切线方程为____y=x-1_____
34.不等式的解集是_________________
35.函数的零点个数为_________3_________
36.若则_____1__________
三解答题:本大题共4小题,共28分.解答应写出文字说明、证明过程或演算步骤。
37.(本小题满分6分)
从夏令营的2名女生和3名男生中任选2人参加公益活动,求选出的2人中至少有一名女生的概率。
7/10
38.(本小题满分6分)
在中,内角A、B、C所对的边分别为a、b、c,已知
求a和A、C
a=2,A=90,C=30
39.(本小题满分8分)
在平面直角坐标系xOy中,椭圆C的中心为原点,焦点在x轴上,离心率为,过的直线交椭圆C于A、B两点,且的周长为16,求椭圆C的标准方程
40.(本小题满分8分)
已知函数
(1)当时试讨论函数的单调性。
(2)求证:对任意的,有。
