高考理科数学(宁夏)卷
宁夏银川市(新版)2024高考数学人教版能力评测(提分卷)完整试卷

宁夏银川市(新版)2024高考数学人教版能力评测(提分卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题2024年某校举行一场射箭比赛,甲乙等8人各射中的环数分别为:9环,4环,6环,5环,7环,10环,8环,9环.则这8个人的成绩的上四分位数是()A.8环B.9环C.7环D.6环第(2)题已知集合,,则()A.B.C.D.第(3)题如图,分别取与x轴,y轴正方向相同的两个单位向量作为基底,若,,则向量的坐标为()A.B.C.D.第(4)题在中,为边的中点,,则()A.B.C.D.第(5)题为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分如图所示,假设得分值的中位数为,众数为,平均值为,则( )A.B.C.D.第(6)题将3个1和3个0随机排成一行,则3个0都不相邻的概率是()A.B.C.D.第(7)题过点作直线,使它与抛物线仅有一个公共点,这样的直线有()A.1条B.2条C.3条D.4条第(8)题一个四棱台的三视图如图所示,其中正视图和侧视图均为上底长为4,下底长为2,腰长为的等腰梯形,则该四棱台的体积为()A.B.C.28D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题下列函数中最小值为6的是()A.B.C.D.第(2)题已知复数满足,且复数对应的点在第一象限,则下列结论正确的是()A.复数的虚部为B.C.D.复数的共轭复数为第(3)题设,向量,向量,则()A.必不互为平行向量B.必不互为垂直向量C.存在,使D.对任意三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题若体积为的正三棱锥的所有顶点都在同一个球面上,则该球体积的最小值为______.第(2)题已知函数(定义域为D,值域为A)有反函数,则方程有解,且的充要条件是满足______________.第(3)题已知实数满足,则的最大值为___________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知数列的前n项和为,,且数列为等差数列.(1)求数列的通项公式;(2)定义:表示不超过x的最大整数.设,求数列的前114项和.第(2)题已知各项均为正数的数列的前n项和为,,且对任意n,恒成立.(1)求证:数列是等差数列,并求数列的通项公式;(2)设,已知,,(2<i<j)成等差数列,求正整数i,j.第(3)题如图,已知抛物线,其焦点为,其准线与轴交于点,以为直径的圆交抛物线于点,连接并延长交抛物线于点,且.(1)求的方程.(2)过点作轴的垂线与抛物线在第一象限交于点,若抛物线上存在点,,使得.求证:直线过定点.第(4)题如图,在多面体中,已知,,均为等边三角形,平面平面ABC,平面平面ABC,H为AB的中点.(1)判断DE与平面ABC的位置关系,并加以证明;(2)求直线DH与平面ACE所成角的正弦值.第(5)题如图所示,圆台的上、下底面圆半径分别为和为圆台的两条不同的母线.分别为圆台的上、下底面圆的圆心,且为等边三角形.(1)求证:;(2)截面与下底面所成的夹角大小为,求异面直线与所成角的余弦值.。
宁夏固原市(新版)2024高考数学人教版真题(评估卷)完整试卷

宁夏固原市(新版)2024高考数学人教版真题(评估卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题已知集合,.则()A.[0,1]B.(1.2]C.D.第(2)题某公司为了调查员工的健康状况,由于女员工所占比重大,按性别分层,用按比例分配的分层随机抽样的方法抽取样本,已知所抽取的所有员工的体重的方差为120,女员工的平均体重为,标准差为6,男员工的平均体重为,标准差为4.若样本中有21名男员工,则女员工的人数为()A.28B.35C.39D.48第(3)题定义:设不等式的解集为A,若A中只有唯一整数,则称A为“和谐解集”.若关于x的不等式在上存在“和谐解集”,则实数m的取值范围为()A.B.C.D.第(4)题已知向量,,则()A.B.C.D.第(5)题“牟合方盖”是我国古代数学家刘徽在研究球的体积过程中构造的一个和谐优美的几何模型.如图1,正方体的棱长为2,用一个底面直径为2的圆柱面去截该正方体,沿着正方体的前后方向和左右方向各截一次,截得的公共部分即是一个牟合方盖(如图2).已知这个牟合方盖与正方体外接球的体积之比为,则正方体除去牟合方盖后剩余部分的体积为()A.B.C.D.第(6)题设集合,,则()A.B.C.D.第(7)题复数,则z的模为()A.B.C.D.第(8)题一个人连续射击次,则下列各事件关系中,说法正确的是()A.事件“两次均击中”与事件“至少一次击中”互为对立事件B.事件“第一次击中”与事件“第二次击中”为互斥事件C.事件“两次均未击中”与事件“至多一次击中”互为对立事件D.事件“恰有一次击中”与事件“两次均击中”为互斥事件二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题已知函数的定义域为是奇函数,分别是函数的导函数,在上单调递减,则()A.B.C.的图象关于直线对称D.第(2)题当且时,不等式恒成立,则自然数可能为()A.0B.2C.8D.12第(3)题如图,在长方形中,,,为的中点,为线段(端点除外)上一动点.现将沿折起,使平面平面.在平面内过点作,为垂足.设,则的取值可以是()A.B.C.D.1三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题若直线l:与圆C:有两个公共点,则k的取值范围为________.第(2)题已知实数,满足,若目标函数取得最大值时的最优解有无数个,则的值为______.第(3)题若,则__________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题如图,已知正三棱锥和正三棱锥有相同的底面,且.(1)若,求二面角的余弦值;(2)若平面,求的长度.第(2)题已知函数(,),曲线在处的切线方程为.(1)求,的值;(2)证明:;(3)已知满足的常数为.令函数(其中是自然对数的底数,),若是的极值点,且恒成立,求实数的取值范围.第(3)题已知函数(1)求不等式的解集;(2)若恒成立,求实数的取值范围.第(4)题已知直线L的倾斜角满足,椭圆满足:焦点在x轴上,长轴长为4,离心率为双曲线的离心率的倒数,直线L过椭圆右焦点,(1)求椭圆的标准方程;(2)求直线L的方程;(3)求直线L与椭圆的相交弦长.第(5)题如图所示,椭圆E的中心为坐标原点,焦点在轴上,且在抛物线的准线上,点是椭圆E上的一个动点,面积的最大值为.(Ⅰ)求椭圆E的方程;(Ⅱ)过焦点作两条平行直线分别交椭圆E于四个点.①试判断四边形能否是菱形,并说明理由;②求四边形面积的最大值.。
宁夏石嘴山市(新版)2024高考数学人教版考试(提分卷)完整试卷

宁夏石嘴山市(新版)2024高考数学人教版考试(提分卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题已知复数,则()A.B.C.D.第(2)题已知:,:,则是的()条件A.充分不必要B.必要不充分C.充要D.既不充分也不必要第(3)题已知角第二象限角,且,则角是()A.第一象限角B.第二象限角C.第三象限角D.第四象限角第(4)题抛物线的准线方程是()A.B.C.D.第(5)题将函数图像上各点的横坐标缩短到原来的,纵坐标不变,再将图像向右平移个单位长度,得到函数的图像,以下方程是函数图像的对称轴方程的是()A.B.C.D.第(6)题已知等差数列{a n}的前n项和为S n,且=,则=()A.B.C.D.第(7)题在中,,则()A.B.C.D.第(8)题设、是椭圆:的左、右焦点,为直线上一点,是底角为的等腰三角形,则的离心率为A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题意大利著名数学家斐波那契在研究兔子的繁殖问题时,发现有这样的一列数:,,,,,,.该数列的特点如下:前两个数均为,从第三个数起,每一个数都等于它前面两个数的和.人们把这样的一列数组成的数列称为斐波那契数列,现将中的各项除以所得余数按原顺序构成的数列记为,则下列结论中正确的是()A.B.C.D.第(2)题过抛物线上一点A(1,-4)作两条相互垂直的直线,与C的另外两个交点分别为M,N,则()A.C的准线方程是B.过C的焦点的最短弦长为8C.直线MN过定点(0,4)D.当点A到直线MN的距离最大时,直线MN的方程为第(3)题定义在上的函数满足,则()A.B.C.为奇函数D.单调递增三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题如图,在梯形中,,将沿直线翻折至的位置,,当三棱锥的体积最大时,过点的平面截三棱锥的外接球所得的截面面积的最小值是_______________.第(2)题设是定义在上、以1为周期的函数,若在上的值域为,则在区间上的值域为___________________ .第(3)题若正实数,满足,则的最大值为______.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知△的三边,,所对的角分别为,,,且.(1)求的值;(2)若△外接圆的半径为14,求△的面积.第(2)题国际上常用体重指数作为判断胖瘦的指标,体重指数是体重(单位:千克)与身高(单位:米)的平方的比值.高中学生由于学业压力,缺少体育锻炼等原因,导致体重指数偏高.某市教育局为督促各学校保证学生体育锻炼时间,减轻学生学习压力,准备对各校学生体重指数进行抽查,并制定了体重指数档次及所对应得分如下表:档次低体重正常超重肥胖体重指数x(单位:)学生得分801008060某校为迎接检查,学期初通过调查统计得到该校高三学生体重指数服从正态分布,并调整教学安排,增加学生体育锻炼时间.4月中旬,教育局聘请第三方机构抽查了该校高三50名学生的体重指数,得到数据如下表:16.316.917.117.518.218.519.019.319.519.820.220.220.520.821.221.421.521.922.322.522.822.923.023.323.323.523.623.824.024.124.124.324.524.624.824.925.225.325.525.725.926.126.426.727.127.628.228.829.130.0请你从肥胖率、体重指数学生平均得分两个角度评价学校采取措施的效果附:参考数据与公式若,则①;②;③第(3)题已知的内角A,B,C的对边分别为a,b,c,.(1)求A;(2)若O是的内心,,且,求面积的最大值.第(4)题在中,内角的对边分别为.(1)若,求的面积;(2)求的值.第(5)题如图,在三棱柱中,,.(1)证明:;(2)若,,,求二面角的余弦值.。
2023年宁夏高考理科数学真题及参考答案

2023年宁夏高考理科数学真题及参考答案一、选择题1.设5212ii iz +++=,则=z ()A .i 21-B .i21+C .i -2D .i+22.设集合R U =,集合{}1<=x x M ,{}21<<-=x x N ,则{}=≥2x x ()A .()N M C U ⋃B .MC N U ⋃C .()N M C U ⋂D .NC M U ⋃3.如图,网格纸上绘制的一个零件的三视图,网格小正方形的边长为1,则该零件的表面积为()A .24B .26C .28D .304.已知()1-=ax xe xe xf 是偶函数,则=a ()A .2-B .1-C .1D .25.设O 为平面坐标系的坐标原点,在区域(){}41,22≤+≤y x y x 内随机取一点,记该点为A ,则直线OA 的倾斜角不大于4π的概率为()A .81B .61C .41D .216.已知函数()()ϕω+=x x f sin 在区间⎪⎭⎫⎝⎛326ππ,单调递增,直线6π=x 和32π=x 为函数()x f y =的图象的两条对称轴,则=⎪⎭⎫⎝⎛-125πf ()A .23-B .21-C .21D .237.甲乙两位同学从6种课外读物中各自选读2种,则这两人选读的课外读物中恰有1种相同的选法共有()A .30种B .60种C .120种D .240种8.已知圆锥PO 的底面半径为3,O 为底面圆心,PB P A ,为圆锥的母线,︒=∠120AOB ,若P AB ∆的面积等于439,则该圆锥的体积为()A .πB .π6C .π3D .π639.已知ABC ∆为等腰直角三角形,AB 为斜边,ABD ∆为等边三角形,若二面角D AB C --为150°,则直线CD 与平面ABC 所成角的正切值为()A .51B .52C .53D .5210.已知等差数列{}n a 的公差为32π,集合{}*∈=N n a S n cos ,若{}b a S ,=,则=ab ()A .1-B .21-C .0D .2111.已知B A ,是双曲线1922=-y x 上两点,则可以作为B A ,中点的是()A .()1,1B .()2,1-C .()3,1D .()4,1-12.已知圆122=+y x O :,2=OP ,过点P 作直线1l 与圆O 相切于点A ,作直线2l 交圆O 于C B ,两点,BC 中点为D ,则PD P A ⋅的最大值为()A .221+B .2221+C .21+D .22+二、填空题13.已知点()51,A 在抛物线px y C 22=:上,则A 到C 的准线的距离为.14.若y x ,满足约束条件⎪⎩⎪⎨⎧≥+≤+-≤-739213y x y x y x ,则y x z -=2的最大值为.15.已知{}n a 为等比数列,63542a a a a a =,8109-=a a ,则=7a .16.已知()()xxa a x f ++=1,()1,0∈a ,若()x f 在()∞+,0为增函数,则实数a 的取值范围为.三、解答题(一)必做题17.某厂为比较甲乙两种工艺对橡胶产品伸缩率处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡胶产品的伸缩率,甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为i i y x ,()10,2,1 =i ,试验结果如下试验序号i 12345678910伸缩率i x 545533551522575544541568596548伸缩率iy 536527543530560533522550576536记i i i y x z -=()10,2,1 =i ,记1021,z z z 的样本平均数为z ,样本方差为2s ,(1)求z ,2s ;(2)判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高(如果1022s z ≥,则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高,否则不认为有显著提高).18.在ABC ∆中,︒=∠120BAC ,2=AB ,1=AC .(1)求ABC ∠sin ;(2)若D 为BC 上一点,且︒=∠90BAD ,求ADC ∆的面积.19.如图,在三棱锥ABC P -中,BC AB ⊥,2=AB ,22=BC ,6==PC PB ,BC AP BP ,,的中点分别为O E D ,,,DO AD 5=,点F 在AC 上,AO BF ⊥.(1)证明:EF ∥平面ADO ;(2)证明:平面ADO ⊥平面BEF ;(3)求二面角C AO D --的正弦值.20.已知椭圆C :()012222>>=+b a bx a y 的离心率为35,点()02,-A 在C 上.(1)求C 的方程;(2)过点()3,2-的直线交曲线C 于Q P ,两点,直线AQ AP ,交y 轴于N M ,两点,求证:线段MN 中点为定点.21.已知函数()()1ln 1+⎪⎭⎫⎝⎛+=x a x x f .(1)当1-=a 时,求曲线()x f 在()()1,1f 的切线方程;(2)是否存在实数b a ,使得曲线⎪⎭⎫⎝⎛=x f y 1关于直线b x =对称,若存在,求出b a ,的值;如果不存在,请说明理由;(3)若()x f 在()∞+,0存在极值,求a 的取值范围.(二)选做题【选修4-4】22.在直角坐标系xOy 中,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线1C 的极坐标方程为⎪⎭⎫ ⎝⎛≤≤=24sin 2πθπθρ,曲线2C :⎩⎨⎧==ααsin 2cos 2y x (α为参数,παπ<<2).(1)写出1C 的直角坐标方程;(2)若直线m x y +=既与1C 没有公共点,也与2C 没有公共点,求m 的取值范围.【选修4-5】23.已知()22-+=x x x f .(1)求不等式()x x f -≤6的解集;(2)在直角坐标系xOy 中,求不等式组()⎩⎨⎧≤-+≤06y x yx f 所确定的平面区域的面积.参考答案一、选择题123456789101112BADDCDCBCBDA1.解:()i i ii i i i i i i z 21112211212252-=--=+=+-+=+++=,则i z 21+=2.解:由题意可得{}2<=⋃x x N M ,则()=⋃N M C U {}2≥x x .3.解:如图所示,在长方体1111D C B A ABCD -中,2==BC AB ,31=AA ,点K J I H ,,,为所在棱上靠近点1111,,,A D C B 的三等分点,N M L O ,,,为所在棱的中点,则三视图所对应的几何体为长方体1111D C B A ABCD -去掉长方体11LMHB ONIC -之后所得的几何体,该几何体的表面积和原来的长方体的表面积相比少2个边长为1的正方体.4.解:∵()1-=ax xe xe xf 是偶函数,则()()=--x f x f ()()[]01111=--=-------axx a x ax x axx e e e x e e x e xe ,又∵x 不恒为0,可得()01=--xa xee ,则()x a x 1-=,∴2=a .5.解:∵区域(){}41,22≤+≤y x y x 表示以()00,O 为圆心,外圆半径2=R ,内圆半径1=r 的圆环,则直线OA的倾斜角不大于4π的部分如阴影所示,在第一象限对应的圆心角4π=∠MON ,结合对称性可得所求概率为41242=⨯=ππp .6.解:∵()()ϕω+=x x f sin 在区间⎪⎭⎫⎝⎛326ππ,单调递增,∴26322πππ=-=T ,且0>ω,则π=T ,22==Tπω.当6π=x 时,()x f 取得最小值,则Z k k ∈-=+⋅,2262ππϕπ,则Z k k ∈-=,652ππϕ,不妨取0=k 则()⎪⎭⎫ ⎝⎛-=652sin πx x f ,则2335sin 125=⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛-ππf .7.解:有1本相同的读物,共有16C 种情况,然后两人各自的另外一种读物相当于在剩余的5种读物里,选出两种进行排列,共有25A 种,根据分布乘法公式则共有⋅16C 12025=A 种.8.解:在AOB ∆中,︒=∠120AOB ,而3==OB OA ,取AC 中点C ,连接PC OC ,,有AB OC ⊥,AB PC ⊥,如图,︒=∠30ABO ,23=OC ,32==BC AB ,由P AB ∆的面积为439得439321=⨯⨯PC ,解得233=PC ,于是6232332222=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=-=OC PC PO ,∴圆锥的体积()πππ663313122=⨯⨯=⨯⨯=PO OA V .9.解:取AB 的中点E ,连接DE CE ,,∵ABC ∆为等腰直角三角形,AB 为斜边,则有AB CE ⊥,又ABD ∆为等边三角形,则AB DE ⊥,从而CED ∠为二面角DAB C --的平面角,即︒=∠150CED ,显然E DE CE =⋂,⊂DE CE ,平面CDE ,又⊂AB 平面ABC ,因此平面CDE ⊥平面ABC ,显然平面CDE ∩平面CE ABC =,直线⊂CD 平面CDE ,则直线CD 在平面ABC 内的射影为直线CE ,从而DCE ∠为直线CD 与平面ABC 所成的角,令2=AB ,则1=CE ,3=DE,在CDE ∆中,由余弦定理得:72331231cos 222=⎪⎪⎭⎫⎝⎛-⨯⨯⨯-+=∠⋅-+=CED DE CE DE CE CD ,由正弦定理得CEDCDDCE DE ∠=∠sin sin ,即7237150sin 3sin =︒=∠DCE ,显然DCE ∠是锐角,7257231sin 1cos 22=⎪⎪⎭⎫ ⎝⎛-=∠-=∠DCE DCE ,∴直线CD 与平面ABC 所成角的正切值为53.10.解:依题意,等差数列{}n a 中,()⎪⎭⎫⎝⎛-+=⋅-+=323232111πππa n n a a n ,显然函数==n a y cos ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+3232cos 1ππa n 的周期为3,而*∈N n ,即n a cos 最多有3个不同取值,又{}{}b a Nn a n ,cos =∈*,而在321cos ,cos ,cos a a a 中,321cos cos cos a a a ≠=或321cos cos cos a a a =≠,于是有⎪⎭⎫ ⎝⎛+=32cos cos πθθ,即有Z k k ∈=⎪⎭⎫ ⎝⎛++,232ππθθ,解得Z k k ∈-=,3ππθ213cos cos cos 3cos 343cos 3cos 2-=-=⎪⎭⎫ ⎝⎛--=⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=ππππππππππk k k k k ab 11.解:由对称性只需考虑()1,1,()2,1,()3,1,()4,1即可,注意到()3,1在渐近线上,()1,1,()2,1在渐近线一侧,()4,1在渐近线的另一侧.下证明()4,1点可以作为AB 的中点.设直线AB 的斜率为k ,显然k 存在.设()41+-=x k y l AB :,直线与双曲线联立()⎪⎩⎪⎨⎧=-+-=194122y x x k y ,整理得()()()094429222=------k x k k xk ,只需满足⎩⎨⎧>∆=+0221x x ,∴()29422=--k k k ,解得49=k ,此时满足0>∆.12.解:如图所示,1=OA ,2=OP ,则由题意可知:︒=∠45APO ,由勾股定理可得122=-=OA OP P A ,当点D A ,位于直线PO 异侧时,设40παα≤≤=∠,OPC ,则:⎪⎭⎫ ⎝⎛+⨯=⎪⎭⎫ ⎝⎛+⋅=⋅4cos cos 214cos πααπαPD P A αααααααα2sin 2122cos 1cos sin cos sin 22cos 22cos 22-+=-=⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--=42sin 2221πα∵40πα≤≤,则4424ππαπ≤-≤-,∴当442ππα-=-时,PD P A ⋅有最大值1.当点D A ,位于直线PO 同侧时,设40παα≤≤=∠,OPC ,则:⎪⎭⎫ ⎝⎛-⨯=⎪⎭⎫ ⎝⎛-⋅=⋅4cos cos 214cos πααπαPD P A αααααααα2sin 2122cos 1cos sin cos sin 22cos 22cos 22++=+=⎪⎪⎭⎫ ⎝⎛+=⎪⎭⎫⎝⎛++=42sin 2221πα∵40πα≤≤,则2424ππαπ≤+≤,∴当242ππα=+时,PD P A ⋅有最大值为221+.二、填空题13.49;14.8;15.2-;16.⎪⎪⎭⎫⎢⎣⎡-1,21513.解:由题意可得:()1252⨯=p ,则52=p ,∴抛物线的方程为x y 52=,准线方程为45-=x ,点A 到C 的准线的距离为49451=⎪⎭⎫ ⎝⎛--.14.作出可行域如下图所示,∵y x z -=2,∴z x y -=2,联立有⎩⎨⎧=+-=-9213y x y x ,解得⎩⎨⎧==25y x 设()2,5A ,显然平移直线x y 2=使其经过点A 此时截距z -最小,则z 最大,代入得8=z .15.解:设{}n a 的公比为()0≠q q ,则q a q a a a a a a 5263542⋅==,显然0≠n a ,则24q a =,即231q q a =,则11=q a ,∵8109-=a a ,则89181-=⋅q a q a ,则()()3351528-=-==q q,则23-=q ,则25517-==⋅=q q q a a .16.⎪⎪⎭⎫⎢⎣⎡-1,215解析:()()()a a a a x f xx+++='1ln 1ln ,由()x f 在()∞+,0为增函数可知()∞+∈,0x 时,()0≥'x f 恒成立,只需()0min ≥'x f ,而()()()01ln 1ln 22>+++=''a a a a x f xx,∴()()()01ln ln 0≥++='>'a a f x f ,又∵()1,0∈a ,∴⎪⎪⎭⎫⎢⎣⎡-∈1,215a .三、解答题(一)必做题17.解:(1)∵i i i y x z -=()10,2,1 =i ,∴9536545111=-=-=y x z ;62=z ;83=z ;84-=z ;155=z ;116=z ;197=z ;188=z ;209=z ;1210=z .()()[]1112201819111588691011011021=++++++-+++⨯=++=z z z z ∵()∑=-=1012101i i z z s ,将各对应值代入计算可得612=s (2)由(1)知:11=z ,612=s,∴5122106121061210222=⨯==s ,121112==z ,∴1022s z ≥∴甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高18.解:(1)根据题意,由余弦定理可得:72112212cos 222222=⎪⎭⎫ ⎝⎛-⨯⨯⨯-+=∠⋅-+=BAC AC AB AC AB BC ∴7=BC 由正弦定理ABC AC A BC ∠=∠sin sin ,即ABC∠=sin 1237,解得1421sin =∠ABC .(2)由三角形面积公式可得430sin 2190sin 21=︒⨯⨯⨯︒⨯⨯⨯=∆∆AD AC AD AB S S ACDABD ,则103120sin 12215151=⎪⎭⎫⎝⎛︒⨯⨯⨯⨯==∆∆ABC ACD S S .19.解:(1)连接OF OE ,,设tAC AF =,则()BC t BA t AF BA BF +-=+=1,BC BA AO 21+-=,AO BF ⊥,则()[]()()0414********=+-=+-=⎪⎭⎫⎝⎛+-⋅+-=⋅t t BC t BA t BC BA BC t BA t AO BF 解得21=t ,则F 为AC 的中点,由F O E D ,,,分别为AC BC P A PB ,,,的中点,于是AB OF AB DE AB DE 2121∥,,∥=,即OF DE OF DE =,∥,则四边形ODEF 为平行四边形,DO EF DO EF =,∥,又⊄EF 平面ADO ,⊂DO 平面ADO ,∴EF ∥平面ADO .(2)由(1)可知EF ∥OD ,则266==DO AO ,,得2305==DO AD ,因此215222==+AD AO OD ,则AO OD ⊥,有AO EF ⊥,又BF AO ⊥,F EF BF =⋂,⊂EF BF ,平面BEF ,则有AO ⊥平面BEF ,又⊂AO 平面ADO ,∴平面ADO ⊥平面BEF .(3)过点O 作BF OH ∥交AC 于点H ,设G BE AD =⋂,由BF AO ⊥得AO HO ⊥,且AH FH 31=,又由(2)知,AO OD ⊥,则DOH ∠为二面角C AO D --平面角,∵E D ,分别为P A PB ,的中点,因此G 为P AB ∆的重心,即有,31,31BE GE AD DG ==又AH FH 31=,即有GF DH 23=,622642622215234cos 2⨯⨯-+=⨯⨯-+=∠P A ABD ,解得14=P A ,同理得26=BE ,于是3222==+BF EF BE ,即有EF BE ⊥,则35262631222=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⨯=GF ,从而315=GF ,21531523=⨯=DH ,在DOH ∆中,215,262321====DH OD BF OH ,于是22221sin ,22232624154346cos 2=⎪⎪⎭⎫ ⎝⎛--=∠-=⨯⨯-+=∠DOH DOH .∴二面角C AO D --的正弦值为22.20.解:(1)由题意可得⎪⎪⎪⎩⎪⎪⎪⎨⎧==+==352222a c e c b a b ,解得⎪⎩⎪⎨⎧===523c b a ,∴椭圆的方程为14922=+x y。
2024年全国甲卷理科综合高考试卷(原卷+答案)

绝密★启用前2024年普通高等学校招生全国统一考试(全国甲卷)(适用地区:四川、宁夏、内蒙古、青海、陕西)理科综合注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案书写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、单选题(每小题6分,共78分)1. 细胞是生物体结构和功能的基本单位。
下列叙述正确的是()A. 病毒通常是由蛋白质外壳和核酸构成的单细胞生物B. 原核生物因为没有线粒体所以都不能进行有氧呼吸C. 哺乳动物同一个体中细胞的染色体数目有可能不同D. 小麦根细胞吸收离子消耗的ATP主要由叶绿体产生2. ATP可为代谢提供能量,也参与RNA的合成,ATP结构如图所示,图中~表示高能磷酸键,下列叙述错误的是()A. ATP转化为ADP可为离子的主动运输提供能量B. 用α位32P标记的ATP可以合成带有32P的RNAC. β和γ位磷酸基团之间的高能磷酸键不能在细胞核中断裂D. 光合作用可将光能转化为化学能储存于β和γ位磷酸基团之间的高能磷酸键3. 植物生长发育受植物激素的调控。
下列叙述错误的是()A. 赤霉素可以诱导某些酶的合成促进种子萌发B. 单侧光下生长素的极性运输不需要载体蛋白C. 植物激素可与特异性受体结合调节基因表达D. 一种激素可通过诱导其他激素的合成发挥作用4. 甲状腺激素在人体生命活动的调节中发挥重要作用。
下列叙述错误的是()A. 甲状腺激素受体分布于人体内几乎所有细胞B. 甲状腺激素可以提高机体神经系统的兴奋性C. 甲状腺激素分泌增加可使细胞代谢速率加快D. 甲状腺激素分泌不足会使血中TSH含量减少5. 某生态系统中捕食者与被捕食者种群数量变化的关系如图所示,图中→表示种群之间数量变化的关系,如甲数量增加导致乙数量增加。
2007-2011年高考理科数学试卷及答案(宁夏卷)
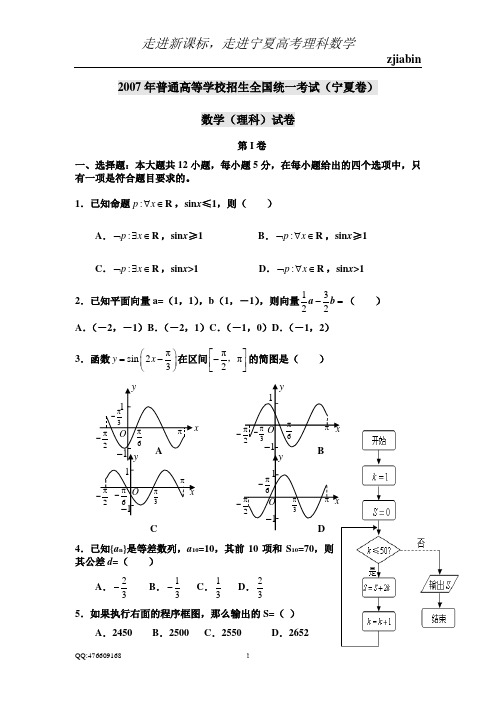
2007年普通高等学校招生全国统一考试(宁夏卷)数学(理科)试卷第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知命题:p x ∀∈R ,sin x ≤1,则( )A .:p x ⌝∃∈R ,sin x ≥1B .:p x ⌝∀∈R ,sin x ≥1C .:p x ⌝∃∈R ,sin x >1D .:p x ⌝∀∈R ,sin x >12.已知平面向量a=(1,1),b (1,-1),则向量1322-=a b ( )A .(-2,-1)B .(-2,1)C .(-1,0)D .(-1,2)3.函数πsin 23y x ⎛⎫=- ⎪⎝⎭在区间ππ2⎡⎤-⎢⎥⎣⎦,的简图是( )A BC D4.已知{a n }是等差数列,a 10=10,其前10项和S 10=70,则其公差d =( )A .23-B .13-C .13D .235.如果执行右面的程序框图,那么输出的S=( )A .2450B .2500C .2550D .2652yx11- 2π-3π- O 6π πyx 11- 2π- 3π- O 6ππ y x 11-2π-3πO 6π- π yx π 2π- 6π- 1 O 1- 3π . .6.已知抛物线22(0)y px p =>的焦点为F ,点P 1(x 1,y 1),P 2(x 2,y 2),P 3(x 3,y 3)在抛物线上,且2x 2=x 1+x 3, 则有( )A .123FP FP FP +=B .222123FP FP FP += C .2132FP FP FP =+ D .2213FPFP FP =· 7.已知x >0,y >0,x ,a ,b ,y 成等差数列,x ,c ,d ,y 成等比数列,则2()a b cd+的最小值是( )A .0B .1C .2D .48.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是()A .34000cm 3 B .38000cm 3C .2000cm 3D .4000cm 3 9.若cos 22π2sin 4αα=-⎛⎫- ⎪⎝⎭,则cos sin αα+的值为( ) A .72-B .12-C .12D .7210.曲线12e x y =在点(4,e 2)处的切线与坐标轴所围三角形的面积为( )A .29e 2B .4e 2C .2e 2D .e 211.甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表s 1,s 2,s 3分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )A .s 3>s 1>s 2B .s 2>s 1>s 3C .s 1>s 2>s 3D .s 2>s 3>s 1 12.一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等。
宁夏银川市(新版)2024高考数学统编版(五四制)真题(自测卷)完整试卷
宁夏银川市(新版)2024高考数学统编版(五四制)真题(自测卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题直三棱柱如图所示,为棱的中点,三棱柱的各顶点在同一球面上,且球的表面积为,则异面直线和所成的角的余弦值为()A.B.C.D.第(2)题已知定义在上的函数,,其中为偶函数,当时,恒成立;且满足:①对,都有;②当时,.若关于的不等式对恒成立,则的取值范围是A.B.C.D.第(3)题若,则()A.1B.-1C.D.第(4)题先后两次掷一枚质地均匀的骰子,事件“两次掷出的点数之和是6”,事件“第一次掷出的点数是奇数”,事件“两次掷出的点数相同”,则()A.A与互斥B.与相互独立C.D.A与互斥第(5)题恩格斯曾经把对数的发明、解析几何的创始和微积分的建立称为十七世纪数学的三大成就.其中对数的发明曾被十八世纪法国数学家拉普拉斯评价为“用缩短计算时间延长了天文学家的寿命”.已知正整数N的70次方是一个83位数,则由下面表格中部分对数的近似值(精确到0.001),可得N的值为()M23711130.3010.4770.845 1.041 1.114A.13B.14C.15D.16第(6)题若M,N为圆上任意两点,P为直线上一个动点,则的最大值是()A.B.C.D.第(7)题已知(是虚数单位),则()A.B.C.D.第(8)题在边长为的正六边形中,若,则()A.1B.C.2D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题已知,为双曲线C:x2–=1的左、右焦点,在双曲线右支上取一点P,使得PF1⊥PF2,直线PF2与y轴交于点Q,连接QF1,△PQF1,的内切圆圆心为I,则下列结论正确的有()A.F1,F2,P,I四点共圆B.△PQF1的内切圆半径为1C.I为线段OQ的三等分点D.PF1与其中一条渐近线垂直第(2)题某市举办“口语易”英语口语竞赛,已知某选手平均得分为8.5分,12位评委对其评分具体如下(满分10分):7.0 7.5 7.8 7.8 8.2 8.3 8.5 8.7 9.1 9.2 9.9 10则下列说法正确的是()A.第75百分位数为9.1B.中位数为8.3C.极差为3D.去掉最高分和最低分,不会影响到这位同学的平均得分第(3)题如图为2017—2020年中国短视频用户规模和增长率、2021年用户规模和增长率预测,据图分析,下列结论正确的为()A.根据预测,2021年中国短视频用户规模将突破8亿人B.2017—2020年中国短视频用户规模逐年增加,但增长速度变缓C.2018年中国短视频用户规模比2017年增加了超过两倍D.2020年中国短视频用户规模与2017年相比较,增长率约为198.3%三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题设点在直线上,点在曲线上,线段的中点为,为坐标原点,则的最小值为________.第(2)题已知数列的首项,且满足,则存在正整数n,使得成立的实数组成的集合为___________第(3)题已知向量,,若,则λ的值为___.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知椭圆的一个焦点与短轴的两端点组成一个正三角形的三个顶点,且椭圆经过点.(1)求椭圆的方程;(2)若直线与圆相切于点,且交椭圆于两点,射线于椭圆交于点,设的面积与的面积分别为.①求的最大值;②当取得最大值时,求的值.第(2)题四名党员教师在暑假中去某社区做志愿者工作,他们中的每人都可以从甲、乙、丙三项工作中随机选择一个,且每人的选择相互独立.(1)设这四名教师中选择工作甲的人数为X,求X的分布列及数学期望;(2)求上述三项工作中恰有一个没被任何人选中的概率.第(3)题已知函数.(1)求函数的单调区间;(2)若恒成立,求实数的取值范围.第(4)题已知且.(1)若,设,比较和的大小;(2)若,求的最小值.第(5)题已知为抛物线:上的一点,直线交于A,B两点,且直线,的斜率之积为2.(1)求的准线方程;(2)求的最小值.。
宁夏银川市2024年数学(高考)部编版能力评测(提分卷)模拟试卷
宁夏银川市2024年数学(高考)部编版能力评测(提分卷)模拟试卷一、单项选择题(本题包含8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题已知函数,设关于的方程有个不同的实数解,则的所有可能的值为A .B .或C .或D .或或第(2)题已知的内角的对边分别是,面积为S ,且,则角的值为( )A.B .C .D .第(3)题如图,已知正三棱柱中,,设,,,分别为棱,,,的中点,则点到平面的距离为( )A .B .C .D .第(4)题已知椭圆的中心为坐标原点,离心率为,过椭圆的上焦点的直线交椭圆于两点,若线段的中点坐标为,则椭圆的标准方程为( )A .B .C .D .第(5)题已知双曲线的一条渐近线与圆交于,两点,若,则的离心率为( )A .B .C.2D .第(6)题已知函数的反函数为,则A .0B .1C .2D .4第(7)题已知在平行四边形中,,,,,则( )A.B .C.D .第(8)题已知,则( )A.B .C .D .二、多项选择题(本题包含3小题,每小题6分,共18分。
在每小题给出的四个选项中,至少有两个选项正确。
全部选对的得6分,选对但不全的得3分,有选错或不答的得0分) (共3题)第(1)题已知函数,则下列结论正确的是( )A .的最小值为eB.在区间上单调递增C .函数有且只有一个零点D.不等式存在唯一整数解第(2)题掷一枚质量均匀的骰子,记事件:掷出的点数为偶数;事件:掷出的点数大于2.则下列说法正确的是()A.B.C.D.第(3)题如图,在四棱锥中,底面是正方形,侧面为等边三角形,,平面平面,点M在线段上运动(不含端点),则下列说法错误的是()A.平面平面B.存在点M使得C.当M为线段中点时,过点A,D,M的平面交于点N,则四边形的面积为D.的最小值为三、填空(本题包含3个小题,每小题5分,共15分。
请按题目要求作答,并将答案填写在答题纸上对应位置) (共3题)第(1)题已知等差数列中,,,则数列的通项公式__________;__________.第(2)题已知随机变量,若,则________.第(3)题已知双曲线C:的左、右焦点分别为,,点M,N分别为C的渐近线和左支上的动点,且的最小值恰为C的实轴长的2倍,则C的离心率为______.四、解答题(本题包含5小题,共77分。
2016宁夏高考数学试卷
2016宁夏高考数学试卷一、设集合P = {x | x² - 2x ≥ 0},Q = {x | 1 < x ≤ 2},则P的补集与Q的交集是( )A. [0,1)B. (0,2]C. (1,2)D. [1,2]答案:A解析:首先解集合P中的不等式x² - 2x ≥ 0,得到x(x - 2) ≥ 0,解得x ≤ 0 或 x ≥ 2。
因此,集合P = {x | x ≤ 0 或 x ≥ 2}。
P的补集是(0, 2)。
然后求P的补集与Q 的交集,即(0, 2) ∩ (1, 2] = [0,1)。
二、已知等差数列{a_n}的前n项和为S_n,公差d不为零,若a_3 + a_4 + a_8 = 3a_5,则d与S_n的关系是( )A. d > 0,S_n > 0B. d > 0,S_n < 0C. d < 0,S_n > 0D. d < 0,S_n < 0答案:A解析:由等差数列的性质,a_3 + a_4 + a_8 = 3a_5 可转化为 (a_1 + 2d) + (a_1 + 3d) + (a_1 + 7d) = 3(a_1 + 4d),即 3a_1 + 12d = 3a_1 + 12d,这是一个恒等式,说明等式成立。
由于题目要求d不为零,且等差数列中项的和为正,说明数列递增,即d > 0。
又因为等差数列的前n项和S_n = n/2 * (2a_1 + (n-1)d),由于d > 0,S_n必然大于0。
三、命题“对于所有n属于自然数,f(n)属于自然数且f(n) ≤ n”的否定形式是( )A. 存在n属于自然数,f(n)不属于自然数且f(n) > nB. 存在n属于自然数,f(n)不属于自然数或f(n) > nC. 存在n属于自然数,f(n)属于自然数且f(n) > nD. 存在n属于自然数,f(n)不属于自然数且f(n) ≤ n答案:C解析:全称命题“对于所有n属于自然数,f(n)属于自然数且f(n) ≤ n”的否定形式是特称命题,即“存在n属于自然数,使得f(n)不满足原命题的条件”。
宁夏吴忠市(新版)2024高考数学部编版真题(评估卷)完整试卷
宁夏吴忠市(新版)2024高考数学部编版真题(评估卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题某大学共有名学生,为了了解学生课外图书阅读量情况,该校随机地从全校学生中抽取名,统计他们每年阅读的书籍数量,由此来估计全体学生当年的阅读书籍数量的情况,下列估计中正确的是()(注:同一组数据用该组区间的中点值作为代表)A.众数为B.平均数为C.中位数为D.该校读书不低于本的人数约为人第(2)题已知函数在区间上单调递增,则实数a的取值范围是()A.B.C.D.第(3)题定义平面向量之间的一种运算“”如下,对任意的,,令,下面说法错误的是( )A.若与共线,则B.C.对任意的,有D.第(4)题已知函数,若不等式恒成立,则实数的取值范围是()A.B.C.D.第(5)题已知集合,,则().A.B.C.D.第(6)题过抛物线的焦点的直线与抛物线相交于M,N两点,若M,N两点到直线的距离之和等于11,则这样的直线()A.不存在B.有且仅有一条C.有且仅有两条D.有无穷多条第(7)题已知集合,,则()A.B.C.D.第(8)题在等差数列中,已知,则()A.4B.6C.8D.10二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题记为正项数列的前项和,为正项数列的前项积,则()A.若数列是等比数列,则数列是等差数列B.若数列是等比数列,则数列是等比数列C.若数列是等差数列,则数列是等比数列D.若数列是等比数列,则数列是等比数列第(2)题下列说法正确的是()A .若随机变量,则B.若随机变量,且,则C.一组数据11,12,12,13,14,15,16,18,20,22的第80百分位数为19D .若,,,则事件与事件相互独立第(3)题已知向量,则()A.若,则B.若,则C.的最大值为5D.若,则三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题已知数列是等差数列,,过点作直线的垂线,垂足为点,则的最大值为__________.第(2)题已知,若是关于的实系数方程的一个根,其中是虚数单位,则___________.第(3)题已知椭圆,C的上顶点为A,两个焦点为,,离心率为.过且垂直于的直线与C交于D,E两点,,则的周长是________________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题如图,在四棱锥中,底面为直角梯形,其中,,,为棱的中点,是棱上一点,且.(1)证明:平面;(2)若,直线与平面所成的角为,求平面与平面夹角的余弦值.第(2)题已知函数.(1)求函数的最小值;(2)证明:对于任意正整数,不等式成立.第(3)题已知曲线的参数方程为(为参数),直线过点.(1)求曲线的普通方程;(2)若直线与曲线交于,两点,且,求直线的倾斜角.第(4)题已知双曲线,焦点到渐近线的距离为2.(1)求双曲线的标准方程;(2)记双曲线的左、右顶点分别为,直线交双曲线于点(点在第一象限),记直线斜率为,直线斜率为,过原点做直线的垂线,垂足为,当为定值时,问是否存在定点,使得为定值,若存在,求此定点.若不存在,请说明理由.第(5)题已知函数.(1)证明:当时,有唯一的极值点为,并求取最大值时的值;(2)当时,讨论极值点的个数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008年普通高等学校统一考试(宁夏卷)数学(理科)一、选择题:本大题共12小题,每小题5分,满分60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知函数y=2sin(ωx+φ)(ω>0)在区间[0,2π]的图像如下:那么ω=A. 1B. 2C. 1/2D. 1/32、已知复数1z i =-,则221z zz -=- A. 2iB. -2iC. 2D. -23、如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为 A. 5/18B. 3/4C.3/2D. 7/84、设等比数列{}n a 的公比2q =,前n 项和为n S ,则42S a = A. 2 B. 4 C.152D.1725、右面的程序框图,如果输入三个实数a 、b 、c ,要求输出这三个数中 最大的数,那么在空白的判断框中,应该填入下面四个选项中的 A. c > x B. x > cC. c > bD. b > c6、已知1230a a a >>>,则使得2(1)1i a x -<(1,2,3)i =都成立的x取值范围是 A.(0,11a ) B. (0,12a ) C. (0,31a ) D. (0,32a )7、0203sin 702cos 10--=A.12B.22C. 2D.328、平面向量b a ,共线的充要条件是A. b a ,方向相同B. b a ,两向量中至少有一个为零向量C. R λ∃∈,a b λ=D. 存在不全为零的实数1λ,2λ,021=+b a λλ9、甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面。
不同的安排方法共有 A. 20种B. 30种C. 40种D. 60种是否 开始输入x=ab>x 输出x结束x=bx=c否 是10、由直线21=x ,x=2,曲线xy 1=及x 轴所围图形的面积为 A. 415 B. 417 C. 2ln 21 D. 2ln 211、已知点P 在抛物线y 2 = 4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为A. (41,-1) B. (41,1) C. (1,2) D. (1,-2) 12、某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a + b 的最大值为A. 22B. 32C. 4D. 52二、填空题:本大题共4小题,每小题5分,满分20分。
13、已知向量(0,1,1)a =-r ,(4,1,0)b =r,||a b λ+=r r0λ>,则λ= ____________14、过双曲线221916x y -=的右顶点为A ,右焦点为F 。
过点F 平行双曲线的一条渐近线的直线与双曲线交于点B ,则△AFB 的面积为______________15、一个六棱柱的底面是正六边形,其侧棱垂直底面。
已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为98,底面周长为3,那么这个球的体积为 _________ 16、从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm ),结果如下: 由以上数据设计了如下茎叶图:①__________________________________________________________________________ ②__________________________________________________________________________甲品种: 271 273 280 285 285 287 292 294 295 301 303 303 307 308 310 314 319 323 325 325 328 331 334 337 352 乙品种:284292295304306307312313315315316318318320 322 322 324 327 329 331 333 336 337 343 356三、解答题:本大题共6小题,满分70分。
解答须写出文字说明,证明过程和演算步骤。
17、(本小题满分12分)已知数列{}n a 是一个等差数列,且21a =,55a =-。
(1) 求{}n a 的通项n a ;(2) 求{}n a 前n 项和n S 的最大值。
18、(本小题满分12分)如图,已知点P 在正方体ABC D -A 1B 1C 1D 1的对角线 BD 1上,∠PDA=60°。
(1) 求DP 与CC 1所成角的大小;(2) 求DP 与平面AA 1D 1D 所成角的大小。
19、(本小题满分12分)A 、B 两个投资项目的利润率分别为随机变量X 1和X 2。
根据市场(1) 在A 、B 两个项目上各投资100万元,Y 1和Y 2分别表示投资项目A 和B 所获得的利润,求方差DY 1、DY 2;(2) 将x (0≤x ≤100)万元投资A 项目,100-x 万元投资B 项目,f(x)表示投资A项目所得利润的方差与投资B 项目所得利润的方差的和。
求f(x)的最小值,并指出x 为何值时,f(x)取到最小值。
(注:D(aX + b) = a 2DX )20、(本小题满分12分)在直角坐标系xOy 中,椭圆C 1:22221(0)x y a b a b+=>>的左、右焦点分别为F 1、F 2。
F 2也是抛物线C 2:24y x =的焦点,点M 为C 1与C 2在第一象限的交点,且25||3MF =。
(1) 求C 1的方程;(2) 平面上的点N 满足12MN MF MF =+uuu r uuu r uuu u r,直线l ∥MN ,且与C 1交于A 、B 两点,若OA uu r ·OB uu u r =0,求直线l 的方程。
21、(本小题满分12分)设函数1()(,)f x ax a b Z x b=+∈+,曲线()y f x =在点(2,(2))f 处的切线方程为3y =。
(1) 求()y f x =的解析式;(2) 证明:曲线()y f x =的图像是一个中心对称图形,并求其对称中心; (3) 证明:曲线()y f x =上任一点的切线与直线1x =和直线y x =所围三角形的面积为定值,并求出此定值。
1A请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题记分。
做答时用2B 铅笔在答题卡上把所选题目对应的题号涂黑。
22、(本小题满分10分)选修4-1:几何证明选讲如图,过圆O 外一点M 作它的一条切线,切点为A ,过A 作直线AP 垂直直线OM ,垂足为P 。
(1)证明:O M ·OP = OA 2;(2)N 为线段AP 上一点,直线NB 垂直直线ON ,且交圆O 于B 点。
过B 点的切线交直线ON 于K 。
证明:∠OKM = 90°。
23、(本小题满分10分)选修4-4:坐标系与参数方程已知曲线C 1:cos ()sin x y θθθ=⎧⎨=⎩为参数,曲线C 2:()x t y ⎧=⎪⎪⎨⎪=⎪⎩为参数。
(1)指出C 1,C 2各是什么曲线,并说明C 1与C 2公共点的个数;(2)若把C 1,C 2上各点的纵坐标都压缩为原来的一半,分别得到曲线1'C ,2'C 。
写出1'C ,2'C 的参数方程。
1'C 与2'C 公共点的个数和C 1与C 2公共点的个数是否相同?说明你的理由。
24、(本小题满分10分)选修4-5:不等式选讲已知函数|4||8|)(---=x x x f 。
(1) 作出函数)(x f y =的图像; (2) 解不等式2|4||8|>---x x 。
参考答案一、选择题 1.B 2.B 3.D 4.C 5.A 6.B 7.C 8.D 9.A10.D11.A12.C二、填空题 13.314.321515.43π 16.1.乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度(或:乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度).2.甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散.(或:乙品种棉花的纤维长度较甲品种棉花的纤维长度更集中(稳定).甲品种棉花的纤维长度的分散程度比乙品种棉花的纤维长度的分散程度更大).3.甲品种棉花的纤维长度的中位数为307mm ,乙品种棉花的纤维长度的中位数为318mm . 4.乙品种棉花的纤维长度基本上是对称的,而且大多集中在中间(均值附近).甲品种棉花的纤维长度除一个特殊值(352)外,也大致对称,其分布较均匀.三、解答题 17.解:(Ⅰ)设{}n a 的公差为d ,由已知条件,11145a d a d +=⎧⎨+=-⎩,解出13a =,2d =-.所以1(1)25n a a n d n =+-=-+. (Ⅱ)21(1)42n n n S na d n n -=+=-+24(2)n =--. 所以2n =时,n S 取到最大值4. 18.解:如图,以D 为原点,DA则(100)DA =,,uu u r ,(001)CC '=,,u u u r .连结BD ,B D ''.在平面BB D D ''中,延长DP 交B D ''于H .设(1)(0)DH m m m =>,,u u u r,由已知60DH DA <>=,o uuu r uu u r, 由cos DA DH DA DH DADH =<>,uu u r uuu r uu u r uuu r uu u r uuu rg 可得2m =解得m =,所以122DH ⎛⎫= ⎪ ⎪⎝⎭,uuu r .(Ⅰ)因为0011cos DH CC +⨯+⨯'<>==,uuu r uuu r所以45DH CC '<>=,o uuu r uuu r. 即DP 与CC '所成的角为45o.(Ⅱ)平面AA D D ''的一个法向量是(010)DC =,,u u u r.因为01101cos 2DH DC ⨯+⨯+⨯<>==,uuu r uuu r , 所以60DH DC <>=,o uuu r uuu r. 可得DP 与平面AA D D ''所成的角为30o. 19.解:(Ⅰ)由题设可知1Y 和2Y 的分布列分别为150.8100.26EY =⨯+⨯=,221(56)0.8(106)0.24DY =-⨯+-⨯=,220.280.5120.38EY =⨯+⨯+⨯=,2222(28)0.2(88)0.5(128)0.312DY =-⨯+-⨯+-⨯=.(Ⅱ)12100()100100x x f x D Y D Y -⎛⎫⎛⎫=+⎪ ⎪⎝⎭⎝⎭2212100100100x x DY DY -⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭22243(100)100x x ⎡⎤=+-⎣⎦2224(46003100)100x x =-+⨯, 当6007524x ==⨯时,()3f x =为最小值.20.解:(Ⅰ)由2C :24y x =知2(10)F ,. 设11()M x y ,,M 在2C 上,因为253MF =,所以1513x +=, 得123x =,1y =.M 在1C 上,且椭圆1C 的半焦距1c =,于是 222248193 1.a b b a ⎧+=⎪⎨⎪=-⎩, 消去2b 并整理得 4293740a a -+=,解得2a =(13a =不合题意,舍去). 故椭圆1C 的方程为22143x y +=. (Ⅱ)由12MF MF MN +=uuu r uuu u r uuu r知四边形12MF NF 是平行四边形,其中心为坐标原点O , 因为l MN ∥,所以l 与OM 的斜率相同,故l的斜率323k ==设l的方程为)y x m =-.由223412)x y y x m ⎧+=⎪⎨=-⎪⎩,,消去y 并化简得 22916840x mx m -+-=.设11()A x y ,,22()B x y ,,12169m x x +=,212849m x x -=.因为OA OB ⊥uu r uu u r,所以12120x x y y +=. 121212126()()x x y y x x x m x m +=+-- 2121276()6x x m x x m =-++22841676699m m m m -=-+g g21(1428)09m =-=.所以m =.此时22(16)49(84)0m m ∆=-⨯->, 故所求直线l的方程为y =-y =+21.解: (Ⅰ)21()()f x a x b '=-+,于是2123210(2)a b a b ⎧+=⎪+⎪⎨⎪-=+⎪⎩,,解得11a b =⎧⎨=-⎩,, 或948.3a b ⎧=⎪⎪⎨⎪=-⎪⎩,因a b ∈Z ,,故1()1f x x x =+-. (Ⅱ)证明:已知函数1y x =,21y x=都是奇函数. 所以函数1()g x x x=+也是奇函数,其图像是以原点为中心的中心对称图形. 而1()111f x x x =-++-. 可知,函数()g x 的图像按向量(11)=,a 平移,即得到函数()f x 的图像,故函数()f x 的图像是以点(11),为中心的中心对称图形. (Ⅲ)证明:在曲线上任取一点00011x x x ⎛⎫+⎪-⎝⎭,. 由0201()1(1)f x x '=--知,过此点的切线方程为2000200111()1(1)x x y x x x x ⎡⎤-+-=--⎢⎥--⎣⎦. 令1x =得0011x y x +=-,切线与直线1x =交点为00111x x ⎛⎫+ ⎪-⎝⎭,. 令y x =得021y x =-,切线与直线y x =交点为00(2121)x x --,. 直线1x =与直线y x =的交点为(11),.从而所围三角形的面积为00000111212112222121x x x x x +---=-=--.所以,所围三角形的面积为定值2.22.解:(Ⅰ)证明:因为MA 是圆O 的切线,所以OA AM ⊥. 又因为AP OM ⊥.在Rt OAM △中,由射影定理知,2OA OM OP =g .(Ⅱ)证明:因为BK 是圆O 的切线,BN OK ⊥.同(Ⅰ),有2OB ON OK =g,又OB OA =, 所以OP OM ON OK =g g ,即ON OMOP OK=. 又NOP MOK =∠∠,所以ONP OMK △∽△,故90OKM OPN ==o∠∠. 23.解:(Ⅰ)1C 是圆,2C 是直线.1C 的普通方程为221x y +=,圆心1(00)C ,,半径1r =. 2C的普通方程为0x y -+=.因为圆心1C到直线0x y -=的距离为1, 所以2C 与1C 只有一个公共点. (Ⅱ)压缩后的参数方程分别为1C ':cos 1sin 2x y θθ=⎧⎪⎨=⎪⎩,(θ为参数); 2C ':24x y ⎧=-⎪⎪⎨⎪=⎪⎩(t 为参数). 化为普通方程为:1C ':2241x y +=,2C ':122y x =+,联立消元得2210x ++=,其判别式24210∆=-⨯⨯=,所以压缩后的直线2C '与椭圆1C '仍然只有一个公共点,和1C 与2C 公共点个数相同. 24.解:(Ⅰ)44()2124848.x f x x x x ⎧⎪=-+<⎨⎪->⎩, ≤,, ≤,图像如下:(Ⅱ)不等式842x x --->,即()2f x >, 由2122x -+=得5x =.由函数()f x 图像可知,原不等式的解集为(5)-∞,.。
