大学理论力学第四章思考题及答案
理论力学第四章习题答案

理论力学第四章习题答案理论力学第四章习题答案在理论力学的学习过程中,习题是非常重要的一部分。
通过解答习题,我们可以巩固理论知识,加深对概念和原理的理解,并培养解决实际问题的能力。
本文将为大家提供理论力学第四章习题的详细答案,希望能够对大家的学习有所帮助。
1. 一个质点在力F作用下做直线运动,已知力的大小与时间的关系为F = kt,其中k为常数。
求质点的速度与时间的关系。
解答:根据牛顿第二定律F = ma,将力的大小与时间的关系代入,得到ma = kt。
由于质点做直线运动,所以速度的变化率等于加速度,即v = ∫a dt。
将上式代入,得到v = ∫(kt/m) dt = (k/m)∫t dt = (k/m)(t^2/2) + C。
其中C为积分常数。
因此,质点的速度与时间的关系为v = (k/m)(t^2/2) + C。
2. 一个质点在力F作用下做直线运动,已知力的大小与位置的关系为F = -kx,其中k为常数。
求质点的加速度与位置的关系。
解答:根据牛顿第二定律F = ma,将力的大小与位置的关系代入,得到ma = -kx。
由于质点做直线运动,所以加速度的变化率等于速度的变化率,即a =dv/dt。
将上式代入,得到dv/dt = -kx/m。
将变量分离,得到dv = (-kx/m) dt。
对两边同时积分,得到∫dv = ∫(-kx/m) dt。
积分后得到v = (-kx^2/2m) + C1,其中C1为积分常数。
再次对上式积分,得到∫v dx = ∫((-kx^2/2m) + C1) dx。
积分后得到x = (-kx^3/6m) + C1x + C2,其中C2为积分常数。
因此,质点的加速度与位置的关系为a = (-kx/m)。
3. 一个质点在势能函数U(x) = kx^2/2下做直线运动,已知质点的质量为m。
求质点的速度与位置的关系。
解答:根据势能函数U(x) = kx^2/2,可以求得力的大小与位置的关系为F = -dU(x)/dx = -kx。
理论力学课后答案4

魏 魏 魏
后
泳 泳 泳
ww
涛 涛 涛
m
课
答
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
案
网
w.
kh
da
xi (2i 1)a cos , yi a sin 轨迹: xi2 yi2 a 2 2 (2i 1)
w.
co
解:以 A1 为对象研究 x a cos , y a sin 同理, Ai (i 2,3,4) 的运动方程为
kh
da
w.
co
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
4.8 飞轮边缘上一点 M ,随飞轮以匀速 v 10 m s 运动。后因刹车,该点以 at 0.1t m s 2 作减速运动。设轮半径 R 0.4m ,求 M 点在减速运动过程中的运 动方程及 t 2s 时的速度、切向和法向加速度。 解:
魏
at
2 2 v vx vy 2500 4t 2
泳 泳 泳
ww
涛 涛 涛
m
加速度的直角分量 ax 0 , a y 2 切向加速度为
dv 4t dt 2500 4t 2 当 t 0s 时, at 0 ,所以
2 2 an a 2 at2 ax ay at2 2 m s 2
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
4.1 一动点按 s t 2 6t 1的规律沿直线运动,式中,时间 t 以秒( s )计,坐标 s 以 米( m )计。试求: (1)最初 5s 内的位移; (2)动点改变运动方向的时刻和所在位置; (3)最初 5s 内动点经过的路程; (4) t 5s 时动点的速度和加速度; (5)动点在哪段时间内作加速运动,哪段时间内作减速运动。
理论力学(胡运康)第四章作业答案
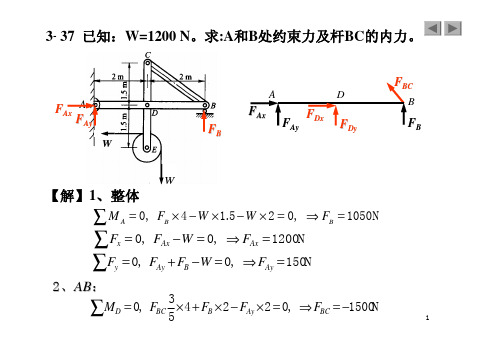
2、AB:
3 M = 0 , F N ∑ D BC × 4 + FB × 2 − FAy × 2 = 0, ⇒ F BC = −1500 5
1
3-39 已知q,M=qa2 。求铰链D受的力;铰链B受的力。
D FDx FDy
qa
C FCy FCx
FDx FDy
FB3
a 3 解: 1、整体 : ∑ M A = 0, FB 3 ⋅ a − qa ⋅ − M = 0, ⇒ FB 3 = qa 2 2 1 M = 0 , F ⋅ a + qa ⋅ a = 0 , ⇒ F = qa 2、DC: ∑ C Dy Dy 2 1 ⇒ FCy = qa ∑ Fy = 0, FDy + FCy − qa = 0, 2
∑ Fy = 0, FAy − 30 + FBC ⋅
3-73 已知M2 、M3 ,AB=d1 、BC=d2 、CD=d3 ,求M1及 A、D处约束力。
FAz FAy
【解】整体:
M3 ⇒ FAy = ∑ M z = 0, M 3 − FAy ⋅ d1 = 0, d1 M2 ⇒ FAz = ∑ M y = 0, M 2 − FAz ⋅ d1 = 0, d1
6
3-53 求桁架中杆BH、CD和GD的内力。
1
FIH 0 FBH
FE
FB 1
FBC
FE
解: FGD = 0 1、整体:
2、1-1面左边:∑ Fy = 0, FE − 60 − FBH
∑M
B
= 0, FE ×15+ 60×10 = 0, ⇒ FE = 26.67kN
1 = 0, ⇒ FBH = −47.1kN 2
∑M
G
《理论力学》第四章 静力学应用专题习题解
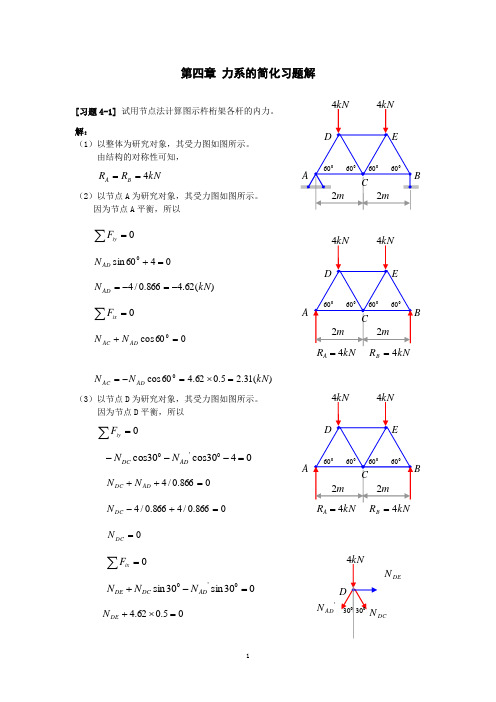
第四章 力系的简化习题解[习题4-1] 试用节点法计算图示杵桁架各杆的内力。
解:(1)以整体为研究对象,其受力图如图所示。
由结构的对称性可知, kN R R B A 4==(2)以节点A 为研究对象,其受力图如图所示。
因为节点A 平衡,所以0=∑iyF0460sin 0=+AD N)(62.4866.0/4kN N AD -=-=0=∑ixF060cos 0=+AD AC N N)(31.25.062.460cos 0kN N N AD AC =⨯=-= (3)以节点D 为研究对象,其受力图如图所示。
因为节点D 平衡,所以 0=∑iyF0430cos 30cos 0'0=---AD D C N N 0866.0/4=++AD D C N N 0866.0/4866.0/4=+-D C N0=DC N0=∑ixF030sin 30sin 0'0=-+AD D C D E N N N 05.062.4=⨯+DE NkN4)(akN4AB RkN 2AC23N A )(31.2kN N DE -=(4)根据对称性可写出其它杆件的内力如图所示。
[习题4-2] 用截面法求图示桁架指定杆件 的内力。
解:(a)(1)求支座反力以整体为研究对象,其受力图如图所示。
由对称性可知,kN R R B A 12==(2)截取左半部分为研究对象,其受力图 如图所示。
因为左半部分平衡,所以0)(=∑i CF M0612422843=⨯-⨯+⨯+⨯N 063243=⨯-++N )(123kN N =kN2AC23N A0=∑ixF0cos cos 321=++N N N αθ01252252421=+⋅+⋅N N012515221=+⋅+⋅N N0512221=++N N ……..(1) 0=∑iyF02812sin sin 21=--++αθN N025*******=+⋅+⋅N N02525121=+⋅+⋅N N052221=++N N0544221=++N N ……..(2) 05832=-N)(963.53/582kN N ==)(399.1652963.5252221kN N N -=-⨯-=--=解:(b )截取上半部分为研究对象,其受力图如图所示。
理论力学答案第四章
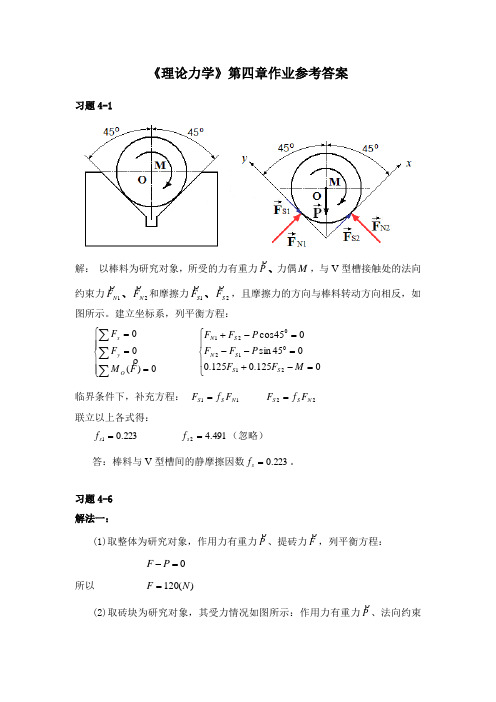
《理论力学》第四章作业参考答案习题4-1解: 以棒料为研究对象,所受的力有重力P、力偶M ,与V 型槽接触处的法向约束力1N F 、2N F 和摩擦力1S F 、2S F,且摩擦力的方向与棒料转动方向相反,如图所示。
建立坐标系,列平衡方程:⎪⎪⎩⎪⎪⎨⎧===∑∑∑0)(00F M F F O y x⎪⎩⎪⎨⎧=-+=--=-+0125.0125.0045sin 045cos 21012021M F F P F F P F F S S S N S N 临界条件下,补充方程: 11N S S F f F = 22N S S F f F = 联立以上各式得:223.01=s f491.42=s f (忽略)答:棒料与V 型槽间的静摩擦因数223.0=s f 。
习题4-6 解法一:(1)取整体为研究对象,作用力有重力P 、提砖力F,列平衡方程:0=-P F所以 )(120N F =(2)取砖块为研究对象,其受力情况如图所示:作用力有重力P、法向约束力NA F 、ND F 和摩擦力SA F 、SD F,由于其滑动趋势向下,所以其摩擦力的方向向上。
列平衡方程:∑=0)(F M D0250125=-SA F P补充方程: NA S SA F f F ≤ 所以)(60N F SA =)(160N F NA ≥(3)取构件AGB 为研究对象,所受的力除提砖力F外,还有砖块对其作用的正压力NAF ' 、摩擦力SA F ' ,G 点的约束力G X F 、G Y F 。
列平衡方程: ∑=0)(F M G03095='-'+NA SAF b F F 其中NAF ' 与砖块所受的力NA F 、SA F ' 与砖块所受的力SA F分别为作用力与反作用力关系,将各力的数值代入得)(110mm b ≤答:距离mm b 110≤时才能把砖夹起。
解法二:取构件GCD 为研究对象,受力情况如图所示。
哈尔滨工业大学 第7版 理论力学 第4章 课后习题答案

解 (1)方法 1,如图 4-6b 所示,由已知得
Fxy = F cos 60° , Fz = F cos 30°
F = F cos 60°cos 30°i − F cos 60°sin 30° j − F sin 60°k = 3 i − 1 Fj − 3 Fk 44 2
41
理论力学(第七版)课后题答案 哈工大.高等教育出版社
A
F
β
MA
C
MB
F
10 N
β M θ − 90° C
MB
(a)
(b)
(c)
图 4-11
解 画出 3 个力偶的力偶矩矢如图 4-11b 所示,由力偶矩矢三角形图 4-11c 可见
MC =
M
2 A
+
M
2 B
=
3 0002 + 4 0002 = 5 000 N ⋅ mm
由图 4-11a、图 4-11b 可得
3 = 250 N 13
FRz = 100 − 200 ×
1 = 10.6 N 5
M x = −300 ×
3 × 0.1 − 200 × 1 × 0.3 = −51.8 N ⋅ m
13
5
M y = −100 × 0.20 + 200 ×
2 × 0.1 = −36.6 N ⋅ m 13
M z = 300 ×
z
F45° F3 F3′ B
F2A
E
F1
C
F5
F6
F F4 45°
D
y
K x
M
(a)
(b)
图 4-9
解 (1) 节点 A 为研究对象,受力及坐标如图 4-9b 所示
力学答案第四章

(1),, ,处势能为零处势能为零N=F =mg×表示弹簧的伸长量,拉伸至弹簧的劲度不变。
拉伸至拉伸,外界做功,弹性力做负功。
缩短,弹性力做正功。
垂直方向的两个分位移(∴∵,∴向右,。
为常量,活塞末速坐标系与作匀速直线运动。
,, 沿∵∴∵∴∴)的作用而发生偏转∴、、做功之和为零。
质点组所力情况如图:为框架的绝对速度。
它。
坐标原点置于弹簧和有势能。
外界压缩弹簧做功使:外力做功:外力做功和地面支持力作用。
(忽略摩擦)。
重力为保不做功,所以机械能守恒。
沿水平方向,说明正好到达抛物线不做功。
( 1 )∵作用,4 ;。
(( 2 )(高度),开始向上运动。
如此往复。
((,碰撞后质点移动的最。
=0.790kg=100m/s 内,问弹簧((为共同速度)((为子弹、小鸟共同速度)和;(是再度下滑到平面轨道的速度)代入此式。
铁箱与地面间无摩擦。
铁箱被加速至时开始做匀速直线运动。
后来,钢球与箱壁发生完全弹性碰撞。
问碰后再经过多长时间钢球与为小球碰撞前后速度。
运动。
另一车厢以从相反方向向左运动并与左车厢碰撞挂钩,货箱在地板上滑行的最大距离为(角散射。
((完全弹性碰撞)(((。
哈尔滨工业大学第7版理论力学第4章课后习题答案_图文(精)

0=∑z M ,0m 075.0m 2.0=+×−×z y x M F F (6解得N 150=Ox F ,N 75=Oy F ,N 500=Oz F ;
m N 100⋅=x M ,m N 5.37⋅−=y M (与图示反向,m N 4.24⋅−=z M (与图示反向4-14图4-14a所示电动机以转矩M通过链条传动将重物P等速提起,链条与水平线
bn20n20cmam90n10n10abmcffa?90mbmcmabc图411解画出3个力偶的力偶矩矢如图411b所示由力偶矩矢三角形图411c可见40003bacmmm由图411a图411b可得mf解mmn00050002222?mm100fmcn50mm100c由图411b图411c可得41433tanbam?m5236873608180412图412a所示手摇钻由支点b钻头a和1个弯曲的手柄组成
6.10250345(R k j i ++−=F主矩
m N 12222
2⋅=++=
z y x O M M M M ,m N 1046.368.51(⋅+−−=k j i O M
4-2 1平行力系由5个力组成,力的大小和作用线的位置如图4-2所示。图中小正方格
的边长为10 mm。求平行力系的合力。
解由题意得合力R F的大小为
解得
kN 4.26−==B A F F (压kN 5.33=C F (拉
x y
P
D
z
A
F C F °30°
45°
15C
°45B F O
(a (b
图4-7
4-8在图4-8a
所示起重机中,已知:
AB=BC=AD=AE ;点A ,B ,D和E等均为球铰链连接,如三角形ABC的投影为AF线,AF与y轴夹角为α。求铅直支柱和各斜杆的内力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章思考题
4.1为什么在以角速度ω转动的参照系中,一个矢量G 的绝对变化率应当写作G ωG G ⨯+=*dt
d dt d ?在什么情况下0=*dt
d G ?在什么情况下0=⨯G ω?又在什么情况下0=dt d G ? 4.2式(4.1.2)和式(4.2.3)都是求单位矢量i 、j 、k 对时间t 的微商,它们有何区别?你能否由式(4.2.3)推出式(4.1.2)?
4.3在卫星式宇宙飞船中,宇航员发现自己身轻如燕,这是什么缘故?
4.4惯性离心力和离心力有哪些不同的地方?
4.5圆盘以匀角速度ω绕竖直轴转动。
离盘心为r 的地方安装着一根竖直管,管中有一物体沿管下落,问此物体受到哪些惯性力的作用?
4.6对于单线铁路来讲,两条铁轨磨损的程度有无不同?为什么?
4.7自赤道沿水平方向朝北或朝南射出的炮弹,落地是否发生东西偏差?如以仰角 40朝北射出,或垂直向上射出,则又如何?
4.8在南半球,傅科摆的振动面,沿什么方向旋转?如把它安装在赤道上某处,它旋转的周期是多大?
4.9在上一章刚体运动学中,我们也常采用动坐标系,但为什么不出现科里奥利加速度?
第四章思考题解答
4.1.答:矢量G 的绝对变化率即为相对于静止参考系的变化率。
从静止参考系观察变矢量G 随转动系以角速度ω相对与静止系转动的同时G 本身又相对于动系运动,所以矢量G 的绝对变化率应当写作
G ωG G ⨯+=*dt d dt d 。
其中
dt
d G *是G 相对于转动参考系的变化率即相对变化率;G ω⨯是G 随动系转动引起G 的变化率即牵连变化率。
若G 相对于参考系不变化,则有0=*dt
d G ,此时牵连运动就是绝对运动,G ωG ⨯=dt
d ;若0=ω即动系作动平动或瞬时平动,则有0=⨯G ω此时相对运动即为绝对运动 dt
d dt d G G *=;另外,当某瞬时G ω//,则0=⨯G ω,此时瞬时转轴与G 平行,此时动系的转动不引起G 的改变。
当动系作平动或瞬时平动且G 相对动系瞬时静止时,则有
0=dt
d G ;若G 随动系转动引起的变化G ω⨯与相对动系运动的变化dt d G *等值反向时,也有0=dt d G 。
4.2.答:式(4.1.2)j i ω=dt d i j ω-=dt
d 是平面转动参考系的单位矢对时间的微商,表示由于动系转动引
起j i ,方向的变化率。
由于动坐标系中的z 轴静止不动。
故有
0=dt d k ;又ω恒沿z 轴方位不变,故不用矢积形式完全可以表示dt d i 和dt
d j 。
式(4.2.3)i ωi ⨯=dt d ,j ωj ⨯=dt d k ωk ⨯=dt
d 是空间转动坐标系的单位矢对时间的微商,表示由于动系转动引起k j i ,,方向的变化率,因动系各轴都转动
0≠dt d k ;又ω在空间的方位随时间改变际不同时刻有不同的瞬时转轴,故必须用矢积表示 dt
d dt d dt d k j i ,,。
(4.1.2)是(4.2.3)的特例,当k ω//代入(4.2.3)j j ωi ω=⨯=dt d ,j ωj ⨯=dt d ,0=dt
d k 即为(4.1.2)式。
不能由式(4.1.2)推出(4.2.3)。
4.3.答:人随卫星式飞船绕地球转动过程中受到惯性离心力作用,此力与地心引力方向相反,使人处于失重状态,故感到身轻如燕。
4.4.答:惯性离心力是随转动坐标系一起转动的物体受到惯性离心力,它作用于随动系一起转动的物体上,它不是物体间的相互作用产生的,也不是产生反作用力,是物体的惯性在非惯性系的反映;离心力是牛顿力,是作用于给曲线运动提供向心力的周围物体上的力,或者说离心力是作用于转动坐标系上的力,它是向心力的反作用力。
4.5.答:如题4.5所示,
题4-5图
由于物体m 相对于圆盘的速度矢量ωv //',故科里奥利力02='⨯-v ωm ;又0==ωω 恒矢量,,故牵连切向惯心力0=⨯-r ω m ;所以物体只受到牵连法向惯性力即惯性离心力的作用,如图示2ωmr F =惯,方向垂直于转轴向外。
4.6.答;单线铁路上,南来北往的列车都要通过,以北半球为例,火车受到的科氏惯性力总是指向运动方向的右侧(南半球相反),从北向南来的列车使西侧铁轨稍有磨损,故两条铁轨的磨损程度并不相同。
4.7.答:抛体的落地偏差是由于科里奥利力m v ω'⨯-2引起的,当炮弹自赤道水平方向朝北或朝正南射出时,出刻v ω'//,科里奥利力为零,但炮弹运行受重力作用改变方向使得ω与v '不平行02≠'⨯-v ωm ,朝北和朝南射出的炮弹都有向东的落地偏差。
若以仰角 40或垂直向上射出,炮弹上升和降落过程中科氏
惯性力方向相反,大小相等,且上升时间等于下降时间,故落地无偏差。
4.8.答:单摆震动面的旋转是摆锤 受到科里奥利力v ω'⨯-m 2的缘故,其中m 是摆锤的质量,ω是地球绕地轴的自转角速度,v '是摆锤的速度。
南半球上摆锤受到的科氏力总是指向起摆动方向的左侧,如题
4.8图是南半球上单摆的示意图,若没有科氏惯性力,单摆将沿AB 摆动,事实上由于科里奥利力的作用单摆从A 向B 摆动逐渐向左侧移动到达C 点,从C 点向回摆动过程中逐渐 左偏到达D 点,以此推论,摆动平面将沿逆时针方向偏转。
科里奥利力很小,每一次摆动,平面的偏转甚微,必须积累很多次摆动,才显出可觉察的偏转。
题4-8图
(图中是为了便于说明而过分夸张的示意图)。
由λ
ωπsin 2='C ,在赤道上纬度∞='=C ,0λ,即在赤道上摆动平面不偏转。
这里不难理解的,若摆动平面沿南北方向,v ω'//,科氏惯性力为零;若单摆平面沿东西方位,则科氏力一定在赤道平面与B 单摆的摆动平面共面,故不会引起摆动平面的偏转。
4.9.答:在上一章刚体运动学中,动系固连于刚体一起转动,但刚体上任一点相对于动坐标系没有相对运动,即各点的相对速度0='v ,故科里奥利加速度02='⨯=v ωa c 。
事实上,科氏加速度是牵连转动与相对运动相互影响而产生的,没有相对运动,就谈不到科里奥利加速度的存在。
