八年级数学一次函数同步练习题
八年级数学一次函数同步练习题
人教新课标八年级数学（上）一、填空题（每题2分，共32分）1．已知一个正比例函数的图象经过点（-1，3），则这个正比例函数的表达式是 ．2．函数y =x 的取值范围是_______________．3．已知一次函数y =2x +4的图像经过点（m ，8），则m ＝________．4．若函数y = -2x m +2 +n -2正比例函数，则m 的值是 ，n 的值为________． 5．一次函数113y x =-+的图象与x 轴的交点坐标是_________，与y 轴的交点坐标是__________． 6．若直线y =kx +b 平行于直线y =5x +3，且过点（2，-1），则k =______，b =______． 7．两直线1y x =-与3y x =-+的交点坐标 ．8．某种储蓄的月利率为0.15%，现存入1000元，则本息和y （元）与所存月数x 之间的函数关系式是 ． 9．某一次函数的图象经过点（1-，3），且函数y 随x 的增大而减小，请你写出一个符合条件的函数解析式______________________．10．现有笔记本500本分给学生，每人5本，则余下的本数y 和学生数x 之间的函数解析式为_________________，自变量x 的取值范围是______________． 11．若一次函数y ＝kx －4当x ＝2时的值为0，则k ＝ ． 12．一次函数12-=x y 一定不经过第 象限．13．已知直线6+=x y 与x 轴,y 轴围成一个三角形,则这个三角形面积为 . 14．如右图：一次函数y kx b =+的图象经过A 、B 两点，则△AOC 的面积为___________． 15．观察下列各正方形图案，每条边上有n (n ＞2)个圆点，每个图案中圆 点的总数是S ．按此规律推断出S 与n 的关系式为 ．二、解答题（共68分）17．（4分）已知一个一次函数，当3x =时，2y =-；当2x =时，3y =-，求这个一次函数的解析式已知，直线y kx b =+经过点A （3，8）和B （6-，4-）．求： （1）k 和b 的值；（2）当3x =-时，y 的值．＝4 S ＝12 n ＝2 S ＝4 n ＝3 S ＝818．（4分）已知正比例函数y kx =．（1）若函数图象经过第二、四象限，则k 的范围是什么？ （2）点（1，－2）在它的图像上，求它的表达式．19．（4分）已知2y -与x 成正比，且当1x =时，6y =-．（1）求y 与x 之间的函数关系式； （2）若点（a ，2）在这个函数图象上，求a ．21．（6分）已知函数(21)3y m x m =++-，（1）若函数图象经过原点，求m 的值；（2）若这个函数是一次函数，且y 随着x 的增大而减小，求m 的取值范围．22．（6分）作出函数24y x =-的图象，并根据图象回答下列问题：（1）当 -2≤x ≤4时，求函数y 的取值范围； （2）当x 取什么值时，y <0，y =0，y>0? （3）当x 取何值时，-4<y <2？23．（6分）图中折线ABC 表示从甲地向乙地打长途电话时所需付的电话费y （元）与通话时间t （分钟）之间的关系图像．（1）从图像知，通话2分钟需付的电话费是 元． （2）当t ≥3时求出该图像的解析式（写出求解过程）． （3）通话7分钟需付的电话费是多少元？24．（6分）已知等腰三角形的周长为12cm ，若底边长为y cm ，一腰长为x cm.． （1）写出y 与x 的函数关系式； （2）求自变量x 的取值范围． 25．（6分）某产品每件成本10元，试销阶段每件产品的销售价x （元）与产品的日销售量y （件）之间的关系如下表：若日销售量y 是销售价x 的一次函数．（1）求出日销售量y （件）与销售价x （元）的函数关系式； （2）求销售价定为30元时，每日的销售利润． 26．（6分）某公司在A 、B 两地分别有库存机器16台和12台，现要运往甲、乙两地，其中甲地15台，乙地13台．从A 地运一台到甲地的运费为500元，到乙地为400元；从B 地运一台到甲地的运费为300元，到乙地为600元．公司应设计怎样的调运方案，能使这些机器的总运费最省？27．（8分）已知直线AB 与x ，y 轴分别交于A 、B （如图），AB =5，OA =3， （1）求直线AB 的函数表达式；（2）如果P 是线段AB 上的一个动点（不运动到A ，B ），过P 作x 轴的垂线，垂足是M ，连接PO ，设OM =x ，图中哪些量可以表示成x 的函数？试写出5个不同的量关于x 的函数关系式．（这里的量是指图中某些线段的长度或某些几何图形的面积等） 28．（8分）2007年5月，第五届中国宜昌长江三峡国际龙舟拉力赛在黄陵庙揭开比赛帷幕．20日上午9时，参赛龙舟从黄陵庙同时出发．其中甲、乙两队在比赛时，路程y （千米）与时间x （小时）的函数关系如图所示．甲队在上午11时30分到达终点黄柏河港． （1）哪个队先到达终点？乙队何时追上甲队？ （2）在比赛过程中，甲、乙两队何时相距最远？时间/时164020八年级数学（上）自主学习达标检测（五）一、填空题1．3y x =- 2．25x ≥ 3．2 4．1,2- 5．（3，0）（0，1）6．5，11- 7．（2，1）8．0.15%1000y x =+ 9．3y x =- 10．5005,100y x x =-≤ 11．2 12．Fg 13．18 14．9 15．1216．44S n =-二、解答题17．（1）1,5k b ==-；（2）8- 18．（1）k ＜0；（2）2y x =- 19．（1）82y x =-+；（2）0a = 20．14x y =-⎧⎨=-⎩21．（1）3m =；（2）m ＜12-22．（1）84y -≤≤；（2）x ＜2，x =2，x ＞2；（3）0＜x ＜3 23．（1）2.4；（2） 1.52y x =-；（3）8.5 24．（1）122y x =-；（2）x ＜6 25．（1）40y x =-+；（2）200元 26．A 地运3台到甲地，运13台到乙地；B 地12台全部运往甲地 27．（1）334y x =-+；（2）23333,482POM PM x S x x =-+=-+13(4)(3)24PMB S x x =--+,34,2PAOBM x Sx =-=28．（1）乙队先达到终点，出发1小时40分钟后（或者上午10点40分）乙队追上甲队；（2）1小时之内，两队相距最远距离是4千米，比赛过程中，甲、乙两队在出发后1小时（或者上午10时）相距最远。
人教版数学2022-2023学年八年级下册第十九章一次函数同步练习题含答案
(3)当y=19.5时，求x的值．
参考答案：
1．D
【分析】先根据 ，且 判断出k的正负，然后根据一次函数的性质判断即可．
【详解】解：∵ ，且 ，
∴k<0，
∴一次函数图象经过一二四象限．
故先D．
【点睛】本题考查了一次函数的图象与性质，对于一次函数y=kx+b（k为常数，k≠0），当k>0时，y随x的增大而增大；当k<0时，y随x的增大而减小．当b＞0，图象与y轴的正半轴相交，当b<0，图象与y轴的负半轴相交，当b=0，图象经过原点．
（3）每分钟的进水量根据前4分钟的图象求出，出水量根据后8分钟的水量变化求解．
（1）
解：设y＝ax．
∵图象过（4，20），
∴4a＝20，
∴a＝5．
∴y随x变化的函数关系式为y＝5x（0≤x≤4）；
（2）
解：设y＝kx+b．
∵图象过（4，20）、（12，30），
∴ ，解得： ，
∴y与x的函数解析式为y＝ x+15（4≤x≤12）；
12．一次函数y=1－5x经过点（0，______）与点( )，0），y随x的增大而______.
三、解答题
13．有一进水管与出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分的进水量和出水量是两个常数，容器内的水量y．单位：L．与时间x．单位：分．之间的关系如图所示：
试题解析：∵函数 的图象过一、二、四象限，
解得-1＜m＜1．
15．(1)y=14+x（4<x<14）
(2)y=20
(3)x=5.5
【分析】（1）根据三角形的周长公式，可得函数关系式，根据三角形三边的关系，可得自变量的取值范围；
八年级数学(下)第十九章《一次函数》同步练习题(含答案)
八年级数学（下）第十九章《一次函数》同步练习（含答案）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．下列函数中，y 是x 的一次函数的是①y =x -6；②y =-3x –1；③y =-0.6x ；④y =7-x ．A ．①②③B ．①③④C ．①②③④D ．②③④ 【答案】C【解析】根据一次函数的定义，可知是一次函数的有①y =x -6；②y =-3x –1；③y =-0.6x ；④y =7-x ，故选C ． 2．如果23(2)2my m x -=-+是一次函数，那么m 的值是 A ．2B ．-2C ．±2D ．±1 【答案】B【解析】由题意得：22031m m -≠⎧⎨-=⎩，解得m =-2，故选B ． 3．下列说法中正确的是A ．一次函数是正比例函数B ．正比例函数不是一次函数C ．不是正比例函数就不是一次函数D ．不是一次函数就不是正比例函数 【答案】D【解析】A ．一次函数不一定是正比例函数，故本选项说法错误；B ．正比例函数是一次函数，故本选项说法错误；C ．不是正比例函数，但有可能是一次函数，故本选项说法错误；C ．不是一次函数就不是正比例函数，故本选项说法正确，故选D ．4．一次函数y =-2x +1的图象经过A ．第一、二、三象限B ．第一、二、四象限C ．第一、三、四象限D ．第二、三、四象限【答案】B【解析】在一次函数y =-2x +1中，k =-2<0，b =1>0，∴一次函数y =-2x +1的图象经过第一、二、四象限，故选B ．5．把直线3y x =-+向上平移m 个单位后，与直线24y x =+的交点在第一象限，则m 的取值范围是A ．1<m <7B ．3<m <4C ．m >1D ．m <4【答案】C 【解析】直线3y x =-+向上平移m 个单位后可得：3y x m =-++，联立两直线解析式得：324y x m y x =-++⎧⎨=+⎩，解得132103m x m y -⎧=⎪⎪⎨+⎪=⎪⎩，∴交点坐标为1210()33m m -+，， ∵交点在第一象限，∴10321003m m -⎧>⎪⎪⎨+⎪>⎪⎩，解得m >1，故选C ． 6．如果函数y =3x +m 的图象一定经过第二象限，那么m 的取值范围是A ．m >0B ．m ≥0C ．m <0D ．m ≤0【答案】A【解析】图象一定经过第二象限，则函数一定与y 轴的正半轴相交，因而0m >，故选A ． 7．关于函数y =-x +1，下列结论正确的是A ．图象必经过点（-1，1）B ．y 随x 的减小而减小C ．当x >1时，y <0D ．图象经过第二、三、四象限 【答案】C【解析】选项A ，∵当x =-1时，y =2，∴图象不经过点（-1，1），选项A 错误；选项B ，∵k =-1<0，∴y 随x 的增大而减小，选项B 错误；选项C ，∵y 随x 的增大而减小，当x =1时，y =0，∴当x >1时，y <0，选项C 正确；选项D ，∵k =-1<0，b =1>0，∴图象经过第一、二、四象限，选项D 错误．故选C ．8．一次函数y =kx +b 的图象如图所示，则k 、b 的值分别为A ．k =−12，b =1B ．k =-2，b=1C．k=12，b=1 D．k=2，b=1【答案】B【解析】由图象可知：过点（0，1），（12，0），代入一次函数的解析式得：112bk b=⎧⎪⎨=+⎪⎩，解得：k=−2，b=1，故选B．二、填空题：请将答案填在题中横线上．9．已知一次函数y=（m-3）x-2的图象经过一、三、四象限，则m的取值范围为__________．【答案】m>3【解析】∵y=（m-3）x-2的图象经过一、三、四象限，∴m-3>0，解得m>3．故答案为：m>3．10．点（-1，y1），（2，y2）是直线y=2x+1上的两点，则y1__________y2（填“>”或“=”或“<”）．【答案】<【解析】∵k=2>0，y将随x的增大而增大，2>−1，∴y1<y2，故y1与y2的大小关系是：y1<y2，故答案为：<．11．已知一次函数的图象与直线y=12x+3平行，并且经过点（-2，-4），则这个一次函数的解析式为__________．【答案】y=12x-3【解析】∵一次函数的图象与直线y=12x+3平行，∴设一次函数的解析式为y=12x+b．∵一次函数经过点（-2，-4），∴12×（-2）+b=-4，解得b=-3，所以这个一次函数的表达式是：y=1 2x-3．故答案为：y=12x-3．12．若点M（x1，y1）在函数y=kx+b（k≠0）的图象上，当-1≤x1≤2时，-2≤y1≤1，则这条直线的函数解析式为__________．【答案】y=x-1或y=-x【解析】∵点M（x1，y1）在在直线y=kx+b上，-1≤x1≤2时，-2≤y1≤1，∴点（-1，-2）、（2，1）或（-1，1）、（2，-2）都在直线上，则有：221k bk b-+=-⎧⎨+=⎩，或122k bk b-+=⎧⎨+=-⎩，解得11kb=⎧⎨=-⎩或1kb=-⎧⎨=⎩，∴y=x-1或y=-x，故答案为：y=x-1或y=-x．三、解答题：解答应写出文字说明、证明过程或演算步骤．13．已知一次函数经过点A（3，5）和点B（-4，-9）．（1）求此一次函数的解析式；（2）若点C（m，2）是该函数上一点，求C点坐标．【解析】（1）设其解析式为y=kx+b（k、b是常数，且k≠0），则5394k bk b=+⎧⎨-=-+⎩，∴k=2，b=−1．∴其解析式为y=2x-1，（2）∵点C（m，2）在y=2x-1上，∴2=2m-1，∴m=32，∴点C的坐标为（32，2）．14．已知一次函数的图象经过点A（2，1），B（-1，-3）．（1）求此一次函数的解析式；（2）求此一次函数的图象与x轴、y轴的交点坐标；（3）求此一次函数的图象与两坐标轴所围成的三角形面积．【解析】（1）根据一次函数解析式的特点，可得出方程组213 k bk b+=⎧⎨-+=-⎩，解得4353 kb⎧=⎪⎪⎨⎪=-⎪⎩，则得到y=43x-53．（2）根据一次函数的解析式y=43x-53，得到当y=0，x=54；当x=0时，y=-53．所以与x轴的交点坐标（54，0），与y轴的交点坐标（0，-53）．（3）在y=43x-53中，令x=0，解得：y=-53，在y=43x-53中，令y=0，解得：x=54．因而此一次函数的图象与两坐标轴所围成的三角形面积是：15525 23424⨯⨯=．15．已知一次函数y=（4-k）x-2k2+32．（1）k为何值时，它的图象经过原点；（2）k为何值时，它的图象经过点（0，-2）；（3）k为何值时，它的图象平行于直线y=-x；（4）k为何值时，y随x的增大而减小．【解析】（1）∵一次函数y=（4-k）x-2k2+32的图象经过原点，∴-2k2+32=0，解得：k=±4，∵4-k≠0，∴k=-4．（2）∵一次函数y=（4-k）x-2k2+32的图象经过（0，-2），∴-2k2+32=-2，解得：k．（3）∵一次函数y=（4-k）x-2k2+32的图象平行于直线y=-x，∴4-k=-1，∴k=5．（4）∵一次函数y=（4-k）x-2k2+32中y随x的增大而减小，∴4-k<0，∴k>4．16．已知一次函数图象经过（-4，-9）和（3，5）两点．（1）求一次函数解析式．（2）求图象和坐标轴交点坐标．并画出图象．（3）求图象和坐标轴围成三角形的面积．（4）若点（2，a）在函数图象上，求a的值．【解析】（1）设一次函数解析式为y=kx+b，把点（3，5），（-4，-9）分别代入解析式，则3549 k bk b+=⎧⎨-+=-⎩，解得21 kb=⎧⎨=-⎩，∴一次函数解析式为y=2x-1．（2）当x=0时，y=-1，当y=0时，2x-1=0，解得：x=0.5，∴与坐标轴的交点为A（0，-1）、B（0.5，0），图象如图，（3）S△AOB1122=⨯⨯|-1|=0.25．（4）∵点（2，a）在图象上，∴a=2×2-1=3，∴a=3．。
4.2 一次函数与正比例函数 北师大版八年级数学上册同步练习1及答案
新版北师大版八年级数学上册第4章《一次函数》同步练习及答案—4.2一次函数与正比例函数（1）
专题一次函数探究题
1.用m根火柴可以拼成如图1所示的x个正方形，还可以拼成如图2所示的2y个正方形，那么用含x的代数式表示y，得______________.
2. 将长为38cm、宽为5cm的长方形白纸按如图所示的方法黏合在一起，黏合部分的白纸宽
为2cm．
（1）求5张白纸黏合的长度；
（2）设x张白纸黏合后的总长为ycm，写出y与x的函数关系式（标明自变量x的取值范围）；
（3）用这些白纸黏合的总长能否为362cm？并说明理由．
参考答案：
1．y=x-【解析】由图1可知：一个正方形有4条边，两个正方形有4+3条边，
∴m=4+3（x-1）=1+3x;由图2可知：一组图形有7条边，两组图形有7+5条边，
∴m=7+5(y-1)=2+5y，所以1+3x=2+5y,即y=x-．
2．解：（1）5张白纸黏合，需黏合4次，重叠2×4=8cm．所以总长为38×5-8=182（cm）.（2）x张白纸黏合，需黏合（x-1）次，重叠2（x-1）cm，所以总长y=38x-2（x-1）=36x+2（x≥1，且x为整数）.
（3）能.当y=362时，得到36x+2=362，解得x=10,即10张白纸黏合的总长为362cm．3．解：（1）由图可以看出图形的周长=上下底的和+两腰长，∴l=3n+2.
（2）n=11时，图形周长为3×11+2=35．。
八年级数学一次函数练习题
八年级数学一次函数练习题精选八年级数学一次函数练习题导语：勤奋是成功之母，懒惰乃万恶之源。
下面是小编为大家整理的：初中数学，希望对大家有所帮助,欢迎阅读，仅供参考，更多相关的知识，请关注CNFLA学习网!一次函数的运算【例一】1.若y=5x+m-3是y关于x的正比例函数，则m=______.2.一台拖拉机开始工作时，油箱中有40升油，如果每小时耗油6升，则油箱中的余油量Q(升)与工作时间t(时)之间的函数关系式为________.3.已知y=(k-2)x|k|-1+2k-3是关于x的一次函数，则这个函数的表达式为_______.4.设地面气温是25℃，如果每升高1千米，气温下降6℃，则气温t(℃)与高度h(千米)的函数关系是( )A.t=25-6tB.t=25+6hC.t=6h-25D.t= t5.水箱内原有水200升，7：30打开水龙头，以2升/分的速度放水，设经t分时，水箱内存水y升.(1)求y关于x的函数关系式和自变量的取值范围.(2)7：55时，水箱内还有多少水?(3)几点几分，水箱内的水恰好放完?6.已知s是t的一次函数，并且当t=1时，s=2;当t=-2时，s=23，•试求这个一次函数的关系式.7.周日上午，小俊从外地乘车回嘉兴.一路上，小俊记下了如下数据：观察时间 9:00(t=0) 9：06(t=6) 9：18(t=18)路牌内容嘉兴90km 嘉兴80km 嘉兴60km(注：“嘉兴90km”表示离嘉兴的距离为90千米)假设汽车离嘉兴的距离s(千米)是行驶时间t(分钟)的一次函数，求s关于t•的函数关系式.8.某饮料厂生产一种饮料，经测算，用1吨水生产的饮料所获利润y(元)是1•吨水买入价x(元)的一次函数.根据下表提供的数据，求y关于x的函数解析式.当水价每吨为10元时，1吨水生产的饮料所获的利润是多少?1吨水的买入价(元) 4 6利润y(元) 200 198一次函数的运算【例二】第1题. 对于任何实数x，点M(x，x-3)一定不在第几象限?答案：点M(x，x-3)在直线y=x-3上，而直线y=x-3不过第二象限，所以，对于任何实数x，点M(x，x-3)一定不在第二象限.第2题. 一次函数，如果，则x的取值范围是( )A. B. C. D.答案：B.第3题. 已知直线y=kx+b(k≠0)与x轴的交点在x轴的正半轴，下列结论：①k>0，b>0;②k>0，b<0;③k<0，b>0;④k<0，b<0.其中正确的结论的个数是( )A.1B.2C.3D.4答案：B第4题. 如图所示，函数y=mx+m的图像中可能是( )答案：D第5题. 当自变量x增大时，下列函数值反而减小的是( )A. y=B.y=2xC.y=D.y=-2+5x答案：C第6题. 正比例函数的图像如图，则这个函数的解析式为( )A.y=xB.y=-2xC.y=-xD.答案：C第7题. 直线y=(2-5k)x+3k-2不过第一象限，则k需满足，写出一个满足上述条件的一个函数的解析式 .答案：，第8题. 直线y=4x-2与x轴的交点是，与y轴的交点是 .答案：第9题. 直线y=(2-5k)x+3k-2若经过原点，则k= ;若直线与x轴交于点(-1，0)，则k= ，答案：第10题. 一次函数的图像经过的象限是____，它与x轴的交点坐标是____，与y轴的交点坐标是____，y随x的增大而____.答案：一、二、四象限，(2，0)，(0，4)，减小第11题. (1)已知关于x的一次函数y=(2k-3)x+k-1的图像与y轴交点在x轴的上方，且y随x的增大而减小，求k的取值范围;(2)已知函数y=(4m-3)x是正比例函数，且y随x的增大而增大，求m的取值范围.答案：(1)依题意，有，解得 ;(2)依题意，得，即时，y随x的增大而增大.第12题. 已知一次函数，当0≤x≤3时，函数y的最大值是( ).A.0B.3C.-3D.无法确定答案：B点拔：画图得的图象是一条线段，又，故y随x的增大而减小，∴当x=0时，y的最大值等于3第13题. 下列图像中，不可能是关于x的一次函数y=mx-(m-3)的图像的是( )答案：C第14题. 在同一坐标内，函数关系式为y=kx+b(k、b为常数且k≠0)的直线有无数条，在这些直线中，不论怎样抽取，至少要抽几条直线，才能保证其中的两条直线经过完全相同的象限( )A.4B.5C.6D.7答案：D第15题. 如图，直线l是一次函数y=kx+b的图像，看图填空：(1) b=______，k=______;(2) x=-20时，y=_______;(3) 当y=-20时，x=_______.答案：第16题. 若一次函数y=kx+b交于y轴的负半轴，且y的值随x 的增大而减小，则k_____0，b______0.(填">"、"="、或"<") 答案：<,<第17题. 下列各点(1，2)，(-2，1)，(1，-2)，(-1， )，在y=-2x 图像上有：____________.答案：(1,-2)第18题. 若一次函数与一次函数的图像的交点坐标为(m，8).则a+b=______.答案：16第19题. 的'图像上有两点，知，你能说出与有什么关系吗?答案：第20题. 如图，函数y=kx-2中，y随x的增大而减小，则它的图像是( )答案：C第21题. 若一次函数 =k +b的图象经过一、三、四象限，则k，b应满足( )A.k>0，b>0B.k>0，b<0C.k<0，b>0D.k<0，b<0答案：B第22题. 一次函数y=-3x-4与x轴交于( )，与y轴交于( )，y随x的增大而___________.答案：，，减少第23题. 如果正比例函数 =3 和一次函数 =2 +k的图象的交点在第三象限，那么k的取值范围是 .答案：k<0第24题. 已知点A(-4，a)、B(-2，b)都在直线y=0.5 +k(k为常数)上，则a与b的大小关系是a b.(填"<""=" 或">")答案：<第25题. 已知正比函数y=kx(k≠0)的函数值y随x的增大而减小，则一次函数y=x+k的图象大致是下图中的( )答案：B第26题. 某校八年级同学到距学校6千米的郊外春游，一部分同学步行，另一部分同学骑自行车，沿相同路线前往.如图，、分别表示步行和骑车的同学前往目的地所走的路程 (千米)与所用时间 (分钟)之间的函数图象，则以下判断错误的是 ( )A.骑车的同学比步行的同学晚出发30分钟B.步行的速度是6千米/时C.骑车的同学从出发到追上步行的同学用了20分钟D.骑车的同学和步行的同学同时到达目的地答案：D第27题. 一次函数y=kx+3的图象与坐标轴的两个交点之间的距离为5，则k的值为.答案：或第28题. 如图，射线、分别表示甲、乙两名运动员在自行车比赛中所行路程 (米)与时间 (分)的函数图象.则他们行进的速度关系是A.甲、乙同速B.甲比乙快C.乙比甲快D.无法确定答案：B第29题. 已知函数轴交点的纵坐标为，且当，则此函数的解析式为.答案：第30题. 甲、乙两同学从地出发，骑自行车在同一条路上行驶到地，他们离出发地的距离(千米)和行驶时间(小时)之间的函数关系的图象如图所示.根据图中提供的信息，有下列说法：(1)他们都行驶了18千米;(2)甲在途中停留了0.5小时;(3)乙比甲晚出发了0.5小时;(4)相遇后，甲的速度小于乙的速度;(5)甲、乙两人同时到达目的地.其中符合图象描述的说法有A.2个B.3个C.4个D.5个答案：C第31题. 我市某出租车公司收费标准如图所示，如果小明只有19元钱，那么他乘此出租车最远能到达公里处.答案：13。
八年级数学(下)第十九章《一次函数——选择方案》同步练习题(含答案)
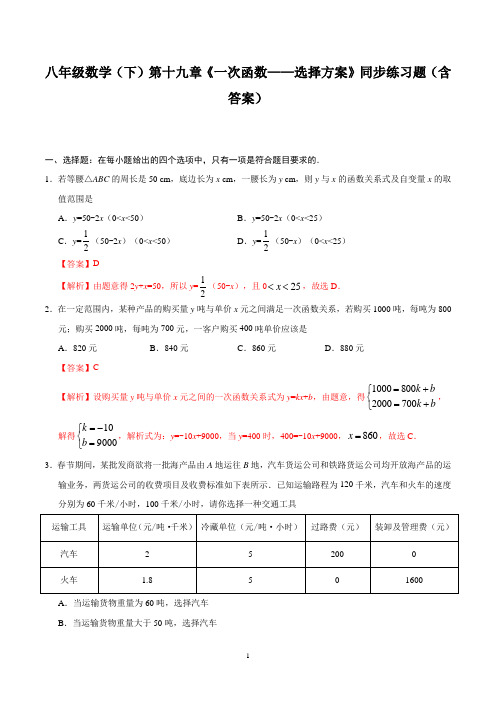
八年级数学（下）第十九章《一次函数——选择方案》同步练习题（含答案）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．若等腰△ABC的周长是50 cm，底边长为x cm，一腰长为y cm，则y与x的函数关系式及自变量x的取值范围是A．y=50-2x（0<x<50）B．y=50-2x（0<x<25）C．y=12（50-2x）（0<x<50）D．y=12（50-x）（0<x<25）【答案】D【解析】由题意得2y+x=50，所以y=12（50-x），且025x<<，故选D．2．在一定范围内，某种产品的购买量y吨与单价x元之间满足一次函数关系，若购买1000吨，每吨为800元；购买2000吨，每吨为700元，一客户购买400吨单价应该是A．820元B．840元C．860元D．880元【答案】C【解析】设购买量y吨与单价x元之间的一次函数关系式为y=kx+b，由题意，得1000800 2000700k bk b=+⎧⎨=+⎩，解得109000kb=-⎧⎨=⎩，解析式为：y=-10x+9000，当y=400时，400=-10x+9000，860x=，故选C．3．春节期间，某批发商欲将一批海产品由A地运往B地，汽车货运公司和铁路货运公司均开放海产品的运输业务，两货运公司的收费项目及收费标准如下表所示．已知运输路程为120千米，汽车和火车的速度分别为60千米/小时，100千米/小时，请你选择一种交通工具A．当运输货物重量为60吨，选择汽车B．当运输货物重量大于50吨，选择汽车C ．当运输货物重量小于50吨，选择火车D ．当运输货物重量大于50吨，选择火车 【答案】D【解析】（1）y 1=2×120x +5×（120÷60）x +200=250x +200， y 2=1.8×120x +5×（120÷100）x +1600=222x +1600； （2）若y 1=y 2，则x =50，∴当海产品不少于30吨但不足50吨时，选择汽车货运公司合算；当海产品恰好是50吨时选择两家公司都一样，没有区别；当海产品超过50吨时选择铁路货运公司费用节省一些，故选D ．4．学校春季运动会期间，负责发放奖品的张也同学，在发放运动鞋（奖品）时，对运动鞋的鞋码统计如下表：如果获奖运动员李伟领取的奖品是43号（原鞋码）的运动鞋，则这双运动鞋的新鞋码是A ．270B ．255C ．260D ．265【答案】D【解析】由题中的表格知，y 是x 的一次函数，可设y 与x 的关系为y =kx +b ， 由题意得22535k 24539b k b =+⎧⎨=+⎩，解得550k b =⎧⎨=⎩，∴y 与x 之间的函数关系式为y =5x +50，当x =43时，y =265，故选D ．5．如图，小明从A 地前往B 地，到达后立刻返回，他与A 地的距离(y 千米)和所用时间(x 小时)之间的函数关系如图所示，则小明出发6小时后距A 地A ．120千米B ．160千米C ．180千米D ．200千米【答案】B【解析】设当46x ≤≤时，y 与x 的函数关系式为y kx b =+，4240100k b k b +=⎧⎨+=⎩，得40400k b =-⎧⎨=⎩， 即当46x ≤≤时，y 与x 的函数关系式为40400y x =-+， 当6x =时，406400160y =-⨯+=， 即小明出发6小时后距A 地160千米，故选B ． 二、填空题：请将答案填在题中横线上．6．甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400 m ，先到终点的人原地休息．已知甲先出发4 min ，在整个步行过程中，甲、乙两人的距离y （m ）与甲出发的时间t （min ）之间的关系如图所示，以下结论：①甲步行的速度为60 m /min ；②乙走完全程用了32 min ；③乙用16 min 追上甲；④乙到达终点时，甲离终点还有300 m ，其中正确的结论有___________（填序号）．【答案】①【解析】由图可得，甲步行的速度为：240÷4=60米/分，故①正确； 乙走完全程用的时间为：2400÷（16×60÷12）=30（分钟），故②错误； 乙追上甲用的时间为：16-4=12（分钟），故③错误；乙到达终点时，甲离终点距离是：2400-（4+30）×60=360米，故④错误，故答案为：①． 7．某体育用品商场为推销某一品牌运动服，先做了市场调查，得到数据如下表：则P 与x 的函数关系式为___________，当卖出价格为60元时，销售量为___________件． 【答案】P =-10x +1000；400件【解析】（1）P 与x 成一次函数关系，设函数关系式为P =kx +b ， 则5005049051k b k b=+⎧⎨=+⎩，解得101000k b =-=⎧⎨⎩ ， ∴P =−10x +1000，经检验可知：当x =52，P =480，当x =53，P =470时也适合这一关系式， ∴所求的函数关系为P =−10x +1000．（2）当x=60时，P=−10×60+1000=400，故答案为：P=−10x+1000；400．三、解答题：解答应写出文字说明、证明过程或演算步骤．8．某移动通讯公司开设了两种通讯业务：“全球通”使用者先缴50元月租费，然后每通话1分钟，再付话费0.4元；“神州行”不缴月租费，每通话1 min付费0.6元．若一个月内通话x min，两种方式的费用分别为y1元和y2元．（1）写出y1，y2与x之间的函数解析式；（2）一个月内通话多少分钟，两种通讯业务费用相同；（3）某人估计一个月内通话300 min，应选择哪种移动通讯业务合算些？【解析】（1）y1=50+0.4x，y2=0.6x．（2）令y1=y2，则50+0.4x=0.6x，解之，得x=250．所以通话250分钟两种费用相同．（3）令x=300，则y1=50+0.4×300=170，y2=0.6×300=180，所以选择全球通合算．9．甲、乙两个厂家生产的办公桌和办公椅的质量、价格一致，每张办公桌800元，每张椅子80元．甲、乙两个厂家推出各自销售的优惠方案，甲厂家：买一张桌子送三张椅子；乙厂家：桌子和椅子全部按原价8折优惠．现某公司要购买3张办公桌和若干张椅子，若购买的椅子数为x张（x≥9）．（1）分别用含x的式子表示甲、乙两个厂家购买桌椅所需的金额；（2）购买的椅子至少多少张时，到乙厂家购买更划算？【解析】（1）根据甲、乙两个厂家推出各自销售的优惠方案：甲厂家所需金额为：3×800+80（x﹣9）=1680+80x；乙厂家所需金额为：（3×800+80x）×0.8=1920+64x．（2）由题意，得：1680+80x≥1920+64x，解得：x≥15．答：购买的椅子至少15张时，到乙厂家购买更划算．10．为响应绿色出行号召，越来越多市民选择租用共享单车出行，已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式，如图描述了两种方式应支付金额y（元）与骑行时间x（时）之间的函数关系，根据图象回答下列问题：（1）求手机支付金额y （元）与骑行时间x （时）的函数关系式；（2）李老师经常骑行共享单车，请根据不同的骑行时间帮他确定选择哪种支付方式比较合算． 【解析】（1）由题意和图象可设：手机支付金额y （元）与骑行时间x （时）的函数解析式为：1y kx b =+，由图可得：0.500.5k b k b +=⎧⎨+=⎩，解得10.5k b =⎧⎨=-⎩，∴手机支付金额y （元）与骑行时间x （时）的函数解析式为：10.5y x =-．（2）由题意和图象可设会员支付y （元）与骑行时间x （时）的函数解析式为：2y ax =， 由图可得：0.75a =，由0.750.5y x y x =⎧⎨=-⎩，可得21.5x y =⎧⎨=⎩， ∴图中两函数图象的交点坐标为（2，1.5）， 又∵0x >，结合图象可得：当02x <<时，李老师用“手机支付”更合算； 当0x =时，李老师选择两种支付分式花费一样多； 当2x >时，李老师选择“会员支付”更合算．11．某工厂生产某种产品，每件产品的出厂价为1000元，其原材料成本价为550元，同时在生产过程中平均每生产一件产品有10千克的废渣产生．为达到国家环要求，需要对废渣进行处理，现有两种方案可供选择：方案一：由工厂对废渣直接进行处理，每处理10千克废渣所用的原料费为50元，并且每月设备维护及损耗费为2000元．方案二：工厂将废渣集中到废渣处理厂统一处理，每处理10千克废渣需付100元的处理费． （1）设工厂每月生产x 件产品．用方案一处理废渣时，每月利润为__________元；用方案二处理废渣时，每月利润为__________元（利润=总收入-总支出）；（2）若每月生产30件和60件，用方案一和方案二处理废渣时，每月利润分别为多少元？ （3）如何根据月生产量选择处理方案，既可达到环保要求又最划算？【解析】（1）由题意可得，用方案一处理废渣时，每月的利润为：x（1000-550）-50x-2000=400x-2000；用方案二处理废渣时，每月利润为：x（1000-550）-100x=350x，故答案为：400x-2000；350x．（2）当x=30时，用方案一处理废渣时，每月的利润为：400×30-2000=10000元；用方案二处理废渣时，每月利润为：350×30=10500元；x=60时，用方案一处理废渣时，每月的利润为：400×60-2000=22000；用方案二处理废渣时，每月利润为：350×60=21000．（3）令400x-2000=350x，解得x=40，即当生产产品数量少于40时，选择方案二；当生产产量大于40时，选择方案一．12．水果商贩小李去水果批发市场采购被誉为“果中之王”的泰顺猕猴桃，他了解到猕猴桃有精品盒与普通盒两种包装，精品盒的批发价格每盒60元，普通盒的批发价格每盒40元，现小李购得精品盒与普通盒共60盒，费用共为3100元。
人教版初中数学八年级下册第十九章《一次函数》19.2一次函数同步练习题(含答案)
故答案为：﹣3或6．
9．y=﹣x﹣1（答案不唯一）
【解析】试题解析：∵y随x的增大而减小，
∴
设一次函数的解析式为
②当a＞0，b＜0时，y=ax+b的图象经过第一、三、四象限；y=bx+a的图象经过第一、二、四象限，无选项符合；
③当a＜0，b＞0时，y=ax+b的图象经过第一、二、四象限；y=bx+a的图象经过第一、三、四象限，B选项符合；
④当a＜0，b＜0时，y=ax+b的图象经过第二、三、四象限；y=bx+a的图象经过第二、三、四象限，无选项符合．
9．某一次函数的图象经过点（﹣2，1），且y轴随x的增大而减小，则这个函数的表达式可能是_____．（只写一个即可）
10．已知直线 与直线 平行，且截距为5，那么这条直线的解析式为_______．
11．直线y=－8x－6可以由直线y=－8x向___平移___个单位得到．
12．如图，在平面直角坐标系中，函数y=2x﹣3和y=kx+b的图象交于点P（m，1），则关于x的不等式2x﹣3＞kx+b的解集是_____．
故选B．
7．C
【解析】如图，作点D关于AB的对称点D′，连接CD′交AB于点E，则此时△CDE的周长最小，
∵点B的坐标为（3，4），四边形ABCO是矩形，D是OA的中点，
∴点C的坐标为（0，4），点D的坐标为（1.5，0），点D′的坐标为（4.5，0），点E的横坐标为3，
设直线CE的解析式为：y=kx+b，则有： ，解得 ，
∴直线CE的解析式为： ，
∴当 时， ，
∴点E的坐标为 .
故选C.
19.2.2 一次函数(1) 人教版数学八年级下册同步练习(含解析)
第十九章 一次函数19.2.2 一次函数(1)基础过关全练知识点1 一次函数的定义1.下列函数关系式中,属于一次函数的是( )A.y =2x -1 B.y =x 2+1C.y =kx +b (k 、b 是常数)D.y =1-2x2.(2022黑龙江哈尔滨期末)当m 为何值时,函数y =(m -3)x 3-|m |+m +2是一次函数( )A.2B.-2C.-2或2D.3知识点2 一次函数的图象与性质3.【教材变式·P92例3变式】下列函数图象中,表示直线y =2x +1的是( )A B C D4.【教材变式·P91思考变式】将直线y =5x 向下平移2个单位长度,所得直线的表达式为( )A.y =5x -2B.y =5x +2C.y =5(x +2)D.y =5(x -2)5.(2020黑龙江牡丹江中考)已知一次函数y =(2m -3)x +3n +1的图象经过第一、二、三象限,则m 、n 的取值是( )A.m >3,n >3B.m >32,n >-13 C.m <32,n <13 D.m >32,n <136.【新独家原创】新定义:[a,b,c]为函数y=ax2+bx+c(a,b,c为实数)的“关联数”.若“关联数”为[m-2,m,-1]的函数为一次函数,对于该一次函数,下列说法正确的是( ) A.它的图象过点(1,0) B.y值随着x值的增大而减小C.它的图象经过第二象限D.当x>1时,y>07.(2022云南八中期末)在一次函数y=(5a2+8)x-3(a为常数)的图象上有A(x1,y1),B(x2,y2),C(x3,y3)三点.若x1<x2<x3,则y1,y2,y3的大小关系为( )A.y1<y2<y3B.y2<y1<y3C.y1<y3<y2D.y3<y2<y18.(2020辽宁丹东中考)已知一次函数y=-2x+b,且b>0,则它的图象不经过第 象限.9.(2021四川眉山中考)一次函数y=(2a+3)x+2的值随x值的增大而减小,则常数a的取值范围是 .10.已知函数y=(2m+1)x+m-3.(1)若函数图象经过原点,求m的值;(2)若该函数的图象与直线y=3x-3平行,求m的值;(3)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围. 能力提升全练11.(2022湖南邵阳中考,8,★☆☆)在直角坐标系中,已知点,m,点,n是直线y=kx+b(k<0)上的两点,则m,n的大小关系是( )A.m<nB.m>nC.m≥nD.m≤n12.(2022河南信阳期末,8,★☆☆)已知点A(x1,y1),B(x2,y2)在直线y=kx+b(k≠0)上,y随x的增大而增大,且kb>0,则在平面直角坐标系内,它的图象大致是( )A B C D13.(2022浙江绍兴中考,9,★★☆)已知(x1,y1),(x2,y2),(x3,y3)为直线y=-2x+3上的三个点,且x1<x2<x3,则以下判断正确的是( ) A.若x1x2>0,则y1y3>0 B.若x1x3<0,则y1y2>0C.若x2x3>0,则y1y3>0D.若x2x3<0,则y1y2>014.(2020四川凉山州中考,7,★★☆)若一次函数y=(2m+1)x+m-3的图象不经过第二象限,则m的取值范围是( ) A.m>-12B.m<3C.-12<m<3 D.―12<m≤315.(2022安徽芜湖一中期末,12,★☆☆)已知点A(x1,y1),B(x2,y2)在一次函数y=(a-2)x+1的图象上,当x1>x2时,y1<y2,则a的取值范围是 .16.(2022重庆期末,12,★★☆)若关于x的分式方程6xx―1=3+axx―1的解为整数,且一次函数y=(7-a)x+a的图象不经过第四象限,则符合题意的整数a的个数为 .素养探究全练17.【几何直观】在平面直角坐标系xOy中,点P的坐标为(m+1,m-1).(1)试判断点P是否在一次函数y=x-2的图象上,并说明理由;(2)如图,一次函数y=-12x+3的图象与x轴、y轴分别相交于点A、B,若点P在△AOB的内部,求m的取值范围.18.【运算能力】一次函数y=(m-2)x+m2-1的图象经过点A(0,3).(1)求m的值,并写出函数解析式;(2)若函数图象与x轴交于点B,直线y=(n+2)x+n2-1也经过点A(0,3),且与x轴交于点C,求线段BC的长.答案全解全析基础过关全练1.D y =2x -1中,2x 不是整式,不是一次函数,y =x 2+1不是一次函数,y =kx +b (k 、b 是常数)中,当k =0时,不是一次函数,y =1-2x 是一次函数.故选D .2.C 由题意得3-|m |=1且m -3≠0,∴m =±2且m ≠3,∴m 的值为2或-2,故选C .3.B ∵k =2>0,b =1>0,∴直线经过第一、二、三象限.故选B .4.A 将直线y =5x 向下平移2个单位长度,所得直线的表达式为y =5x -2.故选A .5.B ∵一次函数y =(2m -3)x +3n +1的图象经过第一、二、三象限,∴2m ―3>0,3n +1>0,解得m >32,n >-13,故选B .6.D 根据题意可得m -2=0,且m ≠0,解得m =2,所以该一次函数表达式为y =2x -1,把x =1代入y =2x -1得到y =1,故该函数图象经过点(1,1),不经过点(1,0),故选项A 错误;函数y =2x -1中,k =2>0,则y 值随着x 值的增大而增大,故选项B 错误;函数y =2x -1中,k =2>0,b =-1<0,则该函数图象经过第一、三、四象限,故选项C 错误;当x >1时,2x -1>1,即y >1,故y >0正确,故选项D 正确.故选D .7.A 一次函数y =(5a 2+8)x -3(a 为常数)中,5a 2+8>0,∴y随x的增大而增大,∵x1<x2<x3,∴y1<y2<y3,故选A.8.答案 三解析 ∵一次函数y=-2x+b,且b>0,∴它的图象经过第一、二、四象限,不经过第三象限.9.答案 a<-32解析 ∵一次函数y=(2a+3)x+2的值随x值的增大而减小,∴2a+3<0,解得a<-32.10.解析 (1)∵函数y=(2m+1)x+m-3的图象经过原点,∴当x=0时,y=0,即m-3=0,解得m=3.(2)∵函数y=(2m+1)x+m-3的图象与直线y=3x-3平行,∴2m+1=3,且m-3≠-3,解得m=1.(3)∵这个函数是一次函数,且y随着x的增大而减小,∴2m+1<0,解得m<-12.能力提升全练11.A ∵点,m,点,n是直线y=kx+b上的两点,且k<0,∴y随x的增大而减小,∵32>72,∴m<n,故选A.12.A ∵点A(x1,y1),B(x2,y2)在直线y=kx+b(k≠0)上,y随x的增大而增大,且kb>0,∴k>0,b>0,∴直线y=kx+b经过第一、二、三象限,故选A.13.D ∵y=-2x+3中,-2<0,∴y随x的增大而减小,当y=0时,x=1.5,∵(x1,y1),(x2,y2),(x3,y3)为直线y=-2x+3上的三个点,且x1<x2<x3,∴若x1x2>0,则x1,x2同号,但不能确定y1y3的正负,故选项A不符合题意;若x1x3<0,则x1,x3异号,但不能确定y1y2的正负,故选项B不符合题意;若x2x3>0,则x2,x3同号,但不能确定y1y3的正负,故选项C不符合题意;若x2x3<0,则x2,x3异号,则x1,x2同时为负,故y1,y2同时为正,故y1y2>0,故选项D符合题意.故选D.14.D 根据题意得2m+1>0,m―3≤0,解得―12<m≤3.故选D.15.答案 a<2解析 ∵当x1>x2时,y1<y2,∴a-2<0,∴a<2,故答案为a<2.16.答案 3解析 ∵一次函数y=(7-a)x+a的图象不经过第四象限,∴7―a>0,a≥0,解得0≤a<7,由分式方程6xx―1=3+axx―1得x=3a―3,∵分式方程6xx―1=3+axx―1的解为整数,且x≠1,∴整数a=0,2,4,∴符合题意的整数a的个数为3.素养探究全练17.解析 (1)∵当x=m+1时,y=m+1-2=m-1,∴点P(m+1,m-1)在函数y=x-2的图象上.(2)∵函数y=-12x+3的图象与x轴、y轴分别相交于点A、B,∴A (6,0),B (0,3),∵点P 在△AOB 的内部,∴0<m +1<6,0<m -1<3,m -1<-12(m +1)+3,∴1<m <73.18.解析 (1)由题意得m 2-1=3,所以m =±2.又m -2≠0,所以m ≠2,所以m =-2,所以y =-4x +3.(2)由题意可得点B ,0.因为直线y =(n +2)x +n 2-1经过点A (0,3),所以n 2-1=3,所以n =±2.又n +2≠0,所以n ≠-2,所以n =2.所以y =4x +3,所以点C 的坐标为―34,0,所以线段BC 的长为34―=32.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一次函数
一、填空题（每题2分，共32分）
1．已知一个正比例函数的图象经过点（-1，3），则这个正比例函数的表达式是 ． 2
．函数y =
x 的取值围是_______________．
3．已知一次函数y =2x +4的图像经过点（m ，8），则m ＝________．
4．若函数y = -2x m +2
+n -2正比例函数，则m 的值是 ，n 的值为________． 5．一次函数1
13
y x =-+的图象与x 轴的交点坐标是_________，与y 轴的交点坐标是__________．
6．若直线y =kx +b 平行于直线y =5x +3，且过点（2，-1），则k =______，b =______． 7．两直线1y x =-与3y x =-+的交点坐标 ．
8．某种储蓄的月利率为0.15%，现存入1000元，则本息和y （元）与所存月数x 之间的函数关系式是 ．
9．某一次函数的图象经过点（1-，3），且函数y 随x 的增大而减小，请你写出一个符合条件的函数解析式______________________．
10．现有笔记本500本分给学生，每人5本，则余下的本数y 和学生数x 之间的函数解析式为_________________，自变量x 的取值围是______________． 11．若一次函数y ＝kx －4当x ＝2时的值为0，则k ＝ ． 12．一次函数12-=x y 一定不经过第 象限．
13．已知直线6+=x y 与x 轴,y 轴围成一个三角形,则这个三角 形面积为 .
14．如右图：一次函数y kx b =+的图象经过A 、B 两点，则△AOC 的面积为___________．
15．根据下图所示的程序计算函数值，若输入的x 值为2
3
，则输出的结果为
16．观察下列各正方形图案，每条边上有n (n ＞2)个圆点，每个图案中圆点的总数是S ．
按此规律推断出S 与n 的关系式为 ．
二、解答题（共68分）
17．（4分）已知一个一次函数，当3x =时，2y =-；当2x =时，3y =-，求这个
一次函数的解析式已知，直线y kx b =+经过点A （3，8）和B （6-，4-）．求： （1）k 和b 的值；（2）当3x =-时，y 的值．
18．（4分）已知正比例函数y kx =．
（1）若函数图象经过第二、四象限，则k 的围是什么？ （2）点（1，－2）在它的图像上，求它的表达式．
19．（4分）已知2y -与x 成正比，且当1x =时，6y =-． （1）求y 与x 之间的函数关系式；
（2）若点（a ，2）在这个函数图象上，求a ．
＝4 S ＝12
n ＝2
S ＝4 n ＝3 S ＝8
20．（4分）利用图象解方程组22
5
y x x y =-⎧⎨
+=-⎩
21．（6分）已知函数(21)3y m x m =++-， （1）若函数图象经过原点，求m 的值；
（2）若这个函数是一次函数，且y 随着x 的增大而减小，求m 的取值围．
22．（6分）作出函数24y x =-的图象，并根据图象回答下列问题： （1）当 -2≤x ≤4时，求函数y 的取值围； （2）当x 取什么值时，y <0，y =0，y>0? （3）当x 取何值时，-4<y <2？
23．（6分）图中折线ABC 表示从甲地向乙地打长途时所需付的费y （元）与通话时间t
（分钟）之间的关系图像．
（1）从图像知，通话2分钟需付的费是 元． （2）当t ≥3时求出该图像的解析式（写出求解过程）． （3）通话7分钟需付的费是多少元？
24．（6分）已知等腰三角形的周长为12cm ，若底边长为y cm ，一腰长为x cm.． （1）写出y 与x 的函数关系式； （2）求自变量x 的取值围．
25．（6分）某产品每件成本10元，试销阶段每件产品的销售价x （元）与产品的日销售量
y （件）之间的关系如下表：
若日销售量y 是销售价x 的一次函数．
（1）求出日销售量y （件）与销售价x （元）的函数关系式； （2）求销售价定为30元时，每日的销售利润．
26．（6分）某公司在A 、B 两地分别有库存机器16台和12台，现要运往甲、乙两地，
其中甲地15台，乙地13台．从A 地运一台到甲地的运费为500元，到乙地为400元；从B 地运一台到甲地的运费为300元，到乙地为600元．公司应设计怎样的调运方案，能使这些机器的总运费最省？
27．（8分）已知直线AB 与x ，y 轴分别交于A 、B （如图），AB =5，OA =3， （1）求直线AB 的函数表达式；
（2）如果P 是线段AB 上的一个动点（不运动到A ，B ），过P 作x 轴的垂线，垂足是M ，连接PO ，设OM =x ，图中哪些量可以表示成x 的函数？试写出5个不同的量关于x 的函数关系式．（这里的量是指图中某些线段的长度或某些几何图形的面积等）
28．（8分）2007年5月，第五届中国长江三峡国
际
龙舟拉力赛在黄陵庙揭开比赛帷幕．20日上午9时，参赛龙舟从黄陵庙同时出发．其中甲、乙两队在比赛时，路程y （千米）与时间x （小时）的函数关系如图所示．甲队在上午11时30分到达终点黄柏河港． （1）哪个队先到达终点？乙队何时追上甲队？ （2）在比赛过程中，甲、乙两队何时相距最远？
时间/时
16
4020。