目标跟踪中非线性滤波算法的研究
多目标跟踪中的相关滤波算法优化研究

多目标跟踪中的相关滤波算法优化研究随着人工智能的发展和应用,多目标跟踪技术已经成为了计算机视觉中重要的研究方向之一。
比如,监控场景中需要同时跟踪多个目标,无人驾驶中需要识别并跟踪行人、车辆等目标物体。
然而,实现准确稳定的多目标跟踪并不是一件容易的事情。
面对大规模多目标、非线性问题、目标遮挡等各种挑战,如何提高多目标跟踪的准确度和实时性成为了研究者们的重要任务之一。
为了解决这些问题,研究人员提出了大量的多目标跟踪算法。
其中,基于相关滤波的算法因为其准确性和实时性的优势,成为了常用的选择。
本文将重点介绍几种相关滤波算法,并探讨它们在不同场景下的优化策略。
一、基础算法--均值滤波算法均值滤波是一种广泛应用于图像处理、信号处理等领域的线性滤波算法。
其基本原理是通过对样本点进行平均处理,来去除背景噪声等不必要信息。
在多目标跟踪中,均值滤波算法的应用相对较少,主要是因为它对非线性的目标运动和遮挡等情况处理效果不佳。
但是,在某些简单场景下,均值滤波算法可以将多个目标的跟踪任务成功实现。
二、基于相关滤波的多目标跟踪算法与均值滤波相比,相关滤波在多目标跟踪中具有更好的性能和精度。
相关滤波的本质是在模板区域内对目标特征进行相关计算,从而实现目标跟踪。
在多目标跟踪中,可以将多个目标的特征描述为多个不同的模板,然后对它们进行相关计算。
常见的相关滤波算法包括MOSSE算法、KCF算法、CSR-DCF算法等。
1. MOSSE算法MOSSE算法是一种基于核相关滤波的多目标跟踪算法。
该算法利用训练集中的数据对模板进行训练,并通过自适应滤波器实现目标跟踪。
其核心思想是在保证跟踪速度的情况下,减小目标特征描述的复杂度,提高目标跟踪的准确性和效率。
但是,在目标特征发生改变、目标运动速度快或者出现遮挡等情况下,MOSSE算法的跟踪效果会受到影响。
2. KCF算法KCF(Kernelized Correlation Filter)算法是一种基于相关滤波的全自动目标跟踪算法。
非线性更新容积高斯求和滤波器在目标跟踪中的应用研究.
第2章 目标跟踪原理及目标的常用模型目标跟踪是指利用传感器观测确定目标位置、轨迹和特性的问题。
传感器可以是任何观测设备,如雷达、声呐、摄像机、红外传感器、超声波、麦克风或其他可以用来收集目标信息的传感器。
目标跟踪的典型目标是确定目标的数目、身份以及目标的状态,如位置、速度、以及特征等。
本章主要对目标的跟踪原理进行介绍,对雷达的目标参数测量进行了简要说明,并根据雷达的测向测距原理建立目标跟踪的数学模型。
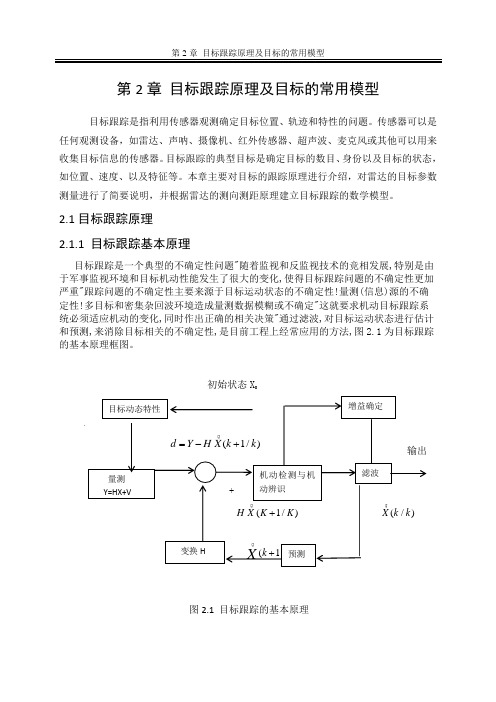
2.1目标跟踪原理2.1.1 目标跟踪基本原理目标跟踪是一个典型的不确定性问题"随着监视和反监视技术的竞相发展,特别是由于军事监视环境和目标机动性能发生了很大的变化,使得目标跟踪问题的不确定性更加严重"跟踪问题的不确定性主要来源于目标运动状态的不确定性!量测(信息)源的不确定性!多目标和密集杂回波环境造成量测数据模糊或不确定"这就要求机动目标跟踪系统必须适应机动的变化,同时作出正确的相关决策"通过滤波,对目标运动状态进行估计和预测,来消除目标相关的不确定性,是目前工程上经常应用的方法,图2.1为目标跟踪的基本原理框图。
初始状态X 0.(1/)d Y H X k k =-+ 输出 + + (1/)H X K K + (/)X k k(1/)k k X +图2.1 目标跟踪的基本原理目标动态特性 量测Y=HX+V变换H 机动检测与机动辨识 增益确定 滤波 预测图2.1中目标动态特性包含位置、速度和加速度的状态向量用X 表示,量测(观测)量Y 被假定为含有量测噪声V 的状态向量的线性组合HX+V,残差(新息)向量d 为量测Y 与状态预测量(1/)H X K K ∧+之差"我们约定,用大写字母X 、Y 表示向量,小写字母x 、y 表示向量的分量"首先由量测量Y 和状态预测量(1/)H X K K ∧+构成残差(新息)向量d,然后根据d 的变化进行机动检测或机动辨识,其次按照某一准则或逻辑调整滤波增益与协方差矩阵或者实时辨识出目标机动特性,最后由滤波算法得到目标的估计值和预测值,从而完成目标跟踪功能。
非线性系统的几种滤波算法研究

Dissertation Submitted to Hangzhou Dianzi Universityfor the Degree of MasterResearch on Several Filtering Algorithms with Non-linear SystemCandidate: Xu DaxingSupervisor: Prof. Wen ChenglinNovember, 2013杭州电子科技大学学位论文原创性声明和使用授权说明原创性声明本人郑重声明:所呈交的学位论文,是本人在导师的指导下,独立进行研究工作所取得的成果。
除文中已经注明引用的内容外,本论文不含任何其他个人或集体已经发表或撰写过的作品或成果。
对本文的研究做出重要贡献的个人和集体,均已在文中以明确方式标明。
申请学位论文与资料若有不实之处,本人承担一切相关责任。
论文作者签名:日期:年月日学位论文使用授权说明本人完全了解杭州电子科技大学关于保留和使用学位论文的规定,即:研究生在校攻读学位期间论文工作的知识产权单位属杭州电子科技大学。
本人保证毕业离校后,发表论文或使用论文工作成果时署名单位仍然为杭州电子科技大学。
学校有权保留送交论文的复印件,允许查阅和借阅论文;学校可以公布论文的全部或部分内容,可以允许采用影印、缩印或其它复制手段保存论文。
(保密论文在解密后遵守此规定)论文作者签名:日期:年月日指导教师签名:日期:年月日摘要随着现代科学技术的快速发展,尤其是通信技术、信息技术和计算机技术等在众多民用和国防领域的广泛应用,使得现代控制系统的信号常表现出非线性、噪声相关和非高斯等复杂特性,从而导致非线性系统的滤波算法设计不仅面临诸多新的问题和挑战,而且又具有重要的理论意义和应用价值。
由于系统噪声的相关性和非高斯特性,使得现有众多非线性滤波算法不能满足该类复杂系统的应用需求,因此如何有效地设计出噪声相关和非高斯情况下的非线性滤波已成为提高非线性滤波方法应用能力的有效途径之一。
基于非线性滤波算法的目标跟踪技术比较研究

基于非线性滤波算法的目标跟踪技术比较研究葛田;陶庆【摘要】with the progress of science and technology, target location and tracking algorithm has been widely used in wireless, aviation, navigation and other fields, such as automotive active safety, mobile phone positioning technology and so on. Common target tracking technology is actually based on monitoring equipment positioning prediction process. However, due to the fact that the trajectory of the target is not controlled, the traditional filtering algorithm can not get accurate results. So tracking technology in recent years began to study the filtering tracking in nonlinear systems, such as extended Kalman filter, particle filter algorithm, etc.. In this paper, the latest research progress of tracking filtering technology is studied, and the filtering model of the nonlinear filtering algorithm in complex environment is studied.%随着科技的进步,目标定位与跟踪算法已经广泛的应用于无线、航空、航海等领域,诸如汽车主动安全、手机定位技术等等。
用于弹道目标跟踪的新的非线性滤波算法

P (k + 1|k ) = λ(k + 1)[F (k ) P (k|k )F T (k ) + Q(k )]
第二, 为了使状态的估计更光滑, 采用平方根函数的特 性, 那么渐消因子的计算被修正为: ìλ0 λ0 ³ 1 λ(k + 1) = í î1 λ0 < 1
λ0 = tr[ N (k + 1)] tr[ M (k + 1)]
(7) (8)
其中,
N (k + 1) = V0 (k + 1) - βR(k + 1)
T T
(9)
M (k + 1) = H (k + 1) ´ [F (k ) P (k|k )F (k ) + Q(k )] H (k + 1)(10) V0 (k + 1) 是残差方差矩阵, 其中, 如下计算: V0 (k + 1) = E[r(k + 1)r T (k + 1)] = ìr(1)r T (1) k = 0 ï í ρV0 (k ) + r(k + 1)r T (k + 1) , k³1 ï 1+ρ î
(1)
基金项目: 国家自然科学基金 (the National Natural Science Foundation of China under Grant No.60574033) ; 国家重点基础研究发展规划 (973) (No.2007CB311006) 。 作者简介: 巫春玲 (1978—) , 女, 博士生, 主要研究方向为雷达目标跟踪、 估计与滤波; 韩崇昭 (1943—) , 男, 教授, 博士生导师。 收稿日期: 2011-03-07; 修回日期: 2011-05-03
非线性滤波算法在雷达信号处理中的应用

非线性滤波算法在雷达信号处理中的应用雷达技术是一种基于电磁波的无线通信技术,广泛应用于民用和军用领域,例如飞机控制、车辆导航和卫星通信等多个领域。
在雷达系统中,信号处理是一个重要的环节,它可以消除噪声、增加信噪比和提高雷达系统的灵敏度。
现代雷达系统中,非线性滤波算法是一种有效的信号处理技术,得到了广泛的应用。
非线性滤波算法与线性滤波算法不同之处在于,非线性滤波算法可以处理非平稳信号、非线性信号和非高斯噪声等不符合线性统计学假设的信号模型。
以常见的经典卡尔曼滤波算法为例,其假设系统和观测噪声均为高斯分布。
此时,若系统和观测噪声不满足高斯分布假设,则卡尔曼滤波算法将无法正确估计状态量。
而非线性滤波算法克服了这一问题,可以适用于更广泛的信号模型。
在雷达信号处理中,非线性滤波算法主要应用于雷达目标探测和跟踪。
常见的非线性滤波算法包括粒子滤波、扩展卡尔曼滤波、无迹卡尔曼滤波和波束滤波等。
下面将分别介绍这些算法的原理和应用。
粒子滤波是一种随机采样技术,通过估计目标状态的概率密度函数来估计其状态。
该算法通过随机采样来生成一组粒子,每个粒子表示一种可能的目标状态,然后利用重要性采样来更新粒子权重。
最后使用加权平均方法通过所有粒子得到目标状态的估计值。
粒子滤波算法适用于非线性非高斯信号和噪声情况下的目标跟踪,并且该算法可以处理非线性非高斯状态转移模型。
扩展卡尔曼滤波是一种基于卡尔曼滤波的非线性滤波算法,它通过泰勒级数将非线性函数近似为一阶导数矩阵。
其主要思想是在非线性函数中使用线性逼近来代替非线性函数,以使得状态转移矩阵保持线性。
然而,扩展卡尔曼滤波仍具有高斯分布假设的缺陷,这使得算法在处理非高斯噪声等情况下效果较差。
无迹卡尔曼滤波是一种基于无迹变换的非线性滤波算法,其主要优点在于可以自适应地选择变换点,避免了扩展卡尔曼滤波中需要对先验和后验信噪比进行人工调整的缺点。
该算法通过变换非线性转移函数,将非线性模型转换为线性模型,并通过卡尔曼滤波来进行状态估计。
目标跟踪中非线性滤波的开题报告

目标跟踪中非线性滤波的开题报告一、选题背景和意义目标跟踪是计算机视觉领域的一个重要研究方向,涉及多个子领域,如目标检测、目标识别、目标追踪等。
其中,目标追踪是将给定目标在连续帧中进行跟踪的过程,对于实时监控、视频分析、自动驾驶等领域具有重要的应用价值。
目标追踪中常用的方法有基于特征点的方法、基于模板匹配的方法、基于卡尔曼滤波的方法、基于粒子滤波的方法等。
其中,非线性滤波在目标跟踪中得到了广泛的应用。
因为目标在实际的图像中往往表现为非线性的,特别是在存在视角、光照、遮挡、形变等复杂情况时,传统的线性滤波方法难以有效地抑制噪声和进行准确的目标追踪。
而非线性滤波方法则可以很好地处理这些复杂情况,提高目标跟踪的稳定性和准确性。
二、主要研究内容本文的主要研究内容是基于非线性滤波的目标跟踪。
具体来说,本文将探讨以下几个方面:(1)非线性滤波方法的基本原理和应用场景。
(2)基于粒子滤波的目标跟踪算法及其优化方法,包括状态空间模型的建立、重采样策略、观测噪声的建模等。
(3)基于卡尔曼滤波的目标跟踪算法及其优化方法,包括线性化处理、动态模型的建立、测量模型的建立等。
(4)实验验证:对比不同算法在目标跟踪数据集上的性能表现,分析不同算法的优劣,验证非线性滤波方法在目标跟踪中的优越性。
三、研究意义(1)本文将深入探究非线性滤波在目标跟踪中的应用,为目标跟踪领域的研究提供新的思路和方法。
(2)通过对比实验验证,可以评估不同算法的优劣,并且可以在实际应用中选择合适的算法以达到更好的目标跟踪效果。
(3)本文的研究成果对于实时监控、视频分析、自动驾驶等领域的应用都具有实际应用价值,因为这些领域在目标追踪方面都有着迫切的需求。
四、预期成果(1)通过对比实验验证,可以评估不同算法的优劣,并且可以在实际应用中选择合适的算法以达到更好的目标跟踪效果。
(2)探索非线性滤波在目标跟踪中的应用方法,提出一种效果优秀的基于非线性滤波的目标跟踪算法。
基于集合卡尔曼滤波的非线性目标跟踪算法

文章编号 : 1 0 0 6—9 3 4 8 ( 2 0 1 3 ) 0 4— 0 3 1 7—0 5
计
算
机
仿
真
2 0 1 3 年4 月
基 于 集 合 卡 尔 曼 滤 波 的非 线 性 目标 跟 踪 算 法
崔 波 , 张 家树 , 杨 宇
( 1 .西南交通大学信 息科学与技术 学院 , 四川 成都 6 1 0 0 3 1 ; 2 .中国电子科技集团公司第三十研究所 , 四川 成都 6 1 0 0 4 1 )
中图分 类号: T P 2 1 2 ቤተ መጻሕፍቲ ባይዱ文献标识码 : B
No n l i n e a r Ta r g e t Tr a c k i n g Al g o r i t hm Ba s e d o n
Ens e mb l e Ka l ma n Fi l t e r
—
a r r i v a l a n d D o p p l e r f r e q u e n c y ’ t o e s t i ma t e t h e t a r g e t s t a t e ,a n d t h e f e a s i b i l i t y nd a v a l i d i t y o f lg a o i r t h m we r e v e r i —
Ka l ma n i f h e r ,a n d t h e a f f e c t i o n o f d i f f e r e n t i n i t i a l e n s e mb l e s o n t a r g e t t r a c k i n g p e r f o ma r n c e w a s d i s c u s s e d,t h e n c o m— p a r i s o n wi t h o t h e r n o n l i n e a r t r a c k i n g a l g o i r t h ms w a s e x e c u t e d .T h e lg a o r i t h m u s e d t h e me a s u r e me n t s o f d i r e c t i o n一0 f
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的粒 子 滤 波 算法 。分 析 了 E KF、P F和 R F算 法 的 原 理 ,比较 了 3种 算 法 的 性 能 差 异 。仿 真 结 果 表 明 ,P 滤 P F 波 精度 优 于 E F, R F在 精 度 和 计 算 复 杂 度 等 方 面 均 优 于 P , 随 着 粒 子 数 目的增 加 , F 和 R F 的 精 度 K 面 P F 且 P P
典 型 问题 , 传统 的解 决方 法是借 助 于 T yo 级数 展开 a lr 的 扩 展 卡 尔 曼 滤 波 ( xe d d Kama ie , 写 E tn e l n F l r 简 t E ) 法 。但 是这 种 滤波 方法 是 基 于 系统 噪声 和量 KF 算 测 噪声 均近 似为 高斯分 布 的假 设 ,对状 态变 量 的均值 和协方 差进行 最 优估 计 ,它需 要计 算模 型 的 J cba ao in 矩 阵 ,从而使 得实 现起 来较 为复杂 。而 且该 方法 只适
用 于弱 非线性 的系统 ,对 于强 非线 性系 统 ,很 容 易导
程 、白噪声激励 的统计特 性和量测误 差的统计 特性l 。 _ 2 ] 它通过 对非 线性 函数 在最佳 估计 点附 近进行 泰勒 展开 并 舍弃高 阶分量 , 从而将 非线性模型线性化 , 因而该种 算 法能够广泛地 应用于各种 非线性系统 。 但 是 ,扩展 卡尔曼 滤 波使用 的只 是非线 性 函数 泰 勒 展开 的第 一 阶展 开式 ,更 高 阶的展 开量通 常 因为其 复杂度 很少 被使用 。而且 它总是 假设 为高斯 分布 ,当 真 实 的后 验 分布不 是 高斯分 布并 且偏 离高斯 分布很 远 时 ,使用 高斯 分 布来 近似就 不能很 好 地描述 真实 的后 验 分布 ,这个 时候 ,使 用 粒子滤 波器 就可 以获得 比扩 展 卡尔曼 滤 波器更 好 的性能 。 2 粒子 滤 波算法 采 样 重 要 性 重 采 样 粒 子 滤 波 (a lg S mpi n I o tneR smpigP ri eFl r 即传统 粒子 滤 mp ra c ea l at l i e ) n c t 波器 ,将重 要性 分 布 函数 P( z , ) 为状态 的 ] z I 取 转 移先验 分布 P( I 一) ,使粒子 的抽 样实 现非常方 便 ,并且 引入 了重 采样 法则 克服权 值 的退化 问题 。这 里 , 示粒 子 i k时刻 的状态 , 表 示粒 子 i 志 -表 z 在 在 时刻 的估 计状 态 。 F递推 过程 由 3部 分组 成 : P ①通过 重 要性 分 布 函数 P( - ) 更 新 ( z J 来 z 预测 ) 粒子 ; 由 ② 似然 函数 P( 『 更 新粒 子 的权 值 ;③ 重采 样 。每 获 .) 2 7 得观测 量 ,预测 粒 子 的权 值根 据对 应粒 子的 似然概率 值来更 新 。在重 采样 过 程 中 ,权值 较 大的粒 子将被采 样 多 次 ,分配相 等权 值 ,然后 根据 系统模 型独 立进行 动态更 新 。这样 理论 上粒 子群 的分 布会 自动逼 近状态 的真 实后验 概率 分 布 。 .
也 不 断提 升 。
关 键 词 :非 线 性 滤 波 ;扩 展 卡 尔 曼 滤 波 ;粒 子 滤 波 ; 正 则 化 粒 子 滤 波 ;状 态估 7 文 献 标 识 码 :A
0 引 言
滤波 的 目的是从 观测测 量 中在线 、实 时地估 计和 预测 出动态 系统 的状态 和误 差的统 计量 。状 态估 计一 直都 是 自动控 制 、通讯 、航 空与航 天 等领 域 的经 典研 究 主 题之一 l 。非线性 估计是 统 计信 号 处理 中 的一个 _ 1 ]
第3 期 ( 总第 1 0期 ) 6 21 0 0年 6月
机 械 工 程 与 自 动 化
M ECHANI CAL ENGI NEERI NG 8 AUT0M AT1 乙 0N
No.3
J n u.
文 章 编 号 : 6 2 6 1 ( 0 0 0 — 0 0 0 1 7— 4 32 1 ) 30 9—3
目标 跟 踪 中非 线 性滤 波算 法 的研 究
赵
原 005) 3 0 1
静 ,黄晋 英 ,王夙 拮
0 0 5 ;2 中北 大 学 机 械 工 程 与 自动 化 学 院 , 山西 太 301 .
( . 中 北 大 学 信 息 与通 信 工 程 学 院 , 山西 太 原 1
摘 要 :介 绍 了 3种 非 线 性估 计 方 法 。在 处 理 目标 跟 踪 等 动 态 系 统 实 时估 计 问题 中,E KF将 系统 进 行 线 性 化 近 似 时存 在 估 计误 差 , 而影 响 目标 跟 踪 的精 度 ; F对 系统 噪声 和 量 测 噪 声 的概 率 分 布 没有 要 求 ; P 是 改 进 从 P RF
致 发散 。因此 有必 要研究 非线 性情 况下 实用 的高精 度 对准 方法 。 粒子 滤波算 法是 一种递 推算 法 , 简单实 用 , 适合 于 系统方 程为非 线性 和噪声 为非 高斯 的情 况 。近 些年 来 ,粒子 滤波算 法经 过很 多研究 者 的改进 ,已被 应用 于惯 性导航 、地 形 匹配和 目标跟 踪 等多个 领域 。 本文 首先 详细地 阐述 了扩展 卡尔 曼 滤波 、传统 粒 子滤 波 以及正 则化粒 子滤 波 的原理及算 法 步骤 ,并从 理论 上对 比了 3 种算 法 的优缺 点 ; 然后 通 过实验 仿真 , 分析 滤波性 能差 异 ;最后 提 出进 一步 的研 究展 望 。 1 扩 展卡 尔曼 滤波算 法
