2020年中考数学试题分类汇编(九个专题)
2020年中考数学试题分类:实数的运算解答题解析

2020年中考数学试题分类汇编:实数的运算解答题解析1.(2020北京)计算:11()|2|6sin 453-+--︒ 【解析】解:原式=5232233=-++2.(2020成都)(12分)(1)计算:212sin 60()|22-︒++;【解答】解:(1)原式2423=+- 423=++-- 3=;3.(2020河北)已知两个有理数:-9和5. (1)计算:(9)52-+; (2)若再添一个负整数m ,且-9,5与m 这三个数的平均数仍小于m ,求m 的值. 【答案】(1)-2;(2)1m =-. 【详解】(1)(9)52-+=422-=-; (2)依题意得(9)53m-++<m解得m >-2∴负整数m=-1.4.(2020江西)(1)计算:21(1|2|2-⎛⎫--+ ⎪⎝⎭【解析】 原式=2)21(121+- =341=+- 19.(202020(2)(3)π+---. 【详解】解:原式341=+-6=.5.(2020乐山)计算:022cos 60(2020)π--︒+-.解:原式=12212-⨯+=2. 6.(2020四川绵阳)(1)计算:125-3+2cos 608()22︒-⨯--【解析】本题考查数式综合运算。
熟练掌握绝对值的化简、二次根式、0指数、三角函数是解题的关键。
解:原式=113-5+25-22-122⨯⨯=3-5+5-2-1=0.7.(2020贵州黔西南)(12分)(1)计算(﹣2)2﹣||﹣2cos45°+(2020﹣π)0;【解答】解:(1)原式=421=41=5﹣2;8.计算:(2020无锡)(1)()22516-+-- 【详解】解:(1)原式=4+5-4=5; 9.(2020长沙)计算:()1131012cos 454-︒⎛⎫---++ ⎪⎝⎭解:()1131012cos 454-︒⎛⎫---++ ⎪⎝⎭=3114-++=710.(2020齐齐哈尔)((10分)(1)计算:sin30°(3)0+||【解答】解:(1)sin30°(3)0+||4﹣1=4;11.(2020重庆A 卷)在整数的除法运算中,只有能整除与不能整除两种情况,当不能整除时,就会产生余数,现在我们利用整数的除法运算来研究一种数——“差一数”.定义:对于一个自然数,如果这个数除以5余数为4,且除以3余数为2,则称这个数为“差一数”. 例如:14524÷=,14342÷=,所以14是“差一数”;19534÷=,但19361÷=,所以19不是“差一数”.(1)判断49和74是否为“差一数”?请说明理由; (2)求大于300且小于400的所有“差一数”. 解:(1)∵49594÷=;493161÷=,∴49不是“差一数”, ∵745144÷=;743242÷=,∴74是“差一数”;(2)∵“差一数”这个数除以5余数为4, ∴“差一数”这个数的个位数字为4或9,∴大于300且小于400的符合要求的数为304、309、314、319、324、329、334、339、344、349、354、359、364、369、374、379、384、389、394、399, ∵“差一数”这个数除以3余数为2,∴“差一数”这个数的各位数字之和被3除余2,∴大于300且小于400的所有“差一数”为314、329、344、359、374、389.12.(2020上海)(10分)计算:(21)﹣2+|3|.【解答】解:原式=(33)2﹣4+3=32﹣4+3=0.13.(2020重庆B 卷)在数的学习过程中,我们总会对其中一些具有某种特性的数充满好奇,如学习自然数时,我们发现一种特殊的自然数——“好数”.定义:对于三位自然数n ,各位数字都不为0,且百位数字与十位数字之和恰好能被个位数字整除,则称这个自然数n 为“好数”. 例如:426是“好数”,因为4,2,6都不为0,且4+2=6,6能被6整除; 643不是“好数”,因为6+4=10,10不能被3整除.(1)判断312,675是否是“好数”?并说明理由;(2)求出百位数字比十位数字大5的所有“好数”的个数,并说明理由. 解:(1)∵3,1,2都不为0,且3+1=4,4能被2整除,∴312是“好数”, ∵6,7,5都不为0,且6+7=12,12不能被5整除,∴675不是“好数”;(2)设十位数字为x ,个位数字为y ,则百位数字为(x+5).其中x ,y 都是正整数,且1≤x ≤4,1≤y ≤9.十位数字与个位数字的和为:2x+5. 当x=1时,2x+5=7,此时y=1或7,“好数”有:611,617 当x=2时,2x+5=9,此时y=1或3或9,“好数”有:721,723,729 当x=3时,2x+5=11,此时y=1,“好数”有:831 当x=4时,2x+5=13,此时y=1,“好数”有:941所以百位数字比十位数字大5的所有“好数”的个数是7.理由如上. 14.(2020新疆生产建设兵团)(6分)计算:(﹣1)2+||+(π﹣3)0.解:(﹣1)2+||+(π﹣3)011﹣2.15.(2020内蒙古呼和浩特)(10分)(1)计算:|1﹣3|﹣2×6+3-21﹣(32)﹣2;【解答】解:(1)原式=3-1-23+2+3-49=45; 16.(2020江苏连云港)(6分)计算2020131(1)()645--+-.【解答】解:原式1542=+-=.17.(2020江苏泰州)(3分)如图,点P 在反比例函数3y x=的图象上,且横坐标为1,过点P 作两条坐标轴的平行线,与反比例函数(0)ky k x=<的图象相交于点A 、B ,则直线AB 与x 轴所夹锐角的正切值为 3 .【解答】解:点P 在反比例函数3y x=的图象上,且横坐标为1,则点(1,3)P , 则点A 、B 的坐标分别为(1,)k ,1(3k ,3),设直线AB 的表达式为:y mx t =+,将点A 、B 的坐标代入上式得133k m t km t =+⎧⎪⎨=-+⎪⎩,解得3m =-,故直线AB 与x 轴所夹锐角的正切值为3,故答案为3.18.(2020四川遂宁)(7分)计算:2sin30°﹣|1|+(21)﹣2﹣(π﹣2020)0. 【解答】解:原式=22(1)+4﹣1=211+4﹣13.19.(2020湖南岳阳)(6分)(2020•岳阳)计算:(21)﹣1+2cos60°﹣(4﹣π)0+|﹣3 |. 【解答】解:原式=2+2×21- 1 +3 =2+1﹣1 +3 =2+3 .20.(2020广西南宁)(6分)计算:﹣(﹣1)+32÷(1﹣4)×2. 解:原式=1+9÷(﹣3)×2=1﹣3×2=1﹣6=﹣5. 21.(6分)(2020•玉林)计算:•(π﹣3.14)0﹣|1|+()2. 【解答】解:原式1﹣(1)+91+9=10.22.(5分)(2020•常德)计算:20+(31)﹣1•4tan45°.【解答】解:原式=1+3×2﹣4×1=1+6﹣4=3. 23.(10分)(2020•徐州)计算:(1)(﹣1)2020+|2|﹣()﹣1; 【解答】解:(1)原式=1+22=1;24.(2020贵州遵义)(1)sin30°﹣(π﹣3.14)0+()﹣2;解:(1)原式1+4=3;25.(2020山西)(10分)(1)计算:(﹣4)2×(﹣21)3﹣(﹣4+1). 解:(1)(﹣4)2×(﹣21)3﹣(﹣4+1)=16×(﹣81)+3=﹣2+3=1;26.(2020东莞)计算:03822cos 60(3.14)π---+--︒.解:原式122212=--+⨯-4=- 27.(2020四川自贡)(8分)计算:|﹣2|﹣(π)0+()﹣1.解:原式=2﹣1+(﹣6)=1+(﹣6)=﹣5.28.(2020四川自贡)(10分)我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法.例如,代数式|x ﹣2|的几何意义是数轴上x 所对应的点与2所对应的点之间的距离:因为|x +1|=|x ﹣(﹣1)|,所以|x +1|的几何意义就是数轴上x 所对应的点与﹣1所对应的点之间的距离. (1)发现问题:代数式|x +1|+|x ﹣2|的最小值是多少?(2)探究问题:如图,点A 、B 、P 分别表示数﹣1、2、x ,AB =3.∵|x +1|+|x ﹣2|的几何意义是线段P A 与PB 的长度之和,∴当点P 在线段AB 上时,P A +PB =3,当点P 在点A 的左侧或点B 的右侧时,P A +PB >3.∴|x +1|+|x ﹣2|的最小值是3. (3)解决问题:①|x ﹣4|+|x +2|的最小值是 6 ;②利用上述思想方法解不等式:|x +3|+|x ﹣1|>4;③当a 为何值时,代数式|x +a |+|x ﹣3|的最小值是2.【解答】解:(1)发现问题:代数式|x +1|+|x ﹣2|的最小值是多少? (2)探究问题:如图,点A 、B 、P 分别表示数﹣1、2、x ,AB =3.∵|x +1|+|x ﹣2|的几何意义是线段P A 与PB 的长度之和,∴当点P 在线段AB 上时,P A +PB =3,当点P 在点A 的左侧或点B 的右侧时,P A +PB >3.∴|x +1|+|x ﹣2|的最小值是3. (3)解决问题:①|x ﹣4|+|x +2|的最小值是6; 故答案为:6;②如图所示,满足|x +3|+|x ﹣1|>4的x 范围为x <﹣3或x >1;③当a 为﹣1或﹣5时,代数式|x +a |+|x ﹣3|的最小值是2. 29.(2020青海)(5分)计算:(31)﹣1+|1﹣3tan45°|+(π﹣3.14)0﹣327. 解:原式=3+|1﹣3|+1﹣3=3+3-1+1-3=3. 30.(2020四川眉山)(8分)计算:(2﹣2)0+(﹣21)﹣2+2sin45°﹣8. 解:原式=1+4+2×22﹣22=5+2﹣22=5﹣2. 31.(2020•怀化)计算:2﹣2﹣2cos45°+|2|.解:原式.32.(2020浙江温州)(10分)(1)计算:|﹣2|+()0﹣(﹣1).【解答】解:(1)原式=2﹣2+1+1 =2;33.(2020海南)(12分)计算:(1)|﹣8|×2﹣1﹣16+(﹣1)2020;(2)(a +2)(a ﹣2)﹣a (a +1).解:(1)|﹣8|×2﹣1﹣16+(﹣1)2020,=8×21﹣4+1, =4﹣4+1,=1;(2)(a +2)(a ﹣2)﹣a (a +1), =a 2﹣4﹣a 2﹣a , =﹣4﹣a .34.(2020•株洲)计算:(41)﹣1+|﹣1|tan60°.【解答】解:原式=4+1=4+1﹣3 =2.35.(2020甘肃定西)计算:0(23)(23)tan 60(23)π+--︒解:原式4331=-=3.。
2020年中考数学试卷(解析版)共9套
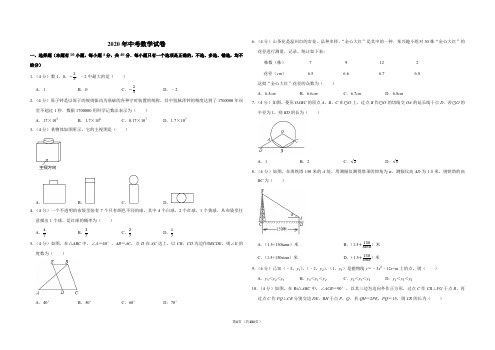
2020年中考数学试卷一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)1.(4分)数1,0,−23,﹣2中最大的是( ) A .1B .0C .−23D .﹣22.(4分)原子钟是以原子的规则振动为基础的各种守时装置的统称,其中氢脉泽钟的精度达到了1700000年误差不超过1秒.数据1700000用科学记数法表示为( ) A .17×105B .1.7×106C .0.17×107D .1.7×1073.(4分)某物体如图所示,它的主视图是( )A .B .C .D .4.(4分)一个不透明的布袋里装有7个只有颜色不同的球,其中4个白球,2个红球,1个黄球.从布袋里任意摸出1个球,是红球的概率为( ) A .47B .37C .27D .175.(4分)如图,在△ABC 中,∠A =40°,AB =AC ,点D 在AC 边上,以CB ,CD 为边作▱BCDE ,则∠E 的度数为( )A .40°B .50°C .60°D .70°6.(4分)山茶花是温州市的市花、品种多样,“金心大红”是其中的一种.某兴趣小组对30株“金心大红”的花径进行测量、记录,统计如下表: 株数(株) 7 9 12 2 花径(cm )6.56.66.76.8这批“金心大红”花径的众数为( )A .6.5cmB .6.6cmC .6.7cmD .6.8cm7.(4分)如图,菱形OABC 的顶点A ,B ,C 在⊙O 上,过点B 作⊙O 的切线交OA 的延长线于点D .若⊙O 的半径为1,则BD 的长为( )A .1B .2C .√2D .√38.(4分)如图,在离铁塔150米的A 处,用测倾仪测得塔顶的仰角为α,测倾仪高AD 为1.5米,则铁塔的高BC 为( )A .(1.5+150tan α)米B .(1.5+150tanα)米 C .(1.5+150sin α)米D .(1.5+150sinα)米 9.(4分)已知(﹣3,y 1),(﹣2,y 2),(1,y 3)是抛物线y =﹣3x 2﹣12x +m 上的点,则( ) A .y 3<y 2<y 1B .y 3<y 1<y 2C .y 2<y 3<y 1D .y 1<y 3<y 210.(4分)如图,在Rt △ABC 中,∠ACB =90°,以其三边为边向外作正方形,过点C 作CR ⊥FG 于点R ,再过点C 作PQ ⊥CR 分别交边DE ,BH 于点P ,Q .若QH =2PE ,PQ =15,则CR 的长为( )A.14B.15C.8√3D.6√5二、填空题(本题有6小题,每小题5分,共30分)11.(5分)分解因式:m2﹣25=.12.(5分)不等式组{x−3<0,x+42≥1的解为.13.(5分)若扇形的圆心角为45°,半径为3,则该扇形的弧长为.14.(5分)某养猪场对200头生猪的质量进行统计,得到频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5kg及以上的生猪有头.15.(5分)点P,Q,R在反比例函数y=kx(常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3.若OE=ED=DC,S1+S3=27,则S2的值为.16.(5分)如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上.在F点观测A点后,沿FN方向走到M点,观测C点发现∠1=∠2.测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则场地的边AB为米,BC为米.三、解答题(本题有8小题,共80分.解答需写出必要的文字说明、演算步骤或证明过程)17.(10分)(1)计算:√4−|﹣2|+(√6)0﹣(﹣1).(2)化简:(x﹣1)2﹣x(x+7).18.(8分)如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.(1)求证:△ABC≌△DCE.(2)连结AE,当BC=5,AC=12时,求AE的长.19.(8分)A,B两家酒店规模相当,去年下半年的月盈利折线统计图如图所示.(1)要评价这两家酒店7~12月的月盈利的平均水平,你选择什么统计量?求出这个统计量.(2)已知A,B两家酒店7~12月的月盈利的方差分别为1.073(平方万元),0.54(平方万元).根据所给的方差和你在(1)中所求的统计量,结合折线统计图,你认为去年下半年哪家酒店经营状况较好?请简述理由.20.(8分)如图,在6×4的方格纸ABCD中,请按要求画格点线段(端点在格点上),且线段的端点均不与点A,B,C,D重合.(1)在图1中画格点线段EF,GH各一条,使点E,F,G,H分别落在边AB,BC,CD,DA上,且EF=GH,EF不平行GH.(2)在图2中画格点线段MN,PQ各一条,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且PQ=√5MN.21.(10分)已知抛物线y=ax2+bx+1经过点(1,﹣2),(﹣2,13).(1)求a,b的值.(2)若(5,y1),(m,y2)是抛物线上不同的两点,且y2=12﹣y1,求m的值.22.(10分)如图,C,D为⊙O上两点,且在直径AB两侧,连结CD交AB于点E,G是AĈ上一点,∠ADC=∠G.(1)求证:∠1=∠2.(2)点C关于DG的对称点为F,连结CF.当点F落在直径AB上时,CF=10,tan∠1=25,求⊙O的半径.23.(12分)某经销商3月份用18000元购进一批T恤衫售完后,4月份用39000元购进一批相同的T恤衫,数量是3月份的2倍,但每件进价涨了10元.(1)4月份进了这批T恤衫多少件?(2)4月份,经销商将这批T恤衫平均分给甲、乙两家分店销售,每件标价180元.甲店按标价卖出a件以后,剩余的按标价八折全部售出;乙店同样按标价卖出a件,然后将b件按标价九折售出,再将剩余的按标价七折全部售出,结果利润与甲店相同.①用含a的代数式表示b.②已知乙店按标价售出的数量不超过九折售出的数量,请你求出乙店利润的最大值.24.(14分)如图,在四边形ABCD中,∠A=∠C=90°,DE,BF分别平分∠ADC,∠ABC,并交线段AB,CD于点E,F(点E,B不重合).在线段BF上取点M,N(点M在BN之间),使BM=2FN.当点P从点D匀速运动到点E时,点Q恰好从点M匀速运动到点N.记QN=x,PD=y,已知y=−65x+12,当Q为BF中点时,y=245.(1)判断DE与BF的位置关系,并说明理由.(2)求DE,BF的长.(3)若AD=6.①当DP=DF时,通过计算比较BE与BQ的大小关系.②连结PQ,当PQ所在直线经过四边形ABCD的一个顶点时,求所有满足条件的x的值.2020年浙江省温州市中考数学试卷参考答案与试题解析一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)1.(4分)数1,0,−23,﹣2中最大的是()A.1B.0C.−23D.﹣2【分析】根据有理数大小比较的方法即可得出答案.【解答】解:﹣2<−23<0<1,所以最大的是1.故选:A.【点评】本题考查了有理数大小比较的方法.(1)在数轴上表示的两点,右边的点表示的数比左边的点表示的数大.(2)正数大于0,负数小于0,正数大于负数.(3)两个正数中绝对值大的数大.(4)两个负数中绝对值大的反而小.2.(4分)原子钟是以原子的规则振动为基础的各种守时装置的统称,其中氢脉泽钟的精度达到了1700000年误差不超过1秒.数据1700000用科学记数法表示为()A.17×105B.1.7×106C.0.17×107D.1.7×107【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.【解答】解:1700000=1.7×106,故选:B.【点评】此题考查科学记数法的表示方法,表示时关键要正确确定a的值以及n的值.3.(4分)某物体如图所示,它的主视图是()A.B.C.D.【分析】根据主视图的意义和画法进行判断即可.【解答】解:根据主视图就是从正面看物体所得到的图形可知:选项A所表示的图形符合题意,故选:A.【点评】考查简单几何体的三视图的画法,主视图就是从正面看物体所得到的图形.4.(4分)一个不透明的布袋里装有7个只有颜色不同的球,其中4个白球,2个红球,1个黄球.从布袋里任意摸出1个球,是红球的概率为()A.47B.37C.27D.17【分析】根据概率公式求解.【解答】解:从布袋里任意摸出1个球,是红球的概率=27.故选:C.【点评】本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.5.(4分)如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作▱BCDE,则∠E的度数为()A.40°B.50°C.60°D.70°【分析】根据等腰三角形的性质可求∠C,再根据平行四边形的性质可求∠E.【解答】解:∵在△ABC中,∠A=40°,AB=AC,∴∠C=(180°﹣40°)÷2=70°,∵四边形BCDE是平行四边形,∴∠E=70°.故选:D.【点评】考查了平行四边形的性质,等腰三角形的性质,关键是求出∠C的度数.6.(4分)山茶花是温州市的市花、品种多样,“金心大红”是其中的一种.某兴趣小组对30株“金心大红”的花径进行测量、记录,统计如下表:株数(株)79122花径(cm) 6.5 6.6 6.7 6.8这批“金心大红”花径的众数为()A.6.5cm B.6.6cm C.6.7cm D.6.8cm【分析】根据表格中的数据,可以得到这组数据的中位数,本题得以解决.【解答】解:由表格中的数据可得,这批“金心大红”花径的众数为6.7,故选:C.【点评】本题考查众数,解答本题的关键是明确众数的含义,会求一组数据的众数.7.(4分)如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为1,则BD的长为()A.1B.2C.√2D.√3【分析】连接OB,根据菱形的性质得到OA=AB,求得∠AOB=60°,根据切线的性质得到∠DBO=90°,解直角三角形即可得到结论.【解答】解:连接OB,∵四边形OABC是菱形,∴OA=AB,∵OA=OB,∴OA=AB=OB,∴∠AOB=60°,∵BD是⊙O的切线,∴∠DBO=90°,∵OB=1,∴BD=√3OB=√3,故选:D.【点评】本题考查了切线的性质,菱形的性质,等边三角形的判定和性质,解直角三角形,熟练正确切线的性质定理是解题的关键.8.(4分)如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为()A.(1.5+150tanα)米B.(1.5+150tanα)米C.(1.5+150sinα)米D.(1.5+150sinα)米【分析】过点A作AE⊥BC,E为垂足,再由锐角三角函数的定义求出BE的长,由BC=CE+BE即可得出结论.【解答】解:过点A作AE⊥BC,E为垂足,如图所示:则四边形ADCE为矩形,AE=150,∴CE=AD=1.5,在△ABE中,∵tanα=BEAE=BE150,∴BE=150tanα,∴BC=CE+BE=(1.5+150tanα)(m),故选:A.【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.9.(4分)已知(﹣3,y1),(﹣2,y2),(1,y3)是抛物线y=﹣3x2﹣12x+m上的点,则()A.y3<y2<y1B.y3<y1<y2C.y2<y3<y1D.y1<y3<y2【分析】求出抛物线的对称轴为直线x=﹣2,然后根据二次函数的增减性和对称性解答即可.【解答】解:抛物线的对称轴为直线x=−−122×(−3)=−2,∵a=﹣3<0,∴x=﹣2时,函数值最大,又∵﹣3到﹣2的距离比1到﹣2的距离小,∴y3<y1<y2.故选:B.【点评】本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的增减性和对称性,求出对称轴是解题的关键.10.(4分)如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q.若QH=2PE,PQ=15,则CR的长为()A.14B.15C.8√3D.6√5【分析】如图,连接EC,CH.设AB交CR于J.证明△ECP∽△HCQ,推出PCCQ=CECH=EPHQ=12,由PQ=15,可得PC=5,CQ=10,由EC:CH=1:2,推出AC:BC=1:2,设AC=a,BC=2a,证明四边形ABQC 是平行四边形,推出AB=CQ=10,根据AC2+BC2=AB2,构建方程求出a即可解决问题.【解答】解:如图,连接EC,CH.设AB交CR于J.∵四边形ACDE,四边形BCJHD都是正方形,∴∠ACE=∠BCH=45°,∵∠ACB=90°,∠BCI=90°,∴∠ACE+∠ACB+∠BCH=180°,∠ACB+∠BCI=90°∴B,C,H共线,A,C,I共线,∵DE∥AI∥BH,∴∠CEP=∠CHQ,∵∠ECP=∠QCH,∴△ECP∽△HCQ,∴PCCQ=CECH=EPHQ=12,∵PQ=15,∴PC=5,CQ=10,∵EC:CH=1:2,∴AC:BC=1:2,设AC=a,BC=2a,∵PQ⊥CRCR⊥AB,∴CQ∥AB,∵AC ∥BQ ,CQ ∥AB , ∴四边形ABQC 是平行四边形, ∴AB =CQ =10, ∵AC 2+BC 2=AB 2, ∴5a 2=100,∴a =2√2(负根已经舍弃), ∴AC =2√5,BC =4√5, ∵12•AC •BC =12•AB •CJ ,∴CJ =2√5×4√510=4, ∵JR =AF =AB =10, ∴CR =CJ +JR =14, 故选:A .【点评】本题考查相似三角形的判定和性质,平行四边形的判定和性质,解直角三角形等知识,解题的关键是学会踢脚线有辅助线,构造相似三角形解决问题,学会利用参数构建方程解决问题,属于中考选择题中的压轴题.二、填空题(本题有6小题,每小题5分,共30分) 11.(5分)分解因式:m 2﹣25= (m +5)(m ﹣5) . 【分析】直接利用平方差进行分解即可. 【解答】解:原式=(m ﹣5)(m +5), 故答案为:(m ﹣5)(m +5).【点评】此题主要考查了运用公式法分解因式,关键是掌握平方差公式:a 2﹣b 2=(a +b )(a ﹣b ). 12.(5分)不等式组{x −3<0,x+42≥1的解为 ﹣2≤x <3 .【分析】先求出不等式组中每一个不等式的解集,再求出它们的公共部分即可求解. 【解答】解:{x −3<0①x+42≥1②,解①得x <3;解②得x ≥﹣2.故不等式组的解集为﹣2≤x <3. 故答案为:﹣2≤x <3.【点评】考查了解一元一次不等式组,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.13.(5分)若扇形的圆心角为45°,半径为3,则该扇形的弧长为 34π .【分析】根据弧长公式l =nπr180,代入相应数值进行计算即可. 【解答】解:根据弧长公式:l =45⋅π×3180=34π, 故答案为:34π.【点评】此题主要考查了弧长的计算,关键是掌握弧长公式.14.(5分)某养猪场对200头生猪的质量进行统计,得到频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5kg 及以上的生猪有 140 头.【分析】根据题意和直方图中的数据可以求得质量在77.5kg 及以上的生猪数,本题得以解决. 【解答】解:由直方图可得,质量在77.5kg 及以上的生猪:90+30+20=140(头), 故答案为:140.【点评】本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.15.(5分)点P ,Q ,R 在反比例函数y =kx (常数k >0,x >0)图象上的位置如图所示,分别过这三个点作x 轴、y 轴的平行线.图中所构成的阴影部分面积从左到右依次为S 1,S 2,S 3.若OE =ED =DC ,S 1+S 3=27,则S 2的值为275.【分析】设CD =DE =OE =a ,则P (k3a ,3a ),Q (k2a ,2a ),R (ka,a ),推出CP =3k 3a ,DQ =k 2a ,ER =ka ,推出OG =AG ,OF =2FG ,OF =23GA ,推出S 1=23S 3=2S 2,根据S 1+S 3=27,求出S 1,S 3,S 2即可. 【解答】解:∵CD =DE =OE , ∴可以假设CD =DE =OE =a , 则P (k 3a,3a ),Q (k2a,2a ),R (ka,a ),∴CP =3k 3a ,DQ =k 2a ,ER =ka,∴OG =AG ,OF =2FG ,OF =23GA , ∴S 1=23S 3=2S 2, ∵S 1+S 3=27,∴S 3=815,S 1=545,S 2=275,故答案为275.【点评】本题考查反比例函数系数k 的几何意义,矩形的性质等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.16.(5分)如图,在河对岸有一矩形场地ABCD ,为了估测场地大小,在笔直的河岸l 上依次取点E ,F ,N ,使AE ⊥l ,BF ⊥l ,点N ,A ,B 在同一直线上.在F 点观测A 点后,沿FN 方向走到M 点,观测C 点发现∠1=∠2.测得EF =15米,FM =2米,MN =8米,∠ANE =45°,则场地的边AB 为 15√2 米,BC 为 20√2 米.【分析】根据已知条件得到△ANE 和△BNF 是等腰直角三角形,求得AE =EN =15+2+8=25(米),BF =FN =2+8=10(米),于是得到AB =AN ﹣BN =15√2(米);过C 作CH ⊥l 于H ,过B 作PQ ∥l 交AE 于P ,交CH 于Q ,根据矩形的性质得到PE =BF =QH =10,PB =EF =15,BQ =FH ,根据相似三角形的性质即可得到结论.【解答】解:∵AE ⊥l ,BF ⊥l , ∵∠ANE =45°,∴△ANE 和△BNF 是等腰直角三角形, ∴AE =EN ,BF =FN ,∴EF =15米,FM =2米,MN =8米,∴AE =EN =15+2+8=25(米),BF =FN =2+8=10(米), ∴AN =25√2,BN =10√2, ∴AB =AN ﹣BN =15√2(米);过C 作CH ⊥l 于H ,过B 作PQ ∥l 交AE 于P ,交CH 于Q , ∴AE ∥CH ,∴四边形PEHQ 和四边形PEFB 是矩形, ∴PE =BF =QH =10,PB =EF =15,BQ =FH , ∵∠1=∠2,∠AEF =∠CHM =90°, ∴△AEF ∽△CHM , ∴CH HM=AE EF=2515=53,∴设MH =3x ,CH =5x , ∴CQ =5x ﹣10,BQ =FH =3x +2,∵∠APB=∠ABC=∠CQB=90°,∴∠ABP+∠P AB=∠ABP+∠CBQ=90°,∴∠P AB=∠CBQ,∴△APB∽△BQC,∴APBQ=PBCQ,∴153x+2=155x−10,∴x=6,∴BQ=CQ=20,∴BC=20√2,故答案为:15√2,20√2.【点评】本题考查了相似三角形的应用,矩形的性质,等腰直角三角形的判定和性质,正确的识别图形是解题的关键.三、解答题(本题有8小题,共80分.解答需写出必要的文字说明、演算步骤或证明过程)17.(10分)(1)计算:√4−|﹣2|+(√6)0﹣(﹣1).(2)化简:(x﹣1)2﹣x(x+7).【分析】(1)直接利用零指数幂的性质以及二次根式的性质、绝对值的性质分别化简得出答案;(2)直接利用完全平方公式以及单项式乘以多项式运算法则计算得出答案.【解答】解:(1)原式=2﹣2+1+1=2;(2)(x﹣1)2﹣x(x+7)=x2﹣2x+1﹣x2﹣7x=﹣9x+1.【点评】此题主要考查了实数运算以及完全平方公式以及单项式乘以多项式运算,正确掌握相关运算法则是解题关键.18.(8分)如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.(1)求证:△ABC≌△DCE.(2)连结AE,当BC=5,AC=12时,求AE的长.【分析】(1)由“AAS”可证△ABC≌△DCE;(2)由全等三角形的性质可得CE=BC=5,由勾股定理可求解.【解答】证明:(1)∵AB∥DE,∴∠BAC=∠D,又∵∠B=∠DCE=90°,AC=DE,∴△ABC≌△DCE(AAS);(2)∵△ABC≌△DCE,∴CE=BC=5,∵∠ACE=90°,∴AE=√AC2+CE2=√25+144=13.【点评】本题考查了全等三角形的判定和性质,勾股定理,熟练掌握全等三角形的判定方法是本题的关键.19.(8分)A,B两家酒店规模相当,去年下半年的月盈利折线统计图如图所示.(1)要评价这两家酒店7~12月的月盈利的平均水平,你选择什么统计量?求出这个统计量.(2)已知A,B两家酒店7~12月的月盈利的方差分别为1.073(平方万元),0.54(平方万元).根据所给的方差和你在(1)中所求的统计量,结合折线统计图,你认为去年下半年哪家酒店经营状况较好?请简述理由.【分析】(1)由要评价两家酒店月盈利的平均水平,即可得选择两家酒店月盈利的平均值,然后利用求平均数的方法求解即可求得答案;(2)平均数,盈利的方差反映酒店的经营业绩,A酒店的经营状况较好.【解答】解:(1)选择两家酒店月盈利的平均值;x A=1+1.6+2.2+2.7+3.5+46=2.5,x B=2+3+1.7+1.8+1.7+3.66=2.3;(2)平均数,方差反映酒店的经营业绩,A酒店的经营状况较好.理由:A酒店盈利的平均数为2.5,B酒店盈利的平均数为2.3.A酒店盈利的方差为1.073,B酒店盈利的方差为0.54,无论是盈利的平均数还是盈利的方差,都是A酒店比较大,故A酒店的经营状况较好.【点评】此题考查了折线统计图的知识.此题难度适中,注意掌握折线统计图表达的实际意义是解此题的关键.20.(8分)如图,在6×4的方格纸ABCD中,请按要求画格点线段(端点在格点上),且线段的端点均不与点A,B,C,D重合.(1)在图1中画格点线段EF,GH各一条,使点E,F,G,H分别落在边AB,BC,CD,DA上,且EF=GH,EF不平行GH.(2)在图2中画格点线段MN,PQ各一条,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且PQ=√5MN.【分析】(1)根据题意画出线段即可;(2)根据题意画出线段即可.【解答】解:(1)如图1,线段EF和线段GH即为所求;(2)如图2,线段MN和线段PQ即为所求.【点评】本题考查了作图﹣应用与设计作图,熟练掌握勾股定理是解题的关键.21.(10分)已知抛物线y=ax2+bx+1经过点(1,﹣2),(﹣2,13).(1)求a,b的值.(2)若(5,y1),(m,y2)是抛物线上不同的两点,且y2=12﹣y1,求m的值.【分析】(1)把点(1,﹣2),(﹣2,13)代入y=ax2+bx+1解方程组即可得到结论;(2)把x=5代入y=x2﹣4x+1得到y1=6,于是得到y1=y2,即可得到结论.【解答】解:(1)把点(1,﹣2),(﹣2,13)代入y=ax2+bx+1得,{−2=a+b+113=4a−2b+1,解得:{a=1b=−4;(2)由(1)得函数解析式为y=x2﹣4x+1,把x=5代入y=x2﹣4x+1得,y1=6,∴y2=12﹣y1=6,∵y1=y2,∴对称轴为x=2,∴m=4﹣5=﹣1.【点评】本题考查了二次函数图象上点的坐标特征,解方程组,正确的理解题意是解题的关键.22.(10分)如图,C,D为⊙O上两点,且在直径AB两侧,连结CD交AB于点E,G是AĈ上一点,∠ADC=∠G.(1)求证:∠1=∠2.(2)点C关于DG的对称点为F,连结CF.当点F落在直径AB上时,CF=10,tan∠1=25,求⊙O的半径.【分析】(1)根据圆周角定理和AB为⊙O的直径,即可证明∠1=∠2;(2)连接DF,根据垂径定理可得FD=FC=10,再根据对称性可得DC=DF,进而可得DE的长,再根据锐角三角函数即可求出⊙O的半径.【解答】解:(1)∵∠ADC=∠G,∴AĈ=AD̂,∵AB为⊙O的直径,∴BĈ=BD̂,∴∠1=∠2;(2)如图,连接DF,∵AĈ=AD̂,AB是⊙O的直径,∴AB⊥CD,CE=DE,∴FD=FC=10,∵点C,F关于DG对称,∴DC=DF=10,∴DE=5,∵tan∠1=25,∴EB=DE•tan∠1=2,∵∠1=∠2,∴tan∠2=25,∴AE=DEtan∠2=252,∴AB=AE+EB=292,∴⊙O的半径为294.【点评】本题考查了圆周角定理、轴对称的性质、解直角三角形,解决本题的关键是掌握轴对称的性质.23.(12分)某经销商3月份用18000元购进一批T恤衫售完后,4月份用39000元购进一批相同的T恤衫,数量是3月份的2倍,但每件进价涨了10元.(1)4月份进了这批T恤衫多少件?(2)4月份,经销商将这批T恤衫平均分给甲、乙两家分店销售,每件标价180元.甲店按标价卖出a件以后,剩余的按标价八折全部售出;乙店同样按标价卖出a件,然后将b件按标价九折售出,再将剩余的按标价七折全部售出,结果利润与甲店相同.①用含a的代数式表示b.②已知乙店按标价售出的数量不超过九折售出的数量,请你求出乙店利润的最大值.【分析】(1)根据4月份用39000元购进一批相同的T恤衫,数量是3月份的2倍,可以得到相应的分式方程,从而可以求得4月份进了这批T恤衫多少件;(2)①根据甲乙两店的利润相同,可以得到关于a、b的方程,然后化简,即可用含a的代数式表示b;②根据题意,可以得到利润与a的函数关系式,再根据乙店按标价售出的数量不超过九折售出的数量,可以得到a的取值范围,从而可以求得乙店利润的最大值.【解答】解:(1)设3月份购进x件T恤衫,18000x+10=390002x,解得,x=150,经检验,x=150是原分式方程的解,则2x=300,答:4月份进了这批T恤衫300件;(2)①每件T恤衫的进价为:39000÷300=130(元),(180﹣130)a+(180×0.8﹣130)(150﹣a)=(180﹣130)a+(180×0.9﹣130)b+(180×0.7﹣130)(150﹣a﹣b)化简,得b=150−a2;②设乙店的利润为w元,w=(180﹣130)a+(180×0.9﹣130)b+(180×0.7﹣130)(150﹣a﹣b)=54a+36b﹣600=54a+36×150−a2−600=36a+2100,∵乙店按标价售出的数量不超过九折售出的数量,∴a≤b,即a≤150−a2,解得,a≤50,∴当a=50时,w取得最大值,此时w=3900,答:乙店利润的最大值是3900元.【点评】本题考查一次函数的应用、分式方程的应用,解答本题的关键是明确题意,利用一次函数的性质和分式方程的知识解答,注意分式方程要检验.24.(14分)如图,在四边形ABCD中,∠A=∠C=90°,DE,BF分别平分∠ADC,∠ABC,并交线段AB,CD于点E,F(点E,B不重合).在线段BF上取点M,N(点M在BN之间),使BM=2FN.当点P从点D匀速运动到点E时,点Q恰好从点M匀速运动到点N.记QN=x,PD=y,已知y=−65x+12,当Q为BF中点时,y=24 5.(1)判断DE与BF的位置关系,并说明理由.(2)求DE,BF的长.(3)若AD=6.①当DP=DF时,通过计算比较BE与BQ的大小关系.②连结PQ,当PQ所在直线经过四边形ABCD的一个顶点时,求所有满足条件的x的值.【分析】(1)推出∠AED=∠ABF,即可得出DE∥BF;(2)求出DE=12,MN=10,把y=245代入y=−65x+12,解得x=6,即NQ=6,得出QM=4,由FQ=QB,BM=2FN,得出FN=2,BM=4,即可得出结果;(3)连接EM并延长交BC于点H,易证四边形DFME是平行四边形,得出DF=EM,求出∠DEA=∠FBE =∠FBC=30°,∠ADE=∠CDE=∠FME=60°,∠MEB=∠FBE=30°,得出∠EHB=90°,DF=EM=BM=4,MH=2,EH=6,由勾股定理得HB=2√3,BE=4√3,当DP=DF时,求出BQ=223,即可得出BQ >BE;②(Ⅰ)当PQ经过点D时,y=0,则x=10;(Ⅱ)当PQ经过点C时,由FQ∥DP,得出△CFQ∽△CDP,则FQDP=CFCD,即可求出x=103;(Ⅲ)当PQ经过点A时,由PE∥BQ,得出△APE∽△AQB,则PEBQ=AEAB,求出AE=6√3,AB=10√3,即可得出x=143,由图可知,PQ不可能过点B.【解答】解:(1)DE与BF的位置关系为:DE∥BF,理由如下:如图1所示:∵∠A=∠C=90°,∴∠ADC+∠ABC=360°﹣(∠A+∠C)=180°,∵DE、BF分别平分∠ADC、∠ABC,∴∠ADE=12∠ADC,∠ABF=12∠ABC,∴∠ADE+∠ABF=12×180°=90°,∵∠ADE+∠AED=90°,∴∠AED=∠ABF,∴DE∥BF;(2)令x=0,得y=12,∴DE=12,令y=0,得x=10,∴MN=10,把y=245代入y=−65x+12,解得:x=6,即NQ=6,∴QM=10﹣6=4,∵Q是BF中点,∴FQ=QB,∵BM=2FN,∴FN+6=4+2FN,解得:FN=2,∴BM=4,∴BF=FN+MN+MB=16;(3)①连接EM并延长交BC于点H,如图2所示:∵FM=2+10=12=DE,DE∥BF,∴四边形DFME是平行四边形,∴DF=EM,∵AD=6,DE=12,∠A=90°,∴∠DEA=30°,∴∠DEA=∠FBE=∠FBC=30°,∴∠ADE=60°,∴∠ADE=∠CDE=∠FME=60°,∴∠DFM=∠DEM=120°,∴∠MEB=180°﹣120°﹣30°=30°,∴∠MEB=∠FBE=30°,∴∠EHB=180°﹣30°﹣30°﹣30°=90°,DF=EM=BM=4,∴MH=12BM=2,∴EH=4+2=6,由勾股定理得:HB=√BM2−MH2=√42−22=2√3,∴BE=√EH2−HB2=√62+(2√3)2=4√3,当DP=DF时,−65x+12=4,解得:x=203,∴BQ=14﹣x=14−203=223,∵223>4√3,∴BQ>BE;②(Ⅰ)当PQ经过点D时,如图3所示:y=0,则x=10;(Ⅱ)当PQ经过点C时,如图4所示:∵BF=16,∠FCB=90°,∠CBF=30°,∴CF=12BF=8,∴CD=8+4=12,∵FQ∥DP,∴△CFQ∽△CDP,∴FQDP=CFCD,∴2+x−65x+12=812,解得:x=103;(Ⅲ)当PQ经过点A时,如图5所示:∵PE∥BQ,∴△APE∽△AQB,∴PE BQ=AE AB,由勾股定理得:AE =√DE 2−AD 2=√122−62=6√3, ∴AB =6√3+4√3=10√3,∴12−(−65x+12)14−x=√310√3,解得:x =143,由图可知,PQ 不可能过点B ;综上所述,当x =10或x =103或x =143时,PQ 所在的直线经过四边形ABCD 的一个顶点.【点评】本题是四边形综合题,主要考查了平行四边形的的判定与性质、勾股定理、角平分线的性质、平行线的判定与性质、相似三角形的判定与性质、含30°角的直角三角形的性质等知识;本题综合性强,难度较大,熟练掌握平行四边形的判定与性质是解题的关键.2020年中考数学试卷一、选择题(本题有10小题,每小题3分,共30分) 1.(3分)实数3的相反数是( ) A .﹣3B .3C .−13D .132.(3分)分式x+5x−2的值是零,则x 的值为( )A .2B .5C .﹣2D .﹣53.(3分)下列多项式中,能运用平方差公式分解因式的是( ) A .a 2+b 2B .2a ﹣b 2C .a 2﹣b 2D .﹣a 2﹣b 24.(3分)下列四个图形中,是中心对称图形的是()A .B .C .D .5.(3分)如图,有一些写有号码的卡片,它们的背面都相同,现将它们背面朝上,从中任意摸出一张,摸到1号卡片的概率是( )A .12B .13C .23D .166.(3分)如图,工人师傅用角尺画出工件边缘AB 的垂线a 和b ,得到a ∥b .理由是( )A .连结直线外一点与直线上各点的所有线段中,垂线段最短B .在同一平面内,垂直于同一条直线的两条直线互相平行C .在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线D .经过直线外一点,有且只有一条直线与这条直线平行7.(3分)已知点(﹣2,a )(2,b )(3,c )在函数y =kx(k >0)的图象上,则下列判断正确的是( ) A .a <b <cB .b <a <cC .a <c <bD .c <b <a8.(3分)如图,⊙O 是等边△ABC 的内切圆,分别切AB ,BC ,AC 于点E ,F ,D ,P 是DF ̂上一点,则∠EPF 的度数是( )A .65°B .60°C .58°D .50°9.(3分)如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x .则列出方程正确的是( )A .3×2x +5=2xB .3×20x +5=10x ×2C .3×20+x +5=20xD .3×(20+x )+5=10x +210.(3分)如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD 与正方形EFGH .连结EG ,BD 相交于点O 、BD 与HC 相交于点P .若GO =GP ,则S 正方形ABCD S 正方形EFGH的值是( )A .1+√2B .2+√2C .5−√2D .154二、填空题(本题有6小题,每小题4分,共24分)11.(4分)点P (m ,2)在第二象限内,则m 的值可以是(写出一个即可) . 12.(4分)数据1,2,4,5,3的中位数是 .13.(4分)如图为一个长方体,则该几何体主视图的面积为 cm 2.14.(4分)如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是°.15.(4分)如图是小明画的卡通图形,每个正六边形的边长都相等,相邻两正六边形的边重合,点A,B,C均为正六边形的顶点,AB与地面BC所成的锐角为β.则tanβ的值是.16.(4分)图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为AC,BD(点A与点B重合),点O是夹子转轴位置,OE⊥AC于点E,OF⊥BD于点F,OE=OF=1cm,AC=BD=6cm,CE=DF,CE:AE=2:3.按图示方式用手指按夹子,夹子两边绕点O转动.(1)当E,F两点的距离最大时,以点A,B,C,D为顶点的四边形的周长是cm.(2)当夹子的开口最大(即点C与点D重合)时,A,B两点的距离为cm.三、解答题(本题有8小题,共66分,各小题都必须写出解答过程)17.(6分)计算:(﹣2020)0+√4−tan45°+|﹣3|.18.(6分)解不等式:5x﹣5<2(2+x).19.(6分)某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如图两幅不完整的统计图表.请根据图表信息回答下列问题:抽取的学生最喜爱体育锻炼项目的统计表类别项目人数(人)A跳绳59B健身操▲C俯卧撑31D开合跳▲E其它22(1)求参与问卷调查的学生总人数.(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数.20.(8分)如图,AB̂的半径OA=2,OC⊥AB于点C,∠AOC=60°.(1)求弦AB的长.(2)求AB̂的长.21.(8分)某地区山峰的高度每增加1百米,气温大约降低0.6℃,气温T(℃)和高度h(百米)的函数关系如图所示.请根据图象解决下列问题:(1)求高度为5百米时的气温;(2)求T关于h的函数表达式;(3)测得山顶的气温为6℃,求该山峰的高度.22.(10分)如图,在△ABC中,AB=4√2,∠B=45°,∠C=60°.(1)求BC边上的高线长.(2)点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.①如图2,当点P落在BC上时,求∠AEP的度数.②如图3,连结AP,当PF⊥AC时,求AP的长.23.(10分)如图,在平面直角坐标系中,已知二次函数y=−12(x﹣m)2+4图象的顶点为A,与y轴交于点B,异于顶点A的点C(1,n)在该函数图象上.(1)当m=5时,求n的值.(2)当n=2时,若点A在第一象限内,结合图象,求当y≥2时,自变量x的取值范围.(3)作直线AC与y轴相交于点D.当点B在x轴上方,且在线段OD上时,求m的取值范围.24.(12分)如图,在平面直角坐标系中,正方形ABOC的两直角边分别在坐标轴的正半轴上,分别过OB,OC 的中点D,E作AE,AD的平行线,相交于点F,已知OB=8.(1)求证:四边形AEFD为菱形.(2)求四边形AEFD的面积.(3)若点P在x轴正半轴上(异于点D),点Q在y轴上,平面内是否存在点G,使得以点A,P,Q,G为顶点的四边形与四边形AEFD相似?若存在,求点P的坐标;若不存在,试说明理由.。
2020年中考数学试题分类:尺规作图 含解析

2020年中考数学试题分类汇编之十七尺规作图一、选择题1.(2020河北)如图1,已知ABC ∠,用尺规作它的角平分线. 如图2,步骤如下,第一步:以B 为圆心,以a 为半径画弧,分别交射线BA ,BC 于点D ,E ; 第二步:分别以D ,E 为圆心,以b 为半径画弧,两弧在ABC ∠内部交于点P ; 第三步:画射线BP .射线BP 即为所求. 下列正确的是( )A. a ,b 均无限制B. 0a >,12b DE >的长 C. a 有最小限制,b 无限制 D. 0a ≥,12b DE <的长 【答案】B【详解】第一步:以B 为圆心,适当长为半径画弧,分别交射线BA ,BC 于点D ,E ; ∴0a >;第二步:分别以D ,E 为圆心,大于12DE 的长为半径画弧,两弧在ABC ∠内部交于点P ; ∴12b DE >的长; 第三步:画射线BP .射线BP 即为所求. 综上,答案为:0a >;12b DE >的长, 故选:B .2.(2020河南).如图,在ABC ∆中,30AB BC BAC ==∠=︒ ,分别以点,A C 为圆心,AC 的长为半径作弧,两弧交于点D ,连接,,DA DC 则四边形ABCD 的面积为( )A. B. 9 C. 6D. 【答案】D 【解析】 【分析】连接BD 交AC 于O ,由已知得△ACD 为等边三角形且BD 是AC 的垂直平分线,然后解直角三角形解得AC 、BO 、BD 的值,进而代入三角形面积公式即可求解. 【详解】连接BD 交AC 于O , 由作图过程知,AD=AC=CD , ∴△ACD 为等边三角形, ∴∠DAC=60º, ∵AB=BC,AD=CD ,∴BD 垂直平分AC 即:BD ⊥AC ,AO=OC ,在Rt △AOB 中,30AB BAC =∠=︒∴BO=AB ·sin30º AO=AB ·cos30º=32,AC=2AO=3, 在Rt △AOD 中,AD=AC=3,∠DAC=60º,∴DO=AD ·sin60º=2,∴ABC ADC ABCD S S S ∆∆=+四边形=11332222⨯⨯+⨯⨯=故选:D .3.(2020贵阳)如图,Rt ABC ∆中,90C ∠=︒,利用尺规在BC ,BA 上分别截取BE ,BD ,使BE BD =;分别以D ,E 为圆心、以大于12DE 为长的半径作弧,两弧在CBA∠内交于点F ;作射线BF 交AC 于点G ,若1CG =,P 为AB 上一动点,则GP 的最小值为( )A. 无法确定B.12C. 1D. 2【答案】C【详解】解:由题意可知,当GP∴AB 时,GP 的值最小, 根据尺规作图的方法可知,GB 是∴ABC 的角平分线, ∴∴C=90°, ∴当GP∴AB 时,GP=CG=1, 故答案为:C .4.(2020广西南宁)(3分)如图,在△ABC 中,BA =BC ,∠B =80°,观察图中尺规作图的痕迹,则∠DCE 的度数为( )A .60°B .65°C .70°D .75°【分析】根据等腰三角形的性质可得∠ACB的度数,观察作图过程可得,进而可得∠DCE 的度数.【解答】解:∵BA=BC,∠B=80°,∴∠A=∠ACB=(180°﹣80°)=50°,∴∠ACD=180°﹣∠ACB=130°,观察作图过程可知:CE平分∠ACD,∴∠DCE=ACD=65°,∴∠DCE的度数为65°故选:B.二、填空题5.(2020天津)如图,在每个小正方形的边长为1的网格中,ABC∆的顶点A,C均落在格点上,点B在网格线上,且53 AB=.(I)线段AC的长等于______;(II)以BC为直径的半圆与边AC相交于点D,若P,Q分别为边AC,BC上的动点,当BP PQ+取得最小值时,请用无刻度的直尺,在如图所示的网格中,画出点P,Q,并简要说明点P,Q的位置是如何找到的(不要求证明)_______.答案)如图,取格点M,N,连接MN,连接BD并延长,与MN相交于点B';连接B C',与半圆相交于点E,连接BE,与AC相交于点P,连接B P'并延长,与BC相交于点Q,则点P,Q即为所求.6.(2020苏州).如图,已知MON ∠是一个锐角,以点O 为圆心,任意长为半径画弧,分别交OM 、ON 于点A 、B ,再分别以点A 、B 为圆心,大于12AB 长为半径画弧,两弧交于点C ,画射线OC .过点A 作ADON ,交射线OC 于点D ,过点D 作DE OC ⊥,交ON 于点E .设10OA =,12DE =,则sin MON ∠=________.【详解】连接AB 交OD 于点H ,过点A 作AG∴ON 于点G , 由尺规作图步骤,可得:OD 是∴MON 的平分线,OA=OB , ∴OH∴AB ,AH=BH , ∴DE OC ⊥, ∴DE∴AB , ∴ADON ,∴四边形ABED 是平行四边形, ∴AB=DE=12, ∴AH=6,8==,∴OB∙AG=AB∙OH , ∴AG=AB OH OB ⋅=12810⨯=485, ∴sin MON ∠=AG OA =2425. 故答案是:2425.7.(2020新疆生产建设兵团)(5分)如图,在x 轴,y 轴上分别截取OA ,OB ,使OA =OB ,再分别以点A ,B 为圆心,以大于12AB 长为半径画弧,两弧交于点P .若点P 的坐标为(a ,2a ﹣3),则a 的值为 3 .【分析】根据作图方法可知点P 在∠BOA 的角平分线上,由角平分线的性质可知点P 到x 轴和y 轴的距离相等,结合点P 在第一象限,可得关于a 的方程,求解即可. 【解答】解:∵OA =OB ,分别以点A ,B 为圆心,以大于12AB 长为半径画弧,两弧交于点P ,∴点P 在∠BOA 的角平分线上, ∴点P 到x 轴和y 轴的距离相等,又∵点P 在第一象限,点P 的坐标为(a ,2a ﹣3), ∴a =2a ﹣3, ∴a =3. 故答案为:3.8.(2020辽宁抚顺)(3分)如图,在Rt △ABC 中,∠ACB =90°,AC =2BC ,分别以点A 和B 为圆心,以大于AB 的长为半径作弧,两弧相交于点M 和N ,作直线MN ,交AC 于点E ,连接BE ,若CE =3,则BE 的长为 5 .9.(2020宁夏)(3分)如图,在△ABC中,∠C=84°,分别以点A、B为圆心,以大于AB的长为半径画弧,两弧分别交于点M、N,作直线MN交AC点D;以点B为圆心,适当长为半径画弧,分别交BA、BC于点E、F,再分别以点E、F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线BP,此时射线BP恰好经过点D,则∠A=32度.三、解答题10.(2020北京)已知:如图,∴ABC为锐角三角形,AB=BC,CD∴AB.求作:线段BP,使得点P在直线CD上,且∴ABP=12BAC .作法:∴以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;∴连接BP.线段BP 就是所求作线段.(1)使用直尺和圆规,依作法补全图形(保留作图痕迹)(2)完成下面的证明.证明:∴CD∴AB,∴∴ABP= .∴AB=AC,∴点B在∴A上.又∴∴BPC=12∴BAC ()(填推理依据)∴∴ABP=12∴BAC【解析】(1)如图所示(2)∠BPC;在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半。
(全国120套)2020年中考数学试卷分类汇编 四边形综合

(全国120套)2020年中考数学试卷分类汇编 四边形综合2、〔2019陕西〕如图,四边形ABCD 的对角线AC 、BD 相交于点O ,且BD 平分AC ,假设BD=8,AC=6,∠BOC=120°,那么四边形ABCD 的面积为 .〔结果保留根号〕 考点:三角形面积的求法及特殊角的应用。
解析:BD 平分AC ,所以OA=OC=3,因为∠BOC=120°, 所以∠DOC=∠A0B=60°,过C 作CH ⊥BD 于H ,过A 作AG ⊥BD 于G ,在△CHO 中,∠C0H=60°, OC=3,所以CH=323,同理:AG=323, 所以四边形ABCD 的面积=3123238=⨯=+∆∆CBD ABD S S 。
3、(2019河南省)如图,在等边三角形ABC 中,6BC cm =,射线AG BC ∥,点E 从点A 出发沿射线AG 以1/cm s 的速度运动,同时点F 从点B 出发沿射线BC 以2/cm s 的速度运动,设运动时间为()t s〔1〕连接EF ,当EF 经过AC 边的中点D 时,求证:ADE CDF ≅ 证明:∵AG BC ∥ ∴EAD ACB ∠=∠ ∵D 是AC 边的中点 ∴AD CD =又∵ADE CDF ∠=∠A BDCO HG第14题图∴ADE CDF ≅〔2〕填空:①当为 s 时,四边形ACFE 是菱形;②当为 s 时,以,,,A F C E 为顶点的四边形是直角梯形。
【解析】①∵当四边形ACFE 是菱形时,∴AE AC CF EF === 由题意可知:,26AE t CF t ==-,∴6t =②假设四边形ACFE 是直角梯形,此时EF AG ⊥过C 作CM AG ⊥于M ,3AG =,可以得到AE CF AM -=, 即(26)3t t --=,∴3t =,此时,C F 与重合,不符合题意,舍去。
假设四边形假设四边形AFCE 是直角梯形,此时AF BC ⊥, ∵△ABC 是等边三角形,F 是BC 中点, ∴23t =,得到32t =经检验,符合题意。
2019-2020年中考数学试题分类汇编解析综合性问题.docx

2019-2020 年中考数学试题分类汇编解析综合性问题一、选择题1.(2014?年山东东营 , 第 10 题 3 分) 如图,四边形 ABCD 为菱形, AB=BD ,点 B、C、D 、G 四个点在同一个圆⊙ O 上,连接 BG 并延长交 AD 于点 F,连接 DG 并延长交 AB 于点 E,BD与 CG 交于点 H,连接 FH ,下列结论:①AE=DF ;② FH∥ AB ;③△ DGH ∽△ BGE ;④当 CG 为⊙ O 的直径时, DF=AF .其中正确结论的个数是()A . 1B . 2 C. 3 D.4考点:圆的综合题.分析:①由四边形ABCD 是菱形, AB=BD ,得出△ ABD 和△ BCD 是等边三角形,再由 B、C、D 、 G 四个点在同一个圆上,得出∠ADE= ∠ DBF ,由△ ADE ≌△ DBF ,得出 AE=DF ,②利用内错角相等∠FBA= ∠ HFB ,求证 FH ∥ AB ,③利用∠ DGH= ∠ EGB 和∠ EDB= ∠FBA ,求证△ DGH ∽△ BGE,④利用 CG 为⊙ O 的直径及 B 、C、D 、G 四个点共圆,求出∠ ABF=120 °﹣ 90°=30°,在RT△AFB 中求出 AF= AB在 RT△ DFB 中求出 FD= BD ,再求得 DF=AF .解答:解:① ∵四边形ABCD 是菱形,∴AB=BC=DC=AD ,又∵ AB=BD ,∴△ ABD 和△BCD 是等边三角形,∴∠ A= ∠ ABD= ∠ DBC= ∠ BCD= ∠ CDB= ∠BDA=60 °,又∵ B、 C、D 、G 四个点在同一个圆上,∴∠ DCH= ∠ DBF ,∠ GDH= ∠BCH ,∴∠ ADE= ∠ ADB ﹣∠ GDH=60 °﹣∠ EDB ,∠ DCH= ∠ BCD ﹣∠ BCH=60 °﹣∠BCH ,∴∠ ADE= ∠ DCH ,∴∠ ADE= ∠ DBF ,在△ADE 和△DBF 中,∴△ ADE ≌△ DBF ( ASA )∴AE=DF故① 正确,②由①中证得∠ ADE= ∠ DBF ,∴∠ EDB= ∠ FBA ,∵ B、 C、D 、 G 四个点在同一个圆上,∠BDC=60 °,∠ DBC=60 °,∴∠ BGC= ∠ BDC=60 °,∠ DGC= ∠DBC=60 °,∴∠ BGE=180 °﹣∠ BGC ﹣∠ DGC=180 °﹣ 60°﹣60°=60°,∴FGD=60 °,∴FGH=120 °,又∵∠ ADB=60 °,∴F、G、H、D 四个点在同一个圆上,∴∠ EDB= ∠ HFB ,∴∠ FBA= ∠ HFB ,∴FH∥ AB ,故② 正确,③ ∵ B、 C、D 、G 四个点在同一个圆上,∠DBC=60 °,∴∠ DGH= ∠ DBC=60 °,∵∠ EGB=60 °,∴∠ DGH= ∠ EGB ,由①中证得∠ ADE= ∠ DBF ,∴∠ EDB= ∠ FBA ,∴△ DGH ∽△ BGE ,故③ 正确,④ 如下图∵CG 为⊙ O 的直径,点 B 、 C、 D、 G 四个点在同一个圆⊙ O 上,∴∠ GBC= ∠ GDC=90 °,∴∠ ABF=120 °﹣90°=30 °,∵∠A=60 °,∴∠ AFB=90 °∴AF= AB ,又∵∠ DBF=60 °﹣ 30°=30 °,∠ ADB=60 °,∴∠ DFB=90 °,∴FD= BD ,∵AB=BD ,∴ DF=AF ,故④ 正确,故选: D.点评:此题综合考查了圆及菱形的性质,等边三角形的判定与性质,全等三角形的判定和性质,运用四点共圆找出相等的角是解题的关键.解题时注意各知识点的融会贯通.2. ( 2014?甘肃白银、临夏, 第 10 题 3 分)如图,边长为 1 的正方形ABCD 中,点 E 在 CB 延长线上,连接ED 交 AB 于点 F,AF=x( 0.2 ≤x≤0.8),EC=y.则在下面函数图象中,大致能反映 y 与 x 之闻函数关系的是()A.B.C.D.考点:动点问题的函数图象.分析:通过相似三角形△EFB∽△ EDC 的对应边成比例列出比例式=,从而得到与 x 之间函数关系式,从而推知该函数图象.解答:解:根据题意知,BF=1﹣x, BE=y﹣ 1,且△ EFB ∽△ EDC,则=,即=,所以 y=(0.2≤x≤0.8),该函数图象是位于第一象限的双曲线的一部分.A、D 的图象都是直线的一部分, B 的图象是抛物线的一部分, C 的图象是双曲线的一部分.故选 C.点评:本题考查了动点问题的函数图象.解题时,注意自变量x 的取值范围.3.( 2014?甘肃兰州 , 第 15 题 4 分)如图,在平面直角坐标系中,四边形OBCD 是边长为4的正方形,平行于对角线BD 的直线 l 从 O 出发,沿x 轴正方向以每秒 1 个单位长度的速度运动,运动到直线l 与正方形没有交点为止.设直线l 扫过正方形OBCD 的面积为S,直线运动的时间为t(秒),下列能反映S 与 t 之间函数关系的图象是()y lA.B.C.D.考点:动点问题的函数图象.分析:根据三角形的面积即可求出S 与 t 的函数关系式,根据函数关系式选择图象.解答:解:①当0≤t≤4 时, S=×t×t=t 2,即 S=t2.该函数图象是开口向上的抛物线的一部分.故 B、C 错误;②当 4<t ≤8 时, S=16﹣×( t﹣ 4)×( t﹣4) =2,即 S=﹣2t t +4t+8 .该函数图象是开口向下的抛物线的一部分.故A错误.故选:D.点评:本题考查了动点问题的函数图象.本题以动态的形式考查了分类讨论的思想,函数的知识和等腰直角三角形,具有很强的综合性.三、解答题1. ( 2014?上海,第 25 题 14 分)如图 1,已知在平行四边形ABCD 中,AB=5 ,BC=8 ,cosB=4 ,5点 P 是边 BC 上的动点,以 CP 为半径的圆 C 与边 AD 交于点 E、 F(点 F 在点 E 的右侧),射线CE 与射线 BA 交于点 G.(1)当圆 C 经过点 A 时,求 CP 的长;(2)联结 AP ,当 AP ∥ CG 时,求弦 EF 的长;( 3)当△ AGE 是等腰三角形时,求圆 C 的半径长.考圆的综合题点:分( 1)当点 A 在⊙ C 上时,点 E 和点 A 重合,过点析:理求出 AC 进而得出答案;( 2)首先得出四边形APCE 是菱形,进而得出 CM A 作 AH ⊥ BC 于 H ,直接利用勾股定的长,进而利用锐角三角函数关系得出 CP 以及 EF 的长;( 3)当∠ AEG= ∠ B 时, A 、E、 G 重合,只能∠ AGE= ∠ AEG ,利用 AD ∥ BC ,得出△ GAE ∽△ GBC,进而求出即可.解解:( 1)如图 1,设⊙ O 的半径为 r,答:当点 A 在⊙ C 上时,点 E 和点 A 重合,过点 A 作 AH ⊥BC 于 H,∴BH=AB?cosB=4 ,∴AH=3 ,CH=4 ,∴AC==5 ,∴此时 CP=r=5 ;(2)如图 2,若 AP ∥CE, APCE 为平行四边形,∵ CE=CP ,∴四边形APCE 是菱形,连接 AC 、EP,则 AC ⊥ EP,∴AM=CM= ,由( 1)知, AB=AC ,则∠ ACB= ∠ B,∴ CP=CE==,∴ EF=2=;(3)如图 3:过点 C 作 CN⊥AD 于点 N,∵cosB= 4,5∴∠ B< 45°,∵∠ BCG < 90°,∴∠ BGC > 45°,∵∠ AEG= ∠ BCG≥ ∠ACB= ∠ B,∴当∠ AEG= ∠B 时, A 、E、 G 重合,∴只能∠ AGE= ∠AEG ,∵AD ∥BC ,∴△ GAE ∽△ GBC,∴=,即=,解得: AE=3 , EN=AN ﹣AE=1 ,∴CE===.点此题主要考查了相似三角形的判定与性质以及勾股定理以及锐角三角函数关系等知识,评:利用分类讨论得出△AGE 是等腰三角形时只能∠ AGE= ∠ AEG 进而求出是解题关键.2. ( 2014?四川巴中,第31 题 12 分)如图,在平面直角坐标系xOy 中,抛物线2y=ax +bx﹣ 4与 x 轴交于点A(﹣ 2, 0)和点 B,与 y 轴交于点 C,直线 x=1 是该抛物线的对称轴.( 1)求抛物线的解析式;( 2)若两动点 M, H 分别从点A, B 以每秒 1 个单位长度的速度沿x 轴同时出发相向而行,当点M 到达原点时,点H 立刻掉头并以每秒个单位长度的速度向点 B 方向移动,当点M 到达抛物线的对称轴时,两点停止运动,经过点M 的直线l⊥ x 轴,交AC或BC于点 P,设点 M 的运动时间为 t 秒( t> 0).求点 M 的运动时间 t 与△ APH 的面积 S的函数关系式,并求出 S 的最大值.考点:二次函数综合题.2分析:( 1)根据抛物线y=ax +bx﹣ 4 与 x 轴交于点A(﹣ 2,0),直线 x=1 是该抛物线的对称轴,得到方程组,解方程组即可求出抛物线的解析式;2( 2)由于点 M 到达抛物线的对称轴时需要 3 秒,所以 t≤3,又当点 M 到达原点时需要秒,且此时点H 立刻掉头,所以可分两种情况进行讨论:①当0< t≤2时,由△ AMP∽△ AOC,得出比例式,求出PM , AH,根据三角形的面积公式求出即可;②当2< t≤3时,过点 P 作 PM⊥x 轴于 M, PF⊥ y 轴于点 F,表示出三角形APH 的面积,利用配方法求出最值即可.解答:( 1)∵抛物线 y=ax2+bx﹣4 与 x 轴交于点 A(﹣ 2,0),直线 x=1 是该抛物线的对称轴,∴,解得:,∴抛物线的解析式是:y=x2﹣ x﹣4,( 2)分两种情况:①当 0<t≤2时,∵ PM ∥ OC,∴△ AMP∽△ AOC,∴=,即=,∴ PM =2t.解方程x2﹣ x﹣ 4=0,得 x1=﹣2, x2=4 ,∵A(﹣ 2, 0),∴ B(4, 0),∴ AB=4﹣(﹣ 2) =6.∵AH=AB﹣ BH=6﹣t ,22∴ S= PM ?AH= ×2t(6﹣ t )=﹣ t +6 t=﹣( t﹣ 3) +9,当 t=2 时 S 的最大值为8;②当 2<t≤3时,过点P 作 PM ⊥ x 轴于 M,作 PF⊥ y 轴于点 F,则△ COB∽△ CFP ,又∵ CO=OB,∴FP=FC=t﹣2, PM =4﹣( t﹣ 2) =6﹣ t,AH =4+ ( t﹣ 2) = t+1,∴ S=PM ?AH= (6﹣ t)(t+1) =﹣ t2 +4t+3= ﹣(t ﹣)2+,当 t=时, S 最大值为.综上所述,点 M 的运动时间 t 与△ APQ 面积 S 的函数关系式是S=, S 的最大值为.点评:本题是二次函数的综合题型,其中涉及到运用待定系数法求二次函数的解析式,三角形的面积,二次函数的最值等知识,综合性较强,难度适中.运用数形结合、分类讨论及方程思想是解题的关键.23. ( 2014?山东威海,第 25 题 12 分)如图,已知抛物线 y=ax +bx+c( a≠0)经过 A(﹣ 1,0),B( 4, 0), C( 0, 2)三点.(1)求这条抛物线的解析式;(2) E 为抛物线上一动点,是否存在点 E 使以 A、 B、 E 为顶点的三角形与△COB 相似?若存在,试求出点 E 的坐标;若不存在,请说明理由;( 3)若将直线 BC 平移,使其经过点 A,且与抛物线相交于点 D,连接 BD,试求出∠ BDA 的度数.考点:二次函数综合题分析:解答:( 1)本题需先根据已知条件,过 C 点,设出该抛物线的解析式为2,y=ax +bx+2再根据过 A,B 两点,即可得出结果;( 2)由图象可知,以 A、 B 为直角顶点的△ ABE 不存在,所以△ ABE 只可能是以点 E 为直角顶点的三角形.由相似关系求出点 E 的坐标;( 3)如图 2,连结 AC,作 DE⊥ x 轴于点 E,作 BF ⊥ AD 于点 F,由 BC∥ AD 设BC 的解析式为 y=kx+b,设 AD 的解析式为 y=kx+n,由待定系数法求出一次函数的解析式,就可以求出 D 坐标,由勾股定理就可以求出BD 的值,由勾股定理的逆定理就可以得出∠ACB=90°,由平行线的性质就可以得出∠ CAD =90°,就可以得出四边形 ACBF 是矩形,就可以得出 BF 的值,由勾股定理求出 DF 的值,而得出 DF =BF 而得出结论.解:( 1)∵该抛物线过点 C( 0, 2),∴可设该抛物线的解析式为y=ax2+bx+2.将 A(﹣ 1, 0), B( 4, 0)代入,得,解得,∴抛物线的解析式为:y=﹣x2 + x+2.( 2)存在.由图象可知,以A、B 为直角顶点的△ABE不存在,所以△ ABE只可能是以点E 为直角顶点的三角形.在 Rt△BOC 中, OC=2, OB=4,∴BC==.在 Rt△BOC 中,设 BC 边上的高为h,则×h=×2×4,∴ h=.∵△ BEA ∽△ COB,设 E 点坐标为( x, y),∴=,∴ y=±2将 y=2 代入抛物线 y=﹣ x2+ x+2,得 x1=0, x2=3 .当 y=﹣2 时,不合题意舍去.∴ E 点坐标为( 0, 2),( 3, 2).( 3)如图 2,连结 AC,作 DE ⊥x 轴于点 E,作 BF ⊥AD 于点 F,∴∠ BED =∠ BFD =∠ AFB=90°.设 BC 的解析式为 y=kx+b,由图象,得,∴,y BC=﹣x+2.由 BC∥ AD ,设 AD 的解析式为y=﹣x+n,由图象,得0=﹣×(﹣1)+n∴n=﹣,y AD =﹣x﹣.2∴﹣x + x+2= ﹣x﹣,解得: x1 =﹣ 1, x2=5∴D(﹣ 1,0)与 A 重合,舍去, D( 5,﹣3).∵ DE ⊥x 轴,∴DE =3,OE=5.由勾股定理,得BD=.∵ A(﹣ 1, 0), B(4, 0), C( 0, 2),∴OA=1,OB=4, OC=2.∴AB=5在 Rt△AOC 中, Rt△ BOC 中,由勾股定理,得AC= , BC=2,∴ AC2=5, BC2=20 ,AB 2=25 ,∴ AC2+BC2=AB 2∴△ ACB 是直角三角形,∴∠ ACB =90°.∵BC∥AD,∴∠ CAF +∠ ACB =180°,∴∠ CAF =90°.∴∠ CAF =∠ ACB =∠ AFB=90°,∴四边形 ACBF 是矩形,∴ AC=BF= ,在 Rt△BFD 中,由勾股定理,得 DF =,∴ DF =BF,∴∠ ADB =45°.点评:本题考查了运用待定系数法求二次函数解析式和一次函数的解析式的运用,相似三角形的性质的运用,勾股定理的运用,矩形的判定及性质的运用,等腰直角三角形的性质的运用,解答时求出函数的解析式是关键.4. ( 2014?山东枣庄,第25 题 10 分)如图,在平面直角坐标系中,二次函数y=x 2﹣ 2x﹣3的图象与x 轴交于 A 、B 两点,与y 轴交于点C,连接 BC ,点 D 为抛物线的顶点,点第四象限的抛物线上的一个动点(不与点 D 重合).P 是( 1)求∠OBC 的度数;( 2)连接CD 、 BD 、DP,延长DP交x 轴正半轴于点E,且S△OCE=S 四边形OCDB,求此时P 点的坐标;( 3)过点考点:分析:P 作PF⊥ x 轴交 BC 于点 F,求线段PF 长度的最大值.二次函数综合题( 1)由抛物线已知,则可求三角形OBC 的各个顶点,易知三角形形状及内角.( 2)因为抛物线已固定,则S四边形OCDB固定,对于坐标系中的不规则图形常用分割求和、填补求差等方法求面积,本图形过顶点作x 轴的垂线及可将其分为直角梯形及直角三角形,面积易得.由此可得 E 点坐标,进而可求ED 直线方程,与抛物线解析式联立求解即得P 点坐标.( 3)PF 的长度即为y F﹣ y P.由P、 F 的横坐标相同,则可直接利用解析式作差.由所得函数为二次函数,则可用二次函数性质讨论最值,解法常规.解答:解:( 1)∵ y=x2﹣ 2x﹣ 3=( x﹣ 3)( x+2 ),∴由题意得, A (﹣ 1, 0), B ( 3,0), C( 0,﹣ 3), D( 1,﹣ 4).在 Rt△OBC 中,∵ OC=OB=3 ,∴△ OBC 为等腰直角三角形,∴∠ OBC=45° .( 2)如图1,过点 D 作DH ⊥x轴于H ,此时S 四边形OCDB =S 梯形OCDH +S△HBD,∵OH=1 , OC=3 ,HD=4 , HB=2 ,∴S 梯形OCDH = ?(OC+HD )?OH= , S△HBD = ?HD?HB=4 ,∴S 四边形OCDB= .∴ S△OCE=S 四边形OCDB = =,∴OE=5 ,∴E( 5, 0).设 l DE: y=kx+b ,∵ D( 1,﹣ 4), E( 5, 0),∴,解得,∴l DE: y=x ﹣ 5.∵DE 交抛物线于 P,设 P( x, y),∴ x2﹣ 2x﹣ 3=x ﹣ 5,解得 x=2 或 x=1( D 点,舍去),∴x P=2 ,代入 l DE: y=x ﹣ 5,∴P(2,﹣ 3).( 3)如图 2,设 l BC: y=kx+b ,∵ B( 3, 0), C( 0,﹣ 3),∴,解得,∴l BC: y=x ﹣ 3.∵F在 BC 上,∴y F=x F﹣ 3,∵P 在抛物线上,∴y P=x P2﹣ 2x P﹣3,∴线段 PF 长度 =y F﹣ y P=x F﹣ 3﹣( x P2﹣ 2x P﹣ 3),∵x P=x F,∴线段 PF 长度 =﹣ x P2+3x P=﹣( x P﹣)2+,( 1< x P≤3),∴当 x P= 时,线段 PF 长度最大为.点评:本题考查了抛物线图象性质、已知两点求直线解析式、直角三角形性质及二次函数最值等基础知识点,题目难度适中,适合学生加强练习.5.( 2014?山东潍坊,第 22 题 12 分)如图 1,在正方形 ABCD 中, E、 F 分别为 BC、CD 的中点,连接 AE、 BF ,交点为 G.(1)求证: AE⊥ BF;(2) 将△ BCF 沿 BF 对折,得到△ BPF(如图 2),延长 FP 交 BA 的延长线于点 Q,求 sin∠BQP 的值;(3)将△ ABE 绕点 A 逆时针方向旋转,使边 AB 正好落在 AE 上,得到△ AHM (如图 3),若AM 和 BF 相交于点N,当正方形ABCD 的面积为 4 时,求四边形GHMN 的面积.考点:相似三角形的判定与性质;全等三角形的判定与性质;正方形的性质;解直角三角形.分析:(1)由四边形 ABCD 是正方形,可得∠ ABE=∠ BCF=90°, AB=BC,又由 BE=CF,即可证得△ ABE ≌△ BCF ,可得∠ BAE=∠ CBF ,由∠ ABF+∠ CBF =90 0可得∠ ABF+∠BAE=90 0,即 AE⊥ BF;(2)由△ BCF ≌△ BPF, 可得 CF=PF,BC=BP,∠ BFE=∠ BFP,由 CD∥AB 得∠ BFC=∠ ABF,从而 QB=QF ,设 PF 为 x,则 BP 为 2x,在 Rt△ QBF 中可求QB 为5x,即可求得答案;2( 3)由AGN(AN) 2可求出△AGN的面积,进一步可求出四边形GHMN 的面积.AHM AM解答: (1) 证明:∵ E、F 分别是正方形ABCD 边 BC、 CD 的中点,∴ CF=BE ,∴ Rt△ ABE≌Rt△ BCF∴∠ BAE=∠CBF又∵∠ BAE+∠ BEA=900,∴∠ CBF +∠ BEA=90 0,∴∠ BGE=90 0,∴AE⊥ BF(2)根据题意得: FP=FC,∠ PFB=∠BFC ,∠ FPB=900,∵CD ∥ AB,∴∠ CFB =∠ ABF,∴∠ ABF=∠ PFB.∴ QF=QB令 PF=k( k>O),则 PB=2k,2225k,∴ sin∠ BQP=BP在 Rt△ BPQ 中,设 QB=x,∴ x =(x-k) +4k ,∴ x=QP2(3) 由题意得:∠ BAE=∠ EAM,又 AE⊥ BF,∴AN=AB=2,∵ ∠ AHM =900, ∴ GN//HM , ∴AGN(AN)2∴AGN(2)24AHM AM155∴四边形 GHMN =S AHM - S AGN=1 一4=4552k 45k52答:四边形GHMN 的面积是 4 .5点评:此题考查了相似三角形的判定与性质、正方形的性质、全等三角形的判定与性质以及三角函数等知识.此题综合性较强,难度较大,注意掌握旋转前后图形的对应关系,注意数形结合思想的应用.6. ( 2014?山东潍坊,第24 题 13 分)如图,抛物线y=ax2+bx+c( a≠O)与 y 轴交于点C(O,4),与 x 轴交于点 A 和点 B,其中点 A 的坐标为(-2,0),抛物线的对称轴x=1 与抛物线交于点 D,与直线BC 交于点 E.(1)求抛物线的解析式;(2)若点 F 是直线 BC 上方的抛物线上的一个动点,是否存在点 F 使四边形 ABFC 的面积为 17,若存在,求出点 F 的坐标;若不存在,请说明理由;(3) 平行于 DE 的一条动直线Z 与直线 BC 相交于点P,与抛物线相交于点Q,若以 D 、E、P、Q 为顶点的四边形是平行四边形,求点P 的坐标。
部编版2020年中考数学试题分项版解析汇编第期专题图形的变换含解析

专题04 图形的变换一、选择题1.(2017山东德州市第11题)如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a >b),M在边BC上,且BM=b,连AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF。
给出以下五种结论:①∠MAD=∠AND;②CP=2-bba;③ΔABM≌ΔNGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共线其中正确的个数是()A.2 B.3 C.4 D.5【答案】D【解析】考点:正方形、全等、相似、勾股定理2.(2017重庆A卷第2题)下列图形中是轴对称图形的是()【答案】C.【解析】试题解析:A 、不是轴对称图形,不合题意; B 、不是轴对称图形,不合题意; C 、是轴对称图形,符合题意; D 、不是轴对称图形,不合题意. 故选C .考点:轴对称图形.3.(2017甘肃庆阳第1题)下面四个手机应用图标中,属于中心对称图形的是( )A .B .C .D .【答案】B .考点:中心对称图形.4.(2017广西贵港第11题)如图,在Rt ABC ∆中,90ACB ∠=o,将ABC ∆绕顶点C 逆时针旋转得到'',A B C M ∆是BC 的中点,P 是''A B 的中点,连接PM ,若230BC BAC =∠=o ,,则线段PM 的最大值是 ( )A .4B .3 C.2 D .1 【答案】B 【解析】试题解析:如图连接PC .在Rt△ABC中,∵∠A=30°,BC=2,∴AB=4,根据旋转不变性可知,A′B′=AB=4,∴A′P=PB′,∴PC=12A′B′=2,∵CM=BM=1,又∵PM≤PC+CM,即PM≤3,∴PM的最大值为3(此时P、C、M共线).故选B.考点:旋转的性质.5.(2017贵州安顺第7题)如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE 交DC于点O,若AO=5cm,则AB的长为()A.6cm B.7cm C.8cm D.9cm【答案】C.【解析】考点:翻折变换(折叠问题);矩形的性质.6.(2017江苏无锡第4题)下列图形中,是中心对称图形的是()A.B.C. D.【答案】C.【解析】试题解析:A、不是中心对称图形,故本选项不符合题意;B、不是中心对称图形,故本选项不符合题意;C、是中心对称图形,故本选项符合题意;D、不是中心对称图形,故本选项不符合题意;故选C.考点:中心对称图形.7.(2017江苏无锡第10题)如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于()A .2B .54 C .53 D .75【答案】D . 【解析】试题解析:如图连接BE 交AD 于O ,作AH ⊥BC 于H .在Rt △ABC 中,∵AC=4,AB=3,∴2234+=5,∵CD=DB , ∴AD=DC=DB=52, ∵12•BC•AH=12•AB•AC, ∴AH=125, ∵AE=AB ,DE=DB=DC ,∴AD 垂直平分线段BE ,△BCE 是直角三角形, ∵12•AD•BO=12•BD•AH, ∴OB=125, ∴BE=2OB=245, 在Rt △BCE 中,22222475()55BC BE -=-= . 故选D .考点:1.翻折变换(折叠问题);2.直角三角形斜边上的中线;3.勾股定理.8.(2017江苏盐城第3题)下列图形中,是轴对称图形的是()【答案】D.【解析】试题解析:D的图形沿中间线折叠,直线两旁的部分可重合,故选D.考点:轴对称图形.9. (2017江苏盐城第6题)如图,将函数y=12(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是()A.y=12(x−2)2−2 B.y=12(x−2)2+7 C.y=12(x−2)2−5 D.y=12(x−2)2+4【答案】D.【解析】试题解析:∵函数y=12(x-2)2+1的图象过点A(1,m),B(4,n),∴m=12(1-2)2+1=112,n=12(4-2)2+1=3,∴A(1,112),B(4,3),过A 作AC ∥x 轴,交B′B 的延长线于点C ,则C (4,112), ∴AC=4-1=3,∵曲线段AB 扫过的面积为9(图中的阴影部分), ∴AC•AA′=3AA′=9, ∴AA′=3, 即将函数y=12(x-2)2+1的图象沿y 轴向上平移3个单位长度得到一条新函数的图象, ∴新图象的函数表达式是y=12(x-2)2+4. 故选D .考点:二次函数图象与几何变换.10.(2017甘肃兰州第14题)如图,在正方形ABCD 和正方形DEFG 中,点G 在CD 上,2DE =,将正方形DEFG 绕点D 顺时针旋转60°,得到正方形'''DE F G ,此时点'G 在AC 上,连接'CE ,则''CE CG +=( )26313236【答案】AA 【解析】试题解析:作G′I⊥CD 于I ,G′R⊥BC 于R ,E′H⊥BC 交BC 的延长线于H .连接RF′.则四边形RCIG′是正方形.∵∠DG′F′=∠IGR=90°, ∴∠DG′I=∠RG′F′, 在△G′ID 和△G′R F 中,DG I RG G D G I G G F F R '=∠''''⎧=⎪∠''⎨=⎪⎩∴△G′ID≌△G′RF, ∴∠G′ID=∠G′RF′=90°, ∴点F 在线段BC 上,在Rt △E′F′H 中,∵E′F′=2,∠E′F′H=30°, ∴E′H=123 易证△RG′F′≌△HF′E′, ∴RF′=E′H,RG′RC=F′H, ∴CH=RF′=E′H, 2 3 26 ∴CE′+26 故选A .考点:旋转的性质;正方形的性质.11.(2017山东烟台第2题)下列国旗图案是轴对称图形但不是中心对称图形的是( )【答案】A.考点:中心对称图形;轴对称图形.12.(2017四川宜宾第7题)如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是()A.3 B.245C.5 D.8916【答案】C.【解析】试题解析:∵矩形ABCD,∴∠BAD=90°,由折叠可得△BEF≌△BAE,∴EF⊥BD,AE=EF,AB=BF,在Rt△ABD中,AB=CD=6,BC=AD=8,根据勾股定理得:BD=10,即FD=10﹣6=4,设EF=AE=x,则有ED=8﹣x,根据勾股定理得:x2+42=(8﹣x)2,解得:x=3(负值舍去),则DE=8﹣3=5,故选C.考点:1. 翻折变换(折叠问题);2.矩形的性质.13.(2017四川自贡第6题0下列图形中,是轴对称图形,但不是中心对称图形的是()【答案】A.考点:1.轴对称图形;2.中心对称图形.14.(2017江苏徐州第题0下列图形中,既是轴对称图形,又是中心对称图形的是()A. B. C. D.【答案】C.【解析】试题解析:A、不是轴对称图形,是中心对称图形,不合题意;B、是轴对称图形,不是中心对称图形,不合题意;C、是轴对称图形,也是中心对称图形,符合题意;D、不是轴对称图形,是中心对称图形,不合题意.故选C.考点:1.中心对称图形;2.轴对称图形.15.(2017浙江嘉兴第7题)若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是()A.向左平移1个单位,再向下平移1个单位-个单位,再向上平移1个单位B.向左平移(221)C.向右平移2个单位,再向上平移1个单位D.向右平移1个单位,再向上平移1个单位【答案】D.【解析】试题解析:过B作射线BC∥OA,在BC上截取BC=OA,则四边形OACB是平行四边形,过B作DH⊥x轴于H,∵B(1,1),22+1=1220),∴C(21)∴OA=OB,∴则四边形OACB是菱形,∴平移点A到点C,向右平移1个单位,再向上平移1个单位而得到,考点:1.菱形的性质;2.坐标与图形变化-平移.16.(2017浙江嘉兴第9题)一张矩形纸片ABCD ,已知3AB =,2AD =,小明按所给图步骤折叠纸片,则线段DG 长为( )A .2B .22C .1D .2【答案】A .【解析】试题解析:∵AB=3,AD=2,∴DA′=2,CA′=1,∴DC′=1,∵∠D=45°,∴DG=2DC′=2,故选A .考点:矩形的性质.17.(2017山东德州第2题)下列图形中,既是轴对称图形又是中心对称图形的是( )【答案】D【解析】试题分析:选项A 和B 是中心对称图形,但不是轴对称图形;选项C 是轴对称图形,但不是中心对称图形;选项D 既是轴对称图形又是中心对称图形。
2020年中考数学试卷分类汇编 代数几何综合

代数几何综合1、(2013年潍坊市压轴题)如图,抛物线c bx ax y ++=2关于直线1=x 对称,与坐标轴同学们:一分耕耘一分收获,只要我们能做到有永不言败+勤奋学习+有远大的理想+坚定的信念,坚强的意志,明确的目标,相信你在学习和生活也一定会收获成功(可删除)交于C B A 、、三点,且4=AB ,点⎪⎭⎫ ⎝⎛232,D 在抛物线上,直线是一次函数()02≠-=k kx y 的图象,点O 是坐标原点.(1)求抛物线的解析式;(2)若直线平分四边形OBDC 的面积,求k 的值.(3)把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线与直线交于N M 、两点,问在y 轴正半轴上是否存在一定点P ,使得不论k 取何值,直线PM 与PN 总是关于y 轴对称?若存在,求出P 点坐标;若不存在,请说明理由.答案:(1)因为抛物线关于直线x=1对称,AB=4,所以A(-1,0),B(3,0),由点D(2,1.5)在抛物线上,所以⎩⎨⎧=++=+-5.1240c b a c b a ,所以3a+3b=1.5,即a+b=0.5,又12=-a b ,即b=-2a,代入上式解得a =-0.5,b =1,从而c=1.5,所以23212++-=x x y . (2)由(1)知23212++-=x x y ,令x=0,得c(0,1.5),所以CD//AB,令kx -2=1.5,得l 与CD 的交点F(23,27k ),令kx -2=0,得l 与x 轴的交点E(0,2k),根据S 四边形OEFC =S 四边形EBDF 得:OE+CF=DF+BE, 即:,511),272()23(272=-+-=+k k k k k 解得(3)由(1)知,2)1(21232122+--=++-=x x x y 所以把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线的解析式为221x y -= 假设在y 轴上存在一点P(0,t),t >0,使直线PM 与PN 关于y 轴对称,过点M 、N 分别向y 轴作垂线MM 1、NN 1,垂足分别为M 1、N 1,因为∠MPO=∠NPO,所以Rt △MPM 1∽Rt △NPN 1, 所以1111PN PM NN MM =,………………(1) 不妨设M(x M ,y M )在点N(x N ,y N )的左侧,因为P 点在y 轴正半轴上, 则(1)式变为NMN M y t y t x x --=-,又y M =k x M -2, y N =k x N -2, 所以(t+2)(x M +x N )=2k x M x N,……(2) 把y=kx-2(k ≠0)代入221x y -=中,整理得x 2+2kx-4=0, 所以x M +x N =-2k, x M x N =-4,代入(2)得t=2,符合条件,故在y 轴上存在一点P (0,2),使直线PM 与PN 总是关于y 轴对称.考点:本题是一道与二次函数相关的压轴题,综合考查了考查了二次函数解析式的确定,函数图象交点及图形面积的求法,三角形的相似,函数图象的平移,一元二次方程的解法等知识,难度较大.点评:本题是一道集一元二次方程、二次函数解析式的求法、相似三角形的条件与性质以及质点运动问题、分类讨论思想于一体的综合题,能够较好地考查了同学们灵活应用所学知识,解决实际问题的能力问题设计富有梯度、由易到难层层推进,既考查了知识掌握,也考查了方法的灵活应用和数学思想的形成2、(绵阳市2013年)如图,二次函数y =ax 2+bx +c 的图象的顶点C 的坐标为(0,-2),交x 轴于A 、B 两点,其中A (-1,0),直线l :x =m (m >1)与x 轴交于D (1)求二次函数的解析式和B 的坐标; (2)在直线l 上找点P (P 在第一象限),使得以P 、D 、B 为顶点的三角形与以B 、C 、O 为顶点的三角形相似,求点P 的坐标(用含m 的代数式表示);(3)在(2)成立的条件下,在抛物线上是否存在第一象限内的点Q ,使△BP Q 是以P 为直角顶点的等腰直角三角形?如果存在,请求出点Q 的坐标;如果不存在,请说明理由解:(1)①二次函数y=ax 2+bx+c 图象的顶点C 的坐标为(0,-2),c = -2 , - b2a = 0 , b=0 ,点A(-1,0)、点B 是二次函数y=ax 2-2 的图象与x 轴的交点,a-2=0,a=2. 二次函数的解析式为y=2x 2-2;②点B 与点A(-1,0)关于直线x=0对称,点B 的坐标为(1,0); (2)∠BOC=∠PDB=90º,点P 在直线x=m 上,设点P 的坐标为(m,p ), OB=1, OC=2, DB= m-1 , DP=|p| ,A B C D O x y l①当△BOC ∽△PDB 时,OB OC = DP DB ,12= |p|m-1 ,p= m-12 或p = 1- m2 ,点P 的坐标为(m ,m-12 )或(m ,1- m2);②当△BOC ∽△BDP 时, OB OC = DB DP ,12= m-1|p|,p=2m-2或p=2-2m,点P 的坐标为(m ,2m-2)或(m ,2-2m );综上所述点P 的坐标为(m ,m-12 )、(m ,1- m2 )、(m ,2m-2)或(m ,2-2m );(3)不存在满足条件的点Q 点Q 在第一象限内的抛物线y=2x 2-2上,令点Q 的坐标为(x, 2x 2-2),x>1, 过点Q 作QE ⊥直线l , 垂足为E ,△BPQ 为等腰直角三角形,PB=PQ ,∠PEQ=∠PDB , ∠EPQ=∠DBP ,△PEQ ≌△BDP ,QE=PD ,PE=BD ,① 当P 的坐标为(m ,m-12 )时,m-x = m-12 , m=0 m=12x 2-2- m-12 = m-1, x= 12 x=1与x>1矛盾,此时点Q 不满足题设条件;② 当P 的坐标为(m ,1- m2)时,x-m= m-12 m=- 29 m=12x 2-2- 1- m 2 = m-1, x=- 56 x=1与x>1矛盾,此时点Q 不满足题设条件;③ 当P 的坐标为(m ,2m-2)时,m-x =2m-2 m= 92m=12x 2-2-(2m-2) = m-1, x=- 52 x=1与x>1矛盾,此时点Q 不满足题设条件; ④当P 的坐标为(m ,2-2m )时,x- m = 2m-2 m= 518 m=12x 2-2-(2-2m) = m-1 x=- 76 x=1与x>1矛盾,此时点Q 不满足题设条件; 综上所述,不存在满足条件的点Q3、(2013•昆明压轴题)如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC 边上,且抛物线经过O,A两点,直线AC交抛物线于点D.(1)求抛物线的解析式;(2)求点D的坐标;(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.考点:二次函数综合题.专题:综合题.分析:(1)由OA的长度确定出A的坐标,再利用对称性得到顶点坐标,设出抛物线的顶点形式y=a(x﹣2)2+3,将A的坐标代入求出a的值,即可确定出抛物线解析式;(2)设直线AC解析式为y=kx+b,将A与C坐标代入求出k与b的值,确定出直线AC解析式,与抛物线解析式联立即可求出D的坐标;(3)存在,分两种情况考虑:如图所示,当四边形ADMN为平行四边形时,DM∥AN,DM=AN,由对称性得到M(3,),即DM=2,故AN=2,根据OA+AN求出ON的长,即可确定出N的坐标;当四边形ADM′N′为平行四边形,可得三角形ADQ全等于三角形N′M′P,M′P=DQ=,N′P=AQ=3,将y=﹣代入得:﹣=﹣x2+3x,求出x的值,确定出OP的长,由OP+PN′求出ON′的长即可确定出N′坐标.解答:解:(1)设抛物线顶点为E,根据题意OA=4,OC=3,得:E(2,3),设抛物线解析式为y=a(x﹣2)2+3,将A(4,0)坐标代入得:0=4a+3,即a=﹣,则抛物线解析式为y=﹣(x﹣2)2+3=﹣x2+3x;(2)设直线AC解析式为y=kx+b(k≠0),将A(4,0)与C(0,3)代入得:,解得:,故直线AC解析式为y=﹣x+3,与抛物线解析式联立得:,解得:或,则点D坐标为(1,);(3)存在,分两种情况考虑:①当点M在x轴上方时,如答图1所示:四边形ADMN 为平行四边形,DM∥AN,DM=AN , 由对称性得到M (3,),即DM=2,故AN=2, ∴N 1(2,0),N 2(6,0);②当点M 在x 轴下方时,如答图2所示:过点D 作DQ⊥x 轴于点Q ,过点M 作MP⊥x 轴于点P ,可得△ADQ≌△NMP, ∴MP=DQ=,NP=AQ=3,将y M =﹣代入抛物线解析式得:﹣=﹣x 2+3x ,解得:x M =2﹣或x M =2+, ∴x N =x M ﹣3=﹣﹣1或﹣1, ∴N 3(﹣﹣1,0),N 4(﹣1,0).综上所述,满足条件的点N 有四个:N 1(2,0),N 2(6,0),N 3(﹣﹣1,0),N 4(﹣1,0). 点评: 此题考查了二次函数综合题,涉及的知识有:待定系数法确定抛物线解析式,一次函数与二次函数的交点,平行四边形的性质,以及坐标与图形性质,是一道多知识点的探究型试题. 4、(2013陕西)在平面直角坐标系中,一个二次函灵敏的图象经过点A (1,0)、B (3,0)两点.(1)写出这个二次函数的对称轴;(2)设这个二次函数的顶点为D ,与y 轴交于点C ,它的对称轴与x 轴交于点E ,连接AD 、DE 和DB ,当△AOC 与△DEB 相似时,求这个二次函数的表达式[提示:如果一个二次函数的图象与x 轴的交点 为)0,(),0,(21x B x A A ,那么它的表达式可表示 为:))((21x x x x a y --=]考点:此题在陕西的中考中也较固定,第(1)问主要考查待定系数法求二次函数的解析式,二次函数与坐标轴的交点坐标,抛物线的对称性等简单问题第二问主要考查二次函数综合应用之点的存在性问题;包括最短距离与面积的最值等(等腰三角形,平行四边形,正方形,相似三角形,相似,全等等问题考查问题的综合能力要求较高,基本上都是转化为求点的坐标的过程(第24题图)y -1 O x 2 -1 1 12 3 -2 3解析:本题中(1)由抛物线的轴对称性可知,与x 轴的两个交点关于对称轴对称,易求出对称轴;(2)由提示中可以设出函数的解析式,将顶点D 与E 的坐标表示出来,从而将两个三角形的边长表示出来,而相似的确定过程中充分考虑到分类即可解决此题; 解:(1)对称轴为直线:x=2(2)∵A (1,0)、B (3,0),所以设)3)(1(--=x x a y 即a ax ax y 342+-=当x=0时,y=3a ,当x=2时,y=a - ∴C (0,3a ),D(2,-a) ∴OC=|3a|, ∵A (1,0)、E (2,0), ∴OA=1,EB=1,DE=}-a|=|a| 在△AOC 与△DEB 中, ∵∠AOC=∠DEB=90° ∴当EBDEOC AO =时,△AOC ∽△DEB ∴1|||3|1a a =时,解得33=a 或33-=a 当DEEBOC AO =时,△AOC ∽△BED ∴||1|3|1a a =时,此方程无解, 综上所得:所求二次函数的表达式为:3334332+-=x x y 或3334332-+-=x x y5、(2013成都市压轴题)在平面直角坐标系中,已知抛物线21y 2x bx c =-++(b,c 为常数)的顶点为P,等腰直角三角形ABC 的顶点A 的坐标为(0,-1),C 的坐标为(4,3),直角顶点B 在第四象限(1)如图,若该抛物线过A,B 两点,求抛物线的函数表达式;(2)平(1)中的抛物线,使顶点P 在直线AC 上滑动,且与AC 交于另一点Q.i )若点M 在直线AC 下方,且为平移前(1)中的抛物线上点,当以M,P,Q 三点为顶点的三角形是等腰三角形时,求出所有符合条件的M 的坐标;ii )取BC 的中点N,连接NP,BQ 试探究PQNP BQ+是否存在最大值?若存在,求出该最大值;所不存在,请说明理由解析:(1)A(0,-1) C(4,3) 则|AC |=22(40)(13)42-+--=ABC 为等腰直角三角形 ∴AB=BC=4 ∴B 点(4,-1)将A,B 代入抛物线方程有1116412c b c =-⎧⎪⎨-⨯++=-⎪⎩⇒12c b =-⎧⎨=⎩ ∴21212y x x =-+- (2)当顶点P 在直线AC 上滑动时,平移后抛物线与AC 另一交点Q 就是A 点沿直线AC 滑动同样的单位下面给予证明:原抛物线2211(44)1(2)122y x x x =--++=--+ 顶点P 为(2,1) 设平移后顶点P 为(a,a-1),则平移后抛物线21()12y x a a '=--+- 联立y=x-1(直线AC 方程)得Q 点为(a-2,a-3)∴|PQ |=22即实际上是线段AP 在直线AC 上的滑动.ⅰ)点M 在直线AC 下方,且M,P,Q 构成等腰直角三角形,那么先考虑使MP,Q 构成等腰直角三角形的M 点的轨迹,再求其轨迹与抛物线的交点以确定M 点.①若∠M 为直角,则M 点轨迹即为AC 下方距AC 为MH 且与AC 平行的直线l 又知|PQ |=22,则|MH |2|PM |=2直线l 即为AC 向下平移|PM |=2个单位 L:y=x-3 联立21212y x x =-+- 得x=15M 点为(1+5,5-2)或(1-5,-5-2)②若∠P=或∠Q 为直角,即PQ 为直角边,MQ ⊥PQ 且,MQ=PQ=22或MP ⊥PQ,且MP=PQ=22,∴M 点轨迹是AC 下方距AC 为22且与AC 平行直线L 直线L 即为AC 向下平移|MP |=4个单位 L:y=x-5 联立21212y x x =-+-得x=4或x=-2 ∴M 点为(4,-1)或(-2,-7)综上所有符合条件的点M 为(1+5,5-2)(4,-1);(1-5,-5-2),(-2,-7)ⅱ)知PQ=22PQMP BQ+有最大值,即NP+BQ 有最小值如下图,取AB 中点M ,连结QM,NM,知N 为中点∴MN 为AC 边中位线,∴MN ∥AC 且MN=12AC=22=PQ ∴MN PQ ∴MNPQ 为平行四边形 即PN=QM ∴QB+PN=BQ+MQ此时,作B 点关于AC 对称的点B ′,连B Q ',B M 'B M '交AC 于点H ,易知B Q '=BQ∴BQ+PN=B Q '+MQ ≥B M '(三角形两边之和大于第三边) 仅当Q 与H 重合时,取等号即BQ+PN 最小值存在 且最小值为B M ' 连结A B '知ABB '∆为等腰直角三角形A B '=4,AM=12AB=2 ∴由勾股定理得25B M '= ∴PQ NP BQ +2210525=6、(2013山西压轴题,26,14分)(本题14分)综合与探究:如图,抛物线213442yx x 与x 轴交于A,B 两点(点B 在点A 的右侧)与y 轴交于点C,连接BC,以BC 为一边,点O 为对称中心作菱形BDEC,点P 是x 轴上的一个动点,设点P 的坐标为(m ,0),过点P 作x 轴的垂线l 交抛物线于点Q(1)求点A,B,C 的坐标(2)当点P 在线段OB 上运动时,直线l 分别交BD ,BC 于点M,N 试探究m 为何值时,四边形CQMD 是平行四边形,此时,请判断四边形CQBM 的形状,并说明理由(3)当点P 在线段EB 上运动时,是否存在点 Q ,使△BDQ 为直角三角形,若存在,请直接写出点Q 的坐标;若不存在,请说明理由 解析:(1)当y=0时,2134042x x ,解得,122,8x x∵点B 在点A 的右侧,∴点A,B 的坐标分别为:(-2,0),(8,0) 当x=0时,y=-4∴点C 的坐标为(0,-4),(2)由菱形的对称性可知,点D 的坐标为(0,4). 设直线BD 的解析式为y =kx +b ,则480b k b .解得,k=12,b=4. ∴直线BD 的解析式为142yx .∵l⊥x 轴,∴点M ,Q 的坐标分别是(m ,142m ),(m ,213442m m ) 如图,当MQ=DC 时,四边形CQMD 是平行四边形. ∴(142m )-(213442m m )=4-(-4) 化简得:240m m .解得,m 1=0,(舍去)m 2=4.∴当m=4时,四边形CQMD 是平行四边形. 此时,四边形CQBM 是平行四边形.解法一:∵m=4,∴点P 是OB 中点.∵l⊥x 轴,∴l∥y 轴. ∴△BPM∽△BOD.∴12BP BM BO BD .∴BM=DM. ∵四边形CQMD 是平行四边形,∴DM CQ∴BM CQ.∴四边形CQBM 为平行四边形. 解法二:设直线BC 的解析式为y=k 1x+b 1,则111480b k b .解得,k 1=12,b 1=-4 ∴直线BC 的解析式为y=12x-4 又∵l⊥x 轴交BC 于点N.∴x=4时,y=-2. ∴点N 的坐标为(4,-2)由上面可知,点M,Q 的坐标分别为:(4,2),Q(4,-6).∴MN=2-(-2)=4,NQ=-2-(-6)=4.∴MN=QN.又∵四边形CQMD 是平行四边形.∴DB∥CQ,∴∠3=∠4, 又∠1=∠2,∴△BMN≌△CQN.∴BN=CN. ∴四边形CQBM 为平行四边形.(3)抛物线上存在两个这样的点Q ,分别是Q 1(-2,0),Q 2(6,-4).7、(2013•内江)如图,在等边△ABC 中,AB=3,D 、E 分别是AB 、AC 上的点,且DE∥BC,将△ADE 沿DE 翻折,与梯形BCED 重叠的部分记作图形L . (1)求△ABC 的面积;(2)设AD=x ,图形L 的面积为y ,求y 关于x 的函数解析式;(3)已知图形L 的顶点均在⊙O 上,当图形L 的面积最大时,求⊙O 的面积.考点: 相似形综合题. 分析: (1)作AH⊥BC 于H ,根据勾股定理就可以求出AH ,由三角形的面积公式就可以求出其值;(2)如图1,当0<x≤1.5时,由三角形的面积公式就可以表示出y 与x 之间的函数关系式,如图2,当1.5<x <3时,重叠部分的面积为梯形DMNE 的面积,由梯形的面积公式就可以求出其关系式;(3)如图4,根据(2)的结论可以求出y的最大值从而求出x的值,作FO⊥DE于O,连接MO,ME,求得∠DME=90°,就可以求出⊙O的直径,由圆的面积公式就可以求出其值.解答:解:(1)如图3,作AH⊥BC于H,∴∠AHB=90°.∵△ABC是等边三角形,∴AB=BC=AC=3.∵∠AHB=90°,∴BH=BC=在Rt△ABC中,由勾股定理,得AH=.∴S△ABC==;(2)如图1,当0<x≤1.5时,y=S△ADE.作AG⊥DE于G,∴∠AGD=90°,∠DAG=30°,∴DG=x,AG=x,∴y==x2,∵a=>0,开口向上,在对称轴的右侧y随x的增大而增大,∴x=1.5时,y最大=,如图2,当1.5<x<3时,作MG⊥DE于G,∵AD=x,∴BD=DM=3﹣x,∴DG=(3﹣x),MF=MN=2x﹣3,∴MG=(3﹣x),∴y=,=﹣;(3),如图4,∵y=﹣;∴y=﹣(x2﹣4x)﹣,y=﹣(x﹣2)2+,∵a=﹣<0,开口向下,∴x=2时,y最大=,∵>,∴y最大时,x=2,∴DE=2,BD=DM=1.作FO⊥DE于O,连接MO,ME.∴DO=OE=1,∴DM=DO.∵∠MDO=60°,∴△MDO是等边三角形,∴∠DMO=∠DOM=60°,MO=DO=1.∴MO=OE,∠MOE=120°,∴∠OME=30°,∴∠DME=90°,∴DE是直径,S⊙O=π×12=π.点评:本题考查了等边三角形的面积公式的运用,梯形的面积公式的运用,勾股定理的运用,圆周角定理的运用,圆的面积公式的运用,等边三角形的性质的运用,二次函数的性质的运用,解答时灵活运用等边三角形的性质是关键.8、(2013•新疆压轴题)如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).(1)求抛物线的解析式;(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D 的坐标,若不存在,请说明理由;(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△A CE的最大面积及E点的坐标.考点:二次函数综合题.专题:代数几何综合题.分析:(1)利用待定系数法求二次函数解析式解答即可;(2)利用待定系数法求出直线AC的解析式,然后根据轴对称确定最短路线问题,直线AC与对称轴的交点即为所求点D;(3)根据直线AC的解析式,设出过点E与AC平行的直线,然后与抛物线解析式联立消掉y得到关于x的一元二次方程,利用根的判别式△=0时,△ACE的面积最大,然后求出此时与AC平行的直线,然后求出点E的坐标,并求出该直线与x轴的交点F 的坐标,再求出AF,再根据直线l与x轴的夹角为45°求出两直线间的距离,再求出AC间的距离,然后利用三角形的面积公式列式计算即可得解.解答:解:(1)∵抛物线y=ax2+bx+3经过点A(1,0),点C(4,3),∴,解得,所以,抛物线的解析式为y=x2﹣4x+3;(2)∵点A、B关于对称轴对称,∴点D为AC与对称轴的交点时△BCD的周长最小,设直线AC的解析式为y=kx+b(k≠0),则,解得,所以,直线AC的解析式为y=x﹣1,∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的对称轴为直线x=2,当x=2时,y=2﹣1=1,∴抛物线对称轴上存在点D(2,1),使△BCD的周长最小;(3)如图,设过点E与直线AC平行线的直线为y=x+m,联立,消掉y得,x2﹣5x+3﹣m=0,△=(﹣5)2﹣4×1×(3﹣m)=0,即m=﹣时,点E到AC的距离最大,△ACE的面积最大,此时x=52,y=﹣34,∴点E的坐标为(52,﹣34),设过点E的直线与x轴交点为F,则F(,0),∴AF=﹣1=94,∵直线AC的解析式为y=x﹣1,∴∠CAB=45°,∴点F到AC的距离为94×=,又∵AC==3,∴△ACE的最大面积=×3×=,此时E点坐标为(52,﹣34).点评:本题考查了二次函数综合题型,主要考查了待定系数法求二次函数解析式,待定系数法求一次函数解析式,利用轴对称确定最短路线问题,联立两函数解析式求交点坐标,利用平行线确定点到直线的最大距离问题.9、(2013凉山州压轴题)如图,抛物线y=ax2﹣2ax+c(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.(1)求抛物线的解析式;(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM 的长;(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值,并直接判断△PCM的形状;若不存在,请说明理由.考点:二次函数综合题.分析:(1)将A(3,0),C(0,4)代入y=ax2﹣2ax+c,运用待定系数法即可求出抛物线的解析式;(2)先根据A、C的坐标,用待定系数法求出直线AC的解析式,进而根据抛物线和直线AC 的解析式分别表示出点P、点M的坐标,即可得到PM的长;(3)由于∠PFC和∠AEM都是直角,F和E对应,则若以P、C、F为顶点的三角形和△AEM 相似时,分两种情况进行讨论:①△PFC∽△AEM,②△CFP∽△AEM;可分别用含m的代数式表示出AE、EM、CF、PF的长,根据相似三角形对应边的比相等列出比例式,求出m的值,再根据相似三角形的性质,直角三角形、等腰三角形的判定判断出△PCM的形状.解答:解:(1)∵抛物线y=ax2﹣2ax+c(a≠0)经过点A(3,0),点C(0,4),∴,解得,∴抛物线的解析式为y=﹣x2+x+4;(2)设直线AC的解析式为y=kx+b,∵A(3,0),点C(0,4),∴,解得,∴直线AC的解析式为y=﹣x+4.∵点M的横坐标为m,点M在AC上,∴M点的坐标为(m,﹣ m+4),∵点P的横坐标为m,点P在抛物线y=﹣x2+x+4上,∴点P的坐标为(m,﹣ m2+m+4),∴PM=PE﹣ME=(﹣m2+m+4)﹣(﹣m+4)=﹣m2+4m,即PM=﹣m2+4m(0<m<3);(3)在(2)的条件下,连结PC,在CD上方的抛物线部分存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似.理由如下:由题意,可得AE=3﹣m,EM=﹣m+4,CF=m,PF=﹣m2+m+4﹣4=﹣m2+m.若以P、C、F为顶点的三角形和△AEM相似,分两种情况:①若△PFC∽△AEM,则PF:AE=FC:EM,即(﹣m2+m):(3﹣m)=m:(﹣ m+4),∵m≠0且m≠3,∴m=.∵△PFC∽△AEM,∴∠PCF=∠AME,∵∠AME=∠CMF,∴∠PCF=∠CMF.在直角△CMF中,∵∠CMF+∠MCF=90°,∴∠PCF+∠MCF=90°,即∠PCM=90°,∴△PCM为直角三角形;②若△CFP∽△AEM,则CF:AE=PF:EM,即m:(3﹣m)=(﹣m2+m):(﹣m+4),∵m≠0且m≠3,∴m=1.∵△CFP∽△AEM,∴∠CPF=∠AME,∵∠AME=∠CMF,∴∠CPF=∠CMF.∴CP=CM,∴△PCM为等腰三角形.综上所述,存在这样的点P使△PFC与△AEM相似.此时m的值为或1,△PCM为直角三角形或等腰三角形.点评:此题是二次函数的综合题,其中涉及到运用待定系数法求二次函数、一次函数的解析式,矩形的性质,相似三角形的判定和性质,直角三角形、等腰三角形的判定,难度适中.要注意的是当相似三角形的对应边和对应角不明确时,要分类讨论,以免漏解.10、(2013•曲靖压轴题)如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,过A、B两点的抛物线为y=﹣x2+bx+c.点D为线段AB上一动点,过点D作CD⊥x 轴于点C,交抛物线于点E.(1)求抛物线的解析式.(2)当DE=4时,求四边形CAEB的面积.(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求此点D坐标;若不存在,说明理由.考点:二次函数综合题.分析:(1)首先求出点A、B的坐标,然后利用待定系数法求出抛物线的解析式;(2)设点C坐标为(m,0)(m<0),根据已知条件求出点E坐标为(m,8+m);由于点E在抛物线上,则可以列出方程求出m的值.在计算四边形CAEB面积时,利用S四边形CAEB=S△ACE+S梯形OCEB﹣S△BCO,可以简化计算;(3)由于△ACD为等腰直角三角形,而△D BE和△DAC相似,则△DBE必为等腰直角三角形.分两种情况讨论,要点是求出点E的坐标,由于点E在抛物线上,则可以由此列出方程求出未知数.解答:解:(1)在直线解析式y=x+4中,令x=0,得y=4;令y=0,得x=﹣4,∴A(﹣4,0),B(0,4).∵点A(﹣4,0),B(0,4)在抛物线y=﹣x2+bx+c上,∴,解得:b=﹣3,c=4,∴抛物线的解析式为:y=﹣x2﹣3x+4.(2)设点C坐标为(m,0)(m<0),则OC=﹣m,AC=4+m.∵OA=OB=4,∴∠BAC=45°,∴△ACD为等腰直角三角形,∴CD=AC=4+m,∴CE=CD+DE=4+m+4=8+m,∴点E坐标为(m,8+m).∵点E在抛物线y=﹣x2﹣3x+4上,∴8+m=﹣m2﹣3m+4,解得m=﹣2.∴C(﹣2,0),AC=OC=2,CE=6,S四边形CAEB=S△ACE+S梯形OCEB﹣S△BCO=×2×6+(6+4)×2﹣×2×4=12.(3)设点C坐标为(m,0)(m<0),则OC=﹣m,CD=AC=4+m,BD=OC=﹣m,则D(m,4+m).∵△ACD为等腰直角三角形,△DBE和△DAC相似∴△DBE必为等腰直角三角形.i)若∠BED=90°,则BE=DE,∵BE=OC=﹣m,∴DE=BE=﹣m,∴CE=4+m﹣m=4,∴E(m,4).∵点E在抛物线y=﹣x2﹣3x+4上,∴4=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣3,∴D(﹣3,1);ii)若∠EBD=90°,则BE=BD=﹣m,在等腰直角三角形EBD中,DE=BD=﹣2m,∴CE=4+m﹣2m=4﹣m,∴E(m,4﹣m).∵点E在抛物线y=﹣x2﹣3x+4上,∴4﹣m=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣2,∴D(﹣2,2).综上所述,存在点D,使得△DBE和△DAC相似,点D的坐标为(﹣3,1)或(﹣2,2).点评:本题考查了二次函数与一次函数的图象与性质、函数图象上点的坐标特征、待定系数法、相似三角形、等腰直角三角形、图象面积计算等重要知识点.第(3)问需要分(第26题图)'类讨论,这是本题的难点.11、(2013年临沂压轴题)如图,抛物线经过5(1,0),(5,0),(0,)2A B C --三点.(1)求抛物线的解析式;(2)在抛物线的对称轴上有一点P ,使PA+PC 的值最小,求点P 的坐标;(3)点M 为x 轴上一动点,在抛物线上是否存在一点N ,使以A,C,M,N 四点构成的四边形为平行四边形?若存在,求点N 的坐标;若不存在,请说明理由.解析:解:(1)设抛物线的解2y ax bx c =++,根据题意,得0,2550,5.2a b c a b c c ⎧⎪-+=⎪++=⎨⎪⎪=-⎩,解得1,22,5.2a b c ⎧=⎪⎪=-⎨⎪⎪=-⎩∴抛物线的解析式为:2152.22y x x =-- ………(3分) (2)由题意知,点A 关于抛物线对称轴的对称点为点B,连接BC 交抛物线的对称轴于点P ,则P 点 即为所求.设直线BC 的解析式为y kx b =+,由题意,得50,5.2k b b +=⎧⎪⎨=-⎪⎩解得 1,25.2k b ⎧=⎪⎪⎨⎪=-⎪⎩∴直线BC 的解析式为15.22y x =- …………(6分) ∵抛物线215222y x x =--的对称轴是2x =,∴当2x =时,153.222y x =-=-∴点P 的坐标是3(2,)2-. …………(7分)(3)存在 …………………………(8分)(i)当存在的点N 在x 轴的下方时,如图所示,∵四边形ACNM 是平行四边形,∴CN ∥x 轴,∴点C 与点N 关于对称轴x=2对称,∵C 点的坐标为5(0,)2-,∴点N 的坐标为5(4,).2- ………………………(11分)(II )当存在的点'N 在x 轴上方时,如图所示,作'N H x ⊥轴于点H ,∵四边形''ACM N 是平行四边形,∴'''',AC M N N M H CAO =∠=∠, ∴Rt △CAO ≌Rt △''N M H ,∴'N H OC =. ∵点C 的坐标为'55(0,),22N H -∴=,即N 点的纵坐标为52, ∴21552,222x x --=即24100x x --= 解得12214,214.x x =+=-∴点'N 的坐标为5(214,)2-和5(214,)2+.综上所述,满足题目条件的点N 共有三个,分别为5(4,).2-,5(214,)2+,5(214,)2- ………………………(13分)12、(2013•宁波压轴题)如图,在平面直角坐标系中,O 为坐标原点,点A 的坐标为(0,4),点B 的坐标为(4,0),点C 的坐标为(﹣4,0),点P 在射线AB 上运动,连结CP 与y 轴交于点D ,连结BD .过P ,D ,B 三点作⊙Q 与y 轴的另一个交点为E ,延长DQ 交⊙Q 于点F ,连结EF ,BF .(1)求直线AB的函数解析式;(2)当点P在线段AB(不包括A,B两点)上时.①求证:∠BDE=∠ADP;②设DE=x,DF=y.请求出y关于x的函数解析式;(3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标:如果不存在,请说明理由.考点:一次函数综合题.分析:(1)设直线AB的函数解析式为y=kx+4,把(4,0)代入即可;(2)①先证出△BOD≌△COD,得出∠BOD=∠CDO,再根据∠CDO=∠ADP,即可得出∠BDE=∠ADP,②先连结PE,根据∠ADP=∠DEP+∠DPE,∠BDE=∠ABD+∠OAB,∠ADP=∠BDE,∠DEP=∠ABD,得出∠DPE=∠OAB,再证出∠DFE=∠DPE=45°,最后根据∠DEF=90°,得出△DEF是等腰直角三角形,从而求出DF=DE,即y=x;(3)当=2时,过点F作FH⊥OB于点H,则∠DBO=∠BFH,再证出△BOD∽△FHB,===2,得出FH=2,OD=2BH,再根据∠FHO=∠EOH=∠OEF=90°,得出四边形OEFH是矩形,OE=FH=2,EF=OH=4﹣OD,根据DE=EF,求出OD的长,从而得出直线CD 的解析式为y=x+,最后根据求出点P的坐标即可;当=时,连结EB,先证出△DEF是等腰直角三角形,过点F作FG⊥OB于点G,同理可得△BOD∽△FGB,===,得出FG=8,OD=BG,再证出四边形OEFG是矩形,求出OD的值,再求出直线CD的解析式,最后根据即可求出点P的坐标.解答:解:(1)设直线AB的函数解析式为y=kx+4,代入(4,0)得:4k+4=0,解得:k=﹣1,则直线AB的函数解析式为y=﹣x+4;(2)①由已知得:OB=OC,∠BOD=∠COD=90°,又∵OD=OD,∴△BOD≌△COD,∴∠BOD=∠CDO,∵∠CDO=∠ADP,∴∠BDE=∠ADP,②连结PE,∵∠ADP是△DPE的一个外角,∴∠ADP=∠DEP+∠DPE,∵∠BDE是△ABD的一个外角,∴∠BDE=∠ABD+∠OAB,∵∠ADP=∠BDE,∠DEP=∠ABD,∴∠DPE=∠OAB,∵OA=OB=4,∠AOB=90°,∴∠OAB=45°,∴∠DPE=45°,∴∠DFE=∠DPE=45°,∵DF是⊙Q的直径,∴∠DEF=90°,∴△DEF是等腰直角三角形,∴DF=DE,即y=x;(3)当BD:BF=2:1时,过点F作FH⊥OB于点H,∵∠DBO+∠OBF=90°,∠OBF+∠BFH=90°,∴∠DBO=∠BFH,又∵∠DOB=∠BHF=90°,∴△BOD∽△FHB,∴===2,∴FH=2,OD=2BH,∵∠FHO=∠EOH=∠OEF=90°,∴四边形OEFH是矩形,∴OE=FH=2,∴EF=OH=4﹣OD,∵DE=E F,∴2+OD=4﹣OD,解得:OD=,∴点D的坐标为(0,),∴直线CD的解析式为y=x+,由得:,则点P的坐标为(2,2);当=时,连结EB,同(2)①可得:∠ADB=∠EDP,而∠ADB=∠DEB+∠DBE,∠EDP=∠DAP+∠DPA,∵∠DEP=∠DPA,∴∠DBE=∠DAP=45°,∴△DEF是等腰直角三角形,过点F作FG⊥OB于点G,精品1 同理可得:△BOD∽△FGB,∴===,∴FG=8,OD=BG,∵∠FGO=∠GOE=∠OEF=90°,∴四边形OEFG是矩形,∴OE=FG=8,∴EF=OG=4+2OD,∵DE=EF,∴8﹣OD=4+2OD,OD=43,∴点D的坐标为(0,﹣43),直线CD的解析式为:y=﹣13x﹣43,由得:,∴点P的坐标为(8,﹣4),综上所述,点P的坐标为(2,2)或(8,﹣4).点评:此题考查了一次函数的综合,用到的知识点是一次函数、矩形的性质、圆的性质,关键是综合运用有关知识作出辅助线,列出方程组.13、(2013四川南充压轴题,21,8分)如图,二次函数y=x2+bx-3b+3的图象与x轴交于A、B两点(点A在点B的左边),交y轴于点C,且经过点(b-2,2b2-5b-1). (1)求这条抛物线的解析式;(2)⊙M过A、B、C三点,交y轴于另一点D,求点M的坐标;(3)连接AM、DM,将∠AMD绕点M顺时针旋转,两边MA、MD与x轴、y轴分别交于点E、F,若△DMF为等腰三角形,求点E的坐标.解析:(1)把点(b-2,2b2-5b-1)代入解析式,得2b2-5b-1=(b-2)2+b(b-2)-3b+3,……………1′解得b=2.∴抛物线的解析式为y=x2+2x-3. ……………2′(2)由x2+2x-3=0,得x=-3或x=1.∴A(-3,0)、B(1,0)、C(0,-3).抛物线的对称轴是直线x=-1,圆心M在直线x=-1上. ……………3′∴设M(-1,n),作MG⊥x轴于G,MH⊥y轴于H,连接MC、MB.∴MH=1,BG=2. ……………4′∵MB=MC,∴BG2+MG2=MH2+CH2,即4+n2=1+(3+n)2,解得n=-1,∴点M(-1,-1)……………5′(3)如图,由M(-1,-1),得MG=MH.∵MA=MD,∴Rt△AMG≌RtDMH,∴∠1=∠2.由旋转可知∠3=∠4. ∴△AME≌△DMF.若△DMF为等腰三角形,则△AME为等腰三角形. ……………6′设E (x ,0),△AME 为等腰三角形,分三种情况: ①AE =AM =5,则x=5-3,∴E (5-3,0);②∵M 在AB 的垂直平分线上,∴MA =ME =MB ,∴E (1,0) ……………7′ ③点E 在AM 的垂直平分线上,则AE =ME .AE =x +3,ME 2=MG 2+EG 2=1+(-1-x )2,∴(x +3)2=1+(-1-x )2,解得x =47-,∴E (47-,0).∴所求点E 的坐标为(5-3,0),(1,0),(47-,0) ……………8′14、(2013四川宜宾压轴题)如图,抛物线y 1=x 2﹣1交x 轴的正半轴于点A ,交y 轴于点B ,将此抛物线向右平移4个单位得抛物线y 2,两条抛物线相交于点C . (1)请直接写出抛物线y 2的解析式;(2)若点P 是x 轴上一动点,且满足∠CPA =∠OBA ,求出所有满足条件的P 点坐标; (3)在第四象限内抛物线y 2上,是否存在点Q ,使得△QOC 中OC 边上的高h 有最大值?若存在,请求出点Q 的坐标及h 的最大值;若不存在,请说明理由.考点:二次函数综合题. 专题:代数几何综合题.分析:(1)写出平移后的抛物线的顶点坐标,然后利用顶点式解析式写出即可; (2)根据抛物线解析式求出点A 、B 的坐标,然后求出∠OBA =45°,再联立两抛物线解析式求出交点C 的坐标,再根据∠CPA =∠OBA 分点P 在点A 的左边和右边两种情况求解;(3)先求出直线OC的解析式为y=x,设与OC平行的直线y=x+b,与抛物线y2联立消掉y得到关于x的一元二次方程,再根据与OC的距离最大时方程有且只有一个根,然后利用根的判别式△=0列式求出b的值,从而得到直线的解析式,再求出与x轴的交点E的坐标,得到OE的长度,再过点C作CD⊥x轴于D,然后根据∠COD的正弦值求解即可得到h的值.解答:解:(1)抛物线y1=x2﹣1向右平移4个单位的顶点坐标为(4,﹣1),所以,抛物线y2的解析式为y2=(x﹣4)2﹣1;(2)x=0时,y=﹣1,y=0时,x2﹣1=0,解得x1=1,x2=﹣1,所以,点A(1,0),B(0,﹣1),∴∠OBA=45°,联立,解得,∴点C的坐标为(2,3),∵∠CPA=∠OBA,∴点P在点A的左边时,坐标为(﹣1,0),在点A的右边时,坐标为(5,0),所以,点P的坐标为(﹣1,0)或(5,0);(3)存在.∵点C(2,3),∴直线OC的解析式为y=x,设与OC平行的直线y=x+b,联立,消掉y得,2x2﹣19x+30﹣2b=0,当△=0,方程有两个相等的实数根时,△QOC中OC边上的高h有最大值,此时x1=x2=×(﹣)=,。
2020年中考数学试题分类:分式及分式方程 含解析

2020年中考数学试题分类汇编之十九分式及分式方程一、选择题1.(2020成都)(3分)已知2x =是分式方程311k x x x -+=-的解,那么实数k 的值为( ) A .3B .4C .5D .6【解答】解:把2x =代入分式方程得:112k-=, 解得:4k =. 故选:B .2.(2020福建)我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.“其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每件椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x 株,则符合题意的方程是( ) A. 62103(1)-=x xB.621031=-x C. 621031-=x xD.62103=x【答案】A【详解】解:由题意得:62103(1)-=x x, 故选A.3.(2020哈尔滨)(3分)方程2152x x =+-的解为( ) A .1x =-B .5x =C .7x =D .9x =【解答】解:方程的两边同乘(5)(2)x x +-得: 2(2)5x x -=-,解得9x =,经检验,9x =是原方程的解. 故选:D . 4.(2020天津)计算221(1)(1)x x x +++的结果是( )A .11x + B .()211x + C .1 D .1x +答案:A5.(2020四川绵阳)甲、乙二人同驾一辆车出游,各匀速驾驶一半路程,共用3小时。
到达目的地后,甲对乙说:我用你所花的时间,可以行使180km ”.乙对甲说:“”我用你花的时间行驶80km ”。
从他们的交谈中可以判断,乙驾驶的时长为( ) A. 1.2小时 B. 1.6小时 C.1.8小时 D.2小时 【解析】本题考查列分式方程解实际问题。
设乙驾驶的时长为x 小时,则甲为(3-x )小时,所以甲的速度为:180x km/h, 乙的速度为803-xkm/h 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
故选:A.
4.(2020河南)如图, ,若 ,则 的度数为()
A. B.
C. D.
【详解】如图,∵ ,
∴∠1+∠3=180º,
∵∠1=70º,
∴∴∠3=180º-70º=110º,
A.130°B.110°C.30°D.20°
答案:B
12.(2020辽宁抚顺)(3分)一个等腰直角三角尺和一把直尺按如图所示的位置摆放,若∠1=20°,则∠2的度数是( )
A.15°B.20°C.25°D.40°
解:∵AB∥CD,
∴∠3=∠1=20°,
∵三角形是等腰直角三角形,
∴∠2=45°﹣∠3=25°,
选:C.
13.(2020吉林)(2分)将一副三角尺按如图所示的方式摆放,则∠α的大小为( )
A.85°B.75°C.65°D.60°
解:如图所示,
∵∠BCD=60°,∠BCA=45°,
∴∠ACD=∠BCD﹣∠BCA=60°﹣45°=15°,
∠α=180°﹣∠D﹣∠ACD=180°﹣90°﹣15°=75°,
故选:B.
14.(2020内蒙古呼和浩特)(3分)命题①设△ABC的三个内角为A、B、C且α=A+B,β=C+A,γ=C+B,则α、β、γ中,最多有一个锐角;②顺次连接菱形各边中点所得的四边形是矩形;③从11个评委分别给出某选手的不同原始评分中,去掉1个最高分、1个最低分,剩下的9个评分与11个原始评分相比,中位数和方差都不发生变化.其中错误命题的个数为( )
A.16°B.28°C.44°D.45°
【解析】延长CD交AB于点F。则∠CFG=∠CDE=72°。∵△ABC是等腰三角形,∠ABC=124°∴∠A=(180°-124°)÷2=28°。∴∠ACD=∠CFG-∠A=72°-28°=44°。故选C.
8.(2020贵阳)如图,直线 , 相交于点 ,如果 ,那么 是()
A. B. C. D.
【答案】A
9.(2020贵州黔西南)(4分)如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37°时,∠1的度数为( )
A.37°B.43°C.53°D.54°
解:∵AB∥CD,∠2=37°,
∴∠2=∠3=37°,
∵∠1+∠3=90°,
∴∠1=53°,
故选:C.
10.(2020长沙)如图,一块直角三角板的60度的顶点A与直角顶点C分别在平行线 上,斜边AB平分 ,交直线GH于点E,则 的大小为( )
故选:D.
3.(2020河北)如图,从笔直的公路 旁一点 出发,向西走 到达 ;从 出发向北走 也到达 .下列说法错误的是()
A.从点 向北偏西45°走 到达
B.公路 的走向是南偏西45°
C.公路 的走向是北偏东45°
D.从点 向北走 后,再向西走 到达
【答案】A
【详解】解:如图所示,过P点作AB的垂线PH,
故命题③错误;
综上:错误的命题个数为1,
故选:B.
15.(2020宁夏)(3分)如图摆放的一副学生用直角三角板,∠F=30°,∠C=是( )
【分析】根据∠A的余角是90°﹣∠A,代入求出即可.
【解答】解:∵∠A=23°,
∴∠A的余角是90°﹣23°=67°.
故选:B.
2.(2020河北)如图,在平面内作已知直线 的垂线,可作垂线的条数有()
A.0条B.1条C.2条D.无数条
【答案】D
【详解】在同一平面内,画已知直线的垂线,可以画无数条;
∵ ,
∴∠2=∠3=110º,
故选:B.
5.(2020江西)如图, ,则下列结论错误的是()
A. B. C. D.
【解析】
由∠1=∠2=65°,可得内错角相等,两直线平行,故A选项正确,∠3和∠BFE互为对顶角,∴∠BFE=35°,∠1为△BEF的外角,∴∠1=∠BFE+∠B,可得∠B=30°,故B选项正确.
选项A:∵BP=AP=6km,且∠BPA=90°,∴△PAB为等腰直角三角形,∠PAB=∠PBA=45°,
又PH⊥AB,∴△PAH为等腰直角三角形,
∴PH= km,故选项A错误;
选项B:站在公路上向西南方向看,公路 的走向是南偏西45°,故选项B正确;
选项C:站在公路上向东北方向看,公路 的走向是北偏东45°,故选项C正确;
②如图,菱形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,
∴HG∥EF,HE∥GF,
∴四边形EFGH是平行四边形,
∵AC⊥BD,
∴HE⊥HG,
∴四边形EFGH是矩形,故命题②正确;
③去掉一个最高分和一个最低分,不影响中间数字的位置,故不影响中位数,
但是当最高分过高或最低分过低,平均数有可能随之变化,同样,方差也会有所变化,
A.0个B.1个C.2个D.3个
解:①设α、β、γ中,有两个或三个锐角,
若有两个锐角,假设α、β为锐角,则A+B<90°,A+C<90°,
∴A+A+B+C=A+180°<180°,
∴A<0°,不成立,
若有三个锐角,同理,不成立,
假设A<45°,B<45°,则α<90°,
∴最多只有一个锐角,故命题①正确;
2020年中考数学试题分类汇编
几何初步(平行线相交线、命题)
平移旋转与折叠
解直角三角形
圆与多边形
分式及分式方程
轴对称与中心对称
尺规作图
最值类题
新概念规律类题
2020年中考数学试题分类汇编之八
几何初步平行线相交线
1、选择题
1.(2020陕西)若∠A=23°,则∠A余角的大小是( )
A.57°B.67°C.77°D.157°
A. B. C. D.
【答案】C
解:∵AB平分 ,∠CAB=60 ,
∴∠DAE=60 ,
∵FD∥GH,
∴∠ACE+∠CAD=180 ,
∴∠ACE=180 -∠CAB-∠DAE=60 ,
∵∠ACB=90 ,
∴∠ECB=90 -∠ACE=30 ,
故选:C.
11.(2020甘肃定西)若 ,则 的补角的度数是()
∠EFC为△CFG的外角,∴∠EFC=∠C+∠CGF,故C选项错误.因为在△CGF中,∠CFG>∠C,∴CG>FG,故D选项正确,所以本题答案为C
6.(2020乐山)如图, 是直线 上一点, ,射线 平分 , .则 ()
A. B. C. D.
【答案】B
7.(2020四川绵阳)在螳螂的示意图中,AB∥DE,△ABC是等腰三角形,∠ABC=124°,∠CDE=72°,则∠ACD=().
