2.4麦克斯韦速度分布
§2.4 麦克斯韦速度分布
• 前面已指出，麦克斯韦是先导出速度分布，然后再从
速度分布得到速率分布的。
• 本节中介绍麦克斯韦速度分布。
• 为了说明速度分布的含义，先介绍速度空间的概念。
§2.4.1 速度空间
§2.4.2 麦克斯韦速度分布
麦克斯韦最早用概率统计的方法导出了理想气体分 子的速度分布，它可表示为
*§2.4.5 绝对零度时金属中自由电子的 速度分布与速率分布 费米球
一速度分布律一般适用于平衡态的理想气体。
*§2.4.3 相对于vp 的速度分量分布 与速率分布 误差函数
*§2.4.4 从麦克斯韦速度分布导出速率分布
（一）以极坐标表示的射击点分布
按极坐标表示的射击点分布。
若用相等的Δr为间隔，
在靶板上画出很多个同心圆，
数出每个圆环中的黑点数ΔN。 以ΔN/NΔr 为纵坐标， r为横坐标画出竖条，如右下图所示。 令Δr 0，得到光滑曲线，
d
Nv
4π
N ( m )3/2 2 π kT
exp(
mv 2 ) v2 2kT
dv
d
Nv
4π
N ( m )3/2 2 π kT
exp(
mv 2 ) v2 2kT
dv
d Nv f (v) d v 4 π( m )3/2 exp( mv 2 ) v2 d v
N
2 π kT
2kT
• 这就是麦克斯韦速率分布.
d
vx
• x 方向速度分量的概率分布曲线如图所示：
•它对称于纵轴，图中打上斜线狭条面积即
f
(vx ) d vx
d
N (vx ) N
( m )1/ 2 2 π kT
第二章分子动力学理论的平衡态理论
这种在大量随机事件的 集合中出现的规律性叫统计 规律性。
少数分子无规律性
大量分子的统计分布 7
二、等概率性与概率的基本性质
1、概率的定义
概率：在总次数趋于无限大时，某事件出现次数对总次数的比率。
No Image
离散变量xi
P(xi)N li m N Ni
连续变量x , x-x+dx区间
d(N x)
§2.3 麦克斯韦速率分布
要深入研究气体的性质，不能光是研究一些平均值，
如t ，V2
等，还应该进一步弄清分子按速率和按能量等的分布情 况。
个别分子的运动是杂乱无章的，但大量分子运动的 集体表现存在着一定的统计规律。
统计物理关心两件事：
1. 平均值; 2. 分布;
几个要用的积分公式 高斯积分
Q xn e a2d x ,x (a0 ,n0 ,1 ,2 ,3 , ) 0
一、分子射线束实验
实验装置
接抽气泵
No Image
No Image
No Image
金属蒸汽
狭缝
No Image
No Image
显
No Image
示
屏
19
二 . 麦克斯韦速率分布函数 1859年麦克斯韦导出了理想气体在无外场的平衡态下，
分子速率分布函数为：
f(v)4(
m3/2 m 2v/2kT 2 m——分子的质量 ) e v T——热力学温度
分子平动动能的平均值
讨论 速率介于v1~v2之间的气体分子的平均速率的计算
v v1~v2
v2 vf (v)dv
v1
v2 f (v)dv
v1
vv1~v2
v2 v f(v)dv
麦克斯韦速度分布
麦克斯韦速度分布在物理学中，麦克斯韦速度分布是一种描述气体分子速度分布的概率分布函数，由苏格兰物理学家詹姆斯·克拉克·麦克斯韦于1860年提出。
该速度分布函数在气体动力学研究中具有重要的意义，可以用来解释多种气体现象和性质。
麦克斯韦速度分布的推导基于经典统计力学，并假设气体分子间的相互作用力很小，即考虑理想气体模型。
根据这个假设，我们可以将气体分子视为质点，并忽略其体积。
此外，麦克斯韦还假设气体分子间没有相对于其平均速度的内在速度趋势，即分子在各个方向上的速度是等概率分布的。
根据这些假设，我们可以得到麦克斯韦速度分布的数学表达式。
设气体分子的速度为v，麦克斯韦速度分布f(v)表示在速度范围v到v+dv 内的气体分子的概率密度。
根据麦克斯韦的推导，麦克斯韦速度分布可以表示为：f(v) = 4πv²(N/mπkT)^(3/2) * exp(-mv²/2kT)其中，N为气体分子数目，m为分子的质量，k为玻尔兹曼常数，T 为气体的绝对温度。
这个表达式可以解释为在速度v附近的各个方向上，单位速度范围内所含的分子数。
麦克斯韦速度分布的数学形式是一个关于速度的二次函数，在速度较低时概率密度逐渐增加，而在速度较高时概率密度逐渐降低。
这个分布函数的特点在于它不仅仅与气体分子的质量有关，还与气体的温度相关。
温度越高，麦克斯韦速度分布函数的峰值越低，峰值处对应的速度越高。
而在相同温度下，分子的质量越大，麦克斯韦速度分布函数的峰值越高，峰值处对应的速度越低。
麦克斯韦速度分布不仅仅可以用来描述气体分子的速度分布，还可以应用于解释气体分子的速度平均值、最概然速度、均方根速度等方面的问题。
例如，在给定温度下，气体分子的平均速度随着分子质量的增大而减小。
最概然速度是速度分布函数的峰值所对应的速度，它对应了气体分子的最有可能的速度值。
均方根速度则是速度分布曲线下方的面积跟速度相关的加权平均速度。
麦克斯韦速率分布
exp(
mv
2
) v dv
2
2kT
⑶ N个分子的气体处于平衡态，以容器为参考系速率在v ~ v+dv 间的分子占总分子数N的百分比（概率）
dN N f (v )dv 4 ( m 2 kT
3 )2
exp(
mv
2
2kT
) v dv 概率
2
2. 麦氏速率分布函数曲线： ⑴
但速率很大 或很小的分子数较少
N
( v ~ v v的分子数 )
则在总分子中分子速率介于
v ~ v+∆v 的分子的概率为：
N N
Pv v v
当∆v→0 时，即得分子速率分布的概率密度函数：
F (v ) dN N dv
相应地，分子速率介于v ~ v+dv的概率即为：
d Pv v d v F ( v ) d v
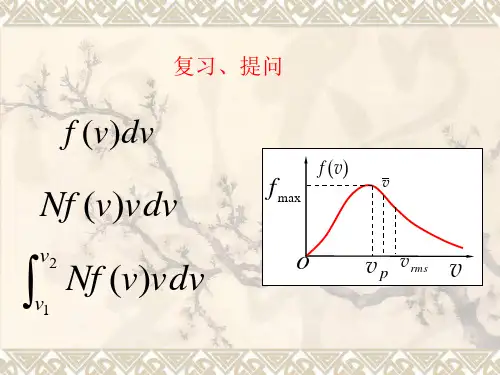
（三）最概然速率vp：
vp 2kT m
2 RT Mm
vrms
f (v )
v
2
3kT m
3 RT Mm
（四）三种速率之比：
v p : v : v rms 1 : 1 . 128 : 1 . 224
v
o
v p v v2
1. 前面讨论理想气体 和 P 时曾用到 vrms v
v rms v 1.085 误差 8.5%
2 RT Mm
vp
意义： 若把整个可能的速率范围分为许多等间隔的小区间， 则在最可几速率vp所在区间中分子数所占比率最大。
3. 称概率密度取极大值时的速率为 最概然速率vp，也称最可几速率
vp
vp
2.4麦克斯韦速度分布
以直角坐标表示的速度空间
●以速度分量vx、vy、vz为坐标轴，
以从原点向代表点所引矢量来表示分子 速度方向和大小的坐标称为速度空间。
●速度空间是人们想像中的空间坐标，所 描述的不是分子的空间位置，而是速度 的大小与方向。
。
二、速度空间中代表点的分布
• ●若把某一瞬时所有分子所对应的速度 矢量代表点都标在速度空间中，就构成 代表点在速度空间中的一种分布图形， 如图所示
•若要求出分子速度x方向分量小于某一数值的 分子数所占的比率，则可对上式积分
v x dN (v ) ux N (0 v x ) 1 2 x ( ) exp(u x )dux 0 0 N N
•引入误差函数erf(x),
erf ( x) (
2
) exp( x 2 )dx
mv x m 1/ 2 m 1/ 2 N( ) exp( )dv x ( ) 2kT 2kT 2kT
2 m vy m vz 2 m exp ) exp dvy ( dvz 2kT 2kT 2kT
到vz+dvz区间内 划出一个体积为dvxdvydvz的微分元，如图所示。 ●数出在这微分元中的代表点的数目 dN（vx、vy、vz）， 并把
f (v x , v y , v z ) dN(v x , v y , v z ) Ndvx dvy dvz
到vy +dvy ，vz
称为坐标为vx、vy、vz处的麦克斯韦速度分布概率密度， ●它表示在dvxdvydvz小体积元 中代表点的相对密集程度。 我们可以这样来求出 dN（vx 、vy 、vz ）
最后说明，由于麦克斯韦在导出麦克斯韦速 度分布律过程中没有考虑到气体分子间的相 互作用，故这一速度分布律一般适用于平衡 态的理想气体。
热学--麦克斯韦速度分布
p1 T1
p2 T2
热分子压差现象
n1 T2
n2 T1
热流逸现象
质量小的分子易于逸出小孔。这就为同位素分离提 供了一种十分有用的方法。 设容器中充满质量分别为m1和m2的两种分子所组成 的混合理想气体，其分子数密度分别为n1及n2。 若m1＜m2，则容器中m1分子减少的速率大于 m2分子 n1 减少的速率，从而使容器中的 n 2 逐步减小，说明 质量大的相对富度将增加。而另一容器中质量小的 同位素相对富度增加。
T=0 K时铜中自由电子平均速率
v 3 3 2E F vF 1.2 10 6 m s 1 4 4 me
§2.5 气体分子碰撞数及其应dt
dA o y vzdt vydt z vy
0
vz
单位体积内的分子数n ,单位面积为dA， 求单位时间内碰在单位面积上的总分子数。
2exp2221zyxidvktmvktmvfiii???二麦克斯韦速度分布三从速度分布导出速率分布二麦克斯韦速度分布三从速度分布导出速率分布ovxvyvzvdv2exp242232ktmvktmndvdvdvdnvddvvvddnzyxvv???dvvktmvktmdvvfndnv????22232exp24金属自由电子模型指出金属中的价电子是无相互作用的自由电子
三、从速度分布导出速率分布
dNv D(v) 4v 2 dv dNv m 3/ 2 mv D (v ) N( ) exp( ) dvx dvy dvz 2kT 2kT
2
vz
v o v
x
vy d v
dNv m 3/ 2 m v2 f (v)dv 4 ( ) exp( ) v 2 dv N 2kT 2kT
麦克斯韦速度分布定律
麦克斯韦速度分布定律麦克斯韦速度分布定律是研究理想气体分子速度分布的重要理论依据。
它是由苏格兰物理学家詹姆斯·麦克斯韦于19世纪中期提出的，对于理解气体分子的运动规律具有重要意义。
麦克斯韦速度分布定律描述了气体分子在给定温度下的速度分布特征，为热力学和统计物理领域的研究提供了极为宝贵的工具。
麦克斯韦速度分布定律的推导基于统计学和概率论的原理，它假设了分子之间的相互作用可以忽略不计。
在这个假设下，理想气体中各个分子的速度是相互独立的，并且服从正态分布。
这意味着，在给定温度下，气体分子的速度存在一个平均值和一个标准差，而速度的分布则呈现出钟形曲线。
根据麦克斯韦速度分布定律，气体分子的速度分布与温度有关，即温度越高，分子的平均速度越大。
具体来说，根据麦克斯韦速度分布定律，一个单原子理想气体的速度分布函数可以表示为：f(v) = 4π(μ/2πkT)^(3/2) * v^2 * exp(-μv^2 / 2kT)其中，f(v)表示速度分布函数，v表示分子速度，μ表示分子的质量，k表示玻尔兹曼常数，T表示温度。
从这个函数的表达式可以看出，速度分布函数是一个关于速度的概率密度函数，可以用来计算速度在某个范围内的概率。
对于正常的气体条件，速度的平均值与大多数分子的速度接近，而速度的标准差则反映了分子速度的分散程度。
麦克斯韦速度分布定律的应用范围非常广泛。
首先，它在热力学和统计物理中被广泛用于描述气体分子的运动和能量分布。
通过分析分子速度的分布特征，可以推导出气体的热力学性质，如压强、内能和热容等。
其次，麦克斯韦速度分布定律还在化学动力学研究中有着重要的应用。
通过对反应物分子的速度分布进行分析，可以预测反应速率和反应机理。
此外，该定律还可以应用于材料科学、天体物理学和等离子体物理学等领域。
尽管麦克斯韦速度分布定律是从理想气体模型出发推导得出的，但它在实际气体中的适用性相当广泛。
实际气体的分子间相互作用虽然不能完全忽略，但在适当条件下，可以将其近似看作理想气体，并利用麦克斯韦速度分布定律进行研究。
2.4 麦克斯韦速度分布律
v x v x dv x 在三维速度空间中， y v y dv y 内这一条件，表示所指的是这 v v v dv z z z
样一些分子，它们的速度矢量的端点都在一定体积元：速度空间， 体积元—微分元 dV dvx dvy dvz 数出这微分元中代表点的数目 dN( v x v y v z )
问题的提出：计算速度分量（速率）为某一定值，介于某一给 定范围内的分子数，即v或vx（vy，vz）的某一 给定范围内的分子 数。 1、相对于vp的速度分量分布的约化形式
具体算vx在0~ vx范围内的分子数 速度分量vx在vx ~ vx+d vx范围内的分子数
速度分量的相对速率
vx 令x v x vp dv x dN v
dN ( v x , v y , v z ) N
f ( v x , v y , v z )dvx dv y dvz
f ( v x , v y , vz )
dN( v x , v y , v z ) Ndvx dvy dvz
（2.31）
dN (v x ) 表示分子处于 N
v x v x dvx
N f ( v x）dvx f（v y）dv y f（v z）dvz
f ( v x , v y , v z )dvx dv y dvz
概率相乘法则：同时或依次发生的，互不相关（或相互 统计独立）事件发生的概率等于各个事件概率之乘积。 §2.4.2 麦克斯韦速度分布（Maxwell velocity distribution）
用速度分量表达： m f ( vk ) e 2kT
m( vx2 v y2 ) 2 kT
dvx dv y
麦克斯韦速度分布律公式
麦克斯韦速度分布律公式麦克斯韦速度分布律麦克斯韦速度分布律是统计物理学中描述理想气体速度分布的重要定律之一。
它描述了在给定温度下，气体分子速度的分布情况。
以下是与麦克斯韦速度分布律相关的公式和解释说明：麦克斯韦速度分布律公式1.麦克斯韦速度分布函数：f(v) = (m / (2 * π * k * T) )^(3/2) * 4 * π * v^2 * exp(-m*v^2 / (2 * k * T))其中，f(v)是速度的概率密度函数，m是分子的质量，k是玻尔兹曼常数，T是气体的温度，v是速度。
2.平均速度：<v> = ∫(v * f(v)) dv计算麦克斯韦速度分布函数与速度的乘积的积分，求得平均速度。
3.均方根速度：vrms = √(3 * k * T / m)均方根速度描述了气体中分子速度的大小，它是所有分子速度平方的平均值的平方根。
麦克斯韦速度分布律解释以下是对麦克斯韦速度分布律公式的解释说明和例子：1.麦克斯韦速度分布函数公式解释：麦克斯韦速度分布函数表示了在给定温度下，速度在不同取值上的概率密度。
函数中的指数项含有一个负号，指数的绝对值大小与速度的平方成正比，即速度越大，对应的指数项越小，概率越小。
这符合物质中分子速度的分布趋势，常见的速度大都集中在某个范围内。
2.平均速度解释：平均速度表示在给定温度下，所有可能速度的加权平均值。
将速度与麦克斯韦速度分布函数相乘后积分，可以得到平均速度。
这意味着在一个气体体系中，速度的概率分布决定了平均速度的大小。
3.均方根速度解释：均方根速度是速度分布的一种描述方式，它描述了速度的大小和分散程度。
均方根速度是气体中所有分子速度平方的平均值的平方根。
根据麦克斯韦速度分布律，均方根速度与温度呈正比，与分子质量的平方根成反比。
总结麦克斯韦速度分布律是描述气体速度分布的重要定律，通过麦克斯韦速度分布函数、平均速度和均方根速度等公式，我们可以计算在给定温度下，气体分子速度的分布情况。
麦克斯韦速率分布律.pptx
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度，
说明下式的物理意义：
(1)nf (v)dv
f (v) dN , n N
Ndv
V
nf (v)dv
dN V
表示单位体积内分布在速率区间 v 内v的 dv
分子数。
第4页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度， 说明下式的物理意义：
(2)Nf (v)dv
f (v) dN Ndv
Nf (v)dv dN
表示分布在速率区间 v v 内的dv分子数。
第5页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度，
说明下式的物理意义：
(3)n v2 f (v)dv
v1
f (v)
dN
,n
N
Ndv
V
n v2 f (v)dv N N N
把这些量值代入，即得
W v＝ 1 v p 50
N＝
N
4
99 100
2
e
99 100
2
1 50
1.66%
第19页/共20页
f (v ) p3
T1
T2
T1 T2 T3
温度越高，速率 大的分子数越多
T3
v v v O
p1 p 2 p3
v
第15页/共20页
气体的三种统计速率
同一温度下不同种气体速率分布比较
f (v)
m1
m1 m2 m3
m2
分子质量越小，速
率大的分子数越多
。
m3
O
v
第16页/共20页
麦克斯韦速度分布定律
麦克斯韦速度分布定律麦克斯韦速度分布定律是描述气体分子速度分布的统计规律之一，由19世纪末的苏格兰物理学家詹姆斯·麦克斯韦提出。
该定律在热力学和统计物理学中有着广泛的应用，能够揭示气体分子运动特征，对于理解气体动力学和热传导等现象具有重要意义。
根据麦克斯韦速度分布定律，理想气体分子的速度服从麦克斯韦-玻尔兹曼速度分布。
其概率密度函数为：f(v) = (m / (2πkT))^(3/2) * 4πv^2 * e^(-mv^2 / (2kT))其中，f(v)表示速度为v的分子的概率密度，m为分子质量，k为玻尔兹曼常数，T为气体温度。
该概率密度函数描述了气体分子速度的分布情况。
根据这一函数，可以得到气体分子不同速度下的概率密度，以及平均速度、平均速度的平方等相关参数。
麦克斯韦速度分布定律具体刻画了速度分布的趋势，从而为研究气体热力学性质提供了重要依据。
根据麦克斯韦速度分布定律可以得到以下几个重要结论：1. 峰值速度：麦克斯韦速度分布定律的概率密度函数在具体速度处取得最大值，即存在一个峰值速度。
这个峰值速度与气体的温度和质量有关，温度越高或质量越小，峰值速度越大。
2. 平均速度：根据麦克斯韦速度分布定律，可以计算出气体分子的平均速度。
平均速度与系统的温度有关，随着温度的升高，平均速度也增加。
3. 速度分散度：麦克斯韦速度分布定律还可以用来计算气体分子速度的分散度。
速度分散度可以通过计算速率最大值附近的速度范围来确定。
由于速度分散度对于描述气体的输运性质至关重要，因此，该定律在研究气体动力学和热学性质时经常被应用。
麦克斯韦速度分布定律是热力学和统计物理学中的重要模型，它将分子速度的概率分布与系统的热力学性质联系在一起。
通过该定律，我们可以更好地理解气体分子的运动规律，研究气体的输运性质和热传导现象。
同时，在工程和科学领域的应用中，麦克斯韦速度分布定律也为材料设计、能源开发和天文物理学等提供了重要指导。
麦克斯韦速度分布函数
麦克斯韦速度分布函数麦克斯韦速度分布函数是一种物理学中使用最广泛的分布函数，它可以用来描述物体的速度分布特征。
简言之，麦克斯韦速度分布函数的作用就是根据不同的物理现象，建立并预测不同物体的速度分布。
它是一种用于描述物理现象的统计分布，比如分子运动、分子电极面等。
麦克斯韦速度分布函数可以用来研究各种相关的物理现象，比如汽油喷射压力，和半导体晶体管的量子效应，二者两者都受到该速度分布函数的影响。
此外，该分布函数也可以用来描述动力学系统中的分子碰撞，以及分子的可能传播速度。
麦克斯韦速度分布函数的数学表达式为：f(v)=4πv^3/Nexp(-v^2/2u^2)，其中N是正则化常数，v是分子速度的模，u^2是有序温度的两倍。
对于一个特定的温度T，其中的N(T)可以作为一个函数表示，可以表示为：N(T)=∫-∞∞ f(v) dv = (2πmkT/h^2)^(3/2)，其中m是分子的质量，k是Boltzmann常数，h是Planck常数。
通过分析麦克斯韦速度分布函数，它具有以下几个特点：第一，分布函数的最大值位于 v=0，其最大值为 4πN/N = 4π。
第二，分布在整个速度空间中是对称的，即 f(v)=f(-v)。
第三，当 v>0，速度分布函数从 0性增加，当 v=√2u，函数极值点出现，即 f(√2u)=4πu^3/N。
第四，当 v>√2u，函数开始下降，当 v→∞，函数最终收敛于 0 。
麦克斯韦速度分布函数在热力学中有着重要的作用，对于理解热力学系统中分子碰撞、热迁移，以及热力学平衡状态的形成，都有着重要的指导意义。
因此，麦克斯韦速度分布函数在描述和研究热力学系统中有着重要的作用。
麦克斯韦速度分布函数可以用于计算分子运动的各种参数，比如分子运动的温度、平均速度、偏度系数以及平均能量的计算等。
此外，它也可以用来研究分子运动的统计性质，因此能够更准确地描述和识别不同系统中分子运动的特征。
综上所述，麦克斯韦速度分布函数在物理学中具有重要的意义，它可以用来描述物理现象，可以计算分子运动的各种参数，也可以用来研究热力学系统的相关物理性质，从而更好地描述物质的热动力特性。
分子动理学的平衡态理论
r 1
r 1
u2 2u u (u)2 u2 (u)2 0,
定义相对均方根偏差[：(u )2 ]1/2 [(u)2 ]1/ 2 (u)rms
u
u
u
6
相对均方根偏差表示了随机变量在平均值附近分散开分布 的程度，也称为涨落、散度或散差。
(5)、概率分布函数
飞镖
F(x)
分布曲线
7
少数分子无规律性
3、Maxwell速率分布本身是统计平均的结果，也会有涨落， 但是很少。Maxwell速率分布可适用于一切处于平衡态的宏 观容器中的理想气体。
4、v
v
f
(v) dv或v
vNi
N
v2 v2 f (v) dv
提供了一种思想方法。
18
§2.4 麦克斯韦速度分布
一、速度空间
vz
dvx
dvz
dvy v
cc
cc
c
6个自由度 t+ r = 3 + 3 = 6
31
定质心位置 需3个平动自由度
cc cc
c
y
转轴
x
z
每一点绕过c 点的轴转动 共有 3个转动自由度
也可以理解成物体 系对三个轴的旋转
先定转轴 2个自由度
再定每个质量元 在垂直轴的平面
内绕轴转的角度 1个自由度
32
例3 由 N 个独立的粒子组成的
大量分子的统计分布
8
§2.3 麦克斯韦速率分布
一、分子射线束实验
实验装置
接抽气泵
2
t l v
vl
Hg
金属蒸汽 狭 缝
l
显 示
屏
9
分子速率分布图 N /(Nv)
麦克斯韦速度分布律
分子的方均根速率： 分子的方均根速率：
v =
2
3kT = m
3 RT
µ
mv 3 = kT 导出。 导出。 也可由 ε t = 2 2
2
•分子的最概然速率：v P = 分子的最概然速率： 分子的最概然速率 •分子的平均速率： 分子的平均速率： 分子的平均速率
v =
2kT = m
8kT = πm
2 RT
∫
0
∞
f ( v )d v = 1
2. 麦克斯韦速率分布律 分子在速度空间分布 概率密度为 FM(v x , v y , v z )， 分子速率处于球壳内的概 率：
dN(v) 2 = 4πv dv ⋅ FM(v x , v y , v z ) N
速率分布函数可写成
dN (v ) 2 f M (v ) = = 4π v FM (v x , v y , v z ) Ndv
•推广到分子按动能的分布： 推广到分子按动能的分布： 推广到分子按动能的分布
dN (v x , v y , v z ) ∝ e
−
εk
kT
dv x dv y d v z
1 2 ε k = m (v 2 + v 2 + v z ) x y 2
动能，分子速度的函数。 动能，分子速度的函数。
dv x dv y dv z ε dN (v x , v y , v z ) − k 速度分布函数： 速度分布函数： (v x , v y , v z ) = F = C e kT Ndv xdv ydv z
vP = 2kT = m 2 RT
µ
8.5.3 平均速率 方均根速率 在温度为T 的平衡态下， 代表： 在温度为 的平衡态下，fM (v )dv 代表： 速率处 区间的分子数占分子总数的百分比。 于v到v+dv区间的分子数占分子总数的百分比。 到 区间的分子数占分子总数的百分比 在该状态下，物理量W(v)的统计平均值： 在该状态下，物理量 的统计平均值： 的统计平均值
麦克斯韦速率分布律
dN m 3 / 2 mv 2 / 2 kT 2 f ( v) 4 ( ) e v Ndv 2 π kT
23 ´ 当m 2 10 g , T 273k , V 800m / s
f (800) 10 什么含义
6
在800-800+dv速率区间，单位速 率区间分子数占总分子数之比
f (v ) d v
0 v0 2 av d v 0
0
1 3 av 0 3
3 a 3 v0
（2）设总分子数为N， 则
v
v 0
Nf (v ) d v N
2
v 0
f (v ) d v
v0 v 0
a 4 1 3 4 3 av d v v 0 ( 3 )v 0 v 0 4 v0 4 4
m 1.45 1.50 1.55 1.60 1.65 1.70 1.75 1.80 1.85 1.90 1.95
总人数1380 1.50-1.55m的人数130
30 25 20 15 10 5 0 25 26 26 26 27
1.51
1.52
1.53
1.54
1.55
1.56
50 40 30 20 10 0
N v d N v 0 N d Nv 0
i
N v 0
d Nv N
v 0
f (v ) d v
8kT 8RT 对麦氏速率分布经计算得： v πm π
v (v ) f (v ) d v
0
规律：任意v 的函数(v)对 全体分子的平均值都可以用 速率分布函数由上式求得：
麦克斯韦速率分布公式
麦克斯韦速率分布公式
给定一个具有一定温度的气体系统，每一个分子都具有不同的速率。
麦克斯韦速率分布公式描述的是在该温度下，不同速率的气体分子的相对
数量。
f(v) = 4π((m/2πkT)^3/2)(v^2)e^(-mv^2/2kT)
其中，f(v)表示速率为v的分子的相对数量密度。
m是气体分子的质量，k是玻尔兹曼常数，T是气体的温度。
这个公式是一个概率密度函数，表示速率为v的分子出现的概率。
整
个函数在速率轴上的曲线形状是一个钟形曲线，也称为高斯分布曲线或正
态分布曲线。
从麦克斯韦速率分布公式可以得到以下一些结论：
1.在给定温度下，速率较小的分子数量较多，速率较大的分子数量较少。
这是因为速率较小的分子相对较容易出现，其运动更容易受到其他分
子的影响。
2.曲线的峰值位置对应着最常见的分子速率，也就是平均速率。
这个
峰值位置随着温度的上升而向右移动，说明气体的平均速率会随着温度的
升高而增加。
3.曲线两侧的高速尾巴逐渐变低，说明高速分子的相对数量逐渐减少。
这是由于高速分子在相互碰撞的过程中更容易发生碰撞，从而损失了能量。
4.曲线的面积总和为1，表示了所有速率的分子的相对数量之和为1
总之，麦克斯韦速率分布公式是一种描述气体分子速率分布的数学模型，它提供了描述不同速率的气体分子在相同温度下的相对数量分布的一
个重要工具。
通过这个公式，我们可以更深入地理解气体分子的运动规律和能量分布。
麦克斯韦速度分布定律
麦克斯韦速度分布定律麦克斯韦速率分布是热学的难点，也是大家初识统计物理时容易感到头疼的知识点，一般而言，考试题会将麦克斯韦分布函数给出，这篇文章对函数形式的推导主要是想帮助同学们加深对麦克斯韦速率分布与速度分布的印象，同时充分理解它们的统计意义。
要想理解麦克斯韦分布，首先我们要理解什么是概率分布函数先看概率密度函数下面是一个典型的概率密度函数图像我们可以将概率密度函数解释为随机变量落在一个区间内的概率与这个区间大小的比值在区间大小趋向于0时的极限分母为f(x)dx，分子为dx概率密度函数满足归一化条件然后是概率分布函数可以看到，概率密度函数就是概率分布函数在某一点的导数重点来了我们讨论的，是连续型变量的概率分布函数，因为粒子的速度/速率是连续变化的连续型变量无法逐个列举就像测分子速率，我们测不出恰好为100m/s的分子数，我们只能测得一个速率范围内的分子数所以我们不能讲分子速率恰好处于100m/s的概率，只能讲分子速率介于某一范围内的概率有了对于概率分布函数的基本认识，我们可以求连续型变量的一些统计值x的某一函数F(x)的平均值为例对于a、c那么图a根据归一化条件A=1/2a对于图cA=1/a对于b则有而麦克斯韦速率分布函数，就建立在最基本的统计理论上比如麦克斯韦分布最关键的概念就是概率密度函数中的f(x)dx下面我们来推导这个f(v)dv的形式首先要推导的是麦克斯韦速度分布函数设三个方向上粒子速度分量为vx、vy、vz由于理想气体处于平衡态，根据气体动理论，有所以由于理想气体处于平衡态，各处气体分子数密度相同，粒子各方向运动概率相同，沿x、y、z轴运动相互独立两边同时取对数对Φ(v^2)求偏导移项，式子左边只留v^2的函数对vy、vz求导的结果形式相同由于vi的任意性，得到令常数为-1/β^2解微分方程得将f(vx)、f(vy)、f(vz)全部代入F(vx,vy,vz)得到速度分布函数的形式为现在我们来求β首先求速度的方均根前面的例题中已经给出了方均根的求法第二步的推导用到了速度空间的概念v到v+dv的速度空间∑dvxdvydvz=4πv^2dv方均根为3β^2/2根据气体动理论得到β^2=m/2kT所以麦克斯韦速度分布为由麦克斯韦速率分布函数，我们可以推出几个重要的速率平均速率结果是根号8kT/πm方均根速率根号3kT/m最概然速率为麦克斯韦速率分布函数取极大值时根号2kT/m至于这些速率的应用，那又是另外一个故事了麦克斯韦分布是热学的重点，希望大家能够真正弄清楚它的意义，而不仅仅是对公式的死记硬背参考资料[1]对麦克斯韦速率分布率的教学研究.石荣彦.江苏教育学院学报.2006.5.p61-p65[2]大学物理中如何讲解麦克斯韦速率分布函数.朱永忠.淮南矿业学院学报.1998.9.p63-p65[3]麦克斯韦速率分布函数的简单推导和讨论.高娟,汤永新,汪月琴.长春大学学报.2014.8.第24卷第8期。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
•
dN（vy）/N = f(vy)dvy • dN（vz）/N = f(vz)dvz 分别表示y及z方向速度分量的概率分布函
数。
●根据处于平衡态的气体的分子混沌性 假设，分子速度没有择优取向，故
f（vx）、f（vy）、f（vz）应具有相同形
• ●分子处于速度空问任一微小范围dvxdvydvz内
的概率是
• f（vx ，vy，vz）与dvxdvydvz的乘积。
§2.4.2 麦克斯韦速度分布 （Maxwell velocity distribution）
麦克斯韦最早用概率统计的方法导出了理想气 体分子的速度分布，这一分布可表示为
• f（vx ，vy，vz）dvxdvydvz=
以从原点向代表点所引矢量来表示分子 速度方向和大小的坐标称为速度空间。
●速度空间是人们想像中的空间坐标，所 描述的不是分子的空间位置，而是速度 的大小与方向。
。
二、速度空间中代表点的分布
• ●若把某一瞬时所有分子所对应的速度 矢量代表点都标在速度空间中，就构成 代表点在速度空间中的一种分布图形， 如图所示
2m kT 3/2ex p m (vx22 k vy 2T vz 2) dxd vyd vzv
•因为f（vx ，vy，vz)=
•
f(vx)dvxdvx·f(vy)dvy·f(vz)dvz
•麦克斯韦速度分布有
f(vi)div 2m kT 1/2ex pm 2ki2T v div
其中i 可分别代表x、y、z。
• ● vz任欲意求的分分子子速数度d的N(xv分x)量, 在vx 到vx+dvx内而vy、、 • 这就是速度空间中垂直于x 轴的无穷大薄平板中
的代表点数，显然可对vy、vz积分后求出：
d( v N x ) N ( v x ) f d x v f( v y ) d y v f( v z) d z
●把分子的速度矢量沿x、y、z方向的投影vx、 vy、vz作直角坐标图，
把所有分子速度矢量的起始点都平移到公共原 点O上。 ●在平移时，矢量的大小、方向都不变。 ●平移后，仅以矢量的箭头端点的点来表示这一 矢量，而把矢量符号抹去。 ●这样的点称为代表点。
如图中的P点所示。
以直角坐标表示的速度空间
●以速度分量vx、vy、vz为 就是所要求的概率
• ●因为vx ，vy，vz相互独立，故
•
dN（vx、vy、vz）/N
•
=f(vx)dvx·f(vy)dvy·f(vz)dvz
• ●显然，速度分布概率密度f（vx ，vy，vz） 是分子分别按速度的x、y、z方向分量分布的
概率密度f(vz)、f(vy)、f(vz)的乘积。
最后要问，分子速度分量处于
vx
到
vx+dvx，vy 到vy+dvy，vz 到vz+dvz范围内的
概率是多少？
•●只需在图中再作一
垂 直 于 vz 轴 的 、 厚 度 为dvz的无穷大薄平板
平板与柱体相交截得一体积为dvxdvydvz的小
立方体，计算出在小立方体中的代表点数
• dN（vx、vy、vz）
条中。
• ●因为分子落在垂直于dvx轴的平板内的概率 是f（vx）dvx，分子落在垂直于vy轴的平板内 的概率是f（vy）dvy。
• ●由相互独立的同时事件概率相乘法则可知，
• 分子落在方柱体内的概率为方柱体内代表点数
dN（vx，vy）与总分子数N的比值
•（
3
）
f(vx)dxv f(vy)dy v d( N v N x,vy)
式。
速度空间中一根截面积为dvx dvy的无穷长
的方条中的概率
（ 2 ） 进 一 步 问 ， 分 子 速 率 介 于 vx 到 vx+dvx，vy 到vy+dvy，而vz在任意的范围 内的分子数 dN（vx，vy）是多少？
●显然这些分子的代表点都落在一根平行
于vz轴、截面积为dvx dvy的无穷长的方
分量如何，只要速
度 x 分 量 在 vx 到 vx+dvx 范 围 内 ， 则
所有这些分子的代
表点都落在此很薄
的无穷 大平板中.
• ●若设此平板中代表点数为dN（vx）， 则dN（vx）/N 表示分子的速度处于vx 到vx+dvx而vy、vz为任意值范围内的概率。
• ●显然这一概率与板的厚度dvx成比例。 • ●并有dN（vx）/N = f(vx)dvx • 称分子x方向速度分量概率分布函数
2.4麦克斯韦速度分布
单击此处添加副标题
§2.4.1速度空间 • 一、速度矢量、速度空间中的代表点 • （1 ) 速度矢量 • ●要描述气体分子的速度大小和方向，
需引入速度矢量这一概念，
• 速度矢量的方向和大小恰与此瞬时该分 子速度的大小、方向一致。
• ●一个分子仅有一个速度矢量。
（1) 速度空间中的代表点
到vz+dvz区间内 划出一个体积为dvxdvydvz的微分元，如图所示。
● 数 出 在 这 微 分 元 中 的 代 表 点 的 数 目 dN（vx、vy、vz），
并把
f(vx,vy,vz)d N N (v d x xd ,v vv y yd ,vz v z)
称为坐标为vx、vy、vz处的麦克斯韦速度分布概率密度，
速度空间中代表点分布与靶板上靶点分布类似：
●前面已指出，在图2.2（a）中，靶点位于x 到 x+dx，y 到y+dy范围内的概率是以
f（x，y）dxdy来表示的，其中dxdy为这一区域 大小，f（x，y）是黑点分布的概率密度。
（1）速度空间中小立方体dvxdvydvz中的概率
●在三维速度空间中，在vx 到vx+dvx，vy 到vy+dvy，vz
●它表示在dvxdvydvz小体积元
中代表点的相对密集程度。
我们可以这样来求出
dN（vx、vy、vz）
（2）速度空间中厚为dvx 无限大平板中的概率
首先问，在N个分子中速度 x分量落在vx 到
vx+dvx范围内而vy ,vz 在任意的范围内的分
子数 dN（vx）是多少？, 在速度空间中划出一个垂直于vx轴的厚度为 dvx的无穷大平板，如图所示. ● 不 管 速 度 的 y、z
N (2 m k)1 T /2ex 2 m k p x)T d ( v xv (2 m k)1 T /2