实验报告:异方差模型的检验和处理
实验三 异方差性的检验及修正
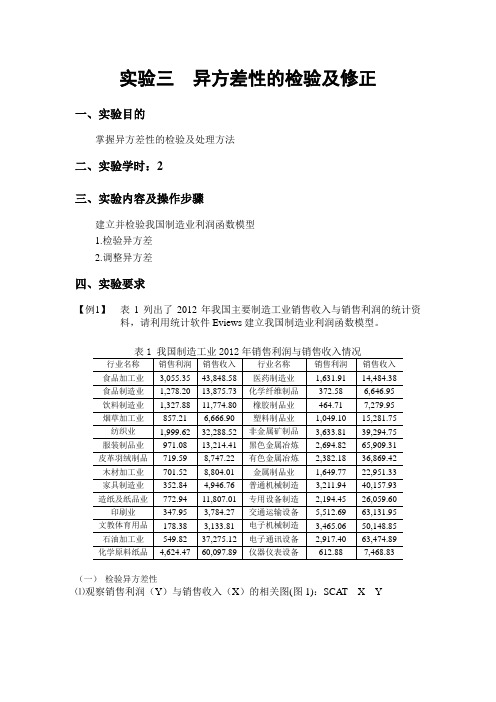
实验三异方差性的检验及修正一、实验目的掌握异方差性的检验及处理方法二、实验学时:2三、实验内容及操作步骤建立并检验我国制造业利润函数模型1.检验异方差2.调整异方差四、实验要求【例1】表1列出了2012年我国主要制造工业销售收入与销售利润的统计资料,请利用统计软件Eviews建立我国制造业利润函数模型。
(一)检验异方差性⑴观察销售利润(Y)与销售收入(X)的相关图(图1):SCAT X Y图1 我国制造工业销售利润与销售收入相关图从图中可以看出,随着销售收入的增加,销售利润的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
⑵残差分析首先将数据排序(命令格式为:SORT 解释变量),然后建立回归方程。
在方程窗口中点击Resids按钮就可以得到模型的残差分布图(或建立方程后在Eviews工作文件窗口中点击resid对象来观察)。
图2 我国制造业销售利润回归模型残差分布图2显示回归方程的残差分布有明显的扩大趋势,即表明存在异方差性。
⒉Goldfeld-Quant检验⑴将样本按解释变量排序(SORT X)并分成两部分(分别有1到10共11个样本合19到28共10个样本)⑵利用样本1建立回归模型1(回归结果如图3),其残差平方和为216231.7。
SMPL 1 10LS Y C X图3 样本1回归结果⑶利用样本2建立回归模型2(回归结果如图4),其残差平方和为63769.67。
SMPL 19 28 LS Y C X图4 样本2回归结果⑷计算F 统计量:12/RSS RSS F =11501152/216231.7=53.19,21RSS RSS 和分别是模型1和模型2的残差平方和。
取05.0=α时,查F 分布表得44.3)1110,1110(05.0=----F ,而44.319.5305.0=>=F F ,所以存在异方差性 ⒊White 检验⑴建立回归模型:LS Y C X ,回归结果如图5。
实验四异方差性的检验与处理

实验四异方差性的检验与处理集团标准化工作小组 [Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]实验四 异方差性的检验及处理(2学时)一、实验目的(1)、掌握异方差检验的基本方法; (2)、掌握异方差的处理方法。
二、实验学时:2学时 三、实验要求(1)掌握用MATLAB 软件实现异方差的检验和处理; (2)掌握异方差的检验和处理的基本步骤。
四、实验原理1、异方差检验的常用方法(1) 用X-Y 的散点图进行判断(2). 22ˆ(,)(,)e x e y 或的图形 ,),x )i i y i i ((e 或(e 的图形)(3) 等级相关系数法(又称Spearman 检验)是一种应用较广的方法,既可以用于大样本,也可与小样本。
检验的三个步骤 ① ˆt t y y=-i e②|i x i i 将e 取绝对值,并把|e 和按递增或递减次序排序,计算Spearman 系数rs ,其中:21ni i d =∑s 26r =1-n(n -1)③ 做等级相关系数的显着性检验。
n>8时,/2(2),t t n α>-反之,若||i i e x 说明与之间存在系统关系,异方差问题存在。
(4) 帕克(Park)检验帕克检验常用的函数形式:若在统计上是显着的,表明存在异方差性。
2、异方差性的处理方法: 加权最小二乘法 如果在检验过程中已经知道:222()()()i i i ji u Var u E u f x σσ===则将原模型变形为:121(i i p pi iy x x uf xβββ=+⋅++⋅+在该模型中:即满足同方差性。
于是可以用OLS估计其参数,得到关于参数12,,,pβββ的无偏、有效估计量。
五、实验举例例101i i iy x u=++若用线性模型,研究不同收入家庭的消费情况,试问原数据有无异方差性如果存在异方差性,应如何处理解:(一)编写程序如下:(1)等级相关系数法(详见文件)%%%%%%%%%%%%%%% 用等级相关系数法来检验异方差性 %%%%%%%%[data,head]=xlsread('');x=data(:,1); %提取第一列数据,即可支配收入xy=data(:,2); %提取第二列数据,即居民消费支出yplot(x,y,'k.'); % 画x和y的散点图xlabel('可支配收入x(千元)') % 对x轴加标签ylabel('居民消费支出y(千元)') % 对y轴加标签%%%%%%%% 调用regres函数进行一元线性回归 %%%%%%%%%%%%xdata=[ones(size(x,1),1),x]; %在x矩阵最左边加一列1,为线性回归做准备[b,bint,r,rint,s]=regress(y,xdata);yhat=xdata*b; %计算估计值y% 定义元胞数组,以元胞数组形式显示系数的估计值和估计值的95%置信区间head1={'系数的估计值','估计值的95%置信下限','估计值的95%置信上限'};[head1;num2cell([b,bint])]% 定义元胞数组,以元胞数组形式显示y的真实值,y的估计值,残差和残差的95%置信区间head2={'y的真实值','y的估计值','残差','残差的95%置信下限','残差的95%置信上限'};[head2;num2cell([y,yhat,r,rint])]% 定义元胞数组,以元胞数组形式显示判定系数,F统计量的观测值,检验的P值和误差方差的估计值head3={'判定系数','F统计量的观测值','检验的P值','误差方差的估计值'};[head3;num2cell(s)]%%%%%%%%%%%%% 残差分析 %%%%%%%%%%%%%%%%%%figure;rcoplot(r,rint) % 按顺序画出各组观测值对应的残差和残差的置信区间%%% 画估计值yhat与残差r的散点图figure;plot(yhat,r,'k.') % 画散点图xlabel('估计值yhat') % 对x轴加标签ylabel('残差r') % 对y轴加标签%%%%%%%%%%%% 调用corr函数计算皮尔曼等级相关系数res=abs(r); % 对残差r取绝对值[rs,p]=corr(x,res,'type','spearman')disp('其中rs为皮尔曼等级相关系数,p为p值');(2)帕克(park)检验法(详见文件)%%%%%%%%%%%%%%% 用帕克(park)检验法来检验异方差性 %%%%%%%[data,head]=xlsread(''); %导入数据x=data(:,1);y=data(:,2);%%%%%% 调用regstats函数进行一元线性回归,linear表带有常数项的线性模型,r表残差ST=regstats(y,x,'linear',{'yhat','r','standres'});scatter(x,.^2) % 画x与残差平方的散点图xlabel('可支配收入(x)') % 对x轴加标签ylabel('残差的平方') %对y轴加标签%%%%%%% 对原数据x和残差平方r^2取对数,并对log(x)和log(r^2)进行一元线性回归ST1=regstats(log(.^2),log(x),'linear',{'r','beta','tstat','fstat'})% 输出参数的估计值% 输出回归系数t检验的P值% 输出回归模型显着性检验的P值(3)加权最小二乘法(详见文件)%%%%%%%%%%% 调用robustfit函数作稳健回归 %%%%%%%%%%%%[data,head]=xlsread(''); % 导入数据x=data(:,1);y=data(:,2);% 调用robustfit函数作稳健回归,返回系数的估计值b和相关统计量stats[b,stats]=robustfit(x,y) %调用函数作稳健回归% 输出模型检验的P值%%% 绘制残差和权重的散点图 %%%%%%%plot,,'o') %绘制残差和权重的散点图xlabel('残差')ylabel('权重'(二)实验结果与分析:第一步::用OLS方法估计参数,并保留残差(1)散点图图可支配收入(x)居民消费支出(y)散点图因每个可支配收入x的值,都有5个居民消费收入y与之对应,所以上述散点图呈现此形状。
实验二、异方差检验与消除实验(异方差检验及异方差的消除的分析过程)

实验二、异方差检验与消除实验(异方差检验及异方差的消除的分析过程)
(1)以上四个对REV回归得:
常数项不显著,去掉常数项再进行回归得结果为:
(2)对REV 2回归得结果为:
常数项不显著,去掉常数项再进行回归得结果为:
从F检验来为来看整个模型不显著
从四个回归的结果看,回归(2)(4)不显著,(1)(3)显著,比较(1)(3)不带常数项的回归,还是选择后一个,方程为:
ABS RESID
()
即异方差的形式为:
2262.153117979i i REV σ==
也即异方差的形式为:
22i i REV σσ=
就把这个形式确定为异方差的形式
要求二、做对ZJ 和GDP1回归的Glejser 检验。
异方差实验报告步骤(3篇)

第1篇一、实验目的1. 掌握异方差性的基本概念和检验方法。
2. 学会运用统计软件进行异方差的检验和修正。
3. 提高对计量经济学模型中异方差性处理能力的实践应用。
二、实验原理1. 异方差性:在回归分析中,若回归模型的误差项(残差)的方差随着自变量或因变量的取值而变化,则称模型存在异方差性。
2. 异方差性的检验方法:图形检验、统计检验(如F检验、Breusch-Pagan检验、White检验等)。
3. 异方差性的修正方法:加权最小二乘法(WLS)、广义最小二乘法(GLS)等。
三、实验步骤1. 数据准备1. 收集实验所需数据,确保数据质量和完整性。
2. 对数据进行初步处理,如剔除异常值、缺失值等。
2. 模型设定1. 根据研究问题,选择合适的回归模型。
2. 利用统计软件(如Eviews、Stata等)进行初步的回归分析。
3. 异方差性检验1. 图形检验:绘制散点图,观察残差与自变量或因变量的关系,初步判断是否存在异方差性。
2. 统计检验:- F检验:检验回归系数的显著性。
- Breusch-Pagan检验:检验残差平方和与自变量或因变量的关系。
- White检验:检验残差平方和与自变量或因变量的多项式关系。
4. 异方差性修正1. 若检验结果表明存在异方差性,则需对模型进行修正。
2. 选择合适的修正方法:- 加权最小二乘法(WLS):根据残差平方与自变量或因变量的关系,计算权重,加权最小二乘法进行回归分析。
- 广义最小二乘法(GLS):根据残差平方与自变量或因变量的关系,选择合适的方差结构,广义最小二乘法进行回归分析。
5. 结果分析1. 对修正后的模型进行回归分析,观察回归系数的显著性、拟合优度等指标。
2. 对实验结果进行分析,解释实验现象,验证研究假设。
6. 实验报告撰写1. 撰写实验报告,包括以下内容:- 实验目的- 实验原理- 实验步骤- 实验结果- 分析与讨论- 结论2. 实验报告应结构清晰、逻辑严谨、语言简洁。
实验异方差模型的检验和处理学生实验报告

4.703427
Durbin-Watson stat
1.930056
Prob(F-statistic)
0.018458
模型【3】
Heteroskedasticity Test: White
F-statistic
14.65680
Prob. F(1,16)
0.0015
Obs*R-squared
Prob.
Y
-0.100666
0.093257
-1.079451
0.3297
C
9534.708
1265.147
7.536443
0.0007
R-squared
0.188998
Mean dependent var
8243.949
Adjusted R-squared
0.026798
S.D. dependent var
19.56939
Log likelihood
-76.19814
Hannan-Quinn criter.
19.41558
F-statistic
5.587862
Durbin-Watson stat
0.656404
Prob(F-statistic)
0.055988
(请对得到的图表进行处理,以上在一页内)
3.White检验法
实验报告
课程名称:计量经济学
实验项目:实验五异方差模型的
检验和处理
实验类型:综合性□设计性□验证性
专业班别:
姓名:
学号:
实验课室:
指导教师:石立
实验日期:
广东商学院华商学院教务处制
EViews计量经济学实验报告异方差的诊断及修正
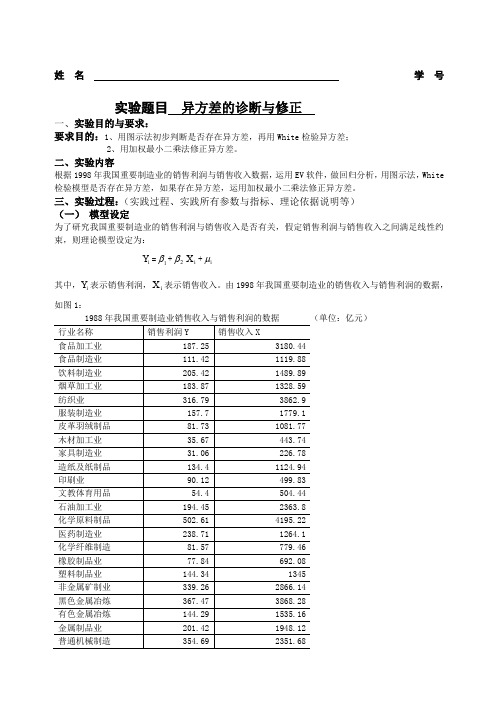
姓名 学号实验题目 异方差的诊断与修正一、实验目的与要求:要求目的:1、用图示法初步判断是否存在异方差,再用White 检验异方差;2、用加权最小二乘法修正异方差。
二、实验内容根据1998年我国重要制造业的销售利润与销售收入数据,运用EV 软件,做回归分析,用图示法,White 检验模型是否存在异方差,如果存在异方差,运用加权最小二乘法修正异方差。
三、实验过程:(实践过程、实践所有参数与指标、理论依据说明等) (一) 模型设定为了研究我国重要制造业的销售利润与销售收入是否有关,假定销售利润与销售收入之间满足线性约束,则理论模型设定为:i Y =1β+2βi X +i μ其中,i Y 表示销售利润,i X 表示销售收入。
由1998年我国重要制造业的销售收入与销售利润的数据,如图1:1988年我国重要制造业销售收入与销售利润的数据 (单位:亿元)Dependent Variable: YMethod: Least Squares Date: 10/19/05 Time: 15:27 Sample: 1 28Included observations: 28Variable Coefficient Std. Error t-Statistic Prob.??C 12.03564 19.517790.6166500.5428 X0.1043930.00844112.366700.0000R-squared0.854696 ????Mean dependent var 213.4650Adjusted R-squared 0.849107 ????S.D. dependent var 146.4895 S.E. of regression 56.90368 ????Akaike info criterion 10.98935 Sum squared resid 84188.74 ????Schwarz criterion 11.08450 Log likelihood -151.8508 ????F-statistic 152.9353 Durbin-Watson stat1.212795 ????Prob(F-statistic)0.000000估计结果为: iY ˆ = 12.03564 + 0.104393i X (19.51779) (0.008441) t=(0.616650) (12.36670)2R =0.854696 2R =0.849107 S.E.=56.89947 DW=1.212859 F=152.9353这说明在其他因素不变的情况下,销售收入每增长1元,销售利润平均增长0.104393元。
异方差性的检验及处理方法
图2显示回归方程的残差分布有明显的扩大趋势,即表明存在异方差性。
⒉Goldfeld-Quant检验
⑴将样本按解释变量排序(SORT X)并分成两部分(分别有1到10共11个样本合19到28共10个样本)
⑵利用样本1建立回归模型1(回归结果如图3),其残差平方和为2579.587。
【实验步骤】
【例1】表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料,请利用统计软件Eviews建立我国制造业利润函数模型。
表1 我国制造工业1998年销售利润与销售收入情况
行业名称
销售利润
销售收入
行业名称
销售利润
销售收入
食品加工业
187.25
3180.44
医药制造业
238.71
1264.1
SMPL 1 10
LS Y C X
图3样本1回归结果
⑶利用样本2建立回归模型2(回归结果如图4),其残差平方和为63769.67。
SMPL 19 28
LS Y C X
图4样本2回归结果
⑷计算F统计量: =63769.67/2579.59=24.72, 分别是模型1和模型2的残差平方和。
取 时,查F分布表得 ,而 ,所以存在异方差性
食品制造业
111.42
1119.88
化学纤维制品
81.57
779.46
饮料制造业
205.42
1489.89
橡胶制品业
77.84
692.08
烟草加工业
183.87
1328.59
塑料制品业
144.34
1345
纺织业
316.79
异方差计量实验报告(3篇)
第1篇一、实验目的本实验旨在通过实际操作,验证计量经济学中异方差性的存在,并掌握相应的检验和修正方法。
通过实验,加深对异方差性概念的理解,提高在实际应用中识别和处理异方差问题的能力。
二、实验内容1. 数据来源与处理- 数据来源:本实验使用某地区某年度的居民消费支出数据,包括居民可支配收入和消费性支出两个变量。
- 数据处理:将原始数据进行整理,剔除异常值,并对数据进行对数化处理,以降低异方差性的影响。
2. 模型设定与估计- 模型设定:根据理论分析,设定居民消费支出与可支配收入之间的线性关系模型为:\[ Y = \beta_0 + \beta_1X + \epsilon \]其中,\( Y \) 为居民消费支出,\( X \) 为可支配收入,\( \beta_0 \)和 \( \beta_1 \) 为模型参数,\( \epsilon \) 为随机误差项。
- 模型估计:采用最小二乘法(OLS)对模型进行估计,得到模型参数的估计值。
3. 异方差性检验- 检验方法:采用以下方法检验模型是否存在异方差性:- 观察法:观察残差图,若残差图呈现出明显的曲线关系,则可能存在异方差性。
- Goldfeld-Quandt 检验:通过分组检验残差平方与解释变量之间的关系,判断是否存在异方差性。
- White 检验:采用 White 检验对模型进行异方差性检验,得到统计量值和p 值。
- 检验结果:根据检验结果,判断模型是否存在异方差性。
4. 异方差性修正- 修正方法:若检验结果表明模型存在异方差性,则采用以下方法进行修正:- 加权最小二乘法(WLS):对模型进行加权最小二乘法估计,以降低异方差性的影响。
- 拉格朗日乘数法(LM):采用 LM 检验对模型进行修正,得到修正后的模型参数估计值。
- 修正结果:根据修正结果,比较修正前后模型参数估计值的变化,并分析修正效果。
三、实验结果与分析1. 模型估计结果- 根据最小二乘法估计,得到模型参数的估计值如下:\[ \beta_0 = 1000, \beta_1 = 0.5 \]- 模型拟合优度为 0.8,说明模型对数据的拟合程度较好。
计量经济学--异方差的检验及修正
经济计量分析实验报告一、实验项目异方差的检验及修正二、实验日期2015.12.06三、实验目的对于国内旅游总花费的有关影响因素建立多元线性回归模型,对变量进行多重共线性的检验及修正后,进行异方差的检验和补救。
四、实验内容建立模型,对模型进行参数估计,对样本回归函数进行统计检验,以判定估计的可靠程度,包括拟合优度检验、方程总体线性的显著性检验、变量的显著性检验,以及参数的置信区间估计。
检验变量是否具有多重共线性并修正。
检验是否存在异方差并补救。
五、实验步骤1、建立模型。
以国内旅游总花费Y 作为被解释变量,以年底总人口表示人口增长水平,以旅行社数量表示旅行社的发展情况,以城市公共交通运营数表示城市公共交通运行状况,以城乡居民储蓄存款年末增加值表示城乡居民储蓄存款增长水平。
2、模型设定为:t t t t t μβββββ+X +X +X +X +=Y 443322110t 其中:t Y — 国内旅游总花费(亿元) t 1X — 年底总人口(万人) t 2X — 旅行社数量(个) t 3X — 城市公共交通运营数(辆)t 4X — 城乡居民储蓄存款年末增加值(亿元)3、对模型进行多重共线性检验。
4、检验异方差是否存在。
六、实验结果(一)、消除多重共线性之后的模型多元线性回归模型估计结果如下:4321000779.0053329.0151924.0720076.0-99.81113ˆX +X +X +X =Y i SE=(26581.73) (0.230790) (0.108223) (0.013834) (0.020502) t =(3.051494) (-3.120046) (1.403805) ( 3.854988) (0.038020)R2=0.969693R2=0.957571F=79.98987(1)拟合优度检验:可决系数R 2=0.969693较高,修正的可决系数R 2=0.957571也较高,表明模型拟合较好。
spss实验--异方差性的检验及处理
实验四 异方差性的检验及处理(2学时)一、实验目的(1)、掌握异方差检验的基本方法; (2)、掌握异方差的处理方法。
二、实验学时:2学时三、实验要求(1)掌握用SPSS 软件实现异方差的检验和处理; (2)掌握异方差的检验和处理的基本步骤。
四、实验原理1、异方差检验的常用方法 (1) 用X-Y 的散点图进行判断(2).22ˆ(,)(,)e x e y 或的图形 ,),x )i i y i i ((e 或(e 的图形)(3).等级相关系数法(又称Spearman 检验)是一种应用较广的方法,既可以用于大样本,也可与小样本。
:i u 0原假设H 是等方差的;:i u 0备择假设H 是异方差; 检验的三个步骤 ①ˆt t y y =- i e②|i x i i 将e 取绝对值,并把|e 和按递增或递减次序排序,计算Spearman 系数rs ,其中:21ni i d =∑s 26r =1-n(n -1)|i x i i 其中, n 为样本容量d 为|e 和的等级的差数。
③ 做等级相关系数的显著性检验。
n>8时,(2)t t n =-0当H 成立时,/2(2),t t n α≤-若认为异方差性问题不存在;/2(2),t t n α>-反之,若||i i e x 说明与之间存在系统关系,异方差问题存在。
(4) 帕克(Park)检验帕克检验常用的函数形式:若α在统计上是显著的,表明存在异方差性。
2、异方差检验的处理方法: 加权最小二乘法如果在检验过程中已经知道:222()()()i i i ji u Var u E u f x σσ===则将原模型变形为:121i i p pi iy x x u βββ=⋅⋅++⋅+ 在该模型中:2211)()()()()i i ji u u ji jiVar u Var u f x f x f x σσ===即满足同方差性。
于是可以用OLS 估计其参数,得到关于参数12,,,p βββ 的无偏、有效估计量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告:异方差模型的
检验和处理
The Standardization Office was revised on the afternoon of December 13, 2020
实验实训报告
课程名称:计量经济学实验
开课学期:2012-2013学年第一学期
开课系(部):经济系
开课实验(训)室:数量经济分析实验室学生姓名:
专业班级:
学号:
重庆工商大学融智学院教务处制
实验题目
实验概述
【实验(训)目的及要求】
通过本次实验,使学生掌握异方差模型的检验方法及校正方法。
其中,检验方法主要掌握图形法检验、怀特检验;校正方法主要掌握加权最小二乘法、White校正法。
【实验(训)原理】
对于不同的样本点,随机误差项的方差不再是常数,而互不相同,则认为出现了异方差性。
异方差的实质表现为随机误差项的方差随着解释变量(引起异方差的解释变量)观测值的变化而变化。
对于出现异方差的原模型主要采用校正其异方差,再对校正后的模型采用普通最小二乘法估计。
实验内容
【实验(训)方案设计】
1、图形法检验:(1)回归分析;(2)得到残差趋势图和残差散点图;(3)分析异方差。
2、使用White检验异方差:(1)回归分析;(2)得到White检验统计量及伴随概率;(3)根据结果判断分析异方差的存在性。
3、在发现存在异方差的基础上,进行异方差的处理:
(1)使用加权最小二乘法校正异方差:①输入回归方程;②在Option中选择加权最小二乘法,并输入权重序列名称;③得到校正后的结果。
(2)使用White校正法解决异方差:①输入回归方程;②在Option中选择White校正;③得到校正后的结果。
【实验(训)过程】(实验(训)步骤、记录、数据、分析)
实验背景
本例用的是四川省2000年各地市州的医疗机构数和人口数。
为了给制定医疗机构的规划提供依据,分析比较医疗机构(Y,单位:个)与人口数量(X,单
位:万人)的关系,建立卫生医疗机构数与人口数的回归模型。
假定医疗机构数与人口数之间满足线性约束,则理论模型设定为
其中,i Y 表示卫生医疗机构数,i X 表示人口数。
【实验(训)过程】(实验(训)步骤、记录、数据、分析)
1、根据实验数据的相关信息建立Workfile ;
在菜单中依次点击File\New\Workfile,在出现的对话框
“Workfilerange ”中选择数据频率。
因为样本数据分析四川省2000年各地市州的医疗机构数和人口数间的关系,属于截面数据,因此,在数据频率选项中选择“Unstructured/Undated ”选项。
在“Datarange ”的“Observations ”中输入21。
2、导入数据;
在菜单栏中选择“Quick\EmptyGroup ”,将X 、Y 的数据从Excel 导入,并将这两个序列的名称分别改为“X ”、“Y ”。
或者在EViews 命令窗口中直接输入“dataXY ”,在弹出的编辑框中将这两个序列的数据从Excel 中复制过来。
3、参数估计;
1) 写出样本回归方程:
()()
t=()()
2)对回归结果的拟合优度及回归系数经济意义进行解释:
上述回归模型解释变量的估计系数表示:人口数每增加1万人,平均说来将增加医疗机构数个。
R 2=,表明医疗机构数变动的%可由人口数量的变化来解释。
上述模型采用截面数据,估计所得的模型可能存在异方差。
4、异方差的诊断:
异方差主要来源于截面数据,通过判断随机误差项的方差与解释变量是否存在某种函数关系进行判断。
由于随机误差项的方差一般未知,通常将残差项的平方作为随机误差项方差的近似估计,判断残差项的平方是否与解释变量存在某种函数关系。
1)图形检验法:2~i i X e —
结果诊断:从图中可以看出,随着人口数量的增加,2~i e 呈递增趋势,表明随机误差项存在递增型异方差。
2)White 检验法(原假设:模型不存在异方差)
(以二元为例:构造如下辅助回归模型:
i i i i i i i i X X a X a X a X a X a a e ε++++++=214224213221102~ 怀特检验的实质,就是检验上述辅助回归模型中的所有参数(常数项除外)是否显着为零。
当原假设成立时,辅助回归的检验统计量
WT g n R g 22()~() χ=⨯。
给定显着性水平α,查表可得临界值。
如果
WT g nR g 22()()αχ=>,则拒绝原模型不存在异方差的原假设;否则接受原假设。
)
检验法的最终结果:
b.结果诊断(05.0=α):
从上表可以看出,0748.182
=nR ,由White 检验知,当05.0=α,查2χ分布表,得临界值9915.5)2(2
05.0=χ,比较计算的2χ统计量与临界值,因为
0748.182=nR >9915
.5)2(205.0=χ,所以拒绝原假设(也可根据p 值进行判断)。
给定显着性水平%5=a ,则在的显着性水平下,White 检验的伴随概率p=<%5=a ,拒绝原模型不存在异方差的原假设,说明模型存在异方差。
5、异方差的处理:
1)阐述加权最小二乘法的基本原理:
加权最小二乘法是对原模型加权,使之变成一个新的不存在异方差性的模型,然后采用OLS 估计其参数。
2)报告加权最小二乘法的修正结果并检验是否消除了异方差。
从11X |e|i 、中选择效果较好的权数,并使用该权数对原模型进行加权以消除异方差,并对消除异方差的模型使用OLS 方法进行估计。
a.修正后的模型:^
316.560 4.442||||||i i i i i Y X e e e =-+ ()()
t=()()
b.修正后模型的White 检验结果如下表所示:
c.进行诊断(05.0=α):
上表最后一行的结果就是怀特检验统计量值及伴随概率。
给定显着性水平0.05a =,则在的显着性水平下,White 检验的伴随概率p=>05.0=α,不能拒绝原模型不存在异方差的原假设,说明修正后的模型不存在异方差。
d.修正后的模型可变为:
e.回归系数的经济含义:
上述回归模型解释变量的估计系数表示:人口数每增加1万人,平均说来将增加医疗机构数大约增加4个。
3)报告White 异方差校正后的修正结果。
采用White 异方差校正只是修正普通最小二乘法所得模型回归系数的标准误(在EquationEstimation 窗口输入ycx ;在Option 中选择
“heteroskedasticity ”,并选择默认的White 选项)
a.校正后的模型最终结果为:
()()
t=()()
b.修正前后回归系数的标准误有何变动:
对照没有校正异方差的估计结果可知,解释变量的回归系数校正后标准误比OLS 估计的结果有所增大,这表明原模型OLS 估计结果低估了回归系数标准差。
指导教师评语及成绩:
成绩:指导教师签名:
批阅日期:。
