(江苏专用)202x版高考数学大一轮复习第五章数列 4 第4讲数列求和文

合集下载

高考数学文优化方案一轮复习课件第5第四数列求和苏教江苏专用

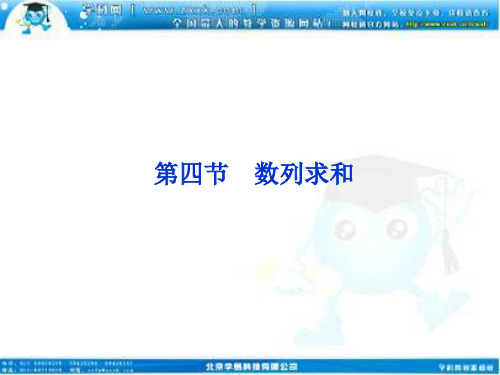
(2)因为 an＝2n＋1，所以 a2n－1＝4n(n＋1)，因此 bn＝4nn1＋1＝14(n1－n＋ 1 1)．故 Tn＝b1＋b2＋…＋bn ＝14(1－12＋12－13＋…＋n1－n＋ 1 1) ＝14(1－n＋ 1 1)＝4nn＋1. 所以数列{bn}的前 n 项和 Tn＝4nn＋1.
{Tn}中的 T1，Tm，Tn 成等比数列．
方法感悟
方法技巧
1．求和问题可以利用等差、等比数列的前n项和公式解决，在具体问题中，既要善于从数列的通项入手观察数列的特点与变化规律，又要注意项数． 2．非等差(比)的特殊数列求和题通常的解题思路是： (1)设法转化为等差数列或等比数列，这一思想方法往往通过通项分解或错位相消来完成．
这是推导等差数列的前n项和公式时所用的方法，就是将一个数列倒过来排列，再把它与原数列相加，就可以得到n个(a1＋an)，其最简单的形式为：若数列{an}中有a1＋an ＝a2＋an－1＝a3＋an－2＝…，就可以用此方法求和．
例1 设函数 y＝f(x)的定义域为 R，其图
象关于点(12，12)成中心对称，令 an＝f(nk)， (n∈N*，n≥2)，k＝1,2,3，…，n－1，…，求数列{an}的前(n－1)项的和．【思路分析】图象关于(12，12)成中心对称，
＝2nn＋1.
(2)由(1)可知，Tn＝2nn＋1，
所以 T1＝13，Tm＝2mm＋1，
若 T1，Tm，Tn 成等比数列，则(2mm＋1)2＝13
(2nn＋1)，即4m2＋m42m＋1＝6nn＋3. 可得n3＝－2m2＋m24m＋1，
所以－2m2＋4m＋1>0，从而：1－ 26<m<1＋ 26，又 m∈N*，且 m>1，所以 m＝2，此时 n＝12. 故可知：当且仅当 m＝2，n＝12 时，数列

2024届苏教版高考数学一轮复习数列求和及综合应用课件

=

+
=2,所以

=2.
所以 a1,a3,a5,…成等比数列;a2,a4,a6,…成等比数列,
所以 S2 018=a1+a2+a3+a4+a5+a6+…+a2 017+a2 018
=(a1+a3+a5+…+a2 017)+(a2+a4+a6+…+a2 018)
=
-

-
+
(-
A.

B.

C.

D.

解析:bn= =

=

=

-

++ (+)(+) + +
选 B.
B )

,前 10 项和为 - + - +…+ - = - = .故
4.数列{an}的前n项和为Sn,已知Sn=1-2+3-4+…+(-1)n-1·n,则S17=
a2a3=8.
(1)求数列{an}的通项公式;
解:(1)由题设知 a1a4=a2a3=8,
又 a1+a4=9,解得
= , = ,
或
(舍去).
=
=
3
设等比数列{an}的公比为 q,由 a4=a1q 得 q=2,
n-1
n-1
故 an=a1q =2 ,n∈N+.
例1-2

苏教版高三数学复习课件5.4 数列的求和

答案：答案：
5． (2010·南京市第九中学调研测试已知数列 n}满足：an＝．南京市第九中学调研测试)已知数列满足：南京市第九中学调研测试已知数列{a 满足则数列{a 的前的前100项的和是项的和是________．则数列 n}的前项的和是．解析：解析：an＝
∴a1＋a2＋…＋a100＝
6．常见的拆项公式有：．常见的拆项公式有：
(1)
(2)
(3) 思考：用裂项相消法求数列前项和的前提是什么项和的前提是什么？思考：用裂项相消法求数列前n项和的前提是什么？提示：数列中的每一项均能分裂成一正一负两项，这是用裂项相消法的前提．提示：数列中的每一项均能分裂成一正一负两项，这是用裂项相消法的前提．
第4课时数列的求和
掌握数列求和的几种常见方法．掌握数列求和的几种常见方法．【命题预测】命题预测】数列的求和在近几年高考中，填空题与解答题都有出现，重点以容易题和中档数列的求和在近几年高考中，填空题与解答题都有出现，题为主，基本知识以客观题出现，综合知识则多以解答题体现，题为主，基本知识以客观题出现，综合知识则多以解答题体现，主要是探索型和综合型题目．复习时，要具有针对性地训练，并以“注重数学思想方法、和综合型题目．复习时，要具有针对性地训练，并以 “ 注重数学思想方法、强化运算能力、重点知识重点训练”的角度做好充分准备．化运算能力、重点知识重点训练”的角度做好充分准备．
1．数列．数列0.9,0.99,0.999，…，，
项和为________． …的前n项和为的前项和为．
解析：数列的通项公式为其前n项和解析：数列的通项公式为an＝1－0.1n，其前项和－

高考数学一轮复习第四章第四讲数列求和课件

已知数列{an} 的首项 a1＝1，且________. (1)求{an} 的通项公式； (2)若 bn＝ana2n＋1，求数列{bn} 的前 n 项和 Tn. 注：如果选择多个条件分别解答，按第一个解答计分.
解：(1)选①(an＋1)2＝a2n－1 ＋4an＋2an－1＋1(n≥2)，an＞0，由(an＋1)2＝a2n－1 ＋4an＋2an－1＋1(n≥2)，可得 (an＋an－1)(an－an－1－2)＝0，因为 an＞0，所以 an－an－1＝2(n≥2)，所以 {an} 是以 1 为首项，2 为公差的等差数列，所以 an＝1＋(n－1)×2＝2n－1.
则数列{bn}的前 2n 项和 T2n＝(b1＋b3＋…＋b2n－1)＋(b2＋ b4＋…＋b2n)
＝(1＋5＋…＋4n－3)＋4113－17＋17－111＋…＋4n1－1－4n1＋3 ＝12n(1＋4n－3)＋1413－4n1＋3 ＝2n2－n＋3(4nn＋3).
考点二裂项相消法求和
[例 2](2022 年全国Ⅰ卷)记 Sn 为数列{an}的前 n 项和，已知 a1＝1，Sann是公差为13的等差数列.
(2)由(1)及 bn＝laong，2ann为，偶n为数奇，数，
得 bn＝n2－ n-1，1，n为n为偶奇数数，， ∴T2n ＝ (0 ＋ 2 ＋ 4 ＋ … ＋ 2n － 2) ＋ (2 ＋ 23 ＋ … ＋ 22n-1) ＝ 0＋22n－2×n＋2(11－－44n)＝23×4n＋n2－n－23＝13×22n+1＋n2－n－32.
【题后反思】
(1)若数列{cn}的通项公式为 cn＝an±bn，且{an}，{bn}为等差或等比数列，可采用分组求和法求数列{cn}的前 n 项和.
(2)若数列{cn}的通项公式为 cn＝abnn，，nn为为偶奇数数，，其中数列 {an}，{bn}是等比数列或等差数列，可采用分组求和法求{an}的前 n 项和.

(江苏专用)2020版高考数学大一轮复习第五章数列4第4讲数列求和课件文

第4讲第五章数列数列求和教材回顾•基础自测0知枳檢理/1.公式法如果一个数列是等差数列或等比数列，则求和时直接利用等差或等比数列的前〃项和公式.2.非等差、等比数列求和的常用方法⑴倒序相加法如果一个数列｛给｝,首末两端等“距离”的两项的和相等或等于同一个常数，那么求这个数列的前n 项和即可用倒序相加法, 等差数列的前〃项和即是用此法推导的.理教材▼ ©(2)分组转化法若一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成，则求和时可用分组转化法，分别求和后相加减.(3)错位相减法如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么这个数列的前〃项和即可用此法来求，等比数列的前n 项和就是用此法推导的.(4)裂项相消法把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得其和.1.数列百，2扌，3舟,喘，…的前兀项和是______________解析：前n项和S“ = (l+2+3 -------------- w) + |+p ------------- *]=n (n + 1)2rt (兀 + 1)」_12 十1 _尹答案:n (n + 1)2+1-寺(1+13寸噪如 S 刑放• (1 + 3寸—=+8」寸— « 匚 =七—十+…+十—卄+十丄-■:首・「圧—Ig E n(z+r)占H£来E[»1厂 I IJ LL•只展昼S温茫…,(z+y)占■…"遐・吃,吃隸门3. （2018-高考江苏卷）已知集合A = {x\x=2n-19 n^}9 B ={x\x=2n9〃丘N*}・将AUB的所有元素从小到大依次排列构成一个数列仏}•记必为数列仏}的前〃项和，贝U使得SQ12给+i成立的n的最小值为___________ 解析：所有的正奇数和2% WN）按照从小到大的顺序排列构成{a tl}9在数列仏}中，2、前面有16个正奇数，即。

高考数学大一轮复习(备考基础查清+热点命题悟通)第五章第四节数列求和配套课件理苏教版

第二十八页，共34页。
[课堂练通考点] 1．数列 112，314，518，7116，…，(2n－1)＋21n，…的前 n 项和 Sn
第四节
数列求和
1．等差数列的前 n 项和公式 Sn＝na12＋an＝ na1＋nn2－1d ；
第一页，共34页。
2．等比数列的前 n 项和公式
Sn＝na1a1－1－，aqnqq＝＝1，a111－－qqn
，q≠1.
3．一些常见数列的前 n 项和公式
nn＋1 (1)1＋2＋3＋4＋…＋n＝ 2 ；
(2)1＋3＋5＋7＋…＋2n－1＝ n2 ；
由(1)知 an＝2n－1，n∈N+，
第十四页，共34页。
所以 bn＝2n2－n 1，n∈N+. 所以 Tn＝12＋232＋253＋…＋2n2－n 1， 12Tn＝212＋233＋…＋2n2－n 3＋22nn－＋11. 两式相减，得 12Tn＝12＋222＋223＋…＋22n－22nn－＋11 ＝32－2n1－1－22nn－＋11，所以 Tn＝3－2n2＋n 3.
(2)由(1)知a2n－11a2n＋1 ＝3－2n11－2n＝122n1－3－2n1－1，从而数列a2n－11a2n＋1的前 n 项和为 12－11－11＋11－13＋…＋2n1－3－2n1－1＝1－n2n.
第二十五页，共34页。
角度四形如 an＝n2nn＋＋122型 4．(2013·江西高考)正项数列{an}的前 n 项和 Sn 满足：S2n－(n2
的等比中项为16. (1)求数列{an}的通项公式； (2)设bn＝log4an，数列{bn}的前n项和为Sn，是否存在正整数 k，使得S11＋S12＋S13＋…＋S1n<k对任意n∈N＋恒成立．若存在，求出正整数k的最小值；不存在，请说明理由．解：(1)设数列{an}的公比为 q，由题意可得 a3＝16， ∵a3－a2＝8，则 a2＝8，∴q＝2.∴an＝2n＋1.

高考数学一轮复习第五章数列4数列求和课件

1．分组求和法一个数列的通项公式是由若干个等差数列或等比数列或可求和的
数列组成，则求和时可用分组求和法，分别求和后相加减．
2．裂项相消法把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵
消，从而求得其和．
12/13/2021
第六页，共四十五页。
3．错位相减法如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么这个数列的前 n 项和即可用此法来求，如等比数列的前 n 项和公式就是用此法推导的． 4．倒序相加法如果一个数列{an}的前 n 项中首末两端等“距离”的两项的和相等或等于同一个常数，那么求这个数列的前 n 项和可用倒序相加法，如等差数列的前 n 项和公式即是用此法推导的．
第九页，共四十五页。
解析：(1)因为数列{an}为等比数列，且公比不等于 1，则其前 n 项和为 Sn＝a111－－qqn＝a11－－aq1qn＝a11－－aqn＋1.
(2)因为 sin21°＋sin289°＝sin22°＋sin288°＝sin23°＋sin287°＝ 1，…，所以 sin21°＋sin22°＋sin23°＋…＋sin287°＋sin288°＋sin289° 可用倒序相加求和．
A．0
B．100
C．－100
D．10 200
12/13/2021
第二十三页，共四十五页。
【解析】 (1)由题意知 S100＝(－1＋3)＋(－5＋7)＋…＋(－ 197＋199)＝2×50＝100.
(2)由题意，得 a1＋a2＋a3＋…＋a100＝12－22－22＋32＋32－ 42－42＋52＋…＋992－1002－1002＋1012＝－(1＋2)＋(3＋2)－(4 ＋3)＋…－(99＋100)＋(101＋100)＝－(1＋2＋…＋99＋100)＋(2 ＋3＋…＋100＋101)＝－50×101＋50×103＝100.

(江苏专用)高考数学总复习第五章第4课时数列通项与求和课件

成等比数列．
Aan ②倒数变换：形如 an＋ 1＝ (A≠ 0， Ban＋ C C≠0)取倒数可转化成①. (4)含有 Sn 和 an 可用公式 an＝ Sn－ Sn－
* ( n ≥ 2 ， n ∈ N )消去 Sn 或 an. 1
2．数列求和常用方法 (1)公式法求和 ①直接由等差、等比数列的求和公式求和． ②掌握一些常见数列前 n 项和 1＋ 2＋ 3 n n＋ 1 2 ＋…＋ n＝__________ ，
课标未作要求，但课本上的分期付款问题的解决，使用的正是此数学模型，从数学建模的角度来说，这一数列还是有研究的必要．
备选例题教师用书独具在数列 {an}中，a1＝ 2，a2＝5，an＋ 2－ 3an
＋1
＋ 2an＝0(n∈ N*)．
(1)若记 bn＝an＋ 1－ an，求证数列 {bn}是等比数列； (2)求数列 {an}的通项公式 an.
考点探究•讲练互动
考点突破
考点1 由简单的递推式求通项例1 根据下列条件求数列的通项
(1)已知a1＝5，an＝2an－1＋3(n≥2)，求
a n； (2)数列{an}的前n项和为Sn，且a1＝1， an＋1＝2Sn，求an.
【解】 (1)在 an＝2an－ 1＋ 3 两边都加上 3 得 an＋ 3＝ 2(an－ 1＋ 3) an＋3 ∴ ＝ 2， an－1＋3
a2 3 a3 4 a4 5 a5 6 解析：由已知得＝，＝，＝，＝， …， a1 1 a2 2 a3 3 a4 4 an n＋ 1 ＝ . an－1 n－ 1 an n n＋ 1 以上 n－1 个式子两边分别相乘得＝， 2 a1 n n＋ 1 n2＋ n ∴ an＝＝ . 2 2 2 n ＋n 答案： 2

高考数学一轮复习4 第4讲数列求和

第4讲数列求和最新考纲考向预测1.熟练掌握等差、等比数列的前n 项和公式及倒序相加求和、错位相减求和法.2.掌握非等差、等比数列求和的几种常见方法.3.能在具体的问题情境中识别数列的等差关系或等比关系，并能用相关知识解决与前n 项和相关的问题.命题趋势数列分组求和、错位相减求和、裂项相消求和仍是今年高考考查的热点，题型仍将是以解答题为主.核心素养数学运算、逻辑推理1．基本数列求和公式(1)等差数列求和公式：S n ＝n （a1＋an ）2＝na 1＋n （n －1）2d ． (2)等比数列求和公式：S n ＝⎩⎨⎧na1，q ＝1，a1－anq 1－q ＝a1（1－qn ）1－q ，q≠1.2．数列求和的五种常用方法 (1)分组转化求和法一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成，则求和时可用分组求和法，分别求和后再相加减．(2)裂项相消法把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得其和．(3)错位相减法如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么这个数列的前n 项和即可用此法来求，如等比数列的前n 项和公式就是用此法推导的．(4)倒序相加法如果一个数列{a n}的前n项中首末两端等“距离”的两项的和相等或等于同一个常数，那么求这个数列的前n项和即可用倒序相加法，如等差数列的前n项和公式即是用此法推导的．(5)并项法一个数列的前n项和中，可两两结合求和，称为并项法求和，形如：(－1)n f(n)类型，可考虑利用并项法求和．常用结论三种常见的拆项公式(1)1n（n＋1）＝1n－1n＋1.(2)1（2n－1）（2n＋1）＝12⎝⎛⎭⎪⎫12n－1－12n＋1.(3)1n＋n＋1＝n＋1－n.常见误区1．在应用错位相减法求和时，要注意观察未合并项的正负号．2．在应用裂项相消法求和时，要注意消项的规律具有对称性，即前面剩多少项，后面就剩多少项．1．判断正误(正确的打“√”，错误的打“×”)(1)当n≥2时，1n2－1＝1n－1－1n＋1.()(2)利用倒序相加法可求得sin21°＋sin22°＋sin23°＋…＋sin288°＋sin289°＝44.5.()(3)若S n＝a＋2a2＋3a3＋…＋na n，当a≠0且a≠1时，求S n的值可用错位相减法求得．()答案：(1)×(2)√(3)√2．数列{1＋2n－1}的前n项和为()A．1＋2n B．2＋2nC．n＋2n－1 D．n＋2＋2n解析：选C.由题意得a n ＝1＋2n －1. 所以S n ＝n ＋1－2n1－2＝n ＋2n －1.3．(多选)设S n 是数列{a n }的前n 项和，且a 1＝－1，a n ＋1＝S n S n ＋1，则( )A ．数列⎩⎨⎧⎭⎬⎫1Sn 为等差数列B ．S n ＝－1nC ．a n ＝⎩⎪⎨⎪⎧－1，n ＝1，1n －1－1n ，n≥2，n ∈N ＋ D.1S1S2＋1S2S3＋…＋1Sn －1Sn＝n －1n解析：选ABCD.S n 是数列{a n }的前n 项和，且a 1＝－1，a n ＋1＝S n S n ＋1，则S n ＋1－S n ＝S n S n ＋1，整理得1Sn ＋1 －1Sn＝－1(常数)，所以数列⎩⎨⎧⎭⎬⎫1Sn 是以1S1＝－1为首项，－1为公差的等差数列，故A 正确；所以1Sn ＝－1－(n －1)＝－n ，故S n ＝－1n ，故B 正确；所以当n ≥2时，a n ＝S n －S n－1＝1n －1－1n (首项不符合通项)，故a n ＝⎩⎪⎨⎪⎧－1，n ＝1，1n －1－1n ，n≥2，n ∈N ＋，故C 正确；因为1Sn －1Sn ＝1（n －1）n ＝1n －1－1n ，所以1S1S2＋1S2S3＋…＋1Sn －1Sn ＝1－12＋12－13＋…＋1n －1－1n ＝n －1n ，故D 正确．4．数列{a n }的前n 项和为S n ，已知S n ＝1－2＋3－4＋…＋(－1)n －1·n ，则S 17＝________．解析：S 17＝1－2＋3－4＋5－6＋…＋15－16＋17＝1＋(－2＋3)＋(－4＋5)＋(－6＋7)＋…＋(－14＋15)＋(－16＋17)＝1＋1＋1＋…＋1＝9.答案：95．(易错题)已知数列{a n }的前n 项和为S n ，且a n ＝n ·2n ，则S n ＝________．解析：因为a n ＝n ·2n ，所以S n ＝1·21＋2·22＋3·23＋…＋n ·2n ，所以2S n ＝1·22＋2·23＋…＋(n －1)·2n ＋n ·2n ＋1，② ①－②，得－S n ＝2＋22＋23＋ (2)－n ·2n ＋1＝2（1－2n ）1－2－n ·2n ＋1＝2n ＋1－2－n ·2n ＋1＝(1－n )2n ＋1－2，所以S n ＝(n －1)2n ＋1＋2.答案：(n －1)2n ＋1＋2分组转化法求和(2020·福州市适应性考试)已知数列{a n }满足a 1＝2，na n ＋1－(n ＋1)a n ＝2n (n ＋1)，设b n ＝an n .(1)求数列{b n }的通项公式；(2)若c n ＝2b n －n ，求数列{c n }的前n 项和．【解】 (1)方法一：因为b n ＝ann 且na n ＋1－(n ＋1)a n ＝2n (n ＋1)，所以b n ＋1－b n ＝an ＋1n ＋1－ann ＝2，又b 1＝a 1＝2，所以{b n }是以2为首项，以2为公差的等差数列．所以b n ＝2＋2(n －1)＝2n .方法二：因为b n ＝ann ，所以a n ＝nb n ，又na n ＋1－(n ＋1)a n ＝2n (n ＋1)，所以n (n ＋1)b n ＋1－(n ＋1)nb n ＝2n (n ＋1)，即b n ＋1－b n ＝2，又b 1＝a 1＝2，所以{b n }是以2为首项，以2为公差的等差数列．所以b n ＝2＋2(n －1)＝2n .(2)由(1)及题设得，c n ＝22n －n ＝4n －n ，所以数列{c n }的前n 项和S n ＝(41－1)＋(42－2)＋…＋(4n －n ) ＝(41＋42＋…＋4n )－(1＋2＋…＋n ) ＝4－4n×41－4－n （1＋n ）2＝4n ＋13－n2＋n 2－43.分组转化法求和的常见类型(1)若a n ＝b n ±c n ，且{b n }，{c n }为等差或等比数列，可采用分组求和法求{a n }的前n 项和．(2)通项公式为a n ＝⎩⎨⎧bn ，n 为奇数，cn ，n 为偶数的数列，其中数列{b n }，{c n }是等比数列或等差数列，可采用分组转化法求和．1．(2020·资阳诊断)已知在数列{a n }中，a 1＝a 2＝1，a n ＋2＝⎩⎨⎧an ＋2，n 是奇数，2an ，n 是偶数，则数列{a n }的前20项和为( )A ．1 121B ．1 122C ．1 123D ．1 124解析：选C.由题意可知，数列{a 2n }是首项为1，公比为2的等比数列，数列{a 2n －1}是首项为1，公差为2的等差数列，故数列{a n }的前20项和为1×（1－210）1－2＋10×1＋10×92×2＝1 123.选C.2．(2020·昆明市三诊一模)设等差数列{a n }的公差为d ，等比数列{b n }的公比为q ，已知a 1＝b 1＝1，b 4＝64，q ＝2d .(1)求数列{a n }，{b n }的通项公式；(2)记c n ＝a 2n －1＋b 2n ，求数列{c n }的前n 项和S n .解：(1)因为b 4＝64，所以b 1q 3＝64，又b 1＝1，所以q ＝4. 又q ＝2d ，所以d ＝2.因为a 1＝1，所以a n ＝a 1＋(n －1)d ＝2n －1， b n ＝b 1q n －1＝4n －1.(2)c n ＝a 2n －1＋b 2n ＝4n －3＋42n －1.所以S n ＝(1＋5＋9＋…＋4n －3)＋(4＋43＋…＋42n －1) ＝n （1＋4n －3）2＋4×（1－42n ）1－42＝2n 2－n ＋42n ＋1－415.错位相减法求和(2020·高考全国卷Ⅰ)设{a n }是公比不为1的等比数列，a 1为a 2，a 3的等差中项．(1)求{a n }的公比；(2)若a 1＝1，求数列{na n }的前n 项和．【解】 (1)设{a n }的公比为q ，由题设得2a 1＝a 2＋a 3, 即2a 1＝a 1q ＋a 1q 2. 所以q 2＋q －2＝0, 解得q ＝1(舍去)或q ＝－2. 故{a n }的公比为－2.(2)记S n 为{na n }的前n 项和．由(1)及题设可得，a n ＝(－2)n －1.所以 S n ＝1＋2×(－2)＋…＋n ×(－2)n －1，－2S n ＝－2＋2×(－2)2＋…＋(n －1)×(－2)n －1＋n ×(－2)n . 可得3S n ＝1＋(－2)＋(－2)2＋…＋(－2)n －1－n ×(－2)n ＝1－（－2）n3－n ×(－2)n.所以S n ＝19－（3n ＋1）（－2）n9.用错位相减法求和的策略和技巧(1)掌握解题“3步骤”(2)注意解题“3关键”①要善于识别题目类型，特别是等比数列公比为负数的情形．②在写出“S n ”与“qS n ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“S n －qS n ”的表达式．③在应用错位相减法求和时，若等比数列的公比为参数，应分公比q ＝1和q ≠1两种情况求解．(2020·安徽省部分重点学校联考)已知等比数列{a n }的各项均为正数，S n 为等比数列{a n }的前n 项和，且9S 2＝5，a 3＝427.(1)求数列{a n }的通项公式a n ；(2)设b n ＝nan ，求数列{b n }的前n 项和T n .解：(1)设等比数列{a n }的公比为q (q >0)，由9S 2＝5得a 1＋a 1q ＝59，又a 3＝a 1q 2＝427，故q21＋q ＝415，所以15q 2－4q －4＝0，解得q ＝23或q ＝－25(舍去)，所以由a 1＋a 1q ＝a 1(1＋q )＝a 1×53＝59，解得a 1＝13，所以a n ＝13⎝ ⎛⎭⎪⎫23n －1.(2)由(1)可知a n ＝13⎝ ⎛⎭⎪⎫23n －1，所以b n ＝3n ⎝ ⎛⎭⎪⎫32n －1.故T n ＝3⎣⎢⎡⎦⎥⎤1×⎝ ⎛⎭⎪⎫320＋2×⎝ ⎛⎭⎪⎫321＋…＋n×⎝ ⎛⎭⎪⎫32n －1①， 32T n ＝3[1×⎝ ⎛⎭⎪⎫321＋2×⎝ ⎛⎭⎪⎫322＋…＋(n －1)×⎝ ⎛⎭⎪⎫32n －1＋n ×⎝ ⎛⎭⎪⎫32n ]②，①－②得，－12T n ＝3[⎝ ⎛⎭⎪⎫320＋⎝ ⎛⎭⎪⎫321＋⎝ ⎛⎭⎪⎫322＋…＋⎝ ⎛⎭⎪⎫32n －1－n ×⎝ ⎛⎭⎪⎫32n ]，化简得T n ＝(6n －12)⎝ ⎛⎭⎪⎫32n＋12.裂项相消法求和角度一形如a n ＝1n ＋k ＋n型数列{a n }满足a 1＝1, a2n ＋2＝a n ＋1(n ∈N *)． (1)证明：数列{a 2n }是等差数列，并求出{a n }的通项公式；(2)若b n ＝2an ＋an ＋1，求数列{b n }的前n 项和．【解】 (1)由a2n ＋2＝a n ＋1得a 2n ＋1－a 2n ＝2，且a 21＝1，所以数列{a 2n }是以1为首项，2为公差的等差数列，所以a 2n ＝1＋(n －1)×2＝2n －1，又由已知易得a n >0，所以a n ＝2n －1(n ∈N *)．(2)b n ＝2an ＋an ＋1＝22n －1＋2n ＋1＝2n ＋1－2n －1，故数列{b n }的前n 项和T n ＝b 1＋b 2＋…＋b n ＝(3－1)＋(5－3)＋…＋(2n ＋1－2n －1)＝2n ＋1－1.裂项求和的基本步骤角度二形如a n ＝1n （n ＋k ）型在①数列{a n }的前n 项和S n ＝12n 2＋52n ；②a 2n －a n －a 2n －1－a n －1＝0(n ≥2，n ∈N *)，a n ＞0，且a 1＝b 2这两个条件中任选一个，补充在下面的问题中，若问题中的M 存在，求出M 的最小值；若M 不存在，说明理由．数列{b n }是首项为1的等比数列，b n ＞0，b 2＋b 3＝12，且____________，设数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1an log3 bn ＋1的前n 项和为T n ，是否存在M ∈N *，使得对任意的n ∈N *，T n ＜M?【解】设公比为q (q ＞0)，因为数列{b n }是首项为1的等比数列，且b n ＞0，b 2＋b 3＝12，所以q 2＋q －12＝0，解得q ＝3(q ＝－4不合题意，舍去)，所以b n ＝3n －1.若选①，由S n ＝12n 2＋52n ，可得S n －1＝12(n －1)2＋52(n －1)(n ≥2)，两式相减可得a n ＝n ＋2(n ≥2)，又a 1＝S 1＝3也符合上式，所以a n ＝n ＋2，所以1anlog3bn ＋1＝1（n ＋2）n ＝12⎝ ⎛⎭⎪⎫1n －1n ＋2，则T n ＝12⎝ ⎛⎭⎪⎫1－13＋12－14＋13－15＋…＋1n －1n ＋2＝34－12⎝ ⎛⎭⎪⎫1n ＋1＋1n ＋2，因为1n ＋1＋1n ＋2＞0，所以T n ＜34，由题意可得M ≥34，又M ∈N *，所以M 的最小值为1.若选②，则由a 2n －a n －a 2n －1－a n －1＝0得(a n －a n －1 －1)·(a n ＋a n －1) ＝0，又a n ＞0，所以a n －a n －1－1＝0，即a n －a n －1＝1，所以数列{a n }是公差为1的等差数列，又a 1＝b 2，则a 1＝3，所以a n ＝n ＋2.所以1anlog3 bn ＋1＝1（n ＋2）n ＝12⎝ ⎛⎭⎪⎫1n －1n ＋2，则T n ＝12⎝ ⎛⎭⎪⎫1－13＋12－14＋13－15＋…＋1n －1n ＋2＝34－12⎝ ⎛⎭⎪⎫1n ＋1＋1n ＋2，因为1n ＋1＋1n ＋2＞0，所以T n ＜34，由题意可得M ≥34，又M ∈N *，所以M 的最小值为1.裂项相消法求和的实质和解题关键裂项相消法求和的实质是先将数列中的通项分解，然后重新组合，使之能消去一些项，最终达到求和的目的，其解题的关键就是准确裂项和消项．(1)裂项原则：一般是前边裂几项，后边就裂几项，直到发现被消去项的规律为止．(2)消项规律：消项后前边剩几项，后边就剩几项，前边剩第几项，后边就剩倒数第几项．[注意] 利用裂项相消法求和时，既要注意检验通项公式裂项前后是否等价，又要注意求和时，正负项相消消去了哪些项，保留了哪些项，切不可漏写未被消去的项．1．已知函数f (x )＝x α的图象过点(4，2)，令a n ＝1f （n ＋1）＋f （n ），n ∈N *.记数列{a n }的前n 项和为S n ，则S 2 020＝( )A. 2 019－1B. 2 020－1C. 2 021－1D. 2 021＋1解析：选C.由f (4)＝2，可得4α＝2，解得α＝12，则f (x )＝x .所以a n ＝1f （n ＋1）＋f （n ）＝1n ＋1＋n＝n ＋1－n ，所以S 2 020＝a 1＋a 2＋a 3＋…＋a 2 020＝(2－1)＋(3－2)＋(4－3)＋…＋ ( 2 021－ 2 020)＝ 2 021－1.2．在①数列{a n }为递增的等比数列，S 3＝7，且3a 2是a 1＋3和a 3＋4的等差中项；②S n ＝2n －1，n ∈N *，这两个条件中任选一个，补充在下面的问题中，并完成解答．已知数列{a n }的前n 项和为S n ，________，b n ＝an ＋1SnSn ＋1，设数列{b n }的前n 项和为T n ，求T n .解：若选①，由已知，得⎩⎪⎨⎪⎧a1＋a2＋a3＝7，（a1＋3）＋（a3＋4）＝2×3a2，解得a 2＝2，设数列{a n }的公比为q ，则a 1q ＝2，所以a 1＝2q ，a 3＝a 1q 2＝2q . 由S 3＝7，可知2q ＋2＋2q ＝7，所以2q 2－5q ＋2＝0，解得q ＝2或q ＝12，易得q >1，所以q ＝2，a 1＝1. 故数列{a n }的通项公式为a n ＝2n －1， S n ＝1－2n 1－2＝2n －1，所以b n ＝an ＋1SnSn ＋1＝2n （2n －1）（2n ＋1－1）＝12n －1－12n ＋1－1，所以T n ＝1－13＋13－17＋…＋12n －1－12n ＋1－1＝1－12n ＋1－1.若选②，当n ＝1时，a 1＝S 1＝1，当n ≥2时，a n ＝S n －S n －1＝2n －1，因为a 1＝1也满足上式，所以a n ＝2n －1，所以b n ＝an ＋1SnSn ＋1＝2n （2n －1）（2n ＋1－1）＝12n －1－12n ＋1－1，所以T n ＝1－13＋13－17＋…＋12n －1－12n ＋1－1＝1－12n ＋1－1.[A 级基础练]1．在数列{a n }中，a 1＝2，a 2＝2，a n ＋2－a n ＝1＋(－1)n ，n ∈N *，则S 60的值为( )A ．990B ．1 000C ．1 100D ．99解析：选 A.n 为奇数时，a n ＋2－a n ＝0，a n ＝2；n 为偶数时，a n ＋2－a n ＝2，a n ＝n .故S 60＝2×30＋(2＋4＋…＋60)＝990.2．在数列{a n }中，a n ＝2n －12n ，若{a n }的前n 项和S n ＝32164，则n ＝( ) A ．3 B ．4 C ．5D ．6解析：选D.由a n ＝2n －12n ＝1－12n 得，S n ＝n －⎝ ⎛⎭⎪⎫12＋122＋…＋12n ＝n －⎝ ⎛⎭⎪⎫1－12n ，则S n ＝32164＝n －⎝ ⎛⎭⎪⎫1－12n ，将各选项中的值代入验证得n ＝6.3．(2020·河北保定期末)在数列{a n }中，若a 1＝1，a 2＝3，a n ＋2＝a n ＋1－a n (n ∈N *)，则该数列的前100项之和是( )A ．18B ．8C ．5D ．2解析：选C.因为a 1＝1，a 2＝3，a n ＋2＝a n ＋1－a n (n ∈N *)，所以a 3＝3－1＝2，a 4＝2－3＝－1，a 5＝－1－2＝－3，a 6＝－3＋1＝－2，a 7＝－2＋3＝1，a 8＝1＋2＝3，a 9＝3－1＝2，…，所以{a n }是周期为6的周期数列，因为100＝16×6＋4，所以S 100＝16×(1＋3＋2－1－3－2)＋(1＋3＋2－1)＝5.故选C.4．(多选)已知数列{a n }为等差数列，首项为1，公差为2.数列{b n }为等比数列，首项为1，公比为2.设c n ＝a bn ，T n 为数列{c n }的前n 项和，则当T n ＜2 019时，n 的取值可能是( )A ．8B ．9C ．10D ．11解析：选AB.由题意，a n ＝1＋2(n －1)＝2n －1，b n ＝2n －1， c n ＝a bn ＝2·2n －1－1＝2n －1，则数列{c n }为递增数列，其前n 项和T n ＝(21－1)＋(22－1)＋(23－1)＋…＋(2n －1) ＝(21＋22＋ (2))－n ＝2（1－2n ）1－2－n ＝2n ＋1－2－n .当n ＝9时，T n ＝1 013＜2 019；当n ＝10时，T n ＝2 036＞2 019. 所以n 的取值可以是8，9. 故选AB.5．已知数列{a n }满足a 1＝1，a n ＋1·a n ＝2n (n ∈N *)，则S 2 020＝( ) A ．22 020－1 B ．3×21 010－3 C ．3×22 021－1D ．3×21 009－2解析：选B.因为a 1＝1，所以a 2＝2a1＝2，又an ＋2·an ＋1an ＋1·an＝2n ＋12n ＝2，所以an ＋2an ＝2.所以a 1，a 3，a 5，…成等比数列；a 2，a 4，a 6，…成等比数列，所以S 2 020＝a 1＋a 2＋a 3＋a 4＋a 5＋a 6＋…＋a 2 019＋a 2 020＝(a 1＋a 3＋a 5＋…＋a 2 019)＋(a 2＋a 4＋a 6＋…＋a 2 020)＝1－21 0101－2＋2（1－21 010）1－2＝3×21 010－3.故选B.6．在等比数列{a n }中，若a 1＝27，a 9＝1243，q >0，S n 是其前n 项和，则S 6＝________．解析：由a 1＝27，a 9＝1243知，1243＝27·q 8，又由q >0，解得q ＝13，所以S 6＝27⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫1361－13＝3649. 答案：36497．中国古代数学著作《算法统宗》中有这样一个问题：“三百七十八里关，初行健步不为难，次日脚痛减一半，六朝才得至其关，要见次日行里数，请公仔细算相还．”其意思为：有一个人走378里路，第一天健步行走，从第二天起脚痛，每天走的路程为前一天的一半，走了6天后到达目的地，请问第二天走了________里．解析：依题意得，该人每天所走的路程依次排列形成一个公比为12的等比数列，记为{a n }，其前6项和等于378，于是有a1⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫1261－12＝378，解得a 1＝192，因此a 2＝12a 1＝96，即该人第二天走了96里．答案：968．已知数列{a n }是等差数列，数列{b n }是等比数列，且b 2＝3，b 3＝9，a 1＝b 1，a 14＝b 4，则{a n }的通项公式为________；设c n ＝a n ＋b n ，则数列{c n }的前n 项和为S n ＝________．解析：设{a n }是公差为d 的等差数列，{b n }是公比为q 的等比数列，由b 2＝3，b 3＝9，可得q ＝b3b2＝3，b n ＝b 2q n －2＝3·3n －2＝3n －1.即有a 1＝b 1＝1，a 14＝b 4＝27，则d ＝a14－a113＝2，则a n ＝a 1＋(n －1)d ＝1＋2(n －1)＝2n －1.c n ＝a n ＋b n ＝2n －1＋3n －1，则数列{c n }的前n 项和为S n ＝[1＋3＋…＋(2n －1)]＋(1＋3＋9＋…＋3n －1)＝12n ·2n ＋1－3n 1－3＝n 2＋3n －12.答案：a n ＝2n －1 n 2＋3n －129．(2020·新高考卷Ⅰ)已知公比大于1的等比数列{a n }满足a 2＋a 4＝20，a 3＝8. (1)求{a n }的通项公式；(2)记b m 为{a n }在区间(0，m ](m ∈N *)中的项的个数，求数列{b m }的前100项和S 100. 解：(1)设{a n }的公比为q .由题设得a 1q ＋a 1q 3＝20，a 1q 2 ＝8. 解得q ＝12(舍去)，q ＝2.由题设得a 1＝2. 所以{a n }的通项公式为a n ＝2n .(2)由题设及(1)知b 1＝0，且当2n ≤m <2n ＋1时，b m ＝n .所以S 100＝b 1＋(b 2＋b 3)＋(b 4＋b 5＋b 6＋b 7)＋…＋(b 32＋b 33＋…＋b 63)＋(b 64＋b 65＋…＋b 100)＝0＋1×2＋2×22＋3×23＋4×24＋5×25＋6×(100－63) ＝480.10．(2020·四川石室中学二诊)已知数列{a n }的前n 项和为S n ，且满足2S n ＝n －n 2(n ∈N *)．(1)求数列{a n }的通项公式；(2)设b n ＝⎩⎪⎨⎪⎧2an （n ＝2k －1），2（1－an ）（1－an ＋2）（n ＝2k ）(k ∈N *)，数列{b n }的前n 项和为T n .若T 2n ＝a ⎝ ⎛⎭⎪⎫14n－12n ＋2＋b 对n ∈N *恒成立．求实数a ，b 的值．解：(1)①当n ＝1时，由2S 1＝2a 1＝1－12得a 1＝0；②当n ≥2时，2a n ＝2S n －2S n －1＝n －n 2－[(n －1)－(n －1)2]＝2－2n ，则a n ＝1－n (n ≥2)，显然当n ＝1时也适合上式，所以a n ＝1－n (n ∈N *)． (2)因为2（1－an ）（1－an ＋2）＝2n （n ＋2）＝1n －1n ＋2，所以T 2n ＝(b 1＋b 3＋…＋b 2n －1)＋(b 2＋b 4＋…＋b 2n )＝(2＋2－2＋…＋22－2n )＋⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫12－14＋⎝ ⎛⎭⎪⎫14－16＋…＋⎝ ⎛⎭⎪⎫12n －12n ＋2＝1－⎝ ⎛⎭⎪⎫14n 1－14＋12－12n ＋2＝116－43⎝ ⎛⎭⎪⎫14n －12n ＋2. 因为T 2n ＝a ⎝ ⎛⎭⎪⎫14n－12n ＋2＋b 对n ∈N *恒成立，所以a ＝－43，b ＝116.[B 级综合练]11．(2020·重庆模拟)数列{a n }满足a n ＋1＝(－1)n ＋1a n ＋2n －1，则数列{a n }的前48项和为( )A ．1 006B ．1 176C ．1 228D ．2 368解析：选B.a n ＋1＝(－1)n ＋1a n ＋2n －1，所以n ＝2k －1(k ∈N *)时，a 2k ＝a 2k －1＋4k －3， n ＝2k ＋1(k ∈N *)时，a 2k ＋2＝a 2k ＋1＋4k ＋1， n ＝2k (k ∈N *)时，a 2k ＋1＝－a 2k ＋4k －1，所以a 2k ＋1＋a 2k －1＝2，a 2k ＋2＋a 2k ＝8k .则数列{a n }的前48项和为2×12＋8(1＋3＋…＋23)＝24＋8×12×（1＋23）2＝1176.故选B.12．(多选)已知数列{a n }的前n 项和为S n ，且有(a 1＋a 2＋…＋a n )a n ＝(a 1＋a 2＋…＋a n －1)a n ＋1(n ≥2，n ∈N*)，a 1＝a 2＝1.数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1log2Sn ＋1·log2Sn ＋2的前n 项和为T n ，则以下结论正确的是 ( )A ．a n ＝1B ．S n ＝2n －1C ．T n ＝n ＋1n ＋3D ．{T n }为增数列解析：选BD.由(a 1＋a 2＋…＋a n )a n ＝(a 1＋a 2＋…＋a n －1)a n ＋1，得S n (S n －S n －1)＝S n－1(S n ＋1－S n )，化简得S 2n ＝S n －1S n ＋1，根据等比数列的性质得数列{S n }是等比数列．易知S 1＝1，S 2＝2，故{S n }的公比为2，则S n ＝2n －1，S n ＋1＝2n ，S n ＋2＝2n ＋1，1log2Sn ＋1·log2Sn ＋2＝1n （n ＋1）＝1n －1n ＋1.由裂项相消法得T n ＝1－1n ＋1＝nn ＋1.故B 正确，C 错误，D 正确．根据S n ＝2n －1知A 选项错误，故答案为BD.13．(2020·山西晋中模拟)已知等差数列{a n }的前n 项和为S n ，a 5＝9，S 5＝25. (1)求数列{a n }的通项公式及前n 项和S n ； (2)设b n ＝(－1)n S n ，求{b n }的前n 项和T n .解：(1)由题意，得S 5＝5（a1＋a5）2＝5·2a32＝5a 3＝25，得a 3＝5，设等差数列{a n }的公差为d ，则 d ＝a5－a35－3＝9－52＝2，所以a n ＝a 3＋(n －3)·d ＝5＋2(n －3)＝2n －1，n ∈N *. 则a 1＝2×1－1＝1，所以S n ＝n·[1＋（2n －1）]2＝n 2.(2)由(1)知，b n ＝(－1)n S n ＝(－1)n n 2， ①当n 为偶数时，n －1为奇数，T n ＝b 1＋b 2＋…＋b n ＝－12＋22－32＋42－…－(n －1)2＋n 2 ＝(22－12)＋(42－32)＋…＋[n 2－(n －1)2]＝(2＋1)(2－1)＋(4＋3)(4－3)＋…＋[n ＋(n －1)][n －(n －1)] ＝1＋2＋3＋4＋…＋(n －1)＋n ＝n （n ＋1）2；②当n 为奇数时，n －1为偶数，T n ＝b 1＋b 2＋…＋b n ＝－12＋22－32＋42－…－(n －2)2＋(n －1)2－n 2 ＝(22－12)＋(42－32)＋…＋[(n －1)2－(n －2)2]－n 2＝(2＋1)(2－1)＋(4＋3)(4－3)＋…＋[(n －1)＋(n －2)][(n －1)－(n －2)]－n 2 ＝1＋2＋3＋4＋…＋(n －2)＋(n －1)－n 2 ＝n （n －1）2－n 2＝－n （n ＋1）2.综上所述，T n ＝(－1)nn （n ＋1）2.14．已知正项数列{a n }的前n 项和为S n ，且4S n ＝(a n ＋1)2. (1)求数列{a n }的通项公式； (2)在①b n ＝1anan ＋1；②b n ＝3n ·a n ；③b n ＝14Sn －1这三个条件中任选一个，补充在下面的问题中并求解．若________，求{b n }的前n 项和T n . 解：(1)因为4S n ＝(a n ＋1)2，所以当n ＝1时，4a 1＝4S 1＝(a 1＋1)2，解得a 1＝1. 当n ≥2时，4S n －1＝(a n －1＋1)2，又4S n ＝(a n ＋1)2，所以两式相减得4a n ＝(a n ＋1)2－(a n －1＋1)2，可得(a n ＋a n －1)(a n －a n －1－2)＝0，因为a n ＞0，所以a n －a n －1＝2，所以数列{a n }是首项为1，公差为2的等差数列，所以a n ＝2n －1，故数列{a n }的通项公式为a n ＝2n －1.(2)若选条件①，b n ＝1anan ＋1＝1（2n －1）（2n ＋1）＝12⎝ ⎛⎭⎪⎫12n －1－12n ＋1，则T n ＝12⎝ ⎛⎭⎪⎫1－13＋13－15＋15－17＋…＋12n －1－12n ＋1＝12⎝ ⎛⎭⎪⎫1－12n ＋1＝n2n ＋1. 若选条件②，b n ＝3n ·a n ＝3n ·(2n －1)，则T n ＝1×3＋3×32＋5×33＋…＋(2n －1)×3n ，上式两边同时乘3，可得3T n ＝1×32＋3×33＋5×34＋…＋(2n －1)×3n ＋1，两式相减得－2T n ＝3＋2×(32＋33＋…＋3n )－(2n －1)× 3n ＋1＝－6＋(2－2n )·3n ＋1，可得T n ＝(n －1)·3n ＋1＋3. 若选条件③，由a n ＝2n －1可得S n ＝（1＋2n －1）×n2＝n 2，所以b n ＝14n2－1＝1（2n －1）（2n ＋1）＝12⎝ ⎛⎭⎪⎫12n －1－12n ＋1，故T n ＝12⎝ ⎛⎭⎪⎫1－13＋13－15＋15－17＋…＋12n －1－12n ＋1 ＝12⎝ ⎛⎭⎪⎫1－12n ＋1＝n2n ＋1. [C 级创新练]15．将正整数20分解成两个正整数的乘积有1×20，2×10，4×5三种，其中4×5是这三种分解中两数差的绝对值最小的，我们称4×5为20的最佳分解．当p×q(p≤q且p，q∈N*)是正整数n的最佳分解时，定义函数f(n)＝q－p，则数列{f(3n)}(n∈N*)的前2 020项和为()A．31 010＋1 B.31 000－14C.31 010－12D．31 010－1解析：选D.由最佳分解的定义，得当n为偶数时，f(3n)＝3n2－3n2＝0；当n为奇数时，f(3n)＝3n＋12－3n－12＝2×3n－12.所以数列{f(3n)}的前2 020 项和S2 020＝2×(30＋31＋32＋…＋31 009)＝2×31 010－13－1＝31 010－1，故选D.16．(多选)已知数列{a n}：12，122，222，322，123，223，323，423，523，623，723，124，224，…(其中第一项是121，接下来的22－1项是122，222，322)，再接下来的23－1项是1 23，223，323，423，523，623，723，依此类推)，其前n项和为S n，则下列判断正确的是()A.210－1210是{a n}的第2 036项B．存在常数M，使得S n＜M恒成立C．S2 036＝1 018D．满足不等式S n＞1 019的正整数n的最小值是2 100解析：选ACD.因为21－1＋22－1＋…＋210－1＝2－2111－2－10＝2 036，所以210－1210是{a n}的第2 036项，所以A正确；因为S n随着n的增大而增大，所以不存在常数M，使得S n＜M恒成立，所以B错误；S2 036＝21－12＋22－12＋…＋210－12＝12×⎝ ⎛⎭⎪⎪⎫2－2111－2－10＝1 018，所以C 正确；由1211＋2211＋…＋n 211＝（1＋n ）n 2211＞1，解得n ≥64，又S 2 036＝1 018，所以满足不等式S n ＞1 019的正整数n 的最小值是2 036＋64＝2 100，所以D 正确．综上，正确的是ACD.。

第04讲数列求和 (精讲)(解析版)-2023年高考数学一轮复习讲练测(新教材新高考)

第04讲数列求和(精讲）目录第一部分：知识点精准记忆第二部分：课前自我评估测试第三部分：典型例题剖析题型一：裂项相消求和法题型二：错位相减求和法题型三：分组求和法题型四：倒序相加求和法第四部分：高考真题感悟1.公式法(1)等差数列前n 项和公式11()(1)22n n n a a n n dS na +-==+; (2)等比数列前n 项和公式111(1)11n n na q S a q q q=⎧⎪=-⎨≠⎪-⎩2.裂项相消求和法:裂项相消求和法就是把数列的各项变为两项之差,使得相加求和时一些正负项相互抵消,前n 项和变成首尾若干少数项之和,从而求出数列的前n 项和.①21111(1)1n n n n n n ==-+++②1111()()n n k k n n k=-++③211111()41(21)(21)22121n n n n n ==---+-+④1111()(1)(2)2(1)(1)(2)n n n n n n n =-+++++1k= 3.错位相减求和法:错位相减法求和：如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么这个数列的前n 项和即可用此法来求.q 倍错位相减法：若数列{}n c 的通项公式n n n c a b =⋅，其中{}n a 、{}n b 中一个是等差数列，另一个是等比数列，求和时一般可在已知和式的两边都乘以组成这个数列的等比数列的公比，然后再将所得新和式与原和式相减，转化为同倍数的等比数列求和．这种方法叫q 倍错位相减法． 4.分组求和法:如果一个数列可写成n n n c a b =±的形式，而数列{}n a ，{}n b 是等差数列或等比数列或可转化为能够求和的数列，那么可用分组求和法. 5.倒序相加求和法:即如果一个数列的前n 项中，距首末两项“等距离”的两项之和都相等，则可使用倒序相加法求数列的前n 项和.1．（2022·福建·厦门一中高二阶段练习）若数列{}n a 满足()11n a n n =+，则{}n a 的前2022项和为（）A ．12023B ．20222023C ．12022D ．20212022【答案】B 解：由题得()11111n a n n n n ==-++，所以{}n a 的前2022项和为11111112022112232022202320232023-+-++-=-=. 故选：B2．（2022·全国·高三专题练习（文））若数列{an }的通项公式为an ＝2n ＋2n －1，则数列{an }的前n 项和为（） A ．2n ＋n 2－1 B ．2n ＋1＋n 2－1 C ．2n ＋n －2 D ．2n ＋1＋n 2－2【答案】D由题可知：设数列{an }的前n 项和为n S 所以12n n S a a a =+++即()()22221321n n n S =+++++++-所以()212[1(21)]122n n n n S -+-=+-故1222n n S n +=-+故选：D3．（2022·全国·高三专题练习（文））设4()42xx f x =+，1231011111111f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭A ．4B ．5C ．6D ．10【答案】B由于()()1144114242x xxx f x f x --+-=+=++，故原式11029565111111111111f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++++= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭. 4．（2022·江苏·高二课时练习）求和：()10132kk =+∑.【答案】2076()10231013232+++3+2+++kk =+=+⋅⋅⋅∑（）（32）（）（32）231030(2222)=++++⋅⋅⋅+102(12)3012-=+- 113022=-+ 2076=题型一：裂项相消求和法例题1．（2022·浙江省淳安中学高二期中）数列的前2022项和为（）A B C 1 D 1【答案】B记的前n项和为nT，则2022140452T=+)112=；故选：B例题2．（2022·河南安阳·高二阶段练习（理））已知{}n a是递增的等差数列，13a=，且13a，4a，1a成等比数列.(1)求数列{}n a的通项公式；(2)设数列11n na a+⎧⎫⎨⎬⎩⎭的前n项和为nT，求证：11156nT≤<.【答案】(1)21na n=+(2)见解析.(1)设{}n a的公差为d，因为13a，4a，1a成等比数列，所以()()222411333331220a a a d d d d=⋅⇒+=+⇒-=，因为{}n a是递增，所以0d>，故2d=，所以21na n=+.(2)()()111111212322123n na a n n n n+⎛⎫==-⎪++++⎝⎭,所以11111111112355721232323nTn n n⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-=-⎪ ⎪ ⎪ ⎪⎢⎥+++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，因为123n+单调递减，所以n T单调递增，故当1n=时，min11()15nT T==，而111123236n nT⎛⎫=-<⎪+⎝⎭，故11156nT≤<.例题3．（2022·辽宁·沈阳市第八十三中学高二阶段练习）已知n S为等差数列{}n a的前n项和，321S=，555S=．(1)求n a、n S；(2)若数列11n na a+⎧⎫⎨⎬⎩⎭的前n项和n T，求满足225nT>的最小正整数n．【答案】(1)an＝4n﹣1，22nS n n=+(2)19(1)设等差数列{an }的公差为d ，则11323212545552a d a d ⨯⎧+=⎪⎪⎨⨯⎪+=⎪⎩，即117211a d a d +=⎧⎨+=⎩，解得134a d =⎧⎨=⎩，故()34141n a n n =+-=-，2(341)22n n n S n n +-==+ (2)由（1）得，1111111414344143n n a a n n n n +⎛⎫=⋅=- ⎪-+-+⎝⎭.故111111111...437471144143n T n n ⎛⎫⎛⎫⎛⎫=-+-++- ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭1114343129n n n ⎛⎫=-= ⎪++⎝⎭，令225n T >有129225n n +>，即241825n n >+，解得18n >，故满足满足225nT >的最小正整数为19例题4．（2022·全国·高三专题练习）已知正项数列{}n a 的前n 项和n S 满足：12(N )n n S a a n +=-∈，且123+1,a a a ,成等差数列.(1)求数列{}n a 的通项公式； (2)令()()()2221N log log n n n b n a a ++=∈⋅，求证：数列{}n b 的前n 项和34n T <.【答案】(1)()2N nn a n +=∈(2)证明见解析(1)由题意：()12,n n S a a n N +=-∈，()-1-112,2,N n n S a a n n +∴=-≥∈ 两式相减得到-1=2(2,)n n a a n n N +≥∈，又0n a >，{}n a ∴是首项为1a ，公比为2的等比数列，再由123+1,a a a ,成等差数列得，得()2132+1a a a =+，即()11122+14a a a =+，则1=2a ，{}n a ∴的通项公式为()2N n n a n +=∈.(2)由题意知，22211111()(2)22log 2log 2n n n b n n n n +===-++⋅1111111111(1)232435112n T n n n n ∴=-+-+-++-+--++ 11113111122124212n n n n ⎛⎫⎛⎫=+--=-+ ⎪ ⎪++++⎝⎭⎝⎭3N ,4n n T +∈∴<例题5．（2022·河南濮阳·高二期末（文））已知数列{}n a 的前n 项和为n S ，12a =，且25a =，()*11232,n n n S S S n n +--+=≥∈N ．(1)求数列{}n a 的通项公式；(2)已知n b 是n a ，1n a +的等比中项，求数列21n b ⎧⎫⎨⎬⎩⎭的前n 项和n T ．【答案】(1)31n a n =-(2)()232nn +(1)当2n ≥时，()()113n n n n S S S S +----=，故13n n a a +-=，又12a =，且25a =， 213a a -=，满足13n n a a +-=，故数列{}n a 为公差为3的等差数列，通项公式为()21331n a n n =+-⨯=-，(2)由题意得：()()23132n b n n =-+，则()()211111313233132n b n n n n ⎛⎫==- ⎪-+-+⎝⎭，则()11111111113255831323232232n nT n n n n ⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪-+++⎝⎭⎝⎭ 例题6．（2022·海南华侨中学高二期中）设等比数列{}n a 满足124a a +=，318a a -=． (1)求{}n a 的通项公式；(2)若()()112311n n n n b a a -+⨯=++，记数列{}n b 的前n 项和为n T ，求n T 的取值范围．【答案】(1)13-=n n a (2)11,42⎡⎫⎪⎢⎣⎭(1)解：设公比为q ，由124a a +=，318a a -=，所以1121148a a q a q a +=⎧⎨-=⎩，解得11a =，3q =，所以13-=n n a ．(2)解：由（1）及()()112311n n n n b a a -+⨯=++，所以()()111231131313131n n n n n n b ---⨯==-++++，所以0112231111111113131313131313131n n n T -=-+-+-++-++++++++011113131231n n =-=-+++ 因为()()1111111111123023123131313131n n n n n n n n n T T -+++-⨯⎛⎫⎛⎫-=---=-=>⎪ ⎪++++++⎝⎭⎝⎭，即n T 单调递增，所以114n T T ≥=，又1112312n n T =-<+，所以1142n T ≤<，即11,42n T ⎡⎫∈⎪⎢⎣⎭；题型二：错位相减求和法例题1．（2022·全国·高三专题练习） 1232482n nnS =++++=（） A ．22n n n -B ．1222n n n +--C ．1212n n n +-+D ．1222n nn +-+【答案】B 由1232482n nn S =++++，得23411111112322222n n S n +⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⨯++⋅ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，两式相减得234111111112222222nn n S n +⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+++++-⋅ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭1111111111222211222212n n n n n n n n n ++++⎛⎫- ⎪--⎛⎫⎛⎫⎝⎭=-=--⋅= ⎪ ⎪⎝⎭⎝⎭-.所以1222n n nn S +--=. 故选：B.例题32．（2022·青海玉树·高三阶段练习（理））已知等差数列{}n a 的前n 项和为n S ，数列{}n b 为等比数列，且111a b ==，32312S b ==． (1)求数列{}n a ，{}n b 的通项公式；(2)若1n n n c a b +=，求数列{}n c 的前n 项和n T ．【答案】(1)32n a n =-，14n n b -=(2)()1414n n T n +=+-(1)设等差数列{}n a 的公差为d ，等比数列{}n b 的公比为q ，由题意得：13312a d +=，解得：3d =，所以()13132n a n n =+-=-，由2312b =得：24b =，所以214a q a ==，所以14n n b -=(2)()1324nn n n c a b n +==-⋅，则()2344474324n n T n =+⨯+⨯++-①， ()2341444474324n n T n +=+⨯+⨯++-②，两式相减得：()23413434343434324n n n T n +-=+⨯+⨯+⨯++⨯--()()111164433241233414n n n n n +++-=+⨯--=-+--，所以()1414n n T n +=+-例题3．（2022·江苏泰州·模拟预测）已知数列{}n a ，{}n b 的前n 项和分别为n S ，n T ，且22n n S a =-，2log =n n n b a a ．(1)求数列{}n a 的通项公式； (2)求证：当2n ≥时，4n n T S ≥+．【答案】(1)2n n a =(2)证明见解析(1)因为22n n S a =-，所以1122a a =-，则12a =，当2n ≥时，1122n n S a --=-，所以1122n n n n n a S S a a --=-=-，化简得12n n a a -=，所以数列{}n a 是以2为首项，2为公比的等比数列，因此2n n a = (2)()12122212n n n S +-==--，22log 2log 22n n nn n n b a a n =⋅=⋅=⋅，则212222nn T n =⨯+⨯++⨯……，所以231212222n n T n +=⨯+⨯++⨯……，两式相减得()231122222n n n T n ++=-⨯-+++⋅……，即()()231121222222212n nn n n T n n ++-=-++++⋅=-+⋅+-……，故()1122n n T n +=-+.所以当2n ≥时，()()()111122222244n n n n n T S n n +++-=-+--=-+≥，所以4n n T S ≥+．例题4．（2022·宁夏·银川一中模拟预测（文））已知数列{}n a 是等差数列，{}n b 是等比数列，且22b =，34b =，11a b =，851a b +=．(1)求数列{}n a 、{}n b 的通项公式； (2)设11n n n a c b ++=，数列{}n c 的前n 项和为n S ，求n S ．【答案】(1)21n a n =-，12n n b -=；(2)1242n n n S -+=-. (1)依题意，等比数列{}n b 的公比322b q b ==，则有2122n n n b b q --==，因此，111a b ==，由851a b +=得85115a b =-=，等差数列{}n a 的公差81281a a d -==-，1(1)21n a a n d n =+-=-，所以数列{}n a 、{}n b 的通项公式分别为：21n a n =-，12n n b -=.(2)由（1）知，111222n n n n n a n nc b -++===，则23123412222n n n S -=+++++，于是得23111231222222n n nn nS --=+++++，两式相减得：23111()11112212122222211222nn n n nn n n S n --+=+++++-=-=--，所以1242n n n S -+=-. 例题5．（2022·辽宁·建平县实验中学高二期中）已知各项均为正数的等比数列{}n a 的前n 项和为n S ，且26S =，314S =． (1)求数列{}n a 的通项公式； (2)若21n nn b a -=，求数列{}n b 的前n 项和n T ．【答案】(1)()*2n n a n =∈N (2)2332n nn T +=-(1)设等比数列{}n a 的公比为q ，当1q =时，1n S na =，所以2126S a ==，31314S a ==，无解．当1q ≠时，()111n n a q S q -=-，所以()()21231316,1114.1a q S q a q S q ⎧-⎪==-⎪⎨-⎪==⎪-⎩解得12a =，2q 或118a =，23q =-（舍）．所以()1*222n n n a n -=⨯=∈N ．(2)21212n n n n n b a --==．所以231135232122222n n nn n T ---=+++++①，则234111352321222222n n n n n T +--=+++++②，①－②得，2341112222212222222n n n n T +-=+++++-234111111212222222nn n +-⎛⎫=+++++- ⎪⎝⎭1111111213234221222212-++⎛⎫- ⎪-+⎝⎭=+⨯-=--n n n n n ．所以2332n nn T +=-．题型三：分组求和法例题1．（2022·新疆克孜勒苏·高一期中）数列112，134 ，158 ，1716 ，．．．，1(21)2n n -+ ，的前n 项和n S 的值等于（）A ．2112nn +-B ．21212nn n -+-C ．22112n n -+-D ．2112nn n -+-【答案】A可得()231111135212222n n S n =++++-+++++()2111121122112212n n n n n ⎛⎫- ⎪+-⎝⎭=+=+--.故选：A.例题2．（2022·辽宁·沈阳市第五十六中学高二阶段练习）数列{n a }中，1(1)(43)n n a n -=--，前n 和为n S ，则6S 为（） A ．-12 B ．16 C ．-10 D ．12【答案】A解：因为1(1)(43)n n a n -=--，所以()()()6123456=+++++S a a a a a a ，()()()159131721=-+-+-，()34=⨯-， 12=-，故选：A例题3．（2022·安徽·合肥一六八中学模拟预测（文））设数列{}n a 的前n 项和为n S ，已知1222,(1)2n n n a a a -+=+-=，则60S =_________. 【答案】960由12(1)2n n n a a -++-=，当n 为奇数时，有22n n a a ++=；当n 为偶数时，22n n a a +-=， ∴数列{}n a 的偶数项构成以2为首项，以2为公差的等差数列，则()()601357575924685860S a a a a a a a a a a a a =+++++++++++++3029152********⨯=⨯+⨯+⨯=，故答案为：960.例题4．（2022·辽宁·鞍山市华育高级中学高二期中）已知数列{}n a 是等差数列，{}n b 是等比数列，23b =，39b =，11a b =，144a b =.(1)求{}n a 、{}n b 的通项公式；(2)设n n n c a b =+，求数列{}n c 的前n 项和n S . 【答案】(1)21n a n =-，13n n b -=(2)2312n n S n -=+(1)设等比数列{}n b 的公比为q ，则323b q b ==，2123n n n b b q --∴==；又111a b ==，14427a b ==，设等差数列{}n a 的公差为d ，则141213a a d -==， ()12121n a n n ∴=+-=-.(2)由（1）得：()1213n n c n -=-+；()()()()112121321133n n n n S a a a b b b n -∴=++⋅⋅⋅++++⋅⋅⋅+=++⋅⋅⋅+-+++⋅⋅⋅+212113312132n n n n n +---=⋅+=+-. 例题5．（2022·湖北·安陆第一高中高二阶段练习）已知等差数列{}n a 的前n 项和为n S ，数列{}n b 为正项等比数列，满足213a b ==，424S S =，26b +是1b 与3b 的等差中项． (1)求数列{}n a ，{}n b 的通项公式；(2)若n n n c a b =+，n T 是数列{}n c 的前n 项和，求n T ．【答案】(1)21n a n =-，3n n b =；(2)2113322n n T n +=+⨯-.(1)设等差数列{}n a 的公差为d ，依题意可知： ()21111314324422a a d a d a d a d =+=⎧=⎧⎪⇒⎨⎨⨯=+=+⎩⎪⎩，所以数列{}n a 的通项公式为()12121n a n n =+-=-，设等比数列{}n b 的公比为q ，依题意可知：()21326b b b +=+，又13b =，所以()2223633230q q q q +=+⇒--=，又0q >，∴3q =，所以数列{}n b 的通项公式为1333n nn b -=⨯=；(2)由（1）可知：()213nn n n c a b n =+=-+所以()()()()()11221212n n n n n T a b a b a b a a a b b b =++++++=+++++++()()2131312113321322nn n n n+-+-=+=+⨯--. 例题6．（2022·重庆八中模拟预测）在等比数列{}n a 中，123,,a a a 分别是下表第一，第二，第三行中的某一个数，且123,,a a a 中的任何两个数不在下表的同一列．(1)写出123,,a a a ，并求数列n a 的通项公式；(2)若数列{}n b 满足2(1)log nn n n b a a =+-，求数列{}n b 的前2n 项和2n S ．【答案】(1)14a =，28a =，316a =，12n n a +=；(2)2224n n ++-.(1)由题意知：14a =，28a =，316a =，因为{}n a 是等比数列，所以公比为2，所以数列{}n a 的通项公式12n n a +=．(2)∵()11122(1)log (1)log (12221)n n nn n n n n n b a a n +++=++-=+-=+-，∴21232n n S b b b b =++++()()23212222345221n n n +=++++⎡-+-+--++⎤⎣⎦()22222122412n n n n +-=+=+--,题型四：倒序相加求和法例题1．（2022·江西·南城县第二中学高二阶段练习（文））德国大数学家高斯年少成名，被誉为数学届的王子.在其年幼时，对123100++++的求和运算中，提出了倒序相加法的原理，该原理基于所给数据前后对应项的和呈现一定的规律生成;因此，此方法也称之为高斯算法.现有函数4()42xx f x =+，则1232018()()()()2019201920192019f f f f ++++等于（） A ．1008 B ．1009 C ．2018 D ．2019【答案】B解：因为4()42xx f x =+，且114444()(1)1424242244--+-=+=+=+++⨯+x x x xx x xf x f x ，令1232018()()()()2019201920192019=++++S f f f f , 又2018201720161()()()()2019201920192019=++++S f f f f ，两式相加得：212018=⨯S ，解得1009S =，故选：B例题2．（2022·江西九江·高二期末（文））德国数学家高斯是近代数学奠基者之一，有“数学王子”之称，在历史上有很大的影响．他幼年时就表现出超人的数学天才，10岁时，他在进行123100++++的求和运算时，就提出了倒序相加法的原理，该原理基于所给数据前后对应项的和呈现一定的规律生成，因此，此方法也称之为高斯算法．已知数列298299-=-n n a n ，则1298+++=a a a （）A ．96B ．97C ．98D ．99【答案】C 令1297989694969897959597=++++=++++S a a a a ， 9897219896949697959597=++++=++++S a a a a ，两式相加得：969496989896949629795959797959597S ⎛⎫⎛⎫=+++++++++ ⎪ ⎪⎝⎭⎝⎭96989496969498969829797959595959797⎛⎫⎛⎫⎛⎫⎛⎫=++++++++=⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭， ∴98S =，故选:C ．例题3．（2022·全国·高三专题练习）已知函数()y f x =满足()(1)1f x f x +-=，若数列{}n a 满足121(0)(1)n n a f f f f f n n n -⎛⎫⎛⎫⎛⎫=+++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则数列{}n a 的前20项和为（）A ．100B ．105C ．110D ．115【答案】D因为函数()y f x =满足()(1)1f x f x +-=， 121(0)(1)n n a f f f f f n n n -⎛⎫⎛⎫⎛⎫=+++⋯⋯++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭①， 121(1)(0)n n n a f f f f f n n n --⎛⎫⎛⎫⎛⎫∴=+++⋯⋯++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭②，由①+②可得21n a n =+，12n n a +∴=，所以数列{}n a 是首项为1，公差为12的等差数列，其前20项和为20120121152+⎛⎫+ ⎪⎝⎭=. 故选：D.例题4．（2022·辽宁·沈阳市第一二〇中学高二期中）已知定义在R 上的函数()320237338982022f x x ⎛⎫=-+ ⎪⎝⎭，则12320221949194919491949f f f f ⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅⋅+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭___________. 【答案】73由()320237338982022f x x ⎛⎫=-+ ⎪⎝⎭，得3320232023202373202373194919493898202238982022f x x x ⎛⎫⎛⎫⎛⎫-=--+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以()33202320237320237373194938982022389820221011f x f x x x ⎛⎫⎛⎫⎛⎫+-=-++-+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，设12320221949194919491949S f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=+++⋅⋅⋅+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭①, 20222021202011949194919491949S f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=+++⋅⋅⋅+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭②, 由+①②，得 1202222021202212194919491949194919491949S f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++⋅⋅⋅+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭+ 即7373732101110111011S =++⋅⋅⋅+，于是有73220221011S =⨯，解得73S =，所以1232022731949194919491949f f f f ⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅⋅+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 故答案为：73.例题5．（2022·黑龙江·鹤岗一中高二阶段练习）已知函数()1e e xx f x =+，数列{}n a 为等比数列，0n a >，1831a =，则()()()()123365ln ln ln ln f a f a f a f a ++++=______．【答案】3652∵()e e 1xx f x =+，∴()()e e e e 1)e (e 1)2e e 1e 1e 1(e 1)(e (e 1)2e x x x x x x x xxx x x x xf x f x -------++++++-=+===++++++． ∵数列{}n a 是等比数列，∴2136523641831a a a a a ====，∴2136523643651183ln ln ln ln ln ln ln 0a a a a a a a +=+==+==．设()()()36512365ln ln ln S f a f a f a =+++，① 则()()()3653653641ln ln ln S f a f a f a =+++，②①＋②，得()()()()()()()()()3651365236436512ln ln ln ln ln ln S f a f a f a f a f a f a =++++++365=，∴3653652S =．故答案为：3652例题6．（2022·全国·高二课时练习）已知()442xx f x =+，求122010201120112011f f f ⎛⎫⎛⎫⎛⎫++⋅⋅⋅+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 【答案】1005.因为()442x x f x =+，所以()1144214242442x x xx f x ---===++⨯+，所以()()11f x f x +-=.令12200920102011201120112011S f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=++⋅⋅⋅++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，倒写得20102009212011201120112011S f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=++⋅⋅⋅++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 两式相加得22010S =，故1005S =.例题7．（2022·全国·高三专题练习）已知函数()21122f x x x =+，数列{}n a 的前n 项和为n S ，点()()*,N n n S n ∈均在函数()f x 的图象上，函数()442x x g x =+.(1)求数列{}n a 的通项公式； (2)求()()1g x g x +-的值；(3)令()*2021n n a b g n ⎛⎫=∈ ⎪⎝⎭N ，求数列{}n b 的前2020项和2020T .【答案】(1)n a n =(2)1(3)1010(1)因为点()()*,N n n S n ∈均在函数()f x 的图象上，所以21122n S n n =+，当2n ≥时，()()2211111112222n n n a S S n n n n n -=-=+----=，当1n =时，111a S ==，适合上式，所以n a n =. (2)因为()442x x g x =+，所以()114214242x x xg x ---==++，所以()()42114242x x x g x g x +-=+=++.(3)由（1）知n a n =，可得20212021n n a n b g g ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，所以2020122020122020202120212021T b b b g g g ⎛⎫⎛⎫⎛⎫=+++=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，① 又因为2020202020191202020191202120212021T b b b g g g ⎛⎫⎛⎫⎛⎫=+++=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，② 因为()()11g x g x +-=，所以①+②，得202022020T =，所以20201010T =.1．记n S 为数列{}n a 的前n 项和，已知11,n n S a a ⎧⎫=⎨⎬⎩⎭是公差为13的等差数列．(1)求{}n a 的通项公式； (2)证明：121112na a a +++<．【答案】(1)()12n n n a +=(2)见解析(1)∵11a =，∴111S a ==,∴111S a =,又∵n n S a ⎧⎫⎨⎬⎩⎭是公差为13的等差数列，∴()121133n n S n n a +=+-=,∴()23n n n a S +=, ∴当2n ≥时，()1113n n n a S --+=，∴()()112133n n n n n n a n a a S S --++=-=-,整理得：()()111n n n a n a --=+, 即111n n a n a n -+=-, ∴31211221n n n n n a a a a a a a a a a ---=⨯⨯⨯⋯⨯⨯ ()1341123212n n n n n n ++=⨯⨯⨯⋯⨯⨯=--，显然对于1n =也成立， ∴{}n a 的通项公式()12n n n a +=；(2)()12112,11n a n n n n ⎛⎫==- ⎪++⎝⎭ ∴12111na a a +++1111112121222311n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-=-< ⎪ ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 2．设{}n a 是公比不为1的等比数列，1a 为2a ，3a 的等差中项．（1）求{}n a 的公比；（2）若11a =，求数列{}n na 的前n 项和．【答案】（1）2-；（2）1(13)(2)9nn n S -+-=. （1）设{}n a 的公比为q ，1a 为23,a a 的等差中项， 212312,0,20a a a a q q =+≠∴+-=，1,2q q ≠∴=-；（2）设{}n na 的前n 项和为n S ，111,(2)n n a a -==-，21112(2)3(2)(2)n n S n -=⨯+⨯-+⨯-++-，①23121(2)2(2)3(2)(1)(2)(2)n n n S n n --=⨯-+⨯-+⨯-+--+-，②①-②得，2131(2)(2)(2)(2)n n n S n -=+-+-++---1(2)1(13)(2)(2)1(2)3n n n n n ---+-=--=--， 1(13)(2)9nn n S -+-∴=. 3．设数列{}n a 满足13a =，134n n a a n +=-．（1）计算2a ，3a ，猜想{}n a 的通项公式并加以证明；（2）求数列{2}nn a 的前n 项和n S ．【答案】（1）25a =，37a =，21n a n =+，证明见解析；（2）1(21)22n n S n +=-⋅+.（1）［方法一］【最优解】：通性通法由题意可得2134945a a =-=-=，32381587a a =-=-=，由数列{}n a 的前三项可猜想数列{}n a 是以3为首项，2为公差的等差数列，即21n a n =+．证明如下：当1n =时，13a =成立；假设()n k k *=∈N 时，21k a k =+成立.那么1n k =+时，1343(21)4232(1)1k k a a k k k k k +=-=+-=+=++也成立. 则对任意的*n N ∈，都有21n a n =+成立；［方法二］：构造法由题意可得2134945a a =-=-=，32381587a a =-=-=．由123,5a a ==得212a a -=．134n n a a n +=-，则134(1)(2)n n a a n n -=--≥，两式相减得()1134n n n n a a a a +--=--．令1n n n b a a +=-，且12b =，所以134n n b b -=-，两边同时减去2，得()1232n n b b --=-，且120b -=，所以20n b -=，即12n n a a +-=，又212a a -=，因此{}n a 是首项为3，公差为2的等差数列，所以21n a n =+．［方法三］：累加法由题意可得2134945a a =-=-=，32381587a a =-=-=．由134n n a a n +=-得1114333n n n n n a a n+++-=-，即2121214333a a -=-⨯，3232318333a a -=-⨯，……1114(1)(2)333n n n n n a a n n ---=--⨯≥．以上各式等号两边相加得1123111412(1)33333n n n a a n ⎡⎤-=-⨯+⨯++-⨯⎢⎥⎣⎦，所以1(21)33n n na n =+⋅．所以21(2)n a n n =+≥．当1n =时也符合上式．综上所述，21n a n =+．［方法四］：构造法21322345,387a a a a =-==-=，猜想21n a n =+．由于134n n a a n +=-，所以可设()1(1)3n n a n a n λμλμ++++=++，其中,λμ为常数．整理得1322n n a a n λμλ+=++-．故24,20λμλ=--=，解得2,1λμ=-=-．所以()112(1)13(21)3211nn n a n a n a +-+-=--=⋅⋅⋅=-⨯-．又130a -=，所以{}21n a n --是各项均为0的常数列，故210n a n --=，即21n a n =+．（2）由（1）可知，2(21)2n n n a n ⋅=+⋅［方法一］：错位相减法231325272(21)2(21)2n n n S n n -=⨯+⨯+⨯++-⋅++⋅，① 23412325272(21)2(21)2n n n S n n +=⨯+⨯+⨯++-⋅++⋅，②由①-②得：()23162222(21)2n n n S n +-=+⨯+++-+⋅()21121262(21)212n n n -+-=+⨯-+⋅⨯-1(12)22n n +=-⋅-，即1(21)22n n S n +=-⋅+.［方法二］【最优解】：裂项相消法112(21)2(21)2(23)2n n n n n n n a n n n b b ++=+=---=-，所以231232222n n nS a a a a =++++()()()()2132431n n b b b b b b b b +=-+-+-++-11n b b +=-1(21)22n n +=-+．［方法三］：构造法当2n ≥时，1(21)2n n n S S n -=++⋅，设11()2[(1)]2n n n n S pn q S p n q --++⋅=+-+⋅，即122nn n pn q p S S ----=+⋅，则2,21,2pq p -⎧=⎪⎪⎨--⎪=⎪⎩，解得4,2p q =-=．所以11(42)2[4(1)2]2n n n n S n S n --+-+⋅=+--+⋅，即{}(42)2n n S n +-+⋅为常数列，而1(42)22S +-+⋅=，所以(42)22nn S n +-+⋅=．故12(21)2n n S n +=+-⋅．［方法四］：因为12(21)2222422n n n n n nn a n n n -=+=⋅+=⋅+，令12n n b n -=⋅，则()()231()0,11n nx x f x x x x x x x-=++++=≠-，()121211(1)()1231(1)nn n n x x nx n x f x x x nx x x +-'⎡⎤-+-+=++++==⎢⎥--⎢⎥⎣⎦'，所以12n b b b +++21122322n n -=+⋅+⋅++⋅1(2)12(1)2n nf n n +==+-+'⋅．故234(2)2222nn S f =++'+++()1212412(1)212n n nn n +-⎡⎤=+⋅-++⎣⎦-1(21)22n n +=-+．。

2024届苏教版高考数学一轮复习数列求和课件1

第四节数列求和
【课标标准】掌握非等差、等比数列求和的几种常见方法．
必备知识·夯实双基
√ √
× √
14破
题后师说
分组转化法求和的两种常见类型
题后师说使用裂项相消法求和时，要注意正负项相消时消去了哪些项，保留了哪些项，切不可漏写未被消去的项，未被消去的项有前后对称的特点，实质上造成正负相消是此法的根源与目的．
则a10＝( )
A．36
B．45
C．55
D．66
答案：C
题后师说形如an＋1－an＝f(n)的数列，利用累加法，即用公式an＝(an－an－1)＋ (an－1－an－2)＋…＋(a2－a1)＋a1(n≥2)，可求数列{an}的通项公式．
答案：A
(2)[2023·山东肥城模拟]已知数列{an}的前n项和为Sn，若nSn＋1＝(n＋ 2)Sn，且a1＝1，求{an}的通项公式．
5
4．[2020·全国卷Ⅰ]设{an}是公比不为1的等比数列，a1为a2，a3的等差中项．
(1)求{an}的公比； (2)若a1＝1，求数列{nan}的前n项和．
专题突破❻ 由数列的递推关系求通项公式
微专题1 累加法
例1 (1)已知数列{an}满足a1＝1，对任意的n∈N*都有an＋1＝an＋n＋1，

第5章第4讲数列求和-2022版高三数学(新高考)一轮复习课件_ppt(56张)

天气骤冷2，0红2旗0 冻结。这句诗形象的写出了色彩鲜明、红白映衬的景象，“掣”字用了拟人的修辞手法，生动形象的写出了塞外天气的恶劣，寒风的呼啸。但在这样的环境下，红
旗却被冻的不会翻动了，更加突出了雪之大、天气之寒冷。从“红”字能反衬出白雪皑皑的景象，而“不翻”则衬托出了天气的寒冷。二是语言清新淡雅而又晶莹明丽，明白晓畅而又情韵悠长。
返回导航
第五章数列
高考一轮总复习 • 数学 • 新高考
返回导航
3．(必修 5P47T4 改编)数列{an}的通项公式是 an＝
1 n＋
n＋1，前
n
项和为
9，则
n＝( B ) A．9
B．99
C．10
D．100
[解析]
因为 an＝
1 n＋
n＋1＝
n＋1－
n.所以 Sn＝a1＋a2＋a3＋…＋an＝(
返回导航
知识梳理 • 双基自测
第五章数列
高考一轮总复习 • 数学 • 新高考
返回导航
知识点一公式法求和
(1)如果一个数列是等差数列或等比数列，则求和时直接利用等差、等比数列的前 n 项和公式．
(2)等差数列的前 n 项和公式： Sn＝na1＋ 2 an＝___n_a_1＋__n__n_2－__1__d__＝___d2_n_2＋__(_a_1_－__d2_)n________.
第五章数列
高考一轮总复习 • 数学 • 新高考
(3)等比数列的前 n 项和公式： na1，q＝1，
Sn＝a11－－aqnq＝_______________，q≠1. 注意等比数列公比 q 的取值情况，要分 q＝1，q≠1.
返回导航
第五章数列
高考一轮总复习 • 数学 • 新高考

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

3．(2018·高考江苏卷)已知集合 A＝{x|x＝2n－1，n∈N*}，B＝ {x|x＝2n，n∈N*}．将 A∪B 的所有元素从小到大依次排列构成一个数列{an}．记 Sn 为数列{an}的前 n 项和，则使得 Sn>12an＋1 成立的 n 的最小值为________．解析：所有的正奇数和 2n(n∈N*)按照从小到大的顺序排列构成 {an}，在数列{an}中，25 前面有 16 个正奇数，即 a21＝25，a38＝ 26.当 n＝1 时，S1＝1<12a2＝24，不符合题意；当 n＝2 时，S2 ＝3<12a3＝36，不符合题意；当 n＝3 时，S3＝6<12a4＝48，不符合题意；当 n＝4 时，S4＝10<12a5＝60，不符合题意；……；
答案：(n－1)2n＋1＋2
2．已知数列{an}：12，13＋23，14＋24＋34，…，110＋120＋130＋…＋190，…，若 bn＝ana1n＋1，那么数列{bn}的前 n 项和 Sn＝________．
解析：an＝1＋2＋n3＋＋1…＋n＝n2，所以 bn＝ana1n＋1＝n（n4＋1）＝4n1－n＋1 1，所以 Sn＝41－12＋12－13＋…＋n1－n＋1 1 ＝41－n＋1 1＝n4＋n1. 答案：n4＋n1
1．数列 112，214，318，4116，…的前 n 项和是________．解析：前 n 项和 Sn＝(1＋2＋3＋…＋n)＋12＋212＋…＋21n＝ n（n2＋1）＋1211－－1212n＝n（n2＋1）＋1－21n. 答案：n（n2＋1）＋1－21n
2．数列2×1 4，4×1 6，6×1 8，…，2n（21n＋2），…的前 n 项和为________．解析：因为 an＝2n（21n＋2）＝14n1－n＋1 1，则 Sn＝141－12＋12－13＋…＋n1－n＋1 1 ＝141－n＋1 1＝4（nn＋1）. 答案的前 n 项和 Sn＝n2＋2 n，n∈N*. (1)求数列{an}的通项公式； (2)设 bn＝2an＋(－1)nan，求数列{bn}的前 2n 项和．
【解】 (1)当 n＝1 时，a1＝S1＝1；当 n≥2 时，an＝Sn－Sn－1 ＝n2＋2 n－（n－1）2＋2 （n－1）＝n. a1 也满足 an＝n，故数列{an}的通项公式为 an＝n.
(2)分组转化法若一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成，则求和时可用分组转化法，分别求和后相加减． (3)错位相减法如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么这个数列的前 n 项和即可用此法来求，等比数列的前 n 项和就是用此法推导的． (4)裂项相消法把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得其和．
当 n＝26 时，S26＝21×（12＋41）＋2×（1－1－225）＝441＋62＝ 503<12a27＝516，不符合题意；当 n＝27 时，S27＝22×（12＋43）＋2×（1－1－2 25）＝484＋62＝546>12a28＝540，符合题意．故使得 Sn>12an＋1 成立的 n 的最小值为 27. 答案：27
(2)由(1)知 an＝n，故 bn＝2n＋(－1)nn. 记数列{bn}的前 2n 项和为 T2n，则 T2n＝(21＋22＋…＋22n)＋(－1 ＋2－3＋4－…＋2n)．记 A＝21＋22＋…＋22n，B＝－1＋2－3＋4－…＋2n，则 A＝2（11－－222n）＝22n＋1－2， B＝(－1＋2)＋(－3＋4)＋…＋[－(2n－1)＋2n]＝n. 故数列{bn}的前 2n 项和 T2n＝A＋B＝22n＋1＋n－2.
3．等比数列{an}的首项为 a，公比为 q，Sn 为其前 n 项的和，求 S1＋S2＋…＋Sn. 解：当 q＝1 时，an＝a，Sn＝na，所以 S1＋S2＋…＋Sn＝(1＋2＋…＋n)a＝n（n2＋1）a. 当 q≠1 时，因为 Sn＝a（11－－qqn），所以 S1＋S2＋…＋Sn
＝1－a q[(1－q)＋(1－q2)＋…＋(1－qn)] ＝1－a q[n－(q＋q2＋…＋qn)] ＝1－a qn－q（11－－qqn）＝1n－aq－aq（（11－－qq）n）2 .
分组转化法求和的常见类型 (1)若 an＝bn±cn，且{bn}，{cn}为等差或等比数列，可采用分组转化法求{an}的前 n 项和． (2)通项公式为 an＝bcnn，，nn为为偶奇数数的数列，其中数列{bn}，{cn}是等比数列或等差数列，可采用分组转化法求{an}的前 n 项和．
第五章数列
第 4 讲数列求和
1．公式法如果一个数列是等差数列或等比数列，则求和时直接利用等差或等比数列的前 n 项和公式． 2．非等差、等比数列求和的常用方法 (1)倒序相加法如果一个数列{an}，首末两端等“距离”的两项的和相等或等于同一个常数，那么求这个数列的前 n 项和即可用倒序相加法，等差数列的前 n 项和即是用此法推导的．
1．已知数列{an}的前 n 项和为 Sn 且 an＝n·2n，则 Sn＝________. 解析：Sn＝1×2＋2×22＋3×23＋…＋n×2n，① 所以 2Sn＝1×22＋2×23＋3×24＋…＋n×2n＋1，② ①－②得－Sn＝2＋22＋23＋…＋2n－n×2n＋1＝2×（1－1－2 2n）－ n×2n＋1，所以 Sn＝(n－1)2n＋1＋2.
1．必明辨的 3 个易错点 (1)在应用等比数列的前 n 项和公式时，注意等比数列公比 q 的取值情况，要分 q＝1 和 q≠1. (2)在应用错位相减法时，注意观察未合并项的正负号． (3)在应用裂项相消法时，要注意消项的规律具有对称性，即前剩多少项则后剩多少项．
2．必会的 2 种方法解决非等差、等比数列的求和，主要有两种思路： (1)转化思想，即将一般数列设法转化为等差或等比数列，这一思想方法往往通过通项分解或错位相减来完成． (2)不能转化为等差或等比数列的数列，往往通过裂项相消法、错位相减法、倒序相加法等来求和．