第四章--能带理论PPT课件
合集下载
能带理论课件

2
k V k
II、能量的二级修正:
Ek(2)
k
Ek0 Ek0
kV k
a. k k n 2
a
kVka 10 aei2a nV()dVn
b. k kn2 kV k 0
a
2
二级微扰能:
E (2) k
k
kV k Ek0 Ek0
n
Vn 2
2 2m
k
2
(k
n a
2
)2
微扰下的电子能量就可写成:
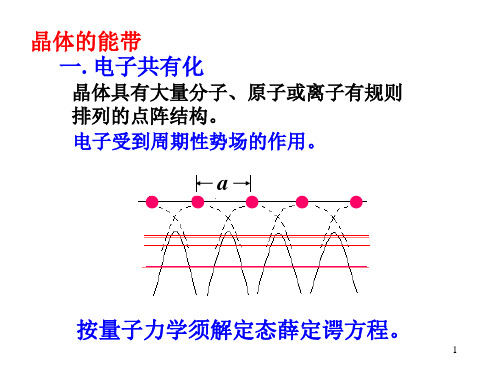
有 N个具有相同能量 的束缚态波函数 ,所以在不考虑原 认为一个电子在离子实和其他电子所形成的势场中运动,称为哈特里—福克自洽场近似,也称为单电子近似。
二、近自由电子近似(Nearly Free Electron)模型
在周期场中,若电子的势能随位置的变化(起伏)比较 小,而电子的平均动能要比其势能的绝对值大得多时,电 子
的运动就几乎是自由的。因此,我们可以把自由电子看成是
它的零级近似,而将周期场的影响看成小的微扰来V求解。
(也称为弱周期V 场(近x)似)V。势场V(x)可用平均势 代替,
E
Ek0
Vn
2Tn
(
2Tn Vn
1)
Ek0 Vn
2Tn
(
2Tn Vn
1)
E i:原来较低的
E
0 k
态微扰使它下降为:
E ii:原来较高的
E
0 k
态微扰使它更高为:
差别为 2 V n
——在近自由电子近似中,在晶体中运动的共有电子被看成
是近自由电子。所有电子及原子实产生的场是具有晶格周期
性的等效势场,周期性势场的起伏对共有化电子
能带理论 PPT课件

电阻率为 10-8Ω•m 以下的物体为导体 电阻率为108Ω•m以上的物体为绝缘体 电阻率介乎上面两者之间的为半导体
引子: ★孤立的原子,其轨道电子的能量由一系列分立 的能级所表征; ★原子结合成固体时,这些原子的能级变扩展而 形成能带; ∴★因一为个在固原体子是内否层导能电级取上决充于满同电价子电,子所能以级相相应对的应的 能内带层能→带价是带满是带否→被电不子参填与满导电;
由于N 很大,新能级中相邻两能级的能量差仅 为 10-22eV,几乎可以看成是连续的,N 个新能 级具有一定的能量范围,通常称为能带。 即:使本来处于同一能量状态的电子产生微小的 能量差异,与此相对应的能级扩展为能带。
通常采用与原子能级相同的符号来表示能带,如1s 带,2p 带等!
三、能带结构
1、能带
★通常情况下,价带为能量最高的 能带;
★价带可能被电子填满,成为满带; ★也可能未被电子填满,形成不满
带或半满带。
空带
带隙
价带
在绝缘体中,价电子刚好填满 最低的一系列能带,最上边的 满带 —— 价带
绝缘体
再高的各能带全部都是空的 —— 空带
导体中,一部分价电子存在于不满带中,这种能 带称为导带
导带
(1)导体:能带结构有三种形式
形式1:价带中只填充了部分电子,在外加电场作用 下,这些电子很容易在该能带中从低能级跃迁到较 高能级 —— 从而形成电流
导带中电子的转移
例如: 金属Li 电子排布1s22s1 每个原子只有一个价电子,整个晶体中的价电子只 能添满半个价带 —— 实际参与导电的是不满带中 的电子 —— 电子导电型导体
这些允许的范围称为能带 不能处于两个能带之间的区域,此区域称为禁带
关于能带的形成,还可以从晶体中各个原子的能级的 相互影响来说明: 能 级:
引子: ★孤立的原子,其轨道电子的能量由一系列分立 的能级所表征; ★原子结合成固体时,这些原子的能级变扩展而 形成能带; ∴★因一为个在固原体子是内否层导能电级取上决充于满同电价子电,子所能以级相相应对的应的 能内带层能→带价是带满是带否→被电不子参填与满导电;
由于N 很大,新能级中相邻两能级的能量差仅 为 10-22eV,几乎可以看成是连续的,N 个新能 级具有一定的能量范围,通常称为能带。 即:使本来处于同一能量状态的电子产生微小的 能量差异,与此相对应的能级扩展为能带。
通常采用与原子能级相同的符号来表示能带,如1s 带,2p 带等!
三、能带结构
1、能带
★通常情况下,价带为能量最高的 能带;
★价带可能被电子填满,成为满带; ★也可能未被电子填满,形成不满
带或半满带。
空带
带隙
价带
在绝缘体中,价电子刚好填满 最低的一系列能带,最上边的 满带 —— 价带
绝缘体
再高的各能带全部都是空的 —— 空带
导体中,一部分价电子存在于不满带中,这种能 带称为导带
导带
(1)导体:能带结构有三种形式
形式1:价带中只填充了部分电子,在外加电场作用 下,这些电子很容易在该能带中从低能级跃迁到较 高能级 —— 从而形成电流
导带中电子的转移
例如: 金属Li 电子排布1s22s1 每个原子只有一个价电子,整个晶体中的价电子只 能添满半个价带 —— 实际参与导电的是不满带中 的电子 —— 电子导电型导体
这些允许的范围称为能带 不能处于两个能带之间的区域,此区域称为禁带
关于能带的形成,还可以从晶体中各个原子的能级的 相互影响来说明: 能 级:
能带理论及其应用ppt课件

分布向电场反方向移动。因为有
dk
e
dt
•
(a)布洛赫振荡:刚有外场时,由于
v(k )
是
k
的周
期函数,故电子速度发生周期性振荡,电子在实空
间位置也发生振荡,此效应称为布洛赫振荡。
• (b)当电子运动时,受到晶格振动、杂质和缺陷 的散射,达到一个稳定的不对称分布,不再振荡。 此时,沿电场正反方向电子数不相等,总的电流不
(1)研究离子运动时,认为电子能跟上离子位置变化,不考 虑其影响——即晶格振动问题,描述原子或离子围绕平衡
位置的小振动问题。
(2)研究电子运动时,假定离子实静止在平衡位置上,晶格 具有严格周期性,而晶格振动对电子影响当作微扰来处
理——即能带理论,研究固体中的电子状态。
单电子近似:含有大量电子的体系中,每个电子受到其
•
出,
l1,
k
l2,l3 为整数),
相邻取值相差很小。
最新版整理ppt
12
•
2. 能带: 对于同一个n的
En(k)
由不同的
k
组成许多靠得很
近的能级组,称为能带。
• 3. 能带结构 对于不同的n,En(k) 形成单电子能谱。En(k) 的总体 称为晶体的能带结构。
1.
所以单电子能谱是由许多能带组成(每个n对应 一个能带)。 • 对值一,个靠能得带很中近的为准En(k连)是续)k 相的邻准能连带续E函n(k)数和(分立 En1(k) 之间可以相接,重叠或分开。
23
紧束缚近似的晶格势场
A
rRm
注:
V(rR m)
r
Rm
Rm 处格点对A处
电子的作用;
a
V
研究生课件-能带理论
设孤立原子的一个能级 Enl ,它最多能容 纳 2 (2 l +1)个电子。
这一能级分裂成由 N条能级组成的能带后, 能带最多能容纳 2N(2l +1)个电子。
6
2N(2l+1)
例如,1s、2s能带,最多容纳 2N个电子。 2p、3p能带,最多容纳 6N个电子。
电子排布时,应从最低的能级排起。
有关能带被占据情况的几个名词:
计算表明: U0b 的数值越大所得到的能带越窄。 由于原子的内层电子受到原子核的束缚较大, 与外层电子相比,它们的势垒强度较大。
所以,内层电子的能带较窄。 外层电子的能带较宽。
26
从 E ~ k 曲线还可以
E
看出: k 值越大,
相应的能带越宽。
E7
k n 2 n 2
Na L (n 0,1,2,)
maU 2
0b
sin
a
a
cos
(
a)
cos(ka)
(4)
式中
2mE
而 k 2 是电子波的角波数*。
(4)式就是电子的能量 E 应满足的方程,也是电子
能量 E与角波数 k 之间的关系式。
注*:有兴趣的读者可参阅〈固体物理基础〉
蔡伯熏编(1990)P 268。
21
maU 2
0b
s
in
a
由周期性边界条件可以推出:布洛赫波函数 的
波数 k 只能取一些特定的分立值。
13
证明如下:
由周期性边界条件 k ( x) k ( x Na)
(3)
按照布洛赫定理:
左边为 右边为
k ( x) ei k xuk ( x)
k
(
x
Na )
这一能级分裂成由 N条能级组成的能带后, 能带最多能容纳 2N(2l +1)个电子。
6
2N(2l+1)
例如,1s、2s能带,最多容纳 2N个电子。 2p、3p能带,最多容纳 6N个电子。
电子排布时,应从最低的能级排起。
有关能带被占据情况的几个名词:
计算表明: U0b 的数值越大所得到的能带越窄。 由于原子的内层电子受到原子核的束缚较大, 与外层电子相比,它们的势垒强度较大。
所以,内层电子的能带较窄。 外层电子的能带较宽。
26
从 E ~ k 曲线还可以
E
看出: k 值越大,
相应的能带越宽。
E7
k n 2 n 2
Na L (n 0,1,2,)
maU 2
0b
sin
a
a
cos
(
a)
cos(ka)
(4)
式中
2mE
而 k 2 是电子波的角波数*。
(4)式就是电子的能量 E 应满足的方程,也是电子
能量 E与角波数 k 之间的关系式。
注*:有兴趣的读者可参阅〈固体物理基础〉
蔡伯熏编(1990)P 268。
21
maU 2
0b
s
in
a
由周期性边界条件可以推出:布洛赫波函数 的
波数 k 只能取一些特定的分立值。
13
证明如下:
由周期性边界条件 k ( x) k ( x Na)
(3)
按照布洛赫定理:
左边为 右边为
k ( x) ei k xuk ( x)
k
(
x
Na )
第四章-能带理论-(Band-Theory)

能带理论 - 3 (Band Theory)
近自由电子适用于价电子束缚较弱的金属晶体, 采用赝 势方法后也可以用来研究半导体的价带和导带;对于价电子 束缚较强的半导体和绝缘体, 通常采用紧束缚近似 (TightBinding Approximation, TBA) 来讨论其电子结构.
1
与利用平面波描写零级近似状态的近自由电子 近似不同, 紧束缚近似中首先把电子看作所属原子 的电子, 晶体环境对电子的影响则作为微扰处理.
N
2
V
2
3
4
3
kF2
kF
3 2n 1/3 .
Fermi 球的表面称为 Fermi 面, Fermi 面的能量
称为Fermi 能 (级). Fermi 能对应的动量和速度分称
为 Fermi 动量和 Fermi 速度.
15
一方面, 三维晶体的能量作为简约波矢的函数, 随波矢方向变换而性质有所变化; 另一方面, 三维BZ 构造复杂, 讨论起来比较困难.
由于对称性的存在, 实际上人们并不需要研究整 个BZ (FBZ). 利用对称性, 人们可以通过研究部分 FBZ的情况来了解整个FBZ.
16
晶体全部对称操作的集合构成空间群.
26
原子中的电子能级是分立的, 可以具体表明各能 级的能量. 固体中, 电子能级形成准连续的能带, 标明 每个能级很困难也没有必要. 这时通常引入能态密度 来描写能级的分布:
状态数
能态密度: N E lim Z
E0 E
能量间隔
27
k 空间等能面 E 和 E + ΔE 之间的状态数为
Z
2V
V
当 取遍晶体所属点群中的所有对称操作, 得到一组
k , 它们是等价的, 称为 k*.
近自由电子适用于价电子束缚较弱的金属晶体, 采用赝 势方法后也可以用来研究半导体的价带和导带;对于价电子 束缚较强的半导体和绝缘体, 通常采用紧束缚近似 (TightBinding Approximation, TBA) 来讨论其电子结构.
1
与利用平面波描写零级近似状态的近自由电子 近似不同, 紧束缚近似中首先把电子看作所属原子 的电子, 晶体环境对电子的影响则作为微扰处理.
N
2
V
2
3
4
3
kF2
kF
3 2n 1/3 .
Fermi 球的表面称为 Fermi 面, Fermi 面的能量
称为Fermi 能 (级). Fermi 能对应的动量和速度分称
为 Fermi 动量和 Fermi 速度.
15
一方面, 三维晶体的能量作为简约波矢的函数, 随波矢方向变换而性质有所变化; 另一方面, 三维BZ 构造复杂, 讨论起来比较困难.
由于对称性的存在, 实际上人们并不需要研究整 个BZ (FBZ). 利用对称性, 人们可以通过研究部分 FBZ的情况来了解整个FBZ.
16
晶体全部对称操作的集合构成空间群.
26
原子中的电子能级是分立的, 可以具体表明各能 级的能量. 固体中, 电子能级形成准连续的能带, 标明 每个能级很困难也没有必要. 这时通常引入能态密度 来描写能级的分布:
状态数
能态密度: N E lim Z
E0 E
能量间隔
27
k 空间等能面 E 和 E + ΔE 之间的状态数为
Z
2V
V
当 取遍晶体所属点群中的所有对称操作, 得到一组
k , 它们是等价的, 称为 k*.
固体物理晶体能带的对称性PPT课件

—— 成键态对应的四个能带交叠在一起形成Si的价带 —— 反键态对应的四个能带交叠在一起形成Si的导带
THANK
YOU
SUCCESS
2019/4/4
04_06 晶体能带的对称性 1 能带关于k的周期性
2 电子波矢 k k n 的布洛赫函数 a
2 E (k ) E (k n ) a
能量本征值
e
m
ik Rm
i ( r Rm )
ikR E (k ) i J ( Rs )e s s
E (k ) i J 0
Rs Nearest
ikR s J ( R ) e s
2 原子能级与能带的对应
2 E (k ) E (k n ) a
2 k' k n a
—— 三维情况中表示
E(k ) E(k Gn )
2 能带的时间反演对称性 可以证明
E ( k ) E ( k )
3 能带的3种表示图式 1) 扩展能区图式 第一能带 E1 (k )
k
a
~
固体物理 Solid State Physics
第四章 能带理论
§4.6晶体能带的对称性
1 模型与微扰计算
—— 紧束缚近似方法的思想
—— 电子在一个原子(格点)附近时 主要受到该原子势场的作用 —— 将其它原子势场的作用看作是微扰
对于确定的 k
晶体中电子的波函数
1 k (r ) N
a
第二能带 E2Hale Waihona Puke (k )2 k ~ a a
2 ~ a a
2) 简约能区图式 —— 对于同一个能带来说能量在k空间具有周期性
固体物理-第四章 能带理论-1(新疆大学李强老师课件)概要

… 禁带
1s
N个钠原子
Xinjiang University Solid State Physics, Dr. Q. Li
允带
N个
钠晶体
2018/11/27
…
第四章 能带理论
讨论固体中电子的运动,能带理论基于以下近似:
绝热近似:由于原子实的质量是电子质量的103~105倍,所 以原子实的运动要比价电子的运动缓慢得多,于是可以忽略 原子实的运动,把问题简化为n个价电子在N个固定不动周期 排列的原子实的势场中运动。 多体问题 →多电子问题 单电子近似:忽略电子之间的相互作用。晶体中的任一电子 都可视为是处在原子实周期势场和其它(n-1)个电子所产生的 等效势场中。 多电子问题→单电子问题 理想晶体假设:忽略晶体中的缺陷和杂质,认为晶格具有严 格的周期性。 等效势场V(r)具有周期性。
新疆大学
固体物理 Solid State Physics
物理科学与技术学院 李强 2009. 1st term
第四章 能带理论
能带理论:研究固体中电子运动的主要理论基础 能带理论定性地阐明了晶体中电子运动的普遍性的 特点。其主要成就:
说明了导体、半导体和绝缘体的区别; 解释了电子输运过程(电导、传热等)中自由 程远大于原子间距; 能带论提供了分析半导体理论问题的基础,推 动了半导体技术的发展。
2018/11/27
R≫a时两个Na原子体系的势能曲线
Xinjiang University Solid State Physics, Dr. Q. Li
第四章 能带理论
以Na晶体为例说明组成晶体时的电子共有化
当N个Na原子组成体心立方晶体时,各个原子间距达到a。
第四章 能带理论.ppt
可以用分离变量法对单个电子独立求解(单电子近似)。
1 单电子所受的势场为: U (r ) u (r ) e
Rn
Ze 2 4 0 r Rm
无论电子之间相互作用的形式如何,都可以假定电子所感受 到的势场具有平移对称性(周期场近似): U (r Rn ) U (r ) 通过上述近似,复杂多体问题变为周期势场下的单电子 问题,单电子薛定谔方程为:
假定在体积 V=L3 中有 N 个带正电荷的离子实,相应地有 NZ 个价电子, 那么该系统的哈密顿量为:
2 2 N 1 1 e ˆ H ' 2 n 2 m 2 4 2 M r r i 1 i, j n 1 0 i j NZ 2 i NZ N 1 1 ( Ze) 2 1 Ze 2 ' 2 m ,n 4 0 Rn Rm i 1 n 1 4 0 ri Rn 2
H ' V ( x) V V
0 (1) ( 2) E E E E 根据微扰理论,电子的能量本征值 k k k k .
一级能量修正
Ek(1) k | H ' | k k | V ( x) V | k
Ek(1)
0 L
1 ikx 1 e [V ( x ) V ] eikx dx L L 1 ikx 1 e V ( x ) eikx dx ] V L L
k r e
ikr
uk r
—— Bloch函数
这里,uk(r) = uk(r +Rl) 是以格矢 Rl 为周期的周期函数。
它确定了波动方程解的基本特点。
4.1
布洛赫定理
二. Bloch 定理的物理证明(定性说明):
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
21
( x ) u ( x )e ikx
2 2m
d
2 ( x ) dx 2
V
( x )
( x )
E
(x dx
(x)
2
(V 0
E
)
(x)
0
K
2
2m(E V0) 2
0
V (x)
V0
1 ( x ) Ae iKx Be iKx
V0
ab 晶格常数c=a+b
2021
22
( x ) u ( x )e ikx
2 2m
d 2 ( x )
dx 2
V
( x)
( x)
E
(x)
2
2
m
d
2 ( x) E ( x) 0
dx 2
18
电子波矢k的取值: a
2 b1 a
分布密度= L 2
(k,rN) a (k,r)
(k, x Na) ei kNa (k, x) (k, x)
e ikNa 1
均匀分布
kN 2a m,m in . t 间隔为b/N 的N个k点。
2m 2m mb
k
Na L 2021 N
19
L1 L2
第四章 能带理论
2021
1
2021
2
2021
3
1. Bloch 定理与周期性边界条件 晶体中电子的运动遵守
Hˆ
(
k,
r
)
E
(k
,
r
)
2 2m
2
V
(r )
(k ,
r)
E
(k ,r )
V
(
r
)
V
(r
R)
R ma1 na2 la3
平移周期性
(k , r ) ???
对易具有共同本征态H的本征态Ψ(k,r)也是Tn的本征态
一维情况
( k ,r n ) a T ˆ n( k ,r ) n( k ,r )
(k, r ma ) Tˆm (k, r) m (k, r) 本征值
[k, r (m n)a] Tˆmn (k, r)
TˆmTˆn (k, r) mn (k, r)
对应同一Tn本征值!
T ˆ n( x ) n( x ) e ik( n x )a e i0 n ka ( x )
当k在一定的取值范围内取值时, k与Tn本征值
一一对应, 其他区域的k重复该区的结果.
2021
12
2 Brillouin Zone
取法:以某个倒易格点为原点,与第一、二….近邻格点连线, 取中垂面围成的区域, 分别是第一、二….布里渊区.
( x) ( x a a ) e ika ( x a )
let z x a, a x z
( x ) e ika ( x a )
e ikx e ikz ( z ) u1 ( z )e ikx u (k , x )e ikx u (k , x ) e ik ( xa ) ( x a )
正格子
倒格子 b1 b2
k点均匀分布
间隔为b1/N1-----X, b2/N2-----Y
倒格子原胞内共有N1N20个21 k点
分布密度=
L1L2
(2)2
S
(2)2
20
3D晶体?
3. 克龙尼克-潘尼问题
V0
ab 晶格常数c=a+b
晶格势场
0 ncax(n1)c V(x) V0 ncxnca
2021
TˆmTˆn (k, r) Tˆm (n (k, r)) nTˆm (k, r)
nm (k, r) mn nm nm
1 2
归一化条件 n
2021
8
为确定λn, 引入周期性边界条件
(k,rN) a(k,r) N总原胞数
晶体总长
晶体两边的物理特性一样
( k ,r N ) T ˆ N a ( k ,r ) N ( k ,r ) ( k ,r )
a1=1
b1=6.28
a2=2
b2=3.14
晶面(10)
倒格矢 G10=b1+0b2
晶面(12)
倒格矢
G12=b1+2b22021
13
第一布里渊区 (简约布里渊区)
布拉非格子
第二布里渊区
布里渊区体积=1个倒易点拥有的体积=倒格子原胞体积
2021
14
2021
15
2021
16
2021
17
2021
2021
4
求解(k?,r) 的特点?
真空中一维自由电子
(k,x)Aeikx
在周期性势场中运动的电子受约束而成Bloch波(调幅平面波)
(k, x) u(k, x)eikx
u(k, x) u(k, x na)
1D
(k ,r )
u(k,r)eik•r
3D
Bloch 定理
u(k,r) u(k, r R)
所以有
(k, xna) Tˆn(k, x) eikna (k, x)
推广到3维
(k,rR ) eik•R (k,r)
Rma1na22021la3
Bloch 定理
10
(k, xna) Tˆn(k, x) eikna (k, x)
?
(k, x) (k, x)eikx (k, x) (k, xa)
Bloch定理 Bloch波
N 1 mn nm;mn nm;N 1
i n m2
n e N
n2 1
1, ei
n为整数
2021
9
i2m n
n e N
Tn本征值, 表相位差
( k ,r n ) a T ˆ n( k ,r )n( k ,r )
2mn2mnambnakna kmb;mint.
N Na N
N
n eikna
一维情况 a •b a b 2
(k ,
r
R)
u(k,r
R)eik•(r R)
u(k ,
r)eik•reik•R
(k ,
r
R)
(k ,
ik•R r )e 2021
r与r+R处差一个相位因5 子
2021
6
Bloch波是晶体具有平移周期性的结果
定义平移算符 Tˆnf(r)f(rn)a f任意函数
Tˆn Hˆ f
u (k , x a ) e ik ( x ) ( x2)021 u (k , x )
11
n eikna 表相位差
a•ba b 2
k mb;mint. N
k倒空间中一点
故当k改变一个倒格失
kk0m;m bint
e i k n e i(s a N m b) nb a e i( 2 s N m n2 )n e i2 n N se i0 n ka
(r)
Tˆn
[
2 2m
2 r
V
( r )]
f
(r)
2 2m
r na
2
V
(r
na
)
f
(r
na
)
2 2m
2 r
V
(r)
f
(r
na
)
Hˆ Tˆn f ( r ) Tˆn Hˆ Hˆ Tˆn
对易具有共同本征态H的Ψ(k,r)也是
Tn的本2征021态
7
Tˆn Hˆ Hˆ Tˆn
