R语言偏最小二乘法判别分析(pls-da)
细胞代谢组学研究及应用进展

细胞代谢组学研究及应用进展【关键词】细胞代谢组学;研究方法与应用;综述【摘要】细胞代谢组学作为代谢组学研究的一个新兴的方向,在病原体感染、肿瘤研究、药物作用机制及药物研发、毒性评价等多个领域都有所应用。
可解决基本的生物学问题,并允许观察细胞内的代谢现象。
现简要综述细胞代谢组学的主要研究方法及其应用方面的研究进展。
1.细胞代谢组学的研究方法细胞代谢组学实验一般可分为几个步骤:细胞增生培养或刺激、淬灭、代谢物提取、样品检测和数据处理。
1.1细胞淬灭细胞淬灭是指快速使细胞内的酶失活,阻止代谢物变化。
理想的淬灭技术应在不损害细胞、不造成细胞内代谢物泄漏的前提下确保胞内酶迅速失活。
Hounoum等考察3种细胞淬灭方式对NSC-34鼠神经元细胞的影响,分别为-40℃甲醇淬灭、-20℃甲醇淬灭及迅速冻存于-80℃后加入4℃甲醇淬灭。
实验结果显示-40℃甲醇是用于该细胞最为理想的淬灭方式;有研究发现甲醇会破坏细胞膜结构,从而导致无法控制的细胞内代谢物泄漏,故常在甲醇中加入缓冲液如HEPES及AMBIC以维持离子强度,避免渗透冲击。
而对于贴壁细胞,液氮冷冻被是停止其酶活性的最佳方法,Zhao等比较了液氮和75%甲醇(-80℃)2种溶液对副溶血性弧菌细胞的淬灭效果,结果发现75%甲醇(-80℃)淬灭时,细胞发生代谢物泄漏;液氮淬灭速度快,且不存在代谢物泄漏问题。
1.2代谢物提取代谢物具有不同的化学和物理性质,如大小、质量、极性、溶解性等,而细胞代谢组学要求找到一种合适的提取方式,尽可能多地把胞内所有代谢物定量提取出来。
因此,提取方法应该有效而没有选择性和破坏性。
提取过程应有效地从细胞中释放代谢物,避免潜在干扰,确保最小代谢物损失。
胞内代谢物通常单独用有机溶剂,或与水结合,或与其他有机溶剂结合,在不同温度条件下提取。
经典的酸性和碱性提取剂也可分别用来提取对酸、碱稳定的化合物。
对于悬浮细胞,常用含水甲醇、含水乙腈或纯甲。
r语言最小二乘法

r语言最小二乘法r语言是一种用于数据分析和统计建模的编程语言,具有丰富的统计函数库和强大的数据处理能力。
其中,最小二乘法(Least Squares Method)是一种常用的数据拟合方法,用于估计线性回归模型中的参数。
本文将详细介绍r语言中最小二乘法的实现过程。
我们需要明确最小二乘法的基本原理。
最小二乘法的目标是通过最小化残差平方和来确定模型参数的最优解。
在线性回归模型中,假设我们有一组自变量x和对应的因变量y,我们希望通过线性模型y = β0 + β1*x + ε 来拟合数据。
其中,β0和β1是模型的参数,ε是误差项。
在r语言中,我们可以使用lm()函数来进行最小二乘法拟合。
下面是一个示例:```# 创建一个示例数据x <- c(1, 2, 3, 4, 5)y <- c(2, 4, 6, 8, 10)# 进行最小二乘法拟合model <- lm(y ~ x)# 查看拟合结果summary(model)```上述代码首先创建了一个示例数据,其中x是自变量,y是因变量。
然后,通过lm()函数进行最小二乘法拟合,将结果保存在model 对象中。
最后,使用summary()函数查看拟合结果。
在输出的结果中,我们可以得到拟合的回归方程的系数估计值、残差平方和、决定系数等信息。
例如,拟合结果中的Coefficients一节显示了回归方程的系数估计值,其中Intercept对应β0,x对应β1。
除了lm()函数,r语言还提供了一些其他函数用于进行最小二乘法拟合,例如lsfit()函数和nls()函数。
lsfit()函数适用于一般的线性回归模型,而nls()函数适用于非线性回归模型。
这些函数的使用方法可以参考官方文档或相关教程。
最小二乘法不仅适用于线性回归模型,还可以用于其他类型的统计建模,例如多项式回归、逻辑回归等。
对于这些模型,r语言同样提供了相应的函数进行拟合。
除了最小二乘法,r语言还提供了其他的统计建模方法,例如广义线性模型(Generalized Linear Model)、岭回归(Ridge Regression)等。
偏最小二乘法

偏最小二乘法 ( PLS)是光谱多元定量校正最常用的一种方法 , 已被广泛应用 于近红外 、 红外 、拉曼 、核磁和质谱等波谱定量模型的建立 , 几乎成为光谱分析中建立线性定量校正模型的通用方法 〔1, 2〕 。
近年来 , 随着 PLS 方法在光谱分析尤其是分子光谱如近红外 、 红外和拉曼中应用 的深入开展 , PLS 方法还被用来解决模式识别 、定量校正模型适用性判断以及异常样本检测等定性分析问题 。
由于 PLS 方法同时从光谱阵和浓度阵中提取载荷和得分 , 克服主成分分析 ( PCA)方法没有利用浓度阵的缺点 , 可有效降维 , 并消除光谱间可能存在的复共线关系 , 因此取得令人非常满意的定性分析结果 〔3 ~ 5〕 。
本文主要介绍PLS 方法在光谱定性分析方面的原理及应用 实例 。
偏最小二乘方法(PLS-Partial Least Squares))是近年来发展起来的一种新的多元统计分析法, 现已成功地应用于分析化学, 如紫外光谱、气相色谱和电分析化学等等。
该种方法,在化合物结构-活性/性质相关性研究中是一种非常有用的手段。
如美国Tripos 公司用于化合物三维构效关系研究的CoMFA (Comparative Molecular Field Analysis)方法, 其中,数据统计处理部分主要是PLS 。
在PLS 方法中用的是替潜变量,其数学基础是主成分分析。
替潜变量的个数一般少于原自变量的个数,所以PLS 特别适用于自变量的个数多于试样个数的情况。
在此种情况下,亦可运用主成分回归方法,但不能够运用一般的多元回归分析,因为一般多元回归分析要求试样的个数必须多于自变量的个数。
§§ 6.3.1 基本原理6.3 偏最小二乘(PLS )为了叙述上的方便,我们首先引进“因子”的概念。
一个因子为原来变量的线性组合,所以矩阵的某一主成分即为一因子,而某矩阵的诸主成分是彼此相互正交的,但因子不一定,因为一因子可由某一成分经坐标旋转而得。
pls (partial least squares analysis):pls(偏最小二乘法)

---------------------------------------------------------------最新资料推荐------------------------------------------------------pls (partial least squares analysis):pls(偏最小二乘法)PLS (PARTIAL LEAST SQUARES ANALYSIS) Introduction Partial Least Squares (PLS) Analysis was first developed in the late 60s by Herman Wold, and works on the assumption that the focus of analysis is on which aspects of the signal in one matrix are related directly to signals in another matrix. It has been developed extensively in chemometrics, and has recently been applied to neuroimaging data. In the application to imaging data, it has been used to identify task-dependent changes in activity, changes in the relations between brain and behaviour, and to examine functional connectivity of one or more brain regions. PLS has similarities to Canonical Correlation in its general configuration, but is much more flexible. This GUI is the first major release of PLS for neuroimaging. It has been in development for some time, and although this version appears stable, there are always things that can be improved. We are also planning several enhancements, such as univariate testing of means and correlations, advanced plotting routines and higher-order analyses. Please check our website regularly to see if there are updates. PLS computes a matrix that defines1/ 11the relation between two (or more) matrices and then analyzes that cross-block matrix. In the case of TaskPLS, the covariance between the image dataset and a set of design contrasts can be calculated (an equivalent procedure is described below). The covariance images are analyzed with Singular Value Decomposition (SVD) to identify a new set of covariance images that correspond to the strongest effects in the data. For BehaviourPLS, task-specific correlations of brain activity and behaviour are computed (across subjects), combined into a single matrix, which is then decomposed with SVD. The resultant patterns identify similarities and differences in brain-behaviour relations. Creating Datamat Regardless of which type of PLS is to be conducted, the data must be in a form such that all data for all subjects and tasks that are to be analyzed are contained in a single matrix. For image data in general, it is assumed images have been standardized in some manner so that they are all the same shape and size. For PET and MRI data, PLS works best if you use the smallest smoothing filter possible (e.g., no more than twice the voxel size). For ERP data, any filtering, or replacing data in bad channels, etc. must also be done before creating the PLS data matrix. The Session Profile part of our program loads brain images or ERP---------------------------------------------------------------最新资料推荐------------------------------------------------------ waveforms, strings each one out into a vector and then stacks the vectors one on top of the other to make the large data matrix (called datamat in the PLS programs). Each image (also called subject data file) represents one subject under one condition. For brain images, the script also eliminates voxels that are zero or non-brain using a threshold, which is specific to each type of image data. Removing the zero and non-brain voxels reduces the size of the datamat considerably and streamlines the computations. Unfortunately, this can restrict the data set if image slices were not prescribed in the same way for all subjects. To make life easy, a mask is created based on the voxels that are common for all subjects. After the datamat is re duced, a vector (‘coords’) is generated to remap the reduced datamat into image space again. PET Images: The code is written assuming you used the SPM99 sterotaxic template with 4x4x4 mm voxels, which creates images having 34 slices each with 40 voxels in the X and 48 voxels in the Y dimensions. For PET scans, the threshold to define brain voxels is 1/4 of the maximum value for a particular subject. The final datamat will have S by C rows and V columns (where S is the number of subjects and C is the number of scans or conditions, V is the number of3/ 11common brain voxels in the image data set). ERP: For ERP data, all channels of a subject data file are strung out into a single vector and the vectors are then stacked one on top of the other. The datamat will have S by C rows and E by T columns (where S is the number of subjects, C is the number of conditions, E is the number of channels, and T is the number of time points in the subject data file). If, after creating the datamat, it becomes clear that a particular set of ERP channels is bad for most of the subjects, those channels can be eliminated from the analysis using the GUI. As well, single subject data can also be eliminated from the analysis using the GUI. fMRI: Creating the datamat for fMRI datasets combines the two approaches above. This allows you to run the analysis either on each subject or as a group. Common voxels across subjects and/or runs are identified, then a single row vector is created for each subject, separately for each condition. The datamat will be S by C rows and V by T columns (where S is the number of subjects, C is the number of conditions, V is the number of common voxels, and T is the number of images defined by the user to account for the lag in the hemodynamic response). TaskPLS: Analysis using Grand Mean Deviation The TaskPLS is designed to identify whole-brain (scalp) patterns of activity that---------------------------------------------------------------最新资料推荐------------------------------------------------------ distinguish tasks. In TaskPLS, a pattern may represent a combination of anticipated effects and some unanticipated ones. The Grand Mean Deviation analysis is based on representing task means as the deviation around the grand mean computed for each voxel and/or time point. The data are thus averaged within a task, leaving out the within-task variability. (We are exploring the possibility of a constrained PLS solution, where a set of apriori contrasts are used to define the solution space). Next the SVD algorithm is used to get the following three components: brainlv (or salience), singular value (s), and designlv (salience for design). The design scores and brain scores (or scalp scores in ERP) are obtained from the formula below: design scores LV(n) = designlv brain scores LV(n) = datamat * brainlv The saliences for design (designlv) and brain (brainlv) are orthonormal, or standardized. To make comparisons across latent variables easier to visualize, we compute unstandardized saliences. This is accomplished by weighting the saliences by their singular values for the latent variable. All eigenimages and ERP salience plots use the unstandardized saliences. TaskPLS is run by clicking the Run PLS Analysis button. All results are saved into a specified file.5/ 11The results will include all data mentioned above, and other useful information. The TaskPLS results can be displayed by clicking the Show PLS Result button in the main GUI window. For PET and Blocked fMRI, the saliences (eigenimages) and bootstrap ratio images are displayed in a montage that includes all the slices for the LV. For Event-Related fMRI, the results are displayed in a montage as follows: each row represents one lag point, thus the number of rows equals the specified temporal window; each column represents the slices in the image. For ERPs, the LV saliences are displayed as a scalp plot, including only the selected electrodes and epoch. In the results window, you will also find options to display: scatterplots of brain (scalp) scores with design scores, designLV bar plots, and bar plots of the singular values and permutation test results. Behaviour PLS: Analysis using Behaviour Data The BehaviourPLS first calculates a correlation vector of behaviour and brain within each task, then stacks these vectors into a single matrix that is decomposed with SVD. Behaviour PLS has the potential to identify commonalities and differences among tasks in brain-behaviour relations. The behaviour matrix contains one or more behavioural measures that are thought to relate to the measured brain activity. The number of rows in the behaviour---------------------------------------------------------------最新资料推荐------------------------------------------------------ matrix and datamat should be the same, with a separate columnfor each behavioural measure. Since this matrix is created outside of the GUI, it is important that the order of subjects and conditions be identical to the order defined using the GUIto create the datamat. As for the TaskPLS, the results window initially contains plots of the unstandardized saliences. Within the results window, you can also display scatterplotsof brain (scalp) scores with behaviour, bar plots showing the magnitude of the brain-behaviour correlation with confidence intervals, and bar plots of the singular values and permutation test results. In the brain (scalp) scores by behaviour plots, the linear fit is also plotted to better view the scatter around the correlation. Tests of Significance PERMUTATION TEST: The significance of the latent variable, as a whole, is assessed using permutation tests. We assess the magnitude of the singular values by asking the question: With any other random set of data, how often is the value for s as large as the one obtained originally? To generate this answer, subjects are randomly reassigned (without replacement) to different conditions, and the PLS is recalculated. Orthogonal procrustes rotation is applied to the resulting BehavLV or7/ 11DesignLV to correct for reflections and rotations of the resampled data, and the singular values are recalculated based on this rotation (Milan and Whittaker 1995). If the probability of obtaining higher singular values is low, the latent variable is considered to be significant. For both task and behaviour, 500 permutations are generally sufficient, although probability estimates are typically stable at about 100 permutations. BOOTSTRAP: Bootstrap estimation is used to assess the reliability of the brain saliences. In this case, subjects are resampled with replacement. A new datamat, and for BehaviourPLS, a new behaviour matrix are created, and the PLS is recalculated. Thus, unlike for the permutation test, the assignment of subjects to conditions is maintained, but the subjects contributing to task-related effects vary. As for the permutation tests, orthogonal procrustes rotation is applied to the resulting BehavLV or DesignLV to correct for reflections and rotations of the resampled data. The bootstrap procedure provides an estimate of the standard error for each salience in all latent variables. If the ratio of a salience to its standard error is greater than 2, the salience can be regarded as reliable. (A salience of 2 is roughly equivalent to a z-score of 2 if the distribution is gaussian).---------------------------------------------------------------最新资料推荐------------------------------------------------------ The bootstrap estimates serve to assess the contribution of each datapoint to the latent variable structure. The estimates of the standard errors are usually stable after 100 resamplings. For the BehaviourPLS only, we also use the bootstrap loop to calculate the confidence intervals around the correlation of brain scores (scalp scores) with each behaviour. The brain score-behaviour correlation is calculated for each sample, and the upper and lower limits of the user-specified confidence interval are generated. This distribution is kept as part of the output, so new confidence intervals can be calculated from the command line if needed. Additional behaviour PLS bootstrap output indicates the number of times the bootstrap sample was recalculated because of zero variability in the bootstrap behaviour matrix (countnewboot) as well as the behaviour/condition combinations that generated the recalculation (badbeh). Occasionally, the resampled behavioural data are skewed, and the resulting confidence intervals do not include the original correlation value . We also provide a very conservative adjustment to the confidence interval calculation that may be informative in those cases (ulcorr_adj; llcorr_adj). However, the correction may not be9/ 11the most optimal, so use with caution. PLS is a new method and it can take some time to understand the results. We can be surprised by what it shows us in the data, but can be puzzled as well. We would encourage you to compare your PLS results with other analytic methods available to you. You will find that most of the answers PLS gives you are there in the data, but may not have been obvious on first pass. It does not identify effects that are not there. Finally, since it is a new method, keep in mind that new analytical tools are being developed all the time. We would greatly appreciate hearing from you on what you found with the analysis, what problems you encountered, and any suggestions for modifications to the code or the analytic approach. Selected References: PLS for neuroimaging: Lobaugh, N. J., R. West, et al. (2019). Spatiotemporal analysis of experimental differences in event-related potential data with partial least squares. Psychophysiology 38(3): 517-30. McIntosh, A. R., F. L. Bookstein, et al. (1996). Spatial pattern analysis of functional brain images using Partial Least Squares. Neuroimage 3: 143-157. McIntosh, A. R., N. J. Lobaugh, et al. (1998). Convergence of neural systems processing stimulus associations and coordinating motor responses. Cerebral Cortex 8: 648-659. PLS in other fields Gargallo, R., C. A. Sotriffer,---------------------------------------------------------------最新资料推荐------------------------------------------------------et al. (1999). Application of multivariate data analysis methods to comparative molecular field analysis (CoMFA) data: proton affinities and pKa prediction for nucleic acids components. J Comput Aided Mol Des 13(6): 611-23. Martin, Y.C., C. T. Lin, et al. (1995). PLS analysis of distance matrices to detect nonlinear relationships between biological potency and molecular properties. J Med Chem 38(16): 3009-15. Streissguth, A. P., F. L. Bookstein, et al. (1993). The enduring effects of prenatal alcohol exposure on child development: Birth through seven years, a partial least squares solution. Ann Arbor, Michigan, The University of Michigan Press. Talbot, M. (1997). Partial Least Squares Regression. position. Royal Statistical Society Journal, Series C: Applied Statistics 44(1): 31-49.11/ 11。
偏最小二乘回归方法(PLS)

偏最小二乘回归方法1 偏最小二乘回归方法(PLS)背景介绍在经济管理、教育学、农业、社会科学、工程技术、医学和生物学中,多元线性回归分析是一种普遍应用的统计分析与预测技术。
多元线性回归中,一般采用最小二乘方法(Ordinary Least Squares :OLS)估计回归系数,以使残差平方和达到最小,但当自变量之间存在多重相关性时,最小二乘估计方法往往失效。
而这种变量之间多重相关性问题在多元线性回归分析中危害非常严重,但又普遍存在。
为消除这种影响,常采用主成分分析(principal Components Analysis :PCA)的方法,但采用主成分分析提取的主成分,虽然能较好地概括自变量系统中的信息,却带进了许多无用的噪声,从而对因变量缺乏解释能力。
最小偏二乘回归方法(Partial Least Squares Regression:PLS)就是应这种实际需要而产生和发展的一种有广泛适用性的多元统计分析方法。
它于1983年由S.Wold和C.Albano等人首次提出并成功地应用在化学领域。
近十年来,偏最小二乘回归方法在理论、方法和应用方面都得到了迅速的发展,己经广泛地应用在许多领域,如生物信息学、机器学习和文本分类等领域。
偏最小二乘回归方法主要的研究焦点是多因变量对多自变量的回归建模,它与普通多元回归方法在思路上的主要区别是它在回归建模过程中采用了信息综合与筛选技术。
它不再是直接考虑因变量集合与自变量集合的回归建模,而是在变量系统中提取若干对系统具有最佳解释能力的新综合变量(又称成分),然后对它们进行回归建模。
偏最小二乘回归可以将建模类型的预测分析方法与非模型式的数据内涵分析方法有机地结合起来,可以同时实现回归建模、数据结构简化(主成分分析)以及两组变量间的相关性分析(典型性关分析),即集多元线性回归分析、典型相关分析和主成分分析的基本功能为一体。
下面将简单地叙述偏最小二乘回归的基本原理。
偏最小二乘法算法

偏最小二乘法1.1基本原理偏最小二乘法(PLS)是基于因子分析的多变量校正方法,其数学基础为主成分分析。
但它相对于主成分回归(PCR)更进了一步,两者的区别在于PLS法将浓度矩阵Y和相应的量测响应矩阵X同时进行主成分分解:X二 TP+EY=UQ+F式中T和U分别为X和Y的得分矩阵,而P和Q分别为X和Y的载荷矩阵,E和F分别为运用偏最小二乘法去拟合矩阵X和Y时所引进的误差。
偏最小二乘法和主成分回归很相似,其差别在于用于描述变量Y中因子的同时也用于描述变量X。
为了实现这一点,数学中是以矩阵Y的列去计算矩阵X的因子。
同时,矩阵Y的因子则由矩阵X 的列去预测。
分解得到的T和U矩阵分别是除去了人部分测量误差的响应和浓度的信息。
偏最小二乘法就是利用各列向量相互正交的特征响应矩阵T和特征浓度矩阵U进行回归:U=TB得到回归系数矩阵,又称矢联矩阵E:B=(TT )F U因此,偏最小二乘法的校正步骤包括对矩阵Y和矩阵X的主成分分解以及对矢联矩阵B的计算。
12主成分分析主成分分析的中心目的是将数据降维,以排除众多化学信息共存中相互重叠的信息。
他是将原变量进行转换,即把原变量的线性组合成几个新变量。
同时这些新变量要尽可能多的表征原变量的数据结构特征而不丢失信息。
新变量是一组正交的,即互不相矢的变量。
这种新变量又称为主成分。
如何寻找主成分,在数学上讲,求数据矩阵的主成分就是求解该矩阵的特征值和特征矢量问题。
卞面以多组分混合物的量测光谱来加以说明。
假设有n个样本包含p个组分,在m个波长下测定其光谱数据,根据比尔定律和加和定理有:如果混合物只有一种组分,则该光谱矢量与纯光谱矢量应该是方向一致,而人小不同。
换句话说,光谱A表示在由p个波长构成的p维变量空间的一组点(n个),而这一组点一定在一条通过坐标原点的直线上。
这条直线其实就是纯光谱b。
因此由ni个波长描述的原始数据可以用一条直线,即一个新坐标或新变量来表示。
如果一个混合物由2个组分组成,各组分的纯光谱用bl,b2 表示,则有:<=c i{b: + Ci2bl有上式看出,不管混合物如何变化,其光谱总可以用两个新坐标轴bl,b2来表示。
R语言实现偏最小二乘回归法partialleastsquares(PLS)回归

R语言实现偏最小二乘回归法partialleastsquares(PLS)回归原文链接:/?p=8652偏最小二乘回归是一种回归形式。
当使用pls时,新的线性组合有助于解释模型中的自变量和因变量。
在本文中,我们将使用pls在“ Mroz”数据集中预测“收入”。
library(pls);library(Ecdat)data("Mroz")str(Mroz)## 'data.frame': 753 obs. of 18 variables:## $ work : Factor w/ 2 levels "yes","no": 2 2 2 22 2 2 2 22 ...## $ hoursw : int 1610 16561980 4561568 20321440 1 0201458 1600 ...## $ child6 : int 1 0 1 01 0 0 000 ...## $ child618 : int 0 2 3 32 0 2 022 ...## $ agew : int 32 30 35 3431 54 37 544839 ...## $ educw : int 12 12 12 1214 12 16 121212 ...## $ hearnw : num 3.35 1.394.55 1.14.59 ...## $ wagew : num 2.65 2.654.04 3.253.6 4.75.95 9.980 4.15 ...## $ hoursh : int 2708 23103072 19202000 10402670 4 1201995 2100 ...## $ ageh : int 34 30 40 5332 57 37 535243 ...## $ educh : int 12 9 12 1012 11 12 8412 ...## $ wageh : num 4.03 8.443.58 3.5410 ...## $ income : int 16310 2180021040 730027300 19495 21152 1890020405 20425 ...## $ educwm : int 12 7 12 712 14 14 377 ...## $ educwf : int 7 7 7 714 7 7 377 ...## $ unemprate : num 5 11 5 59.5 7.55 5 3 5 ...## $ city : Factor w/ 2 levels "no","yes": 1 2 1 12 2 1 11 1 ...## $ experience: int 14 5 15 67 33 11 352421 ...首先,我们必须通过将数据分为训练和测试集来准备数据。
偏最小二乘法回归 PLSR
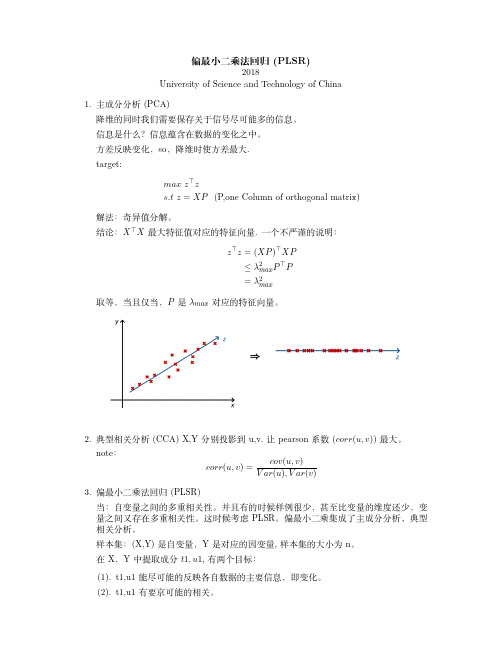
偏最小二乘法回归(PLSR)2018University of Science and Technology of China1.主成分分析(PCA)降维的同时我们需要保存关于信号尽可能多的信息。
信息是什么?信息蕴含在数据的变化之中。
方差反映变化,so ,降维时使方差最大.target:max z ⊤zs.t z =XP (P,one Column of orthogonal matrix)解法:奇异值分解。
结论:X ⊤X 最大特征值对应的特征向量.一个不严谨的说明:z ⊤z =(XP )⊤XP≤λ2max P ⊤P=λ2max取等,当且仅当,P 是λmax 对应的特征向量。
2.典型相关分析(CCA)X,Y 分别投影到u,v.让pearson 系数(corr (u,v ))最大。
note :corr (u,v )=cov (u,v )V ar (u ),V ar (v )3.偏最小二乘法回归(PLSR)当:自变量之间的多重相关性。
并且有的时候样例很少,甚至比变量的维度还少,变量之间又存在多重相关性。
这时候考虑PLSR 。
偏最小二乘集成了主成分分析、典型相关分析。
样本集:(X,Y)是自变量,Y 是对应的因变量,样本集的大小为n 。
在X ,Y 中提取成分t 1,u 1,有两个目标:(1).t1,u1能尽可能的反映各自数据的主要信息,即变化。
(2).t1,u1有要京可能的相关。
结合(1)(2)即是max cov(t1,u1)=corr(t1,u1)∗var(t1)∗var(u1).提取后对数据进行回归,若能满足要求则结束。
若不能,则对残余信息进行第二轮成分的提取。
过程简述:step1:数据的标准化。
(减均值除以方差)step2:maxmize⟨Xp,Y q⟩s.t:∥p∥=1,∥q∥=1拉格朗日求解:L=p⊤X⊤Y q−λ2(∥p∥22−1)−θ2(∥q∥22−1)∂L∂p=X⊤Y q−λp=0(1)∂L∂q=Y⊤Xp−θq=0(2)Then,(p⊤*1)and(q⊤q(2)),we get:λ=θ把1and2联合并带入:maxmize p⊤λp=λs.t:Y⊤XX⊤Y q=λ2qX⊤Y Y⊤Xp=λ2pi.e求最大的奇异值。
