大学物理第三章-动量守恒定律和能量守恒定律-习题及答案
动量守恒定律与能量守恒定律

B
?
vA )
A
由图可得 ? v ? 2v
从而可得水流对管壁作用力的大小为
S
v
vB v
? F ' ? ? F ? ? 2 Sv2 ? ? 1?416? 1? 0 ?20? (3?0)2
?v
? ? 2 ?5? 103 N
作用力的方向则沿直角平分线指向管外侧 .
3-5 保守力与非保守力 势能 3-6 功能原理 机械能守恒定律
习题答案
P51 2-18 已知 m r ?
解:对小球进行受力分析 ,如图.
N ? mg cos? ? mv2 / r
? m g sin ? ? m d v
dt
?
Hale Waihona Puke gsin??dv dt
?
dvd dt
? d?
?
v r
dv
d?
? ? v
vvd
0
?
? gr
? ??
sin
??d
2
第二章牛顿定律
A
O r
?B
α Nv
x
?
mv
2 m
ln
4
2F 3
习题答案
第三章动量守恒定律和能量守恒定律
P94 3-10 解: 依据动量定理 I ?? P
在t=0到t=? /(2? ) 时间内小球动量的增量
?
?
? ? ? p ? I ? 2? Fdt ? 2? ? kxdt
0
0
?
?? 2? ? kA cos? tdt 0
kA ??
?
引力 功
W
?
?
???(?G
m' m )
大学物理 第三章 动量守恒定律和能量守恒定律 3-5 保守力与非保守力
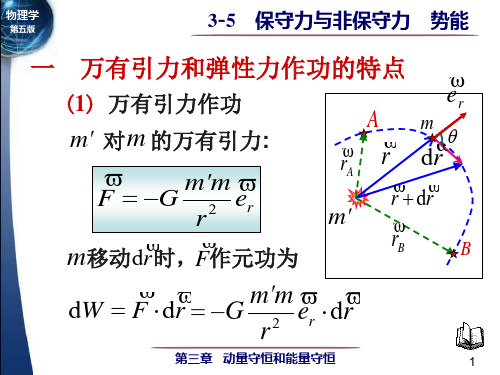
m' m m' m 引力的功 引力的功 WAB = −(−G r ) − (−G r ) B A
A点势能: 点势能: 且令E 设B点为无限远 即rB=∞ 且令 PB=0 点为无限远
m' m WAB = −G rA
= − ( E pB − E pA ) = E pA
功与路径无关,只决定于初末位置。 功与路径无关,只决定于初末位置。 第三章 动量守恒和能量守恒
4
} ⇒ dW
物理学
第五版
3-5 保守力与非保守力 势能 -
F
dW
O
x1
x2
dx
x2 x
W = ∫ Fdx = ∫
x1
x2
x1
1 2 1 2 − kxdx = −( kx2 − kx1 ) 2 2
5
第三章 动量守恒和能量守恒
W p → p0 = −( Ep0 − Ep ) = −∆Ep
E p ( x, y, z) =
∫
E p0 = 0
( x, y,z )
F ⋅ dr
任意一点的势能等于在保守力作用下 从该点到势能零点保守力所作的功
第三章 动量守恒和能量守恒 10
物理学
第五版
3-5 保守力与非保守力 势能 -
W AB = − ( E pB − E pA ) = − ∆ E P
引力的功 引力的功
m' m m' m WAB = −(−G ) − (−G ) rB rA
引力势能 引力势能
m' m Ep = −G r
弹性势能 弹性势能
弹力的功 弹力的功
W AB 1 1 2 2 = − ( kx B − kx A ) 2 2
大学物理第三章-动量守恒定律和能量守恒定律-习题及答案

即:作用在两质点组成的系统的合外力的冲量等于系统内两质点动量之和的增 量,即系统动量的增量。 2.推广:n 个质点的情况
t2 t2 n n n n F d t + F d t m v mi vi 0 i外 i内 i i i 1 i 1 i 1 i 1 t1 t1
yv 2
同乘以 ydy,得
y 2 gdty y
积分 得
y
0
y
gdty
yvdt( yv)
0
1 3 1 gy ( yv) 2 3 2
因而链条下落的速度和落下的距离的关系为
2 v gy 3
1/ 2
7
第4讲
动量和冲量
考虑到内力总是成对出现的,且大小相等,方向相反,故其矢量和必为零, 即
F
i 0
n
i内
0
设作用在系统上的合外力用 F外力 表示,且系统的初动量和末动量分别用
5
第4讲
动量和冲量
P0 和 P 表示,则
t2 n n F d t m v mi vi 0 i i 外力 t1
F外 dt=dPFra bibliotek力的效果 关系 适用对象 适用范围 解题分析
*动量定理与牛顿定律的关系 牛顿定律 动量定理 力的瞬时效果 力对时间的积累效果 牛顿定律是动量定理的 动量定理是牛顿定律的 微分形式 积分形式 质点 质点、质点系 惯性系 惯性系 必须研究质点在每时刻 只需研究质点(系)始末 的运动情况 两状态的变化
1
第4讲
动量和冲量
§3-1 质点和质点系的动量定理
实际上,力对物体的作用总要延续一段时间,在这段时间内,力的作用将 积累起来产生一个总效果。下面我们从力对时间的累积效应出发,介绍冲量、 动量的概念以及有关的规律,即动量守恒定律。 一、冲量 质点的动量定理 1.动量:Momentum——表示运动状态的物理量 1)引入:质量相同的物体,速度不同,速度大难停下来,速度小容易停下;速 度相同的物体,质量不同,质量大难停下来,质量小容易停下。 2)定义:物体的质量 m 与速度 v 的乘积叫做物体的动量,用 P 来表示 P=mv 3)说明:动量是矢量,大小为 mv,方向就是速度的方向;动量表征了物体的 运动状态 -1 4)单位:kg.m.s 5)牛顿第二定律的另外一种表示方法 F=dP/dt 2.冲量:Impulse 1)引入:使具有一定动量 P 的物体停下,所用的时间Δt 与所加的外力有关, 外力大,Δt 小;反之外力小,Δt 大。 2)定义: 作用在物体外力与力作用的时间Δt 的乘积叫做力对物体的冲量, 用 I 来表 示 I= FΔt 在一般情况下,冲量定义为
(完整版)大学物理学(课后答案)第3章

第3章动量守恒定律和能量守恒定律习题一选择题3-1 以下说法正确的是[ ](A)大力的冲量一定比小力的冲量大(B)小力的冲量有可能比大力的冲量大(C)速度大的物体动量一定大(D)质量大的物体动量一定大解析:物体的质量与速度的乘积为动量,描述力的时间累积作用的物理量是冲量,因此答案A、C、D均不正确,选B。
3-2 质量为m的铁锤铅直向下打在桩上而静止,设打击时间为t∆,打击前锤的速率为v,则打击时铁捶受到的合力大小应为[ ](A)mvmgt+∆(B)mg(C)mvmgt-∆(D)mvt∆解析:由动量定理可知,F t p mv∆=∆=,所以mvFt=∆,选D。
3-3 作匀速圆周运动的物体运动一周后回到原处,这一周期内物体[ ] (A)动量守恒,合外力为零(B)动量守恒,合外力不为零(C)动量变化为零,合外力不为零, 合外力的冲量为零(D)动量变化为零,合外力为零解析:作匀速圆周运动的物体运动一周过程中,速度的方向始终在改变,因此动量并不守恒,只是在这一过程的始末动量变化为零,合外力的冲量为零。
由于作匀速圆周运动,因此合外力不为零。
答案选C。
3-4 如图3-4所示,14圆弧轨道(质量为M)与水平面光滑接触,一物体(质量为m)自轨道顶端滑下,M与m间有摩擦,则[ ](A )M 与m 组成系统的总动量及水平方向动量都守恒,M 、m 与地组成的系统机械能守恒(B )M 与m 组成的系统动量不守恒, 水平方向动量守恒,M 、m 与地组成的系统机械能不守恒(C )M 与m 组成的系统动量不守恒, 水平方向动量不守恒,M 、m 与地组成的系统机械能守恒(D )M 与m 组成系统的总动量及水平方向动量都守恒,M 、m 与地组成的系统机械能不守恒解析:M 与m 组成的系统在水平方向上不受外力,在竖直方向上有外力作用,因此系统水平方向动量守恒,总动量不守恒,。
由于M 与m 间有摩擦,m 自轨道顶端滑下过程中摩擦力做功,机械能转化成其它形式的能量,系统机械能不守恒。
第三章 动量守恒定律和能量守恒定律 问题与习题解答

第3章 动量守恒定律和能量守恒定律 问题与习题解答问题:3-1、3-3、3-7、3-10、3-14、3-193-1如图所示,设地球在太阳引力的作用下,绕太阳作匀速圆周运动。
试问:在下述情况下,(1)地球从点A 运动到点B ,(2)地球从点A 运动到点C ,(3)地球从点A 出发绕行一周又返回点A ,地球的动量增量和所受的冲量各为多少? 答:选太阳处为坐标原点O ,且O →C 方向为X 轴正方向,O →B 方向为Y 轴正方向,设地球和太阳的质量分别为,m M ,两者间的距离为r ,地球沿反时针方向作匀速圆周运动的速率为v ,故根据万有引力定律,有:22vm M m Grr=,即v =(1)地球从点A 运动到点B 的动量增量为:()())A B B A P m v v m vi vj i j ∆=-=-=-根据质点的动量定理,地球所受的冲量为:)A B A B I P mi j =∆=-(2)地球从点A 运动到点C 的动量增量和所受的冲量为:()()2A C A C C A P I m v v m vj vj mj ∆==-=--=-(3)同理,地球从点A 出发绕行一周回到A 点的动量增量和所受的冲量为:()0A A A A A A P I m v v ∆==-=3-3在上升气球下方悬挂一梯子,梯子站一人。
问人站在梯子上不动或以加速度向上攀升,气球的加速度有无变化? 答:(1)人不动,则气球的加速度不变。
(2)以气球及梯子(总质量为M )与人(质量为m )为系统,地面为参照系,且设人相对梯子上爬的速度为v 、气球相对地面的速度为V ,人相对地面的速度为v ',则有v v V '=+如果设气球及梯子与人初始为匀速率0v 竖直上升,则可应用动量守恒定律,得0()m v M V m M v '+=+所以, 0()V v m v m M =-+故得气球的加速度为d V m d v a d tm Md t==-⋅+气由此可知,当人相对于梯子的加速度0d v d t=(相对梯子匀速爬上)时0a =气;而当0d v d t>(加速爬上)时,0a <气。
大学物理动量守恒定律和能量守恒定律练习题题

A R=4m O
m=2kg
Bv
不动 v=6m·s-
1
Ff
FN
G=mg
第三章 动量守恒和能量守恒
9
物理学
第五版
第三章补充例题
9 已知在半径为R的光滑球面上,一物
体自顶端静止下滑, 问物体在何处脱离球面?
解
mg
cos
FN
m
v2 R
mgR(1 cos ) 1 mv2
当物体在A处脱离2球
的功.
解
因
vx
dx dt
5,
vy
dy dt
t,
有 v2 t 2 25
应用动能定理,得W
1 2
mv22
1 2
mv12
3J
第三章 动量守恒和能量守恒
7
物理学
第五版
8 如图,物体质
量 m 2 kg ,沿固定
的四分之一圆弧由A静 止滑下,到达B点时的
速率 v 6 m s1,求摩
擦力作的功.
第三章补充例题
x
Fdx
t 6t 1.5t 2dt 2.25t 4
0
0
所以,当 t 2 s 时, 得 W 36 J
第三章 动量守恒和能量守恒
6
物理学
第五版
第三章补充例题
7 质量为m 0.5 kg的质点, 在平面内
运动, 方程为 x 5tm,y 0.5t 2m ,求从
t 2s 到 t 4s 这段时间内,外力对质点作
v1 )
设 M = 200 m, 则 V=0.01v
v0= v1 =v
第三章 动量守恒和能量守恒
1
物理学
第五版
大学物理 第三章 动量守恒定律和能量守恒定律 3-9 质心 质心运动定律
第五版
3-9 质心 -
质心运动定律
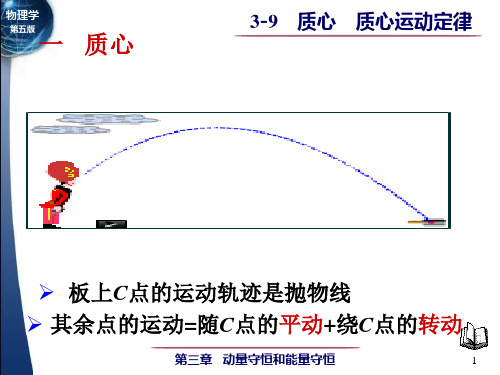
一 质心
1 质心的概念
板上C点的运动轨迹是抛物线 板上 点的运动轨迹是抛物线 其余点的运动=随 点的平动+绕 点的 点的平动 点的转动 其余点的运动 随C点的平动 绕C点的转动
第三章 动量守恒和能量守恒
1
物理学
第五版
3-9 质心 -
质心运动定律
2 质心的位置 由n个质点组成 个质点组成 的质点系, 的质点系,其质心 的位置: 的位置:
13
物理学
第五版
3-9 质心 n n v v v m'vC = ∑ mi vi = ∑ pi = p i =1 i =1
质心运动定律
求一阶导数, 再对时间 t 求一阶导数,得
质心加速度
dp v m'aC = dt v v dp ex 根据质点系动量定理 = Fi dt
第三章 动量守恒和能量守恒
}⇒
x2 = 2 xC
17
第三章 动量守恒和能量守恒
物理学
第五版
3-9 质心 -
质心运动定律
例4 用质心运动定律 y F 来讨论以下问题. 来讨论以下问题. 一长为l 一长为 、密度均匀的 y 柔软链条, 柔软链条,其单位长度的质 c yC 量为 λ .将其卷成一堆放在 地面. 若手提链条的一端, 地面. 若手提链条的一端, o 以匀速v 将其上提.当一端 以匀速 将其上提. 被提离地面高度为 y 时,求手的提力. 求手的提力.
竖直方向作用于链条的合外力为 F − λyg
第三章 动量守恒和能量守恒
20
物理学
第五版
3-9 质心 -
质心运动定律
v 得到 F − yλg = lλ ⋅ l
《大学物理》动量守恒定律和能量守恒定律练习题及答案解析

《大学物理》动量守恒定律和能量守恒定律练习题及答案解析一、选择题1.对动量和冲量,正确的是(B )(A)动量和冲量的方向均与物体运动速度方向相同。
(B)质点系总动量的改变与内力无关。
(C)动量是过程量,冲量是状态量。
(D)质点系动量守恒的必要条件是每个质点所受到的力均为0。
2如图所示,子弹入射在水平光滑地面上静止的木块后而穿出,以地面为参考系,下列说法中正确的是( C )(A)子弹减少的动能转变成木块的动能(B)子弹—木块系统的机械能守恒(C)子弹动能的减少等于子弹克服木块阻力所做的功(D)子弹克服木块阻力所做的功等于这一过程中产生的热。
3.对质点组有下列几种说法:(1)质点组总动量的改变与内力无关(2)质点组总动能的改变与内力无关(3)质点组机械能的改变与内力无关(4)质点组机械能的改变与保守内力无关正确的是( C )(A)(1)和(3)正确(B)(2)和(3)正确(C)(1)和(4)正确(D)(2)和(4)正确4.对于保守力,下列说法错误的是(C)(A)保守力做功与路径无关(B)保守力沿一闭合路径做功为零(C)保守力做正功,其相应的势能增加(D)只有保守力才有势能,非保守力没有势能。
5.对功的概念有以下几种说法:(1)保守力作正功时系统内相应的势能增加.(2) 质点运动经一闭合路径,保守力对质点作的功为零.(3)作用力与反作用力大小相等、方向相反,所以两者所作的功的代数合必为零.在上述说法中:(4)摩擦力一定做负功( C )(A) (1) 、(2)、(4)是正确的.(B) (2) 、(3) 、(4)是正确的.(C)只有(2)是正确的.(D)只有(3)是正确的.6.当重物减速下降时,合外力对它做的功( B )(A)为正值(B)为负值(C)为零(D)无法确定。
7、考虑下列四个实例,你认为哪一个实例中物体和地球构成的系统的机械能不守恒?(A)(A)物体在拉力作用下沿光滑斜面匀速上升(B)物体作圆锥摆运动(C)抛出的铁饼作斜抛运动(不计空气阻力)(D)物体在光滑斜面上自由滑下8.如图所示,圆锥摆的小球在水平面内作匀速率圆周运动,判断下列说法中正确的是( A )(A)重力和绳子的张力对小球都不作功。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学物理第三章-动量守恒定律和能量守恒定律-习题及答案第三章动量守恒定律和能量守恒定律3-1 力)SI (12i F t =作用在质量kg 2=m 的物体上,使物体由原点从静止开始运动,则它在3秒末的动量应为:(A )m/s kg 54?-i (B )m/s kg 54?i(C )m/s kg 27?-i (D )m/s kg 27?i [B] 解:以该物体为研究对象,由质点动量定理=?==-=?30300354d 12d i i F p p p t t t又00=p 故()-13s m kg 54??=i p3-2 一个质点同时在几个力作用下的位移为:)SI (654k j i r +-=? 其中一个力为恒力)SI (953kj i F +--=,则此力在该位移过程中所作的功为(A )67J (B )91J(C )17J (D )-67J [A] 解:()()k j i k j i r F 654953+-?+--=??=A(J) 675425-12=++=3-3 对质点组有以下几种说法:①质点组总动量的改变与内力无关②质点组总动能的改变与内力无关③质点组机械能的改变与保守内力无关在上述说法中:(A )只有①是正确的(B )①、③是正确的(C )①、②是正确的(D )②、③是正确的 [B] 解:由于质点组内力冲量的矢量和为零,所以质点组总动量的改变与内力无关。
由于质点组内力功的代数和不一定为零,由动能定理K E A A ?=+内外,质点组总动能的改变可能与内力相关。
,由功能原理E A A ?=+非保内外,质点系机械能的改变与保守内力无关。
3-4 质点系的内力可以改变(A )系统的总质量(B )系统的总动量(C )系统的总动能(D )系统的总角动量 [C] 解:由质点系动量定理、角动量定理和动能定理k t t t t E A A t t ?=+?=??=??内外外外2121d d LM p F可知质点系内力只能改变系统总动能而不影响其总动量和总角动量。
3-5 设作用在质量为1 kg 的物体上的力)SI (36+=t F 。
如果物体在这一力的作用下,由静止开始沿直线运动,在0到 2.0s 的时间间隔内,这个力作用在物体上的冲量大小I =N.s18。
解:sN 18)33(d )36(d 222=+=+==?t t t t t F I3-6 一颗子弹在枪筒里前进时所受的合力大小为tF 31044005-=(SI )子弹从枪口射出时的速率为300 1s m -?。
假设子弹离开枪口时合力刚好为零,则①子弹走完枪筒全长所用的时间s 003.0=t ,②子弹在枪筒中所受力的冲量sN 6.0?=I ,③子弹的质量kg1023-?=m 。
解:①由子弹离开枪口时所受合力为零,即31044005=?-=t F得子弹在枪筒中运动时间为s 003.010440035=??=t②由冲量定义,子弹在枪筒中所受合力的冲量s N 6.0d 3104400d 003.0050=-==?t t t F I t③以子弹为研究对象,其-10s m 300,0?==v v ,由动量定理:kg1023006.030-?===-=v I m mv mv I3-7 已知地球的半径为R ,质量为M ,现有一质量为m 的物体,在离地面高度为2R处,以地球和物体为系统,若取地面为势能零点,则系统的引力势能为RGmM 32;若取无穷远处为势能零点,则系统的引力势能为RGmM 3-,(G 为万有引力常数)解:物体与地球间引力2r GmM F =系统引力势能等于将物体由场点移动到零势点过程中,保守内力做的功。
取地面为零势点,系统引力势能=??-==RR R RP R GmM r GmM E 32332r d d r F 取无穷远处为零点,系统引力势能∞∞-=?-==RR P R GmM r GmM E 3323r d d r F 3-8 一弹簧原长m 1.00=l ,倔强系数N/m 5=k ,其一端固定在半径为m 1.0=R 的半圆环的端点A ,另一端与一套在半圆环上的小环相连。
在把小环由半圆环中点B 移到另一端C 的过程中,弹簧的拉力对小环所作的功为 -0.207 J 。
解:由保守力做功与相关势能增量的关系-?-=?-=222121B c P l k l k E A将041.02,1.0200=-=?=-=? l R l l R l B c 代入上式得 J207.0041.050211.0502122-=-??-=A3-9 如图所示,一匀质木球固结在一细棒下端,且可绕水平光滑固定轴O 转动,今有一子弹沿着与水平面成一角度的方向击中木球而嵌入其中,则在此击中过程中,木球、子弹、细棒系统的对O 轴的角动量守恒,原因是对该轴合外力矩为零。
木球被击中后棒和球升高的过程中,木球、子弹、细棒、地球系统的机械能守恒。
解:在子弹击中木球过程中,所有外力(重力、轴约O 题3-8图题3-7图题3-9图束力)过轴,对轴力矩为零,故系统对轴角动量守恒。
而在棒和球升高过程中只有保守内力(重力)做功,系统机械能守恒。
3-10 如图,水平地面上一辆静止的炮车发射炮弹。
炮车质量为M ,炮身仰角为α,炮弹质量为m ,炮弹刚出口时,相对于炮身的速率为u ,不计地面摩擦。
(1)求炮弹刚出口时,炮车的反冲速度大小;(2)若炮筒长为l ,求发炮过程中炮车移动的距离。
解:(1)以炮车、炮弹系统为研究对象,以地面为参考系,忽略地面摩擦力,系统在水平方向动量守恒,设炮弹出口时,炮车相对于地面的速度为x v ,则有()0cos =++αu v m Mv x x得M m mu v x +-=αcos (负号表示炮身后退)(2)设发射炮弹过程中,任一时刻炮弹相对于炮身的速率为)(t u ,炮身相对于地面的速度为)(t v x ,则由水平方向动量守恒,可得()()M m t mu t v x +-=αcos在发射炮弹过程中,炮弹相对于炮身移动的距离为弹筒长度,即()?=tl t t u 0d则炮身在此过程中的位移为()()?+-==?ttx t t u Mm m t t v x 00d cos d αM m ml +-=αcos (负号表示炮身后退)3-11 如图所示,质量为M 的滑块正沿着光滑水平地面向右滑动,一质量为m 的小球水平向右飞行,以速率1v (对地)与滑块斜面相碰,碰后竖直向上弹起,速率为2v (对地),若碰撞时间为t ?,试计算此过程中滑块对地的平均作用力和滑块速度增量的大小。
解:以M 和m 系统为研究对象,系统在水平方向不受外力作用,动量定恒。
以地面为参考系,则有()v v M Mv mv ?+=+1式中v 为碰前M 的速率,v ?为M 的速率增量。
由上式得M mv v 1=在竖直方向,系统动量不守恒。
如图所示,系统所题3-10图Mg 题3-11图受外力有N 、Mg 和mg ,由动量定理:mg Mg t mv N mv t mg Mg N ++?==?--22)(根据牛顿第三定律,滑块对地的平均作用力大小为mg Mg t mv N F ++?==2方向竖直向下。
3-12 在X 射线散射实验中,测得入射光子的动量为113s m kg 10177.1--,光子与电子碰撞后沿与入射方向成2/π的方向弹开,动量变为113s m kg 10128.1--。
设碰撞前电子静止,求碰撞后电子的动量。
解:设入射光子动量为0p ,与电子碰撞后光子动量为1p ,电子被碰撞后动量为2p ,如图所示。
以光子和电子为研究对象,碰撞过程中动量守恒:θθsin 0cos 2120210p p p p -==+=p p p联立以上两式,解之得13222120210128.1177.1-?+=+=p p p=)s m kg (10630.1113--78.43177.1128.1arctg arctg 21=??? ??=?=p p θ3-13 一人从10m 深的井中提水。
起始时桶中装有10kg 的水,桶的质量为1kg ,由于水桶漏水,每升高1m 要漏去0.2kg 的水,求水桶匀速地从井中提到井口,人所做的功。
解:以井中水面为坐标原点,取竖直向上为y 轴正方向。
将水桶提到高为y 处瞬时,人用力的大小为ky mg F -=式中m 为满桶水加水桶的质量,k 为每升1m 漏掉的水的重量,即()1m N 2.0-?=g k水桶再升高y d ,力F 做的功为()y ky mg y F A d d d -==设水是从井水面处打起的,则将一桶水提到井口处,力F 做的功为()?-==10d d y ky mg A A题3-12图()J 9811081.92.0211081.911|2121002=-??=??-=ky mgy3-14 如图所示的系统中(滑轮质量不计,轴光滑),外力F 通过不可伸长的绳子和一劲度系数1m N 200-?=k 的轻弹簧缓慢地拉地面上的物体,物体的质量kg 2=M ,初始时弹簧为自然长度。
求在把绳子拉下20cm 的过程中,F 所做的功。
(重力加速度g 取2sm 10-?)解:F 力刚向下拉时,弹簧伸长,物体并未被拉离地面。
设物体开始离地时弹簧伸长0x ,则由Mg kx =0,得()m 1.02001020=?==k Mg x此后物体匀速上升。
力F 的变化为><<=000x x Mgx x kxFF 力向下拉cm 20=h 过程中,做功为()J 3)1.02.0(1021.020021||21d d 20200000=-??+??=+=+=h x x x h x Mgx kx xMg x kx A3-15 如图,长为L 、质量为m 的匀质链条,置于水平桌面上,链条与桌面间的摩擦系数为μ,下垂部分的长度为a 。
链条由静止开始运动,求在链条滑离桌面过程中,重力和摩擦力所做的功和链条离开桌面时的速率。
解:建立如图坐标系,设下垂部分链条长度为x ,受到的重力大小为xg L mP =在链条滑离桌面的过程中,重力所做的功为()-===L aL aP L a L mg x x L mg x P A 2d d 22桌面上链条长为)(x L -,在滑动中受到的摩擦力大小为()Lmgx L f -=μ在链条滑离桌面的过程中,摩擦力所做的功为题3-14图题3-15图()()22d d d a L Lmgxmg Lx L x f A L aL af --=--=-=?=μμl f设链条离开桌面时的速率为v ,由动能定理()()22222122mv L a L mg L a L mg A A f P =---=+μ得()[]222a L a L L g v ---=μ3-16 如图所示,一弹簧劲度系数为k ,一端固定在A 点,另一端连一质量为m 的物体,靠在光滑的半径为a 的圆柱面,弹簧原长为AB 。
