大学物理2-5动量定理
合集下载
大学物理——动量和角动量

x
0
t
M l vdt Mm
X牵
动量守恒定律在空间技术中的应用:火箭飞行
例:火箭在远离星球引力的星际空间加速飞行,因 而不受任何外力的作用,设火箭某一时刻携带的燃 料的质量为 m,喷出的气体相对火箭的速率为 u, 且保持不变,求:火箭在任一时刻的速度。 t + dt t u 解:初态动量 P0 = mv
它受到的火箭对它的作用力:
dp dm F u dt dt
所以根据牛三律火箭获得的推力为
dm F u dt
方向向上
如何提高火 箭的速度?
1.3.4
质心
质心是质点系的质量中心 一、 质心位矢: 质心的定义: 设质点系共有N个质点组成,各质点的 r 质量分别为:m1,m2,…mN ,矢径分别为: 1 , r2 rN 则 质心的矢径定义为: N N y mj m i ri m i ri m1 1 rc i N i 1 c r1 mi m rc mi m2 N i 1
平均冲力: F
t2
Fdt
t1
t 2 t1
m v 2 m v1 t 2 t1
讨论
1)直角坐标系中的分量式( 二维 ):
I x Fx dt P2 x P1 x
t1 t2
I y Fy dt P2 y P1 y
t1
t2
2) 动量定理在碰撞问题中具有特殊重要的意义。 在碰撞过程中由于作用时间极短,作用力(冲力)却 很大. 并且随时间变化很难测定,但可借助始﹑末动 量变化和作用时间来计算平均冲力。
C
dl
dm = dl
= m / (R)
R
·d
大学物理 动量和动量守恒定律

解得
于是滑槽在水平面上移动的距离 S Vdt
0
t
m R M+m
22
大学 物理学
小
微分形式
结
积分形式
t1
•冲量
t2 I = Fdt
•质点的动量定理
dP F dt
I Fdt= P
t1
t2
•质点系的动量定理 F外 d Nhomakorabea dt
I 外= F外dt P
解:取车和人作为系统,该 系统水平方向动量守恒。设 人和车相对于地面的速度分 别为v 和 V,则
0 mv MV
mvdt MVdt mx MX M
0 0
t
t
xX L
L
x
M m
m X L Mm
大学 物理学
例2.13如图所示,在一个水平面上,炮车发射炮弹。 炮身质量为M,仰角为 ,炮弹质量为m。炮弹刚 出口时,相对于炮身的速度为u。不计地面摩擦, 求炮弹刚出口时炮车的速度。 解:取炮车和炮弹为系统。 u 系统所受的外力是重力和 支持力,都沿竖直方向, 所以水平方向动量守恒。 炮弹速度的水平分量为
t1
t2
•动量守恒定律
n 若F外 0, 则P= mi v i 恒 矢 量
i 1
惯性系
若f内 F外 , 则P= mi vi 恒矢量
i 1 n
n
若F外x 0, 则Px= mi vix 恒量
i 1
大学 物理学
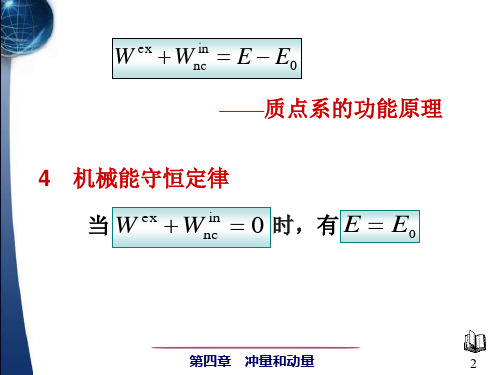
§2-3 功 动能 势能 机械能守恒定律
F
大学 物理学
3. 严格不受外力或外力矢量和为零的系统 是很少见的,但 a.当外力<<内力 且作用时间极短时 (如碰撞),
大学物理第四章冲量动量

x 轴正向相同. 方向与 O 轴正向相同.
= m sin α −m sin α = 0 v v
F' = −F
y
2. 物体系统的动量定理 对两质点分别应用质 点动量定理: 点动量定理:
质点系
v F1
v v F21 F12
m1
v F2
m2
v v v v ∫t1 ( F1 + F12 )dt = m1v1 −m1v10 v t2 v v v ∫ ( F2 + F21 )dt = m2v2 −m2v20
1. 完全弹性碰撞
r r r r m1v1 + m2v2 = m1v10 + m2v20
1 2 1 2 1 2 1 2 m1v1 + m2v2 = m1v10 + m2v20 2 2 2 2
碰后速度
碰前
v m v m1 v10 2 v 20 A B
碰后
(m −m2)v10 +2m2v20 v1 = 1 m +m2 1
v 讨论 (1) 当 ∑i外 ≠ 系统总动量不守恒,但 F , 系统总动量不守恒, 0
i=1
n
0 ∑F外x= i
i =1
n
∑F
i= 1 n
n
i外 y
= 0
∑mv ∑mv
i ix
= ∑ ivi0x m = ∑ ivi0y m = ∑ ivi0z m
i iy
∑F
i= 1
i外 z
= 0
∑mv
i iz
若系统内力>>外力, >>外力 (2) 若系统内力>>外力,以致外力可以忽略不计 时,可以应用动量守恒定律处理问题。 可以应用动量守恒定律处理问题。 式中各速度应对同一参考系而言。 (3) 式中各速度应对同一参考系而言。
= m sin α −m sin α = 0 v v
F' = −F
y
2. 物体系统的动量定理 对两质点分别应用质 点动量定理: 点动量定理:
质点系
v F1
v v F21 F12
m1
v F2
m2
v v v v ∫t1 ( F1 + F12 )dt = m1v1 −m1v10 v t2 v v v ∫ ( F2 + F21 )dt = m2v2 −m2v20
1. 完全弹性碰撞
r r r r m1v1 + m2v2 = m1v10 + m2v20
1 2 1 2 1 2 1 2 m1v1 + m2v2 = m1v10 + m2v20 2 2 2 2
碰后速度
碰前
v m v m1 v10 2 v 20 A B
碰后
(m −m2)v10 +2m2v20 v1 = 1 m +m2 1
v 讨论 (1) 当 ∑i外 ≠ 系统总动量不守恒,但 F , 系统总动量不守恒, 0
i=1
n
0 ∑F外x= i
i =1
n
∑F
i= 1 n
n
i外 y
= 0
∑mv ∑mv
i ix
= ∑ ivi0x m = ∑ ivi0y m = ∑ ivi0z m
i iy
∑F
i= 1
i外 z
= 0
∑mv
i iz
若系统内力>>外力, >>外力 (2) 若系统内力>>外力,以致外力可以忽略不计 时,可以应用动量守恒定律处理问题。 可以应用动量守恒定律处理问题。 式中各速度应对同一参考系而言。 (3) 式中各速度应对同一参考系而言。
大学物理第3章动量与冲量

n Pi P1 P2 ...... Pn mi vi n i 1 i 1
质点系 F2 ( F1 F12 )dt m1v1 m1v10 t1 F21 t2 F12 ( F2 F21 )dt m2 v2 m2 v20 F1 m2
本章教学内容:
3-1 3-2 3-3 3-4 3-5 3-6 3-7 3-8 3-9 冲量与动量定理 动量守恒定律 火箭飞行原理 质心 质心运动定理 质点的角动量和角动量定理 角动量守恒定理 质点系的角动量定理 质心参考系中的角动量
教学基本要求
1、理解并掌握牛顿第二定律的两个积分形式
2、掌握冲量和动量的概念,掌握动量定理及其应用
drc N mi v i m 3、质心的速度 v dt i 1 4、质心的动量 Pc mvc mi vi pi P
C
N N i 1 i 1
i 1
在任何参考系中,质心的动量都等于质点系 的总动量。
dvc mi a i m 5、质心的加速度 ac dt
d (mv ) F dt
动量
mv2 mv1 F t
动量定理 力在Δt时间内的 积累:冲量
动能定理的推导:
质量为M 的物体在水平恒力F 的作用 下,经过时间t,速度由v0 变为 vt, v =v0
————F 作用了时间 t————
F F F F F F F
v =v t
t2
t1
Fdt p2 p1 mv2 mv1
质点的动量定理:在给定的时间内,外力作用在 质点上的冲量,等于质点在此时间内动量的增量 . 注意:动量定理表达的含义有以下几方面: (1) 物体动量变化的大小和它所受合外力冲 量的大小相等。 (2) 物体动量变化的方向和它所受合外力冲 量的方向相同。 (3) 冲量是物体动量变化的原因。
质点系 F2 ( F1 F12 )dt m1v1 m1v10 t1 F21 t2 F12 ( F2 F21 )dt m2 v2 m2 v20 F1 m2
本章教学内容:
3-1 3-2 3-3 3-4 3-5 3-6 3-7 3-8 3-9 冲量与动量定理 动量守恒定律 火箭飞行原理 质心 质心运动定理 质点的角动量和角动量定理 角动量守恒定理 质点系的角动量定理 质心参考系中的角动量
教学基本要求
1、理解并掌握牛顿第二定律的两个积分形式
2、掌握冲量和动量的概念,掌握动量定理及其应用
drc N mi v i m 3、质心的速度 v dt i 1 4、质心的动量 Pc mvc mi vi pi P
C
N N i 1 i 1
i 1
在任何参考系中,质心的动量都等于质点系 的总动量。
dvc mi a i m 5、质心的加速度 ac dt
d (mv ) F dt
动量
mv2 mv1 F t
动量定理 力在Δt时间内的 积累:冲量
动能定理的推导:
质量为M 的物体在水平恒力F 的作用 下,经过时间t,速度由v0 变为 vt, v =v0
————F 作用了时间 t————
F F F F F F F
v =v t
t2
t1
Fdt p2 p1 mv2 mv1
质点的动量定理:在给定的时间内,外力作用在 质点上的冲量,等于质点在此时间内动量的增量 . 注意:动量定理表达的含义有以下几方面: (1) 物体动量变化的大小和它所受合外力冲 量的大小相等。 (2) 物体动量变化的方向和它所受合外力冲 量的方向相同。 (3) 冲量是物体动量变化的原因。
大学物理动量与动量守恒定律

与轨道的摩擦忽略不计)
解: m:表示t时刻煤车和 已落入煤车的煤的总质量;
dm:表示t时刻后dt时间内
F 又落入煤车的煤的质量。
t时刻此系统的水平总量,mv+dm×0=mv t+dt时刻此系统的水平总量,(m+dm)v
Fdt=dp= (m+dm)v—mv=dm v F=dm/dt v=500×3=1500(N)
质点系动量定理 (微分形式)
注意
t2
t1
F外
dt
P2
P1
质点系动量定理 (积分形式)
系统总动量由外力的冲量决定,与内力无关。
用质点系动量定理处理问题可避开内力。
大学 物理学
例2.10一辆装煤车以的v=3m/s速率从煤斗下面通过,
每秒钟落入车厢的煤为△m=500kg,如果使车厢的
速率保持不变,应用多大的牵引力拉车厢?(车厢
大学 物理学
解题步骤: 1.选好系统和过程; 2.进行受力分析,判断守恒条件; 3.确定系统的任意时刻的动量、初动量 或末动量; 4.建立坐标系,列方程求解;
大学
物理学 例2.11 一枚返回式火箭以 2.5103 m·s-1 的
速率相对惯性系S沿水平方向飞行.空气阻
力不计.现使火箭分离为两部分, 前方的仪
大学
物理学 3.严格不受外力或外力矢量和为零的系统 是很少见的,但 a.当外力<<内力 且作用时间极短时(如碰撞), 可认为动量近似守恒。 b.若某个方向上合外力为零,则该方向上动
量守恒,尽管总动量可能并不守恒。
4.动量守恒定律是比牛顿定律更普遍、更基本 的定律,它在宏观和微观领域均适用。 5.用守恒定律作题,应注意分析 过程、系统 和条件。
大学物理 冲量和动量
动量、冲量 、动量定理、动量守恒 动能、功、动能定理、机械能守恒
第四章 冲量和动量
4
物理学
第五版
4-1 质点动量定理
4-2 质点系动量定理
4-3 动量守恒定律 基本要求 1、理解动量定理; 2、掌握动量守恒定律。
第四章 冲量和动量
5
一
4.1 冲量
质点动量定理
力的时间积累
动量 p m v dp d (m v) F dt dt Fdt dp d (m v) t2 F d t p 2 p1 m v 2 m v1
神舟六号发射成功
注:照片摘自新华网
第四章 冲量和动量
30
大作业: P9:一.
P10.全做
课下请预习第六章 并复习前四章
第四章 冲量和动量
31
x
m v1
O
mv2
y
第四章 冲量和动量
11
解
取钢板和球为研究对象,冲力远大于重力。
I F t mv2 mv1
由动量定理有:
Fx t mv2 x mv1x
mv cos (mv cos )
x
m v1
O
2mv cos
Fy t mv2 y mv1 y
分量表示
Iy Iz
t1 t2
t1
说明 某方向受到冲量,该方向上动量就增加.
第四章 冲量和动量
9
F 为恒力
I Ft P
F作用时间很短时,可用力的平均值来代替。 F为恒力时,可以得出:
由此可求平均作用力:
第四章 冲量和动量
大学物理 第四章 冲量和动量

pt 2 I pt 0 I (20i 4 j 8k )N s
上页 下页 返回 退出
【例3】一质量为m的质点作匀速圆周运动,速率为v, 求:质点走过1/4圆弧的过程中,(1)合力对质点的冲 量大小;(2)合力对质点作功。 解:(1) ( 2)
2mv
0
上页 下页 返回 退出
先考虑守恒。 ※动量守恒(合外力0)、 ※机械能守恒(非保守力不作功) 若不满足守恒条件,可选: ※牛顿第二定律 ※动能定理 ※动量定理 动能定理不显含时间,动量定理不显含位移
上页 下页 返回 退出
F 10ti 2(2 t )j 3t k ,质点从静止开始运动,
2
求:(1)2s内受合力的冲量;(2)2s末的动量。
解:(1) I
2 0
[10ti 2(2 t )j 3t k ]dt
2
Fdt
t1
t2
(20i 4 j 8k )N s (2) I pt 2 pt 0
t1
t2
t1 t2
t1
m (F2 f 2 )dt m2v 22 m2v21 1
t2 t1
(F1 f1 )dt m1v12 m1v11
f1
F1
f2
m
2
F2
t2
(F1 F2 )dt (f1 f 2 )dt
(m1v12 m2v 22 ) (m1v11 m1v 21 )
【例4】一力F作用在质量为3kg的质点上,使之沿x轴
运动,运动方程
x 3t 4t t ,求:0---4s内
2 3
(1)力F的冲量大小;(2)力F对质点做功。
解: v 3 8t 3t 2
上页 下页 返回 退出
【例3】一质量为m的质点作匀速圆周运动,速率为v, 求:质点走过1/4圆弧的过程中,(1)合力对质点的冲 量大小;(2)合力对质点作功。 解:(1) ( 2)
2mv
0
上页 下页 返回 退出
先考虑守恒。 ※动量守恒(合外力0)、 ※机械能守恒(非保守力不作功) 若不满足守恒条件,可选: ※牛顿第二定律 ※动能定理 ※动量定理 动能定理不显含时间,动量定理不显含位移
上页 下页 返回 退出
F 10ti 2(2 t )j 3t k ,质点从静止开始运动,
2
求:(1)2s内受合力的冲量;(2)2s末的动量。
解:(1) I
2 0
[10ti 2(2 t )j 3t k ]dt
2
Fdt
t1
t2
(20i 4 j 8k )N s (2) I pt 2 pt 0
t1
t2
t1 t2
t1
m (F2 f 2 )dt m2v 22 m2v21 1
t2 t1
(F1 f1 )dt m1v12 m1v11
f1
F1
f2
m
2
F2
t2
(F1 F2 )dt (f1 f 2 )dt
(m1v12 m2v 22 ) (m1v11 m1v 21 )
【例4】一力F作用在质量为3kg的质点上,使之沿x轴
运动,运动方程
x 3t 4t t ,求:0---4s内
2 3
(1)力F的冲量大小;(2)力F对质点做功。
解: v 3 8t 3t 2
大学物理-力学中的动量

第2级火箭脱落时,火箭组的速率为
V2 = V1 + uln N2 = ulnN1 + ulnN2 = u ln( N 1N 2 )
第 n 级火箭脱落时,火箭组的速率为
Vn = u ln( N1N 2 " N n ) (N1>1, N2>1, · · · Nn>1)
§4 质心 ( Center of Mass)
例:任意三角形的每个顶点有一质量 m,求质心
y
(x1,y1)
o
x2
x
xc
=
mx1 + mx2 3m
=
x1
+ x2 3
yc
=
my1 3m
=
y1 3
例:求半径为 R 的半圆形铁丝的质心。(Semicircular Hoop)
解
xc
=
∫
xdm m
yc
=
∫
ydm m
dm = λdl = m dl = m Rdθ
K M ,V
dm
GG
M − dm,V + dV
K
K
K
x
V气地 = V气箭 + V箭地
P0 = P1 + P2
MV= (M–dm)(V+dV)+ dm(V+dV – u)
MV= MV–Vdm + MdV– dmdV+Vdm +dmdV– udm
MdV = udm
dm = – dM
MdV= – udM
M dV = – u dM
T
m v0 m vm
T
M vM
Δp
mg
Δp
Mg
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t2 F d t t1
d p2
p1
p
p2
p1
动量定理
左侧积分表示力对时间的累积量,叫做冲量。
I t2 Fdt t1
于是得到积分形式
I p2 p1
这就是动量定理:物体在运动过程中所受到的
合外力的冲量,等于物体动量的增量。 动量定理的几点说明:
(1)冲量的方向:
冲量 的I方向一般不是力 在F某(t)一瞬时的方向。
解得 N Mg M 2gh /
代入M、h、的值,求得:
(1) N 3103 (9.8 29.81.5 / 0.1)) N 3103 (9.8 29.81.5 / 0.01)
1.7106牛顿
解法二:考虑从锤自由下落到静止的整个过程, 动量变化为零。
重力作用时间为 2h / g
§2-5 动量定理
微分形式的牛顿第二定律是关于力与加速度的瞬 时关系。某些情况下,并不需要考虑中间过程,仅 需考虑力的累积作用对物体运动状态的影响。这时 候,采用积分形式的牛顿第二定律更有效。这就是 动量定理与动能定理。
1. 动量定理
由牛顿第二定律的微分形式
Fdt d p
考虑一过程,时间从t1 t2,两端积分
的大小,根据动量定理,得到平
F
均冲力: F I /
t1
t2 t
动量定理
(4)对于多个质点组成的质点系,不考虑内力。 (5)动量定理是牛顿第二定律的积分形式,因此其 使用范围是惯性系。
例 题 2-6 质 量 M=3t 的 重 锤 , 从 高 度 h=1.5m处自由落到受锻压的工件上,工
件发生形变。如果作用的时间(1)=0.1s, (2)=0.01s 。试求锤对工件的平均冲力。
解:以物体A和B为系统作为 研究对象,采用隔离法分析受 力,作出绳拉紧时的受力图:
绳子刚好拉紧前的瞬间,物 体A的速度为:
v 2gh
取竖直向上为正方向。
M
T2 T1
Am h
B
BA
mg Mg
动量定理
绳子拉紧后,经过短暂时间的作用,两物体速率
相等 ,V对两个物体分别应用动量定理,得到 (T1 mg)t mV (mv)
(T2Mg)tMV 0 忽略解重得力:(?V),m考虑2到g绳h 不可伸长,有:T1 T2
M m
当物体B上升速度为零时,达到最大高度
2aH 0 V 2
aM mg M m
m2h H M 2 m2
支持力的作用时间为
根据动量定理,整个过程合外力的冲量为零,即
N Mg( 2h / g ) 0 得到解法一相同的结果 N Mg M 2gh /
动量定理
例题2-7 一绳跨过一定滑轮,两端分别拴有质量为m及 的M物体A和B, M大于m。B静止在地面上,当A自由下 落距离h后,绳子才被拉紧。求绳子刚被拉紧时两物体 的速度,以及M能上升的最大高度。
动量定理
(2)在直角坐标系中将矢量方程改为标量方程
Ix
t2 t1
Fx
dt
mv2 x
mv1x
Iy
t2 t1
Fy d t
mv2 y
mv1y
Iz
t2 t1
Fz
dt
mv2 z
mv1z
(3)动量打定击理或在碰打撞击,或设碰撞力问题F的中方用向来保求平均力。 持不变,曲线与t轴所包围的面积 F
就是t1到t2这段时间内力 的F冲量
平均支持力 N
h
解:以重锤为研究对象,分析受力,作 受力图:
Mg
动量定理
解法一:锤对工件的冲力变化范围很大,采用平 均冲力计算,其反作用力用平均支持力代替。
在竖直方向利用动量定理,取竖直向上为正。
(N Mg) Mv Mv0
初状态动量为 M 2gh 末状态动量为0
得到 (N Mg) M 2gh
