潮流计算作业A4汇总
(完整word版)潮流计算方法

由于本人参加我们电气学院的电气小课堂,主讲的是计算机算法计算潮流这章,所以潜心玩了一个星期,下面整理给大家分享下。
本人一个星期以来的汗水,弄清楚了计算机算法计算潮流的基础,如果有什么不懂的可以发信息到邮箱:zenghao616@接下来开始弄潮流的优化问题,吼吼!电力系统的潮流计算的计算机算法:以MATLAB为环境这里理论不做过多介绍,推荐一本专门讲解电力系统分析的计算机算法的书籍---------《电力系统分析的计算机算法》—邱晓燕、刘天琪编著。
这里以这本书上的例题【2-1】说明计算机算法计算的过程,分别是牛顿拉弗逊算法的直角坐标和极坐标算法、P-Q分解算法。
主要是简单的网络的潮流计算,其实简单网络计算和大型网络计算并无本质区别,代码里面只需要修改循环迭代的N即可,这里旨在弄清计算机算法计算潮流的本质。
代码均有详细的注释.其中简单的高斯赛德尔迭代法是以我们的电稳教材为例子讲,其实都差不多,只要把导纳矩阵Y给你,节点的编号和分类给你,就可以进行计算了,不必要找到原始的电气接线图。
理论不多说,直接上代码:简单的高斯赛德尔迭代法:这里我们只是迭代算出各个节点的电压值,支路功率并没有计算。
S_ij=P_ij+Q_ij=V_i(V_i* - V_j*) * y_ij*可以计算出各个线路的功率在显示最终电压幅角的时候注意在MATLAB里面默认的是弧度的形式,需要转化成角度显示。
clear;clc;%电稳书Page 102 例题3-5%计算网络的潮流分布 --- 高斯-赛德尔算法%其中节点1是平衡节点%节点2、3是PV节点,其余是PQ节点% 如果节点有对地导纳支路%需将对地导纳支路算到自导纳里面%------------------------------------------------%%输入原始数据,每条支路的导纳数值,包括自导和互导纳;y=zeros(5,5);y(1,2)=1/(0.0194+0.0592*1i);y(1,5)=1/(0.054+0.223*1i);y(2,3)=1/(0.04699+0.198*1i);y(2,4)=1/(0.0581+0.1763*1i);%由于电路网络的互易性,导纳矩阵为对称的矩阵for i=1:1:5for j=1:1:5y(j,i)=y(i,j);endend%节点导纳矩阵的形成Y=zeros(5,5);%求互导纳for i=1:1:5for j=1:1:5if i~=jY(i,j)=-y(i,j);endendend%求自导纳for i=1:1:5%这句话是说将y矩阵的第i行的所有元素相加,得到自导纳的值 Y(i,i)=sum(y(i,:));end%上面求得的自导纳不包含该节点的对地导纳数值,需要加上Y(2,2)=Y(2,2)+0.067*1i;Y(3,3)=Y(3,3)+0.022*1i;Y(4,4)=Y(4,4)+0.0187*1i;Y(5,5)=Y(5,5)+0.0246*1i;%导纳矩阵的实部和虚部G = real(Y);B = imag(Y);Qc2=0;Qc3=0;%原始节点功率%这里电源功率为正,负荷功率为负S(1)=0;S(2)=-0.217-0.121*1i+Qc2*1i;S(3)=-0.749-0.19*1i+Qc3*1i;S(4)=-0.658+0.039*1i;S(5)=-0.076-0.016*1i;%节点功率的P QP = real(S);Q = imag(S);%下面是两个PV节点的无功初始值Q(2) = 0;Q(3) = 0;U=ones(5,1); %1列5行的‘1’矩阵%节点电压初始值U(1)=1.06;U(2)=1.045;U(3)=1.01;U_reg=U;Sum_YU0=0;%中间变量Sum_YU1=0;%中间变量for cont=1:1:6 %这里的cont是迭代次数for i=2:1:5for j=1:1:iif i~=jSum_YU0 = Sum_YU0 + Y(i,j)*U_reg(j);endendfor j=i+1:1:5Sum_YU1 = Sum_YU1 + Y(i,j)*U(j);endU(i)=( (P(i)-Q(i)*1i ) / conj(U(i)) - Sum_YU0 - Sum_YU1 ) / Y(i,i); U_reg(i)=U(i);%PV节点计算%下面是把求出的U2、U3只保留其相位,幅值不变if i==2angle_U2 = angle(U(2));U(2)=1.045*cos(angle_U2)+1.045*sin(angle_U2)*1i;Q(2)=imag( U(2)*( conj(Sum_YU0) + conj(Sum_YU1) + conj(Y(2,2)*U(2)) ) );endif i==3angle_U3 = angle(U(3));U(3)=1.01*cos(angle_U3)+1.01*sin(angle_U3)*1i;Q(3)=imag( U(3)*( conj(Sum_YU0) + conj(Sum_YU1) + conj(Y(3,3)*U(3)) ) );end% 下面做越界检查%if Q(4)>Q_Max% Q(4) = Q_Max;%end%if Q(4)<Q_Min% Q(4) = Q_Min;%end%下面可以做PV节点收敛判断Sum_YU0 = 0;Sum_YU1 = 0;endend%节点注入无功,流入为正,流出为负Qc2=Q(2)+0.121-1.045^2 * 0.067;Qc3=Q(3)+0.19-1.01^2 * 0.022;%电压幅值和相角angle_U=angle(U)*180/pi;U=abs(U);S_Line=zeros(5,5);%计算平衡节点功率S_BalanceNode=0;for j=1:1:5S_BalanceNode = S_BalanceNode + U(1) * conj(Y(1,j)*U(j));end%下面由上面算出的电压值求线路的功率%这里计算出来的线路功率的有功、无功%for i=1:1:5% for j=i:1:5% if i~=j% S_Line(i,j)=U(i)*( conj(U(i))-conj(U(j)) ) * conj(y(i,j));% end% if i==2% %S_Line(2,j)=S_Line(2,j)+U(2)*conj(0.067*1i);% end% if i==3% %S_Line(3,j)=S_Line(3,j)+U(3)*conj(0.022*1i);% end% end%end计算网络的潮流分布 ---- Newton算法(直角坐标)clear;clc;%电稳书Page 102 例题3-5%计算网络的潮流分布 ---- Newton算法(直角坐标)%其中节点1是平衡节点%节点2、3是PV节点,其余是PQ节点% 如果节点有对地导纳支路%需将对地导纳支路算到自导纳里面%------------------------------------------------%%输入原始数据,每条支路的导纳数值,包括自导和互导纳;y=zeros(5,5);y(1,2)=1/(0.0194+0.0592*1i);y(1,5)=1/(0.054+0.223*1i);y(2,3)=1/(0.04699+0.198*1i);y(2,4)=1/(0.0581+0.1763*1i);%由于电路网络的互易性,导纳矩阵为对称的矩阵for i=1:1:5for j=1:1:5y(j,i)=y(i,j);endend%节点导纳矩阵的形成Y=zeros(5,5);%求互导纳for i=1:1:5for j=1:1:5if i~=jY(i,j)=-y(i,j);endendend%求自导纳for i=1:1:5%这句话是说将y矩阵的第i行的所有元素相加,得到自导纳的值Y(i,i)=sum(y(i,:));end%上面求得的自导纳不包含该节点的对地导纳数值,需要加上Y(2,2)=Y(2,2)+0.067*1i;Y(3,3)=Y(3,3)+0.022*1i;Y(4,4)=Y(4,4)+0.0187*1i;Y(5,5)=Y(5,5)+0.0246*1i;%导纳矩阵的实部和虚部G = real(Y);B = imag(Y);%节点2、3需补偿的无功Qc2=0;Qc3=0;%原始节点功率%这里电源功率为正,负荷功率为负S(1)=0;S(2)=-0.217-0.121*1i+Qc2*1i;S(3)=-0.749-0.19*1i+Qc3*1i;S(4)=-0.658+0.039*1i;S(5)=-0.076-0.016*1i;%节点功率的P QP = real(S);Q = imag(S);%下面是两个PV节点的无功初始值Q(2) = 0;Q(3) = 0;%给点电压初始值e=[1.06,1.045,1.01,1,1];f=[0,0,0,0,0];U=e+f*1i;delta_U=zeros(1,5);delta_P=zeros(1,5);delta_Q=zeros(1,5);delta_PQV=ones(8,1);Sum_GB1=0;Sum_GB2=0;cont=0;while max(delta_PQV > 1e-6),cont=cont+1;%for cont=1:1:3%下面开始计算delta_P/delta_Q/delta_Ufor i=2:1:5for j=1:1:5Sum_GB1=Sum_GB1 + ( G(i,j)*e(j) - B(i,j)*f(j) );Sum_GB2=Sum_GB2 + ( G(i,j)*f(j) + B(i,j)*e(j) );enddelta_P(i)=P(i)-e(i)*Sum_GB1-f(i)*Sum_GB2;if i~=2 && i~=3 %不为节点2,3则计算无功delta_Q(i)=Q(i)-f(i)*Sum_GB1+e(i)*Sum_GB2;endif i==2 || i==3 %这里计算delta_U的值,始终为零delta_U(i)=U(i)^2-( e(i)^2 + f(i)^2 );endSum_GB1=0;Sum_GB2=0;end%___________________________________%%下面计算雅克比矩阵J=zeros(8,8);for ii=2:1:5i=ii-1;for j=1:1:5Sum_GB1=Sum_GB1 + ( G(ii,j)*e(j) - B(ii,j)*f(j) );Sum_GB2=Sum_GB2 + ( G(ii,j)*f(j) + B(ii,j)*e(j) );endfor jj=2:1:5j=jj-1;if ii~=2 && ii~=3 %PQ节点if ii==jjJ(2*i-1,2*i-1)=-Sum_GB1-G(ii,ii)*e(ii)-B(ii,ii)*f(ii);J(2*i-1,2*i)=-Sum_GB2+B(ii,ii)*e(ii)-G(ii,ii)*f(ii);J(2*i,2*i-1)=Sum_GB2+B(ii,ii)*e(ii)-G(ii,ii)*f(ii);J(2*i,2*i)=-Sum_GB1+G(ii,ii)*e(ii)+B(ii,ii)*f(ii);elseJ(2*i-1,2*j-1)=-(G(ii,jj)*e(ii)+B(ii,jj)*f(ii)); J(2*i-1,2*j)=B(ii,jj)*e(ii)-G(ii,jj)*f(ii);J(2*i,2*j-1)=B(ii,jj)*e(ii)-G(ii,jj)*f(ii);J(2*i,2*j)=(G(ii,jj)*e(ii)+B(ii,jj)*f(ii));endelse%PV节点if ii==jjJ(2*i-1,2*i-1)=-Sum_GB1-G(ii,ii)*e(ii)-B(ii,ii)*f(ii);J(2*i-1,2*i)=-Sum_GB2+B(ii,ii)*e(ii)-G(ii,ii)*f(ii);J(2*i,2*i-1)=-2*e(ii);J(2*i,2*i)=-2*f(ii);elseJ(2*i-1,2*j-1)=-(G(ii,jj)*e(ii)+B(ii,jj)*f(ii)); J(2*i-1,2*j)=B(ii,jj)*e(ii)-G(ii,jj)*f(ii);J(2*i,2*j-1)=0;J(2*i,2*j)=0;endendendSum_GB1=0;Sum_GB2=0;end%在求解修正方程之前建议把delta_P和delta_Q,delta_U全部放在一个矩阵delta_PQV=[delta_P(2);delta_U(2);delta_P(3);delta_U(3);delta_P(4) ;delta_Q(4);delta_P(5);delta_Q(5)];%下面求解修正方程;注意矩阵运算时候的左除和右除的区别delta_ef=-J\delta_PQV;%下面修正各个节点的电压for i=2:1:5e(i)=e(i)+delta_ef(2*(i-1)-1);f(i)=f(i)+delta_ef(2*(i-1));end%到这里第一轮迭代完成end%电压幅值和相角U=e+f*1i;angle_U=angle(U)*180/pi;%节点注入无功,流入为正,流出为负Sum_YU=0;for i=2:1:3for j=1:1:5Sum_YU = Sum_YU + Y(i,j)*U(j);endQ(i)=imag( U(i)*conj( Sum_YU ) );Sum_YU=0;endQc2=Q(2)+0.121-1.045^2 * 0.067;Qc3=Q(3)+0.19-1.01^2 * 0.022;U=abs(U);disp(['Iteration times : ' num2str(cont)]);%显示最终的迭代次数牛顿算法求解潮流 (极坐标):clear;clc;%牛顿算法求解潮流 (极坐标)%计算网络的潮流分布%其中节点5是平衡节点%节点1、2、3是PQ节点,节点4是PV节点% 如果节点有对地导纳支路%需将对地导纳支路算到自导纳里面%------------------------------------------------%%输入原始数据,每条支路的导纳数值,包括自导和互导纳;Y=[0.8381-3.7899*1i,-0.4044+1.6203*1i,0,0,-0.4337+2.2586*1i;...-0.4044+1.6203*1i,0.7769-3.3970*1i,-0.3726+1.8557*1i,0,0;...0,-0.3726+1.8557*1i,1.1428-7.0210*1i,-0.5224+4.1792*1i,-0.2739+1. 2670*1i;...0,0,-0.5224+4.1792*1i,0.5499-4.3591*1i,0;...-0.4337+2.2586*1i,0,-0.2739+1.2670*1i,0,0.7077-3.4437*1i];%导纳矩阵的实部和虚部G = real(Y);B = imag(Y);%给点电压初始值U = [1,1,1,1,1.05];angle_U=[0,0,0,0,0];%for i=1:1:5% U(i)=U_abs(i)*cos(angle_U(i))+U_abs(i)*sin(angle_U(i))*1i;%end%原始节点功率%这里电源功率为正,负荷功率为负%下面给点PQ PV节点功率值S=[-0.22-0.14*1i,-0.18-0.09*1i,-0.27-0.13*1i,0.35,0];%节点功率的P QP = real(S);Q = imag(S);%下面是PV节点的无功初始值Q(4) = 0;delta_P=zeros(1,5);delta_Q=zeros(1,5);%delta_angleU=zeros(1,4);%delta_absU=zeros(1,4);delta_PQ=ones(8,1);Sum_GB1=0;Sum_GB2=0;cont=0;%最外层循环,cont代表迭代的次数,这里可以用约束条件来代替%for cont=1:1:4while max(delta_PQ)>1e-6,%下面计算delta_P/delta_Q/delta_Ucont=cont+1;for i=1:1:4for j=1:1:5Sum_GB1=Sum_GB1 + U(j)*( G(i,j)*cos(angle_U(i)-angle_U(j)) + B(i,j)*sin(angle_U(i)-angle_U(j)) );Sum_GB2=Sum_GB2 + U(j)*( G(i,j)*sin(angle_U(i)-angle_U(j)) - B(i,j)*cos(angle_U(i)-angle_U(j)) );enddelta_P(i)=P(i)-U(i)*Sum_GB1;if i~=4 %不为节点四则计算无功delta_Q(i)=Q(i)-U(i)*Sum_GB2;endSum_GB1=0;Sum_GB2=0;end%_______________________________________________________%%下面计算雅克比矩阵J=zeros(7,7);for ii=1:1:4for jj=1:1:4if ii ~= 4 %PQ节点if ii==jjJ(2*ii-1,2*ii-1)=U(ii)^2*B(ii,ii)+Q(ii);J(2*ii-1,2*ii)=-U(ii)^2*G(ii,ii)-P(ii);J(2*ii,2*ii-1)=U(ii)^2*G(ii,ii)-P(ii);J(2*ii,2*ii)=U(ii)^2*B(ii,ii)-Q(ii);elseJ(2*ii-1,2*jj-1)=-U(ii)*U(jj)*( G(ii,jj)*sin(angle_U(ii)-angle_U( jj)) - B(ii,jj)*cos(angle_U(ii)-angle_U(jj)) );J(2*ii-1,2*jj)=-U(ii)*U(jj)*( G(ii,jj)*cos(angle_U(ii)-angle_U(jj)) + B(ii,jj)*sin(angle_U(ii)-angle_U(jj)) );J(2*ii,2*jj-1)=U(ii)*U(jj)*( G(ii,jj)*cos(angle_U(ii)-angle_U(jj)) + B(ii,jj)*sin(angle_U(ii)-angle_U(jj)) );J(2*ii,2*jj)=-U(ii)*U(jj)*( G(ii,jj)*sin(angle_U(ii)-angle_U(jj)) - B(ii,jj)*cos(angle_U(ii)-angle_U(jj)) );endelse%PV节点if ii==jjJ(2*ii-1,2*ii-1)=U(ii)^2*B(ii,ii)+Q(ii);J(2*ii-1,2*ii)=-U(ii)^2*G(ii,ii)-P(ii);elseJ(2*ii-1,2*jj-1)=-U(ii)*U(jj)*( G(ii,jj)*sin(angle_U(ii)-angle_U( jj)) - B(ii,jj)*cos(angle_U(ii)-angle_U(jj)) );J(2*ii-1,2*jj)=-U(ii)*U(jj)*( G(ii,jj)*cos(angle_U(ii)-angle_U(jj)) + B(ii,jj)*sin(angle_U(ii)-angle_U(jj)) );endendendend%在求解修正方程之前建议把delta_ef和delta_ef全部放在一个矩阵delta_PQ=[delta_P(1);delta_Q(1);delta_P(2);delta_Q(2);delta_P(3); delta_Q(3);delta_P(4)];%下面求解修正方程;注意矩阵运算时候的左除和右除的区别J=J(1:7,1:7);delta_ef=-J\delta_PQ;%下面修正各个节点的电压for i=1:1:4if i~=4U(i)=U(i)+delta_ef(2*i)*U(i);endangle_U(i)=angle_U(i)+delta_ef(2*i-1);end%到这里第一轮迭代完成end%下面显示出满足条件后的迭代的次数disp(['Iteration times : ' num2str(cont)]);%下面计算平衡节点5的功率PQfor j=1:1:5Sum_GB1=Sum_GB1 + U(j)*( G(5,j)*cos(angle_U(5)-angle_U(j)) + B(5,j)*sin(angle_U(5)-angle_U(j)) );Sum_GB2=Sum_GB2 + U(j)*( G(5,j)*sin(angle_U(5)-angle_U(j)) - B(5,j)*cos(angle_U(5)-angle_U(j)) );endP(5)=U(5)*Sum_GB1;Q(5)=U(5)*Sum_GB2;%下面将相角用角度表示for i=1:1:5angle_U(i)=angle_U(i)*180/pi;End计算计算法P-Q算法计算潮流:这个算法是由牛顿算法的极坐标形式简化而来。
(完整word版)电力系统潮流计算课程设计
一、问题重述课程设计要求1、在读懂程序的基础上画出潮流计算根本流程图2、经过输入数据,进行潮流计算输出结果3、对不同样的负荷变化,解析潮流分布,写出解析说明。
4、对不同样的负荷变化,进行潮流的调治控制,并说明调治控制的方法,并列表表示调治控制的参数变化。
5、打印利用 DDRTS 进行潮流解析绘制的系统图,以及潮流分布图。
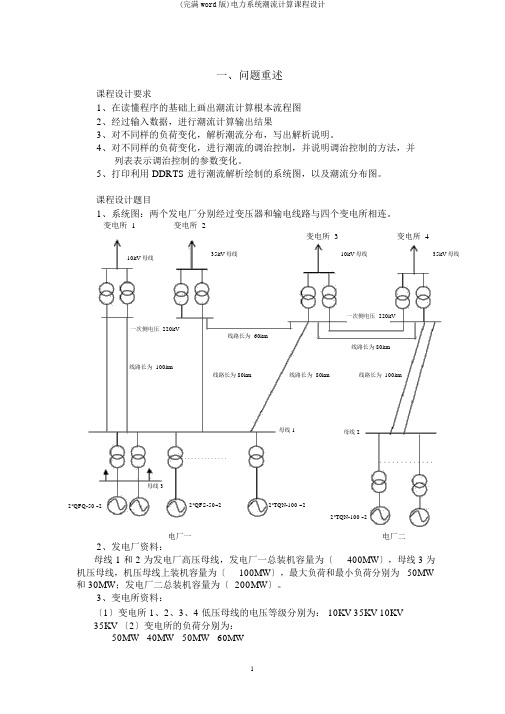
课程设计题目1、系统图:两个发电厂分别经过变压器和输电线路与四个变电所相连。
变电所 1变电所 2变电所 3变电所 435kV 母线10kV 母线35kV 母线10kV 母线一次侧电压 220kV一次侧电压 220kV线路长为 60km线路长为 80km线路长为 100km线路长为 80km线路长为 80km线路长为 100km母线 1母线 2。
母线 32*QFQ-50 -22*QFS-50-22*TQN-100 -22*TQN-100 -2电厂一电厂二2、发电厂资料:母线 1 和 2 为发电厂高压母线,发电厂一总装机容量为〔400MW〕,母线 3 为机压母线,机压母线上装机容量为〔100MW〕,最大负荷和最小负荷分别为 50MW和 30MW;发电厂二总装机容量为〔 200MW〕。
3、变电所资料:〔1〕变电所 1、2、3、4 低压母线的电压等级分别为: 10KV 35KV 10KV35KV 〔2〕变电所的负荷分别为:50MW 40MW 50MW60MW〔3〕每个变电所的功率因数均为cosφ=0.85 ;〔4〕变电所 2 和变电所 4 分别配有两台容量为 75MVA的变压器,短路耗费414KW,短路电压〔 %〕=16.7 ;变电所 1 和变电所 3 分别配有两台容量为63MVA 的变压器,短路耗费为 245KW,短路电压〔 %〕=10.5 ;4、输电线路资料:发电厂和变电所之间的输电线路的电压等级及长度标于图中,单位长度的电阻为,单位长度的电抗为,单位长度的电纳为 2.78 * 10 -6 S 。
电力系统潮计算PPT课件

⑴在 B '中尽量去掉那些对有功功率及电压相角影响较小的因素,如
略去变压器非标准电压比和输电线路充电电容的影响;在 B 中'' 尽
量去掉那些对无功功率及电压幅值影响较小的因素,如略去输电 线路电阻的影响。
⑵为了减少在迭代过程中无功功率及节点电压幅值对有功迭代的影 响,将(2-44)右端U各元素均置为标幺值1.0.
• 潮流计算公式作如下修改:
P i a 1 b 1 u u ii0 c 1 u u ii0 2 P i0 (s) u ij iu jG ijc o ij B s ijs iijn
Q i a 1 b 1 u u ii0 c 1 u u ii0 2 Q i (0 s) u ij iu jG ijs iijn B ijc o ij s
(4)和节点导纳矩阵具有相同稀疏结构的分块雅可比矩阵 在位置上对称,但由于数值上不等,说以,雅可比矩阵式 一个不对称矩阵。
2024/6/4
11
四、牛顿潮流算法的性能分析
• 优点:
⑴收敛速度快。
如果初值选择较好,算法将具有平方收敛性,一般迭代4~5次便 可以收敛到一个非常精确地解,而且其迭代次数与计算的网络规模 基本无关。
方程组的解。而牛顿法出于线性近似,略去了高阶项,因此用每次迭
代所求得的修正量对上一次的估计值加以改进后,仅是向真值接近了
一步而已。
2024/6/4
24
为了推导算法的方便,下面将上述潮流方程写成更普遍的齐次二次方 程的形式。
首先作以下定义:
一个具有n个变量的齐次代数方程式的普遍形式为:
(2-65)
2024/6/4
2024/6/4
3
第三节 牛顿潮流算法
一、牛顿法的基本原理
电力系统牛拉法潮流计算

令 则有
I YV Yn V n n s s
Yn L + D + U
= D-1 (I -YV - LV - UV ) V n n s s n n
ˆ i 1 n 1 S ( k ) ( k ) Y V YV i YisV s ij j ij j ˆ Yii V (k ) j 1 j i 1 i i 1, 2,, n
ji
6
直角坐标功率平衡方程
e jf 如果将节点电压用直角坐标表示,即令 V i i i 则有:
Pi jQi (ei jfi ) (Gij jBij )(e j jf j )
ji
(ei jfi )(ai jbi )
i 1, 2, N
ai (Gij e j Bij f j ) ji bi (Gij f j Bij e j ) ji i 1, 2, N Pi ei ai fi bi i 1, 2, N Qi fi ai ei bi
如何进行潮流计算?
2
潮流计算发展简史
史前时代
手算、交流模拟台 内存需求量小,收敛性差; 收敛性好,内存占用大; Tinney稀疏矩阵技术、节点优化编号;
50年代Y矩阵法(Gauss迭代法)
60年代初Z矩阵法
60年代Newton-Raphson法;
1974年B Stott 提出快速分解法(Fast Decoupled Load Flow);
极坐标潮流方程的已知量和待求量?
13
潮流计算

电力系统潮流计算——9结点算例-PQ法原始数据录入data.txt文档:标号,起始结点,终止结点,支路电阻参数,支路电抗参数,支路对地导纳参数1,2,5,0.0,0.063,0.0,2,5,9,0.019,0.072,0.075,3,6,9,0.012,0.101,0.105,4,3,6,0.0,0.059,0.0,5,6,8,0.039,0.17,0.179,6,4,8,0.017,0.092,0.079,7,5,7,0.032,0.161,0.153,8,4,7,0.01,0.085,0.088,9,1,4,0.0,0.058,0.0,潮流程序chaoliu.txt文档:#include<stdio.h>#include<math.h>#define N 9 /*总结点数*/#define M 6 /*PQ结点数*/#define K 9 /*线路数*/#define eps 1e-4void guass(int n,int m,float c[],float b[][N],float x[]) /*高斯函数*/ {float a[N][N],y[N];int i,j,k;for(i=0;i<m;i++){y[i]=c[i];for(j=0;j<m;j++) a[i][j]=b[i+n][j+n];}for(k=0;k<m-1;k++)for(i=k+1;i<m;i++){for(j=k+1;j<m;j++) a[i][j]=a[i][j]-a[k][j]*a[i][k]/a[k][k];y[i]=y[i]-y[k]*a[i][k]/a[k][k];}for(i=m-1;i>=0;i--){for(j=i+1;j<m;j++) y[i]-=a[i][j]*x[j];x[i]=y[i]/a[i][i];}}struct line{int Lindex;int Headnode;int Endnode;float R;float X;float b;}line[K];struct line *t;main(){float r[N]={0.0};float u[N]={1.04,1.025,1.025,1.0,1.0,1.0,1.0,1.0,1.0};float p[N]={1,1.63,0.85,0.0,0.0,0.0,-1.25,-0.9,-1.0};float q[N]={1,1,1,0.0,0.0,0.0,-0.5,-0.3,-0.35};float g[N][N]={0.0},b[N][N]={0.0};float h[N][N]={0.0};float B[N][N]={0.0};float temp;float H[K][6];float lr,lx,lb1,lg,lb;int i,j;int ku=0,kr=0,kp=1,kq=1;void val(float u[N],float g[N][N],float b[N][N],float r[N],int ku, int kr,float h[N][N]); /*函数申明*/FILE *fp;fp=fopen("data.txt","r");for(i=0;i<K;i++){for(j=0;j<6;j++){ fscanf(fp,"%f,",&temp);H[i][j]=temp;}}fclose(fp);for(i=0;i<K;i++){line[i].Lindex=(int)H[i][0];line[i].Headnode=(int)H[i][1];line[i].Endno de=(int)H[i][2];line[i].R=H[i][3];line[i].X=H[i][4];line[i].b=H[i][5];}for(t=line;t<line+K;t++){i=t->Headnode-1;j=t->Endnode-1;lr=t->R;lx=t->X;lb1=t->b;lg=lr/(lr*lr+lx*lx);lb=-lx/(lr*lr+lx*lx);g[i][i]+=lg;g[j][j]+=lg;b[i][i]+=lb+lb1;b[j][j]+=lb+lb1;h[i][j]=h[j][i]=-lb1;g[i][j]-=lg;g[j][i]-=lg;b[i][j]-=lb;b[j][i]-=lb;}getch();printf("\n=====jie dian dao na ju zhen=====\n");for(i=0;i<N;i++){for(j=0;j<N;j++){B[i][j]=b[i][j];printf("%8f,",B[i][j]);}printf("\n");}printf("\n");getch();printf("\n=====gei ding chu zhi=====\n");for(i=0;i<N;i++)printf("u[%d]=%8f p[%d]=%8f q[%d]=%8f\n",i+1,u[i],i+1,p[i], i+1,q[i]);printf("\n=====die dai qiu jie=====\n");while(kp==1){float ip,iq,max;float dp[N],dq[N],dr[N];float dpu[N],dqu[N];float y1[N-1],y2[M];float x1[N-1],x2[M];for(i=1;i<N;i++) /*算dp对应B',N-1维,除去平衡结点*/{ip=0;for(j=0;j<N;j++)ip=ip+u[j]*(g[i][j]*cos(r[i]-r[j])+b[i][j]*sin(r[i]-r[j]));dp[i]=p[i]-u[i]*ip;dpu[i]=dp[i]/u[i];printf("dp[%d]=%8f\n",i+1,dp[i]);printf("\n");}getch();max=fabs(dpu[1]);for(i=1;i<N;i++){if(fabs(dpu[i])>max)max=fabs(dpu[i]);}if (max>=eps){for(i=0;i<N-1;i++)y1[i]=-dpu[i+1]; /*起值不同,为了对应,故加一*/guass(1,N-1,y1,B,x1);for (i=1;i<N;i++){dr[i]=x1[i-1]/u[i];r[i]=r[i]+dr[i];}printf("\n===== di %d ci die dai hou dian ya xiang jiao chu zhi =====\n",kr+1);for(i=1;i<N;i++)printf("r[%d]=%8f\n",i+1,r[i]);getch();printf("\n\n");kr=kr+1;kq=1;top:for(i=N-M;i<N;i++) /*算dq对应B",仅M维,除去平衡结点和PV结点*/ {iq=0;for(j=0;j<N;j++)iq=iq+u[j]*(g[i][j]*sin(r[i]-r[j])-b[i][j]*cos(r[i]-r[j])); dq[i]=q[i]-u[i]*iq;dqu[i]=dq[i]/u[i];printf("dq[%d]=%8f\n",i+1,dq[i]);printf("\n");}max=fabs(dqu[N-M]);for (i=N-M;i<N;i++){if(fabs(dqu[i])>max)max=fabs(dqu[i]);}if(max>=eps){for(i=0;i<M;i++)y2[i]=-dqu[i+N-M]; /*同上,对应加N-M*/guass(N-M,M,y2,B,x2);for(i=N-M;i<N;i++)u[i]=u[i]+x2[i-(N-M)];printf("\n=====di %d ci die dai dian ya chu zhi=====\n",ku+1); for(i=N-M;i<N;i++)printf("u[%d]=%8f\n",i+1,u[i]);printf("\n\n");ku=ku+1;kp=1;}else{kq=0;if(kp==0)val(u,g,b,r,ku,kr,h);}}else{kp=0;if(kq==0)val(u,g,b,r,ku,kr,h);elsegoto top;}}}void val(float u[N],float g[N][N],float b[N][N],float r[N],int ku, int kr,float h[N][N]) {float ps=0,pv1=0,pv2=0;float qs=0,qv1=0,qv2=0;float p[N][N]={0};float q[N][N]={0};float s[N][N];float dp[N][N]={0};float dq[N][N]={0};float ds[N][N];float dSp=0,dSq=0;int i,j;FILE *fp1;printf("\n=====ping heng jie dian gong lv =====\n");getch();for(i=0;i<N;i++){ps=ps+u[0]*u[i]*(g[0][i]*cos(r[0]-r[i])+b[0][i]*sin(r[0]-r[i]));qs=qs+u[0]*u[i]*(g[0][i]*sin(r[0]-r[i])-b[0][i]*cos(r[0]-r[i]));}printf("sp=%8f+j(%8f)\n",ps,qs);printf("\n=====PV jie dian gong lv=====\n");getch();for(i=0;i<N;i++){pv1=pv1+u[1]*u[i]*(g[1][i]*cos(r[1]-r[i])+b[1][i]*sin(r[1]-r[i]));qv1=qv1+u[1]*u[i]*(g[1][i]*sin(r[1]-r[i])-b[1][i]*cos(r[1]-r[i]));}printf("sv1=%8f+j(%8f)\n",pv1,qv1);for(i=0;i<N;i++){pv2=pv2+u[2]*u[i]*(g[2][i]*cos(r[2]-r[i])+b[2][i]*sin(r[2]-r[i]));qv2=qv2+u[2]*u[i]*(g[2][i]*sin(r[2]-r[i])-b[2][i]*cos(r[2]-r[i]));}printf("sv2=%8f+j(%8f)\n",pv2,qv2);for(i=0;i<N;i++)for(j=0;j<N;j++){p[i][j]=u[i]*u[i]*(-g[i][j])+u[i]*u[j]*(g[i][j]*cos(r[i]-r[j])+b[i][j]*sin(r[i]-r[j]));q[i][j]=u[i]*u[i]*(-h[i][j]+b[i][j])+u[i]*u[j]*(g[i][j]*sin(r[i]-r[j])-b[i][j]*cos(r[i]-r[j]));dp[i][j]=u[i]*u[i]*(-g[i][j])+u[i]*u[j]*(g[i][j]*cos(r[i]-r[j])+b[i][j]*sin(r[i]-r[j]))+u[j]*u[j]*(-g[j][i])+u[j]*u[i]*(g[j][i]*cos(r[j]-r[i])+b[j][i]*sin(r[j]-r[i]));dq[i][j]=u[i]*u[i]*(-h[i][j]+b[i][j])+u[i]*u[j]*(g[i][j]*sin(r[i]-r[j])-b[i][j]*cos(r[i]-r[j])) +u[j]*u[j]*(-h[j][i]+b[j][i])+u[j]*u[i]*(g[j][i]*sin(r[j]-r[i])-b[j][i]*cos(r[j]-r[i]));}printf("\n======die dai hou dian ya yu xiang jiao zhi ======\n");getch();for(i=0;i<N;i++)printf("u[%d]=%8f r[%d]=%8f\n",i+1,u[i],i+1,r[i]);printf("\n=====xian lu gong lv=======\n");for(i=0;i<N;i++){getch();{ for(j=0;j<N;j++){ printf("s[%d][%d]=%8f+j(%8f)\n",i+1,j+1,p[i][j],q[i][j]);printf("\n");}printf("\n");}}printf("\n");printf("\n=====xian lu sun hao=====\n");for(i=0;i<N;i++){getch();{ for(j=i+1;j<N;j++){ printf("ds[%d][%d]=%8f+j%8f\n",i+1,j+1,dp[i][j],dq[i][j]);printf("\n");}printf("\n");}}printf("\n");printf("\n=====wang luo zong sun hao=====\n");getch();for(i=0;i<N;i++){for(j=i+1;j<N;j++){ dSp+=dp[i][j];dSq+=dq[i][j];}}printf("dS=%8f+j(%8f)\n",dSp,dSq);printf("\n======die dai ci shu========\n");printf("ku=%d\n",ku);printf("kr=%d\n",kr);printf("\n=======shu ju bao cun=====\n");fp1=fopen("jieguo.txt","w+");{fprintf(fp1,"xian lu cao liu:\n");for(i=0;i<N;i++){for(j=0;j<N;j++)fprintf(fp1,"s[%d][%d]=%8f+j%8f\n",i+1,j+1,p[i][j],q[i][j]);}fprintf(fp1,"\n");fprintf(fp1,"zhi lu sun hao:\n");for(i=0;i<N;i++){for(j=i+1;j<N;j++)fprintf(fp1,"ds[%d][%d]=%8f+j%8f\n",i+1,j+1,dp[i][j],dq[i][j]);}fprintf(fp1,"\n");fprintf(fp1,"wang luo zong sun hao:\n");fprintf(fp1,"dS=%8f+j(%8f)\n",dSp,dSq);fprintf(fp1,"\n");fprintf(fp1,"PV jie dian gong lv:\n");fprintf(fp1,"sv1=%8f+j(%8f)\n",pv1,qv1);fprintf(fp1,"sv2=%8f+j(%8f)\n",pv2,qv2);fprintf(fp1,"\n");fprintf(fp1,"ping heng jie dian gong lv:\n");fprintf(fp1,"sp=%8f+j(%8f)\n",ps,qs);fprintf(fp1,"\n");fprintf(fp1,"jie dian dian ya yu xiang jiao:\n");for(i=0;i<N;i++)fprintf(fp1,"u[%d]=%8f r[%d]=%8f\n",i+1,u[i],i+1,r[i]); }printf("\n===========THE END==============\n"); getch();。
5-PSASP7.0版潮流计算

可设多个平衡点以改善收敛性和便于几个 孤立子系统同时计算
潮流计算作业定义
潮流计算作业定义
在图上点击右键修改计算数据
潮流计算作业定义
如何模拟各种实际的潮流运行方式?
冬大方式 夏大方式
变压器名 称
变压器9
变压器9
正序电阻
0.000 0.000
正序电抗
0.05860 0.04500
变比
1.000 1.000
数据组 I侧母线 J侧母线
常规 新建
STNB-230 GEN1-230 GEN3-230 STNB-230
线路名称 正序电阻
线路1 线路11
0.017000 0.039000
正序电抗
根据节点电流平衡关系,可得电网导纳矩阵方程:
电网结构和参数 非线性
YY1211
Y12 Y22
Yn1 Yn2
简记为
Y1n
Y2n
VV12
I1 I2
Ynn
Vn
In
YV=I
发电负荷 运行方式
方案决定了电网的规模、结 构、参数等网络数据和发电、 负荷等运行方式数据。
数据组1
数据组2
数据组2 数据组1
方案1: 数据组1+数据组2
方案2: 数据组2+数据组1
数据组1 数据组2
潮流计算作业定义
基本方式作业定义示例
“冬大方案” =“基本网架”+“冬大方式”
“冬小方案” =“基本网架”+“冬小方式”
潮流计算总结[1]1
![潮流计算总结[1]1](https://img.taocdn.com/s3/m/ba10e6d449649b6648d7479c.png)
基本概念④ 运算电源功率、 基本概念④——运算电源功率、运算负荷功率: 运算电源功率 运算负荷功率:
运算电源功率
运算负荷功率
潮流计算分类
同一电压等级 开式网络 不同电压等级
折算
潮 流 计 算
(电压、功率)
同一电压等级 闭式网络 不同电压等级
折算、循环功率
潮流计算——同一电压等级开式网 同一电压等级开式网 潮流计算
两种情形:已知同端 、 : 两种情形:已知同端U、S:递推求解 已知不同端U、 : 已知不同端 、S:迭代求解
同一电压等级 开式网络
折算
潮 流
率 分 点
功
不同电压等级
计 算
(电压、功率)
同一电压等级 闭式网络 不同电压等级
两个步骤: 两个步骤:初步功率分布 最终功率分布
折算、循环功率
潮流计算——环网 环网 潮流计算
将环网从电源处打开成为一个两端供电网络: ①计算初步功率分布 供载功率+循环功率; 供载功率+循环功率; 找到功率分点; 找到功率分点; 将网络分成两个开式网
在多电压等级 环网中存在
②计算最终功率分布 运用开式网潮流计算方法计算各点电压和功率分布 类似已知一端电压和另一端功率的情况) (类似已知一端电压和另一端功率的情况)
基本概念② 电压降落: 基本概念②——电压降落: 电压降落
两种情况下求电压降落(分别已知首端U、S或已知末端U、S)
Ⅰ:已知首端U、S: U
Ⅱ:已知末端U、S: U
这两种情况下电压降落纵、横分量计算公式相同(用已知端的U、S) ( U
基本概念② 电压降落: 基本概念②——电压降落: 电压降落
例2:求各阻抗元件上电压降落的横、纵分量。 2
潮流计算作业A4

电力系统潮流计算综述学院:电气工程学院专业:电力系统及其自动化学号:s姓名:张雪摘要电力系统潮流计算是电力系统分析中最基本的一项计算。
本文对电力系统潮流计算进行了综述。
首先简单回顾了潮流计算的发展历史,对当前基于计算机的各种潮流算法的原理及其优缺点,作了简要介绍和比较,并介绍了它们采用的一些特别技术及程序设计技巧;接着简要分析了三种新型的潮流计算方法的计算原理及优缺点,它们分别是基于人工智能的潮流计算方法、基于L1范数和现代内点理论的电力系统潮流计算方法、基于符号分析的潮流计算方法等。
除此之外还介绍了配电系统潮流计算算法。
关键词:电力系统;潮流计算;综述;新型潮流计算方法;配电系统1 概述电力系统潮流计算是研究电力系统稳态运行的一项基本运算。
它根据给定系统的网络结构及运行条件来确定整个系统的运行状态:主要是各节点电压(幅值和相角),网络中功率分布及功率损耗等。
它既是对电力系统规划设计和运行方式的合理性、可靠性及经济性进行定量分析的依据,又是电力系统静态和暂态稳定计算的基础。
潮流计算经历了一个由手工,利用交、直流计算台到应用数字电子计算机的发展过程。
现在的潮流算法都以计算机的应用为前提。
1956年ward 等人编制成实用的计算机潮流计算程序,标志着电子计算机开始在电力系统潮流计算中应用。
基于导纳矩阵的高斯—塞德尔法是电力系统中最早得到应用的潮流计算方法。
因它对病态条件(所谓具有病态条件的系统是指:重负荷系统;包含有负电抗支路的系统;具有较长辐射型线路的系统;长线路与短线路接在同一节点,且其长度比值又很大的系统;或平衡节点位于网络远端的系统)特别敏感,又发展了基于阻抗阵的高斯—塞德尔法,但此法中阻抗阵是满阵占大量内存,而限制了其应用。
1961年VanNes等人提出用牛顿法求解系统潮流问题,经后人的不断改进,而得到广泛应用并出现了多种变型以满足不同的需要,如快速解耦法、直流法、保留非线性算法等。
同时,60年代初开始出现运用非线性规划的最优潮流算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电力系统潮流计算综述学院:电气工程学院专业:电力系统及其自动化学号:s130********姓名:张雪摘要电力系统潮流计算是电力系统分析中最基本的一项计算。
本文对电力系统潮流计算进行了综述。
首先简单回顾了潮流计算的发展历史,对当前基于计算机的各种潮流算法的原理及其优缺点,作了简要介绍和比较,并介绍了它们采用的一些特别技术及程序设计技巧;接着简要分析了三种新型的潮流计算方法的计算原理及优缺点,它们分别是基于人工智能的潮流计算方法、基于L1范数和现代内点理论的电力系统潮流计算方法、基于符号分析的潮流计算方法等。
除此之外还介绍了配电系统潮流计算算法。
关键词:电力系统;潮流计算;综述;新型潮流计算方法;配电系统1 概述电力系统潮流计算是研究电力系统稳态运行的一项基本运算。
它根据给定系统的网络结构及运行条件来确定整个系统的运行状态:主要是各节点电压(幅值和相角),网络中功率分布及功率损耗等。
它既是对电力系统规划设计和运行方式的合理性、可靠性及经济性进行定量分析的依据,又是电力系统静态和暂态稳定计算的基础。
潮流计算经历了一个由手工,利用交、直流计算台到应用数字电子计算机的发展过程。
现在的潮流算法都以计算机的应用为前提。
1956年ward 等人编制成实用的计算机潮流计算程序,标志着电子计算机开始在电力系统潮流计算中应用。
基于导纳矩阵的高斯—塞德尔法是电力系统中最早得到应用的潮流计算方法。
因它对病态条件(所谓具有病态条件的系统是指:重负荷系统;包含有负电抗支路的系统;具有较长辐射型线路的系统;长线路与短线路接在同一节点,且其长度比值又很大的系统;或平衡节点位于网络远端的系统)特别敏感,又发展了基于阻抗阵的高斯—塞德尔法,但此法中阻抗阵是满阵占大量内存,而限制了其应用。
1961年VanNes等人提出用牛顿法求解系统潮流问题,经后人的不断改进,而得到广泛应用并出现了多种变型以满足不同的需要,如快速解耦法、直流法、保留非线性算法等。
同时,60年代初开始出现运用非线性规划的最优潮流算法。
60年代末Dom-8mel和Tinney提出最优潮流的简化梯度法,70年代有人提出海森矩阵法,80年代SunDl提出最优潮流牛顿算法,还可把解耦技术应用于最优潮流,从而形成解耦型最优潮流牛顿算法,还可把解祸技术应用于最优潮流,从而形成解耦型最优潮流牛顿算法。
随着直流输电技术的发展,交直流联合电力系统的潮流计算方法相应出现。
另外,其它各种潮流算法如最小化潮流算法、随机潮流算法等也不断涌现。
至于用于特殊用途的潮流算法如谐波潮流、适于低压配电网的潮流算法也得到了较快的发展。
潮流算法多种多样,但一般要满足四个基本要求:(i)可靠收敛;(ii)计算速度快;(iii)使用方便灵活;(iv)内存占用量少。
它们也是对潮流算法进行评价的主要依据。
在潮流计算中,给定的量应该是负荷吸收的功率、发电机发出的功率或者发电机的电压。
这样,按照给定量种类的不同,可以将节点分为以下三类[1]:(1)PQ 节点。
给定节点的注入有功功率P 和注入无功功率Q 。
这类节点对应于实际系统中纯负荷节点(如变电所母线)、有功和无功功率都给定的发电机节点(包括节点上带有负荷),以及联络节点(注入有功和无功功率都等于零)。
这类节点占系统中的绝大多数,它们的节点电压有效值和相位未知。
(2)PV 节点。
给定节点的注入有功功率P 和节点电压有效值U ,待求量是节点的注入无功功率Q 和电压的相位θ。
这类节点通常为发电机节点,其有功功率给定而且具有比较大无功容量,它们能依靠自动电压调节器的作用使母线电压保持给定值。
有时将一些装有无功补偿设备的变电站母线也处理为PV 节点。
(3)平衡节点。
在潮流计算中,必须设置一个平衡节点,其电压有效值为给定值,电压相位为θ=0,即系统中其它各点的电压相位都以它为参考;而注入的有功功率和无功功率都是待求量。
实际上,由于所有的PQ 节点和PV 节点的注入有功功率都已经给定,而网络中的总有功功率损耗是未知的,因此平衡节点的注入有功功率必须平衡全系统的有功功率和有功损耗而不能加以给定。
需要注意的是以上介绍的节点分类只是一般的原则,而不是一成不变的。
2 潮流计算主要方法与评价2.1 潮流计算问题的数学模型电力系统潮流的基本方程为[2]:*1n i iij j j iP jQ Y U U =-=∑g(i =1,2,3…n ) (1) 或 *1n j i i ijj j P jQ U Z U =-=∑g (i =1,2,3…n ) (2)其中,ij Y ,ij Z 分别为节点导纳矩阵和节点阻抗矩阵的相应元素,n 为系统节点数。
这就是潮流计算问题最基本的方程式,是一个以节点电压U g为变量的非线性代数方程组。
由此可见,采用节点功率作为节点注入量是造成方程组呈非线性的根本原因。
由于方程组为非线性的,因此必须采用数值计算方法,通过迭代来求解。
根据在计算中对这个方程组的不同应用和处理,就形成了不同的潮流算法。
对于电力系统中的每个节点,要确定其运行状态,需要四个变量:有功注入P 、无功注入Q 、电压模值U 及电压相角θ。
n 个节点总共有4n 个运行变量要确定。
再观察式(1)和式(2),总共包括n 个复数方程式,如果将实部与虚部分开,则形成2n 个变量作为已知量而预先给以指定。
也即对每个节点,要给定其两个变量的值作为已知条件,而另两个变量作为待求量。
按照电力系统的实际运行条件,根据预先给定的变量的不同,电力系统中的节点又可分为PQ 节点、PV 节点及Vθ节点或平衡节点三种类型。
对应于这些节点,分别对其注入有功、无功功率,有功功率及电压模值以及电压模值和相角加以指定;并且对平衡节点来说,其电压相角一般作为系统电压相角的基准(即θ=0o )。
交流电力系统中的复数电压变量可以用两种坐标形式来表示i j i i U U e θ=g(3) 或 i i i U e jf =+g(4) 而复数导纳为ij ij ij Y G jB =+ (5) 将(3)、式(4)以及式(5)代入以导纳矩阵为基础的式(1),并将实部与虚部分开,可得到以下两种形式的潮流方程。
潮流方程的直角坐标形式为:(G e B f )()i i ij i ij j i ij j ij j j i j iP e f G f B e ∈∈=-++∑∑ (6)(i 1,2,,n)=L(G e B f )()i i ij i ij j i ij j ij j j i j iQ f e G f B e ∈∈=--+∑∑ (7)(i 1,2,,n)=L潮流方程的极坐标形式为:U (G cos B sin )i i j ij ij ij ij j iP U θθ∈=+∑ (8)(i 1,2,,n)=LU (G sin B cos )i i j ij ij ij ij j iQ U θθ∈=-∑ (9)(i 1,2,,n)=L以上各式中,j i ∈ 表示∑号后的标号为j 节点必须直接和节点i 相联,并包括j=i 的情况。
这两种形式的潮流方程统称为节点功率方程,是牛顿-拉夫逊等潮流算法所采用的主要数学模型。
对于以上潮流方程中的有关运行变量,还可以按其性质的不同加以分类,这对于进行例如灵敏度分析以及最优潮流的研究等都是比较方便的。
每个节点的注入功率是该节点的电源输入功率Gt P 、Gt Q 和负荷需求功率Li P 、Li Q 的代数和。
负荷需求的功率取决于用户,是无法控制的,所以称之为不可控变量或扰动变量。
而某个电源所发的有功、无功功率则是可以由运行人员控制或改变的变量,是自变量或称为控制变量。
至于各个节点的电压模值或相角,则属于随着控制变量的改变而变化的因变量或状态变量;当系统中各个节点的电压模值及相角都知道以后,则整个系统的运行状态也就完全确定了。
若以p 、u 、x 分别表示扰动变量、控制变量、状态变量,则潮流方程可以用更简洁的方式表示为:f(x,u,p)=0 (10)根据式(10),潮流计算的含义就是针对某个扰动变量p ,根据给定的控制变量u ,求出相应的状态变量x 。
电力系统的潮流计算需要求解一组非线性代数方程。
目前求解非线性代数方程一般采用的是迭代方法,而应用电子数字计算机进行迭代计算可以得到非常精确的结果。
常用的潮流算法有牛顿—拉夫逊法、快速解耦法(PQ 分解法)、直流潮流法、极小化潮流算法、最优潮流算法、保留非线性法、交直流潮流法等。
2.2 牛顿-拉夫逊法牛顿—拉夫逊法简称牛顿法,是求解非线性代数方程的一种有效且收敛速度快的迭代计算方法,而形成雅可比矩阵和求解修正方程式是牛顿法潮流计算中的主体。
牛顿—拉夫逊法将潮流方程f(x)=0用泰勒级数展开,并略去二阶及以上高阶项,然后求解。
其实质是逐次线性化,求解过程的核心是反复形成并求解修正方程。
其迭代格式为:'(k)(k)(k)(k 1)(k)(k)(X )X (X )f f X X X +⎫∆=-⎪⎬=+∆⎪⎭(11) 式中:'(X)f 是(X)f 对于变量X 的一阶偏导数矩阵;k 为迭代次数。
各种形式牛顿法的共同优点是:(1)收敛速度快,具有平方收敛特性,其迭代次数与系统规模基本无关;(2)能求解大部分有病态条件的问题;(3)利用了保持稀疏性技术,所需内存适中。
它是六十年代以来,广泛应用的方法。
但具有以下缺点:(1)由于雅可比矩阵的维数约为节点总数的两倍而且在迭代过程中不断改变,因此在大规模电力系统中应用牛顿法计算潮流比较费时;(2)编程复杂;(3)需要良好的初值(可由高斯-赛德尔法给出),否则不收敛或收敛到无法运行的解上;(4)对重病态条件可能不收敛;而快速分解法则是通过不断简化迭代过程中变化的矩阵来进行潮流计算,一般来说,快速分解法所需要的迭代次数比牛顿法多,但每次迭代的计算工作量远小于牛顿法,因此总的来说迭代求解过程所需要的时间要少得多。
直流潮流算法是一种十分近似的方法,它主要用于系统中有功功率分布的近似估算。
极小化潮流算法是将功率方程式的求解问题转化为一个求函数的极小值问题,然后应用数学规划方法进行求解,极小化潮流算法的主要缺点是所需要的计算机内存计算时间比常规牛顿法更多。
根据f(x)的表达式不同,牛顿法又分功率偏差型算法和电流偏差型算法。
根据复电压变量采用的坐标形式不同,牛顿法又有直角坐标形式、极坐标形式和混合形式。
2.2.1 功率偏差型算法令i j i i U U e θ=g,可得极坐标形式修正方程式为: P H N Q M L U U θ∆∆⎡⎤⎡⎤⎡⎤=-⎢⎥⎢⎥⎢⎥∆∆⎣⎦⎣⎦⎣⎦(12) 令i i i U e jf =+g,可得直角坐标形式修正方程式为:2P H N e Q M L f R S U ⎡⎤∆⎡⎤∆⎡⎤⎢⎥⎢⎥∆=-⎢⎥⎢⎥⎢⎥∆⎣⎦⎢⎥⎢⎥∆⎣⎦⎣⎦ (13) 其特点是每次迭代,雅可比矩阵都需要重新形成。
