数学建模案例分析2 随机存储模型--概率统计方法建模
数学建模概率模型
2
记为X ~ N（， 2 )
背景:如果决定试验结果X的是大量随机因素的总和，假设
各个因素之间近似独立，并且每个因素的单独作用相对均匀 地小，那么X的分布近似正态分布。
如：同龄人的身高、体重、考试分数、某地区年降水量等。
3、数学期望的概念和计算 描述了随机变量的概率取值中心—均值
数学期望
Y gX
E( X ) xk pk k 1
E( X ) xf ( x)dx E(Y ) EgX g( xk ) pk k 1
E(Y ) Eg( X )
g( x) f ( x)dx
4、MATLAB中相关的的概率命令
常见的几种分布的命令字符为： 正态分布：norm 指数分布：exp 泊松分布：poiss 二项分布：bino
G(n)
n
0
[(
a
b)r
(b
c)(n
r
)]
p(r
)drຫໍສະໝຸດ n(ab)np(r
)dr
dG (a b)np(n)
n
(b c) p(r)dr
dn
0
(a b)np(n) n (a b) p(r)dr
n
(b c)0 p(r)dr (a b)n p(r)dr
例3 有10台机床,每台发生故障的概率为0.08,而10台机床工作 独立,每台故障只需一个维修工人排除.问至少要配备几个维修 工人,才能保证有故障而不能及时排除的概率不大于5%。
解：随机变量X示发生故障的机床的台数,则 X ~ B(10,0.08)
即P{X n} 0.95
数学建模—概率模型 ppt课件
数学建模—概率模型
v3统计图(examp05-03) v箱线图（判断对称性） v频率直方图（最常用） v经验分布函数图 v正态概率图（+越集中在参考线附近，越近似正态分布）
v4分布检验 vChi2gof,jbtest,kstest,kstest2,lillietest等 vChi2gof卡方拟合优度检验，检验样本是否符合指定分布。它把观测数据分 组，每组包含5个以上的观测值，根据分组结果计算卡方统计量，当样本够 多时，该统计量近似服从卡方分布。 vjbtest,利用峰度和偏度检验。
3 单因素一元方差分析步骤
（ example07_01.m 判断不同院系成绩均值是否相等）
数据预处理
正态性检验 lillietest （p>0.05接受）
方差齐性检验 vartestn （p>0.05接受）
方差分析
anoval （ｐ＝0 有显著差别）
多重比较：两两比较，找出存在显著差异的学院，multcompare
构造观测值矩阵，每一列对应因素Ａ的一个水平，每一行对应因素Ｂ的一个
水平
方差分析
anova2 得到方差分析表
方差分析表把数据差异分为三部分（或四部分）： 列均值之间的差异引起的变差 列均值之间的差异引起的变差 行列交互作用引起的变差 （随机误差） 后续可以进行多重比较，multcompare，找出哪种组合是最优的
Computer Science | Software Engineering & Information System
数学建模—概率模型
目的：用一个函数近似表示变量之间的不确定关系。 1 一元线性回归分析 做出散点图，估计趋势；计算相关系数矩阵； regress函数，可以得到回归系数和置信区间,做残差分析，剔除异常点，重 新做回归分析 Regstats 多重线性或广义回归分析，它带有交互式图形用户界面，可以处 理带有常数项、线性项、交叉项、平方项等模型 robustfit函数：稳健回归（加权最小二乘法）
概率统计建模方法
第1章概率方法建模简介第2章数据统计描述和分析第3章方差分析第4章回归分析第5章马氏链模型第6章时间序列模型第7章主成分分析及应用第8章判别分析简介及应用主讲：山东大学数学学院陈建良2第1章概率方法建模简介随机性模型，是指研究的对象包含有随机因素的规律，以概率统计为基本数学工具，其结果通常也是在概率意义下表现出来。
随机因素的影响可以用概率、平均值（即数学期望）等的作用来体现。
自然界中的现象总的来说可以概括为两大现象：确定性现象和随机现象在确定性现象中可以忽略随机因素的影响，在随机现象中必须考虑随机因素的影响。
确定性离散模型，主要使用差分方程方法、层次分析方法以及比较简单的图的方法和逻辑方法等方法建立模型；确定性连续模型，主要使用微积分、微分方程及其稳定性、变分法等方法建立模型；§2 概率方法建模实例分析实例一、报童的策略问题1．问题描述报童每天清晨从报站批发报纸零售，晚上将未卖完的报纸退回。
设每份报纸的批发价为b，零售价为a，退回价为c，且设a>b>c，因此报童每售出一份报纸赚(a-b)，退回一份赔(b-c)。
若批少了不够买就会少赚，若批多了买不完就赔钱，报童如何确定每天批发报纸的数量，才能获得最大收入？92. 分析显然应根据需求量来确定批发量。
一种报纸的需求量是一随机变量。
假定报童通过自己的实践经验或其它方式掌握了需求量的随机规律，即在他的销售范围内每天报纸的需求量为X = x 份的概率为P(x)，则通过P(x) 和a, b, c 就可建立关于批发量的优化模型。
3．数学模型设每天批发量为n，因需求量x 是随机的，因此x可以小于、等于或大于n，从而报童每天的收入也是随机的，作为优化模型的目标函数，应考虑他长期（半年、一年等）卖报的日平均收入。
据概率论中的大数定律，这相当于报童每天收入的期望值（以下简称平均收入）。
1011设报童每天批发进n 份报纸时的平均收入为S (n )，若某天需求量x ≤n ，则他售出x 份，退回(n -x )份；若这天需求量x >n ，则n 份报纸全部卖出。
概率统计方法建模PPT课件
第3页/共23页
5.5 随机状态转移模型
状态与状态转移 ➢随机变量Xn：第n年的状态 状态概率 ai (n)
Xn
1, 2,
第n年健康 第n年疾病
ai (n) P(Xn i), i 1, 2, n 0,1,
➢今年处于状态i, 来年处于状态j的概率 pi:j 转移概率
存贮策略是周末库存量为零时订购3架 周末的库存量可 能是0, 1, 2, 3，周初的库存量可能是1, 2, 3。 用马氏链描述不同需求导致的周初库存状态的变化。 动态过程中每周销售量不同，失去销售机会（需求超过 库存）的概率不同。
可按稳态情况（时间充分长以后）计算失去销售机会的 概率和每周的平均销售量。
马氏链的两个重要类型
设状态i是非吸收状态，j是吸收状态，则首达概率f ij (n) 实际上是i经n次转移被j吸收的概率。而
fij = fij (1) + fij(2) + … + fij(n) + …
则是从非吸收状态i出发终将被吸收状态j吸收的概率。 记 F={f ij} 则 F=MR
例如，可以算出前面第二种情况中
第19页/共23页
5. 6 马尔可夫链的应用模型
模型求解 ➢ 估计这种策略下每周的平均销售量
第n周平均售量Rn
需求不超过存 量,销售需求
需求超过存量, 销售存量
3i
Rn [ jP(Dn j, Sn i) iP(Dn i, Sn i)] i1 j 1 3i [ jP(Dn j Sn i) iP(Dn i Sn i)]P(Sn i) i1 j 1
p23 p33
P(Dn k) e1 / k ! (k 0,1, 2 )
概率统计方法建模讲座
f = 94.5863
f = 94.7597
再算一次！！
每天平均的收益的模拟值
随机模拟求最佳订购数量
clear a=2.0;b=1.0;c=0.5;M=[50:150]'; k=length(M);A=zeros(k,1); for J=1:k N=5000;G=zeros(N,1);m=M(J); X=poissrnd(100,N,1); for I=1:N if X(I)>=m G(I)=(a-b)*m; else G(I)=(a-b)*X(I)-(b-c)*(m-X(I)); end end A(J)=mean(G); end [Y,I] = max(A) n=M(I) Y
案例1：如何估计池塘中鱼的数量
一、问题：要估计一个池塘里有多少条鱼，可以采用“标志重捕法”，即：先重池塘中捕出r条，每条鱼都做上记号，经过一段时间后，再从池塘中捕出s条（s>r），统计其中标有记号的鱼的条数t,利用这些信息，估计池塘中鱼的条数N.
需要作哪些假设？
1、实验期间，标记个体不会变化。 2、标记不会对鱼造成伤害。 3、期间没有迁出、迁入、新生和死亡。 4、所有鱼被捕获的概率相等。
随机性存储模型.pptx
Pi
xi s
C2 K C1 C2
（10.34）
成立的最小S值。订货量为Q*=S*—I
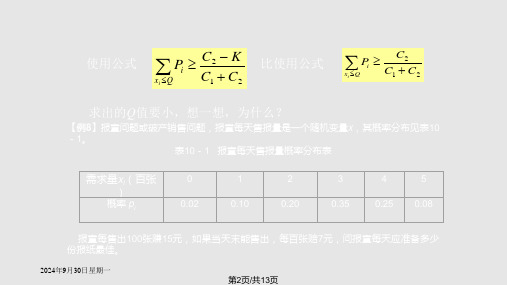
【例10.10】假定在例中月初已有5件产品，问还应该订货多少件。 【解】由例10.9解的结果得知，月初存量为零时应订货S*=20件，在引当初存量I=5件时， 还应该订货Q*=20－5=15件。
2024年9月30日星期一
【解】已知C1=100，C2=180，K=100，泊松分布函数为
P(x) x e , x!
x=0，1，2，…
平均需求量为5，则λ＝5，由式（10.31）得
C2 K 180 100 0.2857 , C1 C2 100 180
4
Q
P(x)
5 x e 5
xQ
x0 x!
查泊松分布表，当Q=4时，
0.20
0.35
0.25 0.08
报童每售出100张赚15元，如果当天末能售出，每百张赔7元，问报童每天应准备多少 份报纸最佳。
2024年9月30日星期一
第2页/共13页
【解】以每天为一个时期，当订货量大于需求量时，存储费为C1=7，当订货量小于 需求量时，因缺货而失去赚钱的机会，因此缺货费为C2=15，不计订货费，利用式 （10.32）可得
第8页/共13页
二、连续型存储模型 离散型存储策略的分析方法同样适合连续型。设需求量x的概率密
度为
(x), 满足
(x)dx 1,x 0
0
1.期初存量为零的情形 当x≤Q时，总存储费期望值为
当 x>Q时，总缺货费期望值为
订货费为C3+KQ，总费用期望值为
Q
C1 0 (Q x)(x)dx
C2 Q (x Q) (x)dx
数学建模方法之概率统计分析法
Obs
Prin1 Prin2 Prin3 Prin4 Prin5 Prin6 1 -0.38118 -0.32367 -0.04450 0.30363 0.00430 0.06437 2 0.57795 -0.35416 0.49279 0.55119 -0.18726 0.17414 3 0.69219 -0.21588 0.40557 0.40041 -0.10461 0.05393 4 0.22635 -0.39419 0.27521 0.63296 0.13851 -0.06481 5 -0.82981 -0.40293 0.47330 -0.42964 -0.55401 -0.35020 6 -1.19410 -0.40627 -0.36848 0.14000 0.02221 0.01063 7 -1.63568 -0.26394 -0.67179 -0.15189 0.01702 -0.03769 8 0.95195 -0.46156 1.61851 -0.92520 0.08394 0.25530 9 0.46501 -0.14888 0.19070 0.16273 -0.30327 0.20883 10 -1.45693 -0.18670 -0.55658 -0.17088 -0.10267 -0.00922 11 -0.29401 3.71727 -0.02727 -0.02382 -0.06419 0.03517 12 0.08041 0.22542 1.71694 0.12718 0.45539 -0.26668 13 -2.11628 -0.16312 -0.90179 -0.16784 0.14422 -0.03334 14 -0.94513 -0.31477 -0.39513 0.09760 0.11375 -0.03132 15 6.74015 -0.06989 -1.12895 -0.16618 0.04080 -0.11394 16 -0.88090 -0.23673 -1.07853 -0.38025 0.29589 0.10482
数学建模概率模型案例
则传送系统效率为：d=s/n=mp/n
=
m[1(1 1)n]
n
m
mn Dm [1(1nn(n1)) ]1n1
n m 2m 2
2m
D87 .5% 当n＝10,m=40
报童的诀窍
问题：报童每天清晨从报社购进报纸零售，晚上 将没有卖掉的报纸退回。设报纸每份的购进价为b， 零售价为a，退回价为c，假设a>b>c。即报童售出
每位被挤掉的乘客获得的赔偿金为常数b。
4 模型建立
先不考虑社会声誉的影响。
公司的经济利益用平均利润（数学期望）S 来衡量
订票的总人数是 m，m有可能超出 n
当有 k个人误机时，
航空公司可能从航班中得到的利润为
s m kg r,
m k n
s n g r (m k n )b , m k n
E ( X )x ip i ( i 1 ,2 , ,n )
连续型随机变量 X 的概率密度函数为 f ( x) 则随机变量 X 的数学期望值为
E(X) xf(x)dx
期望值反映了随机变量取值的“平均”意义！
传送系统的效率
在机械化生产车间里，你可以看到这样的 情景：排列整齐的工作台旁工人们紧张的 生产同一种产品，工作台上方一条传送带 在运转，带上若干个钩子，工人们将产品 挂在经过他上方的钩子上带走，当生产进 入稳态后，请大家构造一个衡量传送系统 效率的指标，并建立模型描述此指标与工 人数量、钩子数量等参数的关系。
mnj1
minPj(m) Pk k0
mJ (a m ) x S r 0 .1 6 n p m 1 b g m k n 0 1 P km n k 1
数学建模 第二章 概率统计模型
参数检验
• 回归系数的检验，即检验每个解释变量对响应变量的影响是否有 统计学上的意义。若有m个回归系数 ，假设检验为：
• 常用的回1归,L系,数m检验方法有Wald统计量：
H0 : b j = 0 H1 : b j ? 0 (j 1,2,L ,m)
• 式中分子为解释变量的参数估计值，分母为参数估计值Wald的标
第二章 概率统计模型
一个例子
• 二战时期，，为了提高飞机的防护能力，英国的科学家、 设计师和工程师决定给飞机增加护甲.
• 为了不过多加重飞机的负载，护甲必须加在最必要的地 方，那么是什么地方呢?
• 统计学家将每架中弹但仍返航的飞机的中弹部位描绘在 图纸上，然后将这些图重叠，形成了一个密度不均的弹 孔分布图.
成一类。
• K均值聚类
K均值聚类首先人为确定分类数，起步于一个初始的分类，然后 通过不断的迭代把数据在不同类别之间移动，直到最后达到预 定的分类数为止。
• 第一步 将所有的样品分成K个初始类； • 第二步 逐一计算每一样品到各个类别中心点的距离，把
各个样品按照距离最近的原则归入各个类别，并计算新 形成类别的中心点。 • 第三步 按照新的中心位置，重新计算每一样品距离新的 类别中心点的距离，并重新进行归类，更新类别中心点。 • 第四步 重复第三步，直到达到一定的收敛标准，或者达 到分析者事先指定的迭代次数为止。
• 模型求解： • 1. 抽取[0,1]之间均匀分布的随机数，确定这次模拟路口停红灯
的车数，例如，抽到0.732，则这个数落在区间（0.671，0.857） 的范围里，所以这次模拟停车数为3； • 2. 计算红灯转为绿灯后，在绿灯延续期间d（如题设5分钟）内， 这部车以速度u通过道口共需时间t=（50/50）*3（分钟），如果 t>d,那么道口发生堵塞，在本次模拟中t=3分钟，没有发生堵塞； • 3. 抽取随机数很多次，如10000次，记下其中多少次发生堵塞， 从而估算出道口发生堵塞的概率。
数学建模概率模型案例
数学建模概率模型案例概率模型是数学建模的重要工具之一，广泛应用于各个领域。
以下是一个基于概率模型的数学建模案例。
问题描述：医院的急诊科接诊员需要根据患者的症状来判断是否需要进行心电图检查。
根据以往的医疗记录，我们知道有一种患者患有心脏病的概率是0.1，有心脏病的患者在进行心电图检查时有90%的准确率，没有心脏病的患者在进行心电图检查时有95%的准确率。
急诊科接诊员在给患者进行评估时会根据患者的症状判断是否需要进行心电图检查，但出于经济和时间的考虑，每天只能对20%的患者进行心电图检查。
问题分析：在这个问题中，我们需要建立一个概率模型来评估患者是否需要进行心电图检查。
我们需要考虑两个因素：患者是否有心脏病以及是否进行了心电图检查。
建立概率模型：1.定义事件：-A：患者有心脏病-B：患者进行了心电图检查-C：急诊科接诊员推荐患者进行心电图检查2.计算概率：-P(A)=0.1，患者有心脏病的概率-P(A')=0.9，患者没有心脏病的概率-P(B，A)=0.9，有心脏病的患者进行心电图检查的准确率-P(B，A')=0.95，没有心脏病的患者进行心电图检查的准确率3.根据贝叶斯定理计算后验概率：-P(A，B)=P(B，A)*P(A)/P(B)-P(A'，B)=P(B，A')*P(A')/P(B)4.根据给定条件计算先验概率：-P(B)=P(B，A)*P(A)+P(B，A')*P(A')5.根据条件概率计算P(C，B)：-P(C，B)=P(C,B)/P(B)进一步分析：根据模型，我们可以进行一些进一步的分析。
1.如果患者没有进行心电图检查，根据模型我们可以计算出他是否有心脏病的概率。
2.如果患者进行了心电图检查，根据模型我们可以计算出他有心脏病的概率。
3.根据模型的输出，急诊科接诊员可以根据患者的症状和推荐指标来判断是否进行心电图检查。
总结：这个案例展示了如何建立一个基于概率模型的数学建模问题。
随机性存储模型
W(Q) Pmin[rQ] KQ C1(Q)
(赢利)=(实际销售货物的收入)-(货物成本)-(支付的存储费用)
赢利的期望值：
E[W(Q)]
QPr(r)dr
P
0
Q
Q (r)drKQ 0QC1(Q-r)(r)dr
0Pr(r)drQPr(r)drQPQ (r)drKQ 0QC1(Q-r)(r)d
k h r0
现利用公式(13-25)解例7的问题。
• 已知：k=7, h=4, P(0)=0.05， k 0.637 kh
• P(1)=0.10，P(2)=0.25，P(3)=0.35
2
3
P(r) 0.40 0.637 P(r) 0.75
r0
r0
知该店应订购日历画片3千张。
例8
• 某店拟出售甲商品，每单位甲商品成本50 元，售价70元。如不能售出必须减价为40 元，减价后一定可以售出。已知售货量r的 概率服从泊松分布(λ=6为平均售出数)
当订货量为2千张时，缺货和滞销两种损 失之和的期望值
• E[C(2)]=(-800)×0.05 + (-400)×0.10+0×0.25 +(-700)×0.35+(-1400)×0.15 +(-2100)×0.10 = －745(元)
• 按此算法列出表13-3。
表13-3
订货量(千张) 0
1
2
解 首先我们来考虑当订购数量为Q时，实际
销售量应该是min[r,Q]。也就是当需求为r而r
小于Q时，实际销售量为r；r≥Q时，实际销
售量只能是Q
需支付的存储费用 C1(Q) 0C1(Q r)
rQ r0
货物的成本为 KQ，本阶段订购量为 Q 赢利为 W(Q)， 赢利的期望值记作 E[W(Q)]。
概率论与数理统计在数学建模中的应用
概率论与数理统计在数学建模中的应用概率论与数理统计在数学建模中的应用——国 冰。
第一节 概率模型一、初等概率模型初等概率模型主要介绍了可靠性模型、传染病流行估计、常染色体遗传模型等三类问题：1、复合系统工作的可靠性问题的数学模型设某种机器的工作系统由N 个部件组成，各部件之间是串联的，即只要有一个部件失灵，整个系统就不能正常工作．为了提高系统的可靠性，在每个部件上都装有主要元件的备用件及自动投入装置(即当所使用元件损坏时，备用元件可自动替代之而开始工作)明显地，备用件越多，整个系统正常工作的可靠性就越大. 但是，备用件过多势必导至整个系统的成本、重量和体积相应增大，工作精度也会降低. 因此，配置的最优化问题便被提出来了：在某些限制性条件之下，如何确定各部件的备用件数量，使整个系统的工作可靠性最大? 这是一个整体系统的可靠性问题.我们假设第i 个部件上装有i x 个备用件(1,2,,)i N =,此时该部件正常工作的概率为()i p x ，那么整个系统正常工作的可靠度便可用1()ni i p p x ==∏ （9.1）来表示.又设第i 个部件上的每个备用件的费用为i C ，重量为i W ，并要求总费用不超过C ，总重量不超过W ，则问题的数学模型便写成为1max ()ni i p p x ==∏合理的决策必须具备三个条件：（1）目标合理；（2）决策结果满足预定目标的要求；（3）决策本身符合效率、满意、有限合理、经济性的原则。
所谓风险型决策是指在作出决策时，往往有某些随机性的因素影响，而决策者对于这些因素的了解不足，但是对各种因素发生的概率已知或者可估算出来，因此这种决策存在一定的风险.①风险决策模型的基本要素决策者——进行决策的个人、委员会或某个组织.在问题比较重大和严肃时，通常应以后者形式出现.方案或策略——参谋人员为决策者提供的各种可行计划和谋略. 如渔民要决定出海打鱼与否便是两个方案或称两个策略.准则——衡量所选方案正确性的标准.作为风险型决策，采用的比较多的准则是期望效益值准则，也即根据每个方案的数学期望值作出判断.对收益讲，期望效益值越大的方案越好；反之对于损失来讲，期望效益值越小的方案越好.事件或状态——不为决策者可控制的客观存在的且将发生的自然状态称为状态(事件)，如下小雨，下大雨和下暴雨即为三个事件或称三种状态，均为人所不可控因素.结果——某事件(状态)发生带来的收益或损失值.②风险决策方法•利用树形图法表示决策过程具有直观简便的特点，将其称为决策树的方法.•充分利用灵敏度分析(即优化后分析)方法对决策结果作进一步的推广和分析.决策树一般都是自上而下的来生成的。
2011概率统计数学建模
概率统计模型§1 概率论模型一、概率的基本知识1、离散型随机变量的概率分布ξ（随机变量）1x2x 3x … n x … 概率P1p2p3p…n p…性质：1,0=≥∑i i p p （1）几个常见的重要分布i.两点分布（贝努里分布或0-1分布） 注：两点分布的分布列就是X 0 1 P p 1-p不论题目有什么区别,只有两种可能,要么是这种结果要么是那种结果,通俗点,要么成功要么失败而二项分布的可能结果是不确定的甚至是没有尽头的,。
ii.二项分布注：如果事件发生的概率是P,则不发生的概率q=1-p ，N 次独立重二项分布公式复试验中发生K 次的概率是P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k), 其中 C(n, k) = n!/(k! * (n-k)!)iii. 普阿松分布（泊松分布）——排队论中常见。
注：若随机变量 X 只取非负整数值，取k （k=0,1,2…）值的概率为（2）期望与方差∑=i i p x E ξ22)()(ξξξE E D -=（3）几个常见的重要分布的期望与方差两点分布（贝努里分布或0-1分布）：p E =ξ，)1(p p D -=ξ 二项分布：np E =ξ，)1(p np D -=ξ 普阿松分布（泊松分布）：λξξ==D E2、连续型随机变量的分布函数与概率密度分布函数：)()(x P x F ≤=ξ，ξ为随机变量 密度函数)(x p ，满足⎰∞-=xdu u p x F )()( （1）几个常见的重要分布i.均匀分布：⎪⎩⎪⎨⎧≤≤-=其它,0,1)(b x a a b x pii ．指数分布：⎩⎨⎧<≥=-0,00,)(x x e x p x λλiii ．正态分布：222)(21)(σμπσ--=x ex p（2）期望与方差⎰+∞∞-=dx x xp E )(ξ22)()(ξξξE E D -=（3）几个常见的重要分布的期望与方差均匀分布：2ba E +=ξ，12)(2ab D -=ξ二项分布：λξ1=E ，21λξ=D普阿松分布（泊松分布）：μξ=E ，2σξ=D（4）实际问题中注意：密度函数（分布函数）的摸拟二、概率论模型实例1．报童问题一个报童每天从邮局订购一种报纸，沿街叫卖。
数学建模 概率统计模型
日常生活中经常遇到的一类问题。它是现代
企业管理的核心问题，贯穿于整个企业管理
的始终。本节将首先简要说明决策的概念和
分类，然后介绍风险型和不确定型决策模型
及其应用。
数
学
4.1.1 决策的概念和类型
建
模
所谓决策，就是从多个备选方案中，选择一个
最优的或满意的方案付诸实施。
例4.1.1（展销会选址问题） 某公司为扩大市场，要举办一个产品展销
会，会址打算选择甲、乙、丙三地，获利情 况除了与会址有关外，还与天气有关，天气 分为晴、阴、多雨三种，据天气预报，估计 三种天气情况可能发生概率为0.2，0.5，0.3 其收益情况见表4.4.1，现要通过分析，确定 会址，使收益最大。
数 学
建 决策问题通常包含以下要素：
模
1.决策者 2.决策的备选方案或策略A1 ， A2，…，Am 3.决策准则，即衡量所选方案正确性的标准。对
数学建模
（Mathematical Modeling)
数 学 建 模
概率统计模型
数
学
建
概率统计模型
模
决策模型
报纸零售商最优购报问题
经济轧钢模型
线性回归模型
排队论模型 建模举例
重点:概率统计模型的建立和求解 难点:概率统计模型的基本原理及数值计算
数
学 建
4.1 决策模型
模
决策问题是人们在政治、经济、技术和
其最大值50对应的行动方案为A1 ，因此用乐观 法的决策结果是执行策略A1 。
数 学
建 解 悲观法：因为每个行动方案在各种状态下的
模 最大效益值为
minj{a1j } min{50,10,5} 5
minj{a2j } min{30,25,0} 0
数学建模案例分析—主成分分析的应用--概率统计方法建模
§8 主成分分析的应用主成分分析的基本思想是通过构造原变量的适当的线性组合，以产生一系列互不相关的新变量，从中选出少数几个新变量并使它们尽可能多地包含原变量的信息（降维），从而使得用这几个新变量替代原变量分析问题成为可能。
即在尽可能少丢失信息的前提下从所研究的m 个变量中求出几个新变量，它们能综合原有变量的信息，相互之间又尽可能不含重复信息，用这几个新变量进行统计分析（例如回归分析、判别分析、聚类分析等等）仍能达到我们的目的。
设有n 个样品，m 个变量（指标）的数据矩阵(1)11121(2)21222()12m m n mn n n nm x x x x x x x x X x x x x ⨯⎛⎫⎛⎫⎪ ⎪ ⎪⎪== ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭寻找k 个新变量12,,,()k y y y k m ≤ ，使得 1、1122,(1,2,,)l l l lm m y a x a x a x l k =+++= 2、12,,k y y y 彼此不相关这便是主成分分析。
主成分的系数向量12(,,,)l l l lm a a a a = 的分量lj a 刻划出第j 个变量关于第l 个主成分的重要性。
可以证明，若12(,,,)T m x x x x = 为m 维随机向量，它的协方差矩阵V 的m 个特征值为120m λλλ≥≥≥≥ ，相应的标准正交化的特征向量为12,,,m u u u ，则12(,,,)T m x x x x = 的第i 主成分为(1,2,,)T i i y u x i m == 。
称1/mi jj λλ=∑为主成分(1,2,,)Ti i y u x i m == 的贡献率，11/k mj jj j λλ==∑∑为主成分12,,k y y y 的累计贡献率，它表达了前k 个主成分中包含原变量12,,,m x x x 的信息量大小，通常取k 使累计贡献率在85%以上即可。
当然这不是一个绝对不变的标准，可以根据实际效果作取舍，例如当后面几个主成分的贡献率较接近时，只选取其中一个就不公平了，若都选入又达不到简化变量的目的，那时常常将它们一同割舍。
数学建模案例分析2 随机存储模型--概率统计方法建模
§2 随机存储模型模型一、销售量为随机的存储模型报童每天清晨从报社购进报纸零售，晚上将没有卖出的报纸退回。
如果购进报纸太少不够卖，会少赚钱；如果购进太多买不完，将要赔钱。
报童应如何确定每天购进的报纸数量，以求获得最大的收入。
模型假设1、报纸每份购进价b ，零售价a ，退回价c ，且c b a >>2、市场需求量是随机的，报童已通过经验掌握了需求量r 的随机规律，r 视为连续随机变量，其概率密度函数)(r p 。
模型建立 记 n —每天购进量，报童每天的收入R 是n 的函数()()()()()⎩⎨⎧>----≤-=r n r n c b r b a r n n b a n R ,, 但目标函数不应是报童每天的收入，而应是他长期卖报的日平均收入。
从大数定律的观点看，这相当于每天收入的期望值，即日平均收入：()()()()[]()()()⎰⎰∞-+----=n n dr r p n b a dr r p r n c b r b a n G 0 ()()()()()()()()⎰⎰∞-+-----=n n dr r p b a n np b a dr r p c b n np b a dn dG 0()()()()⎰⎰∞-+--=n ndr r p b a dr r p c b 0 令0=dndG ，得到 ()()c b b a dr r p drr p n n--=⎰⎰∞又因为()10=⎰∞dr r p ，上式又可表示为 ()ca b a dr r p n--=⎰0 （1） 使报童平均日收入最大购进量n 由（1）确定评注 由()()c b b a dr r p dr r p nn --=⎰⎰∞0，()⎰=ndr r p p 01是卖不完的概率， ()⎰∞=n dr r p p 2是卖完的概率。
上式表明，购进的份数应使卖不完与卖完的概率之比等于卖出一份赚的钱b a -与退回一份赔的钱c b -之比。
概率统计模型(数学建模)
思考： 如何改进模型使“效率”降低？
考虑通过增加钩子数来使效率降低的方法：
在原来放置一只钩子处放置的两只钩子成为一个钩对。一
周期内通过 m 个钩对，任一钩对被任意工人触到的概率
p 1/ m ，不被触到的概率 q 1 p，于是任一钩对为空的概率
工人生产周期相同，但由于各种因素的影响，经过相 当长的时间后，他们生产完一件产品的时刻会不一致， 认为是随机的，并在一个生产周期内任一时刻的可能 性一样。
由上分析，传送系统长期运转的效率等价于一周期的效 率，而一周期的效率可以用它在一周期内能带走的产品 数与一周期内生产的全部产品数之比来描述。
2 模型假设
则
r
Gn
n
0
a
b
r
b
c
n
r
pr
dr
n
a
b
npr
dr
计算
dG dn
a
bnpn
n
0
b
cprdr
a
bnpn
n
a
b
pr
dr
b
c n 0
pr dr
a
b n
pr dr
令 dG 0 ，得到 dn
n
0
n
pr dr pr dr
a b
b c
使报童日平均收入达到最大的购进量 n 应满足上式。
因为
0
pr dr
统计模型
如果由于客观事物内部规律的复杂性及人们认识程度的限 制，无法分析实际对象内在的因果关系，建立合乎机理规 律的模型，那么通常要搜集大量的数据，基于对数据的统 计分析建立模型，这就是本章还要讨论的用途非常广泛的 一类随机模型—统计回归模型。
数学建模_概率统计建模的理论和方法
1 ( x) e 2
x2 2
x .
( x)dx b a a 12
b
X
N ( , 2 ) 时，我们有
b a
P{a X b} p( x)dx
poisspdf（x，λ），计算poisson概率，
例如，poisspdf(0:9,3.87)
问题：Poisson分布是又一类非常重要的用来
计数的离散型分布，它依赖于一个参数 。什么
样的随机变量会服从Poisson分布呢？
10
在给定的观测范围内（例如给定时间内，给定区域内等等）， 事件会发生多少次？把观测范围分成n个小范围： 1.给定事件在每个小范围内可能发生，也可能不发生，发生多少 次取决于小范围的大小； 2.在不同的小范围内发生多少事件相互独立； 3.在小范围里发生的事件数多于一个的概率，和小范围的大小相 比可以忽略不计，用 pn 表示在小范围内事件发生一次的概率。 那么在给定范围内发生的总事件数X近似服从 B(n, pn ) , npn 为给定范围内事件发生次数的近似平均值。令 n ，则
4 5
678Fra bibliotek910
4
可以看出， P{X 6} 1 P{X 6} 0.000864 也就是说，如果供应6个单位的电力，则超负荷工作的 概率只有0.000864，即每
1 1147分钟 20小时 0.000864
中，才可能有一分钟电力不够用。还可以算出，八个或八 个以上工人同时使用电力的概率就更小了，比上面概率的 1/11还要小。 问题：二项分布是一个重要的用来计数的分布。什么 样的随机变量会服从二项分布？ 进行n次独立观测，在每次观测中所关心的事件出现 的概率都是p，那么在这n次观测中事件A出现的总次数 是一个服从二项分布B（n，p）。 5
数学建模简明教程课件：概率模型
31
图 7-4
32
5.决策树的优缺点
•决策树方法的优点：可以生成可以理解的规则；计 算量相对来说不是很大；可以处理连续和种类字段；决策 树可以清晰地显示哪些字段比较重要.
•决策树方法的缺点：对连续性的字段比较难预测； 对有时间顺序的数据，需要很多预处理的工作；当类别太 多时，错误可能就会增加得比较快；一般算法分类的时候 ，只是根据一个字段来分类.
(a b)np(r) d r
0
n
计算
(7.2.2)
d G (a b)np(n)
n
(b c) p(r) d r (a b)np(n)
(a b) p(r) d r
dn
0
n
n
(b c)0 p(r) d r (a b)n p(r) d r
18
令 d G 0 ，得到 dn
n
0
p(r)d r p(r)d r
14
2.问题的分析及假设
众所周知，应该根据需求量确定购进量.需求量是随机 的，假定报童已经通过自己的经验或其它的渠道掌握了需 求量的随机规律，即在他的销售范围内每天报纸的需求量 为r份的概率是f(r)(r＝0，1，2，…).有了f(r)和a，b，c，就 可以建立关于购进量的优化模型了.
假设每天的购进量为n份，因为需求量r是随机的，故r 可以小于n、等于n或大于n，致使报童每天的收入也是随 机的.所以作为优化模型的目标函数，不能是报童每天的收 入，而应该是他长期(几个月或一年)卖报的日平均收入.
26
(4)设定变量： A——试销成功，——试销失败 B——大量销售成功，——大量销售失败
27
3.建立模型 先来计算两个概率，注意到P(A|B)＝0.84，P(B)＝0.6 ，P(A|)＝0.36，代入贝叶斯概率公式：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§2 随机存储模型
模型一、销售量为随机的存储模型
报童每天清晨从报社购进报纸零售，晚上将没有卖出的报纸退回。
如果购进报纸太少不够卖，会少赚钱；如果购进太多买不完，将要赔钱。
报童应如何确定每天购进的报纸数量，以求获得最大的收入。
模型假设1、报纸每份购进价b ，零售价a ，退回价c ，且c b a >>
2、市场需求量是随机的，报童已通过经验掌握了需求量r 的随机规律，r 视为连续随
机变量，其概率密度函数)(r p 。
模型建立 记 n —每天购进量，报童每天的收入R 是n 的函数
()()()()()⎩
⎨⎧>----≤-=r n r n c b r b a r n n b a n R ,, 但目标函数不应是报童每天的收入，而应是他长期卖报的日平均收入。
从大数定律的观点看，这相当于每天收入的期望值，即日平均收入：
()()()()[]()()()⎰⎰∞-+----=n n dr r p n b a dr r p r n c b r b a n G 0 ()()()()()()()()⎰⎰∞-+-----=n n dr r p b a n np b a dr r p c b n np b a dn dG 0 ()
()()()⎰⎰∞-+--=n n
dr r p b a dr r p c b 0 令0=dn
dG ，得到 ()()c b b a dr r p dr
r p n n
--=⎰⎰∞
又因为()10=⎰∞
dr r p ，上式又可表示为 ()c
a b a dr r p n
--=⎰0 （1） 使报童平均日收入最大购进量n 由（1）确定
评注 由()()c b b a dr r p dr r p n
n --=⎰⎰∞0，()⎰=n
dr r p p 01是卖不完的概率， ()⎰∞
=n dr r p p 2是卖完的概率。
上式表明，购进的份数应使卖不完与卖完的概率之比等于卖出一份赚的钱b a -与退回一份赔的钱c b -之比。
模型二、到货时间为随机的存储模型
模型假设1、商品订货费1c ，每件商品单位时间的储存费为2c ，缺货费3c ，单位时间需求量为r ；
2、当储存量降至L 时订货，订货量使下周期初的储存量达到固定值Q ；
3、交货时间x 是随机的，如下图中的,...,21x x ，设x 的概率密度函数()x p 。
模型建立
为使总费用最小，选择合适的目标函数建立模型，确定最佳订货点L 。
t
由储存量()t q 的图形可写出一个订货周期内的储存量和缺货量分别为
()()⎪⎪⎩⎪⎪⎨⎧≥<--=r L x r
Q r L x r rx L Q t q ,2,2222 ()()⎪⎪⎩⎪⎪⎨⎧≥-<=r L x r L rx r L x t q ,2,02 于是得到一个订货周期的平均费用为
()()()()()⎰⎰∞⎥⎦⎤⎢⎣⎡-++--+=r
L r L dx x p r L rx c r Q c dx x p r rx L Q c c L c 0
23222221222 目标函数应取为单位时间的平均费用()L S ，由于订货周期的平均长度为
()()x E r L Q L T +-=
这里()()⎰+∞
=0dx x xp x E
所以 ()()()
L T L c L S = 由0=dL
dS ，可以解出最佳订货点*L 满足方程 ()()
()x rE Q L c L c L +='-**
*。