粗糙集方法
粗糙集理论的模型参数估计方法及其实际应用
粗糙集理论的模型参数估计方法及其实际应用粗糙集理论是一种用于处理不完备、不精确、不确定信息的数学工具，被广泛应用于数据挖掘、模式识别、决策分析等领域。
在粗糙集理论中，模型参数的估计是一个重要的研究内容，本文将介绍几种常用的粗糙集模型参数估计方法，并探讨其在实际应用中的价值。
一、基于最大似然估计的参数估计方法最大似然估计是一种常用的参数估计方法，其基本思想是通过最大化观测数据出现的概率来估计模型参数。
在粗糙集理论中，最大似然估计可以用于估计决策属性的条件概率分布。
具体而言，对于给定的条件属性集合和决策属性，最大似然估计可以通过统计样本中各个条件属性取值与决策属性取值的频率来估计其条件概率分布。
然后，可以利用估计得到的条件概率分布进行决策推理和决策分析。
二、基于贝叶斯估计的参数估计方法贝叶斯估计是一种基于贝叶斯定理的参数估计方法，其基本思想是通过先验知识和观测数据来估计模型参数的后验概率分布。
在粗糙集理论中，贝叶斯估计可以用于估计条件属性的条件概率分布。
具体而言，可以利用先验知识和观测数据来构建条件属性的先验概率分布和似然函数，然后通过贝叶斯定理计算条件属性的后验概率分布。
最后，可以利用估计得到的后验概率分布进行决策推理和决策分析。
三、基于遗传算法的参数估计方法遗传算法是一种模拟生物进化过程的优化算法，其基本思想是通过模拟自然选择、交叉和变异等操作来搜索最优解。
在粗糙集理论中，遗传算法可以用于估计约简算法中的参数。
具体而言，可以将约简算法中的参数作为遗传算法的个体编码，然后通过选择、交叉和变异等操作来搜索最优的参数组合。
最后，可以利用估计得到的最优参数组合进行数据挖掘和模式识别。
四、粗糙集理论在实际应用中的价值粗糙集理论作为一种处理不完备、不精确、不确定信息的数学工具，具有很强的实际应用价值。
首先，粗糙集理论可以用于特征选择和约简，可以帮助我们从大量的属性中选择出最具有代表性和区分性的属性，从而提高数据挖掘和模式识别的效果。
粗糙集理论的模型构建方法及其预测性能评估
粗糙集理论的模型构建方法及其预测性能评估引言：粗糙集理论是一种基于不完全信息的数据分析方法，它可以处理不确定性和模糊性问题，并在决策和预测中发挥重要作用。
本文将介绍粗糙集理论的模型构建方法以及如何评估其预测性能。
一、粗糙集理论的模型构建方法1. 粗糙集理论的基本概念粗糙集理论最基本的概念是等价关系和上近似集、下近似集。
等价关系是指在给定条件下，某个对象的属性值相同，上近似集是指在给定条件下，某个对象的属性值不确定，下近似集是指在给定条件下，某个对象的属性值确定。
通过等价关系和近似集，可以对数据进行粗糙划分。
2. 特征选择特征选择是粗糙集理论中的一个重要步骤，它通过选择最重要的特征来减少数据集的维度。
特征选择可以基于信息增益、相关性等指标进行，选取具有较高区分度的特征。
3. 粗糙集约简粗糙集约简是指通过删除冗余的属性，减少数据集的复杂性，提高数据处理的效率。
约简的目标是找到最小的等价类，使得约简后的数据集仍能保持原始数据集的重要信息。
4. 粗糙集分类模型构建粗糙集分类模型构建是通过学习已知类别的样本，建立一个分类模型，用于对未知类别的样本进行分类。
常用的分类算法有基于规则的分类算法、基于决策树的分类算法等。
二、粗糙集理论的预测性能评估1. 交叉验证交叉验证是一种常用的评估粗糙集模型性能的方法。
它将数据集划分为训练集和测试集，通过训练集训练模型，再通过测试集评估模型的预测性能。
常见的交叉验证方法有k折交叉验证、留一交叉验证等。
2. ROC曲线ROC曲线是一种评估分类模型性能的图形化方法。
它以真正例率（True Positive Rate）为纵轴，假正例率（False Positive Rate）为横轴，通过绘制不同阈值下的真正例率和假正例率，可以评估模型在不同阈值下的预测性能。
3. 混淆矩阵混淆矩阵是一种评估分类模型性能的表格方法。
它以实际类别和预测类别为行列，通过统计真正例、假正例、真负例、假负例的数量，可以计算出模型的准确率、召回率、F1值等指标。
粗糙集理论的使用方法与步骤详解
粗糙集理论的使用方法与步骤详解引言：粗糙集理论是一种用来处理不确定性和模糊性问题的数学工具，它在数据分析和决策支持系统中得到了广泛的应用。
本文将详细介绍粗糙集理论的使用方法与步骤，帮助读者更好地理解和应用这一理论。
一、粗糙集理论概述粗糙集理论是由波兰学者Pawlak于1982年提出的，它是一种基于近似和粗糙程度的数学理论。
粗糙集理论的核心思想是通过对属性间的关系进行分析，识别出数据集中的重要特征和规律。
它主要包括近似集、正域、决策表等概念。
二、粗糙集理论的使用方法1. 数据预处理在使用粗糙集理论之前，首先需要对原始数据进行预处理。
这包括数据清洗、数据变换和数据归一化等步骤，以确保数据的准确性和一致性。
2. 构建决策表决策表是粗糙集理论中的重要概念，它由属性和决策构成。
构建决策表时，需要确定属性集和决策集，并将其表示为一个矩阵。
属性集包括原始数据中的各个属性，而决策集则是属性的决策结果。
3. 确定正域正域是指满足某一条件的样本集合，它是粗糙集理论中的关键概念。
通过对决策表进行分析，可以确定正域，即满足给定条件的样本集合。
正域的确定可以通过计算属性的约简度或者使用启发式算法等方法。
4. 近似集的计算近似集是粗糙集理论中的核心概念，它是指属性集在正域中的近似表示。
通过计算属性集在正域中的近似集，可以确定属性之间的关系和重要程度。
近似集的计算可以使用不同的算法，如基于粒计算、基于覆盖算法等。
5. 属性约简属性约简是粗糙集理论中的一个重要问题，它是指从属性集中选择出最小的子集，保持属性集在正域中的近似表示不变。
属性约简的目标是减少属性集的复杂性，提高数据分析和决策的效率。
属性约简可以通过计算属性的重要度、使用启发式算法或者遗传算法等方法实现。
6. 决策规则的提取决策规则是粗糙集理论中的重要结果，它是从决策表中提取出来的一组条件和决策的组合。
决策规则可以帮助我们理解数据集中的规律和特征，从而做出更好的决策。
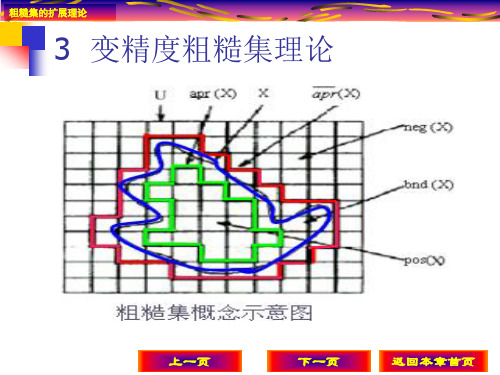
3变精度粗糙集方法
上一页
下一页
返回本章首页
粗糙集的扩展理论
β-粗糙近似
令：β=0.6，则β-粗糙近似分别为:
对论域进行划分，可得如下等价类 U/C={X1, X2, X3, X4, X5} 其中，X1={n1, n4,n6}，X2={n2}，X3={n3}，X4={n5}，X5={n7} U/D={YN,YP} 其中，YN={n1, n2,n3}，YP={n4, n5,n6, n7}
上一页
U n1 n2 n3 n4 n5 n6 n7
a1
1 1 2 1 2 1 2
a3
1 2 1 1 2 1 2
d N N N P P P P
下一页
返回本章首页
粗糙集的扩展理论
由β-约简{a1 ,a3}构造的概率决策规则
表 2.6 由β-约简{a1 ,a3}构造的规则 规则 支持数 １ １ 3 2
下一页
上一页 下一页 返回本章首页
粗糙集的扩展理论
β值与分类精度关系
上一页
下一页
返回本章首页
粗糙集的扩展理论
变精度粗糙集的分类质量
上一页
下一页
返回本章首页
粗糙集的扩展理论
变精度粗糙集中的近似约简
上一页
下一页
返回本章首页
粗糙集的扩展理论
概率规则获取
上一页
下一页
返回本章首页
粗糙集的扩展理论
算例 1
对论域进行划分，可得如下等价类： U/C={X1, X2, X3, X4, X5} 其中：X1={n1,n4,n6}，X2={n2}，X3={n3}，X4={n5}，X5={n7} U/D={YN,YP} 其中：YN={n1,n2,n3}，YP={n4,n5,n6, n7} 求得一个β-约简为{a1,a3 }, β=0.6，则 β{a β=0.6
逻辑函数的粗糙集表达及最小化方法
逻辑函数的粗糙集表达及最小化方法粗糙集理论是Z. Pawlak于1982年提出的，它是一种用来处理不确定性、模糊性和不完备性的一种数学模型。
粗糙集理论的基本思想是，利用一组属性来描述对象，通过这些属性来划分对象之间的相似度和差异度。
在粗糙集理论中，逻辑函数是一种重要的表达形式。
逻辑函数是通过布尔代数的方式来表达逻辑关系的函数形式，例如AND、OR和NOT等。
在粗糙集理论中，逻辑函数通常可以用来表示集合的包含关系或者近似关系。
逻辑函数的表达可以使用联结词来连接属性，例如AND和OR代表交集和并集。
使用逻辑函数可以方便地表示对象之间的相似性和差异性。
例如，对于一些对象a，可以使用逻辑函数来表示与其相似的对象集合，即具有相同属性的对象。
而与其不相似的对象，则可以使用逻辑函数的补运算来表示。
代数化简是一种常见的逻辑函数最小化方法，它通过运用布尔代数的基本定律和规则，对逻辑函数进行逻辑等价变换和化简，以达到最简形式。
代数化简的过程通常包括合并项、消除项和引入项等步骤。
卡诺图是一种图形化的逻辑函数最小化方法，它通过绘制真值表的方式来构造一个二维的格状图，格状图中的每个格子对应一个逻辑函数的项，通过寻找相邻格子之间的距离来合并相似项，从而实现逻辑函数的最小化。
奎因-麦克劳林展开是一种逻辑函数最小化的代数方法，它利用逻辑代数的展开定理，将逻辑函数展开成最简的形式。
展开的过程通常可以通过二项定理和相似项的合并来进行，以达到逻辑函数的最小化。
在实际应用中，根据需求选择合适的逻辑函数表达形式和最小化方法是非常重要的。
不同的逻辑函数表达形式和最小化方法适用于不同的问题和计算环境。
因此，在应用粗糙集理论中，需要根据具体情况选择合适的方法和技术来处理逻辑函数的表达和最小化问题。
综上所述，逻辑函数的粗糙集表达及最小化方法是粗糙集理论中的重要部分，它可以帮助我们处理不确定性、模糊性和不完备性的问题。
逻辑函数的表达使用布尔代数的方式来描述逻辑关系，可以方便地表示对象之间的相似性和差异性。
粗糙集理论与方法
粗糙集理论与方法
粗糙集理论与方法是一种用于处理不确定性和不完全信息的数学方法。
该方法最早由波兰科学家Zdzislaw Pawlak于1982年提出，其基本思想是基于约简和分割的思想对样本空间进行建模和分析。
粗糙集理论主要包括以下几个关键概念和步骤：
1. 近似集：粗糙集理论认为，一个对象可能属于多个不同的概念或类别，且我们不能确定其准确的分类。
因此，利用近似集的概念，我们可以将对象分成精确区域和不确定区域。
精确区域是指可以准确分类的对象，而不确定区域是指不能确定分类的对象。
2. 上近似和下近似：在粗糙集理论中，上近似是指包含所有精确分类对象的集合，而下近似是指包含所有不确定分类对象的集合。
上近似和下近似的交集被称为约简。
3. 属性重要性：对于给定的属性，粗糙集理论可以通过属性重要性来判断其对分类结果的贡献程度。
属性重要性可以通过信息熵、信息增益等指标来度量。
4. 属性约简：属性约简是粗糙集理论中的一个重要步骤，它的目的是通过删除某些不重要的属性来减少样本空间的复杂性，同时保持样本分类的准确性。
属性约简可以通过贪婪算法、遗传算法等进行求解。
粗糙集理论与方法在数据挖掘、决策分析、模式识别等领域具有广泛应用。
它可以处理不完整、不确定、模糊等问题，帮助人们对复杂的数据进行分析和决策。
粗糙集理论的使用方法和步骤
粗糙集理论的使用方法和步骤粗糙集理论是一种用于处理不完全、不确定和模糊信息的数学工具，它在决策分析、数据挖掘和模式识别等领域具有广泛的应用。
本文将介绍粗糙集理论的使用方法和步骤，帮助读者更好地理解和应用这一理论。
一、粗糙集理论的基本概念粗糙集理论是由波兰学者Pawlak于1982年提出的，它的核心思想是通过对数据集进行粗糙化处理，找出数据集中的重要信息，从而进行决策和分析。
在粗糙集理论中，数据集由属性和决策组成，属性是描述对象的特征，决策是对对象进行分类或判断的结果。
二、粗糙集理论的步骤1. 数据预处理：在使用粗糙集理论之前，需要对原始数据进行预处理。
预处理包括数据清洗、数据变换和数据归一化等步骤，旨在提高数据的质量和可用性。
2. 属性约简：属性约简是粗糙集理论的核心步骤之一。
在属性约简过程中，需要根据属性的重要性对属性进行选择和优化。
常用的属性约简方法有基于信息熵的属性约简和基于模糊熵的属性约简等。
3. 决策规则的生成：在属性约简完成后，可以根据属性和决策之间的关系生成决策规则。
决策规则是对数据集中的决策进行描述和判断的规则，可以帮助决策者进行决策和分析。
4. 决策规则的评价：生成的决策规则需要进行评价和优化。
常用的决策规则评价方法有支持度和置信度等指标，通过对决策规则进行评价，可以提高决策的准确性和可靠性。
5. 决策与分析：最后一步是根据生成的决策规则进行决策和分析。
根据决策规则，可以对新的数据进行分类和判断，从而帮助决策者做出正确的决策。
三、粗糙集理论的应用案例粗糙集理论在实际应用中具有广泛的应用价值。
以电商平台为例，可以使用粗糙集理论对用户行为进行分析和预测。
首先，对用户的行为数据进行预处理，包括清洗和归一化等步骤。
然后，通过属性约简找出用户行为中的关键属性，如浏览时间、购买频率等。
接下来，根据属性和决策之间的关系生成决策规则，如用户购买商品的决策规则。
最后，根据生成的决策规则对新的用户行为进行分类和分析，从而提供个性化的推荐和服务。
3变精度粗糙集方法
3变精度粗糙集方法粗糙集方法是为了解决模糊或不确定性问题而发展的一种理论与方法。
在粗糙集方法中，对象的属性值可以是模糊的或精确的，而决策或分类规则可以通过属性之间的相对约束关系来确定。
本文将介绍三个常用的变精度粗糙集方法，并对其进行详细阐述。
1.粗糙集的数学模型：粗糙集的数学模型是基于信息系统理论和近似推理理论。
它可以将不精确或模糊的数据转化为一个或多个精确的决策或分类规则。
其数学模型定义了粗糙集的三个基本元素：信息系统、下近似集和上近似集。
这三个元素构成了粗糙集的主要特性和运算规则。
2.变精度粗糙集的基本概念：在粗糙集方法中，为了处理不确定性或模糊性问题，可以使用变精度技术来调整精确度。
变精度粗糙集是在标准粗糙集的基础上引入了多个精度级别的概念，从而可以根据不同的应用要求对精确度进行调整。
3.粗糙集方法的三个变精度技术：a.基于粗糙集的属性精度：在传统粗糙集方法中，属性的精确度是预先定义的，而在基于粗糙集的属性精度技术中，属性的精确度是由用户根据实际情况进行调整的。
通过调整属性的精确度，可以提高粗糙集方法的分类或决策效果。
b.基于粗糙集的决策精度：传统粗糙集方法中，决策的精确度是通过属性之间的相对约束关系来确定的。
而在基于粗糙集的决策精度技术中，可以通过调整决策的精确度来改善分类或决策结果。
这种技术常常会涉及到模糊推理或概率推理的方法。
c.基于粗糙集的规则精度：在传统粗糙集方法中，规则的精确度是预先定义的。
而在基于粗糙集的规则精度技术中，可以通过调整规则的精确度来提高分类或决策的准确性。
这种技术通常涉及到规则的修剪或合并。
总结起来，粗糙集方法是一种基于信息系统理论和近似推理理论的模糊或不确定性问题处理方法。
它的数学模型定义了信息系统、下近似集和上近似集等三个基本元素，并通过属性精度、决策精度和规则精度等三个变精度技术来提高分类或决策的准确性。
这些方法在实际应用中具有较好的效果，并逐渐成为数据挖掘和智能决策等领域的重要研究方向。
粗糙集理论方法及其应用ppt课件
粗糙集概念示意图
粗糙集理论方法及其应用 病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
2 粗粗糙糙集集理理论论思思想想
粗糙集理论方法及其应用 病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
2.3 粗糙近似
定义 给定一个知识表示系统 S (U, A,V, f ) ， P A，X U ，x U ，集合 X 关于 I 的下近似、 上近似、负区及边界区分别为
apr (X ) {x U : I(x) X} p
aprP (X ) {x U : I(x) X }
neg p ( X ) {x U : I (x) X }
2.2 不可分辨关系 （Indiscribility relation)
❖ 不可分辨关系是一个等 价关系(自反 的、对称 的、传递的）。
❖ 包含对象x的等价类 记为I(x)。等价类与知 识粒度的表达相对应， 它是粗糙集主要概念， 如近似、依赖及约简等， 定义的基础
粗糙集理论方法及其应用 病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
决策属性(D)
U
a1
a2
a3
d
n1
High
Low
Low
Low
n2
Medium
High
Low
High
n3
High
High
High
High
粗糙集理论方法及其应用 病原体侵入机体，消弱机体防御机能，破坏机体内环境的相对稳定性，且在一定部位生长繁殖，引起不同程度的病理生理过程
粗糙集约简方法
粗糙集约简方法简介粗糙集约简方法是数据挖掘领域中一种常用的特征选择方法。
在众多特征选择方法中，粗糙集约简方法以其简单快速、易于理解的特点而受到广泛关注。
它通过粗糙集理论的基本原理，对原始数据集进行约简，从而得到一个更精简的特征子集，提高数据挖掘效率。
粗糙集理论基础粗糙集理论是由波兰学者Pawlak于1982年提出的，是一种处理不确定性信息的方法。
它基于集合论和近似推理，并尝试解决数据集中存在的不确定性和模糊性问题。
在粗糙集理论中，将数据集划分为对象的集合和属性的集合，并使用近似关系来描述属性与对象之间的关系。
约简的概念与意义约简是指通过对原始数据集进行操作，得到一个特征子集，该子集包含了原始数据集中的重要、有用的特征信息，而丢弃了无关、冗余的特征信息。
约简的过程就是在保持数据集中信息完整性和准确性的基础上，减少特征的数量，提高数据挖掘的效率。
约简所起到的作用有以下几个方面： - 减少特征的数量，提高数据挖掘算法的效率和性能； - 去除冗余信息，减少数据挖掘模型的复杂度； - 提高数据可视化效果，减少特征数量可以降低维度，更方便数据的可视化和分析。
粗糙集约简方法的步骤粗糙集约简方法一般包括以下几个步骤：1.确定属性集合和决策集合：首先确定数据集中的属性集合和决策集合。
属性集合是指数据集中待选择的特征集合，决策集合是指用于分类或预测的结果集合。
2.计算属性间的依赖度：使用粗糙集理论中的依赖度指标，计算属性集合中各个属性之间的依赖程度。
具体来说，可以计算属性集合中每个属性与决策集合之间的依赖度，衡量该属性对于分类结果的贡献程度。
3.确定依赖度阈值：根据需求和实际情况，确定一个依赖度阈值。
该阈值可以根据经验选择，也可以通过交叉验证等方法进行确定。
4.生成约简的特征子集：根据依赖度阈值，从属性集合中选择具有较高依赖度的特征，构成约简的特征子集。
5.验证约简的质量：使用约简的特征子集，进行数据挖掘任务，比如分类、预测等。
粗糙集理论的使用方法与建模步骤详解
粗糙集理论的使用方法与建模步骤详解粗糙集理论是一种用于处理不确定性和模糊性问题的数学工具。
它是由波兰数学家Pawlak于1982年提出的，被广泛应用于数据挖掘、模式识别、决策分析等领域。
本文将详细介绍粗糙集理论的使用方法和建模步骤。
一、粗糙集理论的基本概念粗糙集理论的核心思想是通过对数据进行粗糙划分，找出数据之间的相似性和差异性，从而进行有效的分类和决策。
在使用粗糙集理论进行建模之前，我们首先需要了解一些基本概念。
1.1 上近似集和下近似集上近似集是指在给定条件下，能够包含所有与目标属性有关的样本的集合；下近似集是指在给定条件下，能够完全确定与目标属性有关的样本的集合。
1.2 等价类和不可区分关系等价类是指在相同条件下，具有相同目标属性的样本所构成的集合；不可区分关系是指在给定条件下，无法通过已有的属性来区分不同的样本。
二、粗糙集建模的步骤在使用粗糙集理论进行建模时，我们可以按照以下步骤进行操作。
2.1 数据预处理在进行粗糙集建模之前，我们需要对原始数据进行预处理。
预处理包括数据清洗、数据转换、数据归一化等操作，以确保数据的质量和可用性。
2.2 属性约简属性约简是粗糙集建模中的关键步骤。
通过属性约简，我们可以从原始数据中选择出最具代表性的属性，减少冗余信息，提高模型的效率和准确性。
2.3 确定目标属性在进行粗糙集建模时，我们需要明确目标属性。
目标属性是我们希望通过建模来预测或分类的属性。
2.4 确定条件属性条件属性是用来描述和区分不同样本的属性。
在确定条件属性时，我们需要根据实际问题和数据特点选择合适的属性。
2.5 构建上近似集和下近似集通过已知的条件属性和目标属性，我们可以构建上近似集和下近似集。
上近似集包含了所有与目标属性有关的样本，下近似集则包含了能够完全确定与目标属性有关的样本。
2.6 确定等价类和不可区分关系根据上近似集和下近似集，我们可以确定等价类和不可区分关系。
等价类是具有相同目标属性的样本集合，不可区分关系则是无法通过已有的属性来区分不同的样本。
3变精度粗糙集方法
3变精度粗糙集方法粗糙集理论是一种基于信息论和概率统计的数据分析方法，主要用于处理模糊、不确定和不完备信息。
在粗糙集理论中，精度是一个非常重要的指标，可以用来衡量数据集合的精确度和准确度。
在实际应用中，通常需要在不同精度下进行数据分析和挖掘，以获得更加全面和准确的结果。
因此，研究如何在不同精度下进行粗糙集分析是非常重要的。
在本文中，我们将介绍三种常用的变精度粗糙集方法，分别是逐步粗糙集方法、粗糙模糊集方法和动态粗糙集方法。
这些方法在不同的应用场景下具有各自的优势和特点，可以有效地处理不同类型的数据，并可以提高数据分析的效率和准确度。
逐步粗糙集方法是一种常用的变精度粗糙集方法，它通过逐步减少属性的数量来提高数据分析的效率。
具体来说，逐步粗糙集方法将数据集合中的属性按照其重要性进行排序，然后逐步地删除不重要的属性，直到达到所需的精度。
通过这种方式，逐步粗糙集方法可以在不损失太多信息的情况下大幅减少数据的维度，从而提高数据分析的效率和准确度。
另一种常用的变精度粗糙集方法是粗糙模糊集方法，它结合了粗糙集和模糊集的优势，可以有效地处理模糊和不确定性信息。
具体来说，粗糙模糊集方法引入模糊集的概念，将数据的属性值表示为模糊数，然后使用模糊关系来处理属性之间的关系，并通过粗糙集理论来发现数据之间的粗糙关系。
通过这种方式，粗糙模糊集方法可以在处理模糊和不确定性信息时更加有效和准确，从而提高数据挖掘的效率和精度。
最后，动态粗糙集方法是一种基于数据动态变化的变精度粗糙集方法，它可以随着数据的变化而动态调整精度。
具体来说，动态粗糙集方法通过监控数据的变化情况，动态调整精度参数，以适应数据变化的需要。
通过这种方式，动态粗糙集方法可以实现数据的实时监控和管理，从而提高数据分析的灵活性和准确度。
综上所述，逐步粗糙集方法、粗糙模糊集方法和动态粗糙集方法是三种常用的变精度粗糙集方法，它们在处理不同类型的数据和不同应用场景下具有各自的优势和特点。
10.粗糙集方法
可知有：
A ( X ) { f }
A ( X ) {a, b, c} { f } {a, b, c, f }
PosA ( X ) A ( X ) { f }
NEGA ( X ) U A ( X ) {d , e}
BNDA ( X ) A ( X ) A ( X ) {a, b, c}
计算减少一个条件属性相对决策属性的正域
Pos(C \{a1}) (D) {2,5,9,10,11 U } Pos(C \{a2 }) (D) U Posc (D) Pos(C \{a3 }) (D) U Posc (D)
Pos(C \{a4 }) (D) {1,2,3,7,8,9,10,11,12,13} U
a R, x U , fa ( x) Va
（2）等价关系定义
对 于 a A A 中 包 含 一 个 或 多 个 属 （ A 性）， R, x U , y U ，它们的属性值相同， f ( x) f ( y ) 即： 成立，称对象x和y是对属性A的等价关系， 表示为：
a a
(2)集合X的上近似定义
对任意一个子集 X U ，属性A的等价类 Ei [ x]A 有： A ( X ) Ei | Ei A Ei X 或 A ( X ) x | [ x] A X 表示等价类 Ei [ x]A 中的元素x可能属于X， 即x A (X )，则x可能属于X，也可能不属于X。
第 8 章 集合论方法 （一） 粗糙集方法
8.1粗糙集方法
8.1.1粗糙集概念 8.1.2属性约简的粗糙集理论 8.1.3属性约简的粗糙集方法 8.1.4粗糙集方法的规则获取 8.1.5粗糙集方法的应用实例
变精度粗糙集方法
近似集合与真实集合的相似度。
决策规则的生成算法
确定决策规则
根据下近似集和上近似集，通过一定的算法确定决策规则，即根据近似精度进行 分类或决策。
评估决策规则
根据实际需求和数据集，通过一定的算法评估决策规则的准确性和可靠性。
属性约简算法
确定冗余属性
根据数据集和决策规则，通过一定的 算法确定冗余属性，即对决策结果没 有影响的属性。
进行属性约简
根据冗余属性，通过一定的算法进来自 属性约简，即去除冗余属性后得到最 小决策规则集合。
04
变精度粗糙集方法的应 用实例
数据预处理与实例选择
原始数据收集
首先需要收集相关的数据，这些数据可以是 来自不同来源和格式的数据。
数据清洗
对收集到的数据进行清洗，去除重复、错误 或不完整的数据。
数据转换
处理连续属性受限
传统的变精度粗糙集方法主要针对离散属性，对于连续属性的处理能力有限，需要进一 步改进和扩展。
决策规则提取困难
变精度粗糙集方法在提取决策规则方面可能面临挑战，尤其是在处理复杂和不均衡数据 集时，难以得到可靠和有效的决策规则。
未来研究方向与展望
属性约简优化
进一步研究属性约简算法，提高模型在处理大规模数据集时的效率 和准确性。
资源和时间。
03
变精度粗糙集方法的核 心算法
近似集的求解算法
确定下近似集
01
根据给定的数据集和阈值，通过一定的算法确定下近似集，即
确定哪些对象属于集合。
确定上近似集
02
根据给定的数据集和阈值，通过一定的算法确定上近似集，即
确定哪些对象可能属于集合。
计算近似精度
03
根据下近似集和上近似集，通过一定的算法计算近似精度，即
粗糙集理论的核心算法及其在实际问题中的应用
粗糙集理论的核心算法及其在实际问题中的应用粗糙集理论是一种用于处理不确定性和模糊性问题的数学工具，它能够在信息不完备或不准确的情况下进行决策和推理。
本文将介绍粗糙集理论的核心算法，并探讨其在实际问题中的应用。
一、粗糙集理论的核心算法粗糙集理论的核心算法主要包括粗糙集近似算法和粗糙集约简算法。
粗糙集近似算法是粗糙集理论最基本的算法之一，它用于将不完备或不准确的数据集划分为若干个等价类。
该算法基于属性重要性的概念，通过计算属性的正域和反域来确定属性的重要性，从而实现数据集的划分。
粗糙集约简算法是粗糙集理论中的关键算法，它用于从原始数据集中提取出最小的、具有相同决策规则的子集。
该算法通过计算属性的依赖度来确定属性的重要性，从而实现数据集的约简。
二、粗糙集理论在实际问题中的应用粗糙集理论在实际问题中有着广泛的应用，尤其在数据挖掘、模式识别和决策支持等领域。
在数据挖掘中，粗糙集理论可以用于特征选择和数据预处理。
通过粗糙集约简算法，可以从原始数据集中提取出最重要的特征，减少数据维度，提高数据挖掘的效率和准确性。
在模式识别中，粗糙集理论可以用于特征提取和模式分类。
通过粗糙集近似算法，可以对模式进行划分和分类，从而实现对复杂模式的识别和分析。
在决策支持中，粗糙集理论可以用于决策规则的生成和评估。
通过粗糙集约简算法，可以从原始数据集中提取出最简化的决策规则，为决策制定提供支持和指导。
除了以上应用，粗糙集理论还可以用于知识发现、智能推理和不确定性推理等领域。
它的优势在于能够处理不完备或不准确的信息，提供一种有效的决策和推理方法。
总结起来，粗糙集理论的核心算法包括粗糙集近似算法和粗糙集约简算法，它们在实际问题中有着广泛的应用。
通过粗糙集理论，可以处理不完备或不准确的信息，提高数据挖掘、模式识别和决策支持等领域的效率和准确性。
粗糙集理论为我们解决实际问题提供了一种有效的数学工具。
粗糙集下近似计算方法
粗糙集下近似计算方法1. 前言粗糙集理论是一种非常有用的数学工具，可以用来处理诸如分类、聚类、特征选择等问题。
在实际应用中，粗糙集下的近似计算方法被广泛使用，能够有效地解决大规模数据下的问题。
2. 粗糙集理论简介粗糙集理论是基于启发式算法的一种数学工具，主要用于处理不确定性问题。
粗糙集理论的基本假设是，每一个对象都可以用一个或多个属性来描述，这些属性反映了对象的某些特征。
在粗糙集中，对象被描述为属性值的集合。
根据粗糙集的定义，两个对象如果在所有属性上的取值都相等，那么它们就是相等的。
粗糙集理论通过对属性值的划分来确定对象之间的相似性，从而实现了对数据的分类、聚类、特征选择等任务。
3. 粗糙集的近似计算方法在实际应用中，粗糙集理论需要面对大规模的数据，因此需要寻找有效的计算方法来加速计算过程。
粗糙集的近似计算方法是一个重要的解决方案，包括以下几种方法：3.1 粗糙集精简方法粗糙集精简方法是用来减少属性集合中冗余属性的一种方法。
粗糙集的决策属性只与部分属性有关，因此在精简属性集合时可以删除与决策属性无关的属性，从而降低计算复杂度。
3.2 粗糙集标准化方法粗糙集标准化方法是用来将数值型属性转化为离散型属性的一种方法。
由于数值型属性的取值范围广泛，因此在粗糙集的计算中往往需要将其离散化处理。
标准化方法可以根据数据的分布情况来自动将数值型属性离散化，从而改善了计算效率。
3.3 粗糙集快速计算方法粗糙集快速计算方法是通过预处理数据，降低计算复杂度的一种方法。
该方法将数据转化为某种特定形式，从而可以将粗糙集的计算转化为简单的矩阵运算、向量点积等操作，实现了计算的快速计算。
4. 实例分析下面通过一个实例来说明粗糙集的近似计算方法。
4.1 实例描述假设有一个汽车行业的数据集，其中包括车辆品牌、车型、销售地区、价格等属性。
现在需要根据这些属性来进行车辆分类。
4.2 粗糙集分类采用粗糙集分类的步骤如下：1）将数据集进行标准化处理，将数值型属性转化为离散型属性。
构建粗糙集模型的基本步骤与方法
构建粗糙集模型的基本步骤与方法引言：粗糙集理论是一种基于不确定性的数学模型，被广泛应用于数据挖掘、模式识别、决策分析等领域。
构建粗糙集模型是研究者们在实践中积累的经验总结，下面将介绍构建粗糙集模型的基本步骤与方法。
一、数据预处理构建粗糙集模型的第一步是进行数据预处理。
数据预处理是为了清洗数据、填补缺失值、去除异常值等，以保证数据的质量和完整性。
常用的数据预处理方法包括数据清洗、缺失值处理、异常值检测等。
二、属性约简属性约简是构建粗糙集模型的关键步骤之一。
属性约简的目的是通过删除冗余属性，减少数据集的维度，提高模型的效率和可解释性。
常用的属性约简方法有基于信息熵的属性约简、基于粗糙集的属性约简等。
三、决策规则提取决策规则提取是构建粗糙集模型的核心步骤之一。
决策规则提取的目的是从数据集中提取出具有较高可信度和泛化能力的决策规则，用于描述数据集的特征和规律。
常用的决策规则提取方法有基于粗糙集的决策规则提取、基于关联规则的决策规则提取等。
四、模型评估与优化模型评估与优化是构建粗糙集模型的重要环节。
模型评估的目的是评估模型的性能和泛化能力，以确定模型的有效性和可靠性。
常用的模型评估方法有交叉验证、留一法、自助法等。
模型优化的目的是通过调整模型的参数和结构，提高模型的预测能力和稳定性。
常用的模型优化方法有遗传算法、粒子群优化算法等。
五、模型应用与推广构建粗糙集模型的最终目的是将模型应用于实际问题，并推广到更广泛的领域。
模型应用的过程中，需要根据实际需求进行模型调整和优化，以满足实际问题的需求。
模型推广的过程中，需要将模型的思想和方法进行总结和归纳，以便更好地应用于其他领域和问题。
结论：构建粗糙集模型是一个复杂而又有挑战性的过程，需要经验丰富的研究者进行指导和实践。
本文介绍了构建粗糙集模型的基本步骤与方法，包括数据预处理、属性约简、决策规则提取、模型评估与优化、模型应用与推广等。
希望本文能够对研究者们在构建粗糙集模型时提供一定的参考和帮助。
粗糙集方法
粗糙集方法
嘿，朋友！你听说过粗糙集方法吗？这可真是个超级有趣的玩意儿啊！
就比如说咱们整理房间吧。
你看，房间里有各种各样的东西，有些是常用的，就像那些确定的信息；有些呢，你不太确定到底重不重要，这就有点像粗糙集方法里的那些不那么明确的情况。
咱假设有一天，你和几个朋友一起在讨论去哪儿玩。
一个朋友说去爬山，一个朋友说去海边，而你呢有点纠结，不知道该选啥。
这时候就像是粗糙集方法在发挥作用啦！爬山和海边就像是两个不同的条件属性，而你最终的决定就是那个决策属性呀！你得综合考虑各种因素，像天气啊、自己的体力啊等等，这不就是在对这些信息进行分析处理嘛！
粗糙集方法就像是一个聪明的小助手，能帮咱在一堆看似混乱的信息里找到关键的线索。
好比你找工作的时候，各种职位信息、公司要求乱糟糟的一堆，但是通过粗糙集方法，就能帮你理出头绪，找到最适合你的那个工作呀！
哎呀，你说这粗糙集方法是不是超厉害的？它能让咱在面对复杂情况时不再那么迷茫，而是能更有方向、更有把握地做出决定呢！它就像是一把神奇的钥匙，能打开那扇通往清晰思考和正确决策的大门。
别再觉得这是个很难懂的东西啦，其实它就在我们生活的方方面面发挥着作用呢！只要你留心，就能发现它的厉害之处！相信我，你一旦了解了它，肯定会对它超级感兴趣的！
我的观点结论就是：粗糙集方法真的很有用，很值得我们去深入了解和运用！。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A ( X ) A ( X ) BNDA (X )
用图说明正域、负域和边界，每一个小长方形表 示一个等价类。
NEG（X）
Pos（X）
= A ( X )
X
正域
负域
图8.1 正域、负域和边界
BND（X） 边界
任意一个元素 x Pos(X ) ，它一定属于X； 任意一个元素 x NEG，(X )它一定不属于X；集 合X的上近似是其正域和边界的并集，即
[x]A {y | (x, y) IND(A)}
（4）划分的定义
在U中对属性A的所有等价类形成的划分表 示为： A {Ei | Ei [x]A，i＝1，2....}
具有特性： （i.） Ei （ii.）当 i j时，Ei E j （iii.） U＝ Ei
例1
U {a( 体温正常），b（体温正常），c（体
即条件属性C和决策属性D, R=C D V:是属性值的集合， V a是属性的值域。 f ：是 U R V 的一个信息函数，它为每个对
象x的每个属性a赋予一个属性值，即
a R, x U , fa (x) Va
（2）等价关系定义
对 于 a A（ A 中 包 含 一 个 或 多 个 属
性），A R, x U, y U ，它们的属性值相同，
Pos(C \{a2 ,a3}) (D) {3,4,5,6,7,10,12,13,14} U
说明{a2,a3}同时是不可省略的。
3） 在{a2,a3}中只能删除一个属性 即存在两个约简：
redD (C){{a1, a2, a3},{a1, a2, a4 }}
从实例计算可以看出，信息表的属性约简是在 保持条件属性相对决策属性的分类能力不变的 条件下，删除不必要的或不重要的属性。 一般来讲，条件属性对于决策属性的相对约简不 是唯一的，即可能存在多个相对约简。
IND(C \{a4}) {{1,2},{3},{4,14},{5,6},{7},{8},{9},{10},{11},{12},{13}}
计算减少一个条件属性相对决策属性的正域
Pos(C\{a1}) (D) {2,5,9,10,11} U Pos(C \{a2}) (D) U Posc (D) Pos(C\{a3}) (D) U Posc (D) Pos(C\{a4})(D) {1,2,3,7,8,9,10,11,12,13} U
高
无风
P
4
雨
适中
高
无风
P
5
雨
冷
正常
无风
P
6
雨
冷
正常
有风
N
7
多云
冷
正常
有风
P
8
晴
适中
高
无风
N
9
晴
冷
正常
无风
P
10
雨
适中
正常
无风
P
11
晴
适中
正常
有风
P
12
多云
适中
高
有风
P
13
多云
热
正常
无风
P
14
雨
适中
高
有风
N
令 C {a1, a2 , a3, a4}, D {d}
IND(C) {{1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11},{12},{13},{14}}
A ( X ) PosA ( X ) BNDA ( X )
对于元素 xBND(X ) ，是无法确定其是否属于 X，因此对任意元素 x A(X ) ，只知道x可能属 于X。
（4）粗糙集定义
若 A (X ) A(X ) ，即 BND(X ) 即边界为空，称X 为A的可定义集；
否则X为A不可定义的， 即 A (X ) A(X ) ，称X为A的Rough集（粗糙集）
SGF(a,C, D) (C, D) (C {a}, D)
其中 (C {a},D) 表示在缺少属性a后，条件属性与决 策属性的依赖程度。 SGF(a,C, D) 表示C中缺少属性a后，导致不能被准确分 类的对象在系统中所占的比例。
2. SGF(a,C, D性) 质
（1） SGF(a,C, D∈) [0，1]
粗糙集理论用在数据库中的知识发现主要 体现在：
（1）利用等价关系对数据库进行属性约简。
（2）利用集合的上、下近似关系获取分 类规则。
(1)信息表定义
信息表S=(U，R，V，f)的定义为: U:是一个非空有限对象(元组)集合,
U={x1 x2 …xn},其中xi为对象(元组)。 R:是对象的属性集合,分为两个不相交的子集,
粗糙集以等价关系（不可分辨关系）为 基础，用于分类问题。
它用上、下近似两个集合来逼近任意一 个集合，
该集合的边界线区域被定义为上近似集 和下近似集之差集。
上、下近似集可以通过等价关系给出确 定的描述，边界域的含糊元素数目可以 被计算出来。
模糊集（Fuzzy）是用隶属度来描述集合 边界的不确定性，隶属度是人为给定的， 不是计算出来的。
否则称c是C中相对于D必要的。
（5）条件属性C相对于决策属性D的核定义 若 R ，C 如果R中每一个都是相对于D必要的， 则称R是相对于D独立的。如果R相对于D独 立的，且 PosR (D) PosC (D) ，则称R是C中相对于D 的约简，记为redD (C)，所有这样简约的交称为C的D 核，记为：
PosA ( X ) A ( X ) { f }
NEGA (X ) U A (X ) {d,e}
BNDA (X ) A (X ) A (X ) {a,b,c}
8.1.2属性约简的粗糙集理论
属性约简概念 在信息表中根据等价关系，我们可以用等
价类中的一个对象（元组）来代表整个等价 类，这实际上是按纵方向约简了信息表中数 据。
（3）正域定义 设决策属性D的划分 A {y1, y2...yn}，条件属性C 相对于决策属性D的正域定义为：
PosC (D) C _( y j )
（4）条件属性C相对于决策属性D的约简定义 若 c C，如果Pos(C{c}) (D) PosC (D) ， 则称c是C中相对于D不必要的，即可约简的，
（1）约简定义 给定一个信息表IT（U，A），若有属性集 B A 且满足 IND(B) IND(A)， 称B为A的一个约简。记为red（A）
B=red(A)
（2）核定义 属性集A的所有约简的交集称为A的核。记作
core(A) red(A)
Core(A)是A中为保证信息表中对象可精确定义 的必要属性组成的集合，为A中不能约简的重要 属性，它是进行属性约简的基础。
CoreD (C) redD (C)
一般情况下，信息系统的属性约简集有多个，但约 简集中属性个数最少的最有意义。
属性约简实例
气候信息表是4个条件属性（天气a1，温 度a2，湿度a3，风a4）和1个决策属性（类别 d），见表8.1。
NO.
属性
类别
天气
气温
湿度
风
1
晴
热
高
无风
N
2
晴
热
高
有风
N
3
多云
热
②若0< <1,则称D部分依赖于C（D Rough依赖于 C），即在已知条件C下，只能将U上那些属于正 域的个体分类到决策属性D的类别中去。
③若 ＝0，则称D完全不依赖C，即利 用条件C不能分类到D中的类别中去。
2.属性重要度定义 ,CD A，C为条件属性集，D为决策属性集，a∈ ，
属性Ca关于D的重要度定义为：
温正常），d (体温高），e(体温高），f（体 温很高} 对于属性A（体温）的等价关系有：
IND( A) {(a,b), (a, c), (b, c), (d, e), (e, d ), (a, a), (b,b), (c, c), (d, d ), (e, e), ( f , f ),}
属性A的等价类有：
X {a,b,c}{b,c}
例2
对上例1的等价关系A有集合 X {b, c, f } 是粗糙集，计算集合X的下近似、上近似、 正域、负域和边界。 U中关于A的划分为：
A {{a,b,c},{d,e},{ f }}
有：
X {a,b,c}{b,c}
X {d, e}
X {f}{f}
可知有：
A ( X ) { f } A (X ) {a,b,c}{ f } {a,b,c, f }
由此可知，属性a2，a3是相对于决策属性d可省略的， 但不一定可以同时省略， 属性a1和a4是相对决策属性不可省略的，因此：
Core(c) {a1, a4}
2）计算同时减少{a2,a3}的等价关系和正域
IND(C \ {a2, a3}) {{1,8,9},{2,11}.{3,13},{4,5,10},{6,14},{7,12}}
E1 [a]A [b]A [c]A {a,b, c}
E2 [d]A [e]A {d, e}
E3 [ f ]A { f }
U中对属性A的划分为：
A {E1, E2 , E3} {{a,b,c},{d,e},{ f }}
（1）集合X的下近似定义
对任意一个子集 X U 属性A的等价类
第8章
集合论方法
（一） 粗糙集方法
8.1粗糙集方法
8.1.1粗糙集概念 8.1.2属性约简的粗糙集理论 8.1.3属性约简的粗糙集方法 8.1.4粗糙集方法的规则获取 8.1.5粗糙集方法的应用实例
8.1.1粗糙集概念
粗 糙 集 （ Rough Set） 是 波 兰 数 学 家 Z.Pawlak于1982年提出的。
（2）若 SGF(a,C, D)