基于LMS算法的自适应均衡器的MATLAB实现_尹丽丽
LMS算法自适应滤波器的MATLAB仿真与DSP实现

据存储器,64k字的程序存储器.具有高度并行性.用DSP特有的汇编语言实现以上3种LMS算法自适应滤波器.在TMS320C54X的指令系统中,单周期乘/累加指令MAC和循环寻址方式可使滤波器在一个周期内完成每个样值的计算.在实现LMS自适应算法时,由于要计算两组数对应项乘积的累加和,还有要采用循环寻址方式,因此,本文滤波器程序中采用DSP指令中的RPTZ和MAC结合循环寻址方式实现两累加和的运算.RPTZA,#F1LTERMAC℃OFF_DP+0%,*DATA_DP+0%,A其中,RPTZ指令用于将累加器A清零,将立即数10(本实验中滤波器阶数取11)装入到重复计数器,使下条MAC指令重复执行10+1次.MAC指令实现将两存储区数据的乘积累加到累加器A,使存储器的指针以循环寻址的方式指向下一个存储区.其中,FILTER,COFF_DP,DATA—DP分别为自适应滤波器的阶数,自适应滤波器系数缓冲区指针和输入样值缓冲区指针.为了提高算法效率,程序中使用了TMS320C54X特有的LMS指令,来快速实现本文的几种自适应滤波器.设计中,采用1500Hz的期望信号与312Hz的噪声信号叠加作为11个系数的自适应滤波器的一个输入信号,对于每一个时刻r/,,计算自适应滤波器的输出,误差信号是输出信号与期望信号的差值.固定步长LMS算法,变步长LMS算法和归一化LMS算法在SZ—EPP5416评估板上实现的结果如图3所示.70(d)归一化LMS算法滤波结果图3DSP实现结果Fig.3TherealizationDSP图3中,横坐标为仿真时间,竖坐标为波形幅值,图3(a)为输入含噪声的叠加信号,图3(b)为固定步长LMS算法滤波器实现结果,从图3(b)中可以看出,在滤波初始阶段,滤波结果不明显,输入的叠加信号经过自适应滤波器后在初始阶段噪声没有得到明显抑制,存在较大稳态误差,收敛速度比较慢,收敛速度和稳态误差都有待改善.图3(c)为变步长LMS算法滤波结果,从图3(c)中可以看出,在滤波初始阶段,稳态误差已得到改善,但仍有较小稳态误差浮动,初始收敛速度有所加快,输入的叠加信号经过自适应滤波器后噪声得到较明显抑制,滤波性能优于固定步长LMS算法.图3(a)为归一化LMS算法滤波结果,从图3(d)中可以看出,在滤波初始阶段,稳态误差已经得到明显改善,稳态误差浮动已经得到改善,输入的叠加信号经过自适应滤波器后噪声得到更明显抑制,更好的克服了固定步长存在的矛盾.可见,此滤波器滤波效果最为明显.4结论初始收敛速度与稳态误差是衡量自适应滤波算法性能优劣的两个重要技术指标,本文通过对固定步长,变步长LMS算法和归一化LMS算法自适应滤波器进行MATLAB仿真与DSP实现,比较滤波结果,证明了归一化LMS算法能够保证具有更快的收敛速度与更小的稳态误差,能有效去除不相关的独立噪声的干扰,克服了固定步长在增大初始收敛速度与减小稳态误差之间存在的矛盾,优化了自适应滤波器的性能,滤波效果明显.参考文献:【l】1ShireenW,LiT.ADSP-Nmedactivepowerfilterforlowvoltagedistributionsystems田.F_如2tricPowersyBtel璐Research,2008,78:1561—1567.【2】吕振肃,熊景松.一种改进的变步长LMS自适应算法【刀.信号处理,2008,24(1):144-146.LvzS,XiongJS.Anovdi呻r--ovedvariablestep-sizeLMS妇riⅡ姗田.SigllalProcessing,2008,24(1):144一146.【3】KukrerO.№caniIIA.Frequency-response-shapedLMSadaptivefilter田.Digitalsil}IalPro∞s*ing,2006,16:855—869.【4】叶永生,余容桂.一种新的自适应最小均方算法及其应用研究【刀.电测与仪表,2008,45(7):19—22.YeYS。
利用LMS算法的自适应系统仿真

利用LMS算法的自适应系统仿真[摘要] 一待辩识的IIR系统,用一有限长度的FIR滤波器来近似辩识系统,介绍了基于最小均方算法(LMS算法)的自适应均衡器的原理和结构,采用LMS 算法得到N阶FIR滤波器来逼近原IIR滤波器,并且分析了步长,滤波器系数以及自适应过程中的噪声对系统辩识性能的影响,做出了仿真试验结果并分析了仿真试验结果的意义。
[关键词] LMS算法FIR滤波器自适应滤波IIR MATLAB仿真0、引言假定待辨识系统是极点-零点(IIR)系统,要求用一个有限长度的FIR 滤波器来辨识该系统,如下图所示。
已知待辨识系统的传输函数为:(IIR),求FIR 滤波器的系数。
自适应系统辨识的原理图系统设计要求为:首先待辨识系统为IIR滤波器,利用自适应滤波的方法,采用LMS算法得到N阶FIR滤波器来逼近原IIR滤波器,输入信号为高斯白噪声,考察步长、阶数N对自适应滤波器性能的影响。
1、系统设计原理由于LMS算法不需要离线方式的梯度估值或重复使用数据以及它的简单易行性而被广泛采用。
只要自适应系统是线性组合器,且有输入数据向量和期待响应在每次迭代时可利用,对许多自适应处理的应用来说,LMS算法是最好的选择。
我们采用LMS算法自适应调整FIR滤波器的系数,自适应滤波器的结构是具有可调系数的直接型FIR滤波器。
输入信号为功率为1,长度为1000点的高斯白噪声。
为期望响应,为自适应FIR滤波器的输出,误差信号。
对一个FIR滤波器,其可调系数为,为滤波器的阶数。
则输出LMS算法是由最速下降法导出的,求出使均方误差达到最小值时相应的最佳滤波器系数组。
从任意选择的一组初始值开始,接着在每个新的输入采样值进入自适应滤波器后,计算相应的输出,再形成误差信号,并根据如下方程不断修正滤波器系数:其中为步长参数,为时刻输入信号在滤波器的第个抽头处的采样值,是滤波器第个系数的负梯度的近似值。
这就是自适应地调整滤波器系数以便使平方误差最小化的LMS算法。
LMS算法MatLab实现

LMS算法MatLab实现LMS算法MatLab实现LMS⾃适应滤波器是使滤波器的输出信号与期望响应之间的误差的均⽅值为最⼩,因此称为最⼩均⽅(LMS)⾃适应滤波器。
其原理及推导见function [yn,W,en]=LMS(xn,dn,M,mu,itr)% LMS(Least Mean Squre)算法% 输⼊参数:% xn 输⼊的信号序列 (列向量)% dn 所期望的响应序列 (列向量)% M 滤波器的阶数 (标量)% mu 收敛因⼦(步长) (标量) 要求⼤于0,⼩于xn的相关矩阵最⼤特征值的倒数% itr 迭代次数 (标量) 默认为xn的长度,M<itr<length(xn)% 输出参数:% W 滤波器的权值矩阵 (矩阵)% ⼤⼩为M x itr,% en 误差序列(itr x 1) (列向量)% yn 实际输出序列 (列向量)% 参数个数必须为4个或5个if nargin == 4 % 4个时递归迭代的次数为xn的长度itr = length(xn);elseif nargin == 5 % 5个时满⾜M<itr<length(xn)if itr>length(xn) | itr<Merror('迭代次数过⼤或过⼩!');endelseerror('请检查输⼊参数的个数!');end% 初始化参数en = zeros(itr,1); % 误差序列,en(k)表⽰第k次迭代时预期输出与实际输⼊的误差W = zeros(M,itr); % 每⼀⾏代表⼀个加权参量,每⼀列代表-次迭代,初始为0% 迭代计算for k = M:itr % 第k次迭代x = xn(k:-1:k-M+1); % 滤波器M个抽头的输⼊y = W(:,k-1).' * x; % 滤波器的输出en(k) = dn(k) - y ; % 第k次迭代的误差% 滤波器权值计算的迭代式W(:,k) = W(:,k-1) + 2*mu*en(k)*x;end% 求最优时滤波器的输出序列yn = inf * ones(size(xn));for k = M:length(xn)x = xn(k:-1:k-M+1);yn(k) = W(:,end).'* x;endLMS函数的⼀个实例:%function main()close all% 周期信号的产⽣t=0:99;xs=10*sin(0.5*t);figure;subplot(2,1,1);plot(t,xs);grid;ylabel('幅值');title('it{输⼊周期性信号}');% 噪声信号的产⽣randn('state',sum(100*clock));xn=randn(1,100);subplot(2,1,2);plot(t,xn);grid;ylabel('幅值');xlabel('时间');title('it{随机噪声信号}');% 信号滤波xn = xs+xn;xn = xn.' ; % 输⼊信号序列dn = xs.' ; % 预期结果序列M = 20 ; % 滤波器的阶数rho_max = max(eig(xn*xn.')); % 输⼊信号相关矩阵的最⼤特征值mu = rand()*(1/rho_max) ; % 收敛因⼦ 0 < mu < 1/rho[yn,W,en] = LMS(xn,dn,M,mu);% 绘制滤波器输⼊信号figure;subplot(2,1,1);plot(t,xn);grid;ylabel('幅值');xlabel('时间');title('it{滤波器输⼊信号}');% 绘制⾃适应滤波器输出信号subplot(2,1,2);plot(t,yn);grid;ylabel('幅值');xlabel('时间');title('it{⾃适应滤波器输出信号}');% 绘制⾃适应滤波器输出信号,预期输出信号和两者的误差figureplot(t,yn,'b',t,dn,'g',t,dn-yn,'r');grid;legend('⾃适应滤波器输出','预期输出','误差');ylabel('幅值');xlabel('时间');title('it{⾃适应滤波器}');运⾏后的结果如下:。
基于LMS与RLS算法的自适应均衡器性能研究

滤 波 器 ,由 一 条 带 抽 头 的 延 时 线 构 成 ,抽 头 间 隔 等 于 码 元 周 期 ,
每个抽头的延时信号ห้องสมุดไป่ตู้加权送到一个相加电路汇总后输出。
用
表示自适应滤波器在
时刻 n 的权矢量,则滤波器输出信号为:
(3)
自适应均衡器根据自适应算法估计系统特性,并自动调整
滤波器权矢量 ,以达到最佳滤波效果,对未知的时变信道做
出 补 偿 。 本 文 采 用 最 小 均 方 算 法 (LMS) 和 递 推 最 小 二 乘 算 法
雷利华: 博士研究生
(RLS)自 适 应 地 更 新 均 衡 器 的 抽 头 系 数 来 跟 踪 信 道 的 变 化 。
基金项目: 基金申请人: 施浒立; 项目名称: 基于通信卫星的
卫星导航系统的基础研究和理论探索; 基金颁发部门: 科技
b.对
计算: 滤波:
(4)
误差估计:
(5)
权矢量更新:
(6)
其中, 收敛因子是用来控制稳定性和收敛速度的
步长参数。 一般为了获得较好的收敛速度与稳态性能, 通常取
(7)
其中 为接收信号功率,可在接收端进行估计得到。
3.2 递推最小二乘算法(RLS)
基 于 MMSE 准 则 的 自 适 应 算 法 目 标 在 于 使 滤 波 器 输 出 与
器具有很大的参考价值与指导意义。
参考文献
[1]胡广书.数字信号处理—— —理论、算法与实现[M].北京:清华大
学出版社,1997. [2]孙永梅,李晖.数字通信系统中自适应均衡技术的研究[J].信息
技术, 2006,No.4:53-55.
(下转第 111 页)
- 26 - 360元 /年 邮局订阅号:82-946
基于LMS算法的无线信道自适应均衡器
基于LMS 算法的无线信道自适应均衡器一、 无线衰落信道与码间干扰无线信道容易受到噪声、干扰和其他随时间变化的信道因素的影响。
其中,大尺度传播效应(large-scale propagation effects ),包括路径损耗(path loss )和阴影(shadowing )效应,这类衰落比较容易克服。
而由多径引起的小尺度传播效应(small-scale propagation effects),特别是宽带信道下的频率选择性衰落,将使接收信号产生严重的码间干扰,如果不经处理,将无法得到原始信号的精确还原。
宽带通信系统下,如果信号带宽B 远远大于相干带宽c B ,那么在间隔超过相干带宽的两个频率点上的信道幅度特性近似独立。
根据相干带宽c B 与多径信号时延扩展m T σ 的关系,码元周期1s T B ≈ 远远小于1m T cB σ= 。
因此,信道的频率选择性衰落伴随着接收信号严重的码间干扰。
无线通信系统的设计必须以合适的复杂度解决这一问题。
二、 自适应均衡器大多实用的无线通信系统都采用时域均衡作为对抗ISI 的手段。
由于无线信道是时变的,在设计接收机的时候,通常并不能精确地了解信道的冲激响应,因此,所设计的均衡器应该能根据具体的信道特性进行自适应的调整。
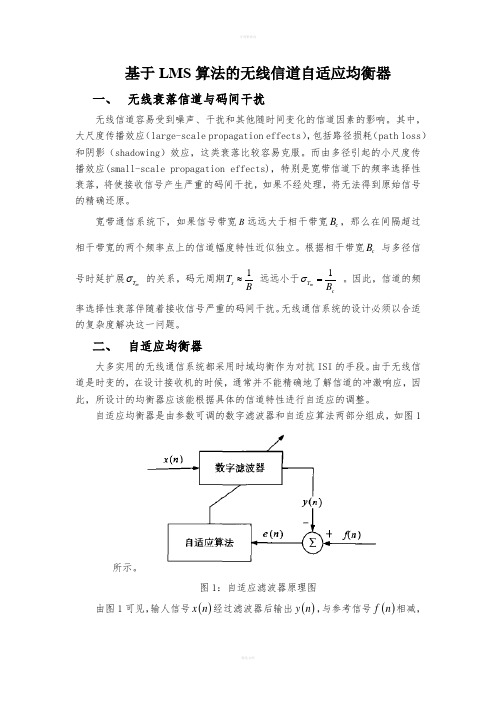
自适应均衡器是由参数可调的数字滤波器和自适应算法两部分组成,如图1所示。
图1:自适应滤波器原理图 由图1可见,输人信号()x n 经过滤波器后输出()y n ,与参考信号()f n 相减,得出误差信号()e n ,然后通过自适应算法调节滤波器系数设置,按照某种算法准则判断误差信号()e n 是否达到最小,重复以上过程,滤波器逐渐掌握了输人信号与噪声规律,通过调节滤波器系数,达到最佳的滤波效果。
参数可调数字滤波器可以是FIR(Finite-duration impulse Response)数字滤波器或IIR(Infinite-duration impulse Response)数字滤波器,也可以是格形数字滤波器。
基于LMS算法的自适应对消器的MATLAB实现
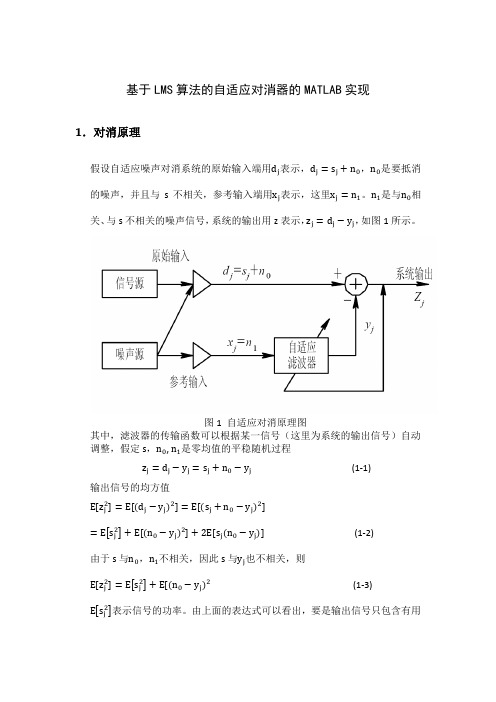
N = 5; w = ones(N,1); u = 0.0026; y = zeros(length(t),1); for k = N:length(t) y(k) = n1(k-N+1:k)'*w; e(k) = d(k) - y(k); w = w + 2*u*e(k).*n1(k-N+1:k); end
% 滤波器阶数 % 初始பைடு நூலகம்滤波器权值 % 步长因子
% 跟新权值
% 图像化仿真效果 subplot(211),plot(t,x);title('被噪声污染的正弦信号'); subplot(212),plot(t,s,'k',t,e,'g'); % 对消噪声后, 误差信号即为对原始信号的估计 legend('原始正弦信号','自适应滤波后的信号'); axis([0 1 -1 1]);title('滤波效果');
图 1 自适应对消原理图 其中,滤波器的传输函数可以根据某一信号(这里为系统的输出信号)自动 调整,假定 s,n0 , n1 是零均值的平稳随机过程 zj = dj − yj = sj + n0 − yj 输出信号的均方值 E[zj2 ] = E[(dj − yj )2 ] = E[(sj + n0 − yj )2 ] = E sj2 + E[(n0 − yj )2 ] + 2E[sj (n0 − yj )] 由于 s 与n0 ,n1 不相关,因此 s 与yj 也不相关,则 E[zj2 ] = E sj2 + E[(n0 − yj )2 (1-3) (1-2) (1-1)
E sj2 表示信号的功率。由上面的表达式可以看出,要是输出信号只包含有用
基于LMS算法的光纤信道自适应均衡器的研究

基于LMS算法的光纤信道自适应均衡器的研究王敬辉;刘剑飞;王蒙军;曾祥烨【摘要】文章分析了影响光纤通信系统性能的主要因素,介绍了在理论分析的基础上建立的单模光纤信道仿真模型;还介绍了判决反馈均衡器(DFE)的基本结构和最小均方(LMS)误差算法,并用MATLAB软件仿真了采用LMS算法对10 Gbit/s光纤信道进行自适应均衡的性能.仿真结果表明,LMS算法简单、高效,能有效消除光纤色散和偏振模色散(PMD)引起的码间干扰,比较适合对均衡速度要求较高的光纤通信系统.【期刊名称】《光通信研究》【年(卷),期】2010(000)002【总页数】3页(P10-12)【关键词】光纤;自适应均衡;色散补偿;最小均方误差【作者】王敬辉;刘剑飞;王蒙军;曾祥烨【作者单位】河北工业大学,信息工程学院,天津,300401;河北工业大学,信息工程学院,天津,300401;河北工业大学,信息工程学院,天津,300401;河北工业大学,信息工程学院,天津,300401【正文语种】中文【中图分类】TN911.5光脉冲沿光纤传播时会产生损耗和失真。
失真主要是由色散引起的,包括多模色散、波导色散、材料色散和偏振模色散(PMD)。
色散导致光纤中的光信号在传输过程中产生失真,并且这种失真会随着传输距离的增加越来越严重。
对数字光纤系统而言,色散造成光脉冲展宽,导致前后脉冲相互重叠,引起数字信号的码间干扰(ISI),造成误码率增大。
随着光纤通信系统传输速率的不断提高,色度色散(CD)和PMD成为制约高速光纤通信系统发展的主要因素。
因此,对高速率、长距离的光纤通信系统必须考虑色散补偿问题,以消除ISI。
1 单模光纤信道的仿真模型对于单模光纤,由于没有多模色散效应,光纤基带传输函数可近似为为dB/km)。
式中,S(λ)为光源频谱;L(λ)为光纤损耗;HC(λ,f)=e-j wlτ(λ),是光纤的频率响应,τ(λ)为单位长度群时延,l为光纤长度。
基于LMS的自适应滤波器典型应用的MATLAB实现

LM S 算法一般包括滤波过程和自适应过程, 这两个过程一起工作组成一个反馈环。 图 1 中, x ( n) 为输入信号, y ( n ) 为输出信号, d ( n ) 为参 考信号或期望信号 , e( n) 是 d ( n) 与 y ( n) 的误 差信号。 自适 应滤波 器的滤 波系数 受误差 信号 e( n) 控制 , 根据 e( n) 的值和自适应算法自动调 整。 推导如下: 假设 x ( n) 是一长度为 M 的序列, 由图 1 有:
e2 ( n ) =
n= 0
[ d( n) k= 0
h( k ) x ( n
- k ) ] 这个平方误差的和 是这个滤波器系数的 二次函数。 因此 , 对于滤波器系数 { h ( k) } 的 最 小化就会产生一组线性方程。 为了求解这组方程 组, 有很多种算法, L MS 算法是其中的一种。 1. 2 LM S 算法的具体步骤 LM S 算法基本上是一种递推算法, 它用任意
2
选择的{ h( k ) } 的初始值作为开始 , 然后将每一新 的输入样本{ x ( n ) } 输入到这个自适应 FIR 滤波 器, 计算相应的输出 { y ( n ) } , 形成误差信号 e( n) = d ( n) - y ( n ) , 并按方程 h n ( k ) = h n- 1 ( k ) + ! N- 1 更新滤波器系数, 这里 称为步长参数, x ( n - k ) 是输入信号在时间 n 位于滤波器的第 k 个样 本, 而 e( n ) x ( n- k) 是对第 k 个滤波器系数的一 个梯度负值的近似( 估计 ) 。 2 MAT LAB 实现 M AT L AB 有专门的函数 ADAPT L MS 实现自 适应滤波 , ADAP T LM S 函数的用法为 : [ y , e, s ] = ADAPT LM S( x , d , s) 其中 y 为滤波器的输出信号 , x 为滤波器的 输入信号 , d 为期望信号, e 为误差信号, s 为包含 构体 [ y, e, S] = adaptlms( x , d, S) ; % 自适应滤 波 st em ( [ b. ∀ , S. coeffs. ∀ ] ) ; % 画出识 别的 系统和未知系统的参数。 e( n) x ( n - k ) , 0 ! k
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第18卷 第3期Vol.18 No.3重 庆 工 学 院 学 报Journal of Chongq ing Institute of Technology2004年6月June.2004【机械与电子】基于LMS算法的自适应均衡器的MATLAB实现尹丽丽,吴跃东(江苏省淮安信息职业技术学院电子信息工程系,江苏淮安 223001)摘要:介绍了基于最小均方算法(LMS算法)的自适应均衡器的原理和结构,针对用硬件实现L MS算法的自适应均衡器存在的诸多缺点,利用MATLAB工具对各种结构形式的自适应均衡器在不同信道模型下的收敛速度和精度进行仿真,并介绍了该仿真程序。
关键词:自适应均衡器;L MS算法;MATLAB中图分类号:TN914 文献标识码:A 文章编号:1671-0924(2004)03-0061-02MATLAB Realization of Automatic AdaptiveEqualizer Based on LMS AlgorithmYIN Li-li,WU Yue-dong(Depart ment of Electronic Information Engineering,Huaian Technicaland Vocational School of Information,Huaian,223001,China)A bstract:This paper introduces the principle and structure of automatic adaptive equalizer based on LMS.As it has many dis-advantages,MATLAB tool can be used to simutate the convergence rate and precision of au kinds of automatic adaptive equaliz-er Under different informati channel madels.algorithm and the ways to realize it with MATLAB.Key words:automatic adaptive equalizer;LMS algorith m;MATLAB0 引言在一个实际的通信系统中,基带传输系统不可能完全满足理想的波形传输无失真条件,因而串扰几乎是不可避免的。
当串扰造成严重影响时,必须对整个系统的传递函数进行校正,使其接近无失真传输条件。
这种校正可以采用串接一个滤波器的方法,以补偿整个系统的幅频和相频特性。
如果这种校正是在频域进行的,称为频域均衡;如果校正是在时域里进行,即直接校正系统的冲激响应,则称为时域均衡。
随着数字信号处理理论和超大规模集成电路的发展,时域均衡正成为如今高速数据传输中所使用的主要方法。
1 系统构成及工作原理目前时域均衡的最常用方法是在基带信号接收滤波器之后插入一个横向滤波器,它由一条带抽头的延时线构成,抽头间隔等于码元周期,每个抽头的延时信号经加权送到一个相加电路汇总后输出,其形式与有限冲激响应滤波器(FIR)相同,如图1所示。
横向滤波器的相加输出经抽样送往判决电路。
每个抽头的加权系数分别为W-N,W-N+1,…,W N,输入波形的抽样值序列为{X k},输出波形的抽样值序列为{Y k},则y k=∑Ni=-NW i X k-i,k=-2N,……,2N。
横向滤波器的特征完全取决于各抽头系数,而抽头系数的调整有两种方法:手工调整和自动调整。
如果接收端知道信道的特性,包括信道冲激响应或频率响应,一般采用比较简单的手动调整方式。
由于无线通信信道具有随机性和时变性,即信道特性事是未知的,信道响应是时变的,这就要求均衡器必须能够实时地跟踪无线通信信道的时变特性,可以根据信道响应自动调整抽头系数,我们称这种可以自动调整滤波器抽头系数的均衡器为自适应均衡器。
收稿日期:2003-11-03作者简介:尹丽丽(1975-),女,安徽人,主要从事电子设计自动化教育与研究.图1 横向滤波器 由于自适应均衡器是对未知的时变信道做出补偿,因而它需要有特别的算法来更新均衡器的抽头系数去跟踪信道的变化。
LMS 算法的判据是最小均方误差,即理想信号d (n )与滤波器输出y (n )之差e (n )的平方值的期望值最小,并且根据这个判据来修改权系数W i (n ),所以被称为最小均方算法(LMS )。
令N 阶FIR 滤波器的抽头系数为W i (n ),滤波器的输入和输出分别为x (n )和y (n ),则FIR 横向滤波器方程可表示为:y (n )=∑Ni =-1W i (n )X (n -i )误差信号:e (n )=d (n )-y (n )可以利用最优化方法中的最速下降法求最佳权系数向量的近似值。
最速下降法,即“下一时刻”权系数向量W (n +1)应该等于“现时刻”权系数向量W (n )加上一个负均方误差梯度- (n )的比例项,即:W (n +1)=W (n )-μ (n )μ为控制收敛速度与稳定性的常数,称之为收敛因子。
按照近似方法,直接取e 2(n )作为均方误差E [e 2(n )]的估计值,即(n )= [e 2(n )]=2e (n ) [e (n )]又 [e (n )]= [d (n )-W T(n )X (n )]=-X (n )所以(n )=-2e (n )X (n )于是W (n +1)=W (n )+2μe (n )X (n )则自适应均衡器的框架图如图2所示:2 MATLAB 实现由于用硬件实现L MS 算法的自适应均衡器存在功率消耗和体积上都较大,实现起来复杂,升级困难等缺点,而MATLAB 具有丰富的库函数,语法简单,编程效率高等优点。
利用MATLAB 工具可以对不同的信道模型进行仿真,并对各种结构形式自适应算法的均衡器在不同信道模型下的收敛速度和精度进行仿真。
基于LMS 算法自适应均衡器的MA TL AB 仿真的程序如下:; y (n )=SU Mw (k )*n (n -k ) k =0,1,2,……,63图2 三抽头LMS 算法自适应均衡 ;; e (n )=d (n )-y (n );; w (k +1)=w (k )+2μ*e (n )* k =0,1,2, (63);仿真时采用的参数如下:;isi =[0.28,1,0.28]; %ISI 信道参数;order =63;%滤波器阶数;snr =30;%AWGN 信道信噪比;len =1000;%训练序列长度;mu =0.02;%调整步长;************************M =(order -1)/2;N =len +length (is i )-1e =zeros (1,N );error =e ;out =zeros (1,N );%FIR 滤波器输出mumber =0;fori =1:100 n =s ign (rang (1,l en )-0.5);%采用P N 码作为训练序列 noise =randn (1,N )/10. (snr /10) ; %加入A WGN(下转第69页)62重庆工学院学报5 结束语通信网的最终目标是实现无论任何人(Whoever)、在任何时间(Whenever)和任何地方(Wherever)、以任何通信方式(Whatever)与世界上的任何人(Whoever)进行通信,即所谓的“5W”,这就是个人通信。
个人通信将各类通信业务与人联系起来,通过各种终端设备随时随地为个人提供各种通信服务。
而实现个人通信的关键技术之一就是要建立发达的智能网。
No.7信令是开放式的模块式结构,它在智能网的交换通信中起着非常重要的作用。
No.7信令不仅仅在智能网、移动智能网中得到广泛应用,而且被应用到IP 业务、ISDN业务以及未来的第三代移动通信。
要检测和维护好未来的这些通信网络,重要的就是要检测对网络高质量运行起神经控制作用的No.7信令,关键技术之一就是要开发出适合中国国情的信令测试仪。
参考文献:[1] 糜正琨,陈锡生.七号公路信令系统[M].北京:人民邮电出版社,1996.16-20.[2] 杨晋儒,吴立贞.No.7信令系统技术手册[Z].北京:人民邮电出版社,2001.[3] 盛友招.现代交换技术[M].北京:机械工业出版社,2003.[4] 元兆瑞,杨放春.基于INAP的智能业务形式化描述和冲突检测[J].通信学报,2001,22(2):87-92.(责任编辑 彭 熙)(上接第62页) y=c onv(is i,x)+noise; wk=zeros(1,order); for n=order:N-M+1 %LMS算法 y1=y(n+M-1:-1:n-m-1); d1=wk*y1'; e(n)=x(n-2)-d1; wk=wk+mu*e(n)*y1; e(n)=10*log10(ads(e(n))); end error=error+eenderror=error(order:N-M+1)/100; %误差4 结束语自适应均衡器被广泛应用于数字通信系统中,而基于LMS算法的自适应均衡器无论是设计还是实现都较为简单,利用MAT-LAB软件来实现,还可以克服硬件电路的成本高、升级困难等缺点,给系统的设计带来很大的方便。
参考文献:[1] Adward B M.高会生译.MATLAB原理与工程应用[M].北京:电子工业出版社,2002.[2] 王金龙.无线通信系统的D SP实现[M].北京:人民邮电出版社,2002.[3] Adrian B.MATLAB for engineers[M].U SA:Addis on WesleyLong-man Inc,2002.[4] 曹志刚,钱亚生.现代通信原理[M].北京:清华大学出版社,1992.[5] 樊昌信.通信原理[M].北京:国防工业出版社,1995.(责任编辑 彭 熙)69董宏成,等:No.7信令在智能网(I N)中的应用。
