中考函数例题4:二次函数综合题将军饮马与切割法求最大面积
2022年中考数学复习专题 将军饮马模型解答题

将军饮马模型解答题1.问题背景:如图()a ,点B A 、在直线l 的同侧,要在直线l 上找一点C ,使AC 与BC 的距离之和最小,我们可以作出点B 关于l 的对称点B ',连接B A '与直线l 交于点C ,则点C 即为所求.(1)实践运用:如图()b ,已知,⊙O 的直径CD 为4,点A 在⊙O 上,︒=∠30ACD ,B 为弧AD 的中点,P 为直径CD 上一动点,则AP BP +的最小值为(2)知识拓展:如图()c ,在ABC Rt ∆中,10=AB ,︒=∠45BAC ,BAC ∠的平分线交BC 于点F E D 、、分别是线段AD 和AB 上的动点,求EF BE +的最小值,并写出解答过程.2.如图已知GH EF //,EF AC ⊥于点C ,EF BD ⊥于点D 交HG 于点K .3=AC ,2=DK ,4=BK .()1若6=CD ,点M 是CD 上一点,当点M 到点A 和点B 的距离相等时,求CM 的长; ()2若213=CD ,点P 是HG 上一点,点Q 是EF 上一点,连接QB PQ AP ,,,求QB PQ AP ++的最小值.3.边作等边BDE ∆,连接AD ,CD .(1)求证:ADE CDB ∆≅∆;(2)若BC AC 边上找一点H ,使得BH EH +最小,并求出这个最小值.4.如图,将一副直角三角板拼放在一起得到四边形ABCD ,其中︒=∠45BAC ,︒=∠30ACD ,点E 为CD 边上的中点,连接AE ,将ADE ∆沿AE 所在直线翻折得到E AD '∆,E D '交AC 于F 点.若cm AB 26=.(1)AE 的长为 cm ;(2)试在线段AC 上确定一点P ,使得EP DP +的值最小,并求出这个最小值;(3)求点'D 到BC 的距离.5.如图,在正方形ABCD 中,点E ,F 分别是边AD ,BC 的中点,连接DF ,过点E 作DF EH ⊥,垂足为H ,EH 的延长线交DC 于点G .(1)猜想DG 与CF 的数量关系,并证明你的结论;(2)过点H 作CD MN //,分别交AD ,BC 于点M ,N ,若正方形ABCD 的边长为10,点P 是MN 上一点,求PDC ∆周长的最小值.6.且2==DE BF .连接AE ,AF ,CE ,CF .(1)求证:四边形AECF 是菱形;(2)求四边形AECF 的面积;(3)如果M 为AF 的中点,P 为线段EF 上的一动点,求PM PA +的最小值.7.已知菱形OBCD 在平面直角坐标系中位置如图所示,点B 的坐标为)0,2(,︒=∠60DOB .(1)点D 的坐标为 ,点C 的坐标为 ;(2)若点P 是对角线OC 上一动点,点)3,0(-E ,求PB PE +的最小值.8.如图,在平面直角坐标系xoy 中,已知直线的解析式为,直线交轴于点,交轴于点.(1)若一个等腰直角三角形的顶点与点重合,直角顶点在第一象限内,请直接写出点的坐标;(2)过点作轴的垂线,在上是否存在一点,使得的周长最小?若存在,请求出点的坐标;若不存在,请说明理由.AC 22.1+-=x y AC x C y A OBD D C B B x l l P AOP ∆P9.在平面直角坐标系中,矩形OACB 的顶点O 在坐标原点,顶点B A 、分别在,x 轴、y 轴的正半轴上,()03,A ,()40,B ,D 为边OB 的中点. (1)若E 为边OA 上的一个动点,求△CDE 的周长最小值;(2)若F E 、为边OA 上的两个动点,且1=EF ,当四边形CDEF 的周长最小时,求点F E 、的坐标.10.如图,在矩形OABC 中,已知A ,C 两点的坐标分别为()0,4A ,()2,0C ,D 为OA 的中点.设点P 是AOC ∠平分线上的一个动点(不与点O 重合).(1)试证明:无论点P 运动到何处,PC 总与PD 相等;(2)当点P 运动到与点B 的距离最小时,求P 的坐标;(3)已知()1,1-E ,当点P 运动到何处时,PDE ∆的周长最小?求出此时点P 的坐标和PDE ∆的周长.11.一次函数b kx y +=的图象与x 、y 轴分别交于点()0,2A ()4,0B ,O 为坐标原点,线段AB OA ,的中点分别为点P D C ,,为直线OB 上一动点.(1)当点P 在直线OB 上运动时,PCD △的面积是否发生变化?请说明理由;(2)当点P 在直线OB 上运动时,PCD △的周长是否发生变化?如果发生变化,求出PCD △的最小周长及周长最小时P 点的坐标;(3)直接写出PCD △为等腰三角形时P 点的坐标;(4)直接写出PCD △为直角三角形时P 点的坐标.12.一次函数2521+-=x y 的图象与反比例函数)0(>k xk y =的图象交于B A 、两点,过点A 作x 轴的垂线,垂足为M ,AOM ∆面积为1.(1)求反比例函数的解析式;(2)在y 轴上求一点P ,使PB PA +的值最小,并求出其最小值和P 点坐标.13.如图,正方形AOCB 在平面直角坐标系xoy 中,点O 为原点,点B 在反比例函数)0(>x xk y =图象上,BOC ∆的面积为8.(1)求反比例函数的关系式;(2)若动点E 从A 开始沿AB 向B 以每秒1个单位的速度运动,同时动点F 从B 开始沿BC 向C 以每秒2个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t 表示,BEF ∆的面积用S 表示,求出S 关于t 的函数关系式;(3)当运动时间为34秒时,在坐标轴上是否存在点P ,使PEF ∆的周长最小?若存在,请求出点P 的坐标;若不存在,请说明理由.14.已知在中边的长与的长与边上的高的和为.试:(1)写出的面积与的长之间的函数解析式及自变量的取值范围;(2)当时求边上的高及此时三角形的面积;(3)当面积为(2)所求结果时,是否存在其周长最小的情形?如果存在,请求出其最小周长,如果不存在请说明理由.15.如图,抛物线522++=bx ax y 经过)0,1(-A ,)0,5(B 两点. (1)求抛物线的解析式,并直接写出抛物线的顶点坐标;(2)在抛物线的对称轴上有一点P ,使PC PA +的值最小,求点P 的坐标;(3)点M 为x 轴上一动点,在抛物线上是否存在一点N ,使以A ,C ,M ,N 四点构成的四边形为平行四边形?若存在,请直接写出N 点的坐标;若不存在,请说明理由.16.如图,直线b kx y +=交x 轴于点()0,1-A ,交y 轴于点()4,0B ,过A ,B 两点的抛物线交x 轴于另一点C .(1)直线的解析式为___________;(2)该抛物线对称轴上有一动点P ,连接PA ,PB ,若PB PA +最小值为5,求此时抛物线的解析式以及点P 坐标;(3)在(2)的条件下,在抛物线对称轴上是否存在点Q ,使ABQ ∆是等腰三角形?若存在,求出符合条件的Q 点坐标;若不存在,请说明理由.ABC ∆BC BC BC 20ABC ∆y BC x x 10=BCBC17.如图,已知抛物线()02≠++=a c bx ax y 的对称轴为1-=x ,且抛物线经过)0,1(A ,)3,0(C 两点,与x 轴交于点B .(1)求抛物线的解析式;(2)在抛物线的对称轴1-=x 上找一点M ,使点M 到点A 的距离与到点C 的距离之和最小,求此时点M 的坐标;(3)设点P 为抛物线对称轴1-=x 上的一个动点,求使BPC ∆为直角三角形的点P 的坐标.18.如图,以D 为顶点的抛物线c bx x y ++-=2交x 轴于B A 、两点,交y 轴于点C ,直线BC 的表达式为3+-=x y .(1)求抛物线的表达式;(2)在直线BC 上有一点P ,使PA PO +的值最小,求点P 的坐标;(3)在x 轴上是否存在一点Q ,使得以Q C A 、、为顶点的三角形与△BCD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由.19.如图,抛物线)(042≠-+=a bx ax y 与x 轴交于)0,4(A )0,1(-B 两点,过点A 的直线4+-=x y 交抛物线于点C .(1)求此抛物线的解析式;(2)在直线AC 上有一动点E ,当点E 在某个位置时,使BDE △的周长最小,求此时E 点坐标;(3)当动点E 在直线AC 与抛物线围成的封闭线A D B C A →→→→上运动时,是否存在使BDE △为直角三角形的情况,若存在,请直接写出符合要求的E 点的坐标;若不存在,请说明理由.20.如图,已知抛物线83212-+=x x y 的图象与x 轴交于A ,B 两点(点A 在点B 的右侧),与y 轴交于点C .(1)求直线BC 的解析式;(2)点F 是直线BC 下方抛物线上的一点,当BCF △的面积最大时,在抛物线的对称轴上找一点P ,使得BFP △的周长最小,请求出点F 的坐标和点P 的坐标;(3)在(2)的条件下,是否存在这样的点),0(m Q ,使得BFQ △为等腰三角形?如果有,请直接写出点Q 的坐标;如果没有,请说明理由.21.如图,直线343+=x y 分别与x 轴, y 轴交于点A , B ,抛物线122++-=x x y 与y 轴交于点C . 若点E 在抛物线122++-=x x y 的对称轴上移动,点F 在直线AB 上移动,求EF CE +的最小值.22.如图,已知抛物线经过点)(3,2-B ,原点O 和x 轴上一点另一点A ,它的对称轴与x 轴交于点)(0,2C .(1)求此抛物线的函数解析式(2)连接CB ,在抛物线的对称轴上找一点E ,使得CE CB =,求点E 的坐标(3)在(2)的条件下,连接BE ,设BE 的中点为G ,在抛物线的对称轴上是否存在一点P ,使得PBG △的周长最小,若存在,求出点P 的坐标,若不存在,请说明理由.23.如图,在平面直角坐标系中,一次函数432+-=x y 的图像与x 轴和y 轴分别相交于B A 、两点.动点P 从点A 出发,在线段AO 上以每秒3个单位长度的速度向点O 作匀速运动,到达点O 停止运动.点A 关于点P 的对称点为点Q ,以线段PQ 为边向上作正方形PQMN .设运动时间为t 秒.(1)当31t =秒时,点Q 的坐标是______; (2)在运动过程中,设正方形PQMN 与△AOB 重叠部分的面积为S ,求S 与t 的函数表达式;(3)若正方形PQMN 对角线的交点为T ,请直接写出在运动过程中PT OT +最小值.24.如图,矩形ABCD 中,6AB cm =,8BC cm =,动点E 从点A 出发,沿AC 向点C 运动,速度为1/cm s ,点E 到达点C 时停止运动,连接DE 并延长交矩形ABCD 的边于点F .点M 与点C 重合,MN DF ⊥于点H 交矩形的边AD 于点N .设点E 运动的时间为()t s .(1)当点F 到达点B 时,求t 的值;(2)当2t =时,求ND 的长;(3)如图2,点M 从点C 开始沿CD 边向点D 运动,速度为1/cm s ,且与点E 同时开始运动,当点M 停止运动时,点E 也停止运动,其他条件不变.①连接FM ,点Q 为FM 的中点,点P 在CD 边上,4CP cm =,请直接写出点F 从点A 运动到点B 的过程中,PQC ∆周长的最小值;②当13EF ED =时,请直接写出线段ND 的长.25.如图,(2,0)B -,(0,4)C ,将BOC ∆绕原点O 顺时针旋转90︒得到DOA ∆,抛物线24y ax bx =++经过A ,B 两点.(1)求抛物线的解析式;(2)将ADO ∆以秒一个单位的速度沿x 轴向左平移,平移后的三角形记为△D O A ''',平移时间为t 秒.①当D '落在抛物线上时,求t 的值;②连接A C ',当t 为何值时,△D A C '''的周长最小?直接写出t 的值和△D A C '''周长的最小值.26.如图①,已知抛物线c bx ax y ++=2的图象经过点)3,0(A 、)0,1(B ,其对称轴为直线l :2=x ,过点A 作x AC ∥轴交抛物线于点C ,AOB ∠的平分线交线段AC 于点E ,点P 是抛物线上的一个动点,设其横坐标为m .(1)若动点P 在直线OE 下方的抛物线上,连结PE 、PO ,当m 为何值时,四边形AOPE 面积最大?当四边形AOPE 面积最大时,在抛物线对称轴直线上找一点M ,使得MP MB -的值最大,并求出这个最大值.(2)如图②,F 是抛物线的对称轴l 上的一点,在抛物线上是否存在点P 使POF △成为以点P 为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.27.阅读材料:“最值问题”是数学中的一类较具挑战性的问题.其实,数学史上也有不少相关的故事,如下即为其中较为经典的一则:海伦是古希腊精通数学、物理的学者,相传有位将军曾向他请教一个问题﹣﹣如图①,从A 点出发,到笔直的河岸l 去饮马,然后再去B 地,走什么样的路线最短呢?海伦轻松地给出了答案:作点A 关于直线l 的对称点'A ,连结B A '交l 于点P ,则B A PB PA '=+的值最小.解答问题:(1)如图,已知菱形ABCD 的边长为12, 60=∠DAB .点P 为AC 线段上一动点,点E 为AD 线段上一动点,求线段PE DP +的最小值.(2)如图,已知菱形ABCD 的边长为12, 60=∠DAB .将此菱形放置于平面直角坐标系中,各顶点恰好在坐标轴上.现有一动点P 从点A 出发,以每秒2个单位的速度,沿A →C 的方向,向点C 运动.当到达点C 后,立即以相同的速度返回,返回途中,当运动到x 轴上某一点M 时,立即以每秒1个单位的速度,沿M →B 的方向,向点B 运动.当到达点B 时,整个运动停止. ①为使点P 能在最短的时间内到达点B 处,试确定点M 的位置,并说明理由.②在①的条件下,设点P 的运动时间为)(s t ,PAB ∆的面积为S ,在整个运动过程中,试求S 与t 之间的函数关系式,并指出自变量t 的取值范围.28.(1)如图1,OC 平分AOB ∠,点D 是射线OA 边上一点,点P 、Q 分别在射线OC 、OB 上运动,已知10=OD ,︒=∠30AOC ,则PQ DP +的最小值是 ;(2)如图2,在菱形ABCD 中,8=AB ,︒=∠60DAB ,点E 是AB 边上的动点,点F 是对角线AC 上的动点,求BF EF +的最小值;(3)如图3,在矩形ABCD 中,8=AB ,4=AD ,点M 是AB 上一动点,点N 是对角线AC 上一动点,请直接写出BN MN +的最小值.29.【探究问题】正的边长为,是它的高线.(1)如图(1),点、分别是正的边和高上的两个动点,求BQ +QP 的最小值;(2)如图(2),点是正高上的一动点,当为何值时,最小?并ABC ∆cm 8AD P Q ABC ∆AB AD M ABC ∆AD AM MC AM +21求出这个最小值;【解决问题】如图(3),、两地相距,是一条沿东西方向向两边延伸的一条铁路.点到的最短距离为.今计划在铁路线上修一个中转站,再在间修一条笔直的公路到地.如果同样的物资在每千米公路上的运费是铁路上的两倍.那么,为使通过铁路由到再通过公路由到的总运费达到最小值,请求出的长.(结果保留根号)30.如图1,已知抛物线2y =++与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,点D 是点C 关于抛物线对称轴的对称点,连接CD ,过点D 作DH x ⊥轴于点H ,过点A 作AE AC ⊥交DH 的延长线于点E .(1)求线段DE 的长度;(2)如图2,试在线段AE 上找一点F ,在线段DE 上找一点P ,且点M 为直线PF 上方抛物线上的一点,求当CPF ∆的周长最小时,MPF ∆面积的最大值是多少;(3)在(2)问的条件下,将得到的CFP ∆沿直线AE 平移得到△C F P ''',将△C F P '''沿C P ''翻折得到△C P F '''',记在平移过称中,直线F P ''与x 轴交于点K ,则是否存在这样的点K ,使得△F F K '''为等腰三角形?若存在求出OK 的值;若不存在,说明理由.31.如图,将边长为6的正三角形纸片ABC 按如下顺序进行两次折叠,展开后,得折痕BE AD ,(如图①),点O 为其交点.(1)探求AO 与OD 的数量关系,并说明理由;(2)如图②,若N P ,分别为BC BE ,上的动点.①当PD PN +的长度取得最小值时,求BP 的长度;②如图③,若点Q 在线段BO 上,1=BQ ,则PD NP QN ++的最小值=.A B km 100AC B AC km 60AC M BM B A M M BAM32.已知,如图,二次函数()0322≠-+=a a ax ax y 图象的顶点为H ,与x 轴交于B A 、两点,点B H 、关于直线l :333+=x y 对称. (1)求B A 、两点坐标,并证明点A 在直线l 上;(2)求二次函数表达式;(3)过点B 作直线BK ∥AH 交直线l 于K 点,N M 、分别为直线AH 和直线l 上的两个动点,连接MK NM NH 、、,求MK NM NH ++的最小值.33.如图,抛物线44y 2+-=x x 与y 轴交于点A ,B 是OA 的中点.一个动点G 从点B 出发,先经过x 轴上的点M ,再经过抛物线对称轴上的点N ,然后返回到点A .如果动点G 走过的路程最短,请找出点M 、N 的位置,并求最短路程.34.如图1,抛物线)0(y 2≠++=a c bx ax 的顶点为)4,1(C ,交x 轴于B A 、两点,交y 轴于点D ,其中点的坐标B 为()0,3.(1)求抛物线的解析式;(2)如图2,过点A 的直线与抛物线交于点E ,交y 轴于点F ,其中点E 的横坐标为2,若直线PQ 为抛物线的对称轴,点G 为直线PQ 上的一动点,则X 轴上是否存在一点F H G D 、、、,使四点所围成的四边形周长最小?若存在,求出这个最小值及点H G 、的坐标;若不存在,请说明理由.35.如图,甲、乙两个单位分别位于一条封闭式街道的两旁,现准备合作修建一座过街天桥.问:(1)桥建在何处才能使由甲到乙的路线最短?(注:桥必须与街道垂直).(2)桥建在何处才能使甲、乙到桥的距离相等?36.如图,二次函数x x y 42-=的图象与x 轴,直线y =x 的一个交点分别为点A .B ,CD 是线段OB 上的一动线段,且22=CD ,过点C .D 的两直线都平行于y 轴,与抛物线相交于点F ,E ,连接EF .(1)点A 的坐标为 ,线段OB 的长= ;(2)设点C 的横坐标为m ,①当四边形CDEF 是平行四边形时,求m 的值;②连接AC .AD ,求m 为何值时,△ACD 的周长最小,并求出这个最小值.37.已知平面直角坐标系中,A B 、两点的坐标分别为)3,2(-、)1,4(-.(1)若0P x (,)是x 轴上的一个动点,当PAB △的周长最短时,求x 的值; (2)若030C a D a +(,),(,)是x 轴上的两个动点,当四边形ABDC 的周长最短时,求a 的值.38.已知点()4,3A ,点B 为直线1-=x 上的动点,设()y B ,1.(1)如图1,若点()0,x C 且31<<x -,AC BC ⊥,求y 与x 之间的函数关系式; (2)在(1)的条件下,y 是否有最大值?若有,请求出最大值;若没有,请说明理由;(3)如图2,当点B 的坐标为)1,1(-时,在x 轴上另取两点F E ,,且1=EF .线段EF 在x 轴上平移,线段EF 平移至何处时,四边形ABEF 的周长最小?求出此时点E 的坐标.40.如图,平面直角坐标系中,直线83+=x y 分别交x 轴,y 轴于B A ,两点,点C 为OB 的中点,点D 在第二象限,且四边形AOCD 为矩形.(1)直接写出点B A ,的坐标,并求直线AB 与CD 交点E 的坐标;(2)动点P 从点C 出发,沿线段CD 以每秒1个单位长度的速度向终点D 运动;同时,动点N 从点A 出发,沿射线AO 以每秒2个单位长度的速度运动,当点C 到达D 点时,两点同时停止运动.过点P 作PH OA ⊥,垂足为H ,连接NP ,设点P 的运动时间为t 秒.①是否存在NPH △的面积为4,如果存在,请说明理由;②点Q 是点B 关于点A 的对称点,问HQ PH BP ++是否有最小值?如果有,求出相应的点P 的坐标;如果没有,请说明理由.41.如图,对称轴为直线2=x 的抛物线经过)0,1(-A ,)5,0(C 两点,与x 轴另一交点为B .已知)1,0(M ,)0,(a E ,)0,1(+a F ,点P 是第一象限内的抛物线上的动点.(1)求此抛物线的解析式;(2)当1=a 时,求四边形MEFP 的面积的最大值,并求此时点P 的坐标;(3)若PCM △是以点P 为顶点的等腰三角形,求a 为何值时,四边形PMEF 周长最小?请说明理由.42.如图1,已知抛物线1(2)()(0)y x x a a a=-+>与x 轴从左至右交于A ,B 两点,与y 轴交于点C .(1)若抛物线过点5(1,)4T -,求抛物线的解析式;(2)在第二象限内的抛物线上是否存在点D ,使得以A 、B 、D 三点为顶点的三角形与ABC ∆相似?若存在,求a 的值;若不存在,请说明理由.(3)如图2,在(1)的条件下,点P 的坐标为(1,1)-,点(6,)Q t 是抛物线上的点,在x 轴上,从左至右有M 、N 两点,且2MN =,问MN 在x 轴上移动到何处时,四边形PQNM 的周长最小?请直接写出符合条件的点M 的坐标.43.如图,已知在平面直角坐标系xoy 中,直角梯形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,2==AB OA ,3=OC ,过点B 作BC BD ⊥,交OA 于点D .将DBC ∠绕点B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于点E 和F .(1)求经过A 、B 、C 三点的抛物线的解析式;(2)当BE 经过(1)中抛物线的顶点时,求CF 的长;(3)在抛物线的对称轴上取两点P 、Q (点Q 在点P 的上方),且1=PQ ,要使四边形BCPQ 的周长最小,求出P 、Q 两点的坐标.44.如图,已知点()84-,A 和点()n ,2B 在抛物线2ax y =上. (1)求a 的值及点B 关于x 轴对称点P 的坐标,并在x 轴上找一点Q ,使得QB AQ +最短,求出点Q 的坐标;(2)平移抛物线2ax y =,记平移后点A 的对应点为A ',点B 的对应点为B ',点()0,2-C 和点()0,4-D 是x 轴上的两个定点.①当抛物线向左平移到某个位置时,B C C A '+'最短,求此时抛物线的函数解析式;②当抛物线向左或向右平移时,是否存在某个位置,5使四边形CD B A ''的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.45.在平面直角坐标系中,已知点()0,2-A ,点()4,0B ,点E 在OB 上,且OBA OAE ∠=∠.(1)如图①,求点E 的坐标;(2)如图②,将AEO △沿x 轴向右平移得到'''O E A △,连接B A '、'BE .①设m '=AA ,其中2m 0<<,试用含m 的式子表示22''BE B A +,并求出使22''BE B A +取得最小值时点'E 的坐标;②当''BE B A +取得最小值时,求点'E 的坐标(直接写出结果即可).46.在菱形中,cm AB 8=,︒60=ABC ∠,点E ,F 分别是BC ,CD 上的动点(不与B ,C ,D 重合),连接AE ,AF .(1)如图1,若CF CE =,求证:AE =AF .(2)如图2,若BC DF BE =+.①AE 与AF 是否相等?并说明理由;②四边形AECF 的面积是2cm .(3)点E 从点B 出发以每秒3cm 的速度沿BC 方向向点C 匀速运动,同时点F 从点D出发以每ABCD秒cm 2的速度沿DC 方向向点C 匀速运动,当其中一点到达终点时另一个点也随之停止运动,又知点P 是ABC ∠平分线上一点,连接EP ,FP ,当FP EP +的值最小时,CE 的长是cm .47.如图,在平面直角坐标系中,抛物线234322+--=x x y 与x 轴交于C B 、两点,与y 轴交于点A ,抛物线的顶点为D .(1)填空:点A 的坐标为;点B 的坐标为;点D 的坐标为;(2)点P 是线段BC 上的动点(点P 不与点C B 、重合).①过点P 作x 轴的垂线交抛物线于点E ,若PC PE =,求点E 的坐标;②在①的条件下,点F 是坐标轴上的点,且点F 到EA 和ED 的距离相等,请直接写出线段EF 的长;③若点Q 是线段AB 上的动点(点Q 不与点B A 、重合),点R 是线段AC 上的动点(点R 不与点C A 、重合),请直接写出PQR △周长的最小值.48.如图,锐角中,,,的面积为.()若点在边上且,,分别为边,上的动点.求PDE △周长的最小值;()假设一只小羊在区域内,从路边某点出发跑到水沟边喝水,然后跑向路边吃草,再跑回出发点处休息,直接写出小羊所跑的最短路程.ABC ∆︒=∠30ACB 5=AB ABC ∆231P AB 103=CP D E AC BC 2ABC ∆AB AC BC49.如图,在直角坐标系中,已知点()10,A ,()44-,B 将点B 绕点A 顺时针方向旋转︒90到点C ,顶点在坐标原点的拋物线经过点B .(1)求抛物线的解析式和点C 的坐标;(2)抛物线上一动点P ,设点P 到x 轴的距离为1d ,点P 到点A 的距离为2d ,试说明112+=d d ;(3) 在(2)的条件下,请探究当点P 位于何处时,△PAC 的周长有最小值,并求出的△PAC 周长的最小值50.如图1,抛物线c bx x y ++-=232,与x 轴交于点A ())0,2(,0,3-B 两点,与y 轴交于点C ,连接AC .(1)求抛物线的解析式;(2)如图2,动点Q 在第一象限的抛物线上运动,连接QO 交线段AC 于点E ,过点A 作直线y AF ∥轴,点F 在x 轴上方,且满足CE AF =.①当AEF ∆是直角三角形时,求线段AF 的长;OE 的值最小时,直接写出线段AF的长.②当OF。
部编数学九年级上册专题13二次函数中的将军饮马(解析版)含答案
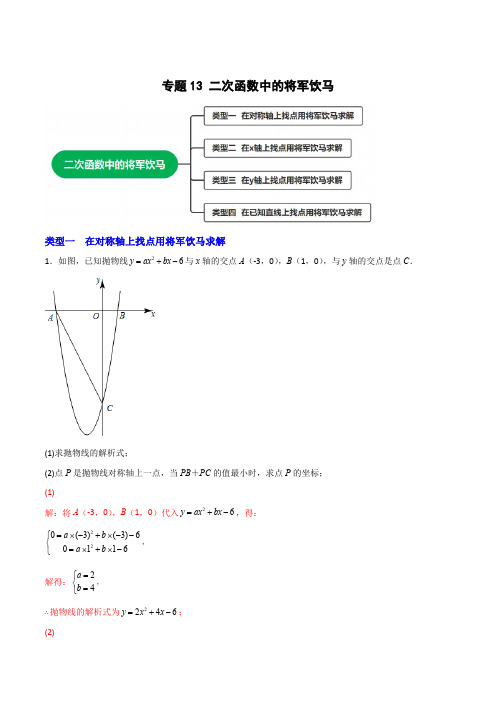
专题13 二次函数中的将军饮马类型一 在对称轴上找点用将军饮马求解1.如图,已知抛物线26y ax bx =+-与x 轴的交点A (-3,0),B (1,0),与y 轴的交点是点C .(1)求抛物线的解析式;(2)点P 是抛物线对称轴上一点,当PB +PC 的值最小时,求点P 的坐标;(1)解:将A (-3,0),B (1,0)代入26y ax bx =+-,得:220(3)(3)60116a b a b ì=´-+´--í=´+´-î,解得:24a b =ìí=î,∴抛物线的解析式为2246y x x =+-;(2)解:∵点P 是抛物线对称轴上一点,∴PA PB =,∴++PB PC PA PC AC =³,∴连接AC ,AC 与对称轴的交点即为点P ,如图.∵对于2246y x x =+-,令0x =,则6y =-,∴C (0,-6),设直线AC 的解析式为(0)y kx b k =+¹,∴036k bb =-+ìí-=î,解得:26k b =-ìí=-î,∴直线AC 的解析式为26y x =--.∵抛物线对称轴为4122x =-=-´,∴对于26y x =--,令1x =-,则2(1)64y =-´--=-,∴P (-1,-4);2.如图,抛物线y =ax 2+bx +c 经过点A (﹣3,0),B (1,0),C (0,﹣3)(1)求抛物线的解析式;(2)若点P为抛物线对称轴上一点,求△PBC周长取得最小值时点P的坐标;(1)由于抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),可设抛物线的解析式为:y=a(x+3)(x﹣1),将C点坐标(0,﹣3)代入,得:a(0+3)(0﹣1)=﹣3,解得a=1,则y=(x+3)(x﹣1)=x2+2x﹣3,所以抛物线的解析式为:y=x2+2x﹣3;(2)如图1中,连接AC交对称轴于P,∵PB=PA,∴PB+PC=PB+PA,∴此时PB+PC最短,△PBC的周长最短,设直线AC解析式为y=kx+b,则330bk b=-ìí-+=î.解得13kb=-ìí=-î,∴直线AC解析式为y=﹣x﹣3,∵对称轴为直线x=﹣1,∴当x=﹣1时,y=−2,∴点P坐标(﹣1,﹣2).3.如图,已知抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2;(1)求抛物线的函数表达式;(2)如果抛物线的对称轴上存在一点P,使得△APC周长的值最小,求此时P点坐标及△APC周长;试题解析:(1)∵AB=2,对称轴为直线x=2,∴点A的坐标为(1,0),点B的坐标为(3,0),∵抛物线y=x2+bx+c与x轴交于点A,B,∴1,3是方程x2+bx+c=0的两个根,由根与系数的关系,得1+3=﹣b,1×3=c,∴b=﹣4,c=3,∴抛物线的函数表达式为y=x2﹣4x+3.(2)连接AC,BC,BC交对称轴于点P,连接PA,如图1,由(1)知抛物线的函数表达式为y=x2﹣4x+3,点A,B的坐标分别为(1,0),(3,0),∴点C的坐标为(0,3),∴,.∵点A,B关于对称轴直线x=2对称,∴PA=PB,∴PA+PC=PB+PC,此时,PB+PC=BC,∴当点P在对称轴上运动时,PA+PC的最小值等于BC,∴△APC周长的最小值.4.如图,抛物线y=ax2+bx+c与x轴相交于点A(-3,0),B(1,0),与y轴交于点C(0,3),点D为抛物线的顶点.(1)直接写出抛物线的函数表达式;(2)如图,抛物线的对称轴上是否存在点F,使得△BCF周长最小,若存在求点F坐标,并求周长的最小值;若不存在,请说明理由;解:(1)将A(-3,0),B(1,0),C(0,3)代入y=ax2+bx+c得:0=933a b ca b cc-+ìï=++íï=î,解得: 123a b c =-ìï=-íï=î所以抛物线的函数表达式: y =-x 2-2x +3(2)存在;∵抛物线的解析式为:y =-x 2-2x +3,∴抛物线的对称轴x =-1,C (0,3),∴ C 1 (-2,3),设直线BC 1的解析式为:y=kx+b ,∵B (1,0),∴320k b k b =-+ìí=+î 解得11k b =-ìí=î,∴ 直线BC 1的解析式为:y=-x+1 ,把x =-1代入直线BC 1的解析式y=-x+1,得y=2,∴F (-1,2);∴CF ==CB ==FB ==∴CBF C CF CB FB D =++=类型二 在x 轴上找点用将军饮马求解5.已知抛物线2(1)3(0)y a x a =--¹的图象与x 轴交于点A 、B (A 在B 的左侧),与y 轴交于点(0,2)C -,顶点为D .(1)试确定a 的值,并直接写出D 点的坐标.(2)试在x 轴上求一点P ,使得PCD V 的周长取最小值.试题解析:(1)∵图像过C 点(0,2)-,∴32a -=-,∴1a =,∴2(1)3y x =--,∴:(1,3)D -.(2)如图,∵PCD C PC CD PD =++V ,∵min ()PC PD PC PD C D ¢¢+=+==,CD =,∴min PCD C =V 6.如图,直线y =﹣x+3与x 轴、y 轴分别交于B 、C 两点,抛物线y =﹣x 2+bx+c 经过B 、C 两点,与x 轴另一交点为A ,顶点为D .(1)求抛物线的解析式;(2)在x 轴上找一点E ,使△EDC 的周长最小,求符合条件的E 点坐标;【详解】(1)直线y=﹣x+3与x 轴、y 轴分别交于B 、C 两点,令x=0,则y=3,令y=0,则x=3,∴点B 、C 的坐标分别为(3,0)、(0,3),将点B 、C 的坐标代入二次函数表达式得:9303b c c -++=ìí=î,解得:23b c =ìí=î,故函数的表达式为:y=﹣x 2+2x+3;(2)如图1,作点C 关于x 轴的对称点C′,连接CD′交x 轴于点E ,此时EC+ED 为最小,则△EDC 的周长最小,令x=0,则﹣x 2+2x+3=0,解得:1213x x =-=,,∴点A 的坐标为(-1,0),∵y=﹣x 2+2x+3()214x =--+,∴抛物线的顶点D 的坐标为(1,4),则点C′的坐标为(0,﹣3),设直线C′D 的表达式为y kx b =+,将C′、D 的坐标代入得43k b b +=ìí=-î,解得:73k b =ìí=-î,∴直线C′D 的表达式为:y=7x ﹣3,当y=0时,x=37,故点E 的坐标为(37,0);7.已知二次函数图象的顶点坐标为M (1,0),直线y =x +m 与该二次函数的图象交于A ,B 两点,其中A 点的坐标为(3,4),B 点在y 轴上.(1)求m 的值及这个二次函数的解析式;(2)在x 轴上找一点Q ,使△QAB 的周长最小,并求出此时Q 点坐标;解:(1)设抛物线的解析式为y=a(x-1)2,∵点A(3,4)在抛物线上,则4=a(3-1)2,解得a=1,∴抛物线的解析式为y=(x-1)2,∵点A(3,4)也在直线y=x+m ,即4=3+m ,解得m=1;(2)直线y=x+1与y 轴的交点B 的坐标为B(0,1),B 点关于x 轴的对称点B′点的坐标为B′(0,-1),设直线AB′的解析式为y=kx+b ,将A 、B′两点坐标代入y=kx+b ,得341k b b +=ìí=-î,解得k=53,b=-1,∴直线AB′的解析式为y=53x-1,当A 、Q 、B′三点在一条直线上时,AQ+BQ 的值最小,即△QAB 的周长最小,Q 点即为直线AB′与x 轴的交点,当y=0时,0=53x-1,解得x=35,Q 点坐标为Q(35,0);类型三 在y 轴上找点用将军饮马求解8.在平面直角坐标系中,抛物线212y x bx c =++经过点(4,0)A -,点M 为抛物线的顶点,点B 在y 轴上,且OA OB =,直线AB 与抛物线在第一象限交于点(2,6)C ,如图.(1)求抛物线的解析式;(2)直线AB 的函数解析式为______,点M 的坐标为______,sin ACO Ð=______.(3)在y 轴上找一点Q ,使得AMQ △的周长最小.请求出点Q 的坐标;【详解】解:(1)将点A 、C 的坐标代入抛物线表达式得:11640214262b c b c ì´-+=ïïíï´++=ïî,解得20b c =ìí=î故抛物线的表达式为:2122y x x =+;(2)点(4,0)A -,4OB OA ==,故点(0,4)B ,设直线AB 的解析式为:(),0y kx b k =+¹,044k b b =-+ì\í=î ,解得,14k b =ìí=î∴直线AB 的表达式为:4y x =+;对于2122y x x =+,函数的对称轴为221222b x a =-=-=-´,把x=2代入2122y x x =+,()()2122222y =´-+´-=-∴顶点(2,2)M --;如图,设抛物线的对称轴交AB 于点E ,连接OE ,把x=-2代入4y x =+,得y=2,(2,2)E \-,E \为线段AB 的中点,OE =,在Rt AOB V 中,OA=OB ,OE AB \^,(2,6)CQ,OC \==在Rt OCE V中,sin OE ACO OC Ð===故答案为:4y x =+;(-2,-2)9.如图,在平面直角坐标系中,抛物线y 12=x 2+bx +c 经过点A (﹣4,0),点M 为抛物线的顶点,点B 在y 轴上,且OA =OB ,直线AB 与抛物线在第一象限交于点C (2,6).(1)求抛物线的解析式;(2)直线AB 的函数解析式为 ,点M 的坐标为 ,连接OC ,若过点O 的直线交线段AC 于点P ,将△AOC 的面积分成1:2的两部分,则点P 的坐标为 ;(3)在y 轴上找一点Q ,使得△AMQ 的周长最小,则点Q 的坐标为 ;解:(1)将点A 、C 的坐标代入抛物线表达式11640214262b c b c ì´-+=ïïíï´++=ïî,解得20b c =ìí=î,故直线AB 的表达式为:y 12=x 2+2x ;(2)点A (﹣4,0),OB =OA =4,故点B (0,4),由点A 、B 的坐标得,直线AB 的表达式为:y =x +4;对于y 12=x 2+2x ,函数的对称轴为x =﹣2,故点M (﹣2,﹣2);OP 将△AOC 的面积分成1:2的两部分,则AP 13=AC 或23AC ,则1233P C y y =或,即12633P y =或,解得:yP =2或4,故点P (﹣2,2)或(0,4);(3)如图所示,作点A 关于y 轴的对称点'A ,连接'A M 与y 轴交于点Q ,连接AQ 、MQ 、AM△AMQ 的周长=AM +AQ +MQ =AM +A ′M 最小,点A ′(4,0),设直线A ′M 的表达式为:y =kx +b ,则4022k b k b +=ìí-+=-î,解得1343k b ì=ïïíï=-ïî,故直线A ′M 的表达式为:y 13=x 43-,令x =0,则y 43=-,故点Q (0,43-);10.如图,已知二次函数y =-12x 2+4x -6.(1)直接写出抛物线与坐标轴的交点坐标;(2)若抛物线的顶点为D ,在y 轴上是否存在一点P ,使得△PAD 的周长最小?若存在,求出△PAD 的周长;若不存在,请说明理由.【详解】当0x =时,与,与y 轴交于点B,140662y ´´=-=-0+-,即(0,6)B -当0y =时, 与x 轴交于点A 、E,有21462x x +0=--解得122,6x x ==,即(2,0)A 、(6,0)E 综上:(2,0)A 、(6,0)E 、(0,6)B -(2)存在.(AD 长度固定,只需找到点P 使PA PD +最小即可,找到点A 关于y 轴的对称点A ¢,连接A D ¢,则A D ¢与y 轴的交点即是点P 的位置.)∴(2,0)A ¢-,(4,2)D ,∴AD =,A D ¢=,∴PAD △周长最小值=【点睛】本题考查二次函数的运用,掌握二次函数的性质,拿出交点坐标和对称轴,结合题意,通过分析可解.类型四 在已知直线上找点用将军饮马求解11.如图,抛物线26y ax bx =+-交x 轴于(2,0),(6,0)A B -两点,交y 轴于点C (0,6)-,点Q 为线段BC 上的动点.(1)求抛物线的解析式;(2)求QA QO+的最小值;解:(1)∵抛物线交x轴于A(−2,0),B(6,0)两点,∴设y=a(x+2)(x−6),将C(0,−6)代入,得:−12a=−6,解得:a=12,∴y=12(x+2)(x−6)=12x2−2x−6,∴抛物线的解析式为y=12x2−2x−6;(2)如图1,作点O关于直线BC的对称点O′,连接AO′,QO′,CO′,BO′,∵OB=OC=6,∠BOC=90°,∴∠BCO=45°,∵O、O′关于直线BC对称,∴BC垂直平分OO′,∴OO′垂直平分BC,∴四边形BOCO′是正方形,∴O′(6,−6),在Rt△ABO′中,AO′10=,∵QA+QO′≥AO′,QO′=QO,∴QO+QA=QA+QO′≥AO′=5,即点Q位于直线AO′与直线BC交点时,QO+QA有最小值10;12.如图抛物线2y=x轴于A、B两点,交y轴于点C,顶点为D.(1)求点A、B、C、D的坐标;V绕AB的中点M旋转180°,得到四边形AEBC;(2)把ABC①求E 的坐标;②试判断四边形AEBC 的形状,并说明理由;(3)试探求:在直线BC 上是否存在一点P ,使得PAD △的周长最小,若存在,求出点P 的坐标,若不存在,请说明理由.【答案】(1)(3,0)A -,(1,0)B ,C ,(D -;(2)①(2,E -;②四边形AEBC 是矩形,理由见解析;(3)存在,3(7P -.【解析】【分析】(1)分别令x=0以及y=0求出A 、B 、C 三点的坐标,再根据二次函数表达式求出顶点D 的坐标;(2)①依题意得出BC ∥AE ,又已知A 、B 、C 的坐标易求出点E 的坐标,②根据旋转的性质证明四边形AEBC 是平行四边形,再利用勾股定理的逆定理得到∠ACB=90°,可得四边形AEBC 是矩形;(3)作点A 关于BC 的对称点A′,连接A′D 与直线BC 交于点P .则可得点P 是使△PAD 周长最小的点,然后求出直线A′D ,直线BC 的函数解析式联立方程求出点P 的坐标.【详解】解:(1)2y x =令0x =,得y =令0y =,即20=,即2230x x +-=,11x \=,23x =-,∴(-3+1)÷2=-1,将x=-1代入2y =,得A \,B ,C ,D 点的坐标分别为(3,0)A -,(1,0)B ,C ,(D -;(2)①过点E 作EF AB ^于F ,Q ,EF \=,(1,0)B Q ,1AF \=,312OF OA AF \=-=-=,(2,E \-;②四边形AEBC 是矩形.理由:∵△ABE 是由△ABC 旋转得到,∴AC=BE ,AE=BC ,∴四边形ACBE 是平行四边形,由(3,0)A -,(1,0)B ,C ,(2,E -,可知:=AB=4,2=,∴222AB AC BC =+,∴∠ACB=90°,四边形AEBC 是矩形;(3)存在.作出点A 关于BC 的对称点A ¢,连接A D ¢与直线BC 交于点P ,则点P 是使PAD D 周长最小的点,3AO =Q ,3FO \=,CO =A F \¢=,\求得(3A ¢,,过A ¢、D 的直线y +过B 、C 的直线y =两直线的交点3(7P -.【点睛】本题综合考查了二次函数的有关知识以及利用待定系数法求出函数解析式,难度中上.13.已知,如图,二次函数()2230y ax ax a a =+-¹图象的顶点为H ,与x 轴交于A 、B 两点(B 点在A 点右侧),点H 、B 关于直线l :y =对称.(1)求A 、B 两点的坐标,并证明点A 在直线l 上;(2)求二次函数解析式;(3)过点B 作直线//BK AH 交直线l 于K 点,M 、N 分别为直线AH 和直线l 上的两个动点,连结HN 、NM 、MK ,求HN+NM+MK 的最小值.【答案】【小题1】A 点坐标为(3,0)-,B 点坐标为(1,0)【小题2】2y x =【小题3】8【解析】【分析】(1)根据一元二次方程求得A点坐标,代入直线求证,(2)通过点H、B关于直线L对称,求得H的坐标,从而解出二次函数的解析式,(3)先求出HN+MN的最小值是MB, 再求出BM+MK的最小值是BQ,即++和的最小值HN NM MK【详解】(1)依题意,得ax2+2ax−3a=0(a≠0),两边都除以a得:即x2+2x−3=0,解得x1=−3,x2=1,∵B点在A点右侧,∴A点坐标为(−3,0),B点坐标为(1,0),答:A. B两点坐标分别是(−3,0),(1,0).证明:∵直线l:y x,当x=−3时,y(3)0-=,∴点A在直线l上.(2)∵点H、B关于过A点的直线l:y x对称,∴AH=AB=4,过顶点H作HC⊥AB交AB于C点,则AC=12,2AB HC==,∴顶点H(1,-,代入二次函数解析式,解得a=,∴二次函数解析式为y=答:二次函数解析式为2y(3)直线AH的解析式为y=+,直线BK的解析式为y=由yyì=ïíï=î解得xy=ìïí=ïî即K,则BK=4,∵点H、B关于直线AK对称,K,∴HN+MN的最小值是MB,过K作KD⊥x轴于D,作点K关于直线AH的对称点Q,连接QK,交直线AH于E,则QM=MK,QE=EKAE⊥QK,∴根据两点之间线段最短得出BM+MK的最小值是BQ,即BQ的长是HN+NM+MK的最小值,∵BK∥AH,∴∠BKQ=∠HEQ=90∘,由勾股定理得QB8 ==∴HN+NM+MK的最小值为8,答:HN+NM+MK和的最小值是8.【点睛】考核知识点:二次函数综合运用.14y=x轴交于点A,与y轴交于点C,抛物线y=ax2﹣+c(a≠0)经过A,B,C三点.(1)求过A,B,C三点抛物线的解析式并求出顶点F的坐标;(2)试探究在直线AC上是否存在一点M,使得△MBF的周长最小?若存在,求出M点的坐标;若不存在,请说明理由.(1)∵直线y=x轴交于点A,与y轴交于点C∴点A(﹣1,0),C(0,∵点A,∴ccìïíïî∴a c ìïíïî∴抛物线的解析式为2x y =∴顶点F (1,).(2)存在理由:延长BC 到点B ′,使B 'C =BC ,连接B 'F 交直线AC 于点M ,则点M 就是所求的点,∵过点B ′作B 'H ⊥∵B点在抛物线2y =∴B (3,0),在Rt △BOC 中,tan ∠OBC∴∠OBC =30°,BC =在Rt △B ′BH 中,B ′H =12BB ′=BH ′H =6,∴OH =3,∴B ′(﹣3,﹣.B ′F 的解析式为y =kx +b ,∴3k b k b ì-+ïí+ïî ,,∴y.y y ìïíïî,解得x y ìïïíïïî,∴M (37∴在直线AC 上存在点M ,使得△MBF 的周长最小,此时M (37.【点睛】考查代数几何的综合运用能力,体现数学知识的内在联系和不可分割的特点.15.如图,抛物线24y ax bx =++与x 轴交于A ,B 两点,与y 轴交于点C .直线2y =经过抛物线上两点D ,E .已知点D ,E 的横坐标分别为1x ,2x 且满足123x x +=,直线BC 的表达式为y x n =-+.(1)求n 的值及抛物线的表达式;(2)设点Q 是直线DE 上一动点,问:点Q 在什么位置上时,QOB △的周长最小?求出点Q 的坐标及QOB △周长的最小值;解:(1)当0x =时,抛物线244y ax bx =++=,∴C (0,4),∵点C 在直线BC 上:y x n =-+上,∴4n =,∵直线BC 与x 轴交点为B ,40x -+=,解得:4x =,∴B (4,0),∵点B 在抛物线上,∴216440a b ++= ①,∵2D E y y ==,∴//DE x 轴,点D 、E 关于抛物线对称轴对称,∵123x x +=,∴抛物线对称轴为:直线12322x x x +==,∴322b a -=②,联立方程①②,216440322a b b a ì++=ïí-=ïî,解得:13a b =-ìí=î,∴抛物线的表达式为234y x x =-++.(2)连接CQ ,如图1,∵C (0,4),点Q 是直线2y =上一动点,∴O 、C 关于直线2y =对称,∴CQ OQ =,∴当点C 、Q 、B 在同一直线上时,OQ BQ CQ BQ BC +=+=最短,当42x -+=时,解得:2x =,∴此时,Q (2,2),∵4OB OC ==,∴==BC∴QOB △周长最小值为:4QOB C OQ BQ OB BC OB =++=+=△.16.如图,抛物线2y ax bx c =++与x 轴交于()1,0A 、()4,0B ,与y 轴交于点()0,3C ,点D 为OC 的中点,点E 、F 分别为x 轴正半轴和抛物线对称轴上的动点,连接DE 、EF 、CF ,求四边形CDEF 周长最小时点E 、F 的坐标.【答案】当四边形CDEF 周长最小时,点E 的坐标5,03æöç÷èø,点F 的坐标为53,24æöç÷èø.【解析】【分析】作点D 关于x 轴的对称点D ¢,作点C 关于抛物线对称轴的对称点C ¢,连接C D ¢¢,交对称轴于点F ,交x 轴于点E .求出直线C D ¢¢的解析为93102y x =-,进一步可得出结论.【详解】如图,作点D 关于x 轴的对称点D ¢,作点C 关于抛物线对称轴的对称点C ¢,连接C D ¢¢,交对称轴于点F ,交x 轴于点E .由对称知C F CF ¢=,D E DE ¢=,\此时四边形CDEF 的周长为CD DE EF CF CD D E EF C F CD C D ¢¢¢¢+++=+++=+.\此时四边形CDEF 的周长最小,最小值为CD C D +¢¢.()1,0A Q ,()4,0B ,\抛物线对称轴为直线52x =.()5,3C ¢\.D Q 为OC 的中点,30,2D æö\ç÷èø.30,2D æö¢\-ç÷èø.设直线C D ¢¢的解析式为y kx b =+.将点C ¢、D ¢的坐标代入可得53,3,2k b b +=ìïí=-ïî解得9,103.2k b ì=ïïíï=-ïî\直线C D ¢¢的解析为93102y x =-.令0y =,则53x =,\点E 的坐标为5,03æöç÷èø.令52x =,则34y =,\点F 的坐标为53,24æöç÷èø.\当四边形CDEF 周长最小时,点E 的坐标5,03æöç÷èø,点F 的坐标为53,24æöç÷èø.【点睛】此题考查了待定系数法求函数解析式,四边形与二次函数的结合,线段的和差最值与二次函数的结合,将不共线的线段转化为共线为解题关键.。
二次函数中的最值问题(将军饮马、面积问题)

二次函数中的将军饮马及面积问题
1、如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC
的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)如果在对称轴上存在一动点E,求当四边形ACEO的面积最小时,点E的坐标;
(2)在直线BC上有一点P,使PO+P A的值最小,求点P的坐标;
(3)如果在直线BC上方抛物线上是否存在一点F,使△BCF的面积是△BCD面积的一半?如果存在,请求出。
如果不存在,请说明理由。
2、在平面直角坐标系中,直线y=x﹣2与x轴交于点B,与y轴交于点C,二次函数y=
x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
(1)求二次函数的表达式;
(2)如图,连接DC,DB,设四边形ABCD的面积为S,求S的最大值;
(3)若E是对称轴上一动点,求EB+ED的最小值.。
二次函数中面积问题的两种考法—2023-2024学年九年级数学上册(人教版)(解析版)

二次函数中面积问题的两种考法类型一、面积最值问题 例.抛物线2y x bx c =−++交x 轴于点(4,0)A ,交y 轴于点(0,4)B .(1)求抛物线的解析式,并直接写出抛物线的对称轴和另一个与x 轴交点C 的坐标;(2)直接写出当0y <时,x 的取值范围.(3)如图,点P 是线段AB 上方抛物线上一动点,当P 点的坐标为_______时,PAB 的面积最大.【答案】(1)234y x x =−++;(1,0)C −;对称轴直线32x = (2)1x <−或>4x(3)()2,2【分析】(1)用待定系数法求函数的解析式即可;(2)根据函数图象即可得出结论;(3)过点P 作PG y ∥轴交AB 于点G ,设2(,34)P t t t −++,则(,4)G t t −+,则22(2)8PAB S t =−−+,再由此求解即可.【详解】(1)将点(4,0)A ,(0,4)B 代入2y x bx c =−++,∴16404b c c −++=⎧⎨=⎩,解得34b c =⎧⎨=⎩,234y x x ∴=−++;令0y =,得2034x x =−++解得:121;4x x =−=∴(1,0)C −,(4,0)A对称轴直线322b x a =−=(2)由(1)得:(1,0)C −,(4,0)A∴当1x <−或>4x 时,0y <(3)设直线AB 的解析式为y kx m =+,∴404k m m +=⎧⎨=⎩,解得14k m =−⎧⎨=⎩,4∴=−+y x ,过点P 作PG y ∥轴交AB 于点G ,设2(,34)P t t t −++,则(,4)G t t −+,223444PG t t t t t ∴=−+++−=−+,2214(4)2(2)82PAB S t t t ∆∴=⨯⨯−+=−−+,当2t =时,PAB 的面积有最大值8,此时(2P ,2).故答案为:()2,2.【点睛】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,胡不归求最短距离的方法是解题的关键. 【变式训练1】如图,抛物线2(1)y x k =++与x 轴相交于A 、B 两点,与y 轴相交于点(0,3)C −.(1)求抛物线的对称轴及k 值;(2)抛物线的对称轴上存在一点P ,使得PA PC +的值最小,求此时点P 的坐标;(3)点M 是抛物线上一动点,且在第三象限,当M 点运动到何处时,四边形AMCB 的面积最大?求出四边形AMCB 的最大面积.【答案】(1)1,4x k =−=−(2)(1,2)P −−(3)315,24M ⎛⎫− ⎪⎝⎭,S 最大,最大值为758【分析】(1)根据解析式可得抛物线的对称轴为直线=1x −,将点(0,3)C −代入解析式,待定系数法即可求解;(2)连接AC ,交对称轴于点P ,根据两点之间,线段最短可得点P 即为所求,求得直线AC 的解析式,令=1x −,即可求解;(3)连接OM ,如图1,设M 点坐标为()2,(1)4x x +−,根据AMO CMO CBO AMCB S S S S =++四边形△△△23375228x ⎛⎫=−++ ⎪⎝⎭,根据二次函数的性质即可求解.【详解】(1)解:抛物线2(1)y x k =++的对称轴为直线=1x −,把(0,3)C −代入2(1)y x k =++得31k −=+,4k ∴=−;(2)连接AC ,交对称轴于点P ,∵两点之间,线段最短,∴PA PC +的最小值为AC 的长,则点P 即为所求对于2y (x 1)4=+−,令0y =,则2(1)40x +-=,解得11x =,23x =−,A ∴点坐标为(3,0)−,B 点坐标为(1,0),设直线AC 的关系式为:y mx b =+,把(3,0)A −,(0,3)C −代入y mx b =+,得303m b b −+=⎧⎨=−⎩,解得13m b =−⎧⎨=−⎩,∴直线AC 的关系式为3y x =−−,当=1x −时,132y =−=−,P ∴点坐标为(1,2)−−;(3)连接OM ,如图1,设M 点坐标为()2,(1)4x x +−,AMO CMO CBO AMCB S S S S =++四边形△△△111222m m AO y CO x OC BO ⨯⨯+⨯⨯+⨯⨯23114(1)3()31222x x ⎡⎤=−++⨯⨯−+⨯⨯⎣⎦239622x x =−−+23375228x ⎛⎫=−++ ⎪⎝⎭, 当32x =−时,S 最大,最大值为758.【点睛】本题考查了二次函数的性质,面积问题,轴对称的性质,熟练掌握二次函数的性质是解题的关键. 【变式训练2】如图,抛物线22y ax x c =−+与x 轴交与()1,0A ,()3,0B −两点.(1)求该抛物线的解析式; (2)设抛物线交y 轴与C 点,在该抛物线的对称轴上是否存在点Q ,使得QAC △的周长最小?若存在,求出Q 点的坐标;若不存在,请说明理由.(3)在第二象限内的抛物线上的是否存在一点P ,使PBC 的面积最大?若存在,求出点P 的坐标及PBC 的面积最大值;若不存在,请说明理由.【答案】(1)223y x x =−−+(2)存在,()1,2Q −;(3)存在,315,24P ⎛⎫− ⎪⎝⎭,PBC 的面积最大值是278【分析】(1)利用待定系数法即可求得二次函数的解析式;(2)根据题意可知,边AC 的长是定值,要想AQC 的周长最小,即是 AQ CQ +最小所以此题的关键是确定点Q 的位置,找到点A 关于对称轴的对称点B ,利用待定系数法求出直线BC 的解析式,直线BC 与对称轴的交点即是所求的点Q ;(3)首先求得BC 的坐标,然后设P 的横坐标是x ,利用a 表示出PBC 的面积,利用二次函数的性质求解;【详解】(1)根据题意得:10930b c b c −++=⎧⎨−−+=⎩,解得23b c =−⎧⎨=⎩,则抛物线的解析式是223y x x =−−+;(2)理由如下:由题知A 、B 两点关于抛物线的对称轴=1x −对称,∴直线BC 与=1x −的交点即为Q 点,此时AQC 周长最小,对于223y x x =−−+,令0x =,则3,故点()0,3C ,设BC 的解析式是y mx n =+,则303m n n −+=⎧⎨=⎩,解得13m n =⎧⎨=⎩,则BC 的解析式是3y x =+.=1x −时,132y =−+=,∴点Q 的坐标是()1,2Q −;(3)过点P 作y 轴的平行线交BC 于点D ,设P 的横坐标是x ,则P 的坐标是()2,23x x x −−+,对称轴与BC 的交点D 是(),3x x +.则()()222333PD x x x x x=−−+−+=−. 则()222139332733222228PBC S x x x x x ⎛⎫=−−⨯=−−=−++ ⎪⎝⎭△, ∵302−<,故PBC 的面积有最大值是278.【点睛】本题考查了待定系数法求函数的解析式以及二次函数的性质,求最值问题一般是转化为函数最值问题求解. (1)求二次函数的表达式;(2)如图1,求AOD △周长的最小值;(3)如图2,过动点D 作DP AC ∥交抛物线第一象限部分于点P ,连接,PA PB ,记PAD 与PBD △的面积和为S ,当S 取得最大值时,求点P 的坐标,并求出此时S 的最大值.【答案】(1)21262y x x =−++(2)12(3)153,2⎛⎫ ⎪⎝⎭,272S =最大值 【分析】(1)根据题意设抛物线的表达式为()()26y a x x =+−,将()0,6代入求解即可;(2)作点O 关于直线BC 的对称点E ,连接EC EB 、,根据点坐特点及正方形的判定得出四边形OBEC 为正方形,()6,6E ,连接AE ,交BC 于点D ,由对称性DE DO =,此时DO DA +有最小值为AE 的长,再由勾股定理求解即可;(3)由待定系数法确定直线BC 的表达式为6y x =−+,直线AC 的表达式为36y x =+,设21,262P m m m ⎛⎫−++ ⎪⎝⎭,然后结合图形及面积之间的关系求解即可.【详解】(1)解:由题意可知,设抛物线的表达式为()()26y a x x =+−, 将()0,6代入上式得:()()60206a =+−,12a =−所以抛物线的表达式为21262y x x =−++;(2)作点O 关于直线BC 的对称点E ,连接EC EB 、,∵()6,0B ,()0,6C ,90BOC ∠=︒,∴6OB OC ==,∵O 、E 关于直线BC 对称,∴四边形OBEC 为正方形,∴()6,6E ,连接AE ,交BC 于点D ,由对称性DE DO =, 此时DO DA +有最小值为AE 的长,10AE ===∵AOD △的周长为DA DO AO ++,2AO =,DA DO +的最小值为10,∴AOD △的周长的最小值为10212+=;(3)由已知点()2,0A −,()6,0B ,()0,6C ,设直线BC 的表达式为y kx b =+,将()6,0B ,()0,6C 代入y kx b =+中,600k b b +=⎧⎨=⎩,解得16k b =−⎧⎨=⎩,∴直线BC 的表达式为6y x =−+,同理可得:直线AC 的表达式为36y x =+,∵PD AC ∥,∴设直线PD 表达式为3y x a =+,由(1)设21,262P m m m ⎛⎫−++ ⎪⎝⎭,代入直线PD 的表达式得:2162a m m =−−+,∴直线PD 的表达式为:21362y x m m =−−+, 由261362y x y x m m =−+⎧⎪⎨=−−+⎪⎩,得22118411684x m m y m m ⎧=+⎪⎪⎨⎪=−−+⎪⎩,∴221111,68484D m m m m ⎛⎫+−−+ ⎪⎝⎭, ∵P ,D 都在第一象限,∴PAD PBD PAB DAB S S S S S =+=−△△△△2211112662284AB m m m m ⎡⎤⎛⎫⎛⎫=−++−−−+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 21398284m m ⎛⎫=⨯−+ ⎪⎝⎭()22339622m m m m =−+=−−2327(3)22m =−−+, ∴当3m =时,此时P 点为153,2⎛⎫ ⎪⎝⎭.272S =最大值.【点睛】题目主要考查二次函数的综合应用,包括待定系数法确定函数解析式,周长最短问题及面积问题,理解题意,熟练掌握运用二次函数的综合性质是解题关键.类型二、求面积问题 例.已知:m ,n 是方程2650x x −+=的两个实数根,且m n <,抛物线2y x bx c =−++的图象经过点(,0)(0,)A m B n ,.(1)求这个抛物线的解析式;(2)设(1)中的抛物线与x 轴的另一交点为C ,抛物线的顶点为D ,试求BCD △的面积;(3)P 是线段OC 上的一点,过点P 作PH x ⊥轴,与抛物线交于H 点,若直线BC 把PCH △分成面积之比为2:3的两部分,请求出P 点的坐标.【答案】(1)245y x x =−−+(2)15(3)点( 1.5,0)P -或2(,0)3P −【分析】(1)利用因式分解法求出一元二次方程的解,从而得到点A B ,的坐标,再代入抛物线解析式即可解答;(2)令抛物线解析式中0y =,可求得点C 坐标,利用公式法求出顶点D 的坐标,过点D 作x 轴的垂线,垂足为点E ,分别求出CDE 、梯形DEOB 、BCO 的面积,利用BCD S △=CDE S +BCO DEOB S S 梯形−解答即可;(3)先利用待定系数法求得直线BC 的解析式,再设直线BC 与PH 相交于点F ,点(,0)P a ,则点2(5),(,45)F a a H a a a +--+,,从而求得25,5PF a FH a a =+=--,最后分两种情况讨论①当:2:3PF HF =时或②当:2:3HF PF =时,分别计算解答即可.【详解】(1)解:2650x x −+=(1)(5)0x x ∴−−=10,50x x ∴−=−=1,5x x ∴==m ,n 是方程2650x x −+=的两个实数根,且m n <,1,5m n ∴==(1,0)(0,5)A B \,把点(1,0)(0,5)A B ,代入抛物线解析式得105b c c −++=⎧⎨=⎩,解得45b c =−⎧⎨=⎩,245y x x \=--+;(2)解:2245=(2)9y x x x =--+-++Q(2,9)D \-令0y =23x ∴+=±1,5x x \==-(5,0)C ∴−如图,过点D 作x 轴的垂线,垂足为点E ,(2,0)E ∴−BCD S △=CDE S +BCO DEOB S S 梯形− 1()1222OB DE OE CE DE CO BO +×=×+-× 1(59)213955222+´=´´+-´´ 27251422=+-114=+15=;(3)解:如图,设直线BC 的解析式为5y kx =+,代入点(-5,0)C 得,550k −+= 1k ∴=5BC y x \=+设直线BC 与PH 相交于点F ,点(,0)P a则点2(5),(,45)F a a H a a a +--+,225,45(5)5PF a FH a a a a a \=+=--+-+=--直线BC 把PCH △分成面积之比为2:3的两部分,分两种情况讨论: ①当:2:3PF HF =时 252=53PF a FH a a +\=--,2210315a a a \--=+2213150a a \++=1.5a ∴=−(5a =−舍去),( 1.5,0)P \-②当:2:3HF PF =时252=53HF a a PF a --\=+ 23a ∴=−,2(,0)3P \- 综上所述,点( 1.5,0)P -或2(,0)3P −.【点睛】本题考查二次函数的图象与性质,涉及待定系数法求一次函数解析式、待定系数法求二次函数解析式、配方法求二次函数顶点坐标、解析法求线段的长等知识,利用等高三角形面积比等于底边比,掌握相关知识是解题关键.(1)当1m =时,求抛物线的顶点坐标;(2)若AC BC ⊥, ①求m 的值;②点P 是x 轴上方的抛物线上的一动点,连结.设PBC 的面积为数,试求点P 的坐标. 【答案】(1)28 ⎪⎝⎭,(2)①2m =;②22P ⎛ ⎝⎭或22P ⎛ ⎝⎭或()2,3P . 【分析】(1)利用待定系数法可求解析式; (2)①根据题意得到()1,0A −,(),0B t ,()0,C m ,然后表示出22221AC OA OC m =+=+,()2222221BC OB OC m n =+=++,()2222AB n =+,根据AC BC ⊥利用勾股定理列方程求解即可;②过点P 作PH x ⊥轴于H ,交BC 于点Q ,先求出BC 的解析式,设点213,222P x x ⎛⎫−++ ⎪⎝⎭,则点1,22Q x x ⎛⎫−+ ⎪⎝⎭,由三角形面积公式可得12PBC S PG OB∆=,由二次函数的性质可求解.【详解】(1)解:∵点()1,0A −,在抛物线212y x nx m =−++图象上,1m =, ∴11021n m ⎧−−+=⎪⎨⎪=⎩,解得:121n m ⎧=⎪⎨⎪=⎩,∴抛物线解析式为:2211119122228y x x x ⎛⎫=−++=−−+⎪⎝⎭, ∴抛物线的顶点坐标为1928⎛⎫ ⎪⎝⎭,;(2)①解:当0y =时,即212x m −++=∴设(),0B t∵()1,0A −∴1212nt n −+=−=−∴21t n =+∴21OB n =+,21122AB n n =++=+ 当0x =时,y m = ∴()0,C m∴OC m =∴22221AC OA OC m =+=+,()2222221BC OB OC m n =+=++,()2222AB n =+∵AC BC ⊥∴222AC BC AB +=,∴()()222212122m m n n ++++=+∴整理得,2210m n −−=将()1,0A −代入212y x nx m =−++得,102n m −−+=可得,12n m =−,∴将12n m =−代入2210m n −−=,得212102m m ⎛⎫−−−= ⎪⎝⎭∴解得2m =或0(舍去) ∴2m =; ②∵2m =∴()0,2C ,()4,0B ,抛物线解析式为213222y x x =−++,∴设直线BC 的解析式为y kx b =+,代入B 、C 坐标得240b k b =⎧⎨+=⎩, 解得:12k =−,∴直线BC 的解析式为122y x =−+,过点P 作PH x ⊥轴于点H ,交BC 于点Q ,如图,设213,222P x x x ⎛⎫−++ ⎪⎝⎭,则1,22Q x x ⎛⎫−+ ⎪⎝⎭, ∴2213112222222PQ x x x x x⎛⎫=−++−−+=−+ ⎪⎝⎭,∴111222CPQ BPQS SSPQ OH PQ BH PQ OB =+=⋅+⋅=⋅()222112442422x x x x x ⎛⎫=−+⨯=−+=−−+ ⎪⎝⎭; ∵102−<,∴抛物线开口向下, ∴4PBCS≤∵S 为正偶数 ∴2S =或4, ∴当2S =时,即()2242x −−+=,解得2x =∴22P ⎛ ⎝⎭或22P ⎛ ⎝⎭; 当4S =时,即()2244x −−+=,解得2x =∴()2,3P综上所述,点P的坐标为22P ⎛+ ⎝⎭或22P ⎛ ⎝⎭或()2,3P . 【点睛】本题是二次函数综合题,考查了待定系数法求解析式,二次函数的性质,一次函数的性质,两点距离公式,利用参数列方程是本题的关键. 设PBC 的面积为求123PP P 的面积.【答案】(1)2222y x x =−−(2)P 的坐标为()2,3−(3)【分析】(1)待定系数法求解析式;(2)作C 关于x 轴的对称点C ',连接B C ',根据C ,C '关于x 轴对称,则2CBC ABC '∠=∠,结合已知条件得出PCB CBC ∠=∠',得出CP BC '∥,求得直线BC '的解析式为122y x =−+,直线CP 解析式为122y x =−−,联立抛物线解析式,进而即可求解.(3)过点P 作PH x ⊥轴交直线BC 于点H ,过1P作PW x ⊥轴交23P P 于W ,求得直线BC 解析式为122y x =−,设132222P m m m ⎛⎫− ⎪⎝⎭,,则122H m m ⎛⎫− ⎪⎝⎭,,当P 在BC 下方时,2211312222222PH m m m m m⎛⎫⎛⎫=−−−−=−+ ⎪ ⎪⎝⎭⎝⎭,此时1(2,3)P −,当P 在BC 上方时,2213112222222PH m m m m m ⎛⎫=−−−−=− ⎪⎝⎭,得出()()23,23,23P P −,进而求得直线23P P 解析式为122y x =+,得出()2,3W ,则16PW=,进而根据三角形面积公式即可求解.【详解】(1)解:把(1,0)A −,(4,0)B 代入212y x bx c =−+得:12840b c b c ⎧++=⎪⎨⎪−+=⎩,解得322b c ⎧=⎪⎨⎪=−⎩, ∴抛物线的解析式为213222y x x =−−;(2)作C 关于x 轴的对称点C ',连接B C ',如图:在213222y x x =−−中,令0x =得2y =−,∴(0,2)C −,C ,C '关于x 轴对称,∴(0,2)C ',2CBC ABC '∠=∠,2PCB ABC ∠=∠, PCB CBC ∴∠=∠',∴CP BC '∥,由(4B ,0),(0,2)C '设直线BC '的解析式为12y k x =+, 则1042k =+,解得:112k =−,∴直线BC '的解析式为122y x =−+,设直线CP 解析式为12y x b=−+,把(0C ,2)−代入得:2b =−,∴直线CP 解析式为122y x =−−, 联立212213222y x y x x ⎧=−⎪⎪⎨⎪=−−⎪⎩得:02x y =⎧⎨=−⎩或23x y =⎧⎨=−⎩,P ∴的坐标为(2,3)−;(3)过点P 作PH x ⊥轴交直线BC 于点H ,过1P作PW x ⊥轴交23P P 于W ,如图:由(4B ,0),(0C ,2)− 设直线BC 的解析式为22y k x =−,则2042k =−,解得:212k =∴直线BC 解析式为122y x =−设132222P m m m ⎛⎫− ⎪⎝⎭,,则122H m m ⎛⎫− ⎪⎝⎭, 当P 在BC 下方时,2211312222222PH m m m m m⎛⎫⎛⎫=−−−−=−+ ⎪ ⎪⎝⎭⎝⎭, ()222112442422S m m m m m ⎛⎫∴=⨯−+⨯−+=−− ⎪⎝=+⎭,10−<,∴当2m =时,S 取最大值4,此时1(2,3)P −; 当P 在BC 上方时,2213112222222PH m m m m m ⎛⎫=−−−−=− ⎪⎝⎭21124822S m m ⎛⎫∴=⨯−⨯= ⎪⎝⎭,解得2m =或2m =−∴()()23,23,23P P −设直线23P P 的解析式为y kx b =+,∴()()3232k b k b =+⎨=−+⎪⎩,解得:122k b ⎧=⎪⎨⎪=⎩,∴直线23P P 解析式为122y x =+,在122y x =+,令2x =得3y =,∴()2,3W ,∴16PW =,∴123PP P的面积为()()16222⨯⨯−−=【点睛】本题考查了二次函数的综合运用,角度问题,面积问题,扎实的计算是解题的关键.课后训练1.如图1,在平面直角坐标系xOy 中,抛物线2y x bx c =++与x 轴分别交于()1,0A m −,()3,0B m −两点,其中点B 在原点左侧,与y 轴交于点()0,3C −.(1)求抛物线的解析式;(2)已知抛物线顶点为P ,点M 在第三象限的抛物线上, ①若直线CM 与直线BP 关于直线y x =对称,求点M 的坐标;②如图2,若直线2y x n =+与抛物线交于点D ,E ,1D E x x −<<,与抛物线线的对称轴l 交于点H ,若DM l ⊥,连接ME ,MH ,求S MEH △的取值范围.【答案】(1)223y x x =+− (2)①57,24M ⎛⎫−− ⎪⎝⎭②2S MEH ≤0<△【分析】(1)根据点,A B 可求出b ,根据点C 可求出c ,即可求解;(2)①先求出直线BP 的解析式,根据题意即可得出直线CM 的解析式,进而可求出点M 的坐标;②建立S MEH△与n的关系即可求解. 【详解】(1)解:由()1,0A m −,()3,0B m −可得抛物线的对称轴为:直线()()1312m m x −+−==− 又对称轴为:直线21bx =−⨯故121b−=−⨯,解得2b =又抛物线与y 轴交于点()0,3C −3c ∴=−所以抛物线的解析式为:223y x x =+− (2)①解:令0y =,则2230x x +−=解得:121,3x x ==− 故()()1,0,3,0A B −()222314y x x x =+−=+−()1,4P ∴−−设直线BP 的解析式为:y mx n =+故有:304m n m n −+=⎧⎨−+=−⎩,解得:26m n =−⎧⎨=−⎩ 所以直线BP 的解析式为:26y x =−− 因为直线CM 与直线BP 关于直线y x =对称所以直线CM 的解析式为:12632x y y x =−−⇒=−−联立直线CM 与抛物线的解析式: 213223y x y x x ⎧=−−⎪⎨⎪=+−⎩解得:1250,2x x ==−当57,24x y =−=−故点57,24M ⎛⎫−− ⎪⎝⎭②解:由题意得:2223y x n y x x =+⎧⎨=+−⎩,解得12x x ==故()),D n En−因为直线2y x n =+与抛物线对称轴l 交于点H 结合(1)可得:()1,2H n −−+因为点D ,点M 关于抛物线对称轴l 对称 故M 的横坐标()(212M x =⨯−−()(()4S 1122222ME E H H MD y y n =⨯⨯−=⨯−⨯=−−△1D Ex x −<<1∴−<解得:32n −≤<- 2S MEH ≤0<△【点睛】本题以二次函数作为背景,综合考查了二次函数的对称性、一次函数的解析式等相关知识点.最后一小问的数学建模思想是学生应该具备的能力.(1)若函数的图象与坐标轴...有两个公共点,且(2)如图,若函数的图象为抛物线,与:(04)l x m m =<<交于点P ,连接点E .设PBE △的面积为1S ,CDE 的面积为①当点P 为抛物线顶点时,求PBC 的面积;②探究直线l 在运动过程中,S −是否存在最大值?若存在,【答案】(1)0或2或4−(2)①6,②存在,163【分析】(1)根据函数与坐标轴交点情况,分情况讨论函数为一次函数和二次函数的时候,按照图像的性质以及与坐标轴交点的情况即可求出a 值.(2)①根据A 和B 的坐标点即可求出抛物线的解析式,即可求出顶点坐标P ,从而求出PH 长度,再利用A 和B 的坐标点即可求出BC 的直线解析式,结合F Px x =即可求出F 点坐标,从而求出PF 长度,最后利用面积法即可求出PBC 的面积.②观察图形,用m 值表示出点P 坐标,再根据平行线分线段成比例求出OD 长度,利用割补法表示出1S 和2S ,将二者相减转化成关于m 的二次函数的顶点式,利用m 取值范围即可求出12S S −的最小值.【详解】(1)解:函数的图象与坐标轴有两个公共点,()()2210a x a xb ∴−+++=, 4a b =,()()22104a a x a x ∴−+++=,当函数为一次函数时,20a −=,2a ∴=.当函数为二次函数时,()()22104a a x a x −+++=,若函数的图象与坐标轴有两个公共点,即与x 轴,y 轴分别只有一个交点时,()()2241424104a b ac a a a ∴∆=−=+−−⋅=+=,14a ∴=−. 当函数为二次函数时,函数的图象与坐标轴有两个公共点, 即其中一点经过原点, 0b ∴=,4a b =,0a ∴=.综上所述,2a =或0.故答案为:0或2或14−. (2)解:①如图所示,设直线l 与BC 交于点F ,直线l 与AB 交于点H .依题意得:2102028a b a b +=⎧⎨+=⎩,解得:18a b =⎧⎨=⎩∴抛物线的解析式为:2228(1)9y x x x =−++=−−+.点P 为抛物线顶点时,(1,9)P ,(0,8)C ,9PH ∴=,1P x =,由()4,0B ,()0,8C 得直线BC 的解析式为28y x =−+, F 在直线BC 上,且在直线l 上,则F 的横坐标等于P 的横坐标,()1,6F ∴,6FH ∴=,1OH =,963PF PH FH ∴=−=−=,413BH OB OH =−=−=1111S S S 313362222PBC PFC PFB P x OH HB PF ∴=+=⋅+⋅=⨯⨯+⨯⨯=.故答案为:6.②12S S −存在最大值,理由如下:如图,设直线x m =交x 轴于H .由①得:4OB =,2AO =,6AB =,8OC =,2AH m =+,()2,28P m m m −++228PH m m ∴=−++, OD x ⊥,PH AB ⊥,OD PH ∴∥,AO OD AH PH ∴=, 即22228OD m m m =+−++,82OD m ∴=−1S S S S PAB AOD EDOB=−−四边形,2S S S OBC EDOB =−四边形, ()()221262828248S S S S S 38222PAB AOD OBC m m m m m −++−⨯∴−=−−=−−=−+,212416S S 333m ⎛⎫∴−=−−+ ⎪⎝⎭, 30−<Q ,04m <<,∴当43m =时,12S S −有最大值,最大值为163. 故答案为:163.【点睛】本题考查了二次函数的综合应用,涉及到函数与坐标轴交点问题,二次函数与面积问题,平行线分线段成比例,解题的关键在于分情况讨论函数与坐标轴交点问题,以及二次函数最值问题. (1)求抛物线的解析式;(2)抛物线上是否存在点D ,使得DOB OBC ∠=∠?若存在,求出所有点在,请说明理由;(3)如图2,点E 是点B 关于抛物线对称轴的对称点,点F 是直线OB EF 与直线OB 交于点G .设BFG 和BEG 的面积分别为1S 和2S ,求【答案】(1)24y x x =− (2)131339⎛⎫ ⎪⎝⎭,或()721,(3)2524【分析】(1)先求得点()55B ,,再利用待定系数法即可求解;(2)分点D 在直线OB 下方、上方两种情况,分别求解即可;(3)如图,分别过点E ,F 作y 轴的平行线,交直线OB 于点M ,N ,则()112B G S FN x x =−,()212B G S EM x x =−,设()24F m m m −,,可表达12S S ,再利用二次函数的性质可得出结论.【详解】(1)解:∵直线y x =经过点()5B t ,, ∴5t =,∴点()55B ,,∵抛物线2y ax bx c =++经过点()40A ,和点()55B ,以及原点,∴164025550a b c a b c c ++=⎧⎪++=⎨⎪=⎩,解得140a b c =⎧⎪=−⎨⎪=⎩,∴抛物线的解析式为24y x x =−;(2)解:∵抛物线()22424y x x x =−=−−, ∴顶点C 的坐标为()24−,,设直线BC 的解析式为:1y kx b =+,则将()55B ,,()24C −,代入1y kx b =+得,115524k b k b +=⎧⎨+=−⎩,解得310k b =⎧⎨=−⎩,∴直线BC 的解析式为:310y x =−.①当点D 在直线OB 的下方时,过点B 作BF x ⊥轴,交x 轴于点F ,延长OD ,交BF 于G ,设BC 交x 轴于点E ,如图,∵()55B ,,∴OF BF =,即45BOF OBF ∠=∠=︒,90OFG BFE ∠=∠=︒,∵DOB OBC ∠=∠,∴GOF EBF ∠∠=,∴()ASA OFG BFE △≌△,∴EF GF =.在310y x =−中,当0y =时,3100x −=,得:103x =, ∴1003E ⎛⎫ ⎪⎝⎭,, 则105533GF EF OF OE ==−=−=, ∴553G ⎛⎫ ⎪⎝⎭,,同理求得直线OG 的解析式为:13y x =, 联立:2134y x y x x ⎧=⎪⎨⎪=−⎩,解得133139x y ⎧=⎪⎪⎨⎪=⎪⎩或00x y =⎧⎨=⎩(舍去), ∴131339D ⎛⎫ ⎪⎝⎭,;②当点D 在直线OB 的上方时,∵DOB OBC ∠=∠,∴∥OD BC ,∵直线BC 的解析式为:310y x =−,∴直线OD 的解析式为:3y x =,联立:234y x y x x =⎧⎨=−⎩,解得:721x y =⎧⎨=⎩或00x y =⎧⎨=⎩(舍去),∴()721 D,.综上,当点D的坐标为131339⎛⎫⎪⎝⎭,或()721,时,使得DOB OBC∠=∠;(3)解:∵点()55B,与点E关于对称轴直线2x=对称,∴()15E−,,如图,分别过点E,F作y轴的平行线,交直线OB于点M,N,∴()11M−−,,6EM=,设()24F m m m−,,则()N m m,,∴()2245FN m m m m m =−−=−+,∵()112B GS FN x x=−,()212B GS EM x x=−,∴()222125115255666224S FN m mm m mS EM−+⎛⎫===−−=−−+⎪⎝⎭,∴当52m=时,12SS的最大值为2524.【点睛】本题属于二次函数综合题,主要考查二次函数的性质,二次函数图象上点的坐标特征,三角形的面积和全等三角形的判定及性质,解题的关键正确表达两个三角形面积的比.。
二次函数九种类型题及解析

1. 在平面直角坐标系xOy中,抛物线y=-x 2+bx+c经过点 A(-1,0),B(3,0),与y轴相交于点C. (1)求这条抛物线的解析式; (2)经过点D(2,2)直线与抛物线交于M,N两点, 若线段MN正好被直线BC平分,求直线MN的解析式; (3)直线x=a上存在点P,使得△PBC为等腰三角形? 若这样的点P有且只有三个,请直接写出符合条件的a 值及其取值范围
1. 如图,二次函数y=x 2+bx+c的图象与x轴交于A、B两点,且A点坐 标为(-3,0),经过B点的直线交抛物线于点D(-2,-3). (1)求抛物线的解析式 (2)过x轴上点E(a,0)(E点在B点的右侧)作直线EF∥BD,交抛 物线于点F,是否存在实数a使四边形BDFE是平行四边形?如果存在, 求出满足条件的a;如果不存在,请说明理由. (3)在二次函数上有一动点P,过点P作PM⊥x轴交线段BD于点M, 判断PM有最大值还是有最小值,如有,求出线段PM长度的最大值 或最小值.
1. 如图,在平面直角坐标系中,抛物线y=ax 2+bx+3与x轴 交于A(-4,0)、B(-l,0)两点,与y轴交于点C,点D 是第三象限的抛物线上一动点. (1)求抛物线的解析式; (2)设点D的横坐标为m,△ACD的面积为S求出S与m的 函数关系式,并确定m为何值时S有最大值,最大值是多 少? (3)若点P是抛物线对称轴上一点,是否存在点P使得 ∠APC=90°?若存在,请直接写出点P的坐标;若不存在, 请说明理由.
1 23 1 如图所示,抛物线y=- x - x+2和直线y= x+2相交于A、C两点,抛物线与 2 2 2 x轴的另一个交点为B,在抛物线的对称轴上是否存在点P,使得△ PBC为直角 三角形,如果存在请求出P点坐标,如果不存在,请说明理由。ຫໍສະໝຸດ 型三:直角三角形的分类讨论:
中考数学二次函数与将军饮马最值问题

二次函数与将军饮马最值问题1.(黑龙江二模)如图,抛物线y=x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).(1)求抛物线的解析式及顶点D的坐标;(2)点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.【解答】解:(1)∵点A(﹣1,0)在抛物线y=x2+bx﹣2上,∴×(﹣1)2+b×(﹣1)﹣2=0,解得:b=﹣,∴抛物线的解析式为:y=x2﹣x﹣2.∵y=x2﹣x﹣2=(x2﹣3x﹣4 )=,∴顶点D的坐标为(,﹣).(2)设点C关于x轴的对称点为C′,直线C′D的解析式为y=kx+n,则,解得:.∴y=﹣x+2.∴当y=0时,﹣x+2=0,解得:x=.∴m=.2.(2022•宁远县模拟)如图,抛物线y=x2+bx+c与x轴交于A,B两点,其中点A的坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.(1)求抛物线的解析式;(2)抛物线的对称轴上有一动点P,求出P A+PD的最小值;【解答】解:(1)∴二次函数y=x2+bx+c的图象经过A(﹣3,0),D(﹣2,﹣3),∴,解得:.∴二次函数解析式为y=x2+2x﹣3;(2)∵抛物线y=x2+2x﹣3的对称轴x=﹣=﹣1,D(﹣2,﹣3),C(0,﹣3),∴C、D关于抛物线的对称轴x=﹣1对称,连接AC与对称轴的交点就是点P,此时P A+PD=P A+PC=AC===3.∴P A+PD的最小值为3;3.(2022•乐业县二模)如图,抛物线y=ax2+bx﹣3与x轴交于A(﹣1,0)、B(3,0)两点,直线l与抛物线交于A、C两点,其中点C的横坐标是2.(1)求抛物线的函数表达式;(2)在抛物线的对称轴上找一点P,使得△PBC的周长最小,并求出点P的坐标;【解答】解:(1)∵抛物线y=ax2+bx﹣3与x轴交于A(﹣1,0)、B(3,0)两点,∴,解得:,∴抛物线的函数表达式为y=x22x﹣3;(2)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的对称轴为x=1,∵A、B关于直线x=1对称,所以AC与对称轴的交点为点P,此时C△PBC=PB+PC+BC=AC+BC,此时△BPC的周长最短,∵点C的横坐标是2,y C=22﹣2×2﹣3=﹣3,∴C(2,﹣3),设直线AC的解析式为y=mx+n(m≠0),∴,解得:,∴直线AC的解析式为y=﹣x﹣1,当x=1时,y=﹣1﹣1=﹣2,∴P(1,﹣2);4.(2022•江阴市校级一模)如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x 轴分别相交于A(﹣1,0)、B(3,0)两点,与y轴相交于点C(0,3).(1)求出这条抛物线的解析式及顶点M的坐标;(2)PQ是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求AQ+QP+PC 的最小值;【解答】解:(1)∵抛物线过点A(﹣1,0),B(3,0),C(0,3),∴设抛物线解析式为y=a(x+1)(x﹣3),将C(0,3)代入,得:3=a(0+1)(0﹣3),解得:a=﹣1,∴y=﹣(x+1)(x﹣3)=﹣x2+2x+3=﹣(x﹣1)2+4,∴该抛物线解析式为y=﹣x2+2x+3,顶点坐标为M(1,4).(2)如图1,将点C沿y轴向下平移1个单位得C′(0,2),连接BC′交抛物线对称轴x=1于点Q′,过点C作CP′∥BC′,交对称轴于点P′,连接AQ′,∵A、B关于直线x=1对称,∴AQ′=BQ′,∵CP′∥BC′,P′Q′∥CC′,∴四边形CC′Q′P′是平行四边形,∴CP′=C′Q′,Q′P′=CC′=1,在Rt△BOC′中,BC′=,==.∴AQ′+Q′P′+P′C=BQ′+C′Q′+Q′P′=BC′+Q′P′=+1,此时,C′、Q′、B三点共线,BQ′+C′Q′的值最小,∴AQ+QP+PC的最小值为+1.5.(2022秋•黄冈月考)如图,抛物线y=﹣x2+bx+c与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D.已知A(﹣1,0),C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上有一点M,使得|MB﹣MC|的值最大,求此点M的坐标;【解答】解:(1)将A(﹣1,0),C(0,3)代入y=﹣x2+bx+c,∴,解得,∴y=﹣x2+2x+3;(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴抛物线的对称轴为直线x=1,∵A、B关于对称轴对称,∴|MB﹣MC|=|MA﹣MC|≤AC,∴当A、C、M三点共线时,|MB﹣MC|有最大值,设直线AC的解析式为y=kx+m,∴,解得,∴y=3x+3,∴M(1,6);6.(2022•常德)如图,已知抛物线过点O(0,0),A(5,5),且它的对称轴为x=2,点B是抛物线对称轴上的一点,且点B在第一象限.(1)求此抛物线的解析式;(2)当△OAB的面积为15时,求B的坐标;(3)在(2)的条件下,P是抛物线上的动点,当P A﹣PB的值最大时,求P的坐标以及P A﹣PB的最大值.【解答】解:(1)∵抛物线过点O(0,0),A(5,5),且它的对称轴为x=2,∴抛物线与x轴的另一个交点坐标为(4,0),设抛物线解析式为y=ax(x﹣4),把A(5,5)代入,得5a=5,解得:a=1,∴y=x(x﹣4)=x2﹣4x,故此抛物线的解析式为y=x2﹣4x;(2)∵点B是抛物线对称轴上的一点,且点B在第一象限,∴设B(2,m)(m>0),设直线OA的解析式为y=kx,则5k=5,解得:k=1,∴直线OA的解析式为y=x,设直线OA与抛物线对称轴交于点H,则H(2,2),∴BH=m﹣2,∵S△OAB=15,∴×(m﹣2)×5=15,解得:t=8,∴点B的坐标为(2,8);(3)设直线AB的解析式为y=cx+d,把A(5,5),B(2,8)代入得:,解得:,∴直线AB的解析式为y=﹣x+10,当P A﹣PB的值最大时,A、B在同一条直线上,∵P是抛物线上的动点,∴,解得:,(舍去),∴P(﹣2,12),此时,P A﹣PB=AB==3.7.(2022春•良庆区校级期末)如图,已知抛物线的解析式为y=﹣x2﹣x+3,抛物线与x轴交于点A和点B,与y轴交点于点C.(1)请分别求出点A、B、C的坐标和抛物线的对称轴;(2)连接AC、BC,将△ABC绕点B顺时针旋转90°,点A、C的对应点分别为M、N,求点M、N的坐标;(3)若点P为该抛物线上一动点,在(2)的条件下,请求出使|NP﹣BP|最大时点P的坐标,并请直接写出|NP﹣BP|的最大值.【解答】解:(1)∵y=﹣x2﹣x+3=﹣(x+4)(x﹣1)=﹣(x+)2+,∴A(﹣4,0),B(1,0),C(0,3),对称轴为直线x=﹣;(2)如图所示:过N作NQ⊥x轴于点Q,由旋转性质得MB⊥x轴,∠CBN=90°,BM=AB=5,BN=BC,∴M(1,5),∠OBC+∠QBN=90°,∵∠OBC+∠BCO=90°,∴∠BCO=∠QBN,又∵∠BOC=∠NQB=90°,BN=BC,∴△OBC≌△QNB(AAS),∴BQ=OC=3,NQ=OB=1,∴OQ=1+3=4,∴N(4,1);(3)设直线NB的解析式为y=kx+b.∵B(1,0)、N(4,1)在直线NB上,∴,解得:,∴直线NB的解析式为:y=x﹣,当点P,N,B在同一直线上时|NP﹣BP|=NB==,当点P,N,B不在同一条直线上时|NP﹣BP|<NB,∴当P,N,B在同一直线上时,|NP﹣BP|的值最大,即点P为直线NB与抛物线的交点.解方程组:,解得:或,∴当P的坐标为(1,0)或(﹣,﹣)时,|NP﹣BP|的值最大,此时最大值为.。
部编数学九年级上册22.26二次函数“将军饮马”问题(基础篇)(人教版)含答案

专题22.26 二次函数“将军饮马”问题(基础篇)(专项练习)一、单选题1.如图,直线y 34=-x +3分别与x 轴,y 轴交于点A 、点B ,抛物线y =x 2+2x ﹣2与y 轴交于点C ,点E 在抛物线y =x 2+2x ﹣2的对称轴上移动,点F 在直线AB 上移动,CE +EF 的最小值是( )A .4B .4.6C .5.2D .5.62.已知抛物线2114y x =+具有如下性质:抛物线上任意一点到定点F (0,2)的距离与到x 轴的距离相等,点M 的坐标为(3,6),P 是抛物线2114y x =+上一动点,则△PMF 周长的最小值是( )A .5B .9C .11D .133.如图,在抛物线2y x =-上有A ,B 两点,其横坐标分别为1,2;在y 轴上有一动点C ,当BC AC +最小时,则点C 的坐标是( )A .(0.0)B .(0,1-)C .(0,2)D .(0,2-)4.如图,抛物线y =﹣x 2+2x +2交y 轴于点A ,与x 轴的一个交点在2和3之间,顶点为B .下列说法:其中正确判断的序号是( )①抛物线与直线y =3有且只有一个交点;②若点M (﹣2,y 1),N (1,y 2),P (2,y 3)在该函数图象上,则y 1<y 2<y 3;③将该抛物线先向左,再向下均平移2个单位,所得抛物线解析式为y =(x +1)2+1;④在x 轴上找一点D ,使AD +BD .A .①②④B .①②③C .①③④D .②③④5.如图,在平面直角坐标系中,已知抛物线2y ax bx =+的对称轴为34x =,且经过点A (2,1),点P 是抛物线上的动点,P 的横坐标为()02m m <<,过点P 作PB x ^轴,垂足为B ,PB 交OA 于点C ,点O 关于直线PB 的对称点为D ,连接CD ,AD ,过点A 作AE ⊥x 轴,垂足为E ,则当m =( )时,ACD D 的周长最小.A .1B .1.5C .2D .2.56.如图,抛物线y=ax2+bx+c交x轴分别于点A(﹣3,0),B(1,0),交y轴正半轴于点D,抛物线顶点为C.下列结论①2a﹣b=0;②a+b+c=0;③当m≠﹣1时,a﹣b>am2+bm;④当△ABC是等腰直角三角形时,a=1-;2⑤若D(0,3),则抛物线的对称轴直线x=﹣1上的动点P与B、D两点围成的△PBD周长最小值为,其中,正确的个数为( )A.2个B.3个C.4个D.5个7.如图,P是抛物线y=x2﹣x﹣4在第四象限的一点,过点P分别向x轴和y轴作垂线,垂足分别为A、B,则四边形OAPB周长的最大值为()A.10B.8C.7.5D.8.如图,已知抛物线y=-x2+px+q的对称轴为x=﹣3,过其顶点M的一条直线y=kx+b 与该抛物线的另一个交点为N(﹣1,1).要在坐标轴上找一点P,使得△PMN的周长最小,则点P的坐标为()A .(0,2)B .(43,0)C .(0,2)或(43,0)D .以上都不正确9.抛物线与直线交于A 、B 两点(点A 在点B 的左侧),动点P 从A 点出发,先到达抛物线的对称轴上的某点E ,再到达x 轴上的某点F ,最后运动到点B .若使点P 运动的总路径最短,则点P 运动的总路径的长为( )A .B .C .D .二、填空题10.如图,抛物线2520533y x x =-+与x 轴分别交于A 、B 两点(点A 在点B 的左侧),与y 轴交于C ,在其对称轴上有一动点M ,连接MA 、MC 、AC ,则当△MAC 的周长最小时,点M 的坐标是_____.11.若抛物线y =﹣x 2+2x +m +1(m 为常数)交y 轴于点A ,与x 轴的一个交点在2和3之间,抛物线顶点为点B .①抛物线y =﹣x 2+2x +m +1与直线y =m +2有且只有一个交点;②若点M (﹣2,y 1)、点N (12,y 2)、点P (2,y 3)在该函数图象上,则y 1<y 2<y 3;③将该抛物线向左平移2个单位,再向下平移2个单位,所得的抛物线解析式为y =﹣(x +1)2+m ;④点A 关于直线x =1的对称点为C ,点D 、E 分别在x 轴和y 轴上,当m =1时,四边形BCDE周长的最小值为3其中正确的是 ___.(填序号)12.如图,在平面直角坐标系中,点A 在抛物线y =x 2﹣2x +2上运动.过点A 作AC ⊥x 轴于点C ,以AC 为对角线作矩形ABCD ,连接BD ,则对角线BD 的最小值为_____.13.如图,抛物线()()13y a x x =+-与x 轴交于A ,B 两点(点A 在B 的左侧),点C 为抛物线上任意一点(不与A ,B 重合),BD 为ABC V 的AC 边上的高线,抛物线顶点E 与点D 的最小距离为1,则抛物线解析式为______.14.如图,在平面直角坐标系中,直线AC :y =43x+8与x 轴交于点A ,与y 轴交于点C ,抛物线y =ax 2+bx+c 过点A ,C ,且与x 轴的另一交点为B ,又点P 是抛物线的对称轴l 上一动点.若△PAC 周长的最小值为,则抛物线的解析式为_____.15.如图,抛物线y =﹣38x 2+34x +3与x 轴交于点A ,B (点A 在点B 的左边),交y 轴于点C ,点P 为抛物线对称轴上一点.则△APC 的周长最小值是_____.16.已知抛物线y =-x 2+2x +3与x 轴交于A 、B 两点,与y 轴交于点C ,P 是抛物线对称轴l 上的一个动点,则PA +PC 的最小值是__________.17.已知二次函数y=12x 2+bx 的图象过点A(4,0),设点C(1,-3),在抛物线的对称轴上求一点P ,使|PA-PC|的值最大,则点P 的坐标为____________。
2022年中考数学二次函数压轴突破 专题02 将军饮马模型(教师版含解析)

将军饮马模型考情分析:通过全国中考试题分析来看,将军饮马的模型多出现在中考二次函数压轴题第二问中出现,难度不大,但需要注意对称点的选择,动点通常在对称轴上,而且已知定点中往往有一个与x 轴的交点.考法主要有以下几种:1.求取最小值时动点坐标2.求最小值.3.求三角形或四边形周长最小值.模型一:两定点一动点如图,A,B 为定点,P 为l 上动点,求AP+BP 最小值解析:作点A 关于直线的对称点A',连接P A',则P A '=P A ,所以P A +PB =P A '+PB当A'、P 、B 三点共线的时候,P A'+PB =A'B ,此时为最小值(两点之间线段最短)PBAA 'ABP 折点端点A 'P BA如图,P 为定点,M 、N 分别为OA 和OB 上的动点,求△PMN 周长最小值解析:分别作点P 关于OA 、OB 的对称点,则△PMN 的周长为PM +MN +NP =P'M +MN +NP '',当P '、M 、N 、P ''共线时,△PMN 周长最小.模型三:两定点两动点如图,P 、Q 为两定点,M 、N 分别为OA 、OB 上的动点,求四边形PQMN 的最小值.解析:∵PQ 是条定线段,∴只需考虑PM +MN +NQ 最小值即可, 分别作点P 、Q 关于OA 、OB 对称, PM +MN +NQ =P 'M +MN +NQ ',当P '、M 、N 、Q '共线时,四边形PMNQ 的周长最小。
BBBB如图,P 为定点,M 、N 分别为OA 、OB 上的动点,求PM +MN 最小值。
解析:作点P 关于OA 对称的点P ',PM +MN =P 'M +MN ,过点P '作OB 垂线分别交OA 、OB 于点M 、N , 得PM +MN 最小值(点到直线的连线中,垂线段最短)模型五:将军饮马有距离例一、如图,A 、D 为定点,B 、C 为直线l 上两动点,BC 为定值,求AB+BC+CD 最小值?解析:BC 为定值,只需求AB+CD 最小即可;平移AB 至CE ,则变成求CE+CD 的最小值,基本将军饮马的模型例二、如图,A 、D 为定点,B 、C 为直线l 1 、l 2上两动点,BC ⊥l 1,求AB+BC+CD 最小值?解析:BC 为定值,只需求AB+CD 最小即可;BB平移CD至BE,则变成求AB+BE最小,基本将军饮马.经典例题剖析:例一:如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点(1,0)A、(5,0)B、(0,4)C三点.(1)求抛物线的解析式和对称轴;(2)P是抛物线对称轴上的一点,求满足PA PC+的值为最小的点P坐标(请在图1中探索);【分析】(1)将点A、B的坐标代入二次函数表达式得:2(1)(5)(65)y a x x a x x=--=-+,即可求解;(2)连接B、C交对称轴于点P,此时PA PC+的值为最小,即可求解;【解答】解:(1)将点A、B的坐标代入二次函数表达式得:2(1)(5)(65)y a x x a x x=--=-+,则54a=,解得:45a=,抛物线的表达式为:224424(65)4555y x x x x=-+=-+,函数的对称轴为:3x=,顶点坐标为16(3,)5-;(2)连接B、C交对称轴于点P,此时PA PC+的值为最小,将点B、C的坐标代入一次函数表达式:y kx b=+得:054k bb=+⎧⎨=⎩,解得:454kb⎧=-⎪⎨⎪=⎩,直线BC的表达式为:445y x=-+,当3x =时,85y =, 故点8(3,)5P ;例二:如图,直线3y x =-+与x 轴、y 轴分别交于B 、C 两点,抛物线2y x bx c =-++经过点B 、C ,与x 轴另一交点为A ,顶点为D .(1)求抛物线的解析式;(2)在x 轴上找一点E ,使EC ED +的值最小,求EC ED +的最小值;【分析】(1)直线3y x =-+与x 轴、y 轴分别交于B 、C 两点,则点B 、C 的坐标分别为(3,0)、(0,3),将点B 、C 的坐标代入二次函数表达式,即可求解;(2)如图1,作点C 关于x 轴的对称点C ',连接CD '交x 轴于点E ,则此时EC ED +为最小,即可求解; 【解答】解:(1)直线3y x =-+与x 轴、y 轴分别交于B 、C 两点,则点B 、C 的坐标分别为(3,0)、(0,3), 将点B 、C 的坐标代入二次函数表达式得:9303b c c -++=⎧⎨=⎩,解得:23b c =⎧⎨=⎩,故函数的表达式为:223y x x =-++,令0y =,则1x =-或3,故点(1,0)A -; (2)如图1,作点C 关于x 轴的对称点C ',连接CD '交x 轴于点E ,则此时EC ED +为最小,函数顶点D 坐标为(1,4),点(0,3)C '-,将C '、D 的坐标代入一次函数表达式并解得: 直线C D '的表达式为:73y x =-, 当0y =时,37x =, 故点3(7E ,0),则EC ED +的最小值为DC '=例三:如图,以D 为顶点的抛物线2y x bx c =-++交x 轴于A 、B 两点,交y 轴于点C ,直线BC 的表达式为3y x =-+. (1)求抛物线的表达式;(2)在直线BC 上有一点P ,使PO PA +的值最小,求点P 的坐标;【分析】(1)先求得点B 和点C 的坐标,然后将点B 和点C 的坐标代入抛物线的解析式得到关于b 、c 的方程,从而可求得b 、c 的值;(2)作点O 关于BC 的对称点O ',则(3,3)O ',则OP AP +的最小值为AO '的长,然后求得AO '的解析式,最后可求得点P 的坐标;【解答】解:(1)把0x =代入3y x =-+,得:3y =,(0,3)C ∴. 把0y =代入3y x =-+得:3x =,(3,0)B ∴,将(0,3)C 、(3,0)B 代入2y x bx c =-++得:9303b c c -++=⎧⎨=⎩,解得2b =,3c =.∴抛物线的解析式为223y x x =-++.(2)如图所示:作点O 关于BC 的对称点O ',则(3,3)O '. O '与O 关于BC 对称,PO PO ∴='.OP AP O P AP AO ∴+='+'.∴当A 、P 、O '在一条直线上时,OP AP +有最小值.设AP 的解析式为y kx b =+,则033k b k b -+=⎧⎨+=⎩,解得:34k =,34b =.AP ∴的解析式为3344y x =+. 将3344y x =+与3y x =-+联立,解得:127y =,97x =,∴点P 的坐标为9(7,12)7.例四:如图,抛物线2y ax bx c =++的图象过点(1,0)A -、(3,0)B 、(0,3)C .(1)求抛物线的解析式;(2)在抛物线的对称轴上是否存在一点P ,使得PAC ∆的周长最小,若存在,请求出点P 的坐标及PAC ∆的周长;若不存在,请说明理由;【分析】(1)由于条件给出抛物线与x 轴的交点(1,0)A -、(3,0)B ,故可设交点式(1)(3)y a x x =+-,把点C 代入即求得a 的值,减小计算量.(2)由于点A 、B 关于对称轴:直线1x =对称,故有PA PB =,则PAC C AC PC PA AC PC PB ∆=++=++,所以当C 、P 、B 在同一直线上时,PAC C AC CB ∆=+最小.利用点A 、B 、C 的坐标求AC 、CB 的长,求直线BC 解析式,把1x =代入即求得点P 纵坐标.【解答】解:(1)抛物线与x 轴交于点(1,0)A -、(3,0)B ∴可设交点式(1)(3)y a x x =+- 把点(0,3)C 代入得:33a -=1a ∴=-2(1)(3)23y x x x x ∴=-+-=-++∴抛物线解析式为223y x x =-++(2)在抛物线的对称轴上存在一点P ,使得PAC ∆的周长最小. 如图1,连接PB 、BC点P 在抛物线对称轴直线1x =上,点A 、B 关于对称轴对称PA PB ∴=PAC C AC PC PA AC PC PB ∆∴=++=++当C 、P 、B 在同一直线上时,PC PB CB +=最小 (1,0)A -、(3,0)B 、(0,3)C221310AC ∴=+=,223332BC =+=1032PAC C AC CB ∆∴=+=+最小设直线BC 解析式为3y kx =+把点B 代入得:330k +=,解得:1k =-∴直线:3BC y x =-+132P y ∴=-+=∴点(1,2)P 使PAC ∆的周长最小,最小值为1032+专题训练1.(2020秋•马山县期中)如图,抛物线2(0)y ax bx c a =++≠与x 轴交于点A 、(1,0)B ,与y 轴交于点C ,直线122y x =-经过点A 、C .抛物线的顶点为D ,对称轴为直线l . (1)求抛物线的解析式;(2)设点G 是y 轴上一点,是否存在点G ,使得GD GB +的值最小,若存在,求出点G 的坐标;若不存在,请说明理由.【分析】(1)利用一次函数的性质求得点A 、C 的坐标,然后把点A 、B 、C 的坐标分别代入二次函数解析式,利用待定系数法求得二次函数解析式;(2)利用轴对称-最短路径方法得点G ,先计算B D '的解析式,令0x =可得点G 的坐标. 【解答】解:(1)如图1,对于直线122y x =-,令0y =,得4x =,令0x =,得2y =-,∴点(4,0)A ,点(0,2)C -,将(4,0)A ,(1,0)B ,(0,2)C -代入抛物线解析式得:164002a b c a b c c ++=⎧⎪++=⎨⎪=-⎩,解得:12522a b c ⎧=-⎪⎪⎪=⎨⎪=-⎪⎪⎩,∴抛物线解析式为215222y x x =-+-;(2)存在.如图3,取点B 关于y 轴的对称点B ',则点B '的坐标为(1,0)-,连接B D ',直线B D '与y 轴的交点G 即为所求的点.22151592()22228y x x x =-+-=--+,∴顶点5(2D ,9)8,设直线B D '的解析式为(0)y kx d k =+≠, 则05928k d k d -+=⎧⎪⎨+=⎪⎩,解得:928928k b ⎧=⎪⎪⎨⎪=⎪⎩,∴直线B D '的解析式为992828y x =+, 当0x =时,928y =, ∴点G 的坐标为9(0,)28. 2.(2019•遵义)如图,抛物线21:2C y x x =-与抛物线22:C y ax bx =+开口大小相同、方向相反,它们相交于O ,C 两点,且分别与x 轴的正半轴交于点B ,点A ,2OA OB =.(1)求抛物线2C 的解析式;(2)在抛物线2C 的对称轴上是否存在点P ,使PA PC +的值最小?若存在,求出点P 的坐标,若不存在,说明理由;【分析】(1)1C 、22:C y ax bx =+开口大小相同、方向相反,则1a =-,将点A 的坐标代入2C 的表达式,即可求解;(2)作点C 关于1C 对称轴的对称点(1,3)C '-,连接AC '交函数2C 的对称轴于点P ,此时PA PC +的值最小,即可求解;【解答】解:(1)令:220y x x =-=,则0x =或2,即点(2,0)B ,1C 、22:C y ax bx =+开口大小相同、方向相反,则1a =-,则点(4,0)A ,将点A 的坐标代入2C 的表达式得:0164b =-+,解得:4b =,故抛物线2C 的解析式为:24y x x =-+;(2)联立1C 、2C 表达式并解得:0x =或3,故点(3,3)C ,作点C 关于2C 对称轴的对称点(1,3)C ',连接AC '交函数2C 的对称轴于点P ,此时PA PC +的值最小为:线段AC '的长度=此时点(2,2)P ;3.(2020秋•金乡县期中)如图,在平面直角坐标系中,二次函数2y x bx c =++的图象与x 轴交于A ,B 两点,与y 轴交于点(0,3)C -,A 点的坐标为(1,0)-.(1)求二次函数的解析式;(2)若Q 为抛物线对称轴上一动点,当Q 在什么位置时QA QC +最小,求出Q 点的坐标,并求出此时QAC ∆的周长.【分析】(1)用待定系数法即可求解;(2)点A 关于函数对称轴的对称点为点B ,连接BC 交函数对称轴于点Q ,连接AQ ,则此时QAC ∆的周长最小,进而求解.【解答】解:(1)(1,0)A -,(0,3)C -在2y x bx c =++上, 则103b c c -+=⎧⎨=-⎩,解得23b c =-⎧⎨=-⎩, ∴二次函数的解析式为223y x x =--;(2)点A 关于函数对称轴的对称点为点B ,连接BC 交函数对称轴于点Q ,连接AQ ,则此时QAC ∆的周长最小,理由:QAC ∆的周长AC AQ QC AB AQ QC BC CQ =++=++=+为最小,由点B 、C 的坐标得,直线BC 的表达式为3y x =-,当1x =时,32y x =-=-,即点(1,2)Q -,则QAC ∆的周长最小值BC AC =+==.4.(2020秋•房县期中)如图,抛物线213y x mx n =-+与x 轴交于A 、B 两点,与y 轴交于点(0,1)C -,且对称轴1x =.(1)求出抛物线的解析式及A ,B 两点的坐标;(2)在对称轴上方是否存在点D ,使三角形ADC 的周长最小?若存在,求出点D 的坐标;若不存在.说明理由(使用图1);【分析】(1)用待定系数法即可求解;(2)连接CB 交对称轴于点D ,此时三角形DAC 周长最小,进而求解;【解答】解:(1)抛物线与y 轴交于点(0,1)C -,且对称轴x l =, 则11231m n -⎧-=⎪⎪⨯⎨⎪=-⎪⎩,解得231m n ⎧=⎪⎨⎪=-⎩, ∴抛物线解析式为212133y x x =--, 令2121033y x x =--=,得:11x =-,23x =, (1,0)A ∴-,(3,0)B ;(2)在对称轴上存在D 使三角形形DAC 的周长最小,连接CB 交对称轴于点D ,此时三角形DAC 周长最小.设BC 的解析式为y kx b =+,把(3,0)B 、(0,1)C -分别代入上式得:130b k b =-⎧⎨+=⎩,解得131k b ⎧=⎪⎨⎪=-⎩, 故直线BC 的解析式为113y x =-, 当1x =时,23y =-, 所以点D 的坐标为2(1,)3-; 5.(2020秋•青羊区校级期中)如图,抛物线25()2y a x h =-+经过点(1,0)A ,(0,3)C . (1)求抛物线与x 轴的另一个交点B 的坐标;(2)如图①,在抛物线的对称轴上是否存在点P ,使得四边形PAOC 的周长最小?若存在,求出此时P 点坐标;若不存在,请说明理由;【分析】(1)根据函数的对称性即可求解;(2)A、B两点关于对称轴对称,连接BC交对称轴于点P,则P点即为所求,进而求解;【解答】解:(1)由抛物线表达式知,函数的对称轴为52x=,而点(1,0)A,根据点的对称性,则512(1)42xB=+⨯-=,故点B的坐标为(4,0);(2)存在,理由:抛物线经过点(1,0)A,(4,0)B,A∴、B关于对称轴对称,如图1,连接BC,BC ∴与对称轴的交点即为所求的点P ,此时PA PC BC +=,∴四边形PAOC 的周长最小值为:OC OA BC ++,(1,0)A ,(4,0)B ,(0,3)C ,设直线BC 解析式为y kx n =+,把B 、C 两点坐标代入可得403k n n +=⎧⎨=⎩,解得343k n ⎧=-⎪⎨⎪=⎩, ∴直线BC 的解析式为334y x =-+, 由抛物线的表达式知,抛物线的对称轴为52x =, 当52x =时,39348y x =-+=, 故点P 的坐标为5(2,9)8; 6.(2019•柳州)如图,直线3y x =-交x 轴于点A ,交y 轴于点C ,点B 的坐标为(1,0),抛物线2(0)y ax bx c a =++≠经过A ,B ,C 三点,抛物线的顶点为点D ,对称轴与x 轴的交点为点E ,点E 关于原点的对称点为F ,连接CE ,以点F 为圆心,12CE 的长为半径作圆,点P 为直线3y x =-上的一个动点. (1)求抛物线的解析式;(2)求BDP ∆周长的最小值;【分析】(1)直线3y x =-,令0x =,则3y =-,令0y =,则3x =,故点A 、C 的坐标为(3,0)、(0,3)-,即可求解;(2)过点B 作直线3y x =-的对称点B ',连接BD 交直线3y x =-于点P ,直线B B '交函数对称轴与点G ,则此时BDP ∆周长BD PB PD BD B B =++=+'为最小值,即可求解;【解答】解:(1)直线3y x =-,令0x =,则3y =-,令0y =,则3x =,故点A 、C 的坐标为(3,0)、(0,3)-,则抛物线的表达式为:2(3)(1)(43)y a x x a x x =--=-+,则33a =-,解得:1a =-,故抛物线的表达式为:243y x x =-+-⋯①;(2)连接DB '交于直线于P ;此时三角形BDP 周长BD PB PD BD DB =++=+'为最小值,(2,1)D ,则点(2,1)G -,即:BG EG =,即点G 是BB '的中点,过点(3,2)B '-,BDP ∆周长最小值BD B D =+'7.(2019•荆州)如图,在平面直角坐标系中,平行四边形OABC 的顶点A ,C 的坐标分别为(6,0),(4,3),经过B ,C 两点的抛物线与x 轴的一个交点D 的坐标为(1,0).(1)求该抛物线的解析式;(2)若AOC ∠的平分线交BC 于点E ,交抛物线的对称轴于点F ,点P 是x 轴上一动点,当PE PF +的值最小时,求点P 的坐标;【分析】(1)由平行四边形OABC 的性质求点B 坐标,根据抛物线经过点B 、C 、D 用待定系数法求解析式.(2)由OE 平分AOC ∠易证得COE AOE OEC ∠=∠=∠,故有CE OC =,求得点E 坐标,进而求得直线OE 解析式.求抛物线对称轴为直线7x =,即求得点F 坐标.作点E 关于x 轴的对称点点E ',由于点P 在x 轴上运动,故有PE PE '=,所以当点F 、P 、E '在同一直线上时,PE PF PE PF FE ''+=+=最小.用待定系数法求直线E F '解析式,即求得E F '与x 轴交点P 的坐标.【解答】解:(1)平行四边形OABC 中,(6,0)A ,(4,3)C6BC OA ∴==,//BC x 轴610B C x x ∴=+=,3B C y y ==,即(10,3)B设抛物线2y ax bx c =++经过点B 、C 、(1,0)D∴10010316430a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩ 解得:19149139a b c ⎧=-⎪⎪⎪=⎨⎪⎪=-⎪⎩∴抛物线解析式为211413999y x x =-+-(2)如图1,作点E 关于x 轴的对称点E ',连接E F '交x 轴于点P (4,3)C5OC ∴= //BC OAOEC AOE ∴∠=∠ OE 平分AOC ∠AOE COE ∴∠=∠OEC COE ∴∠=∠5CE OC ∴==59E C x x ∴=+=,即(9,3)E∴直线OE 解析式为13y x = 直线OE 交抛物线对称轴于点F ,对称轴为直线:149712()9x =-=⨯-7(7,)3F ∴点E 与点E '关于x 轴对称,点P 在x 轴上 (9,3)E '∴-,PE PE '= ∴当点F 、P 、E '在同一直线上时,PE PF PE PF FE ''+=+=最小 设直线E F '解析式为y kx h =+ ∴93773k h k h +=-⎧⎪⎨+=⎪⎩解得:8321k h ⎧=-⎪⎨⎪=⎩ ∴直线8:213E F y x '=-+ 当82103x -+=时,解得:638x = ∴当PE PF +的值最小时,点P 坐标为63(8,0).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考函数例题4:二次函数综合题将来自饮马与切割法求最大面积初中数学中的二次函数中的最短线段或最短周长等问题一般采取利用对称把不在直线一侧的两点对称到直线两侧,则两点之间线段最短,即可得出;最大面积可以用平行于y轴的直线把三角形切成两块,表示出面积并配方求最大值即可可
