CIC插值滤波器的FPGA设计与实现

合集下载

基于FPGA的CIC滤波器的设计与实现

设输入序列为（ｍ），输出序列为Ｙ（ｍ），若输入
采样率为＿厂＝１／Ｔ，输出采样率为＿厂＝，／。内插后的序
列为
以单级ＣＩＣ抽取滤波器为例，积分部分的积分
程为
ＩＲ滤波器，并且反馈系数为１，状态方ｙ（ｍ）：ｆ（予），，＝０， ± ，， ± ２，， … （）器是单级点的Ｉ
符合设计的要求。故在系统中根据需要而设计信号的速率非常重要，而通过内插和抽取就可以改变数字信号的速率，故研究内插和抽取对于软件无线电的
设计非常有必要。运用内插和抽取的就是多速率滤波器 … ，这种常用的多速率滤波器有ＣＩＣ滤波器、ＨＢ滤波器、ＦＩＲ滤波器。本文设计的是ＣＩＣ滤
■
（ＧｕｉｌｉｎＵｎｉｖｅｒｓｉｔｙｏｆＥｌｅｃｔｒｏｎｉｃＴｅｃｈｎｏｌｏｇｙ，ＧｕｉｌｉｎＧｕａｎｇｘｉ５４１００４，Ｃｈｉｎａ）
【Ａｂｓｔｒａｃｔ】Ｔｈｅｄｅｓｉｇｎａｎｄｉｍｐｌｅｍｅｎｔａｒａｔｏｒｃｏｍｂ（ＣＩＣ）ｉｆｌｔｅｒａｒｅｄｅｓｃｒｉｂｅｄ．Ｔｈｅｖｅｉｆｌｏｇｌａｎｇｕａｇｅ
２内插理论

CIC抽取滤波器的MATLAB设计及FPGA实现

CIC抽取滤波器的MATLAB设计及FPGA实现杨翠娥【摘要】CIC抽取滤波器是无线通信中的常用模块,一般用于数字下变频(DDC)系统中.它可以在降低采样速率的同时,完成低通滤波的作用.本论文介绍了CIC抽取滤波器的工作原理,并给出了CIC滤波器的MATLAB程序及仿真结果.最后,利用FPGA高速、高稳定性的特点,在QUAR-TUS设计环境下进行了CIC滤波器的HDL模块设计.【期刊名称】《山西电子技术》【年(卷),期】2017(000)001【总页数】3页(P46-48)【关键词】CIC;抽取;MATLAB;FPGA【作者】杨翠娥【作者单位】太原工业学院,山西太原030008【正文语种】中文【中图分类】TN911.4随着数字通信技术的发展，信号传输的速度越来越快。

这就对数字信号处理提出了更高的要求。

多速率信号处理技术可以在一个数字信号处理系统中采用多个不同的采样率，同时可以实现不同采样率之间的相互转换。

这种技术在降低高速数字系统的复杂度，减少存储量及提高灵活性等方面具有较好的性能。

数字信号的速率可以通过内插和抽取来改变，其中，内插用于上变频系统中，抽取用于下变频系统中。

无论抽取还是内插，都需要设计一个满足抽取或内插(抗混叠)要求的数字滤波器。

该滤波器性能的好坏将影响取样速率变换的效果以及实时处理的能力。

为此，积分级联梳状(CIC)滤波器得到了广泛的应用。

本文将以单级CIC抽取滤波器的设计为例进行CIC抽取滤波器的MATLAB分析设计及FPGA的实现。

积分级联梳状(CIC)抽取滤波器即实现对输入信号采样率的抽取和低通滤波，以完成信号的降速处理。

在数字下变频系统中得到了广泛应用。

CIC抽取滤波器包括积分和梳状两个基本组成部分。

如图1所示。

以单级CIC抽取系统为例，取级数N=1。

积分器实际上是单极点的FIR滤波器，反馈系数为1时的状态方程如下：根据z变换，积分器的传输函数可以表示为：梳状器也是一个对称FIR滤波器，其状态方程可以表示为：式中，D为设计参数，称为微分延迟，其传输函数为：则单级CIC滤波器的传递函数为：其传递函数的幅频特性为：如图2所示为单级CIC滤波器的幅频特性。

基才FPGA的DDC中CIC滤波器的设计

单级ＣＩＣ滤波器的频率响应为：
Ｈ（ｅ）＝ＤＭ ·Ｓｎ（
）·ｓ旷ｔ（）
（２）
式中，Ｓａ（ｘ）＝ｓｌ为抽样函数，且Ｓａ（０）＝１，所以ＣＩＣ
滤波器在ｔｏ＝０处的幅值为Ｄ，即Ｈ（ｅ。）＝Ｄ。
０－２￣／Ｄ的区间为ＣＩＣ滤波器的主瓣，而其他区１９成为旁
ＸＩＡＯＲｕｉ—ｃｈｕａｎ，ＬＩＵＹａｎ—ｐｉｎｇ，ＰＥＮＧＣｈｅｎｇ—ｇｏｎｇ
（ＳｃｈｏｏｌｏｆＩｎｆｏｒｍａｔｉｏｎＥｎｇｉｎｅｅｒｉｎｇ，ＨｅｂｅｉＵｎｉｖｅｒｓｉｔｙｏｆＴｅｃｈｎｏｌｏｇｙ，Ｔｉａｎｊｉｎ３００４０１，Ｃｈｉｎａ）
Ａｂｓｔｒａｃｔ：ＴｈｉｓａｒｔｉｃｌｅｄｅｓｃｒｉｂｅｓｔｈｅｄｅｓｉｇｎｏｆＣＩＣｆｉｌｔｅｒｂａｓｅｄｏｎｔｈｅｓｉｇｎａｌｐｒｏｃｅｓｓｉｎｇｔｈｅｏｒｙ．Ｔｈｉｓａｒｔｉｃｌｅｆｉｒｓｔａｎａｌｙｓｅｓｔｈｅｔｈｅｏｒｙａｎｄｔｈｅｐａｒａｍｅｔｅｒｓｏｆｔｈｅｆｉｌｔｅｒ．ＴｈｅｎｄｅｓｉｇｎｔｈｅＣＩＣｆｉｌｔｅｒｍｅｅｔｔｈｅｓｙｓｔｅｍｒｅｑｕｉｒｅｍｅｎｔｓｗｉｔｈＭａｔｌａｂ．Ｉｎｔｈｅｅｎｄ，ｗｅｃａｒｒｉｅｓｏｕｔｔｈｅｄｅｓｉｇｎｏｆｔｈｅＣＩＣｆｉｌｔｅｒｗｉｔｈＦＰＧＡ．Ｋｅｙｗｏｒｄｓ：ＤＤＣ；ＣＩＣｆｉｌｔｅｒ；ＩＳＯＰｆｉｌｔｅｒ；ＦＰＧＡ
（４）
单极ＣＩＣ滤波器的旁瓣电平是比较大的，只比主瓣低
１３．４６ｄＢ，只也就是意味着阻带衰减很差，一般难以满足实用

改进型CIC抽取滤波器设计与FPGA实现

改进型CIC抽取滤波器设计与FPGA实现张杰;戴宇杰;张小兴;吕英杰【摘要】为了改善级联积分梳状(CIC)滤波器通带不平和阻带衰减不足的缺点,给出一种改进型CIC滤波器.该滤波器在采用COSINE滤波器提高阻带特性的基础上,级联了一个SINE滤波器,补偿了其通带衰减.硬件实现时,采用新的多相分解方法结合非递归结构,不仅大大减少了存储单元数量,还使电路结构更加规则.经仿真和FPGA 验证,改进型CIC滤波嚣使用较少硬件,实现了阻带衰减100.3 dB,通带衰减仅为0.000 1 dB.【期刊名称】《现代电子技术》【年(卷),期】2009(032)010【总页数】3页(P22-24)【关键词】CIC抽取滤波器;COSINE滤波器;SINE滤波器;设计优化;FPGA【作者】张杰;戴宇杰;张小兴;吕英杰【作者单位】南开大学,南开大学微电子所,天津,300071;南开大学,南开大学微电子所,天津,300071;南开大学,南开大学微电子所,天津,300071;南开大学,南开大学微电子所,天津,300071【正文语种】中文【中图分类】TP368.1抽取滤波器是Σ-Δ模/数转换器中的重要组成部分，积分梳状滤波器经常作为第一级滤波器,用以实现抽取和低通滤波[1]。

其优点是实现时不需要乘法器电路，且系数为整数，不需要电路来存储系数，同时通过置换抽取可以使部分电路工作在较低频率，与相同滤波性能的其他FIR滤波器相比，节约了硬件开销[2]。

经过仿真，抽取率为32的一阶积分梳状滤波器第一旁瓣相对于主瓣的衰减最大约为15 dB，这样的阻带衰减根本达不到实用滤波器的设计要求。

为了改变滤波性能，一般采用级联积分梳状滤波器(CIC)[3]。

但经过CIC降频滤波系统降频后会产生信号混叠现象，并且主瓣曲线不平，需要用新的算法或新结构来修正改善这些特性。

1 CIC抽取滤波器原理经典的抽取滤波器为Hogenauer [3]CIC滤波器，其传输函数表达式为：(1)式中：参数M为降频因子，决定了CIC的通带大小；K为滤波器的阶数，对阻带衰减起到加深作用。

Xilinx器件CIC滤波器设计实现

DS613 March 24, 2008

1
Product Specification
CIC Compiler v1.1
Frequency Response Characteristics
The frequency response of a CIC filter is obtained by evaluating Equation 1 at:
implementations • Optional mapping to DSP48/E/A primitives • Synchronous clear input • Clock enable input
General Description
The Xilinx LogicCORETM IP CIC Compiler core v1.1 provides the ability to design and implement Cascaded Integrator-Comb (CIC) filters for a variety of Xilinx FPGA devices. CIC filters, also known as Hogenauer filters, are multi-rate filters often used for implementing large sample rate changes in digital systems. They are typically employed in applications that have a large excess sample rate. That is, the system sample rate is much larger than the bandwidth occupied by the processed signal as in digital down converters (DDCs) and digital up converters (DUCs). Implementations of CIC filters have structures that use only adders, subtractors, and delay elements. These structures make CIC filters appealing for their hardware-efficient implementations of multi-rate filtering.

cic滤波器的fpga实现

cic滤波器的FPGA实现发布时间：2016-01-26 15:07:21技术类别：CPLD/FPGA一、关于多采样率数字滤波器很明显从字面意思上可以理解，多采样率嘛，就是有多个采样率呗。

前面所说的FIR，IIR滤波器都是只有一个采样频率，是固定不变的采样率，然而有些情况下需要不同采样频率下的信号，具体例子我也不解释了，我们大学课本上多速率数字信号处理这一章也都举了不少的例子。

按照传统的速率转换理论，我们要实现采样速率的转换，可以这样做，假如有一个有用的正弦波模拟信号，AD采样速率是f1，现在我需要用到的是采样频率是f2的信号，传统做法是将这个经过f1采样后的信号进行DA转换，再将转换后的模拟信号进行以f2采样频率的抽样，得到采样率为f2的数字信号，至此完成采样频率的转换但是这样的做法不仅麻烦，而且处理不好的话会使信号受到损伤，所以这种思想就被淘汰了，现在我们用到的采样率转换的方法就是抽取与内插的思想。

二、抽取先来总体来解释一下抽取的含义：前面不是说，一个有用的正弦波模拟信号经采样频率为f1的抽样信号抽样后得到了数字信号，很明显这个数字信号序列是在f1频率下得到的，现在，假如我隔几个点抽取一个信号，比如就是5吧，我隔5个点抽取一个信号，是不是就是相当于我采用了1/5倍f1的采样频率对模拟信号进行采样了？所以，抽取的过程就是降低抽样率的过程，但是我们知道，这是在时域的抽样，时域的抽样等于信号在频域波形的周期延拓，周期就是采样频率，所以，为了避免在频域发生频谱混叠，抽样定理也是我们要考虑的因素下面来具体来介绍如上图所示，假如上面就是某一有用信号经采样频率f1抽样得到的频谱，假设这时候的采样频率为8Khz ，可以通过数格子得到，从0到F1处有8个空格，每个空格代表1Khz，有些朋友可能会问，这不是在数字频域吗，单位不是π吗，哪来的hz？是的，这里是数字频域，采样频率F1处对应的是2π，这里只是为了好解释，我们用模拟频率来对应数字频率。

(完整版)CIC滤波器的原理与设计

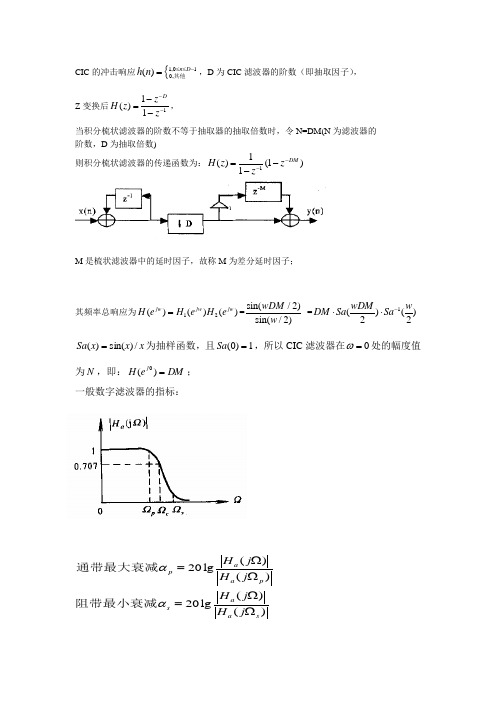
CIC 的冲击响应{1,010,()n D h n ≤≤-=其他，D 为CIC 滤波器的阶数（即抽取因子），Z 变换后11()1Dz H z z ---=-，当积分梳状滤波器的阶数不等于抽取器的抽取倍数时，令N=DM(N 为滤波器的阶数，D 为抽取倍数)则积分梳状滤波器的传递函数为：)1(11)(1DM z zz H ----=M 是梳状滤波器中的延时因子，故称M 为差分延时因子；其频率总响应为12()()()jw jw jwH e H e H e ==sin(/2)sin(/2)wDM w =1()()22wDM wDM Sa Sa -⋅⋅x x x Sa /)sin()(=为抽样函数，且1)0(=Sa ，所以CIC 滤波器在0=ω处的幅度值为N ，即：DM e H j =)(0；一般数字滤波器的指标：()20lg()()20lg ()a pa p a s a s H j H j H j H j ααΩ=ΩΩ=Ω通带最大衰减阻带最小衰减即：CIC 幅频特性响应曲线图由其频率响应函数可以看出其主瓣电平最大为D ，旁瓣电平为21.51()sin(3/2)/sin(3/2)sin(3/2)j DMH e DM DM ωπωπππ=⋅==，旁瓣与主瓣的差值（用dB 数表示）为： dB A DM s 46.1323lg 20lg201===πα 可计算出旁瓣与主瓣的差值约为13.46，意味着阻带衰减很差，单级级联时旁瓣电平很大，为降低旁瓣电平，增加阻带衰减采用级联的方式，N 级频率响应为：)2()2()()2/sin()2/sin()(ωωωωωQ Q Q Qj Q Sa DM Sa DM DM e H -⋅⋅=⎥⎦⎤⎢⎣⎡=，可得到N 级CIC 的旁瓣抑制 dB Q Q A DM Q Qs )46.13(23lg 20)lg(201⨯=⋅==πα 分析一下发现在Q 级联时多出了Q DM 这个处理增益，因此分析一下尽量减少带内容差(通带衰减），即，在通带内，幅度应尽量平缓；下面就它的幅平响应曲线来分析：00()20lg ()()20lg()ps j a p jw a j a s jw a H e H eH e H e αα==1、设在红线w1处抽取的信号带宽很窄，为无混叠信号的带宽,能很好的对窄带信号进行滤波，去除掉高频信号噪声；且在绿线w2=2pi/DM-w1处衰减值足够大，则在其信号带宽内，红线到绿线，信号给CIC 滤波器带来的混叠就可以忽略，计算此时阻带衰减：)2/sin()2/sin(lg 20()(lg 2022012w DM w DM e H e H A jw j ==·引入带宽比例因子b=B/（fs/DM ）, B 为抽取信号的带宽，D 为抽取因子，M 为延时因子；fs 为输入端采样率，则w1=b*2pi/DM ；带入可化简得：b A lg 201-≈；（假设b=0.01;即fs=100MHz ，D=20，信号带宽为50khz,此时衰减为40dB);可见单级的CIC 滤波器的无混叠信号带宽内的阻带衰减能达到40dB;；并不怎么大，适用于较粗略的滤波，适合放在第一级抽取；如果采用级联的方式可以加大无混叠信号带宽；但是满足的通带不够窄；2、在红线w1处幅度不能下降太多，通带内幅值容差不能太大，否则会引起高频失真；设该带内容差为s δ，则,)()(lg 2010jw j s e H e H =δ将w1带入可简化得)sin(lg 20b bs ππδ≈，当N 级时，其带内容差也会增大；由上面分析可知，阻带衰减和带内容差，只与带宽比例因子b 有关，Df Bb s /=,分析可知，在信号带宽一定的前提下，应尽可能采用小的抽取因子，或增大输入采样率；故一般把它放在抽取系统的第一级，所以在配置CIC 时，信号带宽，采样率，抽取因子，综合考虑，下面是阻带衰减和通带衰减的一个表：表1：大抽取因子下的通带衰减由CIC频幅响应图可以发现，幅频特性的零点位于1/M处(M取值为整数)，这说明差分因子M决定了零点的位置；抽取因子D狭定了抽取后信号的采样频率，它同差分延时因子M一起还决定了主瓣和旁瓣的宽度；级数Q可以用来控制阻带衰减，Q越大阻带衰减越大，通带内的混叠就越小，但Q越大，通带内主瓣衰减也越大，所以Q不可太大，不宜超过5级。

FPGA的CIC滤波器的设计

FPGA的CIC滤波器的设计1.原理概述CIC滤波器由差分器、积分器和组合器三部分组成，可有效实现信号的重采样和滤波功能。

其基本原理是将输入信号通过差分器进行差分运算，然后经过积分器进行累积运算，最后通过组合器实现滤波和重采样。

CIC滤波器的特点是具有高的通带增益和截止频率，且不需要乘法器和存储器，适合在FPGA中实现。

2.设计步骤(1)确定CIC滤波器的设计参数，包括增益因子、积分阶数、截止频率等。

(2)根据设计参数计算滤波器的结构参数，包括输入和输出数据宽度、积分器的阶数和阶间差值等。

(3)根据计算结果，设计CIC滤波器的硬件结构，包括差分器、积分器和组合器的实现方法。

(4) 使用HDL语言（如Verilog或VHDL）编写FPGA的CIC滤波器的代码，同时进行功能仿真和波形仿真。

(5)在FPGA开发板上进行综合、布局布线和验证，实现CIC滤波器的硬件设计。

3.设计关键技术(1)差分器设计：差分器实现差分运算，可以简单采用异或门或加减器实现。

需要注意输入信号的幅度范围和差分器的输出范围。

(2)积分器设计：积分器实现累积运算，需要考虑积分阶数、数据宽度和溢出等问题。

可以采用寄存器与加法器的串行或并行结构实现。

(3)组合器设计：组合器实现滤波和重采样功能，需要根据设计参数确定组合器的截止频率和增益系数。

可以采用多级组合器结构实现。

(4)输入输出接口设计：FPGA的CIC滤波器需要与外部系统进行数据交换，因此需要设计合适的输入输出接口，包括数据接口、时钟接口和控制接口等。

4.实现优化技术(1)折叠积分器：为了减少资源占用和延迟，可以采用折叠积分器结构，将多级积分器合并为一个积分器实现。

(2)级联结构：为了增加滤波器的阶数和降低截止频率，可以采用级联结构，将多个CIC滤波器级联实现。

(3)变系数设计：为了实现可调节的滤波参数，可以设计可变系数的CIC滤波器，在运行时动态调整增益因子和积分阶数。

综上所述，FPGA的CIC滤波器设计是一项复杂的数字信号处理任务，需要深入理解CIC滤波器的原理和设计方法，结合FPGA的硬件实现技术进行设计和优化。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

CIC插值滤波器的FPGA设计与实现
摘要：基于多速率信号处理原理，设计了用于下变频的CIC插值滤波器，由于CIC 滤波器结构只用到加法器和延迟器，没有乘法器，很适合用FPGA来实现，所以本文分析了CIC滤波器的原理，性能及影响参数，借助MATLAB设计符合系统要求CIC 滤波器，并利用Modelsim软件建模仿真，验证CIC滤波器性能是否达到要求。

（一）CIC滤波器基本原理
A．CIC滤波器的基本单元
CIC滤波器主要由积分滤波Integrator和梳状滤波Comb两个基本单元部分构成。

典型的CIC滤波器的结构，它由两个基本单元I(积分滤波器)和C（梳状滤波器）级联构成。

本设计主要针对插值滤波器，所以插值滤波器的结构示意图如图1-1所示：
图 1-1 3级级联的CIC插值滤波器结构示意图
积分器和梳状滤波器之间是一个采样率转换器，对于CIC插值器而言，它完成在每一个样值后补上R-1个0值的工作，，对于CIC抽取器来说，它完成在实际的抽取工作，每R个样值中取样一个。

R（插值倍数）,M（延迟因子，一般取1或者2）以及N（级联级数）是影响CIC 滤波器的三个参数，它们的值需根据通带性能的需求而设定。

（二）CIC插值滤波器的设计流程
根据CIC滤波器的原理，本设计的流程如图2-1所示：
图2-1 CIC 插值滤波器的设计流程图
（三）模型的建立和测试
A ．位宽策略
对于数字滤波器，一个不得不考虑的问题是为防止溢出每一级所需的位宽。

对于抽取器来说，CIC 滤波器的输出增益为
(*)N
G R M = （3-1）
所以，在全精度的情况下，最后一级输出的位宽为
2log (*)out in B B N R M =+ （3-2）
其中in B 表示输入数据的宽度，为了保证精度，每一个积分器和梳状滤波器的输入输出位宽都为out B 。

对于插值器而言，输出增益为
212,1,2,....2(*)/,1, 2......2i i N i N i N G R M R i N N N --⎛⎫
== ⎪ ⎪
=++⎝⎭ （3-3）
因此，第i 级为避免溢出所需要的位宽为
2log ()i in i W B G =+ （3-4）
最后一级输出位宽为
22log (*)log out in B B N R M R =+- （3-5）
在实际当中，当差分延时M=1时，为保证稳定，所有积分器的位宽在理论值的基础上加一。

max B 不仅是滤波器输出的最大可能的位数，也是每一级滤波器的最大可能位
数。

但有时候，输出位宽需要根据实际需要引入四舍五入或截取的方法来减少位数。

简单的做法是直接在输出端做四舍五入或者截取，更复杂点的方式是在每一级都做四舍五入或者进行截取。

这自然需要研究一下因四舍五入或截取所引起的滤波器输出端误差，具体的方法就是通过单独研究每一级误差源（指每一级滤波器截取或四舍五入引起的误差）的均值和方差，利用统计特性研究滤波器输出端总的均值和方差。

表 3.1不同参数全精度下的输出位宽
根据实际时的滤波器结构，可以认为误差源有2N+1个：2N个滤波器级因四舍五入或截取所产生的误差源和一个输出寄存器因四舍五入或截取所产生的误差源。

对于CIC滤波器的三个基本单元，都不涉及乘法器，而采样率变换器不使用任何运算单元。

（四）CIC滤波器的matlab仿真
在matlab的程序里，分三部分即根据CIC插值滤波器的原理进行描述。

激励信号采样正弦信号，以及白噪声信号的测试模型。

测试信号的点数，正弦信号的频率和采样率可以根据需要设定。

1.仿真结果
图4-1是CIC插值滤波器的频率响应曲线，其中正弦频率fs=200Hz,采样率Fs=800Hz。

图4-1 CIC插值滤波器的频响曲线
图4-2是正弦信号做完4倍插值前后曲线的比较
图4-2 正弦信号经过CIC插值滤波器前后的信号（N=3，R=4，M=1）
白噪声信号的频率响应曲线如图4-3所示，而经CIC滤波器处理后的白噪声信号频率响应曲线如图4-4所示。

图4-3 白噪声的频率响应
图4-4 白噪声经过CIC插值滤波器处理后的频率响应（N=3，M=1，R=4）
(五) CIC 滤波器的FPGA 实现
1. 接口设计
图5-1 CIC 插值滤波器的接口符号
表5.1：CIC 滤波器的管脚说明
2.子模块的划分和定义
按照MATALB 仿真时的方式，将子模块划分为积分器（interg ），梳状滤波器（comb ）和采样率变换器（in ）三个子模块。

图5-2 子模块的划分框图及接口声明梳状滤波器的实现(M=3)：
图5-3 梳状滤波器RTL框图，N=3
积分滤波器的实现(M=3)：
图5-4 积分滤波器RTL框图，N=3
采样率变换器（插值补零）的实现：
图5-5 采样率变换器RTL框图
其中cnt为计数器,即实现的插值倍数。

3.测试方式
在传统的设计方法中，一般采用图4-2的方式进行测试，这种方式结构简单，目标明确，但是testbench模块以及其激励信号是不可综合的，因而无法在FPGA 上进行测试和调试。

因此本设计testbench的模块流程如下：
图5-6 testbench模块的结构图
这种结构更方便结果的对比，而且是可综合模块，可以在FPGA上进行调试。

4测试结果
图5-7是N=3，R=4，M=1时的4倍插值RTL仿真结果。

从上到下，依次是输入使能，时钟，输入，复位，使能，插值后的正弦波形，插值前的正弦波形。

图5-7 一个周期128采样点的正弦信号4倍插值RTL仿真结果从图中可以看出CIC滤波器很好的完成了正弦信号的插值工作。