一种分析和设计抗混叠滤波器的方法
滤波器设计软件综述

滤波器设计软件综述目前网使用较普遍的滤波器设计软件有FilterShop、Filter Solutions、Filter Wiz Pro、FilterCAD、FilterLab和FilterPro等。
下面分别对这六种设计软件作简要介绍,由于用FilterLab软件来设计和操作简单,本人也大致使用过,因此对该软件作些详细论述。
一、FilterShopFilterShop是一款精确的模拟/数字滤波器设计软件,由美国LinearX Systems 公司所研发。
此软件是一套完整的用于AC电路模拟滤波器的设计软件,可满足对于滤波器设计有独特要求的功能,可提供混合的模拟/数字滤波器设计,以及AC电路模拟器的图表输入和编辑功能,完美的AC电路设计和建模,避免DC偏压电路的缺陷。
具有快速分析和纠正噪声的1200种模式,特殊混合信号组成包括FDNRs,FIR/IIR滤波器,Z-Imp,Pots等。
混合信号源功能以及电路设计能容易的整合和建模,从而作为一个单独的系统。
FilterShop出现在SPICE之后。
然而SPICE是一微观层面的分析工具,FilterShop是一种真正的宏观系统设计工具。
FilterShop已经建立了从基层开始处理的特殊滤波器设计需求,并且提供了大量的其它软件没有的功能。
配备专有的电路模拟引擎,先进的模数混合设计单元,以及一个庞大的目标生成系统——FilterShop在模拟/数字滤波器的设计和分析上展现了一个新的能力水平和技巧。
二、Filter Solutions功能特点:1、高斯、贝赛尔、巴特沃斯、勒让德、切比雪夫I型、切比雪夫Ⅱ型、沙漏、椭圆、升余弦、匹配和延时滤波器。
2、低通、高通、带通、带阻和非对称带通。
3、实时反馈对滤波器分析修正。
4、矢量形式的S和Z变换使得易与Matlab和Matrix-x对接。
5、显示传输函数、零极点图示、时间响应、频率响应和理想滤波器设计的反射系数。
6、S和Z变换的串并联形式。
改进的高性能CIC抗混叠滤波器

2012年第07期,第45卷 通 信 技 术 Vol.45,No.07,2012 总第247期 Communications Technology No.247,Totally改进的高性能CIC抗混叠滤波器皇甫文斌, 朱 江, 王世练(国防科学技术大学 电子科学与工程学院,湖南 长沙410073)【摘 要】这里对一种旋转锐化级联积分梳状滤波器(RSCIC,Rotated Sharpening Cascaded Integrator Comb Filter)进行了研究,RSCIC由锐化级联积分梳状滤波器(SCIC,Sharpening Cascaded Integrator Comb Filter)和旋转内插滤波器(Rotated Sinc Filter)两部分构成。
RSCIC可有效地提高传统积分梳状滤波器(CIC, Cascaded Integrator Comb Filter)的通带和阻带传输性能,特别适合采样率转化。
仿真表明,在同等条件下,RSCIC滤波器的阻带衰减性能比传统的CIC滤波器提高了22 dB,通带抗衰减性能比传统的CIC滤波器提高了0.5 dB。
【关键词】采样率转换;积分梳状滤波器;锐化级联积分梳状滤波器;旋转内插滤波器【中图分类号】TN911.72 【文献标识码】A 【文章编号】1002-0802(2012)07-0119-03 Improved High Performance CIC FilterHUANGFu Wen-bin, ZHU Jiang, WANG Shi-lian(School of Electronic Science and Engineering, National University of Defense Technology,Changsha Hunan 410073, China)【Abstract】CIC(Cascaded Integrator Comb) filter, for its simple hardware, is a most commonly-used multistate filter. However, the large distortion of the pass-band and the attenuation of the stop-band limit its applications, a new cascade structure is studied and proposed. Simulation shows that the proposed structure could improves the stop-band attenuation by 30dB as compared with the traditional CIC Filter. The new structure is quite good in the sampling rate conversion.【Key words】sample rate conversion;CIC;sharpening CIC;rotating sharpening CIC0 引言积分梳状滤波器CIC [1]结构简单,不使用乘法器,且不需要预先存储滤波器系数,是目前用于采样率转换常用的滤波器,但是,单一积分梳状滤波器通带和阻带性能相对较差,无法满足实际应用要求[2]。
便携式数据采集系统中自适应抗混叠滤波器的设计

便携式数据采集系统中自适应抗混叠滤波器的设计谭青;龙杰强【摘要】针对设备监测与故障诊断系统中便携式数据采集系统的设计要求,采用单片8阶椭圆低通滤波器MAX293设计了向AD端集成的内置抗混叠滤波器.提出了独特的自适应抗混叠滤波方案,阐述了其在数据采集过程中的实现原理,设计了相应的硬件实现电路,并给出了滤波过程中非线性相移误差的软件校正方法.【期刊名称】《现代电子技术》【年(卷),期】2007(030)005【总页数】3页(P98-100)【关键词】数据采集;开关电容滤波器;抗混叠滤波;MAX293【作者】谭青;龙杰强【作者单位】中南大学,机电工程学院,湖南,长沙,410083;中南大学,机电工程学院,湖南,长沙,410083【正文语种】中文【中图分类】TN713数据采集系统是设备监测与故障诊断系统的重要组成部分,他为设备的运行状态监测和诊断分析提供原始数据依据。
随着基于计算机的监测与诊断技术的发展,以往大体积、笨重、高价格的数据采集系统已难以适用其新的要求。
近年来,廉价、多功能、便携的数据采集系统的研制成为工业监测与诊断领域的新兴热门。
在某风机在线监测和故障诊断系统中,本文采用USB总线接口设计了内置抗混叠滤波器的便携式数据采集系统。
1 系统组成简介在传统数据采集系统的设计过程中,在传感器输出与AD输入之间,往往需要设计繁琐、复杂的信号调理电路以实现信号数据缓冲、放大、隔直、滤波等功能。
传统的数据采集系统如图1所示。
图1 传统数据采集系统的组成设计者通常是从传感器的标定技术指标出发进行设计,而传感器标定环境与实际工作环境之间存在的差别将影响到整个设计的精度。
随着IC技术和传感器技术的发展,许多传感器产品将放大、隔直、等信号调理电路进行精密IC设计内置,从而将其输出规格化成为标准工业信号4~20 mA,0~5 V。
在环境噪声许可的情况下,这种内置IC传感器产品输出可以与AD产品输入进行直连,从而简化数据采集系统。
(完整版)CIC滤波器的原理与设计
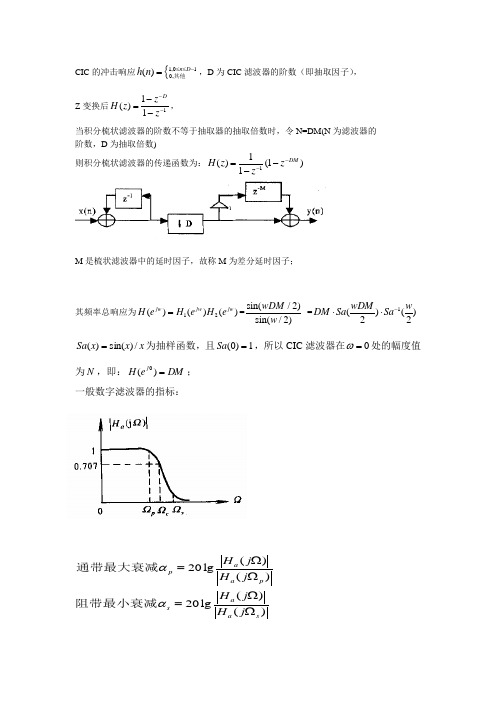
CIC 的冲击响应{1,010,()n D h n ≤≤-=其他,D 为CIC 滤波器的阶数(即抽取因子),Z 变换后11()1Dz H z z ---=-,当积分梳状滤波器的阶数不等于抽取器的抽取倍数时,令N=DM(N 为滤波器的 阶数,D 为抽取倍数)则积分梳状滤波器的传递函数为:)1(11)(1DM z zz H ----=M 是梳状滤波器中的延时因子,故称M 为差分延时因子;其频率总响应为12()()()jw jw jwH e H e H e ==sin(/2)sin(/2)wDM w =1()()22wDM wDM Sa Sa -⋅⋅x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:DM e H j =)(0; 一般数字滤波器的指标:()20lg()()20lg ()a pa p a s a s H j H j H j H j ααΩ=ΩΩ=Ω通带最大衰减阻带最小衰减即:CIC 幅频特性响应曲线图由其频率响应函数可以看出其主瓣电平最大为D ,旁瓣电平为21.51()sin(3/2)/sin(3/2)sin(3/2)j DMH e DM DM ωπωπππ=⋅==,旁瓣与主瓣的差值 (用dB 数表示)为: dB A DM s 46.1323lg 20lg201===πα 可计算出旁瓣与主瓣的差值约为13.46,意味着阻带衰减很差,单级级联时旁瓣电平很大,为降低旁瓣电平,增加阻带衰减采用级联的方式,N 级频率响应为:)2()2()()2/sin()2/sin()(ωωωωωQ Q Q Qj Q Sa DM Sa DM DM e H -⋅⋅=⎥⎦⎤⎢⎣⎡=, 可得到N 级CIC 的旁瓣抑制 dB Q Q A DM Q Qs )46.13(23lg 20)lg(201⨯=⋅==πα 分析一下发现在Q 级联时多出了Q DM 这个处理增益,因此分析一下尽量减少带内容差(通带衰减),即,在通带内,幅度应尽量平缓;下面就它的幅平响应曲线来分析:00()20lg ()()20lg()ps j a p jw a j a s jw a H e H eH e H e αα==1、设在红线w1处抽取的信号带宽很窄,为无混叠信号的带宽,能很好的对窄带信号进行滤波,去除掉高频信号噪声;且在绿线w2=2pi/DM-w1处衰减值足够大,则在其信号带宽内,红线到绿线,信号给CIC 滤波器带来的混叠就可以忽略,计算此时阻带衰减:)2/sin()2/sin(lg 20()(lg 2022012w DM w DM e H e H A jw j ==·引入带宽比例因子b=B/(fs/DM ), B 为抽取信号的带宽,D 为抽取因子,M 为延时因子;fs 为输入端采样率,则w1=b*2pi/DM ;带入可化简得:b A lg 201-≈; (假设b=0.01;即fs=100MHz ,D=20,信号带宽为50khz,此时衰减为40dB);可见单级的CIC 滤波器的无混叠信号带宽内的阻带衰减能达到40dB;;并不怎么大,适用于较粗略的滤波,适合放在第一级抽取;如果采用级联的方式可以加大无混叠信号带宽;但是满足的通带不够窄;2、在红线w1处幅度不能下降太多,通带内幅值容差不能太大,否则会引起高频失真;设该带内容差为s δ,则,)()(lg 2010jw j s e H e H =δ将w1带入可简化得)sin(lg 20b bs ππδ≈,当N 级时,其带内容差也会增大;由上面分析可知,阻带衰减和带内容差,只与带宽比例因子b 有关,Df Bb s /=,分析可知,在信号带宽一定的前提下,应尽可能采用小的抽取因子,或增大输入采样率;故一般把它放在抽取系统的第一级,所以在配置CIC 时,信号带宽,采样率,抽取因子,综合考虑,下面是阻带衰减和通带衰减的一个表:表1:大抽取因子下的通带衰减由CIC频幅响应图可以发现,幅频特性的零点位于1/M处(M取值为整数),这说明差分因子M决定了零点的位置;抽取因子D狭定了抽取后信号的采样频率,它同差分延时因子M一起还决定了主瓣和旁瓣的宽度;级数Q可以用来控制阻带衰减,Q越大阻带衰减越大,通带内的混叠就越小,但Q越大,通带内主瓣衰减也越大,所以Q不可太大,不宜超过5级。
计算阶次分析中避免阶次混叠的滤波定阶方法及其应用

( eat n o Mehn a E g er g Istt o A m rdF reE gne n , e i 0 0 2 C ia D pr met f cai l ni e n , ntue f r oe oc nier g B in 107 , h ) c n i i i jg n
包 含 的阶次 。 为解 决 C T中容 易 出现 的 阶次 混 叠 问 题 , 文 深 O 本
接进行傅里叶分析将产生严重 的频率模糊 现象¨ 2。 I 为了解决这一问题 , 阶次分析应运而生 , 其核心思想是
对振 动信 号进 行等 角度 间 隔采 样 。传 统 的 阶次分 析 方 法是 基于模 拟 电路 的硬件 锁 相 原理 实 现对 模 拟形 式 的 振 动信号 的 等 角度 间 隔采 样 , 最 大 缺 点 是 所 需 设 其 备 较 多 , 场 试 验 过 程 繁 琐 。 随着 计 算 机 运 算 速 度 的 现 提 高 , 生 了 计 算 阶 次 分 析 方 法 ( o ptd Odr 产 C m ue re
旋转机械的振动信号分析是机械故 障诊断的重要
部分 , 由于其往 往是 非平 稳 的 , 对 这些 非 平 稳信 号 直 若
文 献 [ ] 导 了 以角 域重 采 样 为 目标 的 时 域 采 样 频率 8推 确 定方法 , 利 用 时 域采 样 频 率 确 定 后 续 角域 重 采样 并 阶次 , 定 程 度 上 解 决 了 混 叠 的 问题 。但 是 因 角 域 在一 重 采样是 插 值 运算 , 即便 所 用 的采 样 频 率 能满 足 限 制 信 号 阶次 的需 求 , 重采 样 的精 度 会 受 采 样 频 率 大 小 但 的严重影 响 , 至 导致 阶 次谱 图无 法 准 确 反 映信 号 所 甚
设计fir滤波器的方法

设计fir滤波器的方法
设计FIR滤波器的方法主要有以下几种:
1. 正交法:根据滤波器的频率响应要求,将滤波器的频率特性分解成一系列正交基函数,然后通过选取适当的基函数系数来确定滤波器的频率响应。
2. 窗函数法:根据滤波器的频率响应要求,在频域上选取一个窗函数,然后通过窗函数的傅里叶变换来确定滤波器的频率响应。
3. 最小二乘法:根据滤波器的频率响应要求,通过最小化输入输出误差的平方和,利用最小二乘法来确定滤波器的系数。
4. 频率采样法:根据滤波器的频率响应要求,在频域上选取一些特定的频率点,并指定这些点的增益值,然后通过求取这些频率点上的插值样值,从而确定滤波器的系数。
在实际应用中,常常根据具体的滤波器设计要求和计算复杂度的考虑,综合考虑以上方法,采用相关算法进行FIR滤波器的设计,如窗函数法与最小二乘法的结合,频率采样法与正交法的结合等。
滤波器设计中的误差分析与优化方法

滤波器设计中的误差分析与优化方法在滤波器设计过程中,误差是一个不可避免的问题。
由于实际电子组件的特性、制造工艺以及外界干扰等因素的存在,滤波器的性能可能与理论设计有所偏差。
因此,对滤波器误差进行分析和优化非常重要,以确保滤波器的效果和性能能够符合设计要求。
一、误差分析滤波器设计中的误差主要分为以下几类:1. 零点误差:零点是指滤波器的传递函数在某些频率上等于零的点。
在理论设计中,我们希望滤波器的零点位置能够准确地匹配设计要求。
然而,由于电子组件的非理想性和制造误差,滤波器的实际零点位置可能会发生偏移,导致滤波器的频率响应与预期有所差异。
2. 通带误差:通带是指滤波器在指定频率范围内能够传递信号的范围。
通带误差是指滤波器在通带内传输信号时引入的幅度变化误差。
这种误差通常是由于电路的增益非线性、元器件参数的变化或者制造误差等原因引起的。
3. 阻带误差:阻带是指滤波器在指定频率范围内能够抑制信号的范围。
阻带误差是指滤波器在阻带内未能完全抑制信号的误差。
这种误差通常是由于滤波器的阻带衰减能力不足、滤波器结构的非理想性等原因引起的。
4. 相位误差:相位是指滤波器对输入信号引入的时间延迟。
相位误差是指滤波器输出信号的相位与输入信号的相位之间的差异。
相位误差可能会导致信号失真和时域响应的改变。
二、误差优化方法针对滤波器设计中的误差问题,可以采用以下方法进行优化:1. 深入分析滤波器的频率响应特性,了解误差来源。
通过理论分析和仿真实验等手段,分析滤波器误差的具体原因,找出误差来源。
这样可以有针对性地进行优化。
2. 选择合适的电子组件和制造工艺。
不同的电子组件和制造工艺对滤波器的性能和误差有不同的影响。
因此,在滤波器设计中选择合适的电子组件和制造工艺非常重要,可以在一定程度上减小误差。
3. 采用校正技术来减小误差。
校正技术是一种通过调整滤波器的参数或者增加校正电路来减小误差的方法。
通过校正技术,可以在滤波器设计中对误差进行补偿,提高滤波器的性能。
simulink过滤100khz波形参数设计

simulink过滤100khz波形参数设计在Simulink中设计100kHz的滤波器需要考虑滤波器的类型、参数设置以及性能评估。
首先,我们需要选择合适的滤波器类型,如低通、高通、带通或带阻滤波器等。
然后,根据信号的特点和需求来选择合适的滤波器参数,如截止频率、阶数、抗混叠设计和幅度响应等。
最后,利用Simulink进行滤波器的搭建和性能评估。
1.选择滤波器类型:根据100kHz波形的要求,我们选择低通滤波器来剔除在100kHz以外的频率成分。
2.设计滤波器参数:2.1.截止频率:-截止频率决定了滤波器的频率特性,一般选择在滤波后的信号中主要成分基本消失的频率。
-在低通滤波器中,截止频率以上的频率成分会被剔除。
-根据具体需求,选择合适的截止频率,如100kHz附近的值。
2.2.阶数:-阶数决定了滤波器的陡降程度,一般可以选择更高的阶数以增加滤波器的抑制能力。
-阶数越高,滤波器的频率响应越陡峭,但也会带来更多的计算复杂度。
-根据信号特点和计算资源的考虑,选择合适的阶数。
2.3.抗混叠设计:-根据采样定理,要避免混叠,滤波器的截止频率应该小于采样频率的一半。
-如果采样频率为200kHz,则滤波器的截止频率应小于100kHz。
2.4.幅度响应:-幅度响应描述了滤波器在不同频率下的衰减或增益特性。
-根据应用需求,选择合适的幅度响应,如可以选择低通滤波器的平坦或者有特定衰减特性的幅度响应。
3.使用Simulink搭建滤波器:在Simulink中,我们可以使用滤波器模块来搭建滤波器系统。
具体步骤如下:3.1.打开Simulink,并新建一个模型文件。
3.2.在模型中选择滤波器类型,并设置对应的参数,如截止频率、阶数等。
3.3.将输入信号接入滤波器系统,并连接到输出信号。
3.4.运行模型来观察滤波后的波形效果。
4.性能评估:使用Simulink可以方便地进行滤波器的性能评估,包括频率响应、相位响应、幅度响应等。
