25.4圆周角(第二课时圆的内接四边形)
2.2.2 第2课时 圆周角定理2和圆内接四边形

课堂小结
通过这节课的学习,我们学习到哪些知识?
1.直径所对的圆周角是直径;90°的圆周角所对的弦是直径.
2.圆内接四边形的对角互补.
结束寄语
下课了!
•生活是数学的源泉. • 探索是数学的生命线.
解:
∵AB是直径,
C
∴∠C = 90°.
A
O·
B
∴△ABC为直角三角形.
∴∠ABC+ ∠CAB= 90°. ∴∠ABC+ ∠CAB= 90°- ∠CAB = 90°- 65°= 25°.
3.如图,圆内接四边形ABCD的外角 ∠DCE=85°,求∠A的度数.
解 ∵∠DCE=85°, ∴∠BCD=95°. ∵四边形ABCD是圆O的内接四边形, ∴∠BCD+∠A=180°.
解 ∵圆心角∠BOD与圆周角∠BAD所对的弧 为B» D ,∠BO1 D=100°.1 ∴∠BAD= 2∠BOD= 2 ×100°=50°. ∵∠BCD+∠BAD=180°, ∴∠BCD=180°-∠BAD=180°-50°=130°.
练习
1. 如图,AB是圆O的一条直径, ∠CAB=65°, 求∠ABC的度数.
»A B所对的圆周角,
观察:
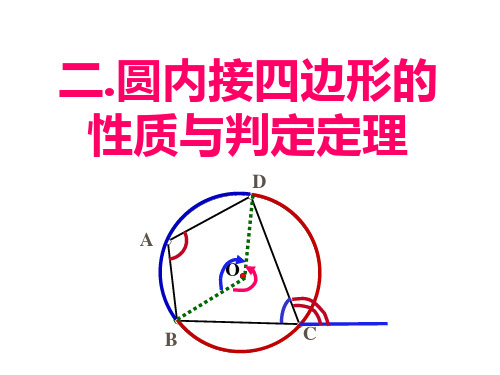
如图,A,B,C,D是⊙O上的四点,顺次连 接A,B,C,D四点,得到四边形ABCD,我 们把四边形ABCD称为圆内接四边形. 这个圆叫作这个四边形的外接圆.
动脑筋
在图的四边形ABCD中,两组对角∠A与∠C, ∠B与∠D有什么关系?
连接OB,OD,
∵∠A所对的弧为 B¼C D ,∠A
所对的弧为 B¼A D ,又 B¼C D
与B¼A D 所对的圆心角之和是圆周
角,
《圆周角》圆PPT(第2课时圆内接四边形的性质)

第二十四章 圆
上一页 返回导航 下一页
证明:∵AD平分∠CAE,
∴∠EAD=∠DAC.
∵∠DAC=∠DBC.
PPT模 板 : /moban/ PPT背 景 : /beijing/
∴∠EAD=∠DBC. PPT素材:/sucai/
地 理 课 件 : /kejian/dili/
历 史 课 件 : /kejian/lishi/
∵四边形ABCD内接于⊙O,
∴∠DAB+∠BCD=180°.
又∵∠EAD+∠DAB=180°,
∴∠EAD=∠BCD,
∴∠DBC=∠DCB,
∴BD=CD.
第二十四章 圆
PPT下 载 : /xiazai/
PPT教 程 : /powerpoint/
资 料 下 载 : /ziliao/
个 人 简 历 : /jianli/
试 卷 下 载 : /shiti/
试 卷 下 载 : /shiti/
教 案 下 载 : /jiaoan/
手 抄 报 : /shouchaobao/
PPT课 件 : /kejian/
语 文 课 件 : /kejian/yuwen/ 数 学 课 件 : /kejian/shuxue/
语 文 课 件 : /kejian/yuwen/ 数 学 课 件 : /kejian/shuxue/
英 语 课 件 : /kejian/yingyu/ 美 术 课 件 : /kejian/meishu/
科 学 课 件 : /kejian/kexue/ 物 理 课 件 : /kejian/wuli/
教 案 下 载 : /jiaoan/
手 抄 报 : /shouchaobao/
PPT课 件 : /kejian/
圆周角_第二课时- 课件

知识回顾 问题探究 课堂小结
探究二: 圆的内接多边形
重点、难点知识★▲
活动2 探索圆的内接四边形四个角之间的关系。
∠A和∠C是四边形ABCD的一组对角,也是⊙O的圆 周角,它们在⊙O中所对的分别是哪两条弧?
这两条弧有什么关系? 从而∠A和∠C具有怎样的数量关系? ∠B和∠D也具有这样的关系吗?
这两条弧的度数之和为360°,从而∠A和∠C之和等 于360°的一半,也就是180°,∠B和∠D之和也为180°。
1 2
OA,根据含30°的
直角三角形三边的关系得到∠OAD=30°,接着根据
三角形内角和定理可计算出∠AOB=120°,然后根据圆周
角定理计算∠APB的度数。
知识回顾 问题探究 课堂小结
探究三 例题分析
活动2 提升型例题
【解题过程】 解:作半径OC⊥AB于D,连结OA、OB,如图, ∵将⊙O沿弦AB折叠,圆弧恰好经过圆心O,
1 ∴∠AOB=90°,∴∠ADB= 2 ∠AOB=45°, ∴∠AEB=180°﹣∠ADB=135°。 ∴此弦所对的圆周角等于45°或135°。
知识回顾 问题探究 课堂小结
探究三 例题分析
活动3 探究型例题
例5.已知弦AB、CD相交于E,»AC 的度数为90°,B»D 的度数为30°,则∠AEC=_6__0_°___。
∴弦AB所对的圆周角的度数为: 1 ∠AOB=20°或180°﹣20°=160°。 2
【思路点拨】由⊙O的弦AB所对的圆心角为40°,根据 圆周角定理与圆的内接四边形的性质,即可求得弦AB 所对的圆周角的度数。
知识回顾 问题探究 课堂小结
探究三 例题分析
活动2 提升型例题
练习4:在⊙O中,若弦AB长2 2 cm,弦心距为 2 cm,则此弦所对的圆周角等于______。
最新人教版九年级数学24.4圆周角第二课时圆内接四边形

圆心角、弧、弦、弦心距之间的关系
在同圆或等圆中, 如果两个圆心角、 两条弧、两条弦 中有有一一组量量相相等等,,那么它们所对应的其 余各组量都分别相等
第二页,共21页。
圆周角的定理:
在同圆或等圆中,同弧或等弧所 对的圆周角相等,都等于这条弧 所对的圆心角的一半。
第三页,共21页。
在圆内接四边形ABCD中,∠A、∠B、∠C的 度数之比是2:3:6,求这个四边形各角的度 数。
解:设∠A、∠B、∠C的度数分别是2x、3x、6x
第十二页,共21页。
1、如图,四边形ABCD为
⊙O的内接四边形,已知
∠BOD=100°,
则∠BAD= 50º
∠BCD=
130ºB
A
A
O D
C
B
2、如图,四边形ABCD内
第九页,共21页。
圆的内接四边形的对角互补,且 任何一个外角等于它的内对角。
如图,那些角互 补,哪两个角相 等?
第十页,共21页。
如图,哪些角相等呢?
4D
∠1=__∠__D_A_B ∠2=_∠__C__D_A ∠3=_∠__B__C_D ∠4=_∠___A_B_ C
A
3
O
B
2
C
1
第十一页,共21页。
2、 如上图(1),若弧BC的度数为1000, 则 ∠BOC=____10_0º,∠A=__ 50º
A
O
B
图1
C
第五页,共21页。
圆内接多边形与多边形的外接圆
一个多边形的所有顶 点都在同一个圆上,这 个多边形叫做圆的内 接多边形,这个圆叫 做这个多边形的外接 圆。
如图,七边形ABCDEFG是
2.圆的内接四边形
综上所述, 综上所述, 点D只能在圆 A 只能在圆 周上, 周上,即A、 、 B、C、D四 、 、 四 点共圆. 点共圆. B
O C
3 四边形存在外接圆的判定定理
说明:在此判定定理的证明中,用到了分类讨论的思想和 说明:在此判定定理的证明中,用到了分类讨论的思想和 分类讨论的思想 反证法.又当问题的结论存在多种情形时, 反证法.又当问题的结论存在多种情形时,通过对每一种 情形分别讨论,最后获得结论的方法,称为穷举法 穷举法. 情形分别讨论,最后获得结论的方法,称为穷举法.于是 圆内接四边形判定定理:如果一个四边形的对角互补, 圆内接四边形判定定理:如果一个四边形的对角互补,那 判定定理 么这个四边形的四个顶点共圆. 么这个四边形的四个顶点共圆.
C P Q A F B
练习2:
1、(1)圆内接平行四边形一定是 矩 形. (2)圆内接梯形一定是等腰梯形. (3)圆内接菱形一定是 正方 形. 2.如果四边形一边上的两个顶点的视角 D 相等,那么四边形的四个顶点共圆. 已知:如图,四边形ABCD中, ABCD ∠ADB=∠ACB. A 求证: A、B、C、D四点共圆. 分析:要用圆内接四边形判定定理或推论 无法找到足够 分析 要用圆内接四边形判定定理或推论,无法找到足够 要用圆内接四边形判定定理 的条件,即直接方法不易证明 于是仿照判定定理 即直接方法不易证明,于是仿照判定定理的证明 的条件 即直接方法不易证明 于是仿照判定定理的证明 反证法 用反证法.
C A D
O1
E B
O2
F
变式1:如图,⊙O1和⊙O2都经过 、B两点.过A点的 如图, 都经过A、 两点 两点. 点的
直线CD与 交于点C, 交于点D. 直线 与⊙O1交于点 ,与⊙O2交于点 .过B点的直线 点的直线 交于点E, 交于点F.求证: EF与⊙O1交于点 ,与⊙O2交于点 .求证:CE//DF. 与
第24章圆-圆周角与内接四边形(教案)

在今天的课堂中,我们探讨了圆周角与内接四边形的性质和应用。回顾整个教学过程,我觉得有几个方面值得反思。
首先,关于课堂导入,我发现通过提问的方式引起学生的兴趣和好奇心非常有效。大多数同学能够积极参与,分享他们在生活中遇到的与圆周角相关的问题。这种导入方式有助于拉近数学与现实生活的距离,让学生感受到学习的实用性。
2.教学难点
-圆周角定理的证明:对于学生来说,理解并掌握圆周角定理的证明过程可能存在困难。教师应通过直观的图形演示和逐步的逻辑推理,帮助学生理解证明的每一步。
-圆内接四边形的判定应用:在实际问题中,学生可能会难以识别哪些四边形是圆内接的,以及如何运用这一性质来解题。
举例:
-对于一个复杂的四边形问题,学生可能需要通过画图、分析角度关系、应用圆内接四边形的性质等多个步骤来解决问题,这要求学生对相关知识有深入的理解和灵活的运用能力。
在实践活动环节,分组讨论和实验操作使学生能够将理论知识应用于实际情境。学生们的积极参与让我感到欣慰。但同时,我也发现有些小组在讨论过程中过于依赖实验操作,而忽略了理论分析。针对这个问题,我计划在接下来的教学中,加强对学生理论分析的引导,让他们在实践中也能够深化对理论的理解。
此外,学生小组讨论环节,同学们提出了许多有创意的想法,展示了他们对圆周角与内接四边形在实际生活中应用的思考。但在讨论过程中,我也注意到有些学生发言不够积极。为了鼓励更多学生参与到讨论中来,我将在下一节课尝试采用一些激励措施,如设立“最佳发言人”等称号,以提高学生的积极性。
其次,在新课讲授环节,我采用了理论介绍、案例分析和重点难点解析相结合的方式。从学生的反馈来看,这种方法有助于他们更好地理解圆周角与内接四边形的性质。但我也注意到,部分学生在理解圆周角定理的证明过程中还存在困难。在今后的教学中,我需要更加关注这部分学生,通过设计更具针对性的教学活动,帮助他们突破难点。
人教版数学九年级上册 24.1.4 圆周角(第二课时)说课课件(共21张PPT)
说课内容
1 2 3 4 5
教材分析 教学目标 重点难点 教学过程 反思生成
教材分析
1. 本节课在教材所处的地位和作用:
圆内接四边形是在研究圆周角之 后的学习内容,从圆内接四边形 的四个角都是圆周角引入,它是 在圆中探求角的相等或互补时常 用的一个重要定理,是学生后续 学习的基础。
教学重点和难点
教学重点
教学难点
圆内接四边形的性质探索及应用
圆内接四边形的性质探索
教法与学法
教法:演示法,引
导启发式教学法
学法:观察、操作与数
学思考归纳相结合;自 主学习与小组合作探究 相结合
教学过程
1
课前热身,引入新知 2 合作探究,获取新知 3 师生合作,应用新知 4 课堂小结,提炼新知 5 课堂检测,体验成功
教学目标
教学目标
知识目标
技能目标
情感目标
通过观察图形认识圆 内接多边形和多边形 的外接圆;探索圆内 接四边形的性质定理 并运用它探求角之间 的关系.
经历圆内接四边形性 质定理的探索过程, 体会从特殊到一般、 数形结合、分类、归 纳、转化等数学思想 方法,发展学生的推 理能力.
鼓励学生敢于实践, 勇于发现,大胆探索, 认识数学的内在联系, 增强学习数学的兴趣。
四边形的外接圆: 图,△ABC是⊙O的 △ABC的外角平分线并
圆内接四边形的性质内:接三角形。 (1)若AD是
交⊙O于点D,连接BD, CD,上述结论还成立吗?
∠BAC的角平分线, 请你补全图形,若结论
交⊙O于点D.
成立,则给出证明;若
求证:BD=CD 结论不成立,则说明理
由。
反思
成功之处:本节课从回顾圆周角定理及推论入手,引入圆
第2课 圆心角与圆周角、圆内接四边形=2021年人教版新九年级数学上册 第二十四章 圆
C .圆心角与圆周角、圆内接四边形学生/课程 年级 学科 数学授课教师日期时段核心内容圆心角与圆周角、圆内接四边形课型一对一/一对N教学目标 1.理解并掌握圆心角、弦、弧之间的关系,能够运用他们的关系分析解决相关的几何问题 2.理解并掌握圆周角的概念以及圆周角定理和推论.并熟练运用解决实际问题。
重、难点1、圆心角与圆周角关系的转换,以及圆周角的推论的运用。
课首沟通1.学校的上课进度如何?你在学习这些内容的过程中都遇到什么问题? 2.上次的作业给我看看,完成了没有?还有不会的题吗?知识导图课首小测1.[单选题] 如图,已知点A (0,1),B (0,﹣1),以点A 为圆心,AB 为半径作圆,交x 轴于点C 和点D ,则DC 的长为( )A .2B .4D .22.[单选题] 已知⊙O的直径AB=10cm ,弦CD=8cm ,AB⊥CD,那么圆心O 到CD 的距离是()A.1cm B.2cm C.3cm D.4cm 3.如图,将半径为的圆形纸片折叠后,圆弧恰好经过圆心,则折痕的长为4.如图,矩形ABCD与圆心在AB上的圆O交于点G、B、F、E,GB=10,EF=8,那么AD=5.⊙O的半径为13 cm,弦AB∥CD,AB=24cm,CD=10cm,那么AB和CD的距离是Cm6.如图,已知AB是⊙O的弦,点C在线段AB上,OC=AC=4,CB=8.求⊙O的半径.导学一:圆心角知识点讲解1:弧、弦、圆心角1.圆心角:顶点在圆心的角叫做圆心角2.定理:(1)在同圆或者等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
(2)在同圆或者等圆中,相等的两条弧所对的圆心角相等,所对的弦也相等。
(3)在同圆或者等圆中,相等的两条弦所对的弧相等,所对的圆心角也相等。
特别注意:只有圆心角与弧存在倍数关系。
与弦不存在倍数关系。
例1. [单选题] 在下图中,下列各角是圆心角的是()A.∠ODC B.∠OCD C.∠AOB D.∠BDC例2. 指出下列哪些是∠AOB所对应的弦和弧?例3. 如图,将圆心角∠AOB绕圆心O旋转到∠A/OB/的位置你能发现哪些等量关系?为什么?完成下面的填空题。
九年级数学人教版上册24.1.4圆周角第2课时圆内接四边形教学设计
2.学生在几何证明过程中的逻辑思维能力,注重培养学生严谨的推理和证明习惯。
3.学生在解决圆内接四边形问题时,对图形的观察和分析能力,引导学生运用性质解决问题。
4.关注学生的学习兴趣和积极性,激发学生的学习动力,提高课堂参与度。
三、教学重难点和教学设想
(一)教学重难点
1.重点:圆内接四边形的性质及其应用。
2.难点:圆内接四边形对角互补的证明过程及其在实际问题中的应用。
(二)教学设想
1.对于重点内容的处理:
a.采用直观演示和动态图示相结合的方式,让学生形象地理解圆内接四边形的性质。
b.通过典型例题的讲解,引导学生运用性质解决实际问题,巩固重点知识。
4.教师对本节课的教学进行总结,指出学生的优点和不足,鼓励学生继续努力。
五、作业布置
为了巩固学生对圆内接四边形性质的理解和应用,以及提高学生的解题能力,特布置以下作业:
1.基础巩固题:
(1)判断以下图形是否为圆内接四边形,并说明理由。
(2)已知圆内接四边形ABCD,求证:∠A+∠C=180°,∠B+∠D=180°。
6.教学拓展:
a.引导学生探究圆内接四边形的性质在生活中的应用,提高学生的应用意识。
b.激发学生对几何学的兴趣,鼓励学生参加数学竞赛和课外活动,拓展知识面。
四、教学内容与过程
(一)导入新课
1.复习导入:通过提问方式复习圆周角定理,引导学生回顾圆周角的概念及其性质。在此基础上,提出问题:“圆内接四边形是否具有特殊的性质?”引发学生思考,为新课的学习做好铺垫。
b.计算题:计算圆内接四边形的对角线长度或角度。
c.应用题:运用圆内接四边形的性质解决实际问题。
《圆周角第2课时圆内接四边形》示范公开课教学设计【部编新人教版九年级数学上册】
《圆内接四边形》教学设计一、教学目标1.理解圆内接多边形的定义,掌握圆内接四边形的概念和性质;2.能运用圆内接四边形的性质证明和计算;3.经历圆内接四边形的性质的探究与证明,渗透“由特殊到一般”的数学思想方法;4.通过学生自主探究、合作交流的学习过程,体验实现自身价值的愉悦和数学的应用.二、教学重难点重点:圆内接四边形的概念及性质.难点:圆内接四边形与圆周角性质的综合应用.三、教学用具多媒体课件四、教学过程设计【回顾】同学们上一节课我们学习了圆周角定理及其推论,一起回顾一下吧.教师并提出问题,引导学生回顾上节课的内容,教师追问:直径是特殊的弦,它所对的圆周角相等,都是90°,那对于一般的弦,它所对的圆周角是否也相等呢?也就是说,同圆或等圆中,同弦或等弦所对的圆周角相等吗?【合作探究】猜想:∠B=∠E,∠D=∠F追问1:能否验证你的猜想呢?预设答案:∵∠B,∠E所对的弧都是AC;∠D,∠F所对的弧都是ABC;根据同弧所对的圆周角相等,得:∠B=∠E,∠D=∠F教师PPT展示,任意作出弦AC所对的4个圆周角,引导学生发现,根据角的顶点在弦的上方还是下方,把4个角归为两类,让学生提出猜想,并验证,最终教师PPT展示验证的过程.追问2:∠B=∠D吗?预设答案:不一定相等.教师提出问题后,引导学生先观察图形:不难发现,∠B是锐角,∠D是钝角.显然不相等.并进一步引导学生发现,若AC是直径,则它所对的圆周角∠B=∠D,从而得出结论:∠B=∠D不一定相等.追问3:∠B和∠D有什么数量关系呢?教师引导学生把问题转化为四边形的一组对角的数量关系,进一步让学生观察这个四边形有什么特点,引导学生发现四边形的四个顶点都在圆上,从而引出圆内接四边形的概念.如果一个四边形的所有顶点都在同一个圆上,这个四边形叫做圆内接四边形.这个圆叫做这个四边形的外接圆.如上图中,四边形ABCD 是⊙O 的内接四边形;⊙O 是四边形ABCD 的外接圆.追问3就转化为了:圆内接四边形的一组对角有什么关系?猜想:互补验证:连接OA ,OC .∵1=12B ∠∠,1=22D ∠∠又∵∠1+∠2=360° ∴∠B +∠D =()11+22∠∠=180° 同理:∠A +∠C =180°教师引导学生猜想,然后学生自主验证、小组交流后,尝试用语言归纳总结出所得结论.教师汇总并补充.圆内接四边形的对角互补.追问4:现在,你能回答课程刚开始的问题了吗?同圆或等圆中,同弦或等弦所对的圆周角相等吗?预设答案:同圆或等圆中,同弦或等弦所对的圆周角相等或互补.教师提出问题,引导学生回顾刚才探究的过程,然后得出结论,需要提醒的是,前面只探究了同弦所对的圆周角,对于同圆或等圆中等弦的情况,学生可自行探究.【延伸】预设答案:相等.证明:∵∠BCE+∠BCD=180°,∠BCD+∠A=180°∴∠BCE=∠A教师引导学生自主探究,小组交流后,尝试用语言总结出所得结论,选代表回答,教师补充.圆内接四边形的一个外角等于它的内对角.圆内接四边形也可扩展到圆内接多边形.如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形.这个圆叫做这个多边形的外接圆.【典型例题】教师提出问题,学生先独立思考,解答.然后再小组交流探讨,教师巡视,如遇到有困难的学生适当点拨,最终教师展示答题过程.例1:如图,四边形ABCD是圆的内接四边形,且ABCD是平行四边形.求证:四边形ABCD是矩形.解:∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D教师给出练习,随时观察学生完成情况并相应指导,最后给出答案,根据学生完成情况适当分析讲解.1.如图在圆内接四边形ABCD中,(1)若∠B=30°,则∠D=__.(2)若∠A∶∠C=5∶4,则∠A=__.答:(1)150°;(2)100°.2.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( ).A.69° B.42°C.48° D.38°答:A.3.若ABCD为圆内接四边形,下列可能成立的是( )A. ∠A∶∠B∶∠C∶∠D= 1∶2∶3∶4B. ∠A∶∠B∶∠C∶∠D= 2∶1∶3∶4C. ∠A∶∠B∶∠C∶∠D= 3∶2∶1∶4D. ∠A∶∠B∶∠C∶∠D=4∶3∶2∶1 答:B.思维导图的形式呈现本节课的主要内容:教科书第88页练习第2、5题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆内接四边形的性质定理
1.如图:圆内接四边形ABCD中, ∵ 弧BCD和弧BAD所对的 圆心角的和是周角. ∴∠A+∠C= 180° 同理∠B+∠D=180° A
O
D
圆内接四边形的性质定理1: 圆的内接四边形的对角互补.
B
C
2.圆内接四边形的性质定理A O.DBCE
圆内接四边形的性质定理2: 圆内接四边形的外角等于它的内角的对角.
二 定理的应用
练习一 :
1、如图,四边形ABCD为⊙O的
A
O
内接四边形,已知∠BOD=100°,
则∠BAD= 50º,∠BCD= 130º .
B
C
D
2、圆内接四边形ABCD中,∠A:∠B:∠C=2:3:4, 则∠A= 60º ∠B= 90º ∠C= 120º ∠D= 90º 设∠ A=2x,则∠ C=4x. ∵ ∠ A+ ∠ C=180º , ∴x=30º . 3、如图,四边形ABCD内接于⊙O, ∠DCE=75º ,则∠BOD= 150º A O
C D
A
O1
E B
O2
F
变式1:如图,⊙O1和⊙O2都经过A、B两点.过A点的
直线CD与⊙O1交于点C,与⊙O2交于点D.过B点的直线 EF与⊙O1交于点E,与⊙O2交于点F.求证:CE//DF.
D A E C
D
O
1
B
O
2
C
A
O2 O1
B
F
F
E
变式2:如图,⊙O1和⊙O2有两个公共点A﹑B.
由例1可知:CE//DF, 又∵CD//EF, 过A﹑B两点的直线分别交⊙O1于C 、E, ∴DCEF为平行四边 形. 交⊙O2于D 、F,且CD∥EF.求证:CE=DF. ∴CE=DF.
25.4圆周角(第二课时) ---圆内接四边形
D A
O
B
C
圆周角定理:圆上一条弧所对的圆周角等于它所对 的圆心角的一半. 圆心角定理:圆心角的度数等于它所对弧的度数. 推论1:在同圆或等圆中,同弧或等弧所对的圆周 角相等;反之,相等的圆周角所对的弧也相等.
推论2:半圆(或直径)所对的圆周角是直角; 反之,90°的圆周角所对的弦是直径.
课堂小结:
1 圆内接四边形的性质
对角互补 外角等于它的内对角
2、解题时应注意两点: (1)注意观察图形,分清四边形的外角和它的内对角 的位置,不要受背景的干扰. (2)证题时,常需添辅助线-----两圆共有一条弦,构 造圆内接四边形.
B
C
D E
练习二:
1、(1)圆内接平行四边形一定是 矩 形. (2)圆内接梯形一定是等腰梯形. (3)圆内接菱形一定是 正方 形.
例1:如图,已知A、B、C、D四点共圆,且AC=BC, E 求证:DC平分∠BDE 1 D C 2 证明: ∵ AC=BC ∴ ∠3= ∠CBA ∵ A、B 、C、D四点共圆 ∴ ∠1= ∠CBA ∵ ∠2= ∠3 ∴ ∠1= ∠2 B A 3
∴ CD平分∠BDE
例2:如图⊙O1与⊙O2都经过A、B两点.经过点 A的直线CD与⊙O1交于点C,与⊙O2交于点D.经 过点B的直线EF与⊙O1交于点E,与⊙O2交于点F. 求证:CE∥DF. 分析:只要证明同旁内角互补即可!
证明:连接AB. 并利用圆内接四边形的性质定理. ∵四边形ABEC是⊙O1的内接四边形,∴ ∠BAD=∠E. 又∵四边形ABFD是⊙O2的内接四边形, ∴ ∠BAD+∠F=180º . ∴ ∠E+∠F=180º . ∴ CE//DF.
A
1.定义:如果多边形的所有顶点都 在一个圆上,那么这个多边形叫做圆内 接多边形,这个圆叫做多边形的外接圆.
O B C
D
A F
A
B O
O B C
C
·
D
E
思考:
(1 ) 任意三角形都有外接圆吗?
(2)一般地,任意四边形都有外接圆吗?
(3)任意矩形是否有外接圆? 那么任意四边形有外接圆吗?
探究:观察下图,这组图中的四边形都内接于圆. 你能发现这些四边形的共同特征吗?
