第2课时 圆周角定理推论2及圆内接四边形的性质
《圆周角定理的推论》课件

所以 AB 为☉O 的直径.
探究点二
圆周角定理的推论2
[例2] 如图所示,AB为☉O的直径,CF⊥AB于点E,交☉O于点D,AF交☉O于点G.求证:
∠FGD=∠ADC.
[导学探究]
1.根据圆内接四边形的性质,可得∠ACD+ ∠AGD =180°,从而可得∠FGD= ∠ACD .
圆内接四边形的对角互补,并且任何一个外角都等于它的相邻内角的对角,这一
结论在探求角的相等或互补关系时常常用到.
点击进入
训练案
BE=DE,求证:AB为☉O的直径.
[导学探究]
,则∠DAE= ∠BAE
90° .
2.欲证 AB 为☉O 的直径,可证明∠AEB=
1.连结 AE,由 BE=DE 可得=
.
证明:如图所示,连结 AE,
因为 BE=DE,
所以=.
所以∠DAE=∠BAE.
因为 AB=AC,
所以 AE⊥BC.
第2课时
圆周角定理的推论
一、圆周角定理的推论
直径
1.90°的圆周角所对的弦是
2.圆内接四边形的对角 互补 .
.
二、外接圆、内接多边形
如果一个圆经过一个多边形的各个顶点,这个圆叫做这个多边形的
个多边形叫做这个圆的 内接多边形 .
外接圆 ,这
探究点一
圆周角定理的推论1
[例1] 已知等腰△ABC的顶点A,B在☉O上,AC=AB,AC,BC分别交☉O于点D,点E,若
2.根据垂径定理,可得=
,则∠ADC=
∠ACD
,从而可得结论.
证明:因为四边形 ACDG 内接于☉O,
所以∠ACD+∠AGD=180°.
圆周角定理和圆内四边形的性质典例精析
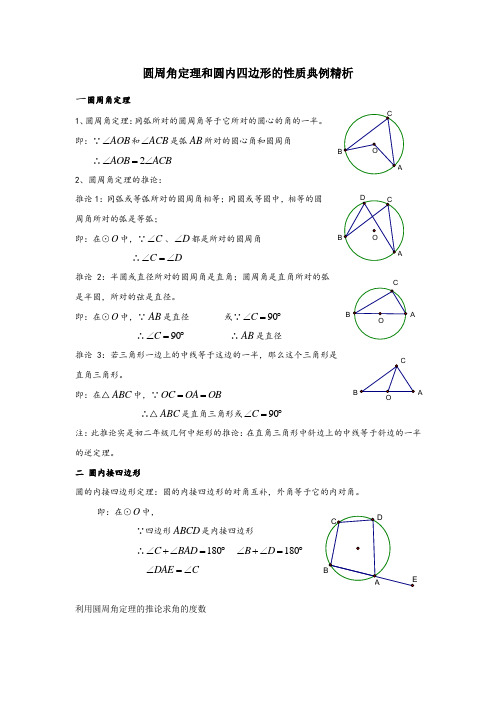
圆周角定理和圆内四边形的性质典例精析一圆周角定理1、圆周角定理:同弧所对的圆周角等于它所对的圆心的角的一半。
即:∵AOB ∠和ACB ∠是弧AB 所对的圆心角和圆周角 ∴2AOB ACB ∠=∠2、圆周角定理的推论:推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧;即:在⊙O 中,∵C ∠、D ∠都是所对的圆周角 ∴C D ∠=∠推论2:半圆或直径所对的圆周角是直角;圆周角是直角所对的弧是半圆,所对的弦是直径。
即:在⊙O 中,∵AB 是直径 或∵90C ∠=︒ ∴90C ∠=︒ ∴AB 是直径推论3:若三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
即:在△ABC 中,∵OC OA OB ==∴△ABC 是直角三角形或90C ∠=︒注:此推论实是初二年级几何中矩形的推论:在直角三角形中斜边上的中线等于斜边的一半的逆定理。
二 圆内接四边形圆的内接四边形定理:圆的内接四边形的对角互补,外角等于它的内对角。
即:在⊙O 中,∵四边形ABCD 是内接四边形∴180C BAD ∠+∠=︒ 180B D ∠+∠=︒ DAE C ∠=∠利用圆周角定理的推论求角的度数BABA O例1 (2016·四川眉山)如图,A、D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC=()A.64° B.58° C.72° D.55°【分析】先根据圆周角定理求出∠B及∠BAC的度数,再由等腰三角形的性质求出∠OAB的度数,进而可得出结论.例2 (2016海南)如图,AB是⊙O的直径,AC、BC是⊙O的弦,直径DE⊥AC于点P.若点D在优弧上,AB=8,BC=3,则DP=.【考点】圆周角定理;垂径定理.【分析】解:由AB和DE是⊙O的直径,可推出OA=OB=OD=4,∠C=90°,又有DE⊥AC,得到OP∥BC,于是有△AOP∽△ABC,根据相似三角形的性质即可得到结论.例3(2016·山东省滨州市)如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD 分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是()A.②④⑤⑥B.①③⑤⑥C.②③④⑥D.①③④⑤【考点】圆的综合题.【分析】①由直径所对圆周角是直角,②由于∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角角,③由平行线得到∠OCB=∠DBC,再由圆的性质得到结论判断出∠OBC=∠DBC;④用半径垂直于不是直径的弦,必平分弦;⑤用三角形的中位线得到结论;⑥得不到△CEF和△BED中对应相等的边,所以不一定全等.利用圆周角定理的推论进行推理论证例4 (2015•烟台)如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且=.(1)试判断△ABC的形状,并说明理由.(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.例5 如图所示,BC是⊙O的直径,AD⊥BC,垂足为D,AB=AF,BF和AD相交于点E;求证:BE=AE.分析:由BC是⊙O的直径,根据直径所对的圆周角是直角,可得∠BAC=90°,又由AD⊥BC,即可得∠BAD=∠C,又由AB=AF,根据圆周角定理,易得∠ABF=∠F=∠C,则可证得∠ABF=∠BAD,继而证得结论.利用圆内接四边形的性质求度数例6(2015湖南邵阳第7题3分)如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC 的大小是()利用圆内接四边形的性质进行推理证明 例 7 (2015南京)(8分)如图,四边形ABCD 是⊙O 的内接四边形,BC 的延长线与AD 的延长线交于点E ,且DC=DE . (1) 求证:∠A=∠AEB .(2) 连接OE ,交CD 于点F ,OE ⊥ CD .求证:△ABE 是等边三角形.圆周角定理与相似三角形的综合例 8 (2016·天津市南开区·一模)如图,AB 是⊙O 的直径,C ,P 是上两点,AB=13,AC=5.(1)如图(1),若点P 是的中点,求PA 的长; (2)如图(2),若点P 是的中点,求PA 的长.(第26题)例 9 (肇庆市2012)如图7,在△ABC 中,AB =AC ,以AB 为直径的⊙O 交AC 于点E ,交BC 于点D ,连结BE 、AD 交于点P . 求证: (1)D 是BC 的中点; (2)△BEC ∽△ADC ; (3)AB ⋅ CE=2DP ⋅AD .圆内接四边形性质的综合应用例10 (2009•内江)如图,四边形ABCD 内接于圆,对角线AC 与BD 相交于点E ,F 在AC 上,AB =AD ,∠BFC =∠BAD =2∠DFC =β.求证:(1)∠ABD =90°-β (2)CD ⊥DF ; (3)BC=2CD .圆周角定理与函数的综合例 1 1 如图,AB 是圆O 的直径,CD 是弦,CD ⊥AB 于点E ,(1)求证:△ACE ∽△CBE ;(2)若AB=4,设OE=x (0<x <2),CE=y ,请求出y 关于x 的函数解析式图7。
九年级数学下册 第2章 圆 2.2 圆心角、圆周角 2.2.2 第2课时 圆周角定理的推论2及圆内接四边形同步练习2 (

第2课时圆周角定理的推论2及圆内接四边形的性质知识点 1 圆周角定理的推论21.如图2-2-32,AB为⊙O的直径,点C在⊙O上,∠A=30°,则∠B的度数为 ( )图2-2-32A.15°B.30°C.45°D.60°2.如图2-2-33,小华同学设计了一个测圆的直径的测量器,将标有刻度的尺子OA,OB在点O处钉在一起,并使它们保持垂直,在测圆的直径时,把点O靠在圆周上,读得刻度OE=8 cm,OF=6 cm,则圆的直径为( )图2-2-33A.12 cm B.10 cm C.14 cm D.15 cm3.2017·福建如图2-2-34,AB是⊙O的直径,C,D是⊙O上位于AB异侧的两点.下列四个角中,一定与∠ACD互余的是( )图2-2-34A.∠ADC B.∠ABDC.∠BAC D.∠BAD4.如图2-2-35,AB为⊙O的直径,CD为⊙O的弦,∠ACD=25°,∠BAD的度数为________.图2-2-355.如图2-2-36,⊙O的直径AB=10 m,C为直径AB下方半圆上一点,∠ACB的平分线交⊙O于点D,连接AD,BD.判断△ABD的形状,并说明理由.图2-2-36知识点 2 圆内接四边形的概念及其性质6.在圆内接四边形ABCD中,若∠A∶∠B∶∠C=1∶2∶5,则∠D的度数为( )A.60°B.120°C.140°D.150°7.2018·济宁如图2-2-37,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )图2-2-37A.50°B.60°C.80°D.100°8.教材练习第3题变式如图2-2-38,四边形ABCD内接于⊙O,E为CD延长线上一点,若∠B=96°,则∠ADE的度数为________.图2-2-389.2017·西宁如图2-2-39,四边形ABCD内接于⊙O,点E在BC的延长线上,若∠BOD =120°,则∠DCE=________°.图2-2-3910.如图2-2-40,A,B,C,D是⊙O上的四点,延长DC,AB相交于点E,且BC=BE.求证:△ADE是等腰三角形.图2-2-4011.2018·武威如图2-2-41,⊙A过点O(0,0),C(3,0),D(0,1),B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是( )图2-2-41A.15°B.30°C.45°D.60°12.2017·株洲如图2-2-42,已知AM为⊙O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交⊙O于点D,E,∠BMD=40°,则∠EOM=________°.图2-2-4213.2016·西宁⊙O的半径为1,弦AB=2,弦AC=3,则∠BAC的度数为________.14.如图2-2-43,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O交于点E,连接AC,CE.(1)求证:∠B=∠D;(2)若AB=4,BC-AC=2,求CE的长.图2-2-4315.如图2-2-44,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.(1)求证:BE=CE;(2)若BD=2,BE=3,求AC的长.图2-2-4416.如图2-2-45,已知⊙O中,弦AB⊥AC,且AB=AC=6,点D在⊙O上,连接AD,BD,CD.(1)如图①,若AD经过圆心O,求BD,CD的长;(2)如图②,若∠BAD=2∠DAC,求BD,CD的长.图2-2-45教师详解详析1.D 2.B3.D [解析] ∵AB 是⊙O 的直径,∴∠BAD +∠ABD =90°.∵∠ACD =∠ABD ,∴∠BAD +∠ACD =90°,故选D.4.65° [解析] ∵AB 为⊙O 的直径,∴∠ADB =90°.∵相同的弧所对应的圆周角相等,且∠ACD =25°,∴∠B =25°.∴∠BAD =90°-∠B =65°.5.解:△ABD 是等腰直角三角形.理由:∵AB 为⊙O 的直径,∴∠ADB =90°.∵CD 是∠ACB 的平分线,∴AD ︵=BD ︵,∴AD =BD ,∴△ABD 是等腰直角三角形.6.B7.D [解析] 如图所示.在优弧BD 上任取一点A (不与点B ,D 重合),连接AB ,AD .因为四边形ABCD 是⊙O 的内接四边形,所以∠A +∠BCD =180°.因为∠BCD =130°,所以∠A =50°.因为∠A 与∠BOD 都对着劣弧BD ,所以∠BOD =2∠A =2×50°=100°.8.96°9.60 [解析] ∵∠BOD =120°,∴∠A =12∠BOD =60°.∵四边形ABCD 是圆内接四边形,∴∠DCE =∠A =60°.10.证明:∵BC =BE ,∴∠E =∠BCE . ∵四边形ABCD 是圆内接四边形, ∴∠A +∠DCB =180°.又∵∠BCE +∠DCB =180°, ∴∠A =∠BCE ,∴∠A =∠E ,∴AD =DE , ∴△ADE 是等腰三角形.11.B [解析] 连接CD ,则CD 为⊙A 的直径,可得∠OBD =∠OCD ,根据点D (0,1),C (3,0),得OD =1,OC =3,由勾股定理得出CD =2,∵OD =12CD ,∴∠OCD =30°,∴∠OBD =30°.故选B.12.80 [解析] 连接EM ,∵AB =AC ,∠BAM =∠CAM ,∴AM ⊥BC .∵AM 为⊙O 的直径,∴∠ADM =∠AEM =90°,∴∠AME =∠AMD =90°-∠BMD =50°,∴∠EAM =40°,∴∠EOM =2∠EAM =80°.13.15°或75° [解析] 作直径AD ,AD =2.如图①,若两条弦在AD 的同侧,分别连接BD ,CD ,则∠B =∠C =90°.∵AB =2,AC =3,∴cos ∠BAD =AB AD =22,cos ∠CAD =AC AD =32,∴∠BAD =45°,∠CAD =30°,∴∠BAC =45°-30°=15°.如图②,若两条弦在AD的两侧,分别连接BD,CD,则∠B=∠C=90°.∵AB=2,AC=3,∴cos∠BAD=22,cos∠CAD=32,∴∠BAD=45°,∠CAD=30°,∴∠BAC=45°+30°=75°.故答案为15°或75°.14.解:(1)证明:∵AB为⊙O的直径,∴∠ACB=90°,∴AC⊥BC.又∵DC=BC,∴AD=AB,∴∠B=∠D. (2)设BC=x,则AC=x-2.在Rt△ABC中,AC2+BC2=AB2,即(x-2)2+x2=42,解得x1=1+7,x2=1-7(舍去).∵∠B=∠E,∠B=∠D,∴∠D=∠E,∴DC=CE.又∵DC=BC,∴CE=BC=1+7.15.解:(1)证明:如图,连接AE.∵AC为⊙O的直径,∴∠AEC=90°,∴AE⊥BC.又∵AB=AC,∴BE=CE.(2)如图,连接DE,∵BE=CE=3,∴BC=6.易知∠BED=∠BAC,而∠DBE=∠CBA,∴△BED∽△BAC,∴BEBA=BDBC,即3BA=26,∴AB=9,∴AC=AB=9.16.解:(1)∵AD经过圆心O,∴∠ACD=∠ABD=90°. ∵AB⊥AC,且AB=AC=6,∴四边形ABDC为正方形,∴BD=CD=AB=AC=6.(2)连接BC,OD,过点O作OE⊥BD.∵AB⊥AC,AB=AC=6,∴BC 为⊙O 的直径,∴BC =6 2,∴BO =CO =DO =12BC =3 2.∵∠BAD =2∠DAC ,∴∠DAC =30°,∠BAD =60°, ∴∠COD =60°,∠BOD =120°,∴△COD 为等边三角形,∠BOE =60°, ∴CD =CO =DO =BO =3 2,则BE =3 62,∵OE ⊥BD ,∴BD =2BE =3 6.。
圆内接四边形的性质与判定ppt课件

圆内接四边形的对角互补
如果一个四边形的对角互补,那么它的四个顶 点共圆.
性质定理2 圆内接边形的外角等于它的内角 的对角。
如果四边形的一个外角等于它的内角的 对角,那么它的四个顶点共圆.
性质定理的逆命题成立吗?
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
(2)如果点D在⊙O内部。 则∠B+∠E=180°
∵∠B+∠ADC=180°∴∠E=∠ADC
同样矛盾。∴点D不可能在⊙O内。
综上所述,点D只能在圆周上,四点共圆。 A D
E O
B
C
(2)
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
假设:四边形ABCD中,∠B+∠D=180°
求证:A,B,C,D在同一圆周上(简称四点共圆).
A
E
D
证明:(1)如果点D在⊙O外部。 则∠AEC+∠B=180°因∠B+∠D=180° B
得∠ D=∠AEC与“三角形外角大于任意
O
C
(1)
不相邻的内角”矛盾。故点D不可能在圆外。
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
o 圆 1与
圆o2都经过A,B两点。经过点A
的直线CD与圆o1交于点C,与圆o2交与点经过点B
的直线EF与圆o1交于点E,与圆o2交与点F.
求证:CE//DF. 证明:连接AB
第2课 圆心角与圆周角、圆内接四边形=2021年人教版新九年级数学上册 第二十四章 圆

C .圆心角与圆周角、圆内接四边形学生/课程 年级 学科 数学授课教师日期时段核心内容圆心角与圆周角、圆内接四边形课型一对一/一对N教学目标 1.理解并掌握圆心角、弦、弧之间的关系,能够运用他们的关系分析解决相关的几何问题 2.理解并掌握圆周角的概念以及圆周角定理和推论.并熟练运用解决实际问题。
重、难点1、圆心角与圆周角关系的转换,以及圆周角的推论的运用。
课首沟通1.学校的上课进度如何?你在学习这些内容的过程中都遇到什么问题? 2.上次的作业给我看看,完成了没有?还有不会的题吗?知识导图课首小测1.[单选题] 如图,已知点A (0,1),B (0,﹣1),以点A 为圆心,AB 为半径作圆,交x 轴于点C 和点D ,则DC 的长为( )A .2B .4D .22.[单选题] 已知⊙O的直径AB=10cm ,弦CD=8cm ,AB⊥CD,那么圆心O 到CD 的距离是()A.1cm B.2cm C.3cm D.4cm 3.如图,将半径为的圆形纸片折叠后,圆弧恰好经过圆心,则折痕的长为4.如图,矩形ABCD与圆心在AB上的圆O交于点G、B、F、E,GB=10,EF=8,那么AD=5.⊙O的半径为13 cm,弦AB∥CD,AB=24cm,CD=10cm,那么AB和CD的距离是Cm6.如图,已知AB是⊙O的弦,点C在线段AB上,OC=AC=4,CB=8.求⊙O的半径.导学一:圆心角知识点讲解1:弧、弦、圆心角1.圆心角:顶点在圆心的角叫做圆心角2.定理:(1)在同圆或者等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
(2)在同圆或者等圆中,相等的两条弧所对的圆心角相等,所对的弦也相等。
(3)在同圆或者等圆中,相等的两条弦所对的弧相等,所对的圆心角也相等。
特别注意:只有圆心角与弧存在倍数关系。
与弦不存在倍数关系。
例1. [单选题] 在下图中,下列各角是圆心角的是()A.∠ODC B.∠OCD C.∠AOB D.∠BDC例2. 指出下列哪些是∠AOB所对应的弦和弧?例3. 如图,将圆心角∠AOB绕圆心O旋转到∠A/OB/的位置你能发现哪些等量关系?为什么?完成下面的填空题。
第2课时圆周角定理的推论

第2课时圆周角定理的推论一、学法点津本节课的内容比拟简单,学好本节课的关键是掌握一些数学思想方法在探究过程中的运用.在探究直径所对的圆周角这一定理时利用度量的方法可以初步探究出“直径所对的圆周角是直角〞这一性质;在探究圆内接四边形的性质时可以利用类比上节课探究圆周角定理的方法进展探究;在探究圆内接四边形的对角互补性质时利用“由特殊到一般〞,先探究对角是直角的特殊情况时的结论,使自己有了初步的感知,然后再对一般的情况进展证明就比拟容易了.二、学点归纳总结(一)知识要点总结1.圆周角定理推论:直径所对的圆周角是直角;90°的圆周角所对的弦是直径.2.圆内接四边形的概念:四个顶点都在圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.3.圆内接四边形的性质:圆内接四边形的对角互补.(二)规律方法总结1.运用圆周角定理的推论作辅助线的口诀记忆法:(1)直径所对的圆周角是直角→“见直径出直角〞;(2)90°的圆周角所对的弦是直径→“见直角连直径〞.2.圆内接四边形的性质的推论:圆内接四边形的任意一个外角等于它的内对角.(三)易错问题误区点拨对圆内接四边形的性质把握不清.【典例】如图3-4-86,∠EAD是圆内接四边形ABCD的一个外角,那么()图3-4-86A.∠EAD=∠B B.∠EAD=∠DC.∠EAD=∠C D.∠EAD=∠B+∠C【错解】D【错解分析】圆内接四边形的两个性质:内角互补;外角等于其内对角.往往容易与三角形外角的性质混淆.【正解】C【正解分析】∵∠EAD是圆内接四边形ABCD的一个外角,∴∠BAD+∠EAD=180°,∠BAD+∠C=180°,∴∠EAD=∠C.应选C.三、稳固拓展练习1.[湖州中考] 如图3-4-87,AB是△ABC外接圆的直径,∠A=35°,那么∠B的度数是(C)图3-4-87A.35°B.45°C.55°D.65°[解析] ∵AB是△ABC外接圆的直径,∴∠C=90°.∵∠A =35°,∴∠B =90°-∠A =55°.应选C.2.[日照中考] 如图3-4-87,在△ABC 中,以BC 为直径的圆分别交边AC ,AB 于E ,D 两点,连接BD ,DE.假设BD 平分∠ABC ,那么以下结论不一定成立的是(D)A .BD ⊥ACB .AC 2=2AB·AEC .△ADE 是等腰三角形D .BC =2AD[解析] ∵BC 是直径,∴∠BDC =90°,∴BD ⊥AC ,故A 正确;∵BD 平分∠ABC ,BD ⊥AC ,∴△ABC 是等腰三角形,∴∠A =∠C ,AD =CD.∵四边形BCDE 是圆内接四边形,∴∠AED =∠C ,∴△ADE ∽△ABC ,△ADE 是等腰三角形,∴AD =DE =CD ,∴AC AE =BC DE =2BC 2DE =2AB AC,∴AC 2=2AB·AE ,故B 正确;由B 的证明过程,可得C 选项正确.应选D.图3-4-88 图3-4-893.[常州中考] 如图3-4-89,△ABC 内接于⊙O ,∠BAC =120°,AB =AC ,BD 为⊙O 的直径,AD =6,那么DC =.[解析] ∵BD 为⊙O 的直径,∴∠BAD =∠BCD =90°.∵∠BAC =120°,∴∠CAD =120°-90°=30°,∴∠CBD =∠CAD =30°.∴∠BDC =90°-∠CBD =90°-30°=60°.∵AB =AC ,∴∠ADB =∠ADC ,∴∠ADB =12∠BDC =12×60°=30°.在Rt △ABD 中,∵AD =6,∴BD =AD÷cos30°=6÷32=4 3.在Rt △BCD 中,DC =12BD =12×43=2 3.故答案为2 3. 4.如图3-4-90,⊙O 是△ABC 的外接圆,AB 是⊙O 的直径,D 为⊙O 上一点,OD ⊥AC ,垂足为E ,图3-4-90连接BD.(1)求证:BD 平分∠ABC ;(2)当∠ODB =30°时,求证:BC =OD.证明:(1)∵OD ⊥AC ,OD 为半径,∴CD ︵=AD ︵,∴∠CBD =∠ABD ,∴BD 平分∠ABC.(2)∵OB =OD ,∴∠OBD =∠ODB =30°,∴∠AOD =∠OBD +∠ODB =30°+30°=60°.又∵OD ⊥AC 于点E ,∴∠OEA =90°,∴∠A =180°-∠OEA -∠AOD =180°-90°-60°=30°.又∵AB 为⊙O 的直径,∴∠ACB =90°.∴在Rt △ACB 中,BC =12AB.又∵OD =12AB ,∴BC =OD. 5.如图3-4-91,四边形ABCD 是⊙O 的内接四边形,DP ∥AC ,交BA 的延长线于点P ,求证:AD·DC =PA·BC.图3-4-91 图3-4-92证明:如图3-4-92,连接BD.∵DP ∥AC ,∴∠PDA =∠DAC.∵∠DAC =∠DBC ,∴∠PDA =∠DBC.∵四边形ABCD 是圆内接四边形,∴∠DAP =∠DCB ,∴△PAD ∽△DCB.∴PA ∶DC =AD ∶BC ,即AD·DC =PA·BC.四、挑战课标中考1.[毕节中考] 如图3-4-93是以△ABC 的边AB 为直径的半圆O ,点C 恰好在半圆上,过点C 作CD ⊥AB 于点D.cos ∠ACD =35,BC =4,那么AC 的长为(D) 图3-4-93A .1 B.203 C .3 D.163[解析] ∵AB 为直径,∴∠ACB =90°,∴∠ACD +∠BCD =90°.∵CD ⊥AB ,∴∠BCD +∠B=90°,∴∠B =∠ACD.∵cos ∠ACD =35,∴cosB =35,∴tanB =43.在Rt △ABC 中,∵BC =4,∴tanB =AC BC =AC 4=43,∴AC =163. [解题策略] 此题考察了圆周角定理以及三角函数的性质.此题难度适中,注意掌握数形结合思想的应用.2.[兰州中考] 如图3-4-94,△ABC 为⊙O 的内接三角形,AB 为⊙O 的直径,点D 在⊙O 上,∠ADC =54°,那么∠BAC 的度数等于__36°__.图3-4-94[解析] ∵∠ABC 与∠ADC 是AC ︵所对的圆周角,∴∠ABC =∠ADC =54°.∵AB 为⊙O 的直径,∴∠ACB =90°,∴∠BAC =90°-∠ABC =90°-54°=36°.[解题策略] 此题考察了圆周角定理与直角三角形的性质.此题比拟简单,注意掌握“在同圆或等圆中,同弧或等弧所对的圆周角相等〞与“直径所对的圆周角是直角〞定理的应用.3.[无锡中考] 如图3-4-95,AB 是半圆O 的直径,C ,D 是半圆O 上的两点,且OD ∥BC ,OD 与AC 交于点E.(1)假设∠B =70°,求∠CAD 的度数;(2)假设AB =4,AC =3,求DE 的长.图3-4-95[解析] (1)根据圆周角定理的推论可得∠ACB =90°,那么∠CAB 的度数即可求得.在等腰三角形AOD 中,根据等边对等角求得∠DAO 的度数,那么∠CAD 的度数即可求得;(2)易证OE 是△ABC 的中位线,利用中位线定理求得OE 的长,那么DE 的长即可求得. 解:(1)∵AB 是半圆O 的直径,∴∠ACB =90°.又∵OD ∥BC ,∴∠AEO =∠ACB =90°,即OE ⊥AC ,∠CAB =90°-∠B =90°-70°=20°,∠AOD =70°.∵OA =OD ,∴∠DAO =∠ADO =180°-∠AOD 2=180°-70°2=55°. ∴∠CAD =∠DAO -∠CAB =55°-20°=35°.(2)在直角三角形ABC 中,BC =AB 2-AC 2=42-32=7.∵OE ⊥AC ,∴AE =EC.又∵OA =OB ,∴OE =12BC =72. 又∵OD =12AB =2,∴DE =OD -OE =2-72. [解题策略] 此题考察了圆周角定理以及三角形的中位线定理,证明OE 是△ABC 的中位线是解(2)题的关键.。
圆内接四边形的定义及性质-九年级数学上册教学课件(人教版)

∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°, 同理∠B+∠D=180°.
推论:圆的内接四边形的对角互补.
图中∠A与∠DCE的大小有何关系?
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
D
∴∠A+∠C=180°, 同理∠B+∠D=180°,
A O
延长BC到点E,有 ∠BCD+∠DCE=180°.
圆内接多边形 如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接多
边形,这个圆叫做这个多边形的外接圆.
探究性质 如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外
接圆.
猜想:∠A与∠C, ∠B与∠D之间的关系为:
∠A+ ∠C=180º, ∠B+ ∠D=180º
思考:如何证明你的猜想呢?
性质1:圆的内接四边形的对角互补.
性质2:圆的内接四边形的任何一个外角都等于它的内对角.
人教版 数学 九年级 上册
理解并掌握圆内接四边形的定义及性质. 能灵活运用圆内接四边形的性质解决相关问题.
圆周角定理
圆周角定理: 一条弧所对的圆周角等于该弧它所对的圆心角的一半;
圆周角定理的推论 同弧或等弧所对的圆周角相等.
圆周角和直径的关系
A2
A
A1
3
半圆或直径所对的圆周角都相等,都等于90°.
证明:∵四边形ACDG内接于⊙O, ∴∠FGD=∠ACD. 又∵AB为⊙O的直径,CF⊥AB于E,∴AB垂 直平分CD, ∴AC=AD, ∴∠ADC=∠ACD, ∴∠FGD=∠ADC.
【点睛】圆内接四边形的性质是沟通角相等关系的重要依据.
如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( A )
人教版九年级数学上册《圆周角》第2课时教学课件

学习目标
1.理解圆内接多边形的定义,掌握圆内接四边形的概念和性质;
2.能运用圆内接四边形的性质证明和计算;
圆
3.经历圆内接四边形的性质的探究与证明,渗透“由特殊到一般”
周
的数学思想方法;
角
4.通过学生自主探究、合作交流的学习过程,体验实现自身价值的
愉悦和数学的应用.
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
B E
O
A
C
DF
∠B∠E ∠D∠F ∠B∠D180° ∠E∠F180°
同圆或等圆中,同弦或等弦所对的圆周角相等或互补.
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
延伸
如图,四边形ABCD是⊙O的内接四边形;∠A与∠BCE 有什么关系?
B
∠BCE∠BCD180°
∠BCD ∠A180°
O
∠A∶∠C5∶4
9
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
随堂练习
2.如图,四边形ABCD内接于⊙O,若∠BOD=138°,
则它的一个外角∠DCEபைடு நூலகம்于( A ).
A.69°
B.42°
C.48° D.38°
A
·O D
B
CE
∠BOD138° ∠A69°
∠A∠DCB180° ∠A∠DCE69°
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
教科书第88页 练习第2、5题
再见
回顾
圆周角定理及其推论
圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半.
推论1:同弧或等弧所对的圆周角相等. 推论2:半圆(或直径)所对的圆周角是直角,
