第4章模糊控制的matlab实现
模糊控制在matlab中的实例

模糊控制在matlab中的实例模糊控制(模糊逻辑控制)是一种基于模糊数学理论的控制方法,它可以用于控制系统的稳定性、精度和响应速度等方面的优化。
在MATLAB 中,可以使用模糊逻辑工具箱(FLUS)来应用模糊控制。
以下是一个简单的实例,展示了如何使用 MATLAB 中的模糊逻辑工具箱来对温度控制系统进行控制:首先,我们需要创建一个温度控制系统,该系统将使用模糊控制来控制传感器的读数。
假设我们有四个传感器,分别为温度传感器、湿度传感器、压力和传感器,每个传感器读数为实数。
```matlab% 创建模型T = [120 100 80 50]; % 温度控制器输出R1 = [1.2 0.8 0.4 0.2]; % 湿度控制器输出R2 = [0.9 0.1 0.3 0.5]; % 压力控制器输出R3 = [1.4 0.6 0.2 0.1]; % 传感器误差P1 = [125 125 125 125]; % 温度控制器输入P2 = [100 100 90 80]; % 湿度控制器输入P3 = [85 85 80 75]; % 压力控制器输入F1 = [0.3 0.2 0.1 0.1]; % 温度控制器输出F2 = [0.4 0.3 0.2 0.1]; % 湿度控制器输出F3 = [0.5 0.4 0.3 0.1]; % 压力控制器输出y1 = [100 85 75 60]; % 实际温度y2 = [120 95 80 70]; % 实际湿度y3 = [135 110 90 80]; % 实际压力% 创建模糊控制器go1 = @(t,u,v) if t > 100 then ((1-v)*F1 + v*R1 +(1+v)*R2)/(1-v)*y1 else 0;go2 = @(t,u,v) if t < 50 then ((1-v)*F3 + v*R1 +(1+v)*R2)/(1-v)*y2 else 0;go3 = @(t,u,v) if t == 0 then ((1-v)*F1 + v*R1 +(1+v)*R2)/(1-v)*y3 else 0;% 创建模糊控制器的优化器var = [0 0 0 0];go1(0,:,:) = var;matlab.模糊控制.优化器.LevenbergMarquardt(var,go1);% 运行模糊控制器[t,u,v] = ode45(go1,[0 1],[120 100 80 50],y1);% 输出结果disp(["实际温度:" num2str(t)]);disp(["实际湿度:" num2str(u)]);disp(["实际压力:" num2str(v)]);```在这个例子中,我们使用 MATLAB 中的 ode45 工具箱来拟合温度控制器和湿度控制器的输出响应函数。
matlab模糊控制实现
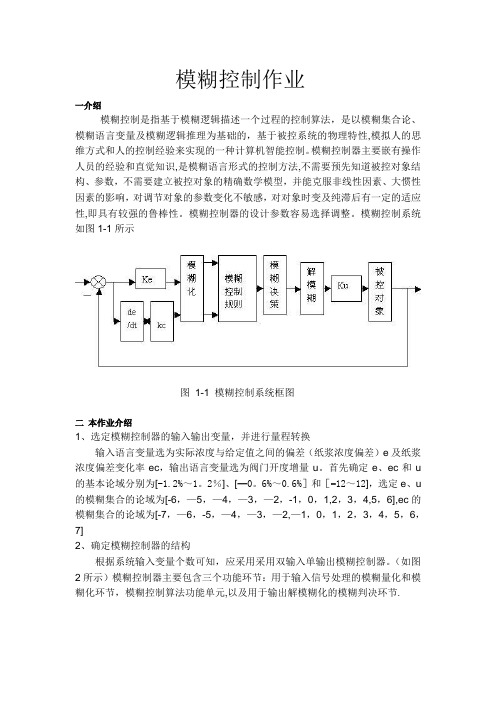
模糊控制作业一介绍模糊控制是指基于模糊逻辑描述一个过程的控制算法,是以模糊集合论、模糊语言变量及模糊逻辑推理为基础的,基于被控系统的物理特性,模拟人的思维方式和人的控制经验来实现的一种计算机智能控制。
模糊控制器主要嵌有操作人员的经验和直觉知识,是模糊语言形式的控制方法,不需要预先知道被控对象结构、参数,不需要建立被控对象的精确数学模型,并能克服非线性因素、大惯性因素的影响,对调节对象的参数变化不敏感,对对象时变及纯滞后有一定的适应性,即具有较强的鲁棒性。
模糊控制器的设计参数容易选择调整。
模糊控制系统如图1-1所示图1-1 模糊控制系统框图二本作业介绍1、选定模糊控制器的输入输出变量,并进行量程转换输入语言变量选为实际浓度与给定值之间的偏差(纸浆浓度偏差)e及纸浆浓度偏差变化率ec,输出语言变量选为阀门开度增量u。
首先确定e、ec和u 的基本论域分别为[-1.2%~1。
2%]、[—0。
6%~0.6%]和[-12~12],选定e、u 的模糊集合的论域为[-6,—5,—4,—3,—2,-1,0,1,2,3,4,5,6],ec的模糊集合的论域为[-7,—6,-5,—4,—3,—2,—1,0,1,2,3,4,5,6,7]2、确定模糊控制器的结构根据系统输入变量个数可知,应采用采用双输入单输出模糊控制器。
(如图2所示)模糊控制器主要包含三个功能环节:用于输入信号处理的模糊量化和模糊化环节,模糊控制算法功能单元,以及用于输出解模糊化的模糊判决环节.ed/dt 图2 双输入单输出模糊控制器3、确定各变量的模糊语言取值及相应的隶属函数,即进行模糊化模糊化是将模糊控制器输入量的确定值转换为相应模糊语言变量值的过程,此相应语言变量均由对应的隶属度函数来定义。
对纸浆浓度偏差e 、纸浆浓度偏差变化率ec 、阀门开度的增量u 进行模糊化,分别用模糊语言变量X 、Y 、Z 进行表示,语言值集合均为{负大,负中,负小,零,正小,正中,正大},用英文缩写进行表示分别为:X={NBe,NMe ,NSe,ZOe ,PSe,PMe ,PBe }Y={ NBec ,NMec,NSec ,ZOec ,PSec ,PMec ,PBec }Z={ NBu ,NMu ,NSu ,ZOu ,PSu,PMu ,PBu }模糊化包括两个任务:第一个任务是进行论域变换,过程参数的实际范围称为基本论域,可以通过变换系数(量化因子)实现由基本论域到量化论域的变换;第二个任务是求得输入对应于语言变量的隶属度。
模糊控制matlab

模糊控制matlab模糊控制是一种基于模糊数学理论的控制方法,它可以有效地处理非线性系统和模糊系统的控制问题。
在模糊控制中,通过将输入、输出和中间变量用模糊集合表示,设计模糊逻辑规则以实现控制目标。
本文将介绍如何用Matlab实现模糊控制,并通过实例讲解其应用和效果。
1. 模糊集合的表示在Matlab中,我们可以使用fuzzy工具箱来构建和操纵模糊系统。
首先,我们需要定义输入和输出的模糊集合。
例如,如果我们要控制一个直线行驶的自动驾驶汽车,可以定义速度和方向作为输入,定义方向盘角度作为输出。
我们可以将速度和方向分别划分为缓慢、中等、快速三个模糊集合,将方向盘角度划分为左转、直行、右转三个模糊集合。
可以使用Matlab的fuzzy工具箱中的fuzzy集合函数实现:slow = fuzzy(fis,'input',[-10 -10 0 20]);gap = fuzzy(fis,'input',[0 20 60 80 100]);fast = fuzzy(fis,'input',[60 80 110 110]);其中,fis为模糊系统对象,输入和输出的模糊集合分别用fuzzy函数定义,分别用输入或输出、模糊集合变量名、模糊集合界限参数表示,如fuzzy(fis,'input',[-10 -10 0 20])表示定义一个输入模糊集合,变量名为slow,其界限参数为[-10 -10 0 20],即表示此模糊集合上下界是[-10,-10]和[0,20]。
2. 设计模糊控制规则在Matlab中,可以使用fuzzy工具箱的ruleviewer函数来设计模糊控制的规则库。
规则库由模糊条件和模糊结论构成,用if-then形式表示。
例如,定义类别均为slow和keep的输入,输出为类别均为left的控制操作的规则如下:rule1 = "if (slow is slow) and (keep is keep) then (left is left);";其中,slow和keep为输入的模糊变量名,left为输出的模糊变量名。
模糊控制在matlab中的实例

模糊控制在matlab中的实例以下是一个模糊控制的MATLAB实例:假设我们要控制一个水平摆,使其保持在垂直状态。
我们可以使用模糊控制器来实现这个任务。
首先,我们需要定义输入和输出变量。
对于输入变量,我们可以选择摆的角度和摆的角速度,对于输出变量,我们可以选择施加到摆上的力。
```matlab% 定义输入变量angle = fuzzymf("angle", [-90 -45 0 45 90], "trimf", [-90 -45 0 45 90]);angular_velocity = fuzzymf("angular_velocity", [-10 -5 0 5 10], "trimf", [-10 -5 0 5 10]);% 定义输出变量force = fuzzymf("force", [-20 -10 0 10 20], "trimf", [-20 -10 0 10 20]);```接下来,我们定义模糊规则。
这些规则描述了如果摆的角度和角速度是什么,我们应该施加多少力,以使摆保持垂直。
```matlab% 定义模糊规则rules = [1 1 3 1;1 2 4 1;1 3 5 2;2 1 2 1;2 23 1;2 3 4 2;3 1 1 2;3 2 2 1;3 3 3 1;4 1 1 3;4 2 2 2;4 3 3 1;5 1 1 3;5 2 2 2;5 3 4 3];% 定义模糊推理引擎fis = mamfis("Name", "Pendulum Fuzzy Controller", "NumInputs", 2, "NumOutputs", 1);fis.Inputs(1).MembershipFunctions = angle;fis.Inputs(2).MembershipFunctions = angular_velocity; fis.Outputs(1).MembershipFunctions = force;fis.Rules = rules;```最后,我们可以使用模糊控制器来控制水平摆。
使用Matlab技术进行模糊控制的基本方法

使用Matlab技术进行模糊控制的基本方法随着科技的不断发展,控制系统越来越广泛地应用于各个领域,帮助我们解决实际问题。
在控制系统中,模糊控制技术因其适应性强、鲁棒性好等特点而备受关注。
而Matlab作为一个强大的计算工具,为我们提供了许多实现模糊控制的功能。
本文将介绍使用Matlab技术进行模糊控制的基本方法。
一、模糊控制的基本理论在介绍使用Matlab进行模糊控制的方法之前,我们先来了解一下模糊控制的基本理论。
模糊控制是一种基于模糊逻辑的控制方法,它模拟人类的思维方式进行控制,通过建立模糊规则库来实现对系统的控制。
在模糊控制中,输入和输出之间的关系由一组模糊规则来描述,这些模糊规则可以通过模糊推理进行计算得到系统的输出。
模糊控制主要有三个基本步骤:模糊化、模糊推理和去模糊化。
模糊化是将输入的实际值通过模糊隶属函数映射成模糊集合。
模糊推理则是根据模糊规则库进行推理计算,得到模糊输出。
最后,去模糊化将模糊输出转换为实际的控制量。
二、使用Matlab进行模糊控制的步骤1. 定义模糊集合和模糊规则库使用Matlab进行模糊控制的第一步是定义模糊集合和模糊规则库。
模糊控制中的模糊集合可以通过Matlab的fuzzymf函数来定义,它可以根据实际问题选择三角形、梯形、高斯函数等不同形状的隶属函数。
模糊规则库则是描述输入和输出之间关系的集合,它由一组模糊规则构成。
在Matlab中,可以使用fuzzylut函数来定义模糊规则库。
这个函数需要指定输入和输出的隶属函数以及规则的后件。
2. 模糊化和模糊推理定义好模糊集合和模糊规则库之后,接下来就是进行模糊化和模糊推理的计算了。
在Matlab中,可以使用fuzzy函数进行模糊化的计算。
这个函数需要输入模糊集合、输入的隶属函数和对应的输入值,然后计算得到模糊输入。
模糊推理可以通过fuzzy函数结合模糊规则库进行计算。
这个函数需要输入模糊规则库、模糊输入和输出的隶属函数,然后计算得到模糊输出。
模糊控制在matlab中的实例

模糊控制在matlab中的实例以下是一个简单的模糊控制器在 MATLAB 中的实例:假设你有一个被控对象,它的输出值 y 取决于输入值 u。
你想要设计一个模糊控制器来控制该对象。
首先,你需要定义模糊控制器的输入和输出变量以及它们的隶属度函数。
示例中,我们定义了两个输入变量 x1 和 x2 以及一个输出变量y,每个变量都由三个隶属度函数组成。
```matlab% 定义输入和输出变量及其隶属度函数x1 = fuzzyvar("input", [-5 5], "bellmf", [1 2 3]);x2 = fuzzyvar("input", [-5 5], "trimf", [-4 0 4]);y = fuzzyvar("output", [-10 10], "trimf", [-8 0 8]);```接下来,我们需要定义规则库。
规则库是一系列模糊规则的集合,每条规则由前提和结论组成。
在这个示例中,我们定义了九条规则,将输入变量 x1 和 x2 映射到输出变量 y。
```matlab% 定义规则库ruleList = ["If (x1 is 1) and (x2 is 1) then (y is -7)";"If (x1 is 1) and (x2 is 2) then (y is -9)";"If (x1 is 1) and (x2 is 3) then (y is -9)";"If (x1 is 2) and (x2 is 1) then (y is -5)";"If (x1 is 2) and (x2 is 2) then (y is -7)";"If (x1 is 2) and (x2 is 3) then (y is -8)";"If (x1 is 3) and (x2 is 1) then (y is -3)";"If (x1 is 3) and (x2 is 2) then (y is -5)";"If (x1 is 3) and (x2 is 3) then (y is -6)";];```现在我们可以创建模糊控制器,并将输入变量和输出变量与规则库相结合。
模糊控制在matlab中的实例

模糊控制在matlab中的实例模糊控制是一种应用广泛的控制方法,它可以处理那些难以精确建立数学模型的系统。
在Matlab中,使用Fuzzy Logic Toolbox工具箱可以方便地实现模糊控制系统。
以下是一个简单的模糊控制器示例,控制一个小车的速度和方向,使得其能够沿着预设的轨迹行驶。
1. 首先,定义输入和输出变量。
这里我们需要控制小车的速度和转向角度。
代码如下:```speed = newfis("speed");speed = addvar(speed,"input","distance",[0 10]);speed = addmf(speed,"input",1,"slow","trimf",[0 0 5]);speed = addmf(speed,"input",1,"fast","trimf",[5 10 10]); speed = addvar(speed,"output","velocity",[-10 10]);speed = addmf(speed,"output",1,"reverse","trimf",[-10-10 -2]);speed = addmf(speed,"output",1,"stop","trimf",[-3 0 3]); speed = addmf(speed,"output",1,"forward","trimf",[2 10 10]);angle = newfis("angle");angle = addvar(angle,"input","position",[-1 1]);angle = addmf(angle,"input",1,"left","trimf",[-1 -1 0]);angle = addmf(angle,"input",1,"right","trimf",[0 1 1]); angle = addvar(angle,"output","steering",[-1 1]);angle = addmf(angle,"output",1,"hard_left","trimf",[-1 -1 -0.5]);angle = addmf(angle,"output",1,"soft_left","trimf",[-1 -0.5 0]);angle = addmf(angle,"output",1,"straight","trimf",[-0.5 0.5 0.5]);angle = addmf(angle,"output",1,"soft_right","trimf",[0 0.5 1]);angle = addmf(angle,"output",1,"hard_right","trimf",[0.5 1 1]);```2. 然后,定义模糊规则。
模糊控制在MATLAB中的实现

模糊控制在MATLAB中的实现模糊控制是一种基于模糊逻辑的控制方法,可以处理输入模糊或模糊输出的问题。
在MATLAB中,模糊控制可以通过Fuzzy Logic Toolbox实现。
Fuzzy Logic Toolbox提供了一套用于设计、模拟和分析模糊逻辑系统的工具。
它允许用户定义模糊集、模糊规则和模糊推理过程,从而实现模糊控制。
在实现模糊控制之前,首先需要确定输入和输出的模糊集以及它们之间的关系。
可以通过定义模糊集合的成员函数来描述输入和输出的模糊集。
常见的成员函数有三角形、梯形、高斯等。
例如,对于一个温度控制系统,可以定义三个模糊集:"冷","舒适"和"热"用于描述温度的状态。
每个模糊集可以具有不同的成员函数。
接下来,需要定义模糊规则,规则用于描述输入和输出之间的关系。
例如,当温度"冷"时,可以设定输出为"加热",当温度"舒适"时,输出为"保持",当温度"热"时,输出为"冷却"。
在MATLAB中,可以使用Fuzzy Logic Toolbox的命令createFIS来创建一个模糊逻辑系统(FIS),并使用addInput和addOutput命令来定义输入和输出的模糊集。
例如,以下代码片段演示了如何创建一个简单的模糊逻辑系统:```MATLABfis = createFIS('fuzzy_system');fis = addInput(fis, [0 100], 'Temperature');fis = addOutput(fis, [0 10], 'Control');fis = addMF(fis, 'input', 1, 'cold', 'trimf', [-10 0 10]);fis = addMF(fis, 'input', 1, 'hot', 'trimf', [40 100 160]);fis = addMF(fis, 'output', 1, 'cool', 'trimf', [-5 0 5]);fis = addMF(fis, 'output', 1, 'maintain', 'trimf', [0 5 10]);fis = addMF(fis, 'output', 1, 'heat', 'trimf', [5 10 15]);ruleList = [1 1 2 3 1;22221;33211];fis = addRule(fis, ruleList);```在定义模糊逻辑系统之后,可以使用evalfis命令对系统进行模糊推理和模糊控制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例:
a=newfis(‘Simple’); a=addvar(a,’input’,’e’,[-6,6]); a=addmf(a,’input’,1,’NL’,’trapmf’,[-6,-6,-5,-3]); a=addmf(a,’input’,1,’NS’,’trapmf’,[-5,-3,-2,0]); a=addmf(a,’input’,1,’ZR’,’trapmf’,[-2,0,2])。
规则分析: 根据水箱水位控制的实际经验,可得到如下控制规则: (1) If e is negative then u is close-fast (2) If e is zero then u is no-chang (3) If e is positive then u is open-fast (4) If e is zero and ec is negative then u is open-slow (5) If e is zero and ec is positive then u is close-slow
4. ruleedit
功能: ruleedit (‘a’) ruleedit (a) 说明:利用ruleedit (‘a’)可打开规则编辑器,从中可 以查看或修改文件a.fis所对应的FIS结构中的规则。 ruleedit (a)格式可用来打开在工作空间中已存在 的名为a的FIS结构所对应的规则编辑器。
3. trimf 功能:三角形隶属度函数 格式:y = trimf(x,[a b c]) 说明:三角函数曲线由3个参数a、 b 、c确定: xa 0 参数a和c确定三角 x a a x b 形的“脚”,而 b a 参数b确定三角形 f x , a ,b , c c x b x c 的“峰” c b 0 xc
wlcontrol=addvar(wlcontrol,'input','e',[-1 1]); wlcontrol=addvar(wlcontrol,'input','ec',[-0.1 0.1]); wlcontrol=addvar(wlcontrol,'output','u',[-1 1]); wlcontrol=addmf(wlcontrol,'input',1,'negative','gaussmf',[0.45 -1]); wlcontrol=addmf(wlcontrol,'input',1,'zero','gaussmf',[0.45 0]); wlcontrol=addmf(wlcontrol,'input',1,'positive','gaussmf',[0.45 1]); wlcontrol=addmf(wlcontrol,'input',2,'negative','gaussmf',[0.045 -0.1]); wlcontrol=addmf(wlcontrol,'input',2,'zero','gaussmf',[0.045 0]); wlcontrol=addmf(wlcontrol,'input',2,'positive','gaussmf',[0.045 0.1]); wlcontrol=addmf(wlcontrol,'output',1,'close-fast','trimf',[-1.5 -1 -0.5]); wlcontrol=addmf(wlcontrol,'output',1,'close-slow','trimf',[-1 -0.5 0]); wlcontrol=addmf(wlcontrol,'output',1,'no-change','trimf',[-0.5 0 0.5]); wlcontrol=addmf(wlcontrol,'output',1,'open-slow','trimf',[0 0.5 1]); wlcontrol=addmf(wlcontrol,'output',1,'open-fast','trimf',[0.5 1 1.5]); rulelist=[1 0 1 1 1;2 0 3 1 1;3 0 5 1 1;2 1 4 1 1;2 3 2 1 1]; wlcontrol=addrule(wlcontrol,rulelist) writefis(wlcontrol); plotfis(wlcontrol)
4.2 水箱水位控制实验
水箱水位模糊推理系统(FIS)的建立 模糊推理系统的任务
对测量数据进行模糊化 建立模糊控制规则表 进行输出信息的模糊判决
建立模糊推理系统,通常采用两类方法: (1)利用Matlab命令行建立模糊推理系统 (2)利用GUI建立模糊推理系统
水位模糊控制系统 设定期望的水位,检测实际的水位,计算水位 误差,由模糊控制器计算得到阀门控制量,即阀门 开度,从而控制阀门,完成水位的控制。
2. fuzzy
功能:调用基本的FIS编辑器。 格式: fuzzy fuzzy(fismat) 说明:FIS编辑器可让用户方便地创建或修改FIS(模 糊推理系统)的高级特性。
3. mfedit 功能:隶属度函数编辑器 格式: mfedit (‘a’) mfedit (a) mfedit 说明: mfedit (‘a’)可打开隶属度函数编辑器,其中 包含文件a.fis的隶属度函数,通过编辑器可对其进行 修改。 mfedit (a)可打开保存在工作空间变量a中的FIS 结构。 mfedit可打开隶属度函数编辑器。
第4章
模糊控制的matlab实现
本实验以Mtlab6.5为开发环境,基于模糊逻辑工具 箱(Fuzzy Logic Toolbox) 通过简单直观的例子,对模 糊控制系统进行分析与研究。
4.1 认识实验
4.1.1 GUI(图形用户界面) 工具箱函数 1. anfisedit 功能:打开ANFIS编辑器的GUI 格式: anfisedit(‘a’) anfisedit(a) anfisedit 说明:利用anfisedit函数打开ANFIS编辑器的GUI, 从中可装入数据集合并训练ANFIS。 利用anfisedit(‘a’)可从磁盘中装入名为a.fis的FIS 文件,并打开ANFIS编辑器。利用anfisedit(a)可按同 样的方式打开FIS结构变量a。
5. 保存FIS结构 用writefis函数可以将Matlab工作空间中的FIS 结构变量wlcontrol保存到磁盘文件中: writefis(wlcontrol) 此文件将以.fis为缺省后缀名。 6. 可以利用下列函数对所建立的FIS进行操作 plotmf(绘制隶属度函数)、surfview(绘制系统输出曲面) plotfis(绘制FIS系统结构)、evalfis(计算FIS输出)、 getfis(获取FIS结构的属性)、showfis(显示FIS结构参数) evalmf(计算隶属度函数)
6. surfview 功能:输出曲面观测器 格式: surfview (‘a’) surfview (a) 说明:利用surfview (‘a’)可打开输出曲面观测器,从 中可查看保存在文件a.fis中的单输入或双输入FIS结 构的输出曲面。
4.1.2 隶属度函数 1. Gaussmf
功能:高斯(Gaussian)型隶属度函数 格式:y=gaussmf(x,[sig c]) 说明:对称的高斯型函数取决于2个参数σ(sig)和c:
4.2.2 利用Matlab命令行建立FIS 1. 建立新的FIS 设所建的FIS结构为wlcontrol,则命令行为:
2.量u,根据它们的论域要求,用add函数添加三 个变量。
3. 添加隶属函数
4. 设计并添加规则列表
2. sigmf 功能:Sigmoid型隶属度函数 格式:y=sigmf(x,[a c]) 说明:Sigmoid型函数由参数a和c确定:
f x, a, c 1 1 e a x c
例: x = 0:0.1:10; y = sigmf(x,[2 4]); plot(x,y); text(0.2,0.88,’sigmf’); text(0.2,0.78,’P = [2 4]’);
5. ruleview
功能:规则观测器和模糊推理框图 格式: ruleview (‘a’) ruleview (a) 说明:利用ruleview(‘a’)可打开a.fis规则状况的规则观 测器,从中可对文件a.fis所对应的FIS结构画出模糊推 理框图,并可显示整个框图。 ruleview (a)格式可用来打开在工作空间中已存在 的名为a的FIS结构所对应的规则观测器。利用可打开 ruleview规则观测器。
4.1.4 Simulink仿真模块 1. fuzblock 功能:模糊逻辑控制器仿真模块 格式: fuzblock 说明:此命令将打开Simulink系统的模糊逻辑模块库, 里面含有有关模糊逻辑器件的演示框图。 2. sffis 功能:Simulink中的模糊推理S函数 格式: output=sffis(t,x,u,flag,fismat) 说明:用此函数可得到一个由Simulink使用的MEX文件
f x, , c e
x c 2
2 2
gaussmf函数的参数以向量[sig,c]形式给出。 例: x = 0:0.1:10; y = gaussmf(x,[2 5]); plot(x,y); text(0.2,0.88,’gaussmf’); text(0.2,0.78,’P = [2 5]’);
