带有非线性扰动的非脆弱奇异时变时滞系统的保性能控制
不确定奇异时滞Lur′e系统的非脆弱保性能控制

1 问题 描 述 和预 备 知 识
考 虑 如下 形 式 的 不确 定 奇 异 时滞 I e系统 :
收 稿 日期 :2 】 一 2 2) 【0 I —( l
作 者 简 介 :吴 保 卫 (9 3 ,男 .陕 西 咸 阳人 ,博 士 生 导 师. 研 究 方 向 :控 制 理论 . 16 -)
, ∞
。
, =f『‘ ) x t + T )u £] t X( Q ( U( R ()I £ ) £ I
() 4
其 中 Q >0 ,R>0是给 定适 当维数 的加 权 阵.
本 文 的 目的是 为不 确定 奇 异时滞 I r , u e系统设 计一 个具 有 增益 扰 动 的反馈 控制 器 :
以下 3个 条件 是等 价 的 :
1 <0 )SI 0 S2 S1; l 0 ) 2 0 SI I )S ;2 I , 2 2 I 2 ;3 2 , I 2 < 一 ss < < —
引理 3‘ s t 1 e a 设 F =F 【(一 1 l t ・ mm ) he i 'E赋 , I ’ “ 0 ,使得 一 >0,则 对所 有 ≠ 0且满 足
文章 编 号 : 1 0 — 2 7 2 1 )2— 0 2— 1 0 1 4 1 (0 10 0 1 1
不确 定 奇 异 时滞 L r u e系统 的 非脆 弱保 性 能控 制
吴保 卫 ,李 俏 , 罗立娑
( 西 师 范 大 学 数 学 与信 息 科 学 学 院 ,陕 西 陕 西安 7I )2 (6 ) R
=
P ( f +D t) () DK() +Q + () K() A() K() +( £ + t) P十 £R t.
【国家自然科学基金】_保性能控制器_基金支持热词逐年推荐_【万方软件创新助手】_20140801
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
推荐指数 8 4 4 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
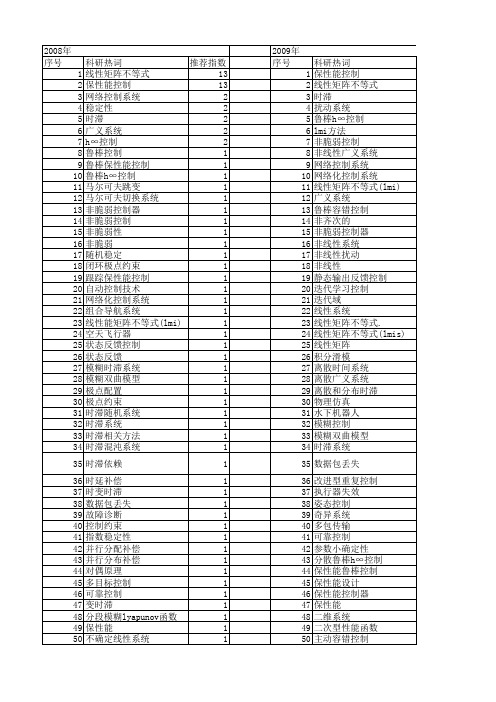
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 推荐指数 线性矩阵不等式 13 保性能控制 13 网络控制系统 2 稳定性 2 时滞 2 广义系统 2 h∞控制 2 鲁棒控制 1 鲁棒保性能控制 1 鲁棒h∞控制 1 马尔可夫跳变 1 马尔可夫切换系统 1 非脆弱控制器 1 非脆弱控制 1 非脆弱性 1 非脆弱 1 随机稳定 1 闭环极点约束 1 跟踪保性能控制 1 自动控制技术 1 网络化控制系统 1 组合导航系统 1 线性能矩阵不等式(lmi) 1 空天飞行器 1 状态反馈控制 1 状态反馈 1 模糊时滞系统 1 模糊双曲模型 1 极点配置 1 极点约束 1 时滞随机系统 1 时滞系统 1 时滞相关方法 1 时滞混沌系统 1 时滞依赖 1 时延补偿 1 时变时滞 1 数据包丢失 1 故障诊断 1 控制约束 1 指数稳定性 1 并行分配补偿 1 并行分布补偿 1 对偶原理 1 多目标控制 1 可靠控制 1 变时滞 1 分段模糊lyapunov函数 1 保性能 1 不确定线性系统 1 不确定性奇异系统 1 t-s模糊系统 1
含区间时变时滞的线性不确定系统非脆弱鲁棒控制

c m b n dwiht ei tg a n q aiy a poo c , ea — e e d n o u t tb l y ciei ni r p s d i em so e o ie t h ne r lie u l p r a h ad ly d p n e t b s a i t rtro sp o o e tr ft t r s i n h ln a ti n q a iy f rl e rs se swih i tr ltme d ly n o —r g l o us o to lri e i n d. i e rmarx i e u lt o i a y tm t ne va i — e a ,a d a n n fa ie r b tc n r le sd sg e n
在控 制器 实 际应 用 的过程 中 , 考虑 到增益 扰动 的存 在 , 制器 的 形式 可 以写为 控
冒
则 标 称 系 统 ( ) 渐 近 稳 定 的 。其 中 6是
三1 ( 1=P A+B K+A ) A+ +△ )P ( K)+( ( ) +Q+ + + 1 2
一
A∑ ( j A 羔 ( + D sE和1 f Ft ) + ) 巨
J j1 =
X (—I xt ) X (—h)2 (一 ) Tf J)1(一 一 Tf 2S xt z I
收 稿 日期 : 1 — 1 0 20 1 1 —3
《 动 技术 应 02 第3 卷 期 自 化 与 用 2 1年 1 第3
控 制 理 论 与 应 用
Co t o n l r The nd Ap ia i n or a pl to s y c
其中.
j AA 【()=A十a) 1 A1 A) +△() ( (
一种控制输入约束下的不确定离散系统非脆弱保性能控制器设计

一种控制输入约束下的不确定离散系统非脆弱保性能控制器设
计
段虹州;韩光信;高兴泉
【期刊名称】《河南科技》
【年(卷),期】2024(51)3
【摘要】【目的】针对考虑扰动及摄动情况下的控制输入约束的不确定离散系统,提出了非脆弱保性能的控制方法。
【方法】首先,以最小化目标函数为性能指标、控制输入饱和范围为约束条件,从而推导出约束状态下的非脆弱保性能控制律。
其次,使用李雅普诺夫方程来构造非线性矩阵不等式。
再次,结合Schur补定理和布谷鸟群智能优化算法对不等式进行求解,得到控制输入约束下的非脆弱保性能控制律的参数。
最后,通过Quanser三自由度陀螺仪平台进行试验验证。
【结果】试验结果表明,本研究所提出方法的稳态误差浮动不超过0.07、跟踪误差不超过0.15。
【结论】该方法在面对扰动及摄动情况时具有更高的鲁棒性,对提升三自由度陀螺仪的稳定性及控制精度具有重要意义。
【总页数】6页(P4-9)
【作者】段虹州;韩光信;高兴泉
【作者单位】吉林化工学院;吉林工业职业技术学院
【正文语种】中文
【中图分类】TP273
【相关文献】
1.一类离散系统的时滞依赖非脆弱保性能控制
2.考虑控制输入约束的鲁棒非脆弱保性能控制
3.切换系统非脆弱保性能H∞控制器设计与仿真
4.结构不确定离散系统的最优非脆弱保成本控制
5.具有控制约束的不确定离散系统最优保性能控制
因版权原因,仅展示原文概要,查看原文内容请购买。
一类非线性不确定奇异时滞系统的鲁棒H∞控制

一类非线性不确定奇异时滞系统的鲁棒H∞控制
焦建民;吴保卫;孙小军
【期刊名称】《西华大学学报(自然科学版)》
【年(卷),期】2009(28)1
【摘要】针对一类含参数不确定性和非线性扰动的奇异时滞系统,研究了状态反馈鲁棒H∞控制器的设计问题.基于Lyapunov稳定性理论和线性矩阵不等式处理方法,给出了系统H∞控制器存在的充分条件和设计方法.所设计的H∞控制器保证了对所有允许的不确定性,相应的闭环系统不仅达到广义二次稳定,而且满足给定的
H∞性能指标.最后,通过数值算例说明了所给方法的有效性.
【总页数】5页(P85-88,91)
【作者】焦建民;吴保卫;孙小军
【作者单位】陕西师范大学数学与信息科学学院,陕西,西安,710062;宝鸡文理学院数学系,陕西,宝鸡,721013;陕西师范大学数学与信息科学学院,陕西,西安,710062;宝鸡文理学院数学系,陕西,宝鸡,721013
【正文语种】中文
【中图分类】TP273
【相关文献】
1.一类不确定Lurie时滞奇异系统的鲁棒H∞控制 [J], 鲁仁全;黄文君;苏宏业;褚健
2.一类不确定性时滞奇异系统鲁棒H∞控制器的设计 [J], 李文姿;吴保卫
3.一类不确定奇异时滞系统的鲁棒方差控制 [J], 侯莉;张高民;王宣战
4.一类非线性不确定时滞系统的时滞相关鲁棒H∞控制 [J], 王岩青;姜长生
5.一类不确定时滞奇异系统的鲁棒非脆弱控制 [J], 李华荣;须文波;李华俊
因版权原因,仅展示原文概要,查看原文内容请购买。
具有输入时滞与状态时滞的非线性不确定奇异系统的保性能控制

具有输入时滞与状态时滞的非线性不确定奇异系统的保性能控制王坤;崔栋【摘要】讨论了一类非线性不确定奇异时滞系统的保性能控制问题.基于线性矩阵不等式及基本不等式的方法,研究了所给定的性能函数及所容许的时滞.设计了一个无记忆反馈控制器,使得闭环系统稳定并且闭环系统的性能指标不大于指标上界.利用线性矩阵不等式的约束条件,给出了闭环系统的保性能的充分条件,用数值算例说明了方法的有效性.【期刊名称】《河北科技大学学报》【年(卷),期】2013(034)005【总页数】6页(P406-411)【关键词】奇异系统;线性矩阵不等式;输入时滞;状态时滞;保性能控制【作者】王坤;崔栋【作者单位】燕山大学理学院,河北秦皇岛066004;燕山大学理学院,河北秦皇岛066004【正文语种】中文【中图分类】O231.2近年来,不确定系统的保性能控制的问题引起了人们的关注。
研究的目的是对不确定系统设计一个控制器,使得其闭环系统不仅对所容许的不确定性渐近稳定,而且相应的闭环系统的性能指标不大于指标上界。
正常系统的保性能控制器的研究已有许多成果[1-6]。
对于奇异系统可以更好的描述实际物理过程,所以对奇异系统的保性能控制的研究更有意义。
文献[7]—文献[9]对于线性奇异系统的保性能控制问题有了一定的发展,文献[10]研究了广义系统的时滞相关非脆弱H∞保成本控制,文献[11]—文献[12]利用Lipschitz条件设计了鲁棒H∞保性能控制器,文献[13]研究了一类不确定非线性奇异系统的保性能控制,未对输入时滞进行研究。
但目前对于均具有状态时滞与输入时滞的不确定奇异系统的非线性扰动的问题的研究还不多见,本文针对这一类非线性不确定奇异时滞系统,基于Lyapunov稳定性理论,线性矩阵不等式以及基本不等式方法设计了闭环系统的保性能控制器,使得闭环系统二次稳定且具有H∞抑制水平γ,保性能的性能指标不大于指标上界。
1 问题描述与预备知识(1)其中:x(t)∈Rn,u(t)∈Rm分别为系统的状态向量和控制向量;ω(t)∈Rp为外界干扰输入向量;z(t)∈Rq为受控输出向量;通常矩阵E∈Rn×n为奇异矩阵,A,Ad,B1,B2,C为适当维数的已知常数矩阵,h为不确定的、非时变的状态时滞,满足0≤h≤h*,h*为时滞h的已知上界;ΔA,ΔAd,ΔB1为时变参数不确定性。
复杂执行器非线性的不确定机器人变参数滑模非脆弱控制

复杂执行器非线性的不确定机器人变参数滑模非脆弱控制李智;刘树博;张志远
【期刊名称】《控制工程》
【年(卷),期】2024(31)2
【摘要】针对机器人面临参数不确定性、复杂执行器非线性及控制器脆弱性的问题,提出了一种基于多项式平方和(sum-of-squares,SOS)理论的变参数滑模非脆弱控制(parameter-varying sliding non-fragile control,PSNC)策略。
首先,建立了具有复杂执行器非线性的机器人数学模型;其次,设计了一种新型伪奇异非脆弱保性能滑模面(non-fragile guaranteed cost sliding surface,NGCSS),基于等效控制法推导了最优保性能滑模面存在的充分条件;最后,设计了非脆弱滑模自适应控制律,并基于Lyapunov方法对闭环系统的稳定性进行了分析。
仿真结果表明,该控制器能够使机器人在复杂执行器非线性、控制器摄动和外部干扰作用下,快速、精确地跟踪期望轨迹,体现出了良好的鲁棒性和非脆弱性。
【总页数】10页(P375-384)
【作者】李智;刘树博;张志远
【作者单位】东华理工大学江西省康复辅具产业技术研究院;东华理工大学机械与电子工程学院
【正文语种】中文
【中图分类】TP273
【相关文献】
1.一类非匹配不确定纯反馈非线性系统新型变幂次趋近律滑模控制
2.基于自适应滑模变结构控制参数不确定永磁同步电机混沌控制
3.非线性不确定机器人复合滑模非脆弱H_(∞)位/力控制
因版权原因,仅展示原文概要,查看原文内容请购买。
不确定性时滞奇异系统的非脆弱保性能控制

(0 2)
考虑 如下形 式 的性 能 函数
. , =【[ f f + f ( ] ( s ( M ) Mf d ) ) (s ) t
其 中 S > , 0是 给定 的加权矩 阵 。 0S > 设计 一具有 增益扰 动 的状 态反馈 控制器
( ) ()≤ , Vt 0 t t , ≥ 将式 ( ) 4 运用 到系统 ( ) , 1 中 可得 闭环系统
维普资讯
第 2 第 2期 8卷 20 0 8年 3月
云南师范大学学报
J u a fYu n nNoma iest o r lo n a r lUnv ri n y
V0 . 8 No 2 12 . Ma .2 08 r 0
不 确 定 性 时滞 奇 异 系统 的非 脆 弱保 性 能控 制
维普资讯
・
6・
云南师范大学学报( 自然科学版)
第2 8卷
() 1h 和 h 是已知的常数 ; () t ≤ D< , M 。 t是在[ 0 上的连续初始函数 ; () A+△A t, t = h ,] A t= ()A ()
A +△A ()E, A , 已知 的具有 适 当维 数 的实 常 数矩 阵 , () △A () 系统 的时 变不 确定 t , A, B是 △A t和 t是 矩阵且满 足 [ () △A () =MF() Ⅳ Ⅳ ] △A t t] t[ 2 其 中 M, Ⅳ 是 实常数 矩阵 , t是未 知 的实时变 矩阵且 满足 Ⅳ ,2 F()
本 文采用 以下记 号 : >0 A> ) 示 A 为半 正 定矩 阵 ( AI ( 0 表 正定 矩 阵 ) 矩 阵 曰 ; 表 示 矩 阵 B的转 置 ;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
其 中 , , , 。 是适 当维 数 的 已知常 数矩 阵 , M E, E, 反映 了不 确定性 的结构信 息 , F() R , 且 £ ∈ 满 足 F () ≤ I J 单位 矩 阵) _ ・ F() (是 ; ( )满 足 i厂 ・ l≤ l x()l, ()∈ R , 厂 l () l - l £ l Vz f G G为给 定常 矩阵 .
条 件和设 计 方法. 最后 , 通过 数值算 例验 证 了所 得方 法 的有效性 .
1 问题 描 述
考 虑 由如下状 态方 程描 述 的一类 不确定 奇异 时变 时滞 系统
f ()一 ( + A A) & f A z( )+ ( A + A A z( — d( ) ) t £ )+ ( B+ △ B) £ ( ) +( B + △ B “( — h() ) t £ )+ Df( £ ) () () 1
性.
ቤተ መጻሕፍቲ ባይዱ
关键 词 : 非线 性扰 动 ;非脆 弱保性 能控 制 ;奇异 时 变时滞 系统 ;L MI
中 图 法 分 类 号 : 0 3 0. 2 2 文 献 标 识 码 :A
0 引 言
时滞 现象 和不 确定性 普遍 存在 于各类 工业 系统 中 , 导致 系统不 确定性 和性 能变差 的 主要 因素 . 是 不 确定 奇异 系统 保性 能控制 研究 的基本 思想 是设 计一个 控 制律 使得 对 应 的闭 环 系统 鲁棒 渐 近稳 定 , 且 相 并 应 的闭环 性能 指标 有一个 性 能上界. 而非 脆弱性 是控 制 律设 计 中的 一个 重要 因素 , 此 , 于 不确 定 奇 异 因 关 时 变时滞 系统 的非 脆弱保 性 能控制 的研 究是具 有实 际 意义 的. 至今 , 有关 这 方 面 的研究 已有 了 丰硕 成果 . 文 献[ ] 究 了带有 非线 性扰 动 的不 确定 奇异 时滞 系统 的保 性 能控 制 问题 , 1研 其研 究 的系统 无 输入 时 滞 ; 文 献 E] 2 研究 了一类非 脆 弱奇异 时滞 系统 的保性 能控制 问题 , 其研 究 的系统不 带有扰 动项 ; 献[ ] 究 了非 文 3研 线 性不 确定 时变 时滞 系统 的鲁棒保 性能 控制 问题 , 其研 究 的系 统时 变 时滞 是 同一个 ; 献 E ] 究 了线 性 文 4研 不 确定 时滞 系统 的保性 能控 制 问题 . 文主要 针对 一类 带有非 线性 扰动 的非脆 弱奇异 时变 时滞 系统 , 本 研究 了其非脆 弱保 性 能控制 问题 , 利用 L a u o y p n v稳 定 性 理论 和 L 方法 , 出 了保 性 能控 制 律 存 在 的充 分 MI 得
() £ 一 () t [ r0 £ , ∈ 一 ,]
其 中 , ∈ R 是奇 异矩 阵 , 且 rn ( 一r E 并 a k E) < ; ()∈ R 是 系统 ( ) zf 1 的状 态 向量 ; ()∈ R £ 是
系统 ( )的控制 输 入 向量 ; A , B , 是 适 当维数 的 已知 矩 阵 ; 1 A, B, D △A, A , △ AB, 是 不确 定 矩 阵 , △B 表 示 系统模 型 中的时 变参数 不确 定性 ; ≤ () d< 。 0≤ 矗 ≤ h< 0 时变 时滞 , 且满 足 () 0 ≤ 。, () 是 并
第 3 O卷
第 2 期
陕 西科 技 大 学 学报
J u na fS a n iUn v r iy o ce c & T c n lg o r lo h a x i e st fS i n e e h oo y
Vo . O No 2 13 .
A pr 2 2 . 01
* 收 稿 日期 :0 11 -5 2 1-20 基 金 项 目 : 家 自然科 学 基 金 项 目( 0 7 1 3 ; 国 1 9 1 2 ) 陕西 省 自然 科 学 基 础 研 究 计划 项 目 (J 8 2 ) SO A O 作 者 简 介 : 阿 曼 ( 9 7 ) 女 , 西 省 周 至 县 人 , 士 , 究 方 向 : 制 理 论 尚 18一 , 陕 硕 研 控
摘 要 : 对 一类 带有非 线性扰 动 的奇异 时 变时滞 系统 , 究 了其 非脆 弱保 性 能控 制 问题 , 针 研 并
运用 L auo y p n v稳 定性理 论和 L MI 法 , 出了 系统 非脆 弱保 性能 控制 律 存在 的 充 分条 件 和 方 得
设计 方 法. 所有容许 的不确 定性 , 对 所设 计的非脆 弱保 性 能控制律 不仅使 得 相应 的 闭环 系统是 渐近 稳 定的 , 并且使得 闭环性 能指标 有性 能上界 . 最后 , 合仿 真 实例 来 说 明所 得 方 法 的可行 结
第 2 期
尚阿 曼 等 : 有 非 线 性 扰 动 的非 脆 弱奇 异 时 变 时 滞 系 统 的 保 性 能 控 制 带
。9 ‘ 5
≤ < 1 () , ≤ < 1 记 r , —ma { h , 一ma { ) ( ) t^ o 一, , £ 是 给定 初 始值 的连续 x d, }卢 x d, , 0 一 , ( ) 7 () z
2 2年 4月 01
文章 编 号 :0 0 5 1 ( 0 2 0 — 0 4 0 1 0—8 1 2 1 }20 9—6
带 有 非 线 性 扰 动 的 非 脆 弱 奇 异 时 变 时 滞 系 统 的 保 性 能 控 制
尚阿 曼 ,吴 保 卫 ,刘 丽丽
( 西师范大学 数学与信息科学学院 , 西 西安 陕 陕 70 6 ) 10 2
