初二数学三角形难题汇总完整版
超难题系列:八年级上册数学《三角形》21道超难题

超难题系列八年级上册数学《三角形》21道超难题一.选择题(共1小题)1.(2020春•南岗区校级月考)如图,在Rt△ABC中,∠BAC=90°,点D在BC上,过D作DF⊥BC交BA的延长线于F,连接AD、CF,若∠CFE=32°,∠ADB=45°,则∠B的大小是()A.32°B.64°C.77°D.87°二.解答题(共21小题)2.(2021春•江都区期中)【概念认识】如图①,在∠ABC中,若∠ABD=∠DBE=∠EBC,则BD,BE叫做∠ABC的“三分线”.其中,BD是“邻AB三分线”,BE是“邻BC三分线”.【问题解决】(1)如图②,在△ABC中,∠A=80°,∠B=45°,若∠B的三分线BD交AC于点D,求∠BDC的度数;(2)如图③,在△ABC中,BP、CP分别是∠ABC邻BC三分线和∠ACB邻BC三分线,且∠BPC=140°,求∠A的度数;【延伸推广】线所在的直线交于点P.若∠A=m°(m>54),∠B=54°,直接写出∠BPC的度数.(用含m的代数式表示)3.(2021•香洲区校级模拟)“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)4.(2019秋•揭阳期末)探究与发现:如图①,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连接DE.(1)当∠BAD=60°时,求∠CDE的度数;(2)当点D在BC(点B、C除外)边上运动时,试猜想∠BAD与∠CDE的数量关系,并说明理由.(3)深入探究:如图②,若∠B=∠C,但∠C≠45°,其他条件不变,试探究∠BAD与∠CDE的数量关系.5.(2019秋•长葛市期末)如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.(1)若∠B=35°,∠ACB=85°,求∠E的度数.(2)当点P在线段AD上运动时,设∠B=α,∠ACB=β(β>α),求∠E的大小.(用含α、β的代数式表示)6.(2019秋•辽阳期末)已知如图①,BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,BQ、CQ分别是∠PBC、∠PCB的角平分线,BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α.(1)当α=40°时,∠BPC= °,∠BQC= °;(2)当α= °时,BM∥CN;(3)如图②,当α=120°时,BM、CN所在直线交于点O,求∠BOC的度数;(4)在α>60°的条件下,直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系:.7.(2019春•高邑县期末)如图,点C、D分别在∠AOB的OA、OB边上运动(不与点O重合).射线CE与射线DF分别在∠ACD和∠CDO内部,延长EC与DF交于点F.(1)若∠AOB=90°,CE、DF分别是∠ACD和∠CDO的平分线,猜想:∠F的度数是否随C,D的运动发生变化?请说明理由.(2)若∠AOB=α°(0<α<180),∠ECD=1 /n ∠ACD,∠CDF=1/n ∠CDO,则∠F= °.(用含α、n的代数式表示)8.(2019春•芙蓉区校级期中)在△ABC中,AD⊥BC于点D,AE平分∠BAC.(1)如图,点D在线段BC上.①若∠B=70°,∠C=30°,则∠DAE= ;②若∠B=α,∠C=β,则∠DAE= .(用含α、β的代数式表示)(2)如图2,若点D在边CB的延长线上时,若∠ABC=α,∠C=β,写出∠DAE与α、β满足的数量关系式,并说明理9.(2018春•南安市期末)阅读理解:请你参与下面探究过程,完成所提出的问题.(Ⅰ)问题引入:如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=70°,则∠BOC= 度;若∠A=α,则∠BOC= (用含α的代数式表示);(Ⅱ)类比探究:如图②,在△ABC中,∠CBO=1/3 ∠ABC,∠BCO=1/3 ∠ACB,∠A=α.试探究:∠BOC与∠A的数量关系(用含α的代数式表示),并说明理由.如图③,BO、CO分别是△ABC的外角∠DBC,∠ECB的n等分线,它们交于点O,∠CBO=1/n ∠DBC,∠BCO=1/n∠ECB,∠A=α,求∠BOC的度数(用含α、n的代数式表示).10.(2018春•镇平县期末)已知a,b,c是△ABC的三边长,a=4,b=6,设三角形的周长是x.(1)直接写出c及x的取值范围;(2)若x是小于18的偶数①求c的长;②判断△ABC的形状.11.(2017秋•开江县期末)如图1,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=82°,则∠BEC= ;若∠A=a°,则∠BEC= .【探究】(1)如图2,在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB,若∠A=a°,(2)如图3,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC和∠A有怎样的关系?请说明理由;(3)如图4,O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?请说明理由.12.(2021春•镇江期末)直线AB、CD为平面内两条直线,点M、点N分别在直线AB、CD上,点P(P不在直线AB、CD上)为平面内一动点.(1)如图1,若AB、CD相交于点O,∠MON=40°;①当点P在△OMN内部时,求证:∠MPN-∠OMP-∠ONP=40°;②小芳发现,当点P在∠MON内部运动时,∠MPN、∠OMP、∠ONP还存在其它数量关系,这种数量关系是;③探究,当点P在∠MON外部时,∠MPN、∠OMP、∠ONP之间的数量关系共有种;(2)如图2,若AB∥CD,请直接写出∠MPN与∠AMP、∠CNP之间存在的所有数量关系是.13.(2021春•永嘉县校级期中)如图1我们称之为“8字形”,请直接写出∠A,∠B,∠C,∠D之间的数量关系:;(3)如图2,∠1+∠2+∠3+∠4+∠5+∠6+∠7= 度(4)如图3所示,已知∠1=∠2,∠3=∠4,猜想∠B,∠P,∠D之间的数量关系,并证明.14.(2021春•安丘市期末)如图①,在△ABC中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.(1)求∠DAE的度数;(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.15.(2020秋•椒江区校级月考)在一个钝角三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“智慧三角形”.如,三个内角分别为120°,40°,20°的三角形是“智慧三角形”.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交射线OB于点C.(1)∠ABO的度数为°,△AOB (填“是”或“不是”)“智慧三角形”;(2)若∠OAC=20°,求证:△AOC为“智慧三角形”;(3)当△ABC为“智慧三角形”时,求∠OAC的度数.(直接写出答案)模型:角平分线模型16.(2020秋•阜平县期中)如图,△ABC中,AD是高,AE、BF是角平分线,它们相17.(2019春•庐江县期末)已知:三角形ABC和同一平面内的点D.(1)如图1,点D在BC边上,DE∥BA交AC于E,DF∥CA交AB于F.若∠EDF=85°,则∠A的度数为°.(2)如图2,点D在BC的延长线上,DF∥CA,∠EDF=∠A,证明:DE∥BA.(3)如图3,点D是三角形ABC外部的一个动点,过D作DE∥BA交直线AC于E,DF∥CA交直线AB于F,直接写出∠EDF与∠A的数量关系(不需证明).18.(2019春•新华区校级期末)直线MN与直线PQ垂直相交于点O,点A在射线OP上运动(点A不与点O重合),(1)如图1,已知AE、BE分别是∠BAO和∠ABO的角平分线,①当∠ABO=60°时,求∠AEB的度数;②点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况:若不发生变化,试求出∠AEB的大小;(2)如图2,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线所在的直线分别相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,请直接写出∠ABO的度数.19.(2018秋•崇左期末)将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.(1)如图(1)若∠BOD=35°,求∠AOC的度数,若∠AOC=135°,求∠BOD的度数.(2)如图(2)若∠AOC=150°,求∠BOD的度数.(3)猜想∠AOC与∠BOD的数量关系,并结合图(1)说明理由.(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由.20.(2019春•永年区期末)如图是一个多边形,你能否用一直线去截这个多边形,使得到的新多边形分别满足下列条件:(画出图形,把截去的部分打上阴影)①新多边形内角和比原多边形的内角和增加了180°.②新多边形的内角和与原多边形的内角和相等.③新多边形的内角和比原多边形的内角和减少了180°.(3)将多边形只截去一个角,截后形成的多边形的内角和为2520°,求原多边形的边数.21.(2019春•潍坊期末)△ABC中,∠C=80°,点D、E分别是△ABC边AC、BC上的点,点P是一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在边AB上,且∠α=50°,如图1,则∠1+∠2= ;(2)若点P在边AB上运动,如图2所示,则∠α、∠1、∠2之间的关系为.(3)若点P运动到边AB的延长线上,如图3,则∠α、∠1、∠2之间有何关系?猜想并说明理由22.(2019春•城厢区校级期末)直线MN与直线PQ垂直相交于O,点A在射线OP 上运动,点B在射线OM上运动.(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;(2)如图2,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F,则∠EAF= °;在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.。
(完整版)初二数学全等三角形专题难题
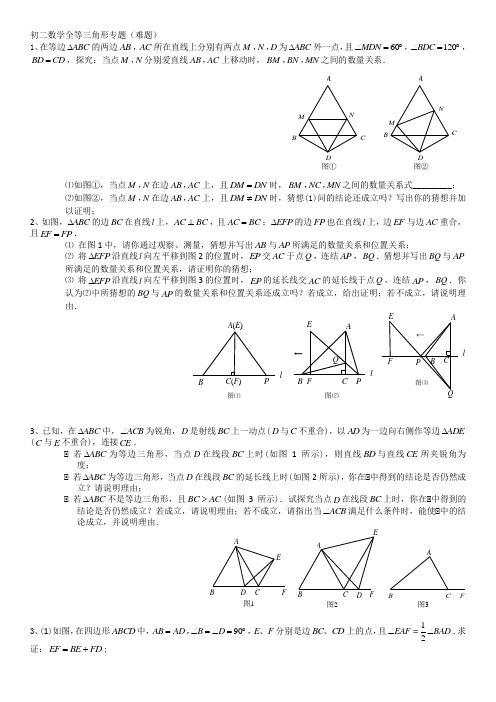
初二数学全等三角形专题(难题) 1、在等边ABC ∆的两边AB ,AC 所在直线上分别有两点M N D ,,为ABC ∆外一点,且60MDN ∠=︒,120BDC ∠=︒,BD CD =,探究:当点M N ,分别爱直线AB AC ,上移动时,BM BN MN ,,之间的数量关系.⑴如图①,当点M N ,在边AB AC ,上,且DM DN =时,BM NC MN ,,之间的数量关系式_________; ⑵如图②,当点M N ,在边AB AC ,上,且DM DN ≠时,猜想(1)问的结论还成立吗?写出你的猜想并加以证明;2、如图,ABC ∆的边BC 在直线l 上,AC BC ⊥,且AC BC =;EFP ∆的边FP 也在直线l 上,边EF 与边AC 重合,且EF FP =.⑴ 在图1中,请你通过观察、测量,猜想并写出AB 与AP 所满足的数量关系和位置关系;⑵ 将EFP ∆沿直线l 向左平移到图2的位置时,EP 交AC 于点Q ,连结AP ,BQ .猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想;⑶ 将EFP ∆沿直线l 向左平移到图3的位置时,EP 的延长线交AC 的延长线于点Q ,连结AP ,BQ .你认为⑵中所猜想的BQ 与AP 的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.3、已知,在ABC ∆中,ACB ∠为锐角,D 是射线BC 上一动点(D 与C 不重合),以AD 为一边向右侧作等边ADE ∆(C 与E 不重合),连接CE .⑴ 若ABC ∆为等边三角形,当点D 在线段BC 上时(如图1所示),则直线BD 与直线CE 所夹锐角为 度;⑴ 若ABC ∆为等边三角形,当点D 在线段BC 的延长线上时(如图2所示),你在⑴中得到的结论是否仍然成立?请说明理由;⑴ 若ABC ∆不是等边三角形,且BC AC >(如图3所示).试探究当点D 在线段BC 上时,你在⑴中得到的结论是否仍然成立?若成立,请说明理由;若不成立,请指出当ACB ∠满足什么条件时,能使⑴中的结论成立,并说明理由.3、(1)如图,在四边形ABCD 中,90AB AD B D =∠=∠=︒,,E F 、分别是边BC CD 、上的点,且12EAF =BAD ∠∠.求证:EF BE FD =+;图①M NDCBA图②MND CBA图⑴lPC (F )B A (E )图⑵Q ←lPFE C B A图⑶←QAEB CF Pl图1FED C B A图2B C D F AE图3B CFA(2) 如图在四边形ABCD 中,180AB AD B+D =∠∠=︒,,E F 、分别是边BC CD 、上的点,且12EAF BAD ∠=∠, (1)中的结论是否仍然成立?不用证明.(3) 如图,在四边形ABCD 中,AB AD =,180B ADC ∠+∠=︒,E F ,分别是边BC CD ,延长线上的点,且12EAF BAD ∠=∠, (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.4、如图,已知⑴ABC 是等边三角形,E 是AC 延长线上一点,选择一点D ,使得⑴CDE 是等边三角形,如果M 是线段AD 的中点,N 是线段BE 的中点, 求证:⑴CMN 是等边三角形.(根据⑴ACD ⑴⑴BCE ,得出AD=BE ,AM=BN ;又⑴AMC ⑴⑴BNC ,可得CM=CN ,⑴ACM=⑴BCN ,证明⑴NCM=⑴ACB=60°即可证明⑴CMN 是等边三角形;)EFDCBAEFD CBAEFDCBA外角的平分线交于点N,DM与MN有怎样的数量关系?点M、N分别在AB、AC上,求AMN∆的周长.BMNM CBA。
初二全等三角形难题压轴题

全等三角形难题易错点剖析一、错用三角对应相等说明全等例1如图,∠CAB=∠DBA,∠C=∠D,E为AC和BD的交点.△ADB与△BCA全等吗?说说理由.错解:△ADB≌△BCA.因为∠C=∠D,∠CAB=∠DBA,∠DAB=CBA,所以△CBE≌△DAE(AAA).分析:两个三角形全等是对的,但说明的理由不正确.三个角对应相等不能作为三角形全等的识别方法.因为三个角对应相等的两个三角形不一定全等.正解:△CBE≌△DAE.因为∠CAB=∠DBA,∠C=∠D,AB=BA(公共边),所以△CAB≌△DBA(AAS).二、错用两边及一角对应相等说明全等例2如图,已知△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD=BE,△ADC与△AEB全等吗?说说理由.错解:△ADC≌△AEB.因为AB=AC,BE=CD,∠BAE=∠CAD,所以△ADC≌△AEB(SSA).分析:错解在把SSA作为三角形全等的识别方法,实际上,SSA不能作为三角形全等的识别条件.因为两边及一边对角相等的两个三角形不一定全等.正解:△ADC≌△AEB.因为AB=AC,D,E为AB,AC的中点,所以AD=AE.在△ADC和△AEB中,因为AB=AC,AD=AE,CD=BE,所以△ADC≌△AEB(SSS).三、错用部分当整体说明全等例3如图,已知AB=AC,BD=CE,试说明△ABE与△ACD全等的理由.错解:因为AB=AC,所以∠B=∠C,在△ABE和△ACD中,因为AB=AC,∠B=∠C,AD=CE,所以△ABE≌△ACD(SAS).分析:错解在把三角形边上的一部分当作说明的条件,这不符合三角形全等的识别方法.正解:△ABE与△ACD全等.因为AB=AC,所以∠B=∠C,因为BD=CE,所以BD+DE=CE+DE,即BE=CD.在△ABE和△ACD中,因为AB=AC,B=C,BE=CD,所以△ABC≌△ACF(SAS).四、错用减法运算说明全等例4如图,已知AC,BD相交于点O,∠A=∠B,∠1=∠2,AD=BC.试说明△AOD≌△BOC.错解:在△ADC和△BCD中,因为∠A=∠B,∠2=∠1,DC=CD,所以△ADC≌△BCD(AAS),所以△ADC-△DEC=△BCD-△DEC,即△A0D≌△B0C.分析:错解在将等式的性质盲目地用到三角形全等中,实际上,三角形全等是不能根据等式的性质说明的.正解:在△ADO和△BCD中,∠A=∠B,∠AOD=∠BOC,AD=BC,所以△AOD≌△BOC(AAS).。
初二数学三角形难题汇总完整版

初二数学三角形难题汇总Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】初二数学三角形测试题一、填空1、(1)全等三角形的_________和_________相等;(2)两个三角形全等的判定方法有:______________________________;另外两个直角三角形全等的判定方法还可以用:_______;(3)如右图,已知AB=DE,∠B=∠E,若要使△ABC≌△DEF,那么还要需要一个条件,这个条件可以是:_____________,理由是:_____________;这个条件也可以是:_____________,理由是:_____________;(4)如右图,已知∠B=∠D=90°,,若要使△ABC≌△ABD,那么还要需要一个条件,这个条件可以是:_____________,理由是:_____________;这个条件也可以是:_____________,理由是:_____________;这个条件还可以是_____________,理由是:_____________;2.如图5,⊿ABC≌⊿ADE,若∠B=40°,∠EAB=80°,∠C=45°,则∠EAC=?,∠D=,∠DAC=?。
3.如图6,已知AB=CD,AD=BC,则≌,≌。
4.如图7,已知∠1=∠2,AB⊥AC,BD⊥CD,则图中全等三角形有_____________;5.如图8,若AO=OB,∠1=∠2,加上条件,则有ΔAOC≌ΔBOC。
7、如图,在一小水库的两测有A、B两点,A、B间的距离不能直接测得,采用方法如下:取一点可以同时到达A、B的点C,连结AC并延长到D,使AC=DC;同法,连结BC并延长到E,使BC=EC;这样,只要测量CD的长度,就可以得到A、B的距离了,这是为什么呢?根据以上的描述,请画出图形,并写出已知、求证、证明。
(专题精选)初中数学三角形难题汇编及答案解析

∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,∠AEB=60°,
∵AB= BC,
∴AE=BE= BC,
∴AE=CE,故①正确;
∴∠EAC=∠ACE=30°
∴∠BAC=90°,
∴S△ABC= AB•AC,故②错误;
∵BE=EC,
∴E为BC中点,O为AC中点,
(专题精选)初中数学三角形难题汇编及答案解析
一、选择题
1.如图,已知 ,若 , , ,下列结论:① ;② ;③ ;④ 与 互补;⑤ ,其中正确的有()
A.2个B.3个C.4个D.5个
【答案】C
【解析】
【分析】
根据平行线的判定得出AC∥DE,根据垂直定义得出∠ACB=∠CDB=∠CDA=90°,再根据三角形内角和定理求出即可.
∴S△ABE=S△ACE=2S△AOE,故③正确;
∵四边形ABCD是平行四边形,
∴AC=CO,
∵AE=CE,
∴EO⊥AC,
∵∠ACE=30°,
∴EO= EC,
∵EC= AB,
∴OE= BC,故④正确;
故正确的个数为3个,
故选:C.
【点睛】
此题考查平行四边形的性质,等边三角形的判定与性质.注意证得△ABE是等边三角形是解题关键.
15.如图,四边形 和 都是正方形,点 在 边上,点 在对角线 上,若 ,则 的面积是()
A.6B.8C.9D.12【答Βιβλιοθήκη 】B【解析】【分析】
根据正方形的性质得到∠DAC=∠ACD=45°,由四边形EFGH是正方形,推出△AEF与△DFH是等腰直角三角形,于是得到DE= EH= EF,EF= AE,即可得到结论.
初二数学三角形-解答题难度:较易76题

初⼆数学三⾓形-解答题难度:较易76题初⼆数学三⾓形-解答题难度:较易 76题⼀、解答题(本⼤题共76⼩题,共608.0分)1. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,DE垂直平分BC,垂⾜为D,交AB于点E.⼜点F在DE的延长线上,且AF=CE.求证:四边形ACEF是菱形.2. 如图,正⽅形⽹格中的每个⼩正⽅形边长都是1,每个⼩格的顶点叫做格点,以格点为顶点分别按下列要求画三⾓形.(1)在图1中,画⼀个三⾓形,使它的三边长都是⽆理数;(2)在图2中,画出⼀个直⾓三⾓形,使它的三边长都是整数;(3)在图3中,画出⼀个中⼼对称图形.3. 在凸多边形中,四边形有2条对⾓线,五边形有5条对⾓线,经过观察、探索、归纳,你认为凸⼋边形的对⾓线条数应该是多少条?简单扼要地写出你的思考过程.4. 如图,已知DE垂直平分AB,分别交AB、BC于D、E两点,AE平分∠BAC,∠B=30°,BE=4,求AC的长.5. ⼀个三⾓形的三边长分别为、、(1)求它的周长(要求结果化简);(2)请你给⼀个适当的x值,使它的周长为整数,并求出此时三⾓形周长的值.6. 如图1,⼀扇窗户打开后⽤窗钩AB可将其固定.(1)这⾥所运⽤的⼏何原理是()(A)三⾓形的稳定性(B)两点之间线段最短;(C)两点确定⼀条直线(D)垂线段最短;(2)图2是图1中窗⼦开到⼀定位置时的平⾯图,若∠AOB=45°,∠OAB=30°,OA=60cm,求点B到OA边的距离.( ≈1.7,结果精确到整数)7. 已知,如图1,AB⊥BD于B,ED⊥BD于D,点C在直线BD上且与F重合,AB=FD,BC=DE(1)请说明△ABC≌△FDE,并判断AC是否垂直FE?(2)若将△ABC 沿BD⽅向平移⾄如图2的位置时,且其余条件不变,则AC是否垂直FE?请说明为什么?8. 如图,在△ABC中,点D是AB的中点,CE⊥AB于点E,∠BCE=60°,∠ACE=45°若DE=10,求CE的长.(结果保留根号)9. 已知正n边形的周长为60,边长为a(1)当n=3时,请直接写出a的值;(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有⼈分别取n等于3,20,120,再求出相应的a与b,然后断⾔:“⽆论n取任何⼤于2的正整数,a与b⼀定不相等.”你认为这种说法对吗?若不对,请求出不符合这⼀说法的n的值.10. 如图,四边形ABCD各个顶点的坐标分别为(-2,8),(-11,6),(-14,0),(0,0).(1)确定这个四边形的⾯积,你是怎么做的?(2)如果把原来ABCD各个顶点纵坐标保持不变,横坐标增加2,所得的四边形⾯积⼜是多少?11. 如图,正⽅形ABCD中,BC=2.点E在CD上,CE=1,将△BCE 绕点B逆时针旋转⾄△BAF的位置,且点F在DA的延长线上.(1)写出旋转⾓度;(2)试判断△BEF的形状;并求出线段EF的长.12. 如图,已知:△ABC中,BC<AC,AB边上的垂直平分线DE交AB于D,交AC于E,AC=9 cm,△BCE的周长为15 cm,求BC的长.13. 如图,在△ABC中,AB=AC,AD平分∠BAC.求证:△ABD≌△ACD.14. 如图:在△ABC中,∠B=90°,AB=BD,AD=CD,求∠CAD的度数.15. 已知:E是AB、CD外⼀点,∠D=∠B+∠E,求证:AB∥CD.16. 看图回答问题:(1)内⾓和为2005°,⼩明为什么说不可能?(2)⼩华求的是⼏边形的内⾓和?(3)错把外⾓当内⾓的那个外⾓的度数你能求吗?是多少度呢?17. ⼀个多边形的外⾓和是内⾓和的,求这个多边形的边数.18. 如果⼀个正多边形的每个外⾓都是24°.(1)求这个多边形的边数.(2)求这个多边形的对⾓线的条数.19. ⼩华从点A出发向前⾛10m,向右转36°然后继续向前⾛10m,再向右转36°,他以同样的⽅法继续⾛下去,他能回到点A 吗?若能,当他⾛回到点A时共⾛多少⽶?若不能,写出理由.20. 如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.求证:(1)△ACD≌△BEC;(2)CF⊥DE.21. 如图,A岛在B岛的北偏东30°⽅向,C岛在B岛的北偏东80°⽅向,A岛在C岛北偏西40°⽅向.从A岛看B、C两岛的视⾓∠BAC是多少?22. 如图所⽰,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选⼀个加以说明.23. 如图,△ACB中,∠ACB=90°,∠1=∠B.(1)试说明CD是△ABC的⾼;(2)如果AC=8,BC=6,AB=10,求CD的长.24. 已知,如图,在△ABC中,BD⊥AC于D,若∠A:∠ABC:∠ACB=3:4:5,试求∠ABD的度数.25. 如图,在△ABC中,∠C=90°,AB的垂直平分线交AC于点D,垂⾜为E,若∠A=30°,CD=2.(1)求∠BDC的度数;(2)求BD的长.26. 阅读材料,并填表:在△ABC中,有⼀点P 1,当P 1、A、B、C没有任何三点在同⼀直线上时,可构成三个不重叠的⼩三⾓形(如图).当△ABC内的点的个数增加时,若其它条件不变,三⾓形内互不重叠的⼩三⾓形的个数情况怎样?完成下表:ABC内点的个数 1 2 3 (1002)构成不重叠的⼩三⾓形的个数 3 5 …27. 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB+BD与DE的长度有什么关系?并加以证明.28. 如图,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,∠CAE:∠EAB=4:1,求∠B的度数.29. 如图,AD为△ABC的⾓平分线,DE⊥AB,DF⊥AC,垂⾜分别为E,F,连接EF,EF交AD于点G、试判断线段AD与EF的位置关系,并证明你的结论.30. 如图1,在△ABC与△BDE中,∠ABC=∠BDE=90°,BC=DE,AB=BD,M、M′分别为AB、BD中点.(1)探索CM与EM′有怎样的数量关系?请证明你的结论;(2)如图2,连接MM′并延长交CE于点K,试判断CK与EK之间的数量关系,并说明理由.31. ⼀个多边形除去⼀个内⾓外,其余各⾓之和为2 750°,求这个多边形的边数及去掉的⾓的度数.32. 如图,已知:AB∥CD,求证:∠B+∠D+∠BED=360°.(⾄少⽤三种⽅法)33. ⼀个n边形的内⾓和⽐它的外⾓和⾄少⼤120°,n的最⼩值是多少?34. 如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,∠CEB=100°.求∠ADC的度数.35. 如图,在△ABC中,AD是BC边上的⾼,AE是∠BAC的平分线,∠B=42°,∠DAE=18°,求∠C的度数.36. 如图,已知AB=AC,DE垂直平分AB交AC、AB于E、D两点,若AB=12cm,BC=10cm,∠A=50°,求△BCE的周长和∠EBC的度数.37. a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请⽤尺规画出O点位置,不写作法,保留痕迹.38. 如图,点A、E、B、D在同⼀条直线上,已知AC∥DF,∠C=∠F=110°,∠ABC=40°(1)求∠D的度数;(2)BC与EF有怎样的位置关系?请说明理由.39. 如图,按规定,⼀块模板中AB、CD的延长线应相交成85°⾓.因交点不在板上,不便测量,⼯⼈师傅连接AC,测得∠BAC=32°,∠DCA=65°,此时AB、CD的延长线相交所成的⾓是不是符合规定?为什么?40. 如图,△ABC中,点D、E分别为AB、AC的中点,连接DE,线段BE、CD相交于点O,若OD=2,求OC的长.41. 在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAB=∠B+30°,求∠AEB.42. 多边形内⾓和与某⼀个外⾓的度数总和是1350°,求多边形的边数.43. 在△ABC中,∠B=3∠A,∠C=5∠A,求△ABC的三个内⾓度数.44. ⼀个多边形每⼀个内⾓都为135°,求这个多边形对⾓线总条数.45. 如图,学校有⼀块三⾓形空地(即△ABC),现准备将它分成⾯积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).46. 如图,AB∥CD,分别探讨下⾯四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选⼀个加以说明.(适当添加辅助线,其实并不难)47. 如图所⽰,求∠A+∠B+∠C+∠D+∠E+∠F的度数.48. 如图,A点在B处的北偏东40°⽅向,C点在B处的北偏东85°⽅向,A点在C处的北偏西45°⽅向,求∠BAC及∠BCA的度数.49. 如图,在△ABC中,BA=BC,∠B=120°,AB的垂直平分线MN交AC于D,求证:AD= DC.50. 如图:△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D,(1)若△BCD的周长为8,求BC的长;(2)若∠ABD:∠DBC=1:1,求∠A的度数.51. 已知⼀个多边形的每⼀个外⾓都等于30°,求这个多边形的边数和它的内⾓和的度数.52. 已知⼀个多边形的内⾓和⽐它的外⾓和的3倍少180°,求这个多边形的边数.53. 如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,求∠DBC的度数.54. 已知:如图,在△ABC中,∠BAC=80°,AD⊥BC于D,AE 平分∠DAC,∠B=60°;求∠DAE的度数.55. 如图,在△ABC中,∠B=47°,三⾓形的外⾓∠DAC和∠ACF 的平分线交于点E,求∠E的度数.56. 如图,已知在三⾓形ABC中,∠C=∠ABC=2∠A,BD是AC边上的⾼,求∠DBC的度数.57. (1)画出△ABC的BC边上的⾼AD;(2)画出△ABC的AB边上的中线CE;(3)画出△ABC的AC边上的⾓平分线BF.58. 如图,在圆O中AB是直径,AT是经过点A的切线,弦CD垂直AB于P点,线段CP的中点为Q,连接BQ并延长交切线AT于T点,连接OT.(1)求证:BC∥OT;(2)若⊙O直径为10,CD=8,求AT的长;(3)延长TO交直线CD于R,若⊙O直径为10,CD=8,求TR的长.59. 已知:如图,在?ABCD中,∠ADC、∠DAB的平分线DF、AE分别与线段BC相交于点F、E,DF与AE相交于点G.(1)求证:AE⊥DF;(2)若AD=10,AB=6,AE=4,求DF的长.60. 已知:如图,在△ABC中,∠C=90°,∠B=30°,AC=6,点D在边BC上,AD平分∠CAB,E为AC上的⼀个动点(不与A、C重合),EF⊥AB,垂⾜为F.(1)求证:AD=DB;(2)设CE=x,BF=y,求y关于x的函数解析式;(3)当∠DEF=90°时,求BF的长?61. (A题)某市经济开发区建有B、C、D三个⾷品加⼯⼚,这三个⼯⼚和开发区A处的⾃来⽔⼚正好在⼀个矩形的四个顶点上,它们之间有公路相通,且AB=CD=900⽶,AD=BC=1700⽶.⾃来⽔公司已经修好⼀条⾃来⽔主管道AN,BC两⼚之间的公路与⾃来⽔管道交于E处,EC=500⽶.若⾃来⽔主管道到各⼯⼚的⾃来⽔管道由各⼚负担,每⽶造价800元.(1)要使修建⾃来⽔管道的造价最低,这三个⼯⼚的⾃来⽔管道路线应怎样设计并在图形中画出;(2)求出各⼚所修建的⾃来⽔管道的最低的造价各是多少元?(B题)如图,已知平⾏四边形ABCD及四边形外⼀直线l,四个顶点A、B、C、D到直线l的距离分别为a、b、c、d.(1)观察图形,猜想得出a、b、c、d满⾜怎样的关系式?证明你的结论.(2)现将l向上平移,你得到的结论还⼀定成⽴吗?请分情况写出你的结论.62. 如图,△ABC是某村⼀遍若⼲亩⼟地的⽰意图,在党的“⼗六⼤”精神的指导下,为进⼀步加⼤农村经济结构调整的⼒度,某村决定把这块⼟地平均分给四位“花农”种植,请你帮他们分⼀分,提供两种分法.要求:画出图形,并简要说明分法.63. 如图:已知△ABC与△DEF是⼀副三⾓板的拼图,A,E,C,D在同⼀条线上.(1)求证EF∥BC;(2)求∠1与∠2的度数.64. 如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂⾜,连接EC.(1)求∠ECD的度数;(2)若CE=5,求BC长.65. 在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,设△ABC的⾯积为s,周长为l,探索与a+b-c的值之间的关系.(1)填表:(2)分析后猜想:若设a+b-c=m(m为正实数),则= (⽤m表⽰);(3)请写出(2)中结论的推导过程.66. 已知:如图△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4cm.求BC的长.67. 将⼀副直⾓三⾓尺如图放置,已知AE∥BC,求∠AFD的度数.68. 已知:如图,在等边三⾓形ABC的AC边上取中点D,BC的延长线上取⼀点E,使CE=CD.求证:BD=DE.69. 如图所⽰,直线AD和BC相交于O,AB∥CD,∠AOC=95°,∠B=50°,求∠A和∠D.70. 先阅读下⾯的内容,再解决问题,例题:若m 2+2mn+2n 2-6n+9=0,求m和n的值.解:∵m 2+2mn+2n 2-6n+9=0∴m 2+2mn+n 2+n 2-6n+9=0∴(m+n) 2+(n-3) 2=0∴m+n=0,n-3=0∴m=-3,n=3问题(1)若x 2+2y 2-2xy+4y+4=0,求x y的值.(2)已知a,b,c是△ABC的三边长,满⾜a 2+b 2=10a+8b-41,且c是△ABC中最长的边,求c的取值范围.71. 如图,BD是∠ABC的平分线,DE∥CB,交AB于点E,∠A=45°,∠BDC=60°,求△BDE各内⾓的度数.72. 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.(1)若BC=10,则△ADE周长是多少?为什么?(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?73. 如图①、②、③中,点E、D分别是正△ABC、正四边形ABCM、正五边形ABCMN 中以C点为顶点的相邻两边上的点,且BE=CD,DB交AE于P点.(1)求图①中,∠APD的度数;(2)图②中,∠APD的度数为,图③中,∠APD的度数为;(3)根据前⾯探索,你能否将本题推⼴到⼀般的正n边形情况?若能,写出推⼴问题和结论;若不能,请说明理由.74. 已知:如图,?ABCD中,E、F分别是边AB、CD的中点.(1)求证:四边形EBFD是平⾏四边形;(2)若AD=AE=2,∠A=60°,求四边形EBFD的周长.75. 已知⼀次函数y= x+2的图象分别与坐标轴相交于A、B两点(如图所⽰),与反⽐例函数y= (x>0)的图象相交于C点.(1)写出A、B两点的坐标;(2)作CD⊥x轴,垂⾜为D,如果OB是△ACD的中位线,求反⽐例函数y= (x>0)的关系式.76. ⼀个等腰三⾓形的周长为32 cm,腰长的3倍⽐底边长的2倍多6 cm.求各边长.。
八年级数学重难点题目

八年级数学重难点题目一、三角形全等证明类题目。
1. 如图,在△ABC和△DEF中,AB = DE,∠A = ∠D,AC = DF。
求证:△ABC≌△DEF。
解析:在△ABC和△DEF中,已知AB = DE,∠A = ∠D,AC = DF。
根据三角形全等判定定理中的“边角边”(SAS),即如果两个三角形的两边及其夹角分别对应相等,那么这两个三角形全等。
所以可以得出△ABC≌△DEF。
2. 已知:如图,∠1 = ∠2,∠3 = ∠4,求证:AC = AD。
解析:因为∠3 = ∠4,所以∠ABC = ∠ABD(等角的补角相等)。
在△ABC和△ABD中,∠1 = ∠2,AB = AB(公共边),∠ABC = ∠ABD。
根据“角边角”(ASA)判定定理,可得△ABC≌△ABD,所以AC = AD。
二、等腰三角形性质与判定类题目。
3. 等腰三角形的一个角为80°,求这个等腰三角形的顶角度数。
解析:当80°角为顶角时,顶角度数就是80°;当80°角为底角时,根据等腰三角形两底角相等,三角形内角和为180°,则顶角为180° - 80°×2 = 20°。
所以顶角度数为80°或20°。
4. 已知:在△ABC中,AB = AC,D是AB上一点,DE⊥BC,E是垂足,ED的延长线交CA的延长线于点F。
求证:AD = AF。
解析:因为AB = AC,所以∠B = ∠C(等腰三角形两底角相等)。
因为DE⊥BC,所以∠B + ∠BDE = 90°,∠C+∠F = 90°。
又因为∠BDE = ∠ADF(对顶角相等),所以∠ADF = ∠F,根据等角对等边,可得AD = AF。
三、勾股定理应用类题目。
5. 已知直角三角形的两条直角边分别为3和4,求斜边的长度。
解析:根据勾股定理a^2+b^2=c^2(其中a、b为直角边,c为斜边)。
初中数学八年级数学《三角形》综合题难题附答案

八年级三角形综合题难题附答案第1节与三角形有关的线段一、三角形的边1、如图,点P是△ABC内部的一点.(1)度量线段AB,AC,PB,PC的长度,根据度量结果比较AB+AC与PB+PC的大小;(2)改变点P的位置,上述结论还成立吗?(3)你能说明上述结论为什么正确吗?【答案】(1)如图有:AB+AC>PB+PC;(2)改变点P的位置,上述结论还成立;(3)如图,连接AP,BP,CP,延长BP交于AC于点E,在△ABE中有,AB+AE>BE=BP+PE △在△CEP中有,PE+CE>PC △△+△得,AB+AE+PE+CE>BP+PE+PC,AB+AC+PE>BP+PE+PC,△AB+AC>BP+PC.二、三角形的高、中线与角平分线1、如图,在△ABC中,AB=AC,BD是腰AC上的中线。
(1)若AB>BC,填空:△AD=_____________;△△ABD的周长与△BEC的周长之差为_________。
(2)若△ABC的周长为20cm,BD将△ABC的周长分成差为4cm的两部分,求△ABC的边长。
【答案】(1)△EC;△AB-BC(2)8cm,8cm,4cm;或16/3cm,16/3cm,28/3cm2、如图,△ABC中,△C=90°,AC=8cm,BC=6cm,AB=10cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm.设运动的时间为t秒.(1)当t=6秒时,CP把△ABC的周长分成相等的两部分?(2)当t=6.5秒时,CP把△ABC的面积分成相等的两部分?(3)当t为何值时,△BCP的面积为12cm2?【答案】(1)6;(2)6.5;(3)2或6.53、如图,已知在Rt△ABC中,△ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE△AD 于E,CF△AD于F,则BE+CF的值()A.不变B.增大C.减小D.先变大再变小【答案】C第2节与三角形有关的角一、三角形的内角和1、△ABC中,∠A=50°,有一块直角三角板PMN放置在△ABC上(P点在△ABC内)使三角板PMN的两条直角边PM、PN恰好分别经过点B和C(如图)(1)填空:∠ABC+∠ACB=______°,∠PBC+∠PCB =______°;(2)试问∠ABP与∠ACP是否存在某种确定的数量关系,写出你的结论.【答案】(1)130;90;(2)∠ABP+∠ACP=40°2、如图①,在△ABC中,∠A=50°,有一块直角三角尺PMN放置在△ABC上(点P在△ABC内),使三角尺PMN的两条直角边PM、PN恰好分别经过点B、C.(1)填空:∠ABC+∠ACB=___,∠PBC+∠PCB=___;(2)试问∠ABP与∠ACP是否存在某种确定的数量关系,请写出你的结论;(3)如图②,改变直角三角尺PMN的位置(点P在△ABC外),三角尺PMN的两条直角边PM、PN仍然分别经过点B、C,(2)中的结论是否仍然成立?若不成立,请写出你的结论,并说明理由.【答案】(1)130;90;(2)∠ABP+∠ACP=40°;(3)发生变化;∠ACP -∠ABP=40°.3、问题情景:如图①,将一块直角三角板PMN放置在△ABC上(点P在△ABC内),使三角尺PMN的两条直角边PM、PN恰好分别经过点B、C.试问∠ABP与∠ACP是否存在某种确定的数量关系?(1)特殊探究:若∠A=50°,则∠ABC+∠ACB=___,∠PBC+∠PCB=_____,∠ABP+∠ACP=_____;(2)类比探究:请探究∠ABP+∠ACP与∠A的数量关系.(3)类比延伸:如图②如图②,改变直角三角尺PMN 的位置(点P在△ABC外),三角尺PMN的两条直角边PM、PN仍然分别经过点B、C,(2)中的结论是否仍然成立?若不成立,请写出你的结论,并说明理由.【答案】(1)130°;90°;40°(2)∠ABP+∠ACP=90°-∠A;(3)不成立;∠ACP -∠ABP=90°-∠A.4、动手操作:(1)如图1,将一块直角三角板DEF放置在直角三角板ABC上,使三角板DEF的两条直角边DE、DF分别经过点B、C,且BC△EF,已知△A=30°,则△ABD +△ACD=______°;(2)如图2,△BDC与△A、△B、△C之间存在着什么关系,并说明理由;(3)灵活应用:请你直接利用以上结论,解决以下列问题:如图3,BE平分△ABD,CE平分△ACD,若△BAC =40°,△BDC=120°,求△BEC的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二数学三角形难题汇
总
Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】
初二数学三角形测试题
一、填空
1、(1)全等三角形的_________和_________相等;
(2)两个三角形全等的判定方法有:______________________________;
另外两个直角三角形全等的判定方法还可以用:_______;
(3)如右图,已知AB=DE,∠B=∠E,
若要使△ABC≌△DEF,那么还要需要一个条件,
这个条件可以是:_____________,理由是:_____________;
这个条件也可以是:_____________,理由是:_____________;
(4)如右图,已知∠B=∠D=90°,,若要使△ABC≌△ABD,那么还要需要一个条件,
这个条件可以是:_____________,理由是:_____________;
这个条件也可以是:_____________,理由是:_____________;
这个条件还可以是_____________,理由是:_____________;
2.如图5,⊿ABC≌⊿ADE,若∠B=40°,∠EAB=80°,
∠C=45°,则∠EAC=?,∠D=,∠DAC=?。
3.如图6,已知AB=CD,AD=BC,则≌,≌。
4.如图7,已知∠1=∠2,AB⊥AC,BD⊥CD,则图中全等三角形有_____________;5.如图8,若AO=OB,∠1=∠2,加上条件,则有ΔAOC≌ΔBOC。
7、如图,在一小水库的两测有A、B两点,A、B间的距离不能直接测得,采用方法如下:取一点可以同时到达A、B的点C,连结AC并延长到D,使AC=DC;同法,连结BC并延长到E,使BC=EC;这样,只要测量CD的长度,就可以得到A、B的距离了,这是为什么呢?根据以上的描述,请画出图形,并写出已知、求证、证明。
