二分法PPT教学课件
合集下载
《算法案例3二分法》课件

算法定义
有序步骤
算法是一系列有序 的步骤
有限性
算法在执行过程中 会在有限步骤内终
止
确定性
算法保证经过有限 次计算后可以得到
确定的结果
算法特性
输入输出
算法具有输入和输 出
确定性
相同输入条件下, 算法的输出结果唯
一
有效性
算法解决问题的方 法必须有效
01 计算机科学
算法是计算机科学的基础
02 人工智能
● 03
第3章 二分法改进
二分法变形
二分查找的变形问题包括根据不同已知条件下的优化以及多 指针二分法的应用。这些变形能够提高算法的效率和适用性。
二分法应用
图论中的应用
优化路径搜索
贪心算法中的 应用
局部最优解
动态规划中的 应用
寻找最优解
01 LeetCode上的经典问题
二分搜索
02 实际项目中的案例
医疗领域的二分法 实践
医疗影像处理中的应用
疾病诊断模型的优化
智能化领域的二分法 实践
智能家居系统中的应用
智能机器人算法优化
二分法在游戏开 发中的应用
在游戏开发中,二分法被广泛应用于解决地图路径规划、资 源分配等问题。游戏引擎中的二分法可以提高游戏性能和体 验,策略游戏中的二分法可以优化AI决策,多人在线游戏中 的二分法能提升服务器响应速度。
《算法案例3二分法》PPT 课件
制作人:PPT创作创作 时间:2024年X月
第1章 算法概述 第2章 二分法原理 第3章 二分法改进 第4章 二分法应用拓展 第5章 实践应用案例 第6章 总结与展望
目录
● 01
第1章 算法概述
什么是算法?
二分法ppt-课件

2.578125
2.5859375
f(2.578125)<0
f(2.5859375)<0
0.03125
0.015625
f(2.578125)<0,f(2.59375)>0
2.58984375
f(2.58984375)>0
0.0078125
因为|2.5625–2.625|=0.0625<0.1,且2.5625、2.625的近似 值均为2.6,所以原方程精确到0.1的近似解为 x1 2.6 同理可知方程精确到0.01的近似解为2.59
课堂小结
1.通过本节课的学习,明确二分法是一种 求一元方程近似解的通法.
2.用二分法求方程的近似解的步骤让我们感受 到数形结合思想,方程思想
作业回馈
1. 借助计算器或计算机,用二分法求 x 方程 0.8 1 ln x 在区间(0,1)内 的近似解(精确度0.1)
2.课本第91页第2题.
f(2.5)<0,f(2.75)>0
f(2.5)<0,f(2.625)>0 f(2.5)<0,f(2.5625)>0 f(2.53125)<0,f(2.5625)>0 f(2.53125)<0,f(2.546875)>0 f(2.53125)<0,f(2.5390625)>0
f(2.625)>0
f(2.5625)>0 f(2.53125)<0 f(2.546875)>0 f(2.5390625)>0 f(2.53515625)>0
x
1
2
3
4
5
6
7
8
二分法-课件(

1、模拟实验,铺垫导入:
1、模拟实验,铺垫导入:
1、模拟实验,铺垫导入:
我在这里
1、模拟实验,铺垫导入:
1、模拟实验,铺垫导入:
哦,找到 了啊!
通过这个小实验,你能快速猜出 商品的价格吗?
1、模拟实验,铺垫导入:
在误差不超过15元的情 况下,你能用什么方法 最快的猜出600-1000元的 手机的价格?
3.1.2利用二分法 求方程近似解
授课人:xxx 班级:xxxxxxxxxxx
1、模拟实验,铺垫导入:
——如何最快找出假币?
16枚金币中有 一枚略轻,是假 币
1、模拟实验,铺垫导入:
1、模拟实验,铺垫导入:
我在这里
1、模拟实验,铺垫导入:
1、模拟实验,铺垫导入:
1、模拟实验,铺垫导入:
我在这里
0.215 0.066 -0.009 0.029 0.01
0.001
0.25 0.125 0.0625 0.03125 0.015625
0.007813
因为2.539 062 5-2.531 25=0.007813<0.01 所以区间(2.531 25,2.539 062 5)的任何值以及端点值都可以表示函数 在精确度为0.01下的近似值。 即:函数的近似解可为2.531 25
3、巩固新知
(1)、借助计算器用二分法求方程2x+3x=7在(1,2)上的近似 解(精确度0.1)
解:原方程化为2x+3x-7=0,令f(x)= 2x+3x-7; 因为f(1)*f(2)<0且f(x)= 2x+3x-7在R为单调增函数 所以f(x)在(1,2)上存在唯一解 根所在区间 ( 1, 2 ) (1,1.5) (1.25,1.5) (1.375,1.5) (1.375,1.4375) 中点值 1.5 1.25 1.375 1.4375 1.40625 中点函数近似值 0.3284 -0.8716 0.0210 -0.1308
用二分法求方程的近似解(很实用)通用课件

使用数学软件实现二分法
总结词
数学软件如Matlab、Mathematica等提 供了强大的符号计算和数值计算功能, 适合用于实现二分法。
VS
详细描述
这些数学软件通常提供了内置的二分法函 数,可以直接调用。用户只需要输入方程 的形式和初始区间,软件会自动调用二分 法函数来求解近似解。
使用在线工具实现二分法
二分法的原理
总结词
二分法基于函数的连续性和零点的存在性定理,通过不断缩小搜索区间来逼近零点。
详细描述
二分法利用了函数在区间端点上的函数值异号的性质,每次迭代都将搜索区间缩小一半,从而以较快 的速度逼近零点。这个过程一直持续到找到满足精度要求的零点或者搜索区间长度小于某个阈值。
二分法的适用范围
总结词
二分法适用于寻找连续函数在某个区间内的零点。
详细描述
二分法要求函数在零点所在的区间内连续,且在区间的端点上的函数值异号。对于一些不满足这些条件的函数, 如分段函数或有多个零点的函数,二分法可能无法找到正确的零点。因此,在使用二分法之前,需要先对函数进 行适当的分析和验证。
02
二分法的基本步骤
确定初始区间
首先需要确定方程有解的初始区间 ,可以通过代入法或观察法得到。
计算中点
在初始区间内取中点,并计算中点 的函数值。
判断中点性质
根据中点的函数值与区间端点的函 数值进行比较,确定下一步的搜索 区间。
迭代搜索
不断重复上述步骤,每次将搜索区 间缩小一半,直到达到所需的精度 要求。
求函数的零点
01
确定初始区间
同样需要确定函数有零点的初 始区间。
02
计算中点
在初始区间内取中点,并计算 中点的函数值。
求函数零点近似解的一种计算方法----二分法_优质PPT课件

依题意得方程x2+(a-1)x+2=0有两个 相异的正数根,
则
(a 1)2
,
1 a 0
得a∈(-∞,1 2 2).
7
bx 5.已知函数f(x)= 2 3x .若方程f(x) +2x=0有两个相等的实数根,则f(x)= .
由 bx +2x=0,得6x2-(b+4) 2 3x
x=0. 4x
11
题型1 函数零点存在性判断
(1)求函数y=x3-2x2-x+2的零点;
(2)判断函数f(x)=log2x+ 1 x+2的零
点的个数.
2
12
( 1 ) 由 y=x3-2x2-x+2=x2 ( x-2 ) (x-2)=(x-2)(x2-1)
=(x-2)(x-1)(x+1). 令 ( x-2 ) ( x-1 ) ( x+1 ) =0 , 解 得 x=2 或 x=1或x=-1. 所以函数y=x3-2x2-x+2的零点为-1,1,2.
基本初等函数(Ⅰ)
函数与方程
1
1.函数的零点 函数y=f(x)的零点是一个 实数,而不是 一个 点,它是函数的图象与x轴交点的横坐标. 2.二分法 用二分法求函数y=f(x)的 零点近似值的 步骤是:
2
第一步,确定区间[a,b],验
证 f(a)、f(b)的正负
,给定精确度ε;
第二步,求区间[a,b]的中点x1; 第三步,计算 f(x1);若 f(x1)=0 , 则x1就是函数的零点;若 f(x1)f(b)<0 , 则令b=x1;若 f(a)f(x1)<0 ,则令a=x1;
第四步,判断是否达到精确度ε,即若 |a-b|<ε,则得到零点近似值a(或b);否则 重复第二、三、四步.
二分法课件
计算f(x0)和f(a0),并判断:
1 1 x0 a0 (b0 a0 ) (a0 b0 ) 2 2
(1)如果f(x0)=0,则x0就是f(x)的零点,计算终止;
(2)如果f(a0)· f(x0)<0,则零点位于区间[a0,x0]
中,令a1=a0,b1=x0;
(3)如果f(a0)· f(x0)>0,则零点位于区间[x0,
由上表的计算可知,区间[0.3125,
0.343755]的左、右端点精确到0.1所取的近
似值都是0.3,因此0.3就是所取函数的精 确到0.1的一个正实数零点的近似值,只需 计算5次即可得到。 同理,所取函数的精确到0.01的一个正 实数零点的近似值为0.32,计算8次可以得
到。
二分法的概念
对于在区间[a,b]上连续不断,且 f(a)*f(b)<0 的函数y=f(x),通过不断把函数f(x)的零点 所在区间一分为二,使区间的两个端点逐 步逼近零点,进而得到零点近似值的方法 叫二分法。
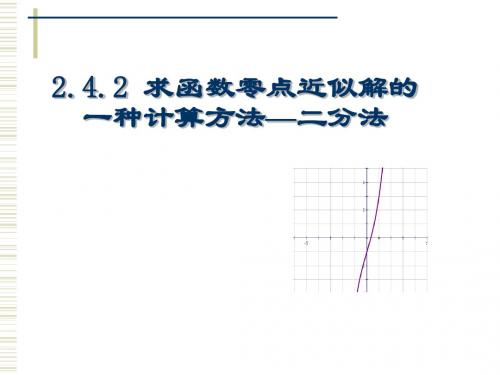
2.4.2 求函数零点近似解的 一种计算方法—二分法
在16世纪,人们找到了三次函 数和四次函数的求根公式,但对于高 于四次的函数,类似的努力却一直没 有成功。 到了19世纪,根据阿贝尔(Abel) 和伽罗瓦(Galois)的研究,人们认 识到高于四次的函数(即高于四次的 代数方程)不存在求根公式,也就是 说,不存在用四则运算即根号表示的 一般公式解。
端点或中点 计算端点或中 横坐标 点的函数值
x4=0.34375 x5=0.328125 f(x4)=0.07187>0 f(x5)=0.0197>0
确定区间
[0.3125,0.343755]
[0.3125,0. 328125]
4.4.2计算函数零点的二分法 课件(共32张PPT)——高中数学湘教版(2019)必修第一册

间为( C)
A. 2.5,3
B.2.25, 2.5
C.2, 2.25
D.不能确定
解析:显然函数 f x x ln x 2x 6在 x 2,3 上是连续不断的曲线,
由于 f (2) 0 , f (2.25) 0 ,所以 f 2 f 2.25 0 , 由零点存在性定理可得: f x x ln x 2x 6的零点所在区间为2, 2.25 , 所以方程 x ln x 2x 6 0 在区间2, 2.25 内一定有根.
2
由于 f 0.625 f 0.75 0 ,可知零点在 0.625,0.75 上.
为了表述清楚,记零点所在区间为 a,b ,其中点 m
1a 2
b . 继续计算列出表
格:
从表中计算数据看出,计算到 10 次,包含零点的区间长度小于 0.002 . 取此区 间中点与零点的距离不超过区间长度的一半,即 0.001 . 于是可取 0.653 作为零点的 近似值,也即方程 x3 3x2 1 0 的一个近似解.
f
1
1
0
,
f
3 2
ln
3 2
0
,即
f
1
f
3 2
0
,
因此,函数
f
x
ln
x
2x
3 的零点所在的一个区间是 1,
3 2
.
故选:C.
4.设函数 f x x ln x 2x 6,用二分法求方程 x ln x 2x 6 0 在 x 2,3 内的近似
解的过程中,计算得 f (2) 0 , f (2.5) 0 , f (2.25) 0 ,则下列必有方程的根的区
由 f 1 1 0和 f 2 ln 2 0 可知, f x 在区间 1, 2 内有一个零点;由 f x 单调递增可知,它只有这一个零点. 用二分法计算,列表如下:
用二分法求方程课件

二分法的基本思想
二分法的基本思想是通过不断将搜索区间一分为二,并根据 函数值在左右端点的符号来判断根所在的子区间,从而逐步 逼近根的近似值。
在每次迭代过程中,选取当前搜索区间的中点,并根据函数 值在该点的正负来判断根所在的子区间,然后舍弃非根所在 的子区间,继续在剩余的子区间上重复该过程,直到达到预 设的精度要求。
定的鲁棒性。
缺点
收敛速度慢
二分法的收敛速度取决于初始区间的 大小和方程的性质,对于一些复杂的 方程,可能需要多次迭代才能得到精 确解。
需要判断根的存在性
对初始区间选择敏感
二分法的收敛速度和精度与初始区间 的选择密切相关,如果初始区间选择 不当,可能会影响最终的求解结果。
在使用二分法之前,需要先判断方程 是否在给定的区间内有根,否则可能 无法收敛。
复杂的非线性方程时具有一定的优势。
END
THANKS
感谢观看
KEEP VIEW
计算中点
在初始区间内选择一个中点,通常是区间的中点。 中点的计算是二分法求解方程的关键步骤之一,需要精确计算中点的坐标。
判断中点处的函数值
判断中点处的函数值是二分法求解方程的重要步骤,根据 函数值的不同情况,可以决定下一步的行动。
如果函数值异号,说明解在区间内,继续进行下一步;如 果函数值同号,说明解不在区间内,需要重新选择初始区 间或调整中点位置。
PART 05
二分法的改进和变种
变种方法一:插值二分法
总结词
通过插值多项式来逼近方程的根,从而提高二分法的收敛速度。
详细描述
插值二分法是在二分法的基础上,利用插值多项式来逼近方程的根。通过构造插值多项式,可以更精 确地估计方程的根的位置,从而加快二分法的收敛速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ATP的形成:
ADP+Pi + 电能
酶
ATP
光能转换成电能
NADPH 、ATP ADP+Pi
C5的再生:
酶
2C3
NADPH
、 ATP
C5 ADP+Pi
再变成活跃的化学能
活跃的化学能变成稳
(ATP、NADPH中)
定的化学能
光反应为碳反应提供NADPH和ATP
联系 碳反应为光反应提供NADP+和ADP和Pi
四、归纳总结
2、不断二分解所在的区间
若 x1 (a,b), 不妨设f (a) 0, f (b) 0
(1)若
f (a b) 0,由
2
f (a) 0 ,则
x1
(a,
a
2
b
)
(2)若
f ( a b) 0 ,由
2
f
(b)
0,则
x1
(
a
2
b
,
b)
(3)若 f (a b) 0 ,则
2
x1
NADPH
• 在电子传递过程中还形成了什么物质? 写出其反应式。
ADP + Pi + 能量(电能) 酶 ATP
• 电能转换成的活跃的化学能,贮存在什么 物质中?
贮存在NADPH 和 ATP 中
• 活跃的化学能意味着什么?
意味着能量很容易释放,供碳反应阶 段合成有机物利用。
• NADPH除了是携带一定能量的物质外, 还具有什么性质? NADPH是强还原剂。
练习: 1求方程x3+3x-1=0的一个近似解(精确到 0.01)
2下列函数的图象与x轴均有交点,其中不能用二分法求其 零点的是(C)
y
y
y
y
x
x
x
x
0
0
0
0
AB
C
D
解1:画y= x 3+3x-1的图象比较困难,
变形为x 3=1-3x,画两个函数的图象如何?
y
有惟一解x0∈(0,1) 1
y=x3
同化作用 (合成代谢)
把从外界获得的营养物 质转变成自身组成物质
贮存能量
新陈代谢
物质代谢
异化作用 (分解代谢)
分解一部分自身组成物 质,把分解的最终产物 排出体外
释放能量
能量代谢
1.同化作用的类型
项目
类型
能量来源
光能自 自 养型
光能
养 化能自
型 养型
体外环境 物质氧化 时所放出 的能量
不同点 物质来源
一、提出问题
能否求解下列方程 (1)lgx=3-x, (2)x2-2x-1=0, (3)x3+3x-1=0 .
能否解出上述方程的近似解?(精确到0.1)
二、方法探究
y y=x2-2x-1
(1)不解方程,如何求方程 x2-2x-1=0 的
x
一个正的近似解 .(精确到0.1)
-1 0 1 2 3
-
2
为糖类等有机物中稳定的化学能
进行部 位
条件
物质 变化
能量变 化
光反应阶段
碳反应阶段
叶绿体基粒囊状结构中 叶绿体基质中
光、色素和酶
ATP、 NADPH 、多种酶
水2H的2O光解色:光素 O2+4H++4eNADPH的形成:
CO2的固定: CO2+C5
C3的还原:2C3
酶
酶
2C3Байду номын сангаас
(CH2O)
NADP++2e+H+ 酶 NADPH
(二)碳反应阶段
碳反应总结
场所: 叶绿体的基质中
条件: 多种酶、 [H] 、ATP
物质变化:
CO2的固定: CO2+C5
酶 2C3
酶
C3的还原:
2C3 NADPH
、ATP
(CH2O) ADP+Pi 糖类
C5的再生:
酶 2C3NADPH 、ATP
ADP+Pi C5
能量变化: ATP和NADPH中活跃的化学能转变
2HNO2+O2 硝化细菌 2HNO3+能量
6CO2+6H2O
C6H12O6+6O2
2.异化作用的类型
需氧型生 物
厌氧型生 物
举例
动物、植物、 人以及绝大多 数微生物
乳酸菌、破伤 风杆菌、大肠 杆菌等细菌以 及动物体内的 寄生虫等
区别
相同点
必须生活在有氧的 环境中,从环境中 摄取氧气,分解自 身成分,释放能量, 维持生命活动
3.下 图是光合作用过程图解,请分析后回答下列问题:
H2O
光
A
B
C D
F CO2
G
E+Pi
J
H
I
①图中B是—O,2 它来自于—水—的分解。
②图中C是—[H—],它被传递到叶绿体的基——质部位,用于—C—3的。还原
③图中D是—AT—P,在叶绿体中合成D所需的能量来自—色的— 素光吸能收 ④图中的H表示光——反,应 H为I提供—N—ADPH和ATP
(3)二分法(bisection method):象上面这种求方程 近似解的方法称为二分法,它是求一元方程近似解的常用 方法。
问题:二分法实质是什么?
用二分法求方程的近似解,实质上就是通 过“取中点”的方法,运用“逼近思想逐步缩 小零点所在的区间。
三、自行探究
利用计算器,求方程 lgx=3- x的近似解.(精确到0.1)
谢谢大家, 再 见!
光反应
光反应包括多个反应,最重要的是发生在 两种叶绿素蛋白质复合体(光系统Ⅰ和光 系统Ⅱ)中的电子被光激发的反应。
• 2H2O→O2+4H++4e- ,水的光解产生的电子 和氢离子最终传递给什么物质,并生成了什
么物质?尝试写出物质变化的反应式。
酶
NADP+ + 2e + H+
三、自行探究
例题:利用计算器,求方程2x=4-x的近似解 (精确到0.1)
怎样找到它的解所在的区间呢? y y=2x
在同一坐标系内画函数y=2x 4
与y=4-x的图象,如图:
y=4-x
得:方程有一个解x0 ∈(0,4) 如果画得很准确,可得x0 ∈(1,2)
1 0
1
2
x
4
提问:能否不画图确定根所在的区间?
f(2.375)<0,f(2.4375)>0 2.375<x1<2.4375
3
二、方法探究
(2)能否简述上述求方程近似解的过程?
对于在区间[a,b]上连续不断,且f (a)f (b)<0的 函数y=f (x),通过不断地把函数f(x)的零点所在的 区间一分为二,使区间的两端点逐步逼近零点, 进而得到零点(或对应方程的根)近似解。
2.75
f(2.75)>0
(2.5,2.75) f(2.5)<0,f(2.75)>0 2.625 f(2.625)>0
(2.5,2.625) f(2.5)<0,f(2.625)>0 2.5625 f(2.5625)<0
(2.5625,2.625) f(2.5625)<0,f(2.625)>0
因为2.5625,2.625精确到0.1的近似值都为2.6,所以原方程的 近似解为x1≈2.6 .
一般生活在缺氧的 环境中,通过无氧 呼吸分解自身成分 获得能量。有氧时, 生命活动将受到抑 制
都必须不断 分解有机物, 释放能量, 供生命活动 的需要
• NADPH用来还原什么?
光反应总结
• 场所:叶绿体的囊状结构(类囊体)薄膜
• 条件: 光、色素、酶
• 过程:
用于暗反应
水的光解:
2H2O
光 色素
O2+4H++4e-
酶
NADPH的形成: NADP++2e+H+
NADPH
ATP的形成: ADP+Pi + 电能 酶(活A跃TP化学能)
碳反应
二氧化碳还原为糖的一系列反应成为碳 循环,又称卡尔文循环。
4. 光合作用过程中,产生ADP和消耗ADP的
部位在叶绿体中依次为
( B)
①外膜
②内膜
③基质
④类囊体膜
A.③②
B.③④
C.①②
D.④③
5. 与光合作用光反应有关的是( A )
①H2O
②ATP ③ADP
A.①②③
B.②③④
④CO2
C.①②④
D.①③④
6.光合作用的过程可分为光反应和碳反应 两个阶段,下列说法正确的是( D) A.叶绿体类囊体膜上进行光反应和碳反应 B.叶绿体类囊体膜上进行碳反应,不进行
至少需要检查接点的个数为
个。
小 结
算法:如果一种计算方法 对某一类问题(不是个
别问题)都有效,计算可以一步一步地进行,每 一步都能得到惟一的结果, 我们常把这一类问题 的求解过程叫做解决这一类问题的一种算法。
算法特点:算法是刻板的、机械的,有时要进行
大量的重复计算,但它的优点是一种通法,只 要按部就班地去做,总会算出结果。更大的优 点是它可以让计算机来实现。
解:画出y=lg x及y=3 -x的图象,观察图象得,方程lgx=3 - x 有唯一解,记为x,且这个解在区间(2,3)内。
三、自行探究
根所在区间 (2,3) (2.5,3)
区间端点函数值符号 f(2)<0,f(3)>0 f(2.5)<0,f(3)>0
