Lingo软件在求解数学优化问题的使用技巧
lingo基本用法(精华版)20分钟学会

Lingo基本用法总结(除集函数部分)LINGO是用来求解线性和非线性优化问题的简易工具。
Lingo免费版可以支持30个未知数,lingo破解版可以支持几万个未知数、几万个约束条件。
当你在windows下开始运行LINGO系统时,会得到类似下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO的默认模型窗口,建立的模型都都要在该窗口内编码实现。
下面举两个例子。
例1.1 如何在LINGO中求解如下的LP问题:在模型窗口中输入如下代码:min=2*x1+3*x2;x1+x2>=350;x1>=100;2*x1+x2<=600;然后点击工具条上的按钮即可。
得到如下结果:所以当x1为250,x2为100时目标函数得到最大值。
算术运算符Lingo中变量不区分大小写,以字母开头不超过32个字符算术运算符是针对数值进行操作的。
LINGO提供了5种二元运算符:^乘方﹡乘/除﹢加﹣减LINGO唯一的一元算术运算符是取反函数“﹣”。
这些运算符的优先级由高到底为:高﹣(取反)^﹡/低﹢﹣运算符的运算次序为从左到右按优先级高低来执行。
运算的次序可以用圆括号“()”来改变。
例:在x1+x2>=350,x1>=100,2*x1+x2<=600的条件下求2*x1+3*x2的最小值在代码窗口中编写min=2*x1+3*x2;x1+x2>=350;x1>=100;2*x1+x2<=600;然后单击上面菜单lingo菜单下solve键即可。
数学函数标准数学函数:@abs(x) 返回x的绝对值@sin(x) 返回x的正弦值,x采用弧度制@cos(x) 返回x的余弦值@tan(x) 返回x的正切值@exp(x) 返回常数e的x次方@log(x) 返回x的自然对数@lgm(x) 返回x的gamma函数的自然对数@sign(x) 如果x<0返回-1;否则,返回1@floor(x) 返回x的整数部分。
LINGO应用教程
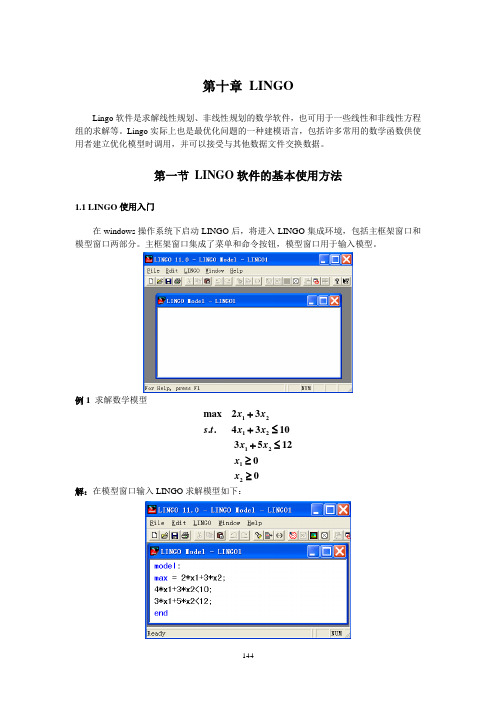
第十章 LINGOLingo 软件是求解线性规划、非线性规划的数学软件,也可用于一些线性和非线性方程组的求解等。
Lingo 实际上也是最优化问题的一种建模语言,包括许多常用的数学函数供使用者建立优化模型时调用,并可以接受与其他数据文件交换数据。
第一节 LINGO 软件的基本使用方法1.1 LINGO 使用入门在windows 操作系统下启动LINGO 后,将进入LINGO 集成环境,包括主框架窗口和模型窗口两部分。
主框架窗口集成了菜单和命令按钮,模型窗口用于输入模型。
例1 求解数学模型12121212max 23..4310351200x x s t x x x x x x ++≤+≤≥≥解:在模型窗口输入LINGO 求解模型如下:输入模型后选择菜单LINGO|Solve 或者按工具栏的,LINGO开始编译模型,如有语法错误将返回一个错误的消息并指明错误出现的位置;如果通过编译,LINGO将激活Solver运算器寻求模型的最优解,首先出现Solver Status状态窗口显示模型求解的运算状态信息:状态窗口显示的信息含义如下:“Global optimal solution found”表示得到全局最优解。
“Objective value: 7.454545”表示最优目标值为7.454545。
“Total solver iterations:2” 表示迭代2次得到结果。
“V alue”给出最优解中各变量的值:x1=1.272727,x2=1.636364。
Reduced Cost 值列出最优单纯形表中判别数所在行的变量的系数,表示当变量有微小变动时,目标函数的变化率。
其中基变量的reduced cost值应为0,对于非基变量xj,相应的reduced cost值表示当某个变量xj 增加一个单位时目标函数减少的量( max型问题)。
本例中此值均为0。
SLACK OR SURPLUS值给出约束条件的松驰变量或剩余变量的值。
2.Lingo优化软件的使用方法

然后再在求解的基础上,在菜单上选择lingo/range(ctr+R), 计算机会自动对每个变量和资源用有量进行范围分析:保 持最优基不变的情况下,变量或约束行的右端允许增加和 减少的量。注意:对整数规划和0-1规划灵敏度分析意义不 大。
Ranges in which the basis is unchanged:
数学模型如下:
max z [ t (i) r (i)]x (i) s(i) y(i)
i 1 i 1
3
3
s.t.
3 c ijx i b( j) j 1,2,3 i 1 x (i) My(i) i 1,2,3 ___ x (i) 0, x Z y(i) 0,1 i 1,2,3
产品1
资源A 资源B 资源C 2 2 1
产品2 产品3
4 3 2 8 4 3
资源量
500 300
单件可变费 固定费用 单件售价
4 100 8
5 150 10
6 200 12
分析问题和设置变量 x(i)表示第i种产品的产量;i=1,2,3 c(i,j)表示第i种产品对第j种资源的消耗量;i=1,23,j=1,23 b(j)表示第j种资源的拥有量; r(i)表示第i种产品的单件可变费用; s(i)表示第i种产品的固定费用; t(i)表示第i种产品的单位售价。 总收益=销售收入-固定费用-可变费用,由于不知道第i种产品 生产与否,所以,必须给定第i种产品的选择变量 y(i)表示第I种产品的生产选择,y(i)=0,表示不生产第i种产品, y(i)=1表示生产第i种产品。
#LT#(小于) #LE#(小于等于) 逻辑运算的结果只有“真”(TRUE)和“假”(FALES), Llingo用1表示True,其它的都是False。
Lingo软件在求解数学优化问题的使用技巧

l 2 + z 3 ≤3 2 5 1 l 1 ̄ <4 0 0 2 + y 2 + z 2≤ 6 0 0
3 3 ̄ <3 0 0
3 1 + 2 y 1 + z l ≤6 0 0
3 2 + 2 y 2 坛 2≤ 8 0o
3 + 2 y 3 3 ≤3 7 5
科技・ 探索・ 争I 毫
S c 科 i e n c e & 技 T e c h 视 n o l o g y 界 V i s i o n
L i n g o 软件在求解数学优化问题的使用技巧
惠高峰 ( 西 安铁路 职 业技术 学 院 , 陕西 西 安 7 1 0 0 1 6 )
【 摘 要】 本文通过求解优化 问题的过程 , 讲述 了L i n g o 软件 的编程 方法和求解过程 中的使 用技 巧 , 用来解决数 学优化 问题 中的计算 f * - I 题,
提 高编程 求解的能 力。
【 关键词 】 L i n g o 软件 ; 线性模 型; 数 学优化 问题
数学优化 问题在管理数学 当中是一个并不 复杂 的问题 . 但是他往 往存在着 大量数学计算 . 学生们遇 到这 样的 问题就会 产生迷 惑 . 这类 问题 的解决实质上现在 已经不在使用人工进行计算 了 . 如何快速的掌 握计算机软件计算 的方法成为一个突 出的问题 . 下 边我们通过例子来 讲述 软件计算 的技 巧 某地 区有三个农场共用一条灌渠 . 每个农场 的可灌溉地及分配到 的最大用水量如下表
农场
1
e = 4 0 0 , 3 0 0 , 1 0 0 ; ENDDAT A
ma x = @s u m( k i n d ( j ) : e ( j ) @s u m ( p l a c e ( i ) : x ( i ) ) ) ; @f o r ( k i n d ( j ) : @s u m( p l a c e ( i ) : x ( i , j ) ) < = c ( j ) ) ; @ f o r ( p l a c e ( i ) : @s u m( k i n d ( j ) : x ( i , j ) ) < = a ( i ) ) ; @f o r ( r , l a c e ( i ) : @s u m( k i n d ( j ) : d ( j ) x ( i J ) ) < = b ( i ) ) ;
lingo案例

LINGO是一种用于线性规划、整数规划、非线性规划、混合整数规划等数学建模和优化问题的软件工具。
它可以用于解决各种实际问题,包括生产计划、物流、资源分配、网络设计等。
以下是一个简单的LINGO案例,以帮助您了解如何使用LINGO进行优化建模和求解问题:**问题描述:**假设有一家制造公司,他们生产两种产品:A和B。
公司有两个工厂,每个工厂都有不同的生产能力和成本。
公司希望确定每个工厂应该生产多少产品A和B,以最大化利润,同时满足生产能力和市场需求的限制。
**问题数据:**- 工厂1的生产能力:最多生产500个A和300个B- 工厂2的生产能力:最多生产400个A和600个B- 产品A的利润:每个A产品的利润为30美元- 产品B的利润:每个B产品的利润为40美元- 生产一个A产品的成本:工厂1为10美元,工厂2为15美元- 生产一个B产品的成本:工厂1为12美元,工厂2为10美元- 市场需求:产品A的市场需求为600个,产品B的市场需求为800个**LINGO建模和求解:**在LINGO中,可以使用数学表达式来建立优化模型。
以下是一个LINGO模型的示例:```SETS:FACTORIES = 1..2;ENDSETSDATA:CAPACITY(FACTORIES) = 500 300400 600;PROFIT = 30 40;COST(FACTORIES) = 10 1512 10;DEMAND = 600 800;ENDDATAVARIABLES:X(FACTORIES) = 0;ENDVARIABLESMAX = @SUM(FACTORIES, PROFIT(FACTORIES) * X(FACTORIES))SUBJECT TOCAPACITY_CONSTRAINT(F)$(FACTORIES): @SUM(FACTORIES, COST(F, FACTORIES) * X(FACTORIES)) <= CAPACITY(F);DEMAND_CONSTRAINT(I)$(FACTORIES): @SUM(FACTORIES,X(FACTORIES)) >= DEMAND(I);POSITIVE_X(F)$(FACTORIES): X(F) >= 0;ENDSUBMODEL:MAX;SOLVE;```上述LINGO模型首先定义了SETS、DATA、VARIABLES和MAX,然后使用SUBJECT TO部分定义了约束条件,最后使用MODEL和SOLVE命令求解优化问题。
lingo软件 优化问题

2.2 LP模型在LINGO中的一个典型输入方式
集合定义部分从 (“SETS:”到 “ENDSETS” ): 定义集合及其属性
MIN
I 1,2,3,4
{400 RP ( I ) 450OP( I ) 20 INV ( I )}
RP( I ) 40, I 1, 2, 3, 4 INV ( I ) INV ( I 1) RP ( I ) OP ( I ) DEM ( I ), I 1, 2, 3, 4 INV (0) 10 INV ( I ) 0 OP ( I ) 0 RP ( I ) 0 I 1 4
Step5 回答问题
Global optimal solution found. Objective value: 78450.00 Total solver iterations: 2 Variable Value Reduced Cost RP1 40.00000 0.000000 RP2 40.00000 0.000000 RP3 40.00000 0.000000 RP4 25.00000 0.000000 OP1 0.000000 20.00000 OP2 10.00000 0.000000 OP3 35.00000 0.000000 OP4 0.000000 50.00000 INV1 10.00000 0.000000 INV2 0.000000 20.00000 INV3 0.000000 70.00000 INV4 0.000000 420.0000 Row Slack or Surplus Dual Price 1 78450.00 -1.000000 2 0.000000 30.00000 3 0.000000 50.00000 4 0.000000 50.00000 5 15.00000 0.000000 6 0.000000 430.0000 7 0.000000 450.0000 8 0.000000 450.0000 9 0.000000 400.0000
lingo讲座.ppt
Erlang繁忙概率。 4.@pel(a,x) 当到达负荷为a,服务系统有x个服务器且不允许排队时的Erlang
繁忙概率。 5.@pfd(n,d,x) 自由度为n和d的F分布的累积分布函数。
如果x<0返回-1;否则,返回1
@floor(x)
返回x的整数部分。
@smax(x1,x2,…,xn) 返回x1,x2,…,xn中的最大值
@smin(x1,x2,…,xn) 返回x1,x2,…,xn中的最小值
概率函数 1.@pbn(p,n,x) 二项分布的累积分布函数。当n和(或)x不是整数时,用线性插
复杂变量:集合
Lingo中没有数组,代之以集合及其属性
集是一群相联系的对象,这些对象也称为集的成员。 一个集可能是一系列产品、卡车或雇员。每个集成员 可能有一个或多个与之有关联的特征,我们把这些特征 称为属性。属性值可以预先给定,也可以是未知的, 有待于LINGO求解。例如,产品集中的每个产品可以有 一个价格属性;卡车集中的每辆卡车可以有一个牵引力 属性;雇员集中的每位雇员可以有一个薪水属性,也可 以有一个生日属性等等。
何时会提升速度?
与数据段不同的是:模型中的变量在这里赋值之后,在模型中 几乎一定会被改变!
(2)Lingo中的运算符与内部函数
三类运算符:算术运算符, 逻辑运算符, 关系运算符
优先级 最高
最低
运算符 #NOT# -(负号) ^ */ + -(减法) #EQ# #NE# #GT# #GE# #LT# #LE# #AND# #OR# <(=) = >(=)
LINGO软件求解优化问题
x 2 y 2 z 30
3 x y 2 z 20
40
2x
y
10
z
50
x , y , z 0
• 2、求解非线性规划
m inf(x24y)2(12x)2
三、Lingo运算符和函数
1、运算符及其优先级
算术运算符 +-*/^
关系运算符 <(=) = >(=)
三、Lingo基本语法
1、定义了目标函数为MIN=.. MAX=.. 2、以一个分号“;”结尾
——除SETS, ENDSETS, DATA , ENDDATA, END之外 3、可以放在约束条件的右端,同时数字也可 放在约束条件的左端。 4、假定各变量非负。 5、注释:“!”
6、<、>为≤、≥
例1:加工奶制品的生产计 划
使用绝对值、符号函数、多个变量求最大/最小值、四舍 五入、取整函数等 • 尽量使用线性模型,减少非线性约束和非线性变量的个数 如x/y <5 改为x<5y • 合理设定变量上下界,尽可能给出变量初始值 • 模型中使用的参数数量级要适当
– 如小于103
练习
• 1、求解线性规划
min( 2 x 3 y 5 z )
SAS软件优化功能 其他
连续优化
离散:整数规划 IP: ILP PIP 0-1
线性规划 LP
二次规划 QP
非线性规划 NLP
LINDO
LINGO
优势:模型表述简单 求解引擎强大
数学规划模型
• 决策变量 x =(x1, x2, …, xn ) • 目标函数 Min Z = f (x)
• 约束条件 s.t x A ( Rn )
5、Options 7个选 项卡
Lingo教程[参照]
LINGO教程LINGO是用来求解线性和非线性优化问题的简易工具。
LINGO内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO高效的求解器可快速求解并分析结果。
§1 LINGO快速入门●安装:实验室的所有电脑都已经事先安装好了Lingo 8(或者9,10,11)。
如果要在自己的电脑上安装这个软件,建议从网上下载一个破解版的,按照提示一步一步地安装完毕。
●简单例子:当你在windows系统下开始运行LINGO时,会得到类似于下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口,建立的模型都要在该窗口内编码实现。
下面举两个例子。
例 1某工厂在计划期内要安排生产I、II两种产品,已知生产单位产品所需的设备台时及A、B两种原材料的消耗,如表所示。
产品I产品II设备 1 28台时原材料A 4 016kg原材料B 0 412kg该工厂每生产一件产品I可获利2元,每生产一件产品II可获利3元,问应该如何安排生产计划使该厂获利最多?我们用下面的数学模型来描述这个问题。
设x_1、x_2分别表示在计划期内产品I、II的产量。
因为设备的有效台时是8,这是一个限制产量的条件,所以在确定产品I、II的产量时,要考虑不超过设备的有效台时数,即可用不等式表示为x_1 + 2x_2 <=8同理,因原材料A、B的限量,可以得到以下不等式4x_1 <=164x_2 <=12该工厂的目标是在不超过所有资源限量的条件下,如何确定产量x_1、x_2以得到最大的利润。
若用z表示利润,这时z=2x_1+3x_2.综合上述,该计划问题可用数学模型表示为:目标函数 max z=2x_1+3x_2约束条件 x_1 + 2x_2 <=84x_1 <=164x_2 <=12x_1、x_2 >=0一般来说,一个优化模型将由以下三部分组成:1.目标函数(Objective Function):要达到的目标。
Lindo 和Lingo 数学软件的简单使用方法
Lindo 和Lingo 数学软件的简单使用方法一、Lindo最新版本:6.1版(注册版)限制:4000个约束、8000个变量、800个整型变量功能:可以求解线性规划、整数规划、混合整数规划、二次规划、目标规划。
我们主要用它来求解整数规划或混合整数规划。
特点:执行速度非常快 例1:求解整数规划问题12121212max 58..65945,0z x x s t x x x x x x =++≤+≤≥且整解:在lindo 的运行窗口中输入 max 5x1+8x2 stx1+x2<6 5x1+9x2<45 end gin 2然后按Solve 菜单或快捷键得运行结果。
OBJECTIVE FUNCTION V ALUE (目标函数最优值) 1) 40.00000VARIABLE V ALUE REDUCED COST (变量增加1时目标函数改变量) X1 0.000000 -5.000000 X2 5.000000 -8.000000ROW SLACK OR SURPLUS DUAL PRICES (行) (松弛变量值) (对偶价格,表示约束右边常数增加1时目标函数改变量)) 2) 1.000000 0.000000 3) 0.000000 0.000000RANGES IN WHICH THE BASIS IS UNCHANGED (灵敏度分析) OBJ COEFFICIENT RANGES (目标函数中变量的系数的变动范围,在此范围内最优解不变) V ARIABLE CURRENT ALLOWABLE ALLOWABLECOEF (当前系数) INCREASE (增加量) DECREASE (减少量) X1 5.000000 0.000000 INFINITY X2 8.000000 0.000000 INFINITYRIGHTHAND SIDE RANGES (约束条件右边常数的变化范围,在此范围内最优基不变) ROW CURRENT ALLOWABLE ALLOWABLERHS (当前系数)INCREASE (增加量) DECREASE (减少量) 2 6.000000 INFINITY 1.000000 (第一个约束) 3 45.000000 INFINITY 0.000000 (第二个约束)注意:1. 软件中已经假设所以的变量是非负的,所以非负约束不必输入; 2. 可以用 FREE 变量 来取消变量的非负限制; 3. 不区分大小写; 4. 约束条件“<=”、“>=”可以用“<”、“>”代替; 5. 变量名不能超过8个字符;6. 变量与系数间可以有空格,但不能有任何运算符号(如*等); 7. 不允许变量出现在一个约束条件的右端; 8. 输入中不能有“()”和“,”;比如4(x1+x2)应写成4x1+4x2等;9. 在一个式中同一变量不能出现一次以上,比如2x1+3x2-x1应简化为x1+3x2;gin 变量 变量为整数变量 gin nint n 模型中的前n 个变量为0/1整数变量,关于变量的顺序可由输出结果查证! 整数变量申明须放在最后(即end 后)例2:集合覆盖问题设有一集合S={1,2,3,4,5},及S 的一个子集簇P={{1,2},{1,3,5},{2,4,5},{3},{1},{4,5}},假设选择P 中各个元素的费用为1、1.5、1.5、0.8、0.8、1,试从P 中选一些元素使之覆盖S 且所选元素费用之和最小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Lingo软件在求解数学优化问题的使用技巧作者:惠高峰
来源:《科技视界》2013年第11期
【摘要】本文通过求解优化问题的过程,讲述了Lingo软件的编程方法和求解过程中的使用技巧,用来解决数学优化问题中的计算问题,提高编程求解的能力。
【关键词】Lingo软件;线性模型;数学优化问题
数学优化问题在管理数学当中是一个并不复杂的问题,但是他往往存在着大量数学计算,学生们遇到这样的问题就会产生迷惑,这类问题的解决实质上现在已经不在使用人工进行计算了,如何快速的掌握计算机软件计算的方法成为一个突出的问题,下边我们通过例子来讲述软件计算的技巧。
某地区有三个农场共用一条灌渠,每个农场的可灌溉地及分配到的最大用水量如下表:
各农场均可种植甜菜、棉花和高粱三种作物,各种作物的用水量、净收益及国家规定的该地区各种作物种植总面积最高限额如下表:
三个农场达成协议,他们的播种面积与其可灌溉面积相等,而各种农场种何种作物并无限制。
问如何制定各农场种植计划才能在上述限制条件下,使本地区的三个农场的总净收益最大。
分析与求解:
LINGO编程如下:
MODEL:
SETS:
place/1..3/:a,b;
kind/1..3/:c,d,e;
plan(place,kind):x;
ENDSETS
DATA:
a=400,600,300;
b=600,800,375;
c=600,500,325;
d=3,2,1;
e=400,300,100;
ENDDATA
max=@sum(kind(j):e(j)*@sum(place(i):x(i,j)));
@for(kind(j):@sum(place(i):x(i,j))
@for(place(i):@sum(kind(j):x(i,j))
@for(place(i):@sum(kind(j):d(j)*x(i,j))
END
得到结果如下:
X(1,1)=0,X(1,2)=300,X(1,3)=0
X(2,1)=258.3333,X(2,2)=12.5,X(2,3)=0
X(3,1)=0,X(3,2)=187.5,X(3,3)=0
最大总净收益为253333.3元。
对本题来说,由于数据少,可以不采用数组形式,可直接采用变量,则建立模型如下: LINGO程序如下:
MODEL:
max=400*(x1+x2+x3)+300*(y1+y2+y3)+100*(z1+z2+z3);
x1+x2+x3
y1+y2+y3
z1+z2+z3
x1+y1+z1
x2+y2+z2
x3+y3+z3
3*x1+2*y1+z1
3*x2+2*y2+z2
3*x3+2*y3+z3
END
得到的解如下:
X1=200,Y1=0,Z1=0;
X2=58.33333,Y2=312.5,Z2=0;
X3=0,Y3=187.5,Z3=0;
最大总净收益为253333.3元。
【参考文献】
[1]肖华勇.实用数学建模与软件应用[M].西安:西北工业大学出版社,2008.
[2]周义仓,郝孝良.数学建模实验[M].西安:西安交通大学出版社,2007. [责任编辑:王静]。
