天线方位角位置随动系统的建模与分析
位置随动系统建模与分析--自控课设教材
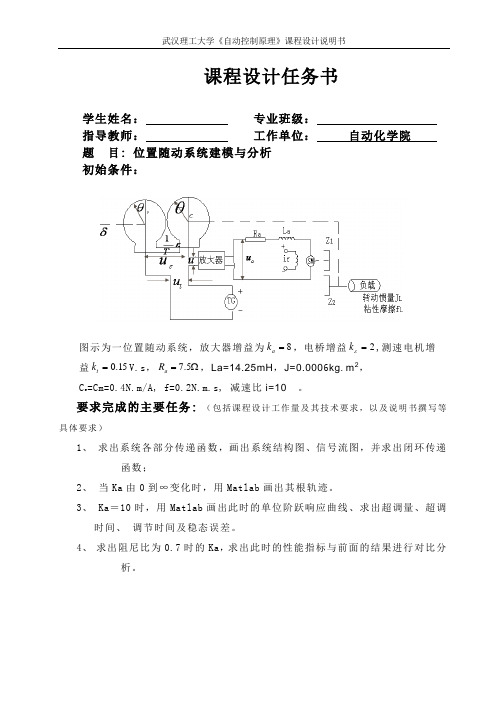
课程设计任务书学生姓名: 专业班级: 指导教师: 工作单位: 自动化学院题 目: 位置随动系统建模与分析 初始条件:图示为一位置随动系统,放大器增益为8=a k ,电桥增益2=εk ,测速电机增 益15.0=t k V.s ,Ω=5.7a R ,La=14.25mH ,J=0.0006kg .m 2, C e =Cm=0.4N.m/A, f=0.2N.m.s, 减速比i=10 。
要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)1、 求出系统各部分传递函数,画出系统结构图、信号流图,并求出闭环传递函数;2、 当Ka 由0到∞变化时,用Matlab 画出其根轨迹。
3、 Ka =10时,用Matlab 画出此时的单位阶跃响应曲线、求出超调量、超调时间、 调节时间及稳态误差。
4、 求出阻尼比为0.7时的Ka ,求出此时的性能指标与前面的结果进行对比分析。
时间安排:指导教师签名:年月日系主任(或责任教师)签名:年月日目录1 位置随动系统原理 (3)1.1 位置随动系统原理框图 (3)1.2 元件结构图分析 (3)1.3 位置随动系统各元件传递函数 (5)1.4 位置随动系统的结构框图 (5)1.5 位置随动系统的信号流图 (6)1.6 相关函数的计算 (6)2根轨迹曲线 (7)2.1参数根轨迹转换 (7)2.2绘制根轨迹 (7)3单位阶跃响应分析 (8)3.1单位阶跃响应曲线 (8)3.2单位阶跃响应的时域分析 (9)4系统性能对比分析 (11)4.1 新系统性能指标计算 (11)4.2 系统性能指标对比分析 (11)5 总结体会 (12)参考文献 (13)位置随动系统建模与分析1 位置随动系统原理1.1 位置随动系统原理框图图1.1位置随动系统原理框图工作原理:用一对电位器作为位置检测元件,并形成比较电路。
两个电位器分别将系统的输入和输出位置信号转换成与位置比例的电压信号,并做出比较。
位置随动系统建模与频率特性分析报告

实用标准文案目录1位置随动系统的分析 (2)1.1位置随动系统建模分析 (2)1.2位置随动系统总体分析 (2)1.2.1随动系统的基本原理图 ...........................................21.2.2随动系统的基本原理结构图 .......................................21.2.3随动系统的基本原理分析 (3)2位置随动系统的原理 (4)2.1位置随动系统各部分基本工作原理 (4)2.1.1环形电桥电位器 .................................................42.1.2放大器 .........................................................52.1.3直流伺服电动机 .................................................62.1.4测速发电机 .....................................................72.1.5减速器 .........................................................82.1.6系统的信号流图 .................................................92.1.7系统的闭环传递函数 (10)3位置随动系统的开环传递函数图像绘制与稳定性判断 (11)3.1开环传递函数伯德图像绘制 (11)3.2开环传递函数奈奎斯特图像绘制 (12)3.3由开环传递函数求出开环系统的截止频率、相角裕度和幅值裕度。
(12)4位置随动系统的闭环传递函数在输入下的响应 (13)4.1闭环传递函数在单位阶跃输入下响应图像绘制 (13)4.2闭环传递函数在斜坡信号输入下响应图像绘制 (14)4.3闭环传递函数输入响应误差分析 (15)5当Ka由0到∞变化时根轨迹的绘制 (16)5.1等效开环传递函数的推导 (16)5.2根轨迹的绘制 (16)6对系统进行超前校正 (17)7心得体会及参考文献 (20)精彩文档.实用标准文案1位置随动系统的分析1.1位置随动系统建模分析在分析系统时由于所给的系统是其原理图,分析的时候很复杂,需要将系统进行建模分析,根据数学公式分析起来就会简单得多。
基于MEMS的角位置无线随动控制系统设计

ቤተ መጻሕፍቲ ባይዱ
传感器 与微 系统 ( T r a n s d u c e r a n d Mi c r o s y s t e m T e c h n o l o g i e s )
2 0 1 3年 第 3 2卷 第 9期
基 于 ME MS的 角 位 置 无 线 随 动 控 制 系 统 设 计
a n d u s u a l l y r e a l i z e d b y s e l s y n . O n s p e c i a l o c c a s i o n s o f d i f f i c u l t wi r i n g , i t i s n e c e s s a r y t o a d o p t wi r e l e s s w a y t o r e a l i z e s e r v o c o n t r o l o n r e mo t e d — e n d me c h a n i c a l s t r u c t u r e . A w i r e l e s s s e r v o c o n t r o l s y s t e m i s d e s i g n e d, a n d a n t i —
i n t e r f e r e n c e a n d t r a c k i n g p r e c i s i o n p r o b l e m o f t h e s y s t e m i s s t u d i e d e x p e r i me n t a l l y . T h e d y n a mi c s i g n a l o f a n g u l a r
i mp l e me n t e d o n ARM M CU.Th e a n t i — i nt e r f e r e n c e o f s y s t e m i s i mpr o v e d b y f r e qu e n c y h o p pi n g p r o g r a m mi n g o n wi r e l e s s t r a ns mi s s i o n mo du l e nRF2 4L0 1. I n a dd i t i o n, u s e DC s e r v o mo t o r t o d iv r e t r a c k i ng me c ha n i s m, a nd r e mo t e
32位置随动系统建模与频率特性分析.

学号:课程设计位置随动系统建模与频率特题目性分析学院自动化学院专业电气工程及其自动化班级姓名指导教师2014 年 1 月18 日课程设计任务书学生姓名: 专业班级:指导教师: 工作单位: 自动化学院题 目: 位置随动系统建模与频率特性分析 初始条件:图示为一位置随动系统,测速发电机TG 与伺服电机SM 共轴,右边的电位器与负载共轴。
放大器增益为Ka=40,电桥增益5K ε=,测速电机增益2t k =,Ra=6Ω,La=12mH ,J=0.006kg.m 2,C e =Cm=0.5N m/A ,f=0.2N m s ,i=0.1。
其中,J 为折算到电机轴上的转动惯量,f 为折算到电机轴上的粘性摩擦系数,i 为减速比。
要求完成的主要任务: (包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)(1) 求出系统各部分传递函数,画出系统结构图、信号流图,并求出闭环传递函数;(2) 用Matlab 画出开环系统的波特图和奈奎斯特图,并用奈奎斯特判据分析系统的稳定性。
(3) 求出开环系统的截止频率、相角裕度和幅值裕度。
(4) 用Matlab 画出系统的单位阶跃响应曲线和单位斜坡响应,并进行误差分析;(5) 对上述任务写出完整的课程设计说明书,说明书中必须进行原理分析,写清楚分析计算的过程及其比较分析的结果,并包含Matlab 源程序或Simulink 仿真模型,说明书的格式按照教务处标准书写。
时间安排:任务时间(天)审题、查阅相关资料,确定设计方案 1.5分析、计算 2.5编写程序2撰写报告 1.5论文答辩0.5指导教师签名:年月日系主任(或责任教师)签名:年月日目录目录 (1)摘要 (2)1 系统建模 (3)1.1 系统机理分析 (3)1.2 系统方框图 (3)1.3系统各部分传递函数 (4)1.3.1 桥式电路 (4)1.3.2 放大器 (5)1.3.3 伺服电机SM (5)1.3.4 减速器 (7)1.3.5测速电机TG (8)1.4 系统信号流图 (8)1.5 系统结构图 (9)1.6 系统传递函数 (9)1.6.1 开环传递函数 (9)1.6.2 闭环传递函数 (9)2 系统频域分析 (10)2.1 用MATLAB绘制波特图 (10)2.2用MATLAB绘制奈奎斯特图 (11)2.3 用奈奎斯特稳定判据分析系统稳定性 (12)2.4 用MATLAB计算稳定裕度 (12)3 系统在不同输入下的响应 (13)3.1 单位阶跃响应 (13)3.1.1 用MATLAB绘制系统的单位阶跃响应曲线 (13)3.1.2 单位阶跃响应误差计算 (14)3.2 单位斜坡响应 (14)3.2.1用MATLAB绘制系统的单位斜坡响应曲线 (14)3.2.2 单位斜坡响应误差计算 (15)结束语 (17)参考文献 (18)摘要本次课程设计的主题是位置随动系统建模与频率特性分析,通过将整个系统分为一个一个的环节,化整为零,逐个分析,对传递函数进行求解,从而得到整个系统的全貌。
天线方位角位置随动系统的建模与分析

天线方位角位置随动系统建摸系统的原理图如图2-7所示,其方块图如图2-8所示。
系统的任务是使输出的天线方位角θ0(t)跟踪输入方位角θi (t)的变化,试建立该系统的数学模型。
系统的参数值如下:电源电压V=10v ;功率放大器的增益和时间常数K 1=1,T 1=0.01s ;伺服电动机的电枢回路电阻R d =8Ω,转动惯量J a =0.02Kg ∙m 2, 粘性摩擦系数f a =0.01N ∙m ∙s/rad , 反电势系数C e =0.5V ∙s/rad ,转矩 系数C m =0.5N ∙m/A ;减速器各齿 轮的齿数为Z 1=25, Z 2= Z 3=250;负载端的转动惯量J L =1 Kg ∙m 2粘性摩擦系数f L =1N ∙m ∙s/rad 。
采用组合系统建摸法,根据原理图2-7可以将系统划分为六个环节:输入电位器,差分放大器,功率放大器,电动机,减速器和输出电位器。
首先建立各个环节的数学模型,然后将它们组合起来则可得系统的数学摸型。
1环节的数学模型(1) 输入电位器与输出电位器由于输入电位器与输出电位器的线路和电位器的结构均相同,故这两个环节的传递函数是一样的。
对电位器环节的输出电压与输入角位移的特性进行线性化处理则可视其为一比例环节。
由图2-7可知;当动触头位于电位器中心时其输出电压为零;朝前或朝后转动5圈其输出电压变化均为10V 。
于是可得它们的传递函数为00()()100.318/()52()i pot i u s u s k v rad s s θπθ====⨯(2) 差分放大器与功率放大器放大器通常工作在放大状态,可不考虑饱和的影响。
差分放大器的时间常数比起功率放大器以及系统的其他环节的时间常数要小得多,可以忽视不计。
故这两个环节的输入输出传递函数分别为差分放大器c e C K s U s U =)()(功率放大器 1()1()10.011do c i u s k u s T s s ==++(3) 电动机在小功率伺服系统中直流电动机的结构图中,由于电动机的电枢回路电感很小,可以忽略不计。
位置随动系统

(1)位置检测器
由电位器RP1和RP2组
成位置(角度)检测器,其
中电位器RP1的转轴与手轮 相连,作为转角给定,电位 器RP2的转轴通过机械机构 与负载部件相连接,作为转 角反馈,两个电位器均由同 一个直流电源供电,这样可 将位置直接转换成电量输出。
(2)电压比较放大器
由放大器1A、2A组成, 其中放大器1A仅起倒相作用, 2A则起电压比较和放大作用, 其输出信号作为下一级功率 放大器的控制信号,并具备
随动系统可以在调速系统的基础上增加一个位置环,位置环是
位置随动系统的主要结构物征。因此,随动系统在结构上往往要比 调速系统复杂一些。
四、位置随动系统的分类
由于位置随机系统的基本特征体现在位置上,体现在位置给定
信号和位置反馈信号及两个综合比较方面,因此可根据这个特征将
它划分两个类型,一类是模拟式随动系统,另一类是数字式随机系 统。 模拟式角位移随动系统的各种参量都是连续变化的模拟量,其 位置检测器可用电位器,自整角机,旋转变压器,感应同步器等。 一般是在调速系统的基础上外加一个位置环组成。 采用数学式检测装置来组成数字式随动系统。在这类系统中, 一般仍可采用模拟的电流环和速度环以保证系统的快速响应,但位 置环是数字式的。
鉴相器的主要功能是进行给定相位 *和反馈相位 的比较,将它们的 偏差量 * 转变成模拟量电压,此模拟量电压的极性应能反映相
位差的极性。鉴相器的输出经变换处理后作为速度控制器的给定经过功率放 大,控制电机和机床工作台向消除偏差的方向移动,因而使 踪 *,也就可以使工作台精确地按指令要求运动。
转子绕组间的相对位置之变化,使输
出电压与转子角呈一定的函数关系。 在不同的自动控制系统中,旋转变压
一种天线水平方位角远程控制系统与实现方法

一种天线水平方位角远程控制系统与实现方法摘要:在通信领域当中,天线水平方位角远程控制系统是一个十分重要的机电一体化自动控制系统,其中包括了连接馈线、驱动单元、主板控制单元、通信控制器等部分,驱动单元则包括了校准机构、传动机构以及机壳部分。
对此,本文提出一种可用于对基站天线水平方位角进行远程控制的机电一体化系统与实现方法,从而实现对天线水平方位角的远程自动化调整,更好的实现基站天线的无线电波信号覆盖可调节范围,并可实现通过一个通信控制器输入发出指令调整天线的水平方位角度,可以在机房就可以对天线的信号覆盖进行调节。
关键词:天线;水平方位角;远程控制系统;实现方法一、天线水平方位角远程控制系统的驱动单元传动结构与设计实现方法在天线水平方位角远程控制系统当中,驱动机构单元包含了法兰转盘、动力输出轴,动力输出轴连接传动机构,在转盘上连接安装天线底板,利用驱动机构,带动天线底板(天线底板上装有电磁波发射单元)转动,从而实现天线覆盖信号波束水平方位转动。
驱动机构上的转盘设计有触碰块,机壳上凸设限位微动开关,触碰块安设计在限位微动开关之间,使其随着驱动机构转动而同步转动。
传动机构当中包含了蜗杆和马达,在马达中设置了传动轴,将传动轴、蜗杆连为一体,利用马达对传动轴进行驱动,从而实现传动轴和蜗杆的同步转动[1]。
传动机构当中的两组齿轮组相互啮合,第一组齿轮与蜗杆啮合,第二齿轮组则在动力输出轴上套设,并与第一齿轮组啮合,在马达驱动下,蜗杆和传动轴同步转动,两组齿轮组与蜗杆同步转动。
最后,动力扭矩传递至动力输出轴,动力输出轴与法兰转盘连接,从而从马达到法兰转盘之间形成一个传动链。
为了实现对天线运输、跌落或振动时对传动机构、齿轮等的保护,应当增设有包含防震锁定机构,其包括馈线帽手把、复位弹簧、锁销套筒等部分。
在转盘中上设置与锁销相配套的套筒,并在机壳中对锁销进行容纳设计。
将复位弹簧的一端顶在机壳上,另一端顶在止推平台上,形成一个常开机构。
基于MATLAB的随动系统的设计及仿真

本科生毕业论文设计题目基于MATLAB的随动系统的设计与仿真作者姓名张蔷薇指导教师李淑娥所在学院职业技术学院专业(系)电气工程及其自动化班级(届)2013届完成日期2013 年5 月4 日目录中文摘要、关键词...................................错误!未定义书签。
英文摘要、关键词. (I)第一章绪论 (1)1.1课题研究背景 (1)1.1.1随动系统现状及历史 (1)1.1.2随动系统的应用 (1)1.2随动系统发展方向及特点 (2)第二章雷达天线位置随动系统的设计 (4)2.1位置随动系统概述 (4)2.2雷达天线位置随动系统的工作原理 (4)2.2.1系统的基本组成 (4)2.2.2该位置随动系统的工作原理 (7)第三章系统的建模与仿真 (8)3.1 MATLAB语言简介 (8)3.1.1MA丁LAB语言概述 (8)3.1.2MATLAB语言的特点 (8)3.2 系统数学传函的建模 (9)3.3基于MATLAB的系统的性能分析及仿真 (11)3.3.1稳定性分析 (11)3.3.2系统时域性能指标分析与仿真 (12)3.3.3系统频域性能分析及仿真 (13)第四章系统的PID校正 (15)4.1PID校正参数的确定 (15)4.1.1比例系数的确定 (15)4.1.2微分时间常数TD的确定 (17)4.1.3积分时间常数TI的确定 (18)4.2加入校正环节后的系统结构图 (19)4.3校正前后系统性能比较及仿真 (20)4.3.1校正后系统稳定性分析 (20)4.3.2校正后系统时域性能分析与比较 (20)4.3.3校正后系统频域性能分析与比较 (21)第五章结束语 (23)致谢 (24)参考文献 (25)基于MATLAB的随动系统的设计与仿真职业技术学院电气工程及其自动化专业指导教师李淑娥作者张蔷薇摘要:随动系统,亦称为伺服系统,是一种用来控制被控对象的某种状态,使被控对象的输出能自动、连续、精确地复现输入信号变化规律的控制系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天线方位角位置随动系统建摸系统的原理图如图2-7所示,其方块图如图2-8所示。
系统的任务是使输出的天线方位角θ0(t)跟踪输入方位角θi (t)的变化,试建立该系统的数学模型。
系统的参数值如下:电源电压V=10v ;功率放大器的增益和时间常数K 1=1,T 1=0.01s ;伺服电动机的电枢回路电阻R d =8Ω,转动惯量J a =0.02Kg ∙m 2, 粘性摩擦系数f a =0.01N ∙m ∙s/rad , 反电势系数C e =0.5V ∙s/rad ,转矩 系数C m =0.5N ∙m/A ;减速器各齿 轮的齿数为Z 1=25, Z 2= Z 3=250;负载端的转动惯量J L =1 Kg ∙m 2粘性摩擦系数f L =1N ∙m ∙s/rad 。
采用组合系统建摸法,根据原理图2-7可以将系统划分为六个环节:输入电位器,差分放大器,功率放大器,电动机,减速器和输出电位器。
首先建立各个环节的数学模型,然后将它们组合起来则可得系统的数学摸型。
1环节的数学模型(1) 输入电位器与输出电位器由于输入电位器与输出电位器的线路和电位器的结构均相同,故这两个环节的传递函数是一样的。
对电位器环节的输出电压与输入角位移的特性进行线性化处理则可视其为一比例环节。
由图2-7可知;当动触头位于电位器中心时其输出电压为零;朝前或朝后转动5圈其输出电压变化均为10V 。
于是可得它们的传递函数为00()()100.318/()52()i pot i u s u s k v rad s s θπθ====⨯(2) 差分放大器与功率放大器放大器通常工作在放大状态,可不考虑饱和的影响。
差分放大器的时间常数比起功率放大器以及系统的其他环节的时间常数要小得多,可以忽视不计。
故这两个环节的输入输出传递函数分别为差分放大器c e C K s U s U =)()(功率放大器 1()1()10.011do c i u s k u s T s s ==++(3) 电动机在小功率伺服系统中直流电动机的结构图中,由于电动机的电枢回路电感很小,可以忽略不计。
图中的J 与f 为折算至电动机轴上系统转动部分的等效转动惯量和等效粘性摩擦系数,其值分别为2212(/)0.021(25/250)0.03a L J J J Z Z =+=+⨯= 2212(/)0.011(25/250)0.02a L f f f Z Z =+=+⨯=将具体参数值代入,于是可求得电动机的电枢(空载)电压与转子角位移之间的传递函数为()/ 2.083()[()][1/(/)]( 1.708)m mm ddo d s e m e m d s C C JR u s s R J f C C s s J f C C R s s θ===+++++(4) 减速器齿轮减速器的传动比为21/i z z ==250/25=10,于是减速器的传递函数为()1/0.1()o m s i s θθ==2 系统的输入输出模型将个环节的数学模型按照信号的传递关系组合起来,则可绘制系统的结构图如图2-8所示。
应用梅森公式或结构图化简,由图则可求得系统的传递函数为32() 6.62()101.71170.8 6.62o ci cs k s s s s k θθ=+++天线方位角位置控制系统的时域分析 在2-5b 已建立该系统的数学模型,其结构如图2-7所示,若系统采用比例控制(即其前置放大器的增益c K 是可调的),试求(1)当c K =1000时系统的时间响应特性;(2)若要求超调量20%pσ=,c K 应调整为何值?并分别应用MA TLAB 和近似估算的方法求系统的暂态性能,说明近似估算的适用条件。
(1)增益c K 的稳定取值范围 天下女子面目可憎言语无味 由系统的传递函数32() 6.62()101.71170.8 6.62o ci cs K s s s s K θθ=+++,可得系统的特征方程为32det()101.71170.8 6.620c sI A s s s K -=+++=于是可构造劳斯表如下:320S 1170.8S 101.71 6.62S 17372.07 6.620S6.62c ccK K K -减速器根据劳斯判据,为确保系统稳定必须使劳斯表第一列的元素不变号,即 17372.07-6.62K c >0 6.62 K c >0故可求得系统在比例控制时,放大器增益的稳定取值范围为0< K c <2624.18。
(2) 当K c =1000时系统暂态特性的分析由题2-5b 系统结构图2-7可得,系统的开、闭环传递函数为0.06620.0388()(0.011)( 1.708)(0.011)(0.591)cck K K G s s s s s s s ==++++32() 6.62()()101.71170.8 6.62o ci cs K s s s s s K θφθ==+++由于K c 远低于其临界值(K er =2624.18),在系统的3个开环极点中功率放大器的极点P o3=-1/0.01=-100远离虚轴(相应的时间常数T 3=0.01很小)可忽略不计,故系统的开、闭环传递函数可简化为22220.06620.06620.0662()'()(0.011)( 1.708)( 1.708)( 1.708)'()66.2()'()1'()1.70866.22cc k k k nk n nK K G s G s s s s s s s s G s s s G s s s s s ωφφξωω=≈≈=++++≈===+++++ (3-9)式中8.14/n rad s ω==, 1.708/(2)0.105n ξω==。
于是可按二阶规范系统的表达式,估算系统的暂态性能如下:0.39p t s == %77.71%100*21/==--ζπζσep44.68s nt s ξω==(3)当要求超调量20%p σ=时系统暂态特性的分析(a) 暂态性能的估算 由于系统响应的超调量远低于第(2)项的相应值(71.77%),可以预计这时的增益K c <<1000,故开环时间常数T3=0.01可忽略不计。
于是系统的开环传递函数可简化为'()0.0662/[( 1.708)]k c G s K s s =+,从而系统的闭环传递函数可近似为2222'()66.2'()1'()1.70866.22k cnk cn nG s K s G s s s K s s ωφξωω===+++++ (3-10)根据对超调量的要求0.2peπξσ-==,则可得系统的阻尼比为ln(1/)0.4558σξ==而2 1.708n s ξω=, 20.0662n c K ω=。
故可求得 1.708/(2) 1.8736/n rad s ωξ==,2/0.066253.03c n K ω==。
于是根据二阶规范系统的性能指标表达式,则可估算系统的暂态性能如下:' 1.88p t s == '20%p σ= 4'4.68s nt s ξω== (b )应用MA TLAB 进行时域分析由式(3-9)和(3-10)应用MA TLAB 程 序A3.1,则可求得系统的实际暂态性能 为p t =1.9s ,p σ=20.8546%,s t =4.4 (s );并绘制系统的单位阶跃响应曲线, 如图3-20所示。
图中实线为按式(3-9) 求得的准确相应曲线,用”.”标出数据点 的为按式(3-10)将系统视为二阶系统 的近似响应曲线。
由图中可见:当K c 远 比其临界值小得多时,忽略小环节时间 常数的影响并进行近似估算,在工程上 是可行的。
MA TLAB 程序A3.1G1=tf(0.0662*53.03,[1,1.708,0.0662*53.03]);G=tf(6.62*53.03,[1,101.71,170.8,6.62*53.03]);T=0:0.1:8;y=step(G ,t);y1=step(G1,t);plot(t,y,’-‘,t,y1,’.’),grid Xlabel(‘t(sec)’)Legend(‘y ’,’y1’)Y=dcgain(G);[yp,p]=max(y);peaktime=t(p) Percentovershoot=100*(yp-Y)/YK=length(t);while(y(k)>0.98*Y&(y(k)<1.02*Y),k=k-1;endSettingtime=t(k)(4)稳态特性分析由式(3-9)可知:系统为1型的,且开环增益K=0.0388K c =38.8(当K c =1000时)或2.06(当K c =53.03)。
于是系统的误差系数为p K =∞ v K K = 0a K =。
因此该系统跟踪阶跃输入信号没有稳态误差;跟踪单位斜坡输入信号的稳态误差为1/38.80.026100011/2.060.48553.03c s c K e K K τ=⎧==⎨=⎩当=时当=时 但无法跟踪抛物线函数或其它变化更快的输入信号,若勉强使用则跟踪误差将随时间而不断地增大,当t →∞时其终值误差将趋于无穷大。
