自动控制原理及其应用答案第二版-课后答案.
自控原理习题答案(第2版)

第1章习题答案1-1 解:自动控制系统:被控对象和控制装置的总体;被控对象:要求实现自动控制的机器、设备和生产过程;扰动:除给定值之外,引起被控制量变化的各种外界因素;给定值:作用于控制系统输入端,并作为控制依据的物理量;反馈:将输出量直接或间接的送到输入端,并与之相比较,使系统按其差值进行调节,使偏差减小或消除。
1-2 解:开环控制有洗衣机的洗衣过程,闭环控制有抽水马桶的蓄水控制、电冰箱制冷系统等。
1-3 解:1-4 解:a与d相连,b与c相连即可;系统原理框图如下所示:1-5 解:系统原理框图如下所示:1-6 解:对控制系统的基本要求是稳定性、准确性和快速性:稳定性是系统正常工作的前提条件;准确性反映控制系统的控制精度,要求过渡过程结束后,系统的稳态误差越小越好;快速性是要求系统的响应速度快,过渡过程时间短,超调量小。
1-7 解:该系统的任务是使工作机械(被控对象)的转角θc(被控量)自动跟踪手柄给定角度θr(给定量)的变化。
该系统的工作原理是:检测电位计与给定电位计的电气特性相同,工作机械的转角θc经检测电位计转换成电压u c,手柄给定角度θr经给定电位计转换成给定电压u r,u c与u r接入放大器前端的电桥。
当工作机械转角θc没有跟踪手柄给定角度θr时,u c与u r两者不相等而产生偏差Δu=u r-u c,Δu经过放大器放大,使电动机转动,通过减速器使得负载产生减小偏差的转动。
当检测电位计检测并转换的u c与u r相等,此时Δu=u r-u c=0,电动机不转,工作机械停在当前位置。
其原理框图如下图所示。
1-8 解:谷物湿度控制系统原理框图如下。
该系统的被控量是谷物湿度,给定量是希望的谷物湿度。
谷物加湿后的实时湿度经湿度检测后送到调节器,若与希望的湿度产生偏差,则通过调节器控制给水阀门的开大或关小,以减小两者的偏差。
谷物在入口端的湿度由前馈通道输入到调节器。
这样若入口处谷物湿度较大,则会使得偏差减小,从而减小阀门的开度;若谷物干燥,会增大偏差,从而加大阀门的开度。
自动控制原理第二版课后答案孟华

自动控制原理第二版课后答案孟华【篇一:自动控制原理_孟华_习题答案】t>第二章2.1 试分别写出图2.68中各无源电路的输入ur(t)与输出uc(t)之间的微分方程。
图2.68 习题2.1图解:(a)ur?ucu?r?u?c)?i2,i1?i2?c?i1,c(ur1r2,r1r2rrr2?c?uc?12cu?r?cuurr1?r2r1?r2r1?r2(b)?r?u?c)?i1,c1(uur?u1?1,uc?i1r2?u1, ?i2,i1?i2?c2ur1??c?(r1c1?r1c2?r2c1)u?c?uc?r1r2c1c2u??r?(r1c1?r2c1)u?r?u r r1r2c1c2u(c)uur?uc?i1,c1(ur?u1)?i2,i1?i2?1r1r2,uc?1i1dt?u1, ?c2??c?(rc????r1r2c1c2u12?r2c2?r2c1)uc?uc?r1r2c1c2ur?(r2c2?r2c1)ur?ur2.2 试证明图2.69(a)所示电路与图2.69(b)所示的机械系统具有相同的微分方程。
图2.69(b)中xr(t)为输入,xc(t)为输出,均是位移量。
(a)(b)图2.69 习题2.2图(a)1ur?uc?r?u?c)?i2,i1?i2?i,uc??i1,c1(uidt?ir2,r1c2???c?(r1c1?r1c2?r2c2)u?c?uc?r1r2c1c2u??r?(r1c1?r2c2)u?r?u r r1r2c1c2u(b)?c?x?1)?k2x1,b1(x?r?x?c)?k1(xr?xc)?b2(x?c?x?1), b2(xb1b2bbbbbbb??c?(1?2?2)x?c?xc?12??r?(1?2)x?r?xrxxk1k2k1k2k1k1k2k1k22.3 试分别求出图2.70中各有源电路的输入ur(t)与输出uc(t)之间的微分方程。
(a) (b)(c)图2.70 习题2.3图解:(a)uur?r??c?cur1r2,uc?r???r2cur2ur r1(b)uurr?c,r2cu?c?uc??2ur ??c?cur1r2r1uc??ur1u?c??r2cu?r?ur r2??rdt,r1cur1cr1(c)2.4 某弹簧的力-位移特性曲线如图2.71所示。
自动控制原理第二版课后答案
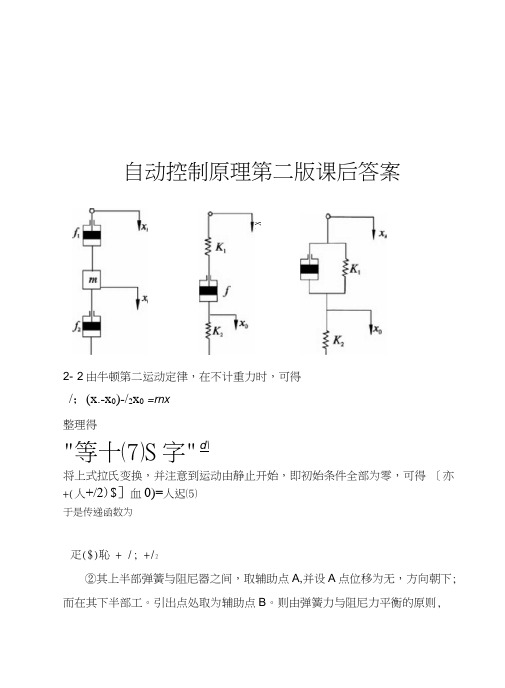
自动控制原理第二版课后答案X.2- 2由牛顿第二运动定律,在不计重力时,可得/;(x.-x0)-/2x0=rnx整理得"等十⑺S字" d\将上式拉氏变换,并注意到运动由静止开始,即初始条件全部为零,可得[亦+(人+/2)$]血0)=人迟⑸于是传递函数为疋($)恥 + /; +/2②其上半部弹簧与阻尼器之间,取辅助点A,并设A点位移为无,方向朝下; 而在其下半部工。
引出点处取为辅助点B。
则由弹簧力与阻尼力平衡的原则,从A和B两点可以分别列出如下原始方程:K](兀-x) = /(x-x c)消去中间变量X,可得系统微分方程佔+心)牛+ K心0 = 牛at at对上式取拉氏变换,并计及初始条件为零,得系统传递函数为K ⑸一/(&+£)$+&瓦③以引出点作为辅助点,根据力的平衡原则,可列出如下原始方程: 蜀(兀-X)+ /(乙-对)=丘%移项整理得系统微分方程/贽+ (陌+ 0)心=令+瓦兀对上式进行拉氏变换,并注意到运动由静止开始,即X r(。
) = X0(。
)= °则系统传递函数为X。
(£)_ fz K\ 兀G) 一冷+ (K]+0)2-3r 並'C 2s=1 (&C°s 十 1)一 1 {T.S + 1)・・・——(T.s + 1)所以.5(s)_ S _ C“ -_⑺s + l)®s + l)'5(s) Z 1 + Z 2 尽 |1(匚「J 尽C Q S + ^S + I)込s + 1)T 、s +1 C 2s 2(b) 以幻和fl 之间取辅助点A,并设A 点位移为方向朝下;根据力的平 衡原则,可列出如下原始方程:解:(a):利用运算阻抗法得:Z] =R 』R.——1 _ C\s泾尽+丄R 】 RiGs +1+1K2(X.-X0)+ f2(x. - x0) = /;(x0 -x) (1)A:1x = /;(x(> -x) (2)所以K2(x i-X0)4-/2(X,--X0)=K x x (3)対(3)式两边取微分得恳2(乙—攵。
自动控制原理答案完全版_第二版
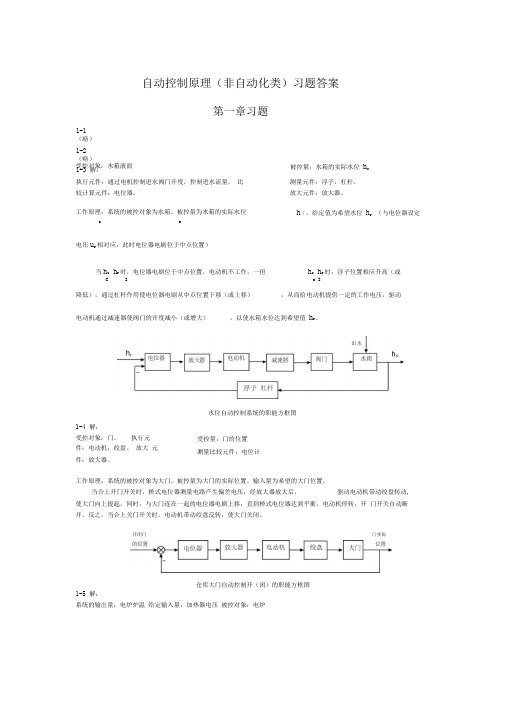
自动控制原理(非自动化类)习题答案第一章习题被控量:水箱的实际水位 h c执行元件:通过电机控制进水阀门开度,控制进水流量。
比较计算元件:电位器。
h 「。
给定值为希望水位 h r (与电位器设定cr电压u r 相对应,此时电位器电刷位于中点位置)当h c h r 时,电位器电刷位于中点位置,电动机不工作。
一但h c h r 时,浮子位置相应升高(或CIc I降低),通过杠杆作用使电位器电刷从中点位置下移(或上移) ,从而给电动机提供一定的工作电压,驱动电动机通过减速器使阀门的开度减小(或增大),以使水箱水位达到希望值 h r 。
水位自动控制系统的职能方框图受控量:门的位置 测量比较元件:电位计工作原理:系统的被控对象为大门。
被控量为大门的实际位置。
输入量为希望的大门位置。
当合上开门开关时,桥式电位器测量电路产生偏差电压,经放大器放大后,驱动电动机带动绞盘转动,使大门向上提起。
同时,与大门连在一起的电位器电刷上移,直到桥式电位器达到平衡,电动机停转,开 门开关自动断开。
反之,当合上关门开关时,电动机带动绞盘反转,使大门关闭。
1-5 解:系统的输岀量:电炉炉温 给定输入量:加热器电压 被控对象:电炉1-1 (略) 1-2(略)1-3 解: 受控对象:水箱液面 测量元件:浮子,杠杆。
放大元件:放大器。
工作原理:系统的被控对象为水箱。
被控量为水箱的实际水位1-4 解:受控对象:门。
执行元件:电动机,绞盘。
放大 元件:放大器。
开闭门门实际仓库大门自动控制开(闭)的职能方框图放大元件:电压放大器,功率放大器,减速器比较元件:电位计测量元件:热电偶职能方框图:KK3 2 Ts (T 1)s s K1K 3电位器电压放大炉温热电偶第二章习题2-1解:对微分方程做拉氏变换:X,(s) R(s) C(s) N,(s)X 2 (s) Q X/s)X 3 (s) X2 (s) X5(s TsX4 (s) X 3 (s)X5 (s) X4 (s) K2 N2(s k 3 X5 (s) s2C (s) sC(s) C(s) / R(s) 功率放大加热器'电机电炉R(s)绘制上式各子方程的方块图如下图所示:C(s) / N i (s) C(s) / R(s),K 2K 3TSTs 3~~T 1)s 2s K 1K 32-2解:对微分方程做拉氏变换X i (s) K[R(s) C (s)] X 2 (s)sR(s)(s 1) X 3(s) X i (s) X 2 (s) (Ts 1)X 4 (s)X 3 (s) X 5 (s)C(s) X 4 (s) N (s) X 5 (s) (Ts 1) N(s)(b) C (s)字红R(s) 1 G 1G 3 G G 4 G 2 G 3 G 2G 4X3(s) 绘制上式各子方程的方块如下图:将方块图连接得出系统的动态结构图:..R(s)1(s 1):Ts 1)C(s)N (s) 02-3解:(过程略)K____________C(s) (s 1)<Js 1) (s 1XTs 1) K ____________ Ts 2(T s1)s (K 1)C(s) / N 2 (s)R(s) ms fs K(c)誤 R(s) G 2 G 1G 2 1 G-i G 2G-I (d 普 R(s)G 1 G 2 1 G 2G 3(e)R^ R(s)G 1G 2G 3G 4 1 G<|G 2 G 2G 3 G 3G 4 G 1G 2G 3G 4 2-4 解:(1)求 C/R ,令 N=0 KK K 3s(Ts 1) C (s) / R(s) G(s)1 G(s) 求C/N ,令R=0,向后移动单位反馈的比较点 K C(s) / N (s) (K n G n K 1 0 ) — J s 1 亠 K 1G(s)K 1K 2 K 3 Ts 2K i K 2 K 3K n K 3s K 1K 2 K 3G K 2 n2 一Ts 2s K 1K 2 K 3 Ts 1 s (2)要消除干扰对系统的影响C(s) / N (s) K n K3s K1K2 K3GnTs 2 s K 1K 2 K 3G n (s) KnsK 1K 22-5 解:(a ) (1 )系统的反馈回路有三个,所以有3L a L 1 L 2 L 3 a 1G 1G 2G 5 G 2G 3G 4 G 4G 2G 5三个回路两两接触,可得 1 L a 1 GG 2G 5 G 2G 3G 4 G 4G 2G 5(2) 有两条前向通道,且与两条回路均有接触,所以P P 2 G 1G 2G 3,11, 2 1(3) 闭环传递函数C/R 为GGG 3 11 G 1G 2G 5 G 2G 3G 4 G 4G 2G 5(b)(1) 系统的反馈回路有三个,所以有3L aa 1L 1L 3 G 1G 2 G 1 G 1三个回路均接触,可得 1 L a 1 G-i G 2 2G-)(2 )有四条前向通道,且与三条回路均有接触,所以R G 1G 2 , 11P 2G, 21PG2,3 1P 4G 1,41(3)闭环传递函数C/R 为C G 1G 2 G 1 G 2 GG-i G 2 G 2 R 1 G 1G 22G 1 1 G-|G 2 2G.2-6解:用梅逊公式求,有两个回路,且接触,可得1L a 1 GG 2G 3 G 2,可得第三章习题采用K 0 , K H 负反馈方法的闭环传递函数为1OK o要使过渡时间减小到原来的 0.1倍,要保证总的放大系数不变,则:(原放大系数为10,时间常数为0.2)3-2解:系统为欠阻尼二阶系统(书上改为“单位负反馈……”,“已知系统开环传递函数”)% e / 1 $100%100% 1C(s) G-|G 2G 3 G 2G 3 R(s) 1 G 1G 2G 3 G 2 C (s)(1 G 2 )G 3N 2 (s) 1 GG 2G 3 G 2 E(s) 1 G 2 G 2G 3 R(s) 1 G-|G 2G :3 G 2 E(s) C(s) (1 G 2 G N 2 (s)N 2 (s)1 G 1G 2G 3 G 2C (s) NQC(s) / R(s)C(s) 1 (1 GG 2G 3 G 2 ) 1N 3 (s) 1 G 1G 2G 3 G 2 E(s) C(s) G 2G 3 G 1G 2G 3 N 1 (s) N 1(s) 1 G 1G 2G 3 G 2E(s)C(s) 1N 3 (s)N 3 (s)3-1解:(原书改为G(s) 100.2s 1)(s)C(s) K G(s) R(s) 01 G(S )K H1 10K H 0.2s1 10K10K 。
自动控制原理及其应用(第2版)黄坚第二章习题课

第二章习题课
(2-9)
2-9 若系统在单位阶跃输入作用时,已知初 若系统在单位阶跃输入作用时, 始条件为零的条件下系统的输出响应, 始条件为零的条件下系统的输出响应,求 系统的传递函数和脉冲响应。 系统的传递函数和脉冲响应。 -t 1 -2t R(s)= s c(t)=1-e +e r(t)=I(t) 1 - 1 + 1 = (s2+4s+2) 解: C(s)= s s+2 s+1 s(s+1)(s+2) (s2+4s+2) G(s)=C(s)/R(s)= (s+1)(s+2) (s2+4s+2) =1+ 2 - 1 脉冲响应: 脉冲响应 C(s)= (s+1)(s+2) s+2 s+1 c(t)= (t)+2e-2t-e-t δ
第二章习题课
(2) dy(t) 2 dt +y(t)=t
(2-4)
y(0)=0
第二章习题课
(2-5)
2-5 试画题图所示电路的动态结构图, 试画题图所示电路的动态结构图, c 并求传递函数。 并求传递函数。 i1 (1) 解: + R
Ur(s)
Cs _
I1(s)
+ +
i2
1
+
I(s)
R2
Uc(s)
+ i uo -
第二章习题课
(b) 解: (ui-u1) i=i1+i2 i= R
1
(2-1)
u1 L i
R1 C
+
ui
i1 i2
R2
+ uo -
大学_自动控制原理第二版(王敏 王金城著)课后答案下载

自动控制原理第二版(王敏王金城著)课后答案下载自动控制原理第二版(王敏王金城著)课后答案下载1控制系统导论1.1自动控制的基本原理1.1.1一个实例1.1.2控制系统方框图1.2自动控制系统的分类1.2.1按信号的传递路径来分1.2.2按系统输入信号的变化规律来分1.2.3按系统传输信号的性质来分1.2.4按描述系统的数学模型来分1.2.5其他分类方法1.3对控制系统的基本要求1.4自动控制的发展简史1.4.1经典控制理论阶段1.4.2现代控制理论阶段1.4.3大系统控制理论阶段1.4.4智能控制阶段__小结习题12控制系统数学模型2.1导论2.2控制系统的微分方程2.2.1微分方程式的建立2.2.2非线性方程的线性化2.3控制系统的传递函数2.3.1传递函数的概念2.3.2传递函数的性质2.3.3典型环节及其传递函数 2.4控制系统结构图与信号流图 2.4.1控制系统的结构图2.4.2控制系统的信号流图2.4.3控制系统的传递函数2.5应用Matlab控制系统仿真 2.5.1举例2.5.2传递函数2.5.3结构图模型__小结习题23控制系统的时域分析法3.1二阶系统的瞬态响应及性能指标 3.1.1典型输入信号3.1.2系统的性能指标3.1.3瞬态响应分析3.1.4线性定常系统的重要特性3.2增加零极点对二阶系统响应的影响 3.3反馈控制系统的稳态误差3.3.1稳态误差的概念3.3.2稳态误差的计算3.3.3主扰动输入引起的稳态误差3.3.4关于降低稳态误差问题3.4劳斯赫尔维茨稳定性判据3.4.1稳定性的概念3.4.2劳斯判据3.4.3赫尔维茨判据3.5控制系统灵敏度分析3.6应用Matlab分析控制系统的性能 __小结习题34根轨迹法4.1根轨迹的基本概念4.2绘制根轨迹的基本规则4.3控制系统根轨迹的`绘制4.4广义根轨迹4.4.1以非K?为变参数的根轨迹4.4.2正反馈系统的根轨迹4.4.3非最小相位系统的根轨迹4.5线性系统的根轨迹分析方法4.5.1主导极点的概念4.5.2增加开环零极点对根轨迹的影响 4.6利用Matlab绘制系统的根轨迹__小结习题45线性系统的频域分析5.1频率特性的概念5.2开环系统频率特性的图形表示 5.2.1幅相频率特性曲线5.2.2对数频率特性曲线5.3奈奎斯特稳定判据5.3.1奈奎斯特稳定判据的数学基础 5.3.2奈奎斯特稳定判据5.4控制系统的相对稳定性5.4.1相对稳定性5.4.2稳定裕度的求取……6线性系统的校正方法7线性离散控制系统8非线性系统理论9状态空间分析与综合10鲁棒控制系统附录Matlab简介参考文献自动控制原理第二版(王敏王金城著):内容提要本书还结合自动控制理论的基本概念的讲解,应用了Matlab及控制系统工具箱进行计算机辅助教学,通过例题、习题介绍Matlab在控制系统分析、综合及仿真中的应用。
《自动控制原理》第二版课后习题答案
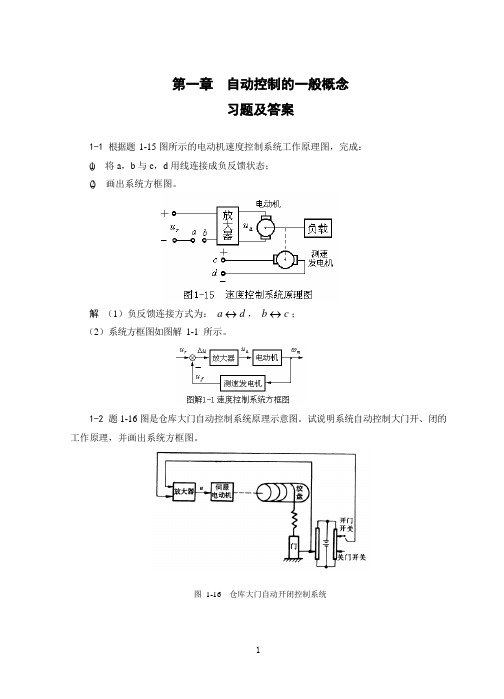
k (x x ) f ( dx1 dy )
(1)
1
1
dt dt
对B点有
f ( dx1 dy ) k y dt dt 2
(2)
联立式(1)、(2)可得:
dy k1k2 y k1 dx dt f (k1 k2 ) k1 k2 dt
电压。
在正常情况下,炉温等于某个期望值T °C,热电偶的输出电压u f 正好等于给定电压ur 。 此时, ue ur u f 0 ,故u1 ua 0 ,可逆电动机不转动,调压器的滑动触点停留在某 个合适的位置上,使uc 保持一定的数值。这时,炉子散失的热量正好等于从加热器吸取的热
量,形成稳定的热平衡状态,温度保持恒定。
第一章 自动控制的一般概念 习题及答案
1-1 根据题 1-15 图所示的电动机速度控制系统工作原理图,完成: (1) 将 a,b 与 c,d 用线连接成负反馈状态; (2) 画出系统方框图。
解 (1)负反馈连接方式为: a d , b c ;
(2)系统方框图如图解 1-1 所示。
1-2 题 1-16 图是仓库大门自动控制系统原理示意图。试说明系统自动控制大门开、闭的 工作原理,并画出系统方框图。
图 1-16 仓库大门自动开闭控制系统
1
解 当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏 差电压经放大器放大后,驱动伺服电动机带动绞盘转动,将大门向上提起。与此同时,和大 门连在一起的电刷也向上移动,直到桥式测量电路达到平衡,电动机停止转动,大门达到开 启位置。反之,当合上关门开关时,电动机带动绞盘使大门关闭,从而可以实现大门远距离 开闭自动控制。系统方框图如图解 1-2 所示。
当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失),则出现以下
自动控制原理及其应用第二版课后答案

自动控制原理及其应用第二版课后答案【篇一:《自动控制原理》黄坚课后习题答案】ss=txt>uo-u+o(a)解:i1=i-i2u1=ui-uouuu-ui=i1==211dud(u-u)i2=c=c(b)解:(u-u)i=i1+i2i=udui1=i2=c2duu1-uo=21u-uud(u-u)-c=12dudur2(ui-uo )=r1u0-cr1r2(-)duducr1r2+r1uo+r2u0=cr1r2+r2uidud2uuuduu--21112=2+cud2udu+(c+=12+(1+2)uo12duu+c2duo+22-2 求下列函数的拉氏变换。
(1) f(t)=sin4t+cos4t(2) f(t)=t3+e4t434t解:l[t+e](3) f(t)=tneat解:l[tneat]=(4) f(t)=(t-1)2e2t解:l[(t-1)2e2t]=e-(s-2)2-3求下列函数的拉氏反变换。
(1) f(s)=aa解:a1=(s+2)=-1a2=2 -f(t)=2e-3t-e-2t(2) f(s)=aaa解:a1=(s+1)=-1a2[=2a3s=-2=-2f(t)=-2e-2t-te-t+2e-t(3) f(s)=2as+aa解:f(s)(s2=a1s+a2j=a1s+aj-2-5j+1=ja1+a2-5j-1=-a1+ja2a1=1a2=-5a3=f(s)s=1++f(t)=1+cost-5sint(4) f(s)=解:=a+a+a+aa1a3a4a2ad[2]s=-1f(t)=e-t-e-t++e-3t(2-4)求解下列微分方程。
a2=5 a3=-4y(t)=1+5e-2t-4e-3t并求传递函数。
2-5试画题图所示电路的动态结构图,c+sc)r2r+rrscu(s)==c1+(+sc)r212121(2)cl1=-r2 /lsl2=-/lcs2l3=-1/scr1l1l3=r2/lcr1s2c112122-8 设有一个初始条件为零的系统,系统的输入、输出曲线如图,求g(s)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+ ui -
i1 R1 R2
+ uo i2 -
IC(s)=CsUC(s)
[UI(s)-UO(s)]Cs=IC(s)
UI(s)
UI(s) sC
1+ sC )R2 (R 1 IC(s) + I2(s) + I1(s)
UO(s)
-
1 R1
R2
UO(s)
1 ( +sC)R2 UO(s) R1 R2+R1R2sC = = 1 UI(s) R1+R2+R1R2sC ( sC)R + 1+ R 2 1
6+2s2+12s ∴ Y(s)= 2 s(s +5s+6) A1=sY(s)
s=0
1 s
(2-4-2)
求下列微分方程。
d3y(t) d2y(t) dy(t) 初始条件: +4 2 +29 =29, 3 dt dt dt · · y(0)=0 , y(0)=17 , · y(0)=-122 解:
2-5-a 试画题2-1图所示电路的动态结构图,并 求传递函数。 + uc - 解:ui=R1i1+uo ,i2=ic+i1 duc ic=C dt UI(s)=R1I1(s)+UO(s) I2(s)=IC(s)+I1(s) UI(s)-UO(s) 即: =I1(s) R1
(2-4-1) 求下列微分方程。 A3=(s+3)Y(s) A2=(s+2)Y(s) s=-2
s=-3
d2y(t) dy(t) +5 dt +6y(t)=6 ,初始条件: 2 dt · y(0)=y(0)=2 。 A1=1 , A2=5 , A3=-4 ∴ y(t)=1+5e-2t-4e-3t
′ 解:s2Y(s)0)-Y(0)+5sY(s)-5Y(0)+6Y(s)=
2-3-3 函数的拉氏变换。
∴ f(t)=1+cost-5sint
2s2-5s+1 F(s)= s(s2+1) 解:F(s)(s2+1) s=+j =A1s+A2 A1=1, A2=-5
s=+j s=0
A3=F(s)s
=1
s -5 1 F(s)= s + 2 + 2 s +1 s +1
2-3-4 函数的拉氏变换。
解:L[t3+e4t]= (3) f(t)=tneat 解:L[tneat]= n! (s-a)n+1 3! 1 3! 1 + s-4 = 4 + s-4 3+1 s s
(4) f(t)=(t-1)2e2t 2 2 2t -(s-2) 解:L[(t-1) e ]=e (s-2)3
2-3-1 函数的拉氏变换。 s+1 F(s)=(s+1)(s+3) s+1 解:A1=(s+2) (s+1)(s+3) A2=(s+3) s+1 (s+1)(s+3)
s=-3 s=-2
= -1
=2
2 - 1 F(s)= s+3 s+2
f(t)=2e-3t-e-2t
2-3-2 函数的拉氏变换。 s F(s)= (s+1)2(s+2) s d [ s est] st 解:f(t)= e +lim (s+1)2 s=-2 s -1 ds s+2 st st 2 -2t st) =-2e +lim( e + e s -1 s+2 (s+2)2 =-2e-2t-te-t+2e-t =(2-t)e-t-2e-2t
第二章习题课
(2-1b)
2-1(b) 试建立图所示电路的动态微分方 程。 duc CL d2uo duo du L ic= = +C o L 2 R 1 uL= dt R2 dt dt R2 dt + + 2 uo C CL d uoR2 duo uo u u + +C i1= i o i2= R ui=u1+uo 2 dt - R2 R2 dt - 2 输入量为ui,输出量为uo。 duc d(ui-uo) u1=i1R1 ic=C dt = dt diL uo u =L L dt iL=i2= i1=iL+ic R2
求下列函数的拉氏变换。 (1) f(t)=sin4t+cos4t w 解:∵L[sinwt]= 2 2 w +s s L[coswt]= 2 2 w +s
习题课一 (2-2)
4 + s ∴L[sin4t+cos4t]= s2+16 s2+16 s+4 = 2 s +16
(2) f(t)=t3+e4t
第二章习题课
(2-1a)
2-1(a) 试建立图所示电路的动态微分方 程。 u
+
c
-
i1=i2-ic
+ d1(ui-uo+ ) + uo R u1u =[ -C R2 ]R1+uo ui u dt i R2 o - - -
C
解:
C C i1 R1 R2
ic
+ uo i2 -
dui du。 o 输入量为 u ,输出量为 u i=u 1+uo i o R2ui=uoR1-Cdt R1R2+C dt R1R2u +u R o 2 duc d(ui-uo) uo u1=i1R1 duo ic=C dui dt = dt i2= R uoR1+C dt R1R2+uoR 2 2=R2ui+C dt R1R2
2-5-b 试画出题 2-1图所示的电路 的动态结构图,并 求传递函数。 解:ui=R1I1+uc uo ∴ iL= R2 UL(s)=sLIL(s)
+ ui -
R1 C
L
R2
+ uo -
uc=uo+uL i1=iL+ic
diL uL=L dt duc ic=C dt
Ui(s)=R1I1(s)+UC(s)
UC(s)=UO(s)+UL(s) I1(s)=IL(s)+IC(s)
UO(s) I2(s)= R2 UI(s)+UC(S) I1(s)= 即: R1 IL(s)=I1(s)-IC(s)
Ui 1 R1 I1
s+2 2 1 -3t 3 -t t -t (4) F(s)= = + e - e - e 2 s(s+1) (s+3) 3 12 4 2 s+2 s+2 st st 解:f(t)= e + e 2 2 (s+1) (s+3) s=0 s(s+1) s=-3 s+2 est ] d[ s(s+3) + lim s -1 ds st 2 st (s+2)te 2 1 -3t (-s -4s-6)e = + e +lim [ + 2 ] 2 2 s -1 3 12 (s +3) s +3s
