用excel进行线性规划的灵敏度分析学习资料
实验1用Excel求解线性规划模型

实验一、用Excel求解线性规划模型线性规划问题用手工求解工作量很大,而且没有较高的数学基础很难理解其计算过程和方法,但是借助Excel“规划求解”工具,就能轻而易举地求得结果。
Excel最多可解200个变量、600个约束条件的问题。
下面我们以一实例介绍利用Excel规划求解工具怎样快速解决具体的经济决策问题。
一、实验目的1、掌握如何建立线性规划模型。
2、掌握用Excel求解线性规划模型的方法。
3、掌握如何借助于Excel对线性规划模型进行灵敏度分析,以判断各种可能的变化对最优方案产生的影响。
4、读懂Excel求解线性规划问题输出的运算结果报告和敏感性报告。
二、实验内容1、[工具][规划求解]命令规划求解加载宏是Excel的一个可选安装模块,在安装Excel时,只有在选择“完全/定制安装”时才可选择装入这个模块。
在安装完成进入Excel后还要用[工具][加载宏]命令选中“规划求解”,以后在[工具]菜单下就增加了一条[规划求解]命令。
使用[规划求解]命令的一般步骤为:第一步:在选取[工具][规划求解]命令后,弹出图1所示“规划求解参数”对话框,其中各选项说明如表1。
图1“规划求解参数”对话框选项名说明设置目标单元格选取计算问题的目标函数,并含有计算公式的单元格等于按问题目标进行选择。
如利润问题,选取“最大值”可变单元格决策变量所在各单元格、不含公式,可以有多个区域或单元格约束增加、修改、删除各个约束等式或不等式,一个一个地与图2切换填入或修改添加选择后弹出图2所示对话框更改选择后弹出图3所示对话框删除删除所选定的约束条件选项决定采用线性模型还是非线性模型求解约束条件中的单元格引用位置,可从键盘直接录入,也可用鼠标拖放选取。
图2图3第二步:完成图1所示的一切填入项目后,单击“选项”按钮,在弹出的“规划求解选项”对话框中若是线性模型则选取“采用线性规模”选项按钮,再单击“确定”按钮回到图1。
图4第三步:在图1中单击“求解”按钮,经计算完成后弹出“规划求解结果”对话框(图5)。
excel求解线性规划和灵敏度分析实训过程记录及学习收获

excel求解线性规划和灵敏度分析实训过程记录及学习收获线性规划是一种数学优化模型,用于对一组线性限制条件下的线性目标函数进行优化。
Excel 能够进行线性规划问题的求解和灵敏度分析,以下是实习过程的记录和收获总结:1. 实训任务我们的实训任务是一个有饲料限制的生产计划问题,其中需要决定生产哪些种类的产品、购买何种原材料、以及在何时生产这些产品,以使得利润最大化。
任务中给定了各种产品需要的原材料数量,各种原材料的数量与价格,及一些限制条件,例如生产时间,最小生产量等。
2. Excel求解线性规划问题Excel中求解线性规划问题的函数是“Solver”,首先需要打开Excel中的“数据”选项卡,然后在“分析”工具中找到“Solver”。
进入“Solver参数”对话框后,需要输入目标函数和限制条件,并且设置决策变量的可变性、约束条件的类型和数量。
最后根据需要设置求解的约束条件和目标函数的目标方向,点击“求解”即可。
在我们的实训任务中,我们首先需要设置约束条件,限制了各种产品需要的原材料数量,并且确保生产时间在规定范围内。
然后我们需要设置各个决策变量的可变性,例如选择生产哪些产品,购买何种原材料以及在何时生产这些产品等。
最后将目标函数设置为生产的利润最大化,并且设置约束条件为“>=0”,以确保决策变量的可行性。
点击“求解”即可得出最优解。
3. Excel灵敏度分析Excel的灵敏度分析功能可以帮助我们了解线性规划问题的各个变量对于目标函数的影响程度。
Excel中灵敏度分析的函数是“规划求解器的报告”,在对话框中选择“接受解决方案”,然后勾选“制作规划求解器报告”选项,即可生成报告。
在报告中,我们可以看到各个决策变量的最优解以及目标函数的最优值。
同时,报告中还包括影响目标函数的变量的“系数范围”和“变化量”,我们可以通过调整这些参数来预测目标函数的变化情况。
4. 学习收获通过这次实训,我学会了如何使用Excel求解线性规划问题以及如何进行灵敏度分析。
实验二___线性规划灵敏度分析

实验二线性规划模型及灵敏度分析(一)实验目的:掌握使用Excel软件进行灵敏度分析的操作方法。
(二)实验内容和要求:用Excel软件完成案例。
(三)实例操作:(1)建立电子表格模型;(2)使用Excel规划求解功能求解问题并生成“敏感性报告”;(3)结果分析:哪些问题可以直接利用“敏感性报告”中的信息求解,哪些问题需要重新规划求解,并对结果提出你的看法;(4)在Word文档中书写实验报告,包括线性规划模型、电子表格模型、敏感性报告和结果分析等。
案例1 市场调查问题某市场调查公司受某厂的委托,调查消费者对某种新产品的了解和反应情况。
该厂对市场调查公司提出了以下要求:(1)共对500个家庭进行调查;(2)在被调查家庭中,至少有200个是没有孩子的家庭,同时至少有200个是有孩子的家庭;(3)至少对300个被调查家庭采用问卷式书面调查,对其余家庭可采用口头调查;(4)在有孩子的被调查家庭中,至少对50%的家庭采用问卷式书面调查;(5)在没有孩子的被调查家庭中,至少对60%的家庭采用问卷式书面调查。
对不同家庭采用不同调查方式的费用如下表所示:市场调查费用表家庭类型调查费用(元)问卷式书面调查口头调查有孩子的家庭50 30没有孩子的家庭40 25问:市场调查公司应如何进行调查,使得在满足厂方要求的条件下,使得总调查费用最少?案例2 经理会议建议的分析某公司生产三种产品A1,A2,A3,它们在B1,B2两种设备上加工,并耗用C1,C2两种原材料,已知生产单位产品耗用的工时和原材料以及设备和原材料的每天最多可使用量如下表所示:生产三种产品的有关数据资源产品A1 产品A2 产品A3 每天最多可使用量设备B1(min) 1 2 1 430设备B2(min) 3 0 2 460原料C1(kg) 1 4 0 420原料C2(kg) 1 1 1 300每件利润(元) 30 20 50已知每天对产品A2的需求不低于70件,对A3不超过240件。
90. 如何在Excel中进行敏感性分析?

90. 如何在Excel中进行敏感性分析?90、如何在 Excel 中进行敏感性分析?在当今的数据驱动时代,Excel 作为一款强大的电子表格软件,被广泛应用于各种数据分析和决策支持场景。
敏感性分析作为一种重要的分析方法,可以帮助我们了解模型中输入变量的变化对输出结果的影响程度,从而为决策提供更可靠的依据。
接下来,让我们一起深入探讨如何在 Excel 中进行敏感性分析。
首先,我们需要明确敏感性分析的概念。
简单来说,敏感性分析就是研究当模型中的某个或某些输入变量发生变化时,输出结果会如何相应地改变。
这对于评估模型的稳定性和可靠性,以及识别关键的影响因素非常有帮助。
在 Excel 中进行敏感性分析,通常可以采用以下几种方法:一、数据表格法这是一种较为直观和简单的方法。
假设我们有一个销售预测模型,其中销售量、单价和成本是影响利润的主要因素。
我们可以在 Excel 中创建一个数据表,将这三个变量放在列标题上,然后在不同的行中输入它们可能的取值。
接着,通过公式计算出每个组合下的利润。
这样,我们就可以直观地看到不同变量取值对利润的影响。
例如,假设利润的计算公式为:利润=(销售量单价)成本。
我们可以在 Excel 中输入如下公式:在 B2 单元格输入:=B1C1 D1然后通过向下填充或复制公式,得到不同变量组合下的利润值。
通过观察这个数据表,我们可以快速了解每个变量对利润的影响程度,例如销售量增加 10%时利润的变化情况,或者单价降低 5%时利润的变化情况。
二、单变量求解当我们想要知道当输出结果达到某个特定值时,某个输入变量应该取什么值时,可以使用单变量求解功能。
比如,我们仍然以销售预测模型为例,已知当前的销售量、单价和成本,以及计算出的利润。
现在假设我们希望利润达到一个特定的目标值,比如 10000 元,然后想知道在这种情况下,单价应该调整为多少。
操作步骤如下:首先,在 Excel 中输入利润的计算公式,然后选择“数据”选项卡中的“假设分析”,再点击“单变量求解”。
用Excel求解LP线性规划问题PPT学习教案

对话框“规划求解参 数”
第6页/共12页
①在“设置目标单元格”栏后的空白中填入$C$5, 并选中“最小”;
对话框“规划求解参 数”
②在“可变单元格(B)”栏后的空白中 填入$A$1:$B$1;
第7页/共12页
③光标指向“约束”栏,按“添加”,出现“添 加约束”对话框(如下图),
对话框“改变约束”
依次填入约束关系,每输完一条,按“添加”,输入所有约束条 件后,按“确定”,
输入系数
第3页/共12页
3、LP模型的EXCEL输入(两种 方法)
在C2单元格中输入“=A2*A$1+B2*B$1”,并复制到C3、C4、C5 中,使它们分别变为 “=A3*A$1+B3*B$1” 、“=A4*A$1+B4*B$1” 和 “=A5*A$1+B5*B$1”。
第4页/共12页
利用EXCEL的SUMPRODUCT函 数进行计算
第8页/共12页
又退回到下图状态,在下图中可以选“更改”、 “删除”、“全部重设”来编辑约束条件及其他
设置。
填入了参数的对话框“规划求解参数 ”
第9页/共12页
④在上图中按“求解”,即进入求解过程, 求解结束,出现“规划求解结果”对话框(如
下图),选择“保存规划求解结果”后,
对话框“规划求解结果”
求解的结果
第11页/共12页
工作表中可变单元格、目标单 元格以及计算约束条件的单元 格均发生变化。如不想破坏原 始数据,可选择“恢复为原 值”,同时第1选0页/共中12页“报告”框中 的“运算结果报告”,或选
灵敏度分析的EXCEL求解(N12)

练习:《Sytech 国际公司》问题
案例概述:
Sytech 国际公司是一家在同行业中处于领先地位的计 算机和外围设备的制造商。公司的主导产品分类如下:大型 计算机(MFRAMES)、小型计算机(MINIS)、个人计算机( PCS)、和打印机(PRINTERS)。公司的两个主要市场是北 美和欧洲。
公司一直按季度作出公司最初的重要决策。公司必须按 照营销部门的需求预测来对分布在全球的三个工厂调整产量 ,公司下一季度需求预测如下:
资源
价格(美元/吨) 联合/非联合 卡车/铁路 可挥发性(%) 生产容量(千吨)
阿什利
49.5 联合 铁路
15 300
贝德福德 50
联合 卡车
16 600
康索 61
非联合 铁路 18 510
邓比 63.5 联合 卡车 20 655
厄勒姆 66.5
非联合 卡车 21 575
弗洛伦斯 71
联合 卡车
22 680
1
0
0
0
1
1
506 <=
18
20
21
22
23
25
19
>=
决策变量
阿什利A贝德福德B 康索C 邓比D 厄勒姆E 弗洛伦斯F加斯顿G 霍普特H 合计
购买数量(千吨)
56
600
0
16
104
0
450
0
1226 =
<=
<=
<=
<=
<=
<=
<=
<=
生产容量(千吨)
300
600
510
655
575
运筹学04-运用Spreadsheet求解线性规划及灵敏度分析

使用敏感性报告进行灵敏度分析
如果单位椅子的价格从15$增加到18$,那么已求得的最优解、最优 目标值会变化么?该系数在什么范围内变化才不会影响最优解?
A B C D E F G H I 5 6 可变单元格 7 8 单元格 名字 9 $B$14 决策变量 chair 10 $C$14 决策变量 Table 11
“单元格”是指决策变量所在单元格的地址 “名字”是决策变量的名称 “终值”是决策变量的终值,即最优解 “递减成本”(reduced cost) 不做解释 “目标式系数”目标函数中的系数,为已知条件 “允许的增量”与“允许的减量”表示目标函数中的系数 在增量与减量的变化范围内变化时,最优解保持不变。 (最优值变化)
“允许变化范围”是指其他条件不变,仅在该变量变化范围内
约束条件右边变化对目标值的影响
A B C D E F G H I 11 12 约束 13 14 单元格 名字 15 $B$19 Large bricks 使用量 16 $B$20 small bricks 使用量 17 终 阴影 约束 允许的 允许的 值 价格 限制值 增量 减量 6 5 6 2 2 8 5 8 4 2
线性规划 网络模型(如:邮递员送信,最短路) 整数规划(如:指派问题-N项任务N个对象)
4.4 用Excel solver求解 求解
中的“ 用Excel中的“规划求解”功能 中的 规划求解”
几个Excel中的命令
公式的输入:“=” 单元格的地址:绝对地址和相对地址
$A$8,A8
求和:
=sum(A1,A2,F6) =SUM(B2:B22)
运用Spreadsheet求解线性规划 Spreadsheet求解 第四章 运用Spreadsheet求解线性规划
Excel灵敏度分析实验
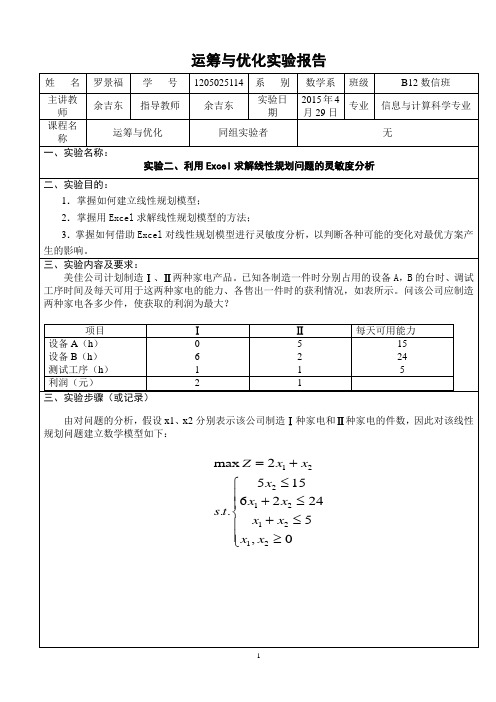
图4
添加约束
图5
规划求解参数的设置
(5)在图 4“规划求解参数”对话框中单击“选项” ,弹出“规划求解选项”对话框,在该对 话框中勾选“采用线性模型”和“假定非负”选项,然后点击“确定” ,如图 6 所示。
5
图6
规划求解选项的设置
(6)设置完成后,单击“规划求解参数”对话框中的“求解”进行求解,弹出“线性求解结果” 对话框,如图 7 所示;单击“线性求解结果”对话框中的“确定” ,得到该线性规划模型的结果,如 图 8 所示。
2
3
图2
调用 SUMPRODUCT()函数的结果
(3)单击“工具”中的“加载宏” ,弹出的“加载宏”对话框,在对话框中选择“规划求解” 选项,最后单击“确定” ,如图 3 所示。
图3
加载宏选择规划求解
4
(4)在工具菜单中选择“规划求解”命令,弹出“规划求解参数”窗口,在该对话框中目标单 元格选择“D2” ,问题类型选择“最大值” ,在“可变单元格”中选择“$B$8:$C$8” 。点击“添加” 按钮,弹出“添加约束”对话框,在该对话框中添加本模型所给出的约束条件,如图 4 所示。然后 单击“确定” ,得到规划求解参数的设置,如图 5 所示。
图 1 两种产品问题的电子表格模型 ( 2 )将目标方程和约束条件的对应公式输入到 D2 , D4 , D5 , D6 各单元格中,格式为 SUMPRODUCT(D2:C2,B8:C8) , SUMPRODUCT(D4:C4,B8:C8) , SUMPRODUCT(D5:C5,B8:C8) , SUMPRODUCT(D6:C6,B8:C8),回车后以下单元格均显示数字“0” ,如图 2 所示。
运筹与优化实验报告
姓 名 罗景福 学 号 1205025114 系 别 数学系 班级 B12 数信班 主讲教 实验日 2015 年 4 余吉东 指导教师 余吉东 专业 信息与计算科学专业 师 期 月 29 日 课程名 运筹与优化 同组实验者 无 称 一、实验名称: 实验二、利用 Excel 求解线性规划问题的灵敏度分析 二、实验目的: 1.掌握如何建立线性规划模型; 2.掌握用 Excel 求解线性规划模型的方法; 3.掌握如何借助 Excel 对线性规划模型进行灵敏度分析,以判断各种可能的变化对最优方案产 生的影响。 三、实验内容及要求: 美佳公司计划制造Ⅰ、Ⅱ两种家电产品。已知各制造一件时分别占用的设备 A,B 的台时、调试 工序时间及每天可用于这两种家电的能力、各售出一件时的获利情况,如表所示。问该公司应制造 两种家电各多少件,使获取的利润为最大? 项目 设备 A(h) 设备 B(h) 测试工序(h) 利润(元) 三、实验步骤(或记录) Ⅰ 0 6 1 2 Ⅱ 5 2 1 1 每天可用能力 15 24 5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用excel进行线性规划的灵敏度分析学习资料
线性规划是一种数学优化方法,它提供了一种有效的方法来解决最优化问题。
灵敏度
分析是线性规划中的一个非常重要的概念,它是用来研究一些关键参数的变化对于最优解
的影响。
在Excel中进行线性规划和灵敏度分析非常方便,本文将介绍如何在Excel中进
行线性规划的灵敏度分析。
首先,我们需要先了解Excel中进行线性规划的基本步骤。
以最简单的线性规划模型
为例,我们可以用以下模型来说明:
目标函数:Maximize f(x,y)=4x+3y
约束条件:
2x+y <= 8
x,y >= 0
要在Excel中求解这个问题,我们需要遵循以下步骤:
1. 打开Excel,输入目标函数和约束条件。
公式应放在单元格中,约束条件应按行排列,用每行的最后一个单元格来设置限制。
还应设置变量的初始值,并将目标单元格格式
设置为“最大值”或“最小值”。
2. 选择“数据”选项卡,在“分析”组内选择“规划问题”选项。
在弹出的窗口中,选择“线性规划”选项,并单击“确定”按钮。
3. 在线性规划窗口中,选择“目标单元格”和变量单元格,然后选择要优化的运算
符(如“大于等于”或“小于等于”)。
选择“添加”按钮向模型添加约束条件,直到所
有限制都添加完毕。
单击“求解”按钮,Excel将显示变量的最优解、目标函数的最优解
以及约束条件的最佳值。
在完成线性规划模型的求解后,我们可以进行灵敏度分析来研究模型中不同参数的变
化对最终解的影响。
在Excel中进行灵敏度分析有以下步骤:
1. 求出每个决策变量的最优值和目标函数的最优值。
2. 使用Excel的数据表功能,建立一个数据表,将要变化的参数输入到数据表中。
可以一次性变化多个参数。
3. 将数据表的单元格链接到原始模型中的输入参数单元格。
4. 使用Excel的数据表的“展示数据表”功能,查看各参数的最优解或其他解所对应的目标函数的值。
5. 根据结果进行分析,确定哪些参数对最终结果有最大的影响。
总之,在Excel中进行线性规划的灵敏度分析,可以帮助您评估模型对输入参数的敏感程度,并找到解决方案的可能变化范围。
灵敏度分析也可以帮助您确定需要进行调整或优化的变量,以便在实际应用中取得更好的结果。
