20XX年中考数学创新思维训练试题及答案(3)
数学初升高思维训练答案

数学初升高思维训练答案一、选择题1. 下列哪个选项不是整数?A. 0B. 3C. -5D. 2.5答案:D2. 如果一个数的平方等于它本身,那么这个数可能是:A. 1B. -1C. 0D. 所有选项答案:D3. 一个等差数列的首项是3,公差是2,那么第5项的值是:A. 7B. 9C. 11D. 13答案:C4. 一个圆的半径是5,那么这个圆的面积是:A. 25πB. 50πC. 75πD. 100π答案:B5. 下列哪个表达式的结果不是整数?A. \( \sqrt{16} \)B. \( (-3)^2 \)C. \( \frac{10}{2} \)D. \( \frac{7}{3} \)答案:D二、填空题6. 一个直角三角形的两个直角边分别是3和4,那么斜边的长度是______ 。
答案:57. 如果一个数的立方等于它本身,那么这个数可能是 ______ 。
答案:1 或 -1 或 08. 一个数的绝对值是5,那么这个数可能是 ______ 或 ______ 。
答案:5 或 -59. 一个正数的倒数是它自己,那么这个数是 ______ 。
答案:110. 如果一个数的相反数是它自己,那么这个数是 ______ 。
答案:0三、解答题11. 证明:对于任意实数x,\( x^2 \geq 0 \)。
证明:假设x为任意实数,那么x的平方\( x^2 \)可以表示为:\( x^2 = (x - 0)(x - 0) \)。
由于实数的乘积总是非负的,所以:\( x^2 \geq 0 \)。
12. 解不等式:\( 2x - 5 > 3x + 1 \)。
解:将不等式两边的x项放在一边,常数项放在另一边:\( 2x - 3x > 1 + 5 \),\( -x > 6 \),两边同时乘以-1(注意不等号方向要翻转):\( x < -6 \)。
13. 一个等比数列的首项是2,公比是3,求第6项的值。
解:等比数列的通项公式为:\( a_n = a_1 \times r^{(n-1)} \),其中\( a_1 \)是首项,r是公比,n是项数。
2020年七年级数学创新思维竞赛试卷及答案解析

第 1 页 共 13 页
2020年七年级数学创新思维竞赛试卷
一、选择题(共8小题,每小题5分,满分40分)
1.(5分)a 代表有理数,那么,a 和﹣a 的大小关系是( )
A .a 大于﹣a
B .a 小于﹣a
C .a 大于﹣a 或a 小于﹣a
D .a 不一定大于﹣a
2.(5分)如图,分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图,
则组成这个几何体的小正方体的个数是( )
A .3个或4个
B .4个或5个
C .5个或6个
D .6个或7个
3.(5分)9点12分时,时钟的分针和时针的夹角(小于180°的角)为( )
A .150°
B .154°
C .156°
D .162°
4.(5分)从长度分别为1,3,5,7,9个单位的5条线段中任取3条作边,能组成三角形
的概率为( )
A .15
B .25
C .12
D .310
5.(5分)如图,是5×5的网格图,任意上下左右相邻的两点间距离都是1,则以网格图中
的格点为顶点画正方形,共能画出面积互不相等的正方形的个数是( )
A .8
B .9
C .10
D .11
6.(5分)如图是测量一颗玻璃球体积的过程:
(1)将300mL 的水倒进一个容量为500mL 的杯子中;
(2)将四颗相同的玻璃球放入水中,结果水没有满;
(3)再加一颗同样的玻璃球放入水中,结果水满溢出.
根据以上过程,推测这样一颗玻璃球的体积在( )。
数学中考创新思维训练四

1.如图,已知⊙O 1经过⊙O 2的圆心O 2,且与⊙O 2相交于A 、B 两点,点C 为弧AO 2B 上的一动点(不运动至A 、B ),连结AC ,并延长交⊙O 2于点P ,连结BP 、PC(1)当点C(2)请猜想△BCP 2.如图,已知AB 是⊙O 的直径,直线垂足为D 。
(1)求证:∠BAE=∠DAF(2)若把直线MN 请把不必证明)3L ,AA 1⊥L ,BB 1⊥L ,CC 1⊥L ,DD 1⊥L 。
求证:现将L 向上平移,则以上的结论还成立吗? 4.如图,AD 是⊙O 的直径,BC 切⊙O 于E ,F(1)求证:AE·AB=AF·AC (2)如果将直线BC 向上或向下平移(与AD仍然垂直)且AB ,AC 交⊙O 于E ,F ,则AE·AB=AF·AC 还成立吗?5.已知,如图,点C 为线段AB 上一点,△ACM,△CBN 是等边三角形,则图(1)中存在结论AN=BM (1)现将△ACM 绕C 点按逆时针方向旋转1800,使A 点落在CB 上,请在画出符合题意的图(2)(2)在(2)中所得的图形中,结论“AN=BM”是否还成立?若成立,请证明;若不成立,请说明理由 (3)在(2)得到的图形中,设MA 的延长线与BN 相交于D 点,请你判断△ABD 与四边形MDNC的形状,并证明你的结论6.A 的直线7直线y与x ?8已知⊙O 于E 9⊙O 210A 、11AC 、P P请直接应用上述信息解决下列问题: 如图(2)当点P 在△ABC 内、如图(3),当点P 在△ABC 外这两种情况时,上述结论是否还成立?若成立,请给予证明;若不成立,则h 1、h 2、h 3,与h之间又有怎样的关系;请写出你猜想,不需证明。
12.已知,AB⊙O 的直径,P 为AB 延长线上的一个动点,过点P 作⊙O 的切线,设切点为C ,(1)当点P 在AB 延长线上的位置,如图1所示时,连结AC ,作∠APC 的平分线,交AC 于点D ,请你测量出∠CDP 的度数,(2)当点P 在AB 延长线的位置如图2和图3所示时,连结AC ,请你分别在这两个图中用尺规作出∠APC 的平分线,设此角平分线交AC 于点D ,然后在这两个图中分别测量出∠CDP 的度数;猜想:∠CDP 的度数是否随点P 在AB 延长线上的位置的变化而变化?请对你的猜想加以证明, ? ? 13.AB 是⊙O 的直径,C 是⊙O 上一点,连结AC ,过点C 作直线CD⊥AB 于D (AD<DB ),点E 是DB 上任意一点(点D 、B除外),直线CE 交⊙O 于点F ,连结AF 与直线CD 交于点G 。
2024中考数学复习—思维训练题(含参考答案)

中考复习—思维训练题一.试题(共17题)1.已知a ,b 是方程2350x x −−=的两根,则代数式3222671a a b b −+++的值是( ) A .25−B .24−C .35D .362.已知方程2230x x +−=的解是11x =,23x =−,则给出另一个方程2(23)2(23)30x x +++−=,它的解是( ) A .1−或3B .1或3C .1−或3−D .1或3−3.平面直角坐标系中,函数0)y x =<与4y x =+的图象交于点(,)P a b ,则代数式11a b−的值是( )A .BC .D 4.著名数学家华罗庚说过:“数形结合百般好,隔裂分家万事非.”请运用这句话中提到的思想方法判断方程2324x x x−=−的根的情况是( ) A .有三个实数根 B .有两个实数根 C .有一个实数根 D .无实数根5.华罗庚说过:“数形结合百般好,隔裂分家万事非.”请运用这句话中提到的思想方法判断方程2124x x x+=−+的根的情况是( ) A .有三个实数根 B .有两个实数根 C .有一个实数根 D .无实数根6.判断方程3|2|2x x =−−的根的情况是( ) A .有四个实数根 B .有两个实数根 C .有一个实数根 D .无实数根7.构建几何图形解决代数问题是“数形结合”思想的重要体现,在计算tan15︒时,如图,在Rt ABC ∆中,90C ∠=︒,30ABC ∠=︒,延长CB 使BD AB =,连接AD ,得15D ∠=︒,所以tan152AC CD ︒====−tan 22.5︒的值为( )A1+ BC1− D .128.已知1x 、2x 、3x 为方程323940x x x +−−=的三个实数根,则下列结论一定正确的是( )A .1230x x x <B .1230x x x +−>C .1230x x x −−>D .1230x x x ++<9.如图是一些有规律的图案,它们由一些线段组成.图1中有3条线段,图2中有7条线段,图3中有15条线段,⋯,以此类推,第6个图中有( )条线段.A .63B .65C .127D .25510.如图所示,由一些点组成形如三角形的图形,每条“边”(包括两个顶点)有(1)n n >个点,每个图形总共的点数是S ,当8n =时,S 的值是( )A .18B .21C .24D .2711.我国宋朝时期的数学家杨辉,曾将大小完全相同的圆弹珠逐层堆积,形成“三角垛”,图1有1颗弹珠;图2有3颗弹珠;图3有6颗弹珠,往下依次是第4个图,第5个图,⋯;若用n a 表示图n 的弹珠数,其中1n =,2,3,⋯,则12320231111(a a a a +++⋯+= )A .40442023B .40422023C .20211011D .2023101212.关于x 的方程(2)(3)x x m −−=有两个不相等的实数根1x ,212()x x x <,则下列结论一定正确的是( )A .14m >−B .12522x x += C .当0m >时,1223x x <<< D .当0m >时,1223x x <<<13.已知2x =−,代数式244x x ++的值为 .14.若x =3231x x x +++的值为 . 15.已知实数a ,b 满足2222(21)(21)80a b a b +++−=,试求222a b +的值. 解:设222a b m +=.原方程可化为(1)(1)80m m +−=,即281m =,解得9m =±. 2220a b +,2229a b ∴+=.上面的这种方法称为“换元法”,换元法是数学学习中最常用的一种思想方法,在结构较复杂的数和式的运算中,若把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂问题简单化.请根据以上阅读材料,解决问题.已知实数x ,y 满足2222(221)()3x y x y +−+=,则22332x y +−的值为 . 16.若21m n +=,则2366m mn n ++的值为 .17.当代数式235x x ++的值为7时,代数式23911x x +−的值为 .思维片2024参考答案与试题解析一.试题(共17题)1.已知a ,b 是方程2350x x −−=的两根,则代数式3222671a a b b −+++的值是( ) A .25−B .24−C .35D .36【解答】解:a ,b 是方程2350x x −−=的两根, 2350a a ∴−−=,2350b b −−=,3a b +=, 235a a ∴−=,235b b =+, 3222671a a b b ∴−+++22(3)3571a a a b b =−++++ 10106a b =++10()6a b =++ 1036=⨯+ 36=.故选:D .2.已知方程2230x x +−=的解是11x =,23x =−,则给出另一个方程2(23)2(23)30x x +++−=,它的解是( ) A .1−或3B .1或3C .1−或3−D .1或3−【解答】解:方程2230x x +−=的解是11x =,23x =−, ∴方程2(23)2(23)30x x +++−=,231x +=,233x +=−, 22x =−,26x =−,11x =−,23x =−,故选:C .3.平面直角坐标系中,函数(0)y x x =<与4y x =+的图象交于点(,)P a b ,则代数式11a b−的值是( )A .B .3C .3D .3【解答】解:把点(,)P a b 分别代入0)y x x=−<与4y x =+中,得b =,4b a =+,即ab =,4b a −=,∴11b a a b ab −−===故选:A .4.著名数学家华罗庚说过:“数形结合百般好,隔裂分家万事非.”请运用这句话中提到的思想方法判断方程2324x x x−=−的根的情况是( ) A .有三个实数根 B .有两个实数根 C .有一个实数根 D .无实数根【解答】解:画出函数3y x=和函数242y x x =−+的图象如图,观察图象,函数3y x=和函数242y x x =−+的图象有一个交点, 所以,方程2324x x x−=−有一个实数根, 故选:C .5.华罗庚说过:“数形结合百般好,隔裂分家万事非.”请运用这句话中提到的思想方法判断方程2124x x x+=−+的根的情况是( ) A .有三个实数根 B .有两个实数根 C .有一个实数根 D .无实数根【解答】解:方程变形为2142x x x=−+−, ∴21(2)2x x=−−+,把解方程理解为求反比例函数1y x=图象与抛物线2(2)2y x =−−+的交点的横坐标, 反比例函数图象分布在第一、三象限,在第一象限,抛物线的顶点(2,2)在反比例函数图象上方,且抛物线的开口向下,如图, ∴反比例函数1y x=图象与抛物线2(2)2y x =−−+有3个交点, ∴原方程有3个实数解.故选:A .6.判断方程3|2|2x x =−−的根的情况是( ) A .有四个实数根 B .有两个实数根 C .有一个实数根 D .无实数根【解答】解:3|2|2x x =−−, 20x ∴−>,2(2)3x ∴−=,2x ∴−,解得2x =,经检验,2x =+是原方程的解. 故方程3|2|2x x =−−的根的情况是有一个实数根.故选:C .7.构建几何图形解决代数问题是“数形结合”思想的重要体现,在计算tan15︒时,如图,在Rt ABC ∆中,90C ∠=︒,30ABC ∠=︒,延长CB 使BD AB =,连接AD ,得15D ∠=︒,所以tan152AC CD ︒====−tan 22.5︒的值为( )A 1+BC 1−D .12【解答】解:在Rt ABC ∆中,90C ∠=︒,45ABC ∠=︒,延长CB 使BD AB =,连接AD ,得22.5D ∠=︒,设1AC BC ==,则AB BD ==,tan 22.51AC CD ∴︒===, 故选:C .8.已知1x 、2x 、3x 为方程323940x x x +−−=的三个实数根,则下列结论一定正确的是( )A .1230x x x <B .1230x x x +−>C .1230x x x −−>D .1230x x x ++<【解答】解:323940x x x +−−=,当0x =时,40−≠, 24390x x x∴+−−=, 1x ∴、2x 、3x 可以看作是抛物线239y x x =+−与反比例函数4y x=的三个交点的横坐标,由函数图象可知1230x x x>,1230x x x++<,根据已知条件无法判定1230x x x+−>,1230x x x−−>,故选:D.9.如图是一些有规律的图案,它们由一些线段组成.图1中有3条线段,图2中有7条线段,图3中有15条线段,⋯,以此类推,第6个图中有()条线段.A.63B.65C.127D.255【解答】解:由图可知,图1中有3条线段,图2中有7条线段,734=+,图3中有15条线段:15724=+⨯,图4中有31条线段:311544=+⨯,图5中有63条线段:633184=+⨯,则第6个图中有线段:63164127+⨯=(条),故选:C.10.如图所示,由一些点组成形如三角形的图形,每条“边”(包括两个顶点)有(1)n n>个点,每个图形总共的点数是S,当8n=时,S的值是()A .18B .21C .24D .27【解答】解:根据题意分析可得: 2n =时,3S =, 3n =时,6S =, 4n =时,9S =, 5n =时,12S =,...此后,n 每增加1,S 就增加3个. 故当8n =时,(81)321S =−⨯=. 故选:B .11.我国宋朝时期的数学家杨辉,曾将大小完全相同的圆弹珠逐层堆积,形成“三角垛”,图1有1颗弹珠;图2有3颗弹珠;图3有6颗弹珠,往下依次是第4个图,第5个图,⋯;若用n a 表示图n 的弹珠数,其中1n =,2,3,⋯,则12320231111(a a a a +++⋯+= )A .40442023B .40422023C .20211011D .20231012【解答】解:当1n =时,11212a ⨯==, 当2n =时,22(12)231222a +⨯=+==, 当3n =时,33(13)3412322a +⨯=++==, 当4n =时,44(14)45123422a +⨯=+++==, ⋯当2023n =时:20232023(12023)202320241234202322a +⨯=+++++==; 12320231111a a a a +++⋅⋅⋅+222221223344520232024=+++++⨯⨯⨯⨯⨯111112()1223344520232024=+++++⨯⨯⨯⨯⨯1111111112(1)223344520232024=−+−+−+−++− 12(1)2024=− 20231012=; 故选:D .12.关于x 的方程(2)(3)x x m −−=有两个不相等的实数根1x ,212()x x x <,则下列结论一定正确的是( ) A .14m >−B .12522x x += C .当0m >时,1223x x <<< D .当0m >时,1223x x <<<【解答】解:由(2)(3)x x m −−=得2560x x m −+−=, 1x ∴,2x 为2560x x m −+−=的两个不相等的实数根, ∴△2(5)4(6)0m =−−−>,解得14m >−,选项A 正确;抛物线256y x x m =−+−的对称轴为直线5522x −=−=, ∴12522x x +=,选项B 正确; 当0m >时,抛物线(2)(3)y x x =−−与直线y m =交点在x 轴上方, 抛物线开口向上,1212x x ∴<<<,选项D 正确.故选:ABD .13.已知2x =−,代数式244x x ++的值为 3 . 【解答】解:原式2(2)x =+.当2x =−时,原式222)3=−+=, 故答案为3.14.若12x =,则代数式3231x x x +++的值为 3 . 【解答】解:322231(1)1x x x x x x +++=+++,当x =原式2211213=++==+=. 故答案为:3.15.已知实数a ,b 满足2222(21)(21)80a b a b +++−=,试求222a b +的值.解:设222a b m +=.原方程可化为(1)(1)80m m +−=,即281m =,解得9m =±.2220a b +,2229a b ∴+=.上面的这种方法称为“换元法”,换元法是数学学习中最常用的一种思想方法,在结构较复杂的数和式的运算中,若把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂问题简单化.请根据以上阅读材料,解决问题.已知实数x ,y 满足2222(221)()3x y x y +−+=,则22332x y +−的值为52. 【解答】解:设22x y m +=,原方程可化为(21)3m m −=,即2230m m −−=,解得11m =−,232m =, 220x y +, ∴2232x y +=, 22332x y ∴+−3322=⨯− 52=, 故答案为:52.16.若21m n +=,则2366m mn n ++的值为 3 .【解答】解:21m n +=,2366m mn n ∴++3(2)6m m n n =++316m n =⨯+36m n =+3(2)m n =+31=⨯3=,故答案为:3.17.当代数式235x x ++的值为7时,代数式23911x x +−的值为 5− .【解答】解:由题意得,2357x x ++=, 232x x ∴+=,23911x x ∴+−23(3)11x x =+−3211=⨯−611=−5=−,故答案为:5−.。
中考数学创新题集锦含答案.doc
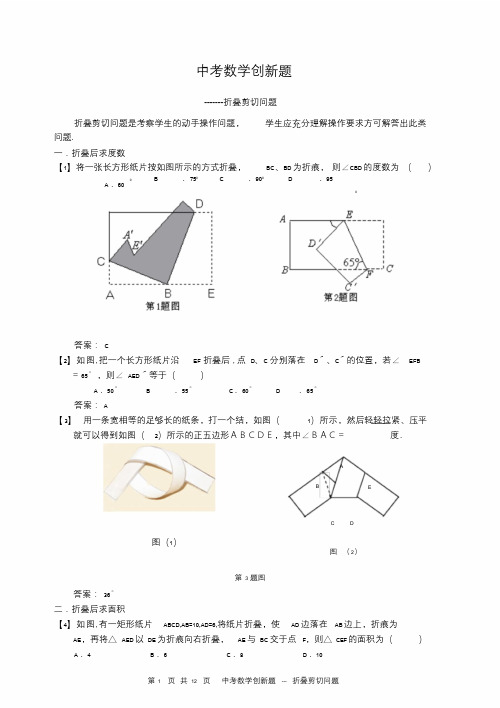
中考数学创新题-------折叠剪切问题折叠剪切问题是考察学生的动手操作问题,学生应充分理解操作要求方可解答出此类问题.一.折叠后求度数【1】将一张长方形纸片按如图所示的方式折叠,BC、BD为折痕,则∠CBD的度数为()0 B .750 C .900 D .95A.60答案:C【2】如图, 把一个长方形纸片沿EF 折叠后, 点D、C 分别落在D′、C′的位置,若∠EFB =65°,则∠AED′等于()A.50° B .55°C.60° D .65°答案:A【3】用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC=度.AB EC D图(1)图(2)第3 题图答案:36°二.折叠后求面积【4】如图, 有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD 边落在AB 边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF的面积为()答案:C【5】如图,正方形硬纸片ABCD的边长是4,点E、F 分别是AB、BC的中点,若沿左图中的虚线剪开,拼成如下右图的一座“小别墅”,则图中阴影部分的面积是A.2 B .4 C .8 D .10答案:B【6】如图a,ABCD是一矩形纸片,AB=6cm,AD=8cm,E 是AD上一点,且AE=6cm。
操作:(1)将AB向AE折过去,使AB与AE重合,得折痕AF,如图b;(2)将△AFB以BF 为折痕向右折过去,得图c。
则△GFC的面积是()A E D AB D B DAGB FC F C F C图a 图b 图c第6 题图2 B.2 cm 2 C.3 c m2 D.4 cm2A.1cm答案:B三.折叠后求长度【7】如图,已知边长为 5 的等边三角形ABC纸片,点 E 在AC边上,点 F 在AB边上,沿着EF折叠,使点 A 落在BC边上的点D的位置,且ED BC ,则CE的长是()(A)10 3 15 (B)10 5 3A(C)5 3 5 (D)20 10 3EFB CD答案:D 第7 题图四.折叠后得图形【8】将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是()第8 题图A.矩形 B .三角形 C .梯形 D .菱形答案:D【9】在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形又能拼成三角形和梯形的是()A. B. C. D.第9 题图答案:D【10】小强拿了张正方形的纸如图(1),沿虚线对折一次如图(2),再对折一次得图(3),然后用剪刀沿图(3)中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是( )第10 题图答案:D【11】如图,把矩形ABCD对折,折痕为MN(图甲),再把 B 点叠在折痕MN上的B'处。
初三数学中考创新思维训练三

一、细心填一填(本大题共有12小题,15空,每空2分,共30分.请把结果直接填在题中的横线上.只要你理解概念,仔细运算,积极思考,相信你一定会填对的!)1.3的相反数是_________,-2的绝对值是___________. 2.4的算术平方根是__________,-8的立方根是___________.3.据中新社报道:2010年我国粮食产量将达到540 000 000 000千克,这个粮食产量用科学记数法可表示为______________________千克.4.分解因式:x 2-4=_________________. 5.函数y =12x +中,自变量x 的取值范围是___________________; 函数y中,自变量x 的取值范围是___________________.6.如图,已知a ∥b ,∠1=40?,则∠2=_________?.7.一n 边形的内角和等于1080?,那么这个正n 边形的边数n =_________.8.为发展农业经济,致富奔小康,养鸡专业户王大伯2004年养了2000只鸡. 上市前,他随机抽取了10只鸡,称得重量统计如下:根据统计知识,估计王大伯这批鸡的总重量约为_____________千克.9.如图,在⊙O 中,弦AB =1.8cm ,圆周角∠ACB =30?,则⊙O 的直径 为__________cm.10.有一直角梯形零件ABCD ,AD ∥BC ,斜腰DC 的长为10cm , ∠D =120?,则该零件另一腰AB 的长是___________cm.11.两个完全相同的长方体的长、宽、高分别为5cm 、4cm 、3cm ,把它们叠放在一起组成一个新的长方体,在这些长方体中,表 面积最大是__________cm 2.12.一串有黑有白,其排列有一定规律的珠子,被盒子遮住了一部分 (如图),则这串珠子被盒子遮住的部分有_________粒. 二、精心选一选(本大题共8小题,每题3分,共24分. 在每题所给出的四个选项中,只有一项是符合题意的.把所选项前的字母代号填在题后的括号内. 相信你一定会选对!)13.如图,a 、b 、c 在数轴上对应的点分别为A 、B 、C ,则下列结论正确的是 ( ) A.ab <0 B. a -b >0 C. abc <0 D. c (a -b )<014 )A C D 15.下列各式中,与分式x y x--的值相等的是( ) A .x x y + B .x x y -- C .x x y -+ D .x x y- 16.已知一次函数y =kx +b的图像如图所示,则当x <0时,y 的取值范围是( )A. y >0B. y <0(第6题)ba c21A BCD(第10题)B A C(第13题)(第9题)C. -2<y <0D. y <-217.下面的平面图形中,是正方体的平面展开图的是( )1819)A B .为了了解全国中学生的睡眠状况,采用普查方式 C .为了了解人们保护水资源的意识,采用抽样调查的方式D .对栽人航天器“神州五号”零部件的检查,采用抽样调查的方式20.中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏. 游戏规则如下:在20个商标牌中,有5个商标牌的背面注明一定的奖金额,其余商标牌的背面是一张哭脸,若翻到哭脸就不得奖. 参与这个游戏的观众有三次翻牌的机会(翻过的牌不能再翻). 某观众前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是( )A .14 B .15 C .16D .320三、认真答一答(本大题共7小题,满分58分. 只要你认真思考, 仔细运算,一定会解答正确的!) 21.(本题共有3小题,每小题5分,共15分)(1)计算:(-2)3+12(2004)0tan60?.(2)解不等式: 12(x -2)<3-x .(3)解方程组:{4,2 5.x y x y -=+=22.(本题满分6分)在如图的12×24的方格形纸中(每个小方格的边长都是1个单位)有一ΔABC . 现先把ΔABC 分别向右、向上平移8个单位和3个单位得到ΔA 1B 1C 1;再以点O 为旋转中心把ΔA 1B 1C 1按顺时针方向旋转90o 得到ΔA 2B 2C 2. 请在所给的方格形纸中作出ΔA 1B 1C 1和 ΔA 2B 2C 2.23.(本题满分8分)如图,给出四个等式:①AE =AD ;②AB =AC 个作为结论.(1(2)请你至少写出三个这样的正确命题. 24.(本题满分6分)某产品每件成本10间的关系如下表:若日销量y (件)是销售价x (元)的一次函数.(1)求出日销量y (件)与销售价x (元)的函数关系式;(2)要使每日的销售利润最大,每件产品的销售价应定位多少元?此时每日的销售利润是多少? 25.(本题满分6分)如图,有两个可以自由转动的均匀转盘A 、B ,转盘A 被均匀地分成4等分,每份分别标上1,2,3,4四个数字;转盘B 被均匀地分成6等份,每份分别标上1,2,3,4,5,6六个数字. 有人为甲、乙两人设计了一个游戏,其规则如下:A.B. C. D.(1)同时自由转动转盘A、B;(2)转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数字作成积. 如果得到的积是偶数,那么甲胜;如果得到的积是奇数,则乙胜(如果转盘A指针指向3,转盘B指针指向5,3×5=15,按规则乙胜).你认为这样的规则是否公平?请说明理由;如果不公平,请你设计一个公平的规则,并说明理由.(2)①填写下表:②根据所填表中数据呈现的规律,猜想出用x表示y的二次函数关系式:___________;(3)当水面宽度为36m时,一艘吃水深度(船底部到水面的距离)为1.8m的货船能否在这个河段安全通过?为什么?27.(本题满分9分)某生活小区的居民筹集资金1600元,计划在一块上、下底分别为.(1)他们在ΔAMD和ΔBMC地带上种植太阳花,单价为8元/cm2160元,请计算种满ΔBMC地带所需的费用;(2)若其余地带要种的有玫瑰和茉莉花两种花木可供选择,刚好用完所筹集资金?(3)若梯形ABCD为等腰梯形,面积不变(如图),使得ΔAPB≌ΔDPC,且SΔAPD=SΔBPC,,并说出你的理由.四、动脑想一想(本大题共有2小题,共18分. )28.(本题满分8分)如图,在平面直角坐标系中,直线l的解析式为y,关于x2x2-2(m+2)x+2m+5=0(m>0)有两个相等的实数根.(1)试求出m的值,并求出经过点A(0,-m)和点D(m,0)的直线解析式;(2)在线段AD上顺次取两B、C,使AB=CD-1,试判断ΔOBC的形状;(3)设直线l与直线AD交于点P,图中是否存在与ΔOAB相似的三角形?如果存在,请直接写出来;如果不存在,请说明理由.29.(本题满分10分)如图,正方形ABCD的边长为12,划分成12×12个小正方形. 将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)C图乙×(n -1)的正方形. 如此摆放下去,最后直到纸片盖住 正方形ABCD 的右下角为止. 请你认真观察思考后回答下 列问题:(1)由于正方形纸片边长n 的取值不同,完成摆放时所使用正方形纸 片的张数也不同,请填写下表:(2)设正方形ABCD 被纸片盖住的面积(重合部分只计一次)为S 1,未被盖住的面积为S 2.①当n =2时,求S 1∶S 2的值;②是否存在使得S 1=S 2的n 值?若存在,请求出这样的n 值;若不存在,请说明理由.参考答案一、细心填一填(本大题共有12小题,15空,每空2分,共30分.请把结果直接填在题中的横线上.只要你理解概念,仔细运算,积极思考,相信你一定会填对的!)1.-3,2 2. 2,-2 3. 5.4×10114. (x +2)(x -2)5. x ≠-2, x ≥36. 1407. 8 二、精心选一选(本大题共8小题,每题3分,共24分. 在每题所给出的四个选项中,只有一项是符合题意的.把所选项前的字母代号填在题后的括号内. 相信你一定会选对!)13. C 14. B 15. D 16. D 17. C 18. A 19. C 20. C三、认真答一答(本大题共7小题,满分58分. 只要你认真思考, 仔细运算, 一定会解答正确的!)21. (1)-9;(2)x <83;(3){3,1.x y ==- 22.ΔA 1B 1C 1和ΔA 2B 2C 2如图所示.23.(1)如果AE=AD ,AB=AC ,那么∠B =∠C . 证明:在ΔABE 和ΔACD 中,∵AE=AD ,∠A =∠A ,AB=AC ,∴ΔABE ≌ΔACD(2)①如果AE=AD ,AB=AC ,那么OB=OC . ②如果AE=AD ,∠B =∠C ,那么AB=AC . ③如果OB=OC ,∠B =∠C ,那么AE=AD . 24.(1)y =-x +40;(2)当销售价定为25元/件时日销售利润最大,为225元.25.这个游戏不公平.把游戏中由A 、B 两个转盘中所指的两个数字的“积”改成“和”,游戏就公平了. 因为在A 盘和B 盘中指针所指的两个数字作和共有24种情况,而A 盘中每个数字与B 盘中的数字作和得到偶数和奇数的结果都是3,这样这24个和中,偶数和奇数的种数都是12,所以甲和乙获胜的可能性是一样的,这对他们就公平了.26.(1)如图所示; (2)①;②y =200x 2;(3)当水面宽度为36m ,即x =18m 时,y =1.62m<1.8m , 所以这艘货船不能安全通过该河段.27.(1)∵梯形ABCD 中,AD ∥BC ,∴∠MAD =∠MCB ,∠MDA =∠MBC ,∴ΔMAD ∽ΔMCB ,∴S ΔMAD ∶S ΔMBC =1∶4. ∵种植ΔMAD 地带花费160元,∴S ΔMAD =160÷8=20(m 2),∴S ΔMBC =80(m 2), ∴种植ΔMBC 地带花费640元.(2)设ΔMAD 的高为h 1,ΔMBC 的高为h 2,梯形ABCD 的高为h ,则S ΔMAD =12×10 h 1=20,∴h 1=4;S ΔMBC =12×10 h 2=80,∴h 2=8,∴h =h 1+h 2=12,∴S 梯形ABCD =12×(AD +BC ) h =180,∴S ΔMAB + S ΔMCD =180-(20+80)=80(m 2).∵160+640+80×12=1760(元),160+640+80×10=1600, ∴应种植茉莉花刚好用完所筹集的资金.(3)点P 在AD 、BC 的中垂线上. 此时,PA=PD ,PB=PC . ∵AB=DC ,∴ΔAPB ≌ΔDPC .设ΔAPD 的高为x ,则ΔBPC 的高为(12-x ), ∴S ΔAPD =12×10 x =5x , S ΔBPC =12×20(12-x )=10(12-x ),由S ΔAPD = S ΔBPC ,即5x =10(12-x ),可得x =8.∴当点P 在AD 、BC 的中垂线上,且与AD 的距离为8cm 时,S ΔAPD = S ΔBPC . 28.(1)由题意得Δ=[-2(m +2)]2-4×2×(2m +5)=0,∴m=.∵m >0,∴m.∴点A (0、D0). 设经过A 、D 两点的直线解析式为y =kx +b ,则0,b b ==+⎧⎪⎨⎪⎩解得1,k b ==⎧⎨⎩∴y =x. (2)作OE ⊥AD 于E ,由(1)得OA=OD,∴AD=∴OE=AE=ED=12AD =. ∵AB=CD-1,∴BE=EC =1,∴OB=OC .在Rt ΔOBE 中,tan ∠OBE=OE BE=ΔOBC 为等边三角形.(3)存在,ΔODC 、ΔOPC 、ΔOPA . 29.(1)依此为11,10,9,8,7(2)S 1=n 2+(12-n )[n 2-(n -1)2]= -n 2+25n -12. ①当n =2时,S 1=34,S 2=110,∴S 1∶S 2=17∶55; ②若S 1=S 2,则有-n 2+25n -12=12×122,即n 2-25n +84=0,解得n 1=4, n 2=21(舍去)。
初三数学思维训练题
初中数学思维训练一、平面图形的运动1、平移2、翻折3、旋转二、分类讨论三、新题型四、函数解析式的确定1、已知函数解析式的确定——待定系数法——关键是求点的坐标(几何法、解析法综合运用)2、未知函数解析式的确定——列方程(直接法、间接法、参数法)利用面积、勾股定理、平行线截得比例线段、相似性(全等)等方法找到等量关系——求函数定义域(解析式法、极限法)五、探索问题千变万化,但少不了对图形的分析和研究,运用数学数形结合的思想,化动为静、化繁为简的转化思想,分类讨论的思想,用几何和代数的方法求出x的值。
PDABCMNE初三数学思维训练题(一)一、平移1. 如图,在Rt △ABC 中,AB =6cm ,BC =4cm ,点D 是斜边AB 上的中点,把△ADC 沿着AB 方向平移1cm 得△EFP ,EP 与FP 分别交边BC 于点H 和点G ,则GH = cm . 2. 如图,在△ACB 中,∠CAB=90°,AC=AB =3,将△ABC 沿直线BC 平移,顶点A 、C 、B 平移后分别记为A 1、C 1、B 1,若△ACB 与△A 1C 1B 1重合部分的面积2,则CB 1= .3. 如图,把Rt △ABC 放在直角坐标系内,其中∠CAB =90°,BC =5,点A 、B 的坐标分别为(1,0)、(4,0),将△ABC 沿x 轴向右平移,当点C 落在直线26y x =-上时,线段BC 扫过的面积为 cm 2 .二、翻折4. 如图所示,将边长为2的正方形纸片折叠,折痕为EF ,顶点A 恰好落在CD 边上的中点P 处,B 点落在点Q 处,PQ 与CF 交于点G . 设C 1为△PCG 的周长,C 2为△PDE 的周长,则C 1 :C 2 = .5. 如图,Rt △ABC 中,∠C=90°,AC=3,3cot 4A =,点D 、E 分别是边BC 、AC 上的点,且∠EDC=∠A ,将△ABC 沿DE 对折,若点C 恰好落在边AB 上,则DE 的长为 .6. 如图,在ABC ∆中,MN ∥AC ,直线MN 将ABC ∆分割成面积相等的两部分.将BMN ∆沿直线MN 翻折,点B 恰好落在点E 处,联结AE ,若AE ∥CN ,则:AE NC = .H GA BCP AC BEBC三、旋转7. 如图,在Rt △ABC 中,90ACB ∠=︒,点O 在AB 上,且6CA CO ==,1cos 3CAB ∠=,若将△ABC 绕点A 顺时针旋转得到Rt △AB’C’,且C’落在CO 的延长线上,联结'BB 交CO 的延长线于点F ,则BF = .8. 如图,在ABC ∆中,90C ∠=o ,10AB =,3tan 4B =,点M 是AB 边的中点,将ABC ∆绕着点M 旋转,使点C 与点A 重合,点A 与点D 重合,点B 与点E 重合,得到DEA ∆,且AE 交CB 于点P ,那么线段CP 的长是 .9. 如图,将△ABC 绕顶点C 旋转至△DEC 位置,使顶点D 恰好落在边AB 上,已知AC=3,BC=4,︒=∠90ACB ,则=∠BED cot _______________.四、分类讨论10. 已知等腰三角形的周长为20,一个内角的余弦值为23,那么这个等腰三角形的腰长等于 .11. 抛物线23y ax bx =++的顶点在坐标轴上,则a = .12. 在△ABC 中,5AB =,4AC =,3BC =,D 是边AB 上的一点,E 是边AC 上的一点(D 、E与端点不重合),如果△CDE 与△ABC 相似,那么CE =五、新题型13. 若等腰三角形的顶角为θ,则定义msad nθ=,其中m 、n 分别表示这个等腰三角形的底边长和腰长,请根据定义推算: ① 若已知锐角θ满足4tan 3θ=,则sad θ= ; ②36sad ︒= . 14. 下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第n 个图案中白色正方形的个数为___________.CABO F 'C 'B EDCBA…… 第n 个15. 现规定一种新的运算“*”:b a b a *=,如23239*==,则132*=( ) (A ) 18 (B ) 8 (C ) 16 (D ) 32初三数学思维训练题(二)一、函数型综合题1.已知抛物线23y ax bx =++与x 的交点为A (1,0)、B (3,0),与y 轴交于点C. (1)求出抛物线的解析式及顶点P 的坐标;(2)若点M 在抛物线的对称轴上,且∠AMP=∠ACB ,求点M 的坐标;(3)若点G 在线段OC 上,且OG=2CG ,抛物线的对称轴与x 轴相交于点E ,点F 为射线AG 上一点,且△ABF 与△AEG 相似,求出点F 的坐标;(4)设点Q 是抛物线上的一个动点,当点Q 在第四象限时,△ACQ 的面积为158,求点Q 的坐标.二、几何型综合题1、已知:点A 、B 都在半径为9的圆O 上,P 是射线OA 上一点,以PB 为半径的圆P 与圆O 相交的另一个交点为C ,直线OB 与圆P 相交的另一个交点为D ,2cos 3AOB ∠=. (1)求:公共弦BC 的长度;(2)如图,当点D 在线段OB 的延长线上时,设AP=x ,BD=y ,求y 关于x 的函数解析式,并写出它的定义域;(3)如果直线PD 与射线CB 相交于点E ,且△BDE 与△BPE 相似,求线段AP 的长.OAPB CD(第(2)小题图)H参考答案:初三数学思维训练题(一)(1)23; (2) 或; (3) 16; (4) 4:3; (5) 12548; (6) :1 ; (7) 14; (8)74; (9) 724; (10) 6 或; (11) 3或7 或-1; (12) 2或3625或258;(13)(14) )5n+3 ; (15) A. 初三数学思维训练题(二) 一、函数型综合题(1)243y x x =-+;2(2)1y x =--;顶点P (2,-1); (2)M 1(2,2)M 2(2,-2);(3)(-1,4)或34(,)55 ;(4)53(,)24-二、几何型综合题(1)BC =(2)y 关于x 的函数解析式为463y x =-,定义域为92x >.(3)线段AP 的长为9292.。
雅礼创新思维数学试卷初三
一、选择题(每题5分,共50分)1. 下列哪个数是奇数?A. 0B. 2C. 3D. 42. 已知函数f(x) = 2x - 1,则f(3)的值为:A. 5B. 6C. 7D. 83. 在直角三角形ABC中,∠A = 90°,AB = 3cm,BC = 4cm,则AC的长度为:A. 5cmB. 6cmC. 7cmD. 8cm4. 下列哪个图形是正方形?A. 正三角形B. 矩形C. 等腰三角形D. 等边三角形5. 已知等差数列{an}的首项为2,公差为3,则第10项an的值为:A. 29B. 32C. 35D. 386. 下列哪个数是无理数?A. √2B. 2√3C. √9D. √167. 下列哪个图形是中心对称图形?A. 等腰三角形B. 矩形C. 正方形D. 圆8. 已知一元二次方程x^2 - 5x + 6 = 0的解为x1和x2,则x1 + x2的值为:A. 5B. 6C. 7D. 89. 下列哪个图形是轴对称图形?A. 等腰三角形B. 矩形C. 正方形D. 圆10. 已知函数f(x) = x^2 - 2x + 1,则f(2)的值为:A. 1B. 3C. 5D. 7二、填空题(每题5分,共50分)1. 已知数列{an}的通项公式为an = 2n - 1,则第5项an的值为______。
2. 在直角三角形ABC中,∠A = 30°,∠B = 60°,AB = 2cm,则AC的长度为______cm。
3. 已知等差数列{an}的首项为3,公差为-2,则第10项an的值为______。
4. 下列哪个数是有理数?______(写出数字)5. 已知函数f(x) = 3x + 2,则f(-1)的值为______。
6. 在直角坐标系中,点P(2, -3)关于x轴的对称点坐标为______。
7. 已知一元二次方程x^2 - 4x + 3 = 0的解为x1和x2,则x1 x2的值为______。
中年级数学思维竞赛试卷【含答案】
中年级数学思维竞赛试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 若a、b为实数,且a≠b,则下列哪个选项一定成立?A. a²=b²B. a+b=0C. a-b≠0D. (a+b)²=02. 已知函数f(x)=x²-2x+1,则f(x)的最小值为?A. 0B. 1C. -1D. 23. 设集合A={1,2,3},B={2,3,4},则A∩B的结果是?A. {1,2,3}B. {2,3,4}C. {2,3}D. {1,4}4. 若|a|=3,|b|=4,则|a+b|的最大值为?A. 7B. 5C. 3D. 45. 二项式展开式(x+y)⁶中x⁴y²的系数为?A. 15B. 20C. 30D. 60二、判断题(每题1分,共5分)1. 若两个实数的和为0,则这两个实数互为相反数。
()2. 一元二次方程ax²+bx+c=0(a≠0)的解一定是实数。
()3. 任何实数的平方都是非负数。
()4. 若函数f(x)在区间[a,b]上单调递增,则f(a)≤f(x)≤f(b)。
()5. 若向量a与向量b垂直,则a·b=0。
()三、填空题(每题1分,共5分)1. 若log₂x=3,则x=______。
2. 若sinθ=1/2,且θ在第二象限,则cosθ=______。
3. 若等差数列{an}的前n项和为Sn=n²+2n,则a1=______。
4. 二项式展开式(x+y)⁴中x³y的系数为______。
5. 若矩阵A=[[1,2],[3,4]],则A的行列式det(A)=______。
四、简答题(每题2分,共10分)1. 简述一元二次方程的求根公式。
2. 解释什么是等差数列?给出等差数列的通项公式。
3. 简述三角函数的定义及其在单位圆上的表示。
4. 解释什么是矩阵的逆矩阵?如何求一个矩阵的逆矩阵?5. 简述函数的极值和最值的定义及其关系。
初中数学新思维练习题
初中数学新思维练习题1. 有理数的运算- 计算下列有理数的和:\( \frac{1}{2} + \left(-\frac{3}{4}\right) + \frac{5}{8} \)。
- 求出 \( 3x - 5 \) 与 \( 2x + 4 \) 的差,并简化结果。
2. 代数式求值- 已知 \( a = 2 \) 和 \( b = -3 \),计算 \( a^2 - b^2 \) 的值。
- 若 \( x = 5 \),求 \( 3x^2 - 2x + 1 \) 的值。
3. 一元一次方程- 解方程 \( 2x + 3 = 7 \)。
- 找出 \( x \) 的值,使得 \( 5x - 6 = 9 \)。
4. 二元一次方程组- 解下列方程组:\[\begin{cases}x + y = 10 \\2x - y = 4\end{cases}\]- 找出 \( x \) 和 \( y \) 的值,使得:\[\begin{cases}3x + 2y = 8 \\x - y = 1\end{cases}\]5. 几何图形的性质- 已知一个等腰三角形的底边长为 6 厘米,两腰长为 5 厘米,计算其周长。
- 若一个矩形的长为 8 厘米,宽为 4 厘米,求其面积和周长。
6. 函数与图像- 画出函数 \( y = 2x + 1 \) 在 \( x \) 轴上的图像,并标出\( x = 1 \) 和 \( x = -1 \) 时的点。
- 确定函数 \( y = x^2 - 4x + 3 \) 的顶点坐标。
7. 概率初步- 一个袋子里有 5 个红球和 3 个蓝球,随机抽取一个球,抽到红球的概率是多少?- 抛一枚公平硬币两次,两次都是正面朝上的概率是多少?8. 数据统计- 一组数据为:10, 12, 15, 18, 20,计算这组数据的平均数和中位数。
- 给定一组数据:8, 12, 15, 18, 22,计算其众数和方差。
