2017_2018学年高中数学第一章立体几何初步1.2直观图学案北师大
2016-2017学年高中数学 第一章 立体几何初步 1.2 直观图学案 北师大版必修2

直观图【课时目标】1.了解斜二测画法的概念.2.会用斜二测画法画出一些简单的平面图形和立体图形的直观图.用斜二测画法画水平放置的平面图形直观图的规则:(1)在已知图形中取互相垂直的x轴和y轴,两轴相交于点O.画直观图时,把它们画成对应的x′轴与y′轴,两轴交于点O′,且使∠x′O′y′=45°(或135°),它们确定的平面表示水平面.(2)已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x′轴或y′轴的线段.(3)已知图形中平行于x轴的线段,在直观图中保持原长度不变,平行于y轴的线段,长度为原来的一半.一、选择题1.下列结论:①角的水平放置的直观图一定是角;②相等的角在直观图中仍然相等;③相等的线段在直观图中仍然相等;④两条平行线段在直观图中对应的两条线段仍然平行.其中正确的有( )A.①② B.①④ C.③④ D.①③④2.具有如图所示直观图的平面图形ABCD是( )A.等腰梯形 B.直角梯形C.任意四边形 D.平行四边形3.如图,正方形O′A′B′C′的边长为1 cm,它是水平放置的一个平面图形的直观图,则原图的周长是( )A.8 cm B.6 cmC.2(1+3) cm D.2(1+2) cm4.下面每个选项的2个边长为1的正△ABC的直观图不是全等三角形的一组是( )5.如图甲所示为一个平面图形的直观图,则此平面图形可能是图乙中的( )6.一个水平放置的平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则该平面图形的面积等于( )A .12+22B .1+22C .1+ 2D .2+ 2二、填空题7.利用斜二测画法得到: ①三角形的直观图是三角形;②平行四边形的直观图是平行四边形; ③正方形的直观图是正方形; ④菱形的直观图是菱形.以上结论,正确的是______________.8.水平放置的△ABC 的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB 边上的中线的实际长度为____________.9.如图所示,为一个水平放置的正方形ABCO ,它在直角坐标系xOy 中,点B 的坐标为(2,2),则在用斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为________.三、解答题10.如图所示,梯形ABCD 中,AB∥CD,AB =4 cm ,CD =2 cm ,∠DAB=30°,AD =3 cm ,试画出它的直观图.11.已知正三角形ABC的边长为a,求△ABC的直观图△A′B′C′的面积.能力提升12.在水平放置的平面α内有一个边长为1的正方形A′B′C′D′,如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.直观图与原图形的关系1.斜二测画法是联系直观图和原图形的桥梁,可根据它们之间的可逆关系寻找它们的联系:(1)在求直观图的面积时,可根据斜二测画法,画出直观图,从而确定其高和底边等;而求原图形的面积可把直观图还原为原图形;(2)此类题易混淆原图形与直观图中的垂直关系而出错,在原图形中互相垂直的直线在直观图中不一定垂直,反之也是.所以在求面积时应按照斜二测画法的规则把原图形与直观图都画出来,找出改变量与不变量.用斜二测画法画出的水平放置的平面图形的直观图的面积是原图形面积的24倍.2.在用斜二测画法画直观图时,平行线段仍然平行,所画平行线段之比仍然等于它的真实长度之比,但所画夹角大小不一定是其真实夹角大小.§2直观图答案作业设计1.B [由斜二测画法的规则判断.] 2.B 3.A [根据直观图的画法,原几何图形如图所示,四边形OABC 为平行四边形, OB =22,OA =1,AB =3,从而原图周长为8 cm .]4.C [可分别画出各组图形的直观图,观察可得结论.] 5.C6.D [如图1所示,等腰梯形A′B′C′D′为水平放置的原平面图形的直观图,作D′E′∥A′B′交B′C′于E′,由斜二测直观图画法规则,直观图是等腰梯形A′B′C′D′的原平面图形为如图2所示的直角梯形ABCD ,且AB =2,BC =1+2,AD =1,所以S ABCD =2+2.]图1 图27.①②解析 斜二测画法得到的图形与原图形中的线线相交、相对线线平行关系不会改变,因此三角形的直观图是三角形,平行四边形的直观图是平行四边形.8.2.5解析 由直观图知,原平面图形为直角三角形,且AC =A′C′=3,BC =2B′C′=4,计算得AB =5,所求中线长为2.5.9.22解析画出直观图,则B′到x′轴的距离为 22·12OA =24OA =22. 10.解 (1)如图a 所示,在梯形ABCD 中,以边AB 所在的直线为x 轴,点A 为原点,建立平面直角坐标系xOy .如图b 所示,画出对应的x′轴,y′轴,使∠x′O′y′=45°.(2)在图a 中,过D 点作DE⊥x 轴,垂足为E .在x′轴上取A′B′=AB =4 cm ,A′E′=AE =323≈2.598 cm ;过点E′作E′D′∥y′轴,使E′D′=12ED ,再过点D′作D′C′∥x′轴,且使D′C′=DC =2 cm .(3)连接A′D′、B′C′,并擦去x′轴与y′轴及其他一些辅助线,如图c 所示,则四边形A′B′C′D′就是所求作的直观图.11.解 先画出正三角形ABC ,然后再画出它的水平放置的直观图, 如图所示.由斜二测画法规则知B′C′=a ,O′A′=34a .过A′引A′M⊥x′轴,垂足为M ,则A′M=O′A′·sin 45°=34a×22=68a .∴S △A′B′C′=12B′C′·A′M=12a×68a =616a 2. 12.解 四边形ABCD 的真实图形如图所示,∵A′C′在水平位置,A′B′C′D′为正方形, ∴∠D′A′C′=∠A′C′B′=45°, ∴在原四边形ABCD 中,DA⊥AC,AC⊥BC,∵DA=2D′A′=2, AC =A′C′=2,∴S 四边形ABCD =AC·AD=22.。
2016-2017学年高中数学 第一章 立体几何初步 1.2 直观图学案2(无答案)北师大版必修2

§直观图【学习目标】1 理解斜二测画法步骤,学会用斜二测画法会画水平放置的平面图形和立体图形图形的直观图,为学好立体几何打好基础.2提高识图能力立体图形图形,培养空间想象能力3 学会欣赏图形美,培养学习数学的兴趣【重点难点】重点用斜二测画法空间几何体的直观图; 难点是将直观图还原为实物图【知识链接】1 在初中,如何用尺规画正六边形和正五边形?2在初中,研究平面图形特征时,总是先画出直观示意图,我们现在研究立体图形时,也是先画出立体图形的直观示意图.那么如何在纸张上用平面图形去直观地表示立体图形图形? 本节来学习空间几何体的的画法--------------斜二测画法【学法指导】观察尝试法【学习过程】一水平放置的平面图形直观图的画法;1.自学例1,并回答下列问题⑴共需哪几步?(老师按同学们所想在黑板上按步骤画)⑵什么叫斜二测画法? 测斜二测画法规则是什么?请填空:①②③⑶谈谈你对斜二测画法的字面意思的理解,“斜”“二测”分别指的是什么?2.变式练习(1).试用斜二测画法画水平放置圆的直观图,请按斜二测画法的步骤画出,不写步骤(2)画出水平放置正五边形的直观图二. 空间几何体的直观图的画法1 自学例1,并回答下列问题共需哪几步? , , 分别是① ,②③2变式练习(1)试画出底面半径为1.5厘米高为3厘米的圆柱的直观图2 (2) 试画出底面为正方形,高与底面相等的四棱锥的直观图(不写画法,保留作图过程)【回顾小结】1 知识要点2 方法与步骤【课堂检测】1利用斜二测画法画边长为2厘米的正方形的直观图,正确的是 ( )2 如图,直观图表示的平面图形是 ( )(A)任意三角形;(B)锐角三角形;(C)直角三角形; (D)钝角三角形3 由斜二测画法所得的直观图,下列说法不正确的是( )①等腰三角形的直观图仍为等腰三角形 ②梯形的直观图不是梯形 ③正三角形的直观图一定为等腰三角形 ④平行四边形仍为平行四边形 4 把如图所示的水平放置的直观图梯形ABCD 还原为真正的平面图形【作业布置】课本P12习题1-2 A 组1,2,3【自我反思】xA B C D。
2017-2018学年高中数学北师大版2学案:第一章立体几何初步1.5平行关系含答案
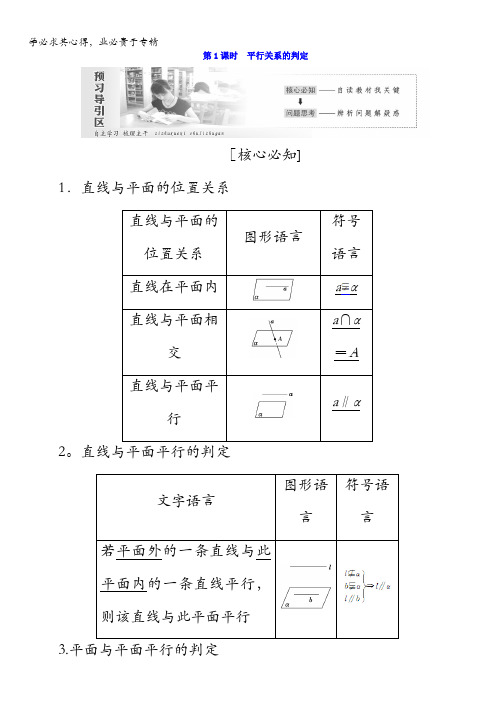
第1课时平行关系的判定[核心必知] 1.直线与平面的位置关系直线与平面的位置关系图形语言符号语言直线在平面内aα直线与平面相交a∩α=A直线与平面平行a∥α2。
直线与平面平行的判定文字语言图形语言符号语言若平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行3.文字语言图形语言符号语言如果一个平面内有两条相交直线都平行于另一个平面,则两平面平行[问题思考]1.若直线a平行于平面α内的无数条直线,则直线a平行于平面α吗?提示:不一定,因为直线a在平面α内时,与a平行的直线也有无数条.2.对于平面与平面平行的判定定理中,若把“相交”去掉,这两个平面是否一定平行,为什么?提示:不一定.如图中,平面α内的两条直线a,b均平行于β,而α与β却相交.讲一讲1。
如图,在四棱锥P.ABCD中,底面ABCD是矩形,E,F分别是PB,PC的中点.证明:EF∥平面PAD。
[尝试解答]证明:在△PBC中,E,F分别是PB,PC的中点,∴EF∥BC.又BC∥AD,∴EF∥AD。
又∵AD平面PAD,EF平面PAD,∴EF∥平面PAD。
1.判断或证明线面平行的方法(1)定义法:证明直线与平面无公共点(不易操作);(2)判定定理法:aα,bα,a∥b⇒a∥α;(3)排除法:证明直线与平面不相交,直线也不在平面内.2.证明线线平行的方法(1)利用三角形、梯形中位线的性质;(2)利用平行四边形的性质;(3)利用平行线分线段成比例定理.练一练1.如图,P是平行四边形ABCD所在平面外一点,Q是PA的中点,求证:PC∥平面BDQ.证明:连接AC交BD于O,连接QO。
∵四边形ABCD是平行四边形,∴O为AC的中点.又Q为PA的中点,∴QO∥PC。
显然QO平面BDQ,PC平面BDQ,∴PC∥平面BDQ.讲一讲2。
如图所示,正方体ABCD.A1B1C1D1中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点.求证:平面AMN∥平面EFDB.[尝试解答] 证明:如图所示,连接MF。
高中数学 第一章 立体几何初步 1.2 直观图课件 北师大

[规律方法] (1)画水平放置的平面多边形的直观图的关键是确定多边形的顶 点位置.顶点位置可以分为两类:一类是在轴上或在与轴平行的线段上,这类顶 点比较容易确定;另一类是不在轴上且不在与轴平行的线段上,这类顶点一般通 过过此点作与轴平行的线段,将此点转到与轴平行的线段上来确定.
(2)要画好对应平面图形的直观图,首先应在原图形中确定直角坐标系,然后 在此基础上画出水平放置的平面坐标系.
[自主练习] 1.关于直观图画法的说法中,不正确的是( ) A.原图形中平行于x轴的线段,其对应线段仍平行于x′轴,其长度不变 B.原图形中平行于y轴的线段,其对应线段仍平行于y′轴,其长度不变 C.画与坐标系xOy对应的坐标系x′O′y′时,∠x′O′y′可画成135° D.作直观图时,由于选轴不同,所画直观图可能不同 解析: 根据斜二测画法的规则可知B不正确. 答案: B
2.利用斜二测画法画边长为 3 cm 的正方形的直观图,正确的是图中的( )
解析: 正方形的直观图应为平行四边形,且一组对边为 3 cm,另一组对边 为32 cm.
答案: C
3.如图为△ABO 水平放置的直观图△A′B′O′,由图判断△ABO 中,AB, BO,BD,OD 由小到大的顺序是_________________________________
[提示] 不相等,当角度不一样时,如图.
1.体会平面图形和空间几何体的直观图的含义. 2.会用斜二测画法画水平放置的平面图形的直观图. 3.会用斜二测画法画空间几何体的直观图.
用斜二测画法画水平放置的平面图形的直观图的步骤
[强化拓展] 水平放置的平面图形的直观图与原图形相比,平行关系是不变的,角的大小, 线线垂直关系等都有可能变化.
合作探究·课堂互动
高中数学第一章立体几何初步2直观图学案北师大版必修2201

§2 直观图学习目标 1.掌握斜二测画法的作图规则.2.会用斜二测画法画出简单几何体的直观图.知识点 斜二测画法思考1 边长2 cm 的正方形ABCD 水平放置的直观图如下,在直观图中,A ′B ′与C ′D ′有何关系?A ′D ′与B ′C ′呢?在原图与直观图中,AB 与A ′B ′相等吗?AD 与A ′D ′呢?答案 A ′B ′∥C ′D ′,A ′D ′∥B ′C ′,A ′B ′=AB ,A ′D ′=12AD .思考2 正方体ABCD -A 1B 1C 1D 1的直观图如图所示,在此图形中各个面都画成正方形了吗?答案 没有都画成正方形.梳理 (1)水平放置的平面图形直观图的画法 斜二测画法规则:①在已知图形中建立平面直角坐标系xOy ,画直观图时,它们分别对应x ′轴和y ′轴,两轴相交于点O ′,使∠x ′O ′y ′=45°,它们确定的平面表示水平平面.②已知图形中平行于x 轴或y 轴的线段,在直观图中分别画成平行于x ′轴或y ′轴的线段. ③已知图形中平行于x 轴的线段,在直观图中保持原长度不变;平行于y 轴的线段,长度为原来的12.(2)立体图形直观图的画法1.用斜二测画法画水平放置的∠A 时,若∠A 的两边分别平行于x 轴和y 轴,且∠A =90°,则在直观图中,∠A =45°.( × )2.用斜二测画法画平面图形的直观图时,平行的线段在直观图中仍平行,且长度不变.( × )3.在斜二测画法中平行于y 轴的线段在直观图中长度保持不变.( × )类型一 水平放置的平面图形的直观图 例1 画出如图水平放置的直角梯形的直观图.考点 平面图形的直观图 题点 平面图形的直观图 解 画法:(1)在已知的直角梯形OBCD 中,以底边OB 所在直线为x 轴,垂直于OB 的腰OD 所在直线为y 轴建立平面直角坐标系.画出相应的x ′轴和y ′轴,使∠x ′O ′y ′=45°,如图(1)(2)所示;(2)在x ′轴上截取O ′B ′=OB ,在y ′轴上截取O ′D ′=12OD ,过点D ′作x ′轴的平行线l ,在l 上沿x ′轴正方向取点C ′使得D ′C ′=DC .连接B ′C ′,如图(2);(3)去掉辅助线,所得四边形O ′B ′C ′D ′就是直角梯形OBCD 的直观图,如图(3).引申探究若得本例中的直角梯形改为等腰梯形,画出其直观图. 解 画法:(1)如图所示,取AB 所在直线为x 轴,AB 中点O 为原点,建立平面直角坐标系,画出对应的x ′轴和y ′轴,使∠x ′O ′y ′=45°;(2)以O ′为中点在x ′轴上取A ′B ′=AB ,在y ′轴上取O ′E ′=12OE ,以E ′为中点画出C ′D ′∥x ′轴,并使C ′D ′=CD ;(3)连接B ′C ′,D ′A ′,所得的四边形A ′B ′C ′D ′就是水平放置的等腰梯形ABCD 的直观图.反思与感悟 在画水平放置的平面图形的直观图时,选取适当的平面直角坐标系是关键之一,一般要使平面多边形尽可能多的顶点落在坐标轴上,以便于画点.原图中不平行于坐标轴的线段可以通过作平行于坐标轴的线段来作出其对应线段.关键之二是确定多边形顶点的位置,借助于平面直角坐标系确定顶点后,只需把这些顶点顺次连接即可. 跟踪训练1 已知正五边形ABCDE ,如图,试画出其直观图.考点 平面图形的直观图 题点 平面图形的直观图 解 画法:(1)在图(1)中作AG ⊥x 轴于点G ,作DH ⊥x 轴于点H .(2)在图(2)中画相应的x ′轴与y ′轴,两轴相交于点O ′,使∠x ′O ′y ′=45°. (3)在图(2)中的x ′轴上取O ′B ′=OB ,O ′G ′=OG ,O ′C ′=OC ,O ′H ′=OH ,y ′轴上取O ′E ′=12OE ,分别过G ′和H ′作y ′轴的平行线,并在相应的平行线上取G ′A ′=12GA ,H ′D ′=12HD .(4)连接A ′B ′,A ′E ′,E ′D ′,D ′C ′,并擦去辅助线G ′A ′,H ′D ′,x ′轴与y ′轴,便得到水平放置的正五边形ABCDE 的直观图A ′B ′C ′D ′E ′(如图(3)).类型二 直观图的还原与计算例2 如图所示,梯形A 1B 1C 1D 1是一平面图形ABCD 的直观图.若A 1D 1∥O ′y ′,A 1B 1∥C 1D 1,A 1B 1=23C 1D 1=2,A 1D 1=O ′D 1=1.试画出原四边形的形状,并求出原图形的面积.考点 平面图形的直观图 题点 由直观图还原平面图形解 如图,建立平面直角坐标系xOy ,在x 轴上截取OD =O ′D 1=1,OC =O ′C 1=2. 在过点D 的y 轴的平行线上截取DA =2D 1A 1=2. 在过点A 的x 轴的平行线上截取AB =A 1B 1=2. 连接BC ,即得到了原图形.由作法可知,原四边形ABCD 是直角梯形,上、下底长度分别为AB =2,CD =3,直角腰的长度AD =2,所以面积为S =2+32×2=5.反思与感悟 (1)由直观图还原为平面图的关键是找与x ′轴,y ′轴平行的直线或线段,且平行于x ′轴的线段还原时长度不变,平行于y ′轴的线段还原时放大为直观图中相应线段长的2倍,由此确定图形的各个顶点,顺次连接即可.(2)若一个平面多边形的面积为S ,其直观图的面积为S ′,则有S ′=24S 或S =22S ′.利用这一公式可由原图形面积求其直观图面积或由直观图面积求原图形面积.跟踪训练 2 (1)如图所示,一个水平放置的三角形的斜二测直观图是等腰直角三角形A ′B ′O ′,若O ′B ′=1,那么原三角形ABO 的面积是( )A.12B.22 C. 2 D .2 2 考点 平面图形的直观图 题点 与直观图有关的计算 答案 C解析 直观图中等腰直角三角形直角边长为1,因此面积为12,又直观图与原平面图形面积比为2∶4,所以原图形的面积为2,故选C.(2)如图所示,矩形O ′A ′B ′C ′是水平放置的一个平面图形的直观图,其中O ′A ′=6 cm ,C ′D ′=2 cm ,则原图形是________.(填四边形的形状)考点 平面图形的直观图 题点 由直观图还原平面图形 答案 菱形解析 如图所示,在原图形OABC 中,应有OA =O ′A ′=6(cm),OD =2O ′D ′=2×22=42(cm),CD =C ′D ′=2(cm),∴OC =OD 2+CD 2=(42)2+22=6(cm),∴OA =OC ,又OA ∥BC ,OA =BC , 故四边形OABC 是菱形. 类型三 简单几何体的直观图例3 画出底面是正方形,侧棱均相等的四棱锥的直观图. 考点 简单几何体的直观图 题点 简单几何体的直观图 解 画法:(1)画轴.画x 轴,y 轴,z 轴,三轴相交于点O ,使∠xOy =45°(或135°),∠xOz =90°,如图①.(2)画底面,以O为中心在xOy平面内,画出正方形直观图ABCD.(3)画顶点.在Oz轴上截取OP使OP的长度是原四棱锥的高.(4)成图.顺次连接PA,PB,PC,PD,并擦去辅助线,将被遮住的部分改为虚线,得四棱锥的直观图如图②.反思与感悟简单几何体直观图的画法(1)画轴:通常以高所在直线为z轴建系.(2)画底面:根据平面图形直观图的画法确定底面.(3)确定顶点:利用与z轴平行或在z轴上的线段确定有关顶点.(4)连线成图.跟踪训练3 用斜二测画法画棱长为2 cm的正方体ABCD-A′B′C′D′的直观图.考点简单几何体的直观图题点简单几何体的直观图解画法:(1)画轴.如图①,画x轴,y轴,z轴,三轴相交于点O,使∠xOy=45°,∠xOz=90°.(2)画底面.以点O为中心,在x轴上取线段MN,使MN=2 cm;在y轴上取线段PQ,使PQ =1 cm.分别过点M和N作y轴的平行线,过点P和Q作x轴的平行线,设它们的交点分别为A,B,C,D,四边形ABCD就是正方体的底面ABCD.(3)画侧棱.过A,B,C,D各点分别作z轴的平行线,并在这些平行线上沿Oz轴方向分别截取2 cm长的线段AA′,BB′,CC′,DD′.(4)成图.顺次连接A′,B′,C′,D′,并加以整理(去掉辅助线,将被遮挡的部分改为虚线),得到正方体的直观图(如图②).1.利用斜二测画法画出边长为3 cm的正方形的直观图,图中正确的是( )考点平面图形的直观图题点平面图形的直观图答案 C解析正方形的直观图应是平行四边形,且相邻两边的边长之比为2∶1.2.下列关于直观图的说法不正确的是( )A.原图形中平行于y轴的线段,对应线段平行于直观图中y′轴,长度不变B.原图形中平行于x轴的线段,对应线段平行于直观图中x′轴,长度不变C.在画与直角坐标系xOy对应的x′O′y′时,∠x′O′y′可以画成45°D.在画直观图时,由于选轴的不同所画的直观图可能不同考点平面图形的直观图题点平面图形的直观图答案 A解析平行于y轴的线段,直观图中长度变为原来的一半,故选A.3.有一个长为5 cm,宽为4 cm的矩形,则其用斜二测画法得到的直观图的面积为________cm2. 考点平面图形的直观图题点与直观图有关的计算答案5 2解析该矩形直观图的面积为24×5×4=52(cm2).4.如图,水平放置的△ABC的斜二测直观图是图中的△A′B′C′,已知A′C′=6,B′C′=4,则AB边的实际长度是________.考点平面图形的直观图题点与直观图有关的计算答案10解析在原图中,AC=6,BC=4×2=8,∠AOB=90°,∴AB=62+82=10.5.画出一个正三棱台的直观图.(尺寸:上、下底面边长分别为1 cm,2 cm,高为2 cm) 考点简单几何体的直观图解画法:(1)作水平放置的下底面等边三角形的直观图△ABC,其中O为△ABC的重心,BC=2 cm,线段AO与x轴的夹角为45°,AO=2OD.(2)过O作z轴,使∠xOz=90°,在Oz轴上截取OO′=2 cm,作上底面等边三角形的直观图△A′B′C′,其中B′C′=1 cm,连接AA′,BB′,CC′,得正三棱台的直观图.1.画水平放置的平面图形的直观图,关键是确定直观图的顶点.确定点的位置,可采用直角坐标系.建立恰当的坐标系是迅速作出直观图的关键,常利用图形的对称性,并让顶点尽量多地落在坐标轴上或与坐标轴平行的直线上.2.用斜二测画法画图时要紧紧把握住:“一斜”、“二测”两点:(1)一斜:平面图形中互相垂直的Ox、Oy轴,在直观图中画成O′x′、O′y′轴,使∠x′O′y′=45°.(2)二测:在直观图中平行于x轴的长度不变,平行于y轴的长度取一半,记为“横不变,纵折半”.一、选择题1.关于斜二测画法所得直观图,以下说法正确的是( )A.等腰三角形的直观图仍是等腰三角形B.正方形的直观图为平行四边形C.梯形的直观图不是梯形D.正三角形的直观图一定为等腰三角形考点平面图形的直观图答案 B解析 由直观图的性质知,B 正确.2.若把一个高为10 cm 的圆柱的底面画在x ′O ′y ′平面上,则圆柱的高应画成( ) A .平行于z ′轴且长度为10 cm B .平行于z ′轴且长度为5 cm C .与z ′轴成45°且长度为10 cm D .与z ′轴成45°且长度为5 cm 考点 简单几何体的直观图 题点 柱、锥、台的直观图 答案 A解析 由直观图的性质知,与z 轴平行的线段长度不变,高与原长相等. 3.如图所示为一平面图形的直观图,则此平面图形可能是下图中的( )考点 平面图形的直观图 题点 由直观图还原平面图形 答案 C解析 在x 轴上或与x 轴平行的线段在新坐标系中的长度不变,在y 轴上或平行于y 轴的线段在新坐标系中的长度变为原来的12,并注意到∠xOy =90°,∠x ′O ′y ′=45°,因此由直观图还原成原图形为选项C.4.下面每个选项的2个边长为1的正△ABC 的直观图不是全等三角形的一组是( )题点平面图形的直观图答案 C解析可分别画出各组图形的直观图,观察可得结论.5.已知一个正方形的直观图是一个平行四边形,其中有一边长为4,则此正方形的面积为( )A.16 B.64C.16或64 D.无法确定考点平面图形的直观图题点与直观图有关的计算答案 C解析等于4的一边在原图形中可能等于4,也可能等于8,所以正方形的面积为16或64. 6.水平放置的△ABC,有一边在水平线上,它的斜二测直观图是正三角形A′B′C′,则△ABC 是( )A.锐角三角形B.直角三角形C.钝角三角形D.任意三角形考点平面图形的直观图题点由直观图还原平面图形答案 C解析如图所示,斜二测直观图还原为平面图形,故△ABC是钝角三角形.7.用斜二测画法画出的某平面图形的直观图如图所示,AB平行于y′轴,BC,AD平行于x′轴.已知四边形ABCD的面积为2 2 cm2,则原平面图形的面积为( )A.4 cm2B.4 2 cm2C.8 cm2D.8 2 cm2考点平面图形的直观图题点与直观图有关的计算答案 C解析依题意可知∠BAD=45°,则原平面图形为直角梯形,且上下底边的长分别与BC,AD 相等,高为梯形ABCD的高的22倍,所以原平面图形的面积为8 cm2.8.已知两个底面半径相等的圆锥,底面重合在一起(底面平行于水平面),其中一个圆锥顶点到底面的距离为2 cm,另一个圆锥顶点到底面的距离为3 cm,则其直观图中这两个顶点之间的距离为( )A.2 cm B.3 cm C.2.5 cm D.5 cm考点简单几何体的直观图题点柱、锥、台的直观图答案 D解析圆锥顶点到底面的距离即圆锥的高,故两顶点间距离为2+3=5(cm),在直观图中与z 轴平行的线段长度不变,仍为5 cm.故选D.二、填空题9.水平放置的△ABC的斜二测直观图如图所示,已知B′C′=4,A′C′=3,B′C′∥y′轴,则△ABC中AB边上的中线的长度为________.考点平面图形的直观图题点与直观图有关的计算答案73 2解析由斜二测画法规则知AC⊥BC,即△ABC为直角三角形,其中AC=3,BC=8,所以AB=73,AB边上的中线长度为732.10.在如图所示的直观图中,四边形O′A′B′C′为菱形且边长为2 cm,则在坐标系xOy 中原四边形OABC为______(填形状),面积为________ cm2.考点平面图形的直观图题点与直观图有关的计算答案矩形8解析由题意结合斜二测画法,可得四边形OABC为矩形,其中OA=2 cm,OC=4 cm,∴四边形OABC的面积为S=2×4=8(cm2).11.如图所示,四边形OABC 是上底为2,下底为6,底角为45°的等腰梯形,用斜二测画法画出这个梯形的直观图O ′A ′B ′C ′,则在直观图中,梯形的高为________.考点 平面图形的直观图 题点 与直观图有关的计算 答案22解析 作CD ,BE ⊥OA 于点D ,E ,则OD =EA =OA -BC2=2,又∠COD =45°, ∴OD =CD =2,∴在直观图中梯形的高为2×12×sin 45°=22.三、解答题12.如图所示,画出水平放置的四边形OBCD 的直观图.考点 平面图形的直观图 题点 平面图形的直观图 解 画法:(1)过点C 作CE ⊥x 轴,垂足为E ,如图(1)所示.画出对应的x ′轴,y ′轴,使∠x ′O ′y ′=45°,如图(2)所示;(2)如图(2)所示,在x ′轴正半轴上取点B ′,E ′,使得O ′B ′=OB ,O ′E ′=OE .在y ′正半轴上取一点D ′,使得O ′D ′=12OD .过E ′作E ′C ′∥y ′轴,使E ′C ′=12EC ;(3)连接B ′C ′,C ′D ′,并擦去x ′轴与y ′轴及其他一些辅助线,如图(3)所示,四边形O ′B ′C ′D ′就是所得直观图.13.一个机器部件,它的下面是一个圆柱,上面是一个圆锥,并且圆锥的底面与圆柱的上底面重合,圆柱的底面直径为3 cm ,高为3 cm ,圆锥的高为3 cm ,画出此机器部件的直观图. 考点 简单几何体的直观图 题点 简单几何体的直观图 解 画法:(1)如图①.画x 轴,y 轴,z 轴,三轴相交于点O ,使∠xOy =45°,∠xOz =90°. (2)画圆柱的两底面.在xOy 平面上画出底面圆O ,使直径为3 cm ,在z 轴上截取OO ′,使OO ′=3 cm ,过O ′作Ox 的平行线O ′x ′,Oy 的平行线O ′y ′,利用O ′x ′与O ′y ′画出底面圆O ′,使其直径为3 cm.(3)画圆锥的顶点.在z 轴上取一点P ,使PO ′等于圆锥的高3 cm.(4)成图.连接A ′A ,B ′B ,PA ′,PB ′,擦去辅助线,将被遮挡的部分改为虚线,得到此几何体(机器部件)的直观图,如图②.四、探究与拓展14.如图所示,一个水平放置的正方形ABCO ,在直角坐标系xOy 中,点B 的坐标为(2,2),则用斜二测画法画出正方形的直观图中,顶点B ′到x ′轴的距离为______.考点 平面图形的直观图 题点 与直观图有关的计算 答案22解析 画出直观图,则B ′到x ′轴的距离为22·12OA =24OA =22.15.在水平放置的平面α内有一个边长为1的正方形A′B′C′D′,如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.考点平面图形的直观图题点与直观图有关的计算解四边形ABCD的真实图形如图所示,∵A′C′在水平位置,A′B′C′D′为正方形,∴∠D′A′C′=∠A′C′B′=45°,∴在原四边形ABCD中,DA⊥AC,AC⊥BC,∵DA=2D′A′=2,AC=A′C′=2,∴S四边形ABCD=AC·AD=2 2.精美句子1、善思则能“从无字句处读书”。
2017-2018学年高中数学 第一章 立体几何初步 1.7 简单几何体的再认识学案 北师大版必修2

第1课时 柱、锥、台的侧面展开与面积[核心必知]1.圆柱、圆锥、圆台的侧面展开图及侧面积公式几何那么台体、锥体、柱体的侧面积公式有什么联系?提示:根据以上关系,在台体的侧面积公式中,令c ′=c ,可以得到柱体的侧面积公式,令c ′=0,可得到锥体的侧面积公式,其关系如下所示:S 柱侧=ch ′c =c ′,S 台侧=12(c +c ′)h ′――→c ′=0S 锥侧=12ch ′.3.棱柱的侧面积一定等于底面周长与侧棱长的乘积吗?提示:不一定.由棱柱的概念与性质可知棱柱的侧面展开图是一个平行四边形,此平行四边形的一边为棱柱的底面周长,另一边长为棱柱的侧棱长,但此平行四边形若不是矩形,则它的面积并不等于这两边长的乘积,所以棱柱的侧面积并不一定等于底面周长与侧棱长的乘积,只有直棱柱的侧面积才等于底面周长与侧棱长的乘积.讲一讲1.(1)圆柱的侧面展开图是边长为6π和4π的矩形,则圆柱的表面积为( ) A .6π(4π+3) B .8π(3π+1)C .6π(4π+3)或8π(3π+1)D .6π(4π+1)或8π(3π+2)(2)圆锥的中截面把圆锥侧面分成两部分,则这两部分侧面积的比为( ) A .1∶1 B .1∶2 C .1∶3 D .1∶4[尝试解答] (1)选C 圆柱的侧面积S 侧=6π×4π=24π2.①以边长为6π的边为轴时,4π为圆柱底面周长,则2πr =4π,即r =2,∴S 底=4π,S 全=S 侧+2S 底=24π2+8π=8π(3π+1).②以边长为4π的边为轴时,6π为圆柱底面周长,则2πr =6π,即r =3,∴S 底=9π,∴S 全=S 侧+2S 底=24π2+18π=6π(4π+3).(2)选C 如图所示,PB 为圆锥的母线,O 1,O 2分别为截面与底面的圆心.∵O 1为PO 2的中点,∴PO 1PO 2=PA PB =O 1A O 2B =12, ∴PA =AB ,O 2B =2O 1A . ∵S 圆锥侧=12×2π·O 1A ·PA ,S 圆台侧=12×2π·(O 1A +O 2B )·AB ,∴S 圆锥侧S 圆台侧=O 1A ·PA O 1A +O 2B ·AB =13.1.求柱、锥、台的表面积(或全面积)就是求它们的侧面积和(上、下)底面积之和. 2.求几何体的表面积问题,通常将所给几何体分成基本的柱、锥、台,再通过这些基本柱、锥、台的表面积,进行求和或作差,从而获得几何体的表面积.练一练1.圆台的上、下底面半径分别是10 cm 和20 cm ,它的侧面展开图的扇环的圆心角是180°,那么圆台的表面积是多少?解:如图所示,设圆台的上底面周长为c ,因为扇环的圆心角是180°,故c =π·SA =2π×10, 所以SA =20(cm), 同理可得SB =40(cm), 所以AB =SB -SA =20(cm), 所以S 表面积=S 侧+S 上+S 下 =π(r 1+r 2)·AB +πr 21+πr 22 =π(10+20)×20+π×102+π×202=1 100π(cm 2).故圆台的表面积为1 100π cm 2.讲一讲2.五棱台的上、下底面均是正五边形,边长分别是8 cm 和18 cm ,侧面是全等的等腰梯形,侧棱长是13 cm ,求它的侧面积.[尝试解答] 如图是五棱台的其中一个侧面,它是一个上底、下底分别为8 cm 和18 cm ,腰长为13 cm 的等腰梯形,由点A 向BC 作垂线,设垂足为E ,由点D 向BC 作垂线,设垂足为F ,易知BE =CF .∵BE +EF +FC =2BF -AD =BC , ∴BF =BC +AD 2=18+82=13.∴BE =BF -AD =13-8=5.又AB =13,∴AE =12.∴S 四边形ABCD =12(AD +BC )·AE =12×(18+8)×12=156(cm 2).故其侧面积为156×5=780(cm 2).要求锥体、柱体、台体的侧面积及表面积,需根据题目中的已知条件寻求锥体、柱体、台体的侧面积及表面积公式所需条件,然后应用公式进行解答.练一练2.已知正三棱锥V ABC 的主视图,俯视图如图所示,其中VA =4,AC =23,求该三棱锥的表面积.VA =VB =VC =4,则VD =VB 2-BD 2=42-32=13,∴S △VBC =12×VD ×BC =12×13×23=39,S △ABC =12×(23)2×32=33, ∴三棱锥V ABC 的表面积为3S △VBC +S △ABC =339+33=3(39+3).讲一讲3.已知一个圆锥的底面半径为R ,高为H ,在其内部有一个高为x 的内接圆柱. (1)求圆柱的侧面积;(2)x 为何值时,圆柱的侧面积最大?[尝试解答] 如图是圆锥及内接圆柱的轴截面图.(1)设所求圆柱的底面半径为r , 则r R =H -x H ,∴ r =R -RHx ,∴S 圆柱侧=2πrx =2πRx -2πR H·x 2. (2)∵S 圆柱侧是关于x 的二次函数, ∴当x =-2πR -2πR H=H2时,S 圆柱侧有最大值, 即当圆柱的高是圆锥的高的一半时,它的侧面积最大.解决组合体的表面积问题,要充分考虑组合体各部分的量之间的关系,将其转化为简单多面体与旋转体的表面积问题进行求解.练一练3.已知底面半径为 3 cm ,母线长为 6 cm 的圆柱,挖去一个以圆柱上底面圆心为顶点,下底面为底面的圆锥,求所得几何体的表面积.解:如图,由题意易知圆锥的母线长为3 cm.则S =S 底+S 柱侧+S 圆锥侧=π×(3)2+2π×3×6+π×3×3 =(3+62+33)π(cm 2).如图所示,圆柱OO ′的底面半径为2 cm ,高为4 cm ,点P 为母线B ′B 的中点,∠AOB =23π,试求一蚂蚁从A 点沿圆柱表面爬到P 点的最短路程.[巧思] 将圆柱的侧面展开,将A 、P 两点转化到同一个平面上解决.[妙解] 将圆柱侧面沿母线AA ′剪开展平为平面图,如图,则易知最短路径为平面图中线段AP .在Rt △ABP 中,AB ∴AP =AB 2+BP 21.矩形的边长分别为1和2,分别以这两边为轴旋转,所形成的几何体的侧面积之比为( )A .1∶2B .1∶1C .1∶4D .4∶1解析:选B 以边长为1的边为轴旋转得到的圆柱的侧面积S 1=2π×2×1=4π,以边长为2的边为轴旋转得到的圆柱的侧面积S 2=2π×1×2=4π, ∴S 1∶S 2=4π∶4π=1∶1.2.一个圆台的母线长等于上、下底面半径和的一半,且侧面积是32π,则母线长为( )A .2B .2 2C .4D .8解析:选C 设圆台的母线长为l ,上、下底面半径分别为r ,R , 则l =12(r +R ).又32π=π(r +R )l =2πl 2, ∴l 2=16, ∴l =4.3.(北京高考)某三棱锥的三视图如图所示,该三棱锥的表面积是( )A .28+6 5B .30+6 5C .56+12 5D .60+12 5解析:选B 由题中的三视图知,该三棱锥的立体图形如图所示.由题中所给条件,可求得S △ABD =12×4×5=10,S △ACD =S △BCD =12×4×5=10,AC =BC =41,AB =25,可求得△ABC 中AB 边上的高为41-5=6,所以S △ABC =12×6×25=6 5.综上可知,该三棱锥的表面积为S △ABD +S △ACD +S △BCD +S △ABC =30+6 5.4.圆锥的侧面展开图是半径为R 的半圆,则圆锥的高是________. 解析:设底面半径是r ,则2πr =πR ,∴r =R 2,∴圆锥的高h =R 2-r 2=32R .答案:32R 5.若一个底面是正三角形的三棱柱的主视图如图所示,则其表面积等于________.解析:根据题意可知,该棱柱的底面边长为2,高为1,侧棱和底面垂直,故其表面积S =34×22×2+2×1×3=6+2 3. 答案:6+2 36.一个几何体的三视图如图所示.已知主视图是底边长为1的平行四边形,左视图是一个长为3,宽为1的矩形,俯视图为两个边长为2的正方形拼成的矩形.求该几何体的表面积S .解:由三视图可知,该平行六面体中,两底面半径都缩小为原来的1n倍,那么它的侧面积变为原来的( )A .1倍B .n 倍C .n 2倍 D.1n倍解析:选A 由S 侧=π(r ′+r )l .当r ,r ′缩小1n倍,l 扩大n 倍时,S 侧不变.2.已知正四棱锥底面边长为6,侧棱长为5,则此棱锥的侧面积为( ) A .12 B .36C .24D .48解析:选D 正四棱锥的斜高h ′=52-32=4,S 侧=4×12×6×4=48.3.长方体的对角线长为214,长、宽、高的比为3∶2∶1,那么它的表面积为( ) A .44 B .88 C .64 D .48解析:选B 设长,宽,高分别为3x,2x ,x ,则对角线长为9x 2+4x 2+x 2=14x =214,∴x =2.∴表面积S =2(6x 2+3x 2+2x 2)=88.4.圆柱的一个底面积为S ,侧面展开图是一个正方形,那么这个圆柱的侧面积是( ) A .4πS B .2πS C .πS D.233πS解析:选A 设圆柱的底面半径为R ,则S =πR 2, ∴R =Sπ,则圆柱的母线长l =2πR =2S π.S 侧面积=(2πR )2=4π2R 2=4π2×Sπ=4πS .5.(重庆高考)某几何体的三视图如下图所示,则该几何体的表面积为( )A .180B .200C .220D .240解析:选D 几何体为直四棱柱,其高为10,底面是上底为2,下底为8,高为4,腰为5的等腰梯形,故两个底面面积的和为12×(2+8)×4×2=40,四个侧面面积的和为(2+8+5×2)×10=200,所以直四棱柱的表面积为S =40+200=240,故选D.二、填空题6.已知圆台的上、下底面半径和高的比为1∶4∶4,母线长为10,则圆台的侧面积为________.解析:设上底面半径为r ,则下底面半径为4r ,高为4r ,如图.∵母线长为10,∴有102=(4r )2+(4r -r )2,解得r =2. ∴S 圆台侧=π(r +4r )×10=100π. 答案:100π7.已知棱长为1,各面都是正三角形的四面体,则它的表面积是________. 解析:由条件可知,四面体的斜高为32, 所以其表面积为S 表=4×12×1×32= 3.答案: 38.如图,直三棱柱的主视图面积为2a 2,则左视图的面积为________.a 的正三角形,该三角形的高为32a .左视图是一矩,故左视图的面积为32a ×2a =3a 2. 现需将其外壁用油漆刷一遍,已知每平方米用漆0.2 m ,π取3.14,结果精确到0.01 kg)解:由三视图知建筑物为一组合体,自上而下分别是圆锥和四棱柱,并且圆锥的底面半径为3 m ,母线长为5 m ,四棱柱的高为4 m ,底面是边长为3 m 的正方形.圆锥的表面积为πr 2+πrl =3.14×32+3.14×3×5=28.26+47.1=75.36(m 2); 四棱柱的一个底面积为32=9(m 2); 四棱柱的侧面积为4×4×3=48(m 2). 所以外壁面积=75.36-9+48=114.36(m 2), 需油漆114.36×0.2=22.872≈22.87(kg), 答:共需油漆约22.87 kg.10.正四棱台两底面边长分别为a 和b (a <b ).(1)若侧棱所在直线与上、下底面正方形中心的连线所成的角为45°,求棱台的侧面积; (2)若棱台的侧面积等于两底面面积之和,求它的高.解:(1)如图,设O 1,O 分别为上,下底面的中心,过C 1作C 1E ⊥AC 于E ,过E 作EF ⊥BC 于F ,连接C 1F ,则C 1F 为正四棱台的斜高.由题意知∠C 1CO =45°,CE =CO -EO =CO -C 1O 1=22(b -a ). 在Rt △C 1CE 中,C 1E =CE =22(b -a ), 又EF =CE ·sin 45°=12(b -a ),∴斜高C 1F =C 1E 2+EF 2=⎣⎢⎡⎦⎥⎤22b -a 2+⎣⎢⎡⎦⎥⎤12b -a 2=32(b -a ).∴S 侧=12(4a +4b )×32(b -a )=3(b 2-a 2).(2)∵S 上底+S 下底=a 2+b 2, ∴12(4a +4b )·h 斜=a 2+b 2, ∴h 斜=a 2+b 2a +b.又EF =b -a2,h =h 2斜-EF 2=ab a +b. 第2课时 柱、锥、台的体积[核心必知]柱、锥、台的体积公式(2)如果圆锥的底面半径是r ,高是h ,那么它的体积是:V 圆锥=3πr 2h .(3)如果圆台上、下底面半径分别是r ′、r ,高是h ,那么它的体积是:V 圆台=13πh (r2+rr ′+r ′2).讲一讲1.已知直三棱柱ABC A 1B 1C 1中,点C 到AB 的距离为3 cm ,侧面ABB 1A 1的面积为8 cm 2,求直三棱柱的体积.[尝试解答] 法一:如图,设点C 到AB 的距离为d ,侧面ABB 1A 1的面积为S 1,则△ABC 的面积S =12|AB |d .∴直三棱柱的体积V =Sh =S |AA 1| =12|AB |d |AA 1|=12|AB |·|AA 1|d =12S 1 d =12(cm 3). 法二:补上一个相同的直三棱柱可以得到一个直四棱柱ABCD A 1B 1C 1D 1.可以看成以A 1ABB 1为底面的四棱柱D 1DCC 1A 1ABB 1.则ABB 1A 1的面积就是底面积,C 到AB 的距离即为高. ∴四棱柱D 1DCC 1A 1ABB 1的体积V =24(cm 3), 则直三棱柱的体积为12(cm 3).(1)直棱柱的侧面与对角面都是矩形,所以方法一利用侧面积与点到直线的距离的乘积求得体积.(2)四棱柱的底面与侧面是相对而言的,即任何一组对面都可以作为底面.所以方法二采用了“补形”求得四棱柱的体积(间接求解).练一练1.一个正方体的底面积和一个圆柱的底面积相等,且侧面积也相等,求正方体和圆柱的体积之比.解:设正方体边长为a ,圆柱高为h ,底面半径为r ,则有⎩⎪⎨⎪⎧a 2=πr 2, ①2πrh =4a 2, ②由①得r =ππa , 由②得πrh =2a 2, ∴V 圆柱=πr 2h =2ππa 3,∴V 正方体∶V 圆柱=a 3∶(2ππa 3)=π2∶1=π∶2.讲一讲2.如图,已知四棱锥P ABCD 的底面为等腰梯形,AB ∥CD ,AC ⊥BD ,垂足为H ,PH 是四棱锥的高.若AB =6,∠APB =∠ADB =60°,求四棱锥P ABCD 的体积.[尝试解答] 因为ABCD 为等腰梯形,AB ∥CD ,AC ⊥BD ,AB =6, 所以HA =HB = 3. 因为∠APB =∠ADB =60°,所以PA =PB =6,HD =HC =3可得PH =PA 2-AH 2=3,等腰梯形ABCD 的面积为S =12AC 所以四棱锥的体积为V =13×(2+求锥体的体积,要选择适当的底面和高,然后应用公式V =13Sh 进行计算即可,常用方法为割补法和等积变换法:(1)割补法:求一个几何体的体积可以将这个几何体分割成几个柱体、锥体,分别求出柱体和锥体的体积,从而得出几何体的体积.(2)等积变换法:利用三棱锥的任一个面可作为三棱锥的底面. ①求体积时,可选择容易计算的方式来计算; ②利用“等积性”可求“点到面的距离”. 练一练2.已知三角形ABC 的边长分别是AC =3,BC =4,AB =5,以AB 所在直线为轴,将此三角形旋转一周,求所得几何体的体积.∵△ABC 为直角三角形,且AB 为斜边,∴绕AB 边旋转一周,所得几何体为两个同底的圆锥,且圆锥的底面半径r =125.∴V 锥=13·AB ·πr 2=13×5×π×⎝ ⎛⎭⎪⎫1252=485π.讲一讲3.圆台上底的面积为16π cm 2,下底半径为6 cm ,母线长为10 cm ,那么,圆台的侧面积和体积各是多少?[尝试解答] 首先,圆台的上底的半径为4 cm , 于是S 圆台侧=π(r +r ′)l =100π(cm 2). 其次,如图,圆台的高h =BC =BD 2-OD -AB 2=102--2=46(cm),所以V 圆台=13h (S +SS ′+S ′)=13×46×(16π+16π×36π+36π) =3046π3(cm 3).求台体的体积关键是求出上、下底面的面积和台体的高,要注意充分运用棱台内的直角梯形和圆台的轴截面(等腰梯形)等求相关量之间的关系.因为台体是由锥体用平行于底面的平面截得的几何体,所以它的体积也可以转化为两个锥体的体积之差.练一练3.正四棱台的上下底面边长分别为6 cm 和12 cm ,侧面积为180 cm 2,求棱台的体积. 解:如图,分别过正四棱台的底面中心O 1,O 作O 1E 1⊥B 1C 1,OE ⊥BC ,垂足分别为E 1,E ,则E 1E 为正四棱台的斜高.由于正四棱台的侧面积为180 cm 2,所以12×4×(6+12)|E 1E |=180,解得|E 1E |=5.在直角梯形O 1OEE 1中,O 1E 1=3,OE =6,E 1E =5,解得O 1O =4.所以正四棱台的体积为V =13h (S +SS ′+S ′)=13×4×(62+6×12+122)=336(cm 3).如图所示,在长方体ABCD A ′B ′C ′D ′中,用截面截下一个棱锥C A ′DD ′,求棱锥C A ′DD ′的体积与剩余部分的体积之比.[解] 法一:设AB =a ,AD =b ,DD ′=c , 则长方体ABCD A ′B ′C ′D ′的体积V =abc , 又S △A ′DD ′=12bc ,且三棱锥C -A ′DD ′的高为CD =a , ∴V 三棱锥C -A ′DD ′=13S △A ′D ′D ·CD =16abc .则剩余部分的体积V 剩=abc -16abc 故V 三棱锥C -A ′D ′D ∶V 剩=16abc ∶56ADD ′A ′BCC ′B ′,设它的底面,高是h ,′DD ′=13×12Sh =16Sh .-6=6Sh ∴棱锥C -A ′DD ′的体积与剩余部分的体积之比为16Sh ∶56Sh =1∶5.1.正方体的表面积为96,则正方体的体积是( ) A .48 6 B .64 C .16 D .96解析:选B 设正方体的棱长为a ,则6a 2=96,解得a =4,则正方体的体积是a 3=64. 2.(山东高考)一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如右图所示,则该四棱锥侧面积和体积分别是( )A .45,8B .45,83C .4(5+1),83D .8,8解析:选B 由题意可知该四棱锥为正四棱锥,底面边长为2,高为2,侧面上的斜高为22+12=5,所以S 侧=4×⎝ ⎛⎭⎪⎫12×2×5=45,V =13×22×2=83.3.(重庆高考)某几何体的三视图如图所示,则该几何体的体积为( )A.13+πB.23+π C.13+2π D.23+2π 解析:选A 由三视图可知该几何体是由一个半圆柱和一个三棱锥组成的.由图中数据可得三棱锥的体积V 1=13×12×2×1×1=13,半圆柱的体积V 2=12×π×12×2=π,∴V =13+π.4.一个几何体的三视图如图所示,则这个几何体的体积为________.解析:该空间几何体是一个底面为梯形的四棱柱,其底面积是1+22×2=3,高为1,故其体积等于3.答案:35.圆台的上、下底面半径和高的比为1∶4∶4,母线长为10,则圆台的体积为________. 解析:设圆台的上底面半径为r , 则(3r )2+(4r )2=100,解之得r =2.∴S 上=πr 2=4π,S 下=π(4r )2=16πr 2=64π,h =4r =8.∴V =13(4π+64π+16π)×8=224π.答案:224π6.已知一个三棱台的两底面是边长分别为20 cm 和30 cm 的正三角形,侧面是全等的′中,O ′、O 分别为上、下底面的中心,D 、D ′分别BCC ′B ′的高,75DD ′.又A ′B ′=20 cm ,AB =30 cm ,则上、下底面面积之和为S 上+S 下=34(202+302)=3253(cm 2).由S 侧=S 上+S 下得,75DD ′=3253(cm 2),所以DD ′=1333(cm). 在直角梯形O ′ODD ′中,OD =5 3 cm ,O ′D ′=1033cm ,O ′O =D ′D 2-OD -O ′D2=⎝ ⎛⎭⎪⎫13332-⎝⎛⎭⎪⎫53-10332=43(cm),即棱台的高h =4 3 cm.由棱台的体积公式,可得棱台的体积为V =h3(S +S ′+SS ′)=433·⎝ ⎛⎭⎪⎫34·302+34·202+34·20·30 =1 900(cm 3).一、选择题1.已知圆锥的母线长是8,底面周长为6π,则它的体积是( ) A .955π B .955 C .355π D .355解析:选C 设圆锥底面圆的半径为r ,则2πr =6π,∴r =3. 设圆锥的高为h ,则h =82-32=55, ∴V 圆锥=13πr 2h =355π.2.在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是( )A.23B.76C.45D.56解析:选D 用过共顶点的三条棱中点的平面截该正方体,所得三棱锥的体积为13×⎝ ⎛⎭⎪⎫124=148,故剩下的凸多面体的体积为1-8×148=56. 3.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )A .6B .9C .12D .18解析:选B 由三视图可知该几何体为底面是斜边为6的等腰直角三角形,高为3的三棱锥,其体积为13×12×6×3×3=9.4.(浙江高考)已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )A .108 cm 3B .100 cm 3C .92 cm 3D .84 cm 3解析:选B 根据几何体的三视图可知,所求几何体是一个长方体截去一个三棱锥,∴几何体的体积V =6×6×3-13×12×4×4×3=100 cm 3.30°的直角三角形的最短直角边、较长直角边、斜边所在的直线)CD =32,旋转所得几何体V 2=13π×12×3=33π,V 3=13π(32)2×2=12π. V 1∶V 2∶V 3=1∶33∶12=6∶23∶3. 二、填空题6.如图已知底面半径为r 的圆柱被一个平面所截,剩下部分母线长的最大值为a ,最小值为b ,那么圆柱被截后剩下部分的体积是________.解析:采取补体方法,相当于一个母线长为a +b 的圆柱截成了两个体积相等的部分,所以剩下部分的体积V =πr2a +b2.答案:πr 2a +b27.一个圆锥形容器和一个圆柱形容器的轴截面的尺寸如图所示,两容器盛有液体的体积正好相等,且液面高均为h ,则h =________.解析:锥体的底面半径和高都是h ,圆柱体的底面半径是a 2,高为h ,依题意得π3h 2·h=π·(a 2)2·h ,解得h =32a .答案:32a 8.已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是________.解析:此几何体的直观图如图,ABCD 为正方形,边长为20 cm ,S 在底面的射影为CD 中点E ,SE =20 cm ,V S ABCD =13S ABCD ·SE =8 0003cm 3.答案:8 0003 cm 3三、解答题9.如图所示,是一个底面直径为20 cm 的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为6 cm ,高为20 cm 的一个圆锥体铅锤,当铅锤从水中取出后,杯里的水将下降多少?(π=3.14)解:因为玻璃杯是圆柱形的,所以铅锤取出后,水面下降部分实际是一个小圆柱,这个圆柱的底面与玻璃的底面一样,是一直径为20 cm 的圆柱,它的体积正好等于圆锥体铅锤的体积,这个小圆柱的高就是水面下降的高度.因为圆锥形铅锤的体积为13×π×⎝ ⎛⎭⎪⎫622×20=60π(cm 3),设水面下降的高度为x ,则小圆柱的体积为π×(20÷2)2×x =100πx (cm 3),所以有方程60π=100πx ,解此方程得x =0.6(cm).答:铅锤取出后,杯中水面下降了0.6 cm.10.若E ,F 是三棱柱ABC A 1B 1C 1侧棱BB 1和CC 1上的点,且B 1E =CF ,三棱柱的体积为m ,求四棱锥A BEFC 的体积.解:如图所示,连接AB 1,AC 1.∵B 1E =CF ,∴梯形BEFC 的面积等于梯形B 1EFC 1的面积. 又四棱锥A BEFC 的高与四棱锥A B 1EFC 1的高相等, ∴V A BEFC =VA B 1EFC 1=12VA BB 1C 1C .又VA A 1B 1C 1=13S △A 1B 1C 1·h ,VABC A 1B 1C 1=m ,∴VA A 1B 1C 1=m3,∴VA BB 1C 1C =VABC A 1B 1C 1-VA A 1B 1C 1=23m ,∴V A BEFC =12×23m =m 3,即四棱锥A BEFC 的体积是m3.第3课时 球[核心必知]1.球的表面积公式:S 球面=4πR 2. 2.球的体积公式:V 球=43πR 3.[问题思考]用一个平面去截球体,截面的形状是什么?该截面的几何量与球的半径之间有什么关系?提示:可以想象,用一个平面去截球体,截面是圆面,在球的轴截面图中,截面圆与球的轴截面的关系如图所示.若球的半径为R ,截面圆的半径为r ,OO ′=d . 在Rt △OO ′C 中,OC 2=OO ′2+O ′C 2, 即R 2=r 2+d 2.讲一讲1.已知过球面上三点A 、B 、C 的截面到球心的距离等于球半径的一半,且AC =BC =6,AB =4,求球面面积与球的体积.[尝试解答] 如图所示,设球心为O ,截面圆圆心O 1,球半径为R , 连接OO 1,则OO 1是球心到截面的距离.由于OA =OB =OC =R , 则O 1是△ABC 的外心.设M 是AB 的中点,由于AC =BC , 则O 1在CM 上.设O 1M =x O 1C =CM -O 1M 又O 1A =O 1C 解得x =724.在Rt △OO 1A 故S 球面=4πR计算球的表面积和体积的关键是求出球的半径,这里就要充分利用球的截面的性质进行求解.已知条件中的等量关系,往往是建立方程的依据,这种解题的思想值得重视.练一练1.过球的半径的中点,作一垂直于这条半径的截面,已知此截面的面积为48π cm 2,试求此球的表面积和体积.解:如图,设截面圆的圆心为O 1, 则OO 1⊥O 1A ,O 1A 为截面圆的半径,OA 为球的半径.∵48π=π·O 1A 2,∴O 1A 2=48. 在Rt △AO 1O 中,OA 2=O 1O 2+O 1A 2,即R 2=⎝ ⎛⎭⎪⎫12R 2+48,∴R =8(cm),∴S 球=4πR 2=4π×64=256π(cm 2),V 球=43πR 3=20483π(cm 3).讲一讲2.轴截面是正三角形的圆锥内有一个内切球,若圆锥的底面半径为1 cm ,求球的体积. [尝试解答]如图所示,作出轴截面,O 是球心,与边BC 、AC 相切于点D 、E . 连接AD ,OE ,∵△ABC 是正三角形, ∴CD =12AC .∵CD =1 cm ,∴AC =2 cm ,AD = 3 cm , ∵Rt △AOE ∽Rt △ACD , ∴OE AO =CDAC.设OE =r ,则AO =(3-r ), ∴r3-r =12, ∴r =33cm , V 球=43π(33)3=4327π(cm 3), 即球的体积等于4327π cm 3.解决与球有关的接、切问题时,一般作一个适当的截面,将问题转化为平面问题解决,这类截面通常是指圆锥的轴截面、球的大圆、多面体的对角面等,在这个截面中应包括每个几何体的主要元素,且这个截面包含体和体之间的主要位置关系和数量关系.练一练2.如图,半球内有一个内接正方体,正方体的一个面在半球的底面圆内,若正方体棱长为6,求球的表面积和体积.解:作轴截面如图所示,CC′=6,AC=2·6=23,设球的半径为R,则R2=OC2+CC′2=(3)2+(6)2=9,∴R=3,∴S球=4πR2=36π,V球=43πR3=36π.一个球内有相距9 cm的两个平行截面,面积分别为49π cm2和400π cm2,求球的表面积.[错解] 如图所示,设OD=x,由题知π·CA2=49π,∴CA=7 cm.π·BD2=400π,∴BD=20 cm.设球半径为R,则有(CD+DO)2+CA2=R2=OD2+DB2,即(9+x)2+72=x2+202,∴x=15,R=25.∴S球=4πR2=2 500π cm2.[错因] 本题错解的原因在于考虑不周,由于球心可能在两个截面之间,也可能在两个截面的同一侧,因此解决此题要分类讨论.[正解] (1)当球心在两个截面的同侧时,解法同错解.(2)当球心在两个截面之间时,如图所示,设OD =x ,则OC =9-x ,设球半径为R ,可得x 2+202=(9-x )2+72=R 2, 此方程无正数解,即此种情况不可能. 综上可知,球的表面积是2 500π cm 2.1.球的表面积扩大2倍,球的体积扩大( ) A .2倍 B. 2 倍 C .2 2 倍 D .3 2 倍解析:选C 球的表面积扩大2倍,半径扩大2倍,从而体积扩大(2)3=22倍. 2.两个球的半径之比为1∶3,那么两个球的表面积之比为 ( ) A .1∶9 B .1∶27 C .1∶3 D .1∶1解析:选A 设两球的半径分别为R 1,R 2. ∵R 1∶R 2=1∶3,∴两个球的表面积之比为S 1∶S 2=4πR 21∶4πR 22=R 21∶R 22=1∶9.3.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一个球面上,则这个球的表面积是( )A .202πB .252πC .50πD .200π解析:选C 设球的半径为R ,则2R =33+42+52=5 2. ∴S 球=4πR 2=π·(2R )2=50π.4.(福州高一检测)已知正四棱锥O ABCD 的体积为322,底面边长为3,则以O 为球心,OA 为半径的球的表面积为________.解析:过O 作底面ABCD 的垂线段OE ,则E 为正方形ABCD 的中心.由题意可知13×(3)2×OE =323,所以OE =322,故球的半径R =OA =OE 2+EA 2=6,则球的表面积S=4πR 2=24π.答案:24π5.圆柱形容器内盛有高度为8 cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是________cm.解析:设球的半径为r cm ,则有8πr 2+3×43πr 3=πr 2×6r ,由此解得r =4.答案:46.某个几何体的三视图如图所示(单位:m):(1)求该几何体的表面积(结果保留π); (2)求该几何体的体积(结果保留π).解:由三视图可知,该几何体是一个四棱柱和一个半球构成的组合体,且半球的直径为2,该四棱柱为棱长为2的正方体.(1)该几何体的表面积为S =2πR 2+6×2×2-π×R 2=π+24 (m 2).(2)该几何体的体积为V =12×43πR 3+23=23π+8 (m 3).一、选择题1.用与球心距离为1的平面去截球,所得截面面积为π,则球的体积为( ) A.323π B.8π3C .82π D.823π解析:选D 所得截面圆的半径为r =1,因此球的半径R =12+12=2,球的体积为 43πR 3=823π. 2.若三个球的表面积之比是1∶2∶3,则它们的体积之比是( ) A .1∶2∶3 B .1∶2∶ 3 C .1∶22∶3 3 D .1∶4∶7解析:选C ∵三个球的表面积之比是1∶2∶3, 即r 21∶r 22∶r 23=1∶2∶3.∴r 1∶r 2∶r 3=1∶2∶3, ∴V 1∶V 2∶V 3=1∶22∶3 3.3.平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )A.6π B .43π C .46π D .63π解析:选B 设球的半径为R ,由球的截面性质得R =22+12=3,所以球的体积V =43πR 3=43π.4.设三棱柱的侧棱垂直于底面,所有棱的长都为a ,顶点都在一个球面上,则该球的表面积为( )A .πa 2 B.73πa 2C.113πa 2 D .5πa 2解析:选B 正三棱柱内接于球,则球心在正三棱柱两底面中心连线的中点处,在直角三角形中可得R =⎝ ⎛⎭⎪⎫a 22+⎝ ⎛⎭⎪⎫33a 2=712a , ∴S =4πR 2=4π×7a 212=7π3a 2.5.(新课标全国卷Ⅰ)如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm ,如果不计容器的厚度,则球的体积为( )A.500π3 cm 3B.866π3 cm 3C.1 372π3 cm 3 D.2 048π3cm 3解析:选 A 解题时,先根据已知条件分析出正方体的上底面到球心的距离为(R -2) cm(其中R 为球半径),再利用球半径、球心距、和截面圆半径构成的直角三角形求出球半径,进而计算出球的体积.设球半径为R cm ,根据已知条件知正方体的上底面与球相交所得截面圆的半径为4 cm ,球心到截面的距离为(R -2) cm ,所以由42+(R -2)2=R 2,得R =5,所以球的体积V =43πR 3=43π×53=500π3cm 3,选择A.二、填空题6.一个平面截一球得到直径为6 cm 的圆面,球心到这个平面的距离为4 cm ,则球的3OA =5. 答案:37.一个底面直径是32 cm 的圆柱形水桶装入一些水,将一个球放入桶内完全淹没,水面上升了9 cm ,则这个球的表面积是________.解析:球的体积等于以16 cm 为底面半径,高为9 cm 的圆柱的体积,设球的半径为R ,所以43πR 3=π·162·9,解得R =12(cm),所以S 球=4πR 2=576π cm 2.答案:576π cm 28.如图所示,正四棱锥S ABCD 的底面边长和各侧棱长都为2,点S ,A ,B ,C ,D 都在同一个球面上,则该球的体积为________.解析:∵正四棱锥的底面边长和侧棱长都为2,∴其高为1,由对称性可知,棱长为2的正八面体也内接于此球,∴球的半径为1,体积为43π.答案:43π三、解答题9.如图,ABCD 是正方形,是以A 为圆心的弧,将正方形ABCD 以AB 为轴旋转一周,求图中Ⅰ、Ⅱ、Ⅲ三部分旋转所得旋转体的体积之比.解:Ⅰ生成圆锥,Ⅱ生成的是半球去掉圆锥Ⅰ,Ⅲ生成的是圆柱去掉扇形ABD 生成的半球.设正方形的边长为a ,Ⅰ、Ⅱ、Ⅲ三部分旋转所得旋转体的体积分别为V Ⅰ、V Ⅱ和V Ⅲ,则V Ⅰ=13πa 3,V Ⅱ=43πa 3÷2-13πa 3=13πa 3,V Ⅲ=πa 3-43πa 3÷2=13πa 3.三部分所得旋转体的体积之比为1∶1∶1.10.如图,半径为R 的半圆O 的直径为直角梯形垂直于两底的腰,且半圆O 分别切AB ,BC ,CD 于点A 、E 、D .将半圆与梯形绕AD 所在直线旋转一周,得到一个球和一个圆台,若球的表面积与圆台的侧面积的比为3∶4,求圆台的体积.解:设圆台的上、下底的半径分别为r 1、r 2,母线长为l .由题意知,圆台的高h =2R ,DC =CE =r 1,AB =BE =r 2,OE =R ,∠BOC =90°.OE ⊥BC . ∵在Rt △COB 中,CE ·BE =OE 2,BC =CE +BE , ∴r 1r 2=R 2,l =r 1+r 2.又∵S 球=4πR 2,S 圆台侧=π(r 1+r 2)l 且S 球∶S 圆台侧=3∶4, ∴4πR 2∶πl (r 1+r 2)=3∶4. ∴(r 1+r 2)2=163R 2,∴V 台=13πh (r 21+r 22+r 1r 2)=π3×2R [(r 1+r 2)2-r 1r 2]=π3×2R ×⎝ ⎛⎭⎪⎫163R 2-R 2=269πR 3. 故圆台的体积为269πR 3.1.空间几何体的结构及其三视图和直观图空间几何体是研究空间线、面、体的几何载体,正确理解几何体的概念,掌握几何体的特征是解题成功的关键.对三视图的考查,高考中不可能去画三视图或画几何体,但观察三视图,想象几何体是可能的,这类题目只要把握三视图和几何体之间的关系是不难解决的.2.平行关系(1)判定线线平行的方法:①利用线线平行的定义证明共面而且无公共点(结合反证法); ②利用平行公理4; ③利用线面平行性质定理;④利用线面垂直的性质定理(若a ⊥α,b ⊥α,则a ∥b );⑤利用面面平行的性质定理(若α∥β,α∩γ=a ,β∩γ=b ,则a ∥b );⑥利用平行四边形的性质,三角形、梯形中位线,线段对应成比例等.(2)判定线面平行的方法:①线面平行的定义(无公共点);②利用线面平行的判定定理(aα,bα,a∥b⇒a∥α);③面面平行的性质定理(α∥β,aα⇒a∥β);④面面平行的性质(α∥β,aα,aβ,a∥α⇒a∥β).(3)判定面面平行的方法:①平面平行的定义(无公共点);②面面平行的判定定理(若a∥β,b∥β,a、bα,且a∩b=A⇒α∥β);③面面平行的判定定理的推论(若a∥a′,b∥b′,aα,bα且a∩b=A,a′β,b′β,且a′∩b′=A′,则α∥β);④线面垂直的性质定理(若a⊥α,a⊥β⇒α∥β);⑤平面平行的性质(传递性:α∥β,β∥γ⇒α∥γ).3.平行关系相互转化的示意图4.垂直关系(1)证明线面垂直的主要方法有:①利用线面垂直的定义;②利用判定定理:m,nα,m∩n=A,l⊥m,l⊥n⇒l⊥α;③利用面面平行的性质定理:α∥β,a⊥α⇒a⊥β;④利用面面垂直的性质定理:α⊥β,α∩β=l,aα,a⊥l⇒a⊥β;⑤利用线面垂直判定定理的推论:a∥b,a⊥α⇒b⊥α.(2)证明面面垂直的方法就是利用判定定理先转化为证明线面垂直.(3)直线和平面垂直、平面和平面垂直是直线和平面相交、平面和平面相交的特殊情况.对这种情况的认识,既可以从直线和平面、平面和平面的夹角为90°来讨论,又可以从已有的线线垂直、线面垂直关系出发进行推理和论证.无论是线面垂直还是面面垂直,都。
2017_2018版高中数学第一章立体几何初步2直观图学案北师大版必修2
例3 如下图,梯形A1B1C1D1是一平面图形ABCD的直观图.假设A1D1∥O′y′,A1B1∥C1D1,A1B1= C1D1=2,A1D1=O′D1=1.试画出原四边形的形状,并求出原图形的面积.
D.在画直观图时,由于选轴的不同所画的直观图可能不同
3.假设一个三角形采纳斜二测画法,取得的直观图的面积是原三角形面积的( )
A. 倍 B.2倍 C. 倍 D. 倍
4.如图,水平放置的△ABC的斜二测直观图是图中的△A′B′C′,已知A′C′=6,B′C′=4,那么AB边的实际长度是________.
(3)画侧棱.过A,B,C,D各点别离作z轴的平行线,并在这些平行线上沿Oz轴方向别离截取2 cm长的线段AA′,BB′,CC′,DD′.
(4)成图.按序连接A′,B′,C′,D′,并加以整理(去掉辅助线,将被遮挡的部份改成虚线),取得正方体的直观图(如图②).
当堂训练
1.C 2.A 3.A 4.10
例3 解 如图,成立直角坐标系xOy,在x轴上截取OD=O′D1=1,OC=O′C1=2.
在过点D的y轴的平行线上截取DA=2D1A1=2.
在过点A的x轴的平行线上截取AB=A1B1=2.
连接BC,即取得了原图形.
由作法可知,原四边形ABCD是直角梯形,上、下底长度别离为AB=2,CD=3,直角腰的长度AD=2,
A. B.
C. D.2
类型三 空间几何体的直观图
例4 画出底面是正方形,侧棱均相等的四棱锥的直观图.
反思与感悟 简单几何体直观图的画法
(1)画轴:通常以高所在直线为z轴建系.
2017_2018版高中数学第一章立体几何初步1简单几何体学案北师大版必修2
1 简单几何体学习目标 1.明白得旋转体与多面体的概念.2.把握球、圆柱、圆锥、圆台的结构特点.3.把握棱柱、棱锥、棱台的大体性质.知识点一两平面平行和直线与平面垂直的概念试探1 如何概念两平面平行?试探2 如何判定直线与平面垂直?梳理(1)________________的两个平面平行.(2)若是一条直线与一个平面内的__________________都垂直,那么这条直线与那个平面垂直.知识点二旋转体与多面体旋转体一条__________绕着它所在的平面内的一条定直线旋转所形成的曲面叫作____________;封闭的旋转面围成的几何体叫作______________多面体把若干个________________围成的几何体叫作________________知识点三常见的旋转体及概念试探1 以直角三角形的一条直角边所在的直线为轴旋转180°所得的旋转体是圆锥吗?试探2 可否由圆锥取得圆台?梳理名称图形及表示定义相关概念球记作:球O球面:以________________所在的直线为旋转轴,将半圆旋转所形成的________叫作球面.球体:球面所围成的几何体叫作球体,简称球球心:半圆的________.球的半径:连接球心和球面上任意一点的线段.球的直径:连接__________上两点并且过______的线段圆柱记作:圆柱OO′以________所在的直线为旋转轴,其余各边旋转而形成的________所围成的几何体叫作圆柱高:在__________上这条边的长度.底面:垂直于____________的边旋转而成的________.侧面:__________________的边旋转而成的曲面.母线:__________________的边,无论转到什么位置都叫作侧面的母线圆锥记作:圆锥OO′以直角三角形的__________所在的直线为旋转轴,其余各边旋转而形成的________所围成的几何体叫作圆锥圆台记作:圆台OO′以直角梯形__________________所在的直线为旋转轴,其余各边旋转而形成的________所围成的几何体叫作圆台专门提示:(1)通过旋转体轴的截面称为该几何体的轴截面.(2)圆柱的母线相互平行,圆锥的母线相交于圆锥的极点,圆台的母线延长后相交于一点.知识点四常见的多面体及相关概念试探观看以下多面体,试指明其类别.梳理(1)棱柱①概念要点:(ⅰ)两个面________________;(ⅱ)其余各面都是________________;(ⅲ)每相邻两个四边形的公共边都________________.②相关概念:底面:两个________________的面.侧面:除底面外的其余各面.侧棱:相邻______________的公共边.极点:底面多边形与________的公共极点.③记法:如三棱柱ABC-A1B1C1.④分类及特殊棱柱:(ⅰ)按底面多边形的边数分,有____________________、________________、________________、……. (ⅱ)直棱柱:侧棱________于底面的棱柱.(ⅲ)正棱柱:底面是________________的直棱柱.(2)棱锥①概念要点:(ⅰ)有一个面是________________;(ⅱ)其余各面是三角形;(ⅲ)这些三角形有一个________________.②相关概念:底面:除去棱锥的侧面余下的那个________________.侧面:除底面外的其余__________面.侧棱:相邻两个________的公共边.极点:________的公共极点.③记法:如三棱锥S-ABC.④分类及特殊棱锥:(ⅰ)按底面多边形的边数分,有________、__________、__________、……,(ⅱ)正棱锥:底面是______________,且各侧面________的棱锥.(3)棱台①概念要点:用一个______________________的平面去截棱锥,________与________之间的部份.②相关概念:上底面:原棱锥的________.下底面:原________的底面.侧棱:相邻的________的公共边.极点:________与底面的公共极点.③记法:如三棱台ABC-A1B1C1.④分类及特殊棱台:(ⅰ)按底面多边形的边数分,有____________________、________________、________________、……,(ⅱ)正棱台:由________________截得的棱台.类型一旋转体的概念例1 以下命题正确的选项是________.(填序号)①以直角三角形的一边所在直线为旋转轴旋转一周所得的旋转体是圆锥;②以直角梯形的一腰所在直线为旋转轴旋转一周所得的旋转体是圆台;③圆柱、圆锥、圆台的底面都是圆;④以等腰三角形的底边上的高线所在的直线为旋转轴,其余各边旋转一周形成的几何体是圆锥;⑤半圆面绕其直径所在直线旋转一周形成球;⑥用一个平面去截球,取得的截面是一个圆面.反思与感悟(1)判定简单旋转体结构特点的方式①明确由哪个平面图形旋转而成.②明确旋转轴是哪条直线.(2)简单旋转体的轴截面及其应用①简单旋转体的轴截面中有底面半径、母线、高等表现简单旋转体结构特点的关键量.②在轴截面中解决简单旋转体问题表现了化空间图形为平面图形的转化思想.跟踪训练1 以下命题:①圆柱的轴截面是过母线的截面中最大的一个;②用任意一个平面去截圆锥取得的截面必然是一个圆;③圆台的任意两条母线的延长线,可能相交也可能不相交;④球的半径是球心与球面上任意一点的连线段.其中正确的个数为( )A.0 B.1C.2 D.3类型二多面体及其简单应用例2 (1)以下关于多面体的说法正确的个数为________.①所有的面都是平行四边形的几何体为棱柱;②棱台的侧面必然可不能是平行四边形;③底面是正三角形,且侧棱相等的三棱锥是正三棱锥;④棱台的各条侧棱延长后必然相交于一点;⑤棱柱的每一个面都可不能是三角形.(2)如下图,长方体ABCD-A1B1C1D1.①那个长方体是棱柱吗?若是是,是几棱柱?什么缘故?②用平面BCNM把那个长方体分成两部份,各部份形成的几何体仍是棱柱吗?若是是,是几棱柱,并用符号表示;若是不是,说明理由.(提示:能够证明BC綊MN)引申探讨假设用一个平面去截本例(2)中的四棱柱,能截出三棱锥吗?反思与感悟(1)棱柱的识别方式①两个面相互平行.②其余各面都是四边形.③每相邻两个四边形的公共边都相互平行.(2)棱锥的识别方式①有一个面是多边形.②其余各面都是有一个公共极点的三角形.③棱锥仅有一个极点,它是各侧面的公共极点.④对几类特殊棱锥的熟悉(ⅰ)三棱锥是面数最少的多面体,又称四面体.它的每一个面都能够作为底面.(ⅱ)各棱都相等的三棱锥称为正四面体.(ⅲ)正棱锥有以下性质:侧面是全等的等腰三角形,极点与底面正多边形中心的连线与底面垂直.(3)棱台的识别方式①上、下底面相互平行.②各侧棱延长交于一点.跟踪训练2 以下说法正确的选项是( )A.有两个面相互平行,其余四个面都是等腰梯形的六面体是棱台B.两底面平行,而且各侧棱也相互平行的几何体是棱柱C.棱锥的侧面能够是四边形D.棱柱中两个相互平行的平面必然是棱柱的底面1.以下几何体中棱柱有( )A.5个B.4个C.3个D.2个2.关于以下几何体,说法正确的选项是( )A.图①是圆柱B.图②和图③是圆锥C.图④和图⑤是圆台D.图⑤是圆台3.下面有关棱台说法中,正确的选项是( )A.上下两个底面平行且是相似四边形的几何体是四棱台B.棱台的所有侧面都是梯形C.棱台的侧棱长必相等D.棱台的上下底面可能不是相似图形4.等腰三角形ABC绕底边上的中线AD所在的直线旋转一周所得的几何体是( )A.圆台B.圆锥C.圆柱D.球5.假设一个圆锥的轴截面是等边三角形,其面积为3,那么那个圆锥的母线长为________.1.圆柱、圆锥、圆台的关系如下图.2.棱柱、棱锥、棱台概念的关注点(1)棱柱的概念有以下两个要点,缺一不可:①有两个平面(底面)相互平行;②其余各面(侧面)每相邻两个面的公共边(侧棱)都相互平行.(2)棱锥的概念有以下两个要点,缺一不可:①有一个面(底面)是多边形;②其余各面(侧面)是有一个公共极点的三角形.(3)用一水平平面截棱锥可取得棱台.答案精析问题导学知识点一试探1 两平面无公共点.试探2 直线和平面内的任何一条直线都垂直.梳理(1)无公共点(2)任何一条直线知识点二平面曲线旋转面旋转体平面多边形多面体知识点三试探1 不是.以直角三角形的一条直角边所在的直线为轴旋转180°所得的旋转体是圆锥的一半,不是整个圆锥.试探2 用平行于圆锥底面的平面截去一个圆锥能够取得.梳理半圆的直径曲面圆心球面球心矩形的一边曲面一条直角边曲面垂直于底边的腰曲面旋转轴旋转轴圆面不垂直于旋转轴不垂直于旋转轴知识点四试探(1)五棱柱;(2)四棱锥;(3)三棱台.梳理(1)①(ⅰ)相互平行(ⅱ)四边形(ⅲ)相互平行②相互平行两个侧面侧面④(ⅰ)三棱柱四棱柱五棱柱(ⅱ)垂直(ⅲ)正多边形(2)①(ⅰ)多边形(ⅲ)公共极点②多边形三角形侧面侧面④(ⅰ)三棱锥四棱锥五棱锥(ⅱ)正多边形全等(3)①平行于棱锥底面底面截面②截面棱锥侧面侧面④(ⅰ)三棱台四棱台五棱台(ⅱ)正棱锥题型探讨例1 ④⑤⑥解析①以直角三角形的一条直角边所在直线为旋转轴旋转一周才能够取得圆锥;②以直角梯形垂直于底边的腰所在直线为旋转轴旋转一周可取得圆台;③它们的底面为圆面;④⑤⑥正确.跟踪训练1 C例2 3解析①中两个四棱柱放在一路,如以下图所示,能保证每一个面都是平行四边形,但并非是棱柱.故①错;②中棱台的侧面必然是梯形,不可能为平行四边形,②正确;依照棱锥的概念知,③正确;依照棱台的概念知,④正确;棱柱的底面能够是三角形,故⑤错.正确的个数为3.(2)解①长方体是棱柱,是四棱柱.因为它有两个平行的平面ABCD与A1B1C1D1,其余各面都是四边形,而且每相邻两个四边形的公共边相互平行,符合棱柱的概念.②用平面BCNM把那个长方体分成两部份,其中一部份有两个平行的平面BB1M与CC1N,其余各面都是四边形,而且每相邻两个四边形的公共边相互平行,符合棱柱的概念,因此是三棱柱,可用符号表示为三棱柱BB1M-CC1N;另一部份有两个平行的平面ABMA1与DCND1,其余各面都是四边形且每相邻两个四边形的公共边相互平行,符合棱柱的概念,因此是四棱柱,可用符号表示为四棱柱ABMA1-DCND1.引申探讨解如图,几何体B-A1B1C1确实是三棱锥.跟踪训练2 B [A中所有侧棱不必然交于一点,故A不正确;B正确;C中棱锥的侧面必然是三角形,故C不正确;D中棱柱的侧面也可能平行,故D不正确.]当堂训练1.D [由棱柱的概念知,①③为棱柱.]2.D [由旋转体的结构特点知,D正确.]3.B [由棱台的结构特点知,B正确.]4.B [中线AD⊥BC,左右双侧对称,旋转体为圆锥.]5.2解析如下图,设等边三角形ABC为圆锥的轴截面,由题意知,圆锥的母线长即为△ABC的边长,且S△ABC=34AB2,∴3=34AB2,∴AB=2.故答案为2.。
[推荐学习]2018-2019学年高中数学 第一章 立体几何初步 1.2 直观图训练案 北师大版必修
1.2 直观图[A.基础达标]1.给出以下几个结论:①水平放置的角的直观图一定是角; ②相等的角在直观图中仍相等; ③相等的线段在直观图中仍相等;④若两条线段平行,则在直观图中对应的两条线段仍平行. 其中叙述正确的个数是( )A .1B .2C .3D .4解析:选B.由斜二测画法的规则知,结论①与④是正确的,故选B. 2.如图所示的直观图的原平面图形ABCD 是( )A .任意梯形B .直角梯形C .任意四边形D .平行四边形解析:选B.原图形ABCD 中,必有AB ⊥AD ,AD ∥BC ,且AD >BC ,故ABCD 是直角梯形. 3.如图所示的直观图是将正方体模型放置在你的水平视线的左下角而绘制的,其中正确的是( )解析:选A.根据把模型放在水平视线的左下角绘制的特点,并且由几何体的直观图画法及立体图形中虚线的使用知A 正确.4.水平放置的△ABC 的斜二测直观图如图所示,已知B ′C ′∥O ′y ′,B ′C ′=4,A ′C ′=3,则△ABC 中AB 边上的中线的长度为( )A.732B.73C .5 D.52解析:选A.把直观图还原成平面图形如图,得△ABC 为直角三角形,BC =8,AC =3,则AB 边上的中线为12 82+32=732.5.如图,正方形O ′A ′B ′C ′的边长为1 cm ,它是水平放置的一个平面图形的直观图,则原图形的周长为( )A .6 cmB .8 cmC .(2+32)cmD .(2+23)cm解析:选B.如图,原图形为OABC ,且OA =O ′A ′=1 cm ,OB =2O ′B ′=2 2 cm ,于是OC =AB =(22)2+12=3(cm), 故OABC 的周长为2×(1+3)=8(cm). 6.如图,△A ′B ′C ′为水平放置的△ABC 的直观图,则△ABC 中,最长的边为________.解析:由B ′C ′∥y ′轴,A ′B ′∥x ′轴知,△ABC 为直角三角形,∠B 为直角,AC 为斜边,故最长边为AC .答案:AC7.一个建筑物上部为四棱锥,下部为长方体,且四棱锥的底面与长方体的上底面尺寸一样,已知长方体的长、宽、高分别为20 m ,5 m ,10 m ,四棱锥的高为8 m ,若以长、宽、高所在直线分别为x ,y ,z 轴建立坐标系,按1∶500的比例画出它的直观图,那么直观图中长方体的长、宽、高和棱锥的高应分别为________.解析:由比例可知长方体的长、宽、高和棱锥的高应分别为4 cm ,1 cm ,2 cm 和1.6 cm ,再结合直观图,图形的尺寸应为4 cm ,0.5 cm ,2 cm ,1.6 cm.答案:4 cm ,0.5 cm ,2 cm ,1.6 cm8.如图所示是△AOB 用斜二测画法画出的直观图,则△AOB 的面积是________.解析:画出原图形△AOB (图略),则S △AOB =12×4×16=32.答案:329.如图所示,在平面直角坐标系中,各点坐标为O (0,0),A (1,3),B (3,1),C (4,6),D (2,5).试画出四边形ABCD 的直观图.解:(1)先画x ′轴和y ′轴,使∠x ′O ′y ′=45°(如图1).(2)在原图中作AE ⊥x 轴,垂足为E (1,0).(3)在x ′轴上截取O ′E ′=OE ,作A ′E ′∥y ′轴,截取E ′A ′=1.5.(4)同理确定点B ′,C ′,D ′,其中B ′G ′=0.5,C ′H ′=3,D ′F ′=2.5. (5)连线成图(去掉辅助线)(如图2).10.画一个上、下底面边长分别为0.8 cm、1.5 cm,高为1.5 cm的正三棱台的直观图.解:(1)画轴.画x轴、y轴、z轴三轴相交于O,使∠xOy=45°,∠xOz=90°;(2)画下底面.在y轴上正方向上截取线段OC,使OC=34cm,在y轴负半轴上截取OD=38cm,过D作线段AB∥x轴,使D为AB中点,AB=1.5 cm,连接BC,CA,则△ABC为正三棱台的下底面;(3)画上底面.在z轴上截取线段OO′,使OO′=1.5 cm.过O′点作O′x′∥Ox,O′y′∥Oy.建立坐标系x′O′y′,在x′O′y′中,重复(2)的步骤得上底面A′B′C′(取O′D′=315cm,A′B′=0.8 cm,O′C′=2315cm).(4)连线成图.连接AA′,BB′,CC′,擦去辅助线,被遮线画为虚线,则三棱台ABC-A′B′C′为要求画的三棱台的直观图.[B.能力提升]1.如图水平放置的正方形ABCO,在直角坐标系xOy中,点B的坐标为(2,2),则由斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为( )A.22B.1C. 2 D.2解析:选A.如图,由斜二测画法可知,在新坐标系x′O′y′中,B′C′=1,∠x′C′B′=45°,过B′作x′轴的垂线,垂足为D,在Rt△B′DC′中,B′D=B′C′sin 45°=1×22=22.2.如图所示是水平放置的三角形的直观图,D为△ABC中BC边上的中点,则平面图中AB,AD,AC三条线段中( )A.最长的是AB,最短的是ACB.最长的是AC,最短的是ABC.最长的是AB,最短的是ADD.最长的是AC,最短的是AD解析:选B.由斜二测画法的规则知,题图还原后如图所示,是一个∠B为直角的直角三角形,则AB 为一条直角边,由图可知,AC >AD >AB .3.如图,已知A (-1,0),B (2,0),C (0,2),则△ABC 的直观图的面积为________.解析:由已知得△ABC 的面积S =12·AB ·CO =12×3×2=3,于是其直观图的面积S ′=24S =24×3=324. 答案:3244.如图所示,四边形ABCD 是一平面图形水平放置的直观图.在直观图中,四边形ABCD 是一直角梯形,AB ∥CD ,AD ⊥CD ,且BC 与y ′轴平行.若AB =6,CD =4,则这个平面图形的实际面积是________.解析:由斜二测画法规则知,该图的平面图形A ′B ′C ′D ′也是一直角梯形,其中B ′C ′⊥C ′D ′,A ′B ′=6,C ′D ′=4,B ′C ′=2BC =2·6-4sin 45°=42,所以原平面图形A ′B ′C ′D ′的面积为S A ′B ′C ′D ′=12(6+4)×42=20 2.答案:20 25.如图为一几何体的展开图,沿图中虚线将它们折叠起来,请画出其直观图.解:由题设中所给的展开图可以得出,此几何体是一个四棱锥,其底面是一个边长为2的正方形,垂直于底面的侧棱长为2,其直观图如图所示.6.(选做题)如图所示,梯形ABCD 中,AB ∥CD ,AB =4 cm ,CD =2 cm ,∠DAB =30°,AD =3 cm ,试画出它的直观图.解:画法步骤:(1)如图①所示,在梯形ABCD 中,以边AB 所在的直线为x 轴,点A 为原点, 建立平面直角坐标系xOy .如图②所示,画出对应的x ′轴,y ′轴,使∠x ′O ′y ′=45°. (2)在图①中,过D 点作DE ⊥x 轴, 垂足为E .在图②中,在x ′轴上取A ′B ′=AB =4 cm ,A ′E ′=AE =323≈2.598 cm ;过点E ′作E ′D ′∥y ′轴,使E ′D ′=12ED =12×32=0.75 cm ,再过点D ′作D ′C ′∥x ′轴,且使D ′C ′=DC =2 cm.(3)连接A ′D ′,B ′C ′,并擦去x ′轴与y ′轴及其他一些辅助线,如图③所示,则四边形A ′B ′C ′D ′就是所求作的直观图.。
高中数学第一章立体几何初步章末复习学案北师大版必修
第一章立体几何初步章末复习学习目标 1.整合知识结构,梳理知识网络,进一步巩固、深化所学知识.2.熟练掌握平行关系与垂直关系,能自主解决一些实际问题.3.掌握几何体的直观图,能计算几何体的表面积与体积.1.空间几何体的结构特征及其侧面积和体积名称定义图形侧面积体积多面体棱柱有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行S直棱柱侧=Ch,C为底面的周长,h为高V=Sh棱锥有一个面是多边形,其余各面都是有一个公共顶点的三角形S正棱锥侧=12Ch′,C为底面的周长,h′为斜高V=13Sh,h为高棱台用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分S正棱台侧=12(C+C′)h′,C,C′V=13(S上+S下+S上S下)h,h为底面的周长,h′为斜高为高旋转体圆柱以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体S侧=2πrh,r为底面半径,h为高V=Sh=πr2h 圆锥以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体S侧=πrl,r为底面半径,h为高,l为母线V=13Sh=13πr2h圆台用平行于圆锥底面的平面去截圆锥,底面和截面之间的部分S侧=π(r1+r2)l,r1,r2为底面半径,l为母线V=13(S上+S下+S上S下)h=13π(r21+r22+r1r2)h球以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体S球面=4πR2,R为球的半径V=43πR32.空间几何体的直观图(1)斜二测画法:主要用于水平放置的平面图形或立体图形的画法.它的主要步骤:①画轴;②画平行于x、y、z轴的线段分别为平行于x′、y′、z′轴的线段;③截线段:平行于x、z轴的线段的长度不变,平行于y轴的线段的长度变为原来的一半.(2)转化思想在本章应用较多,主要体现在以下几个方面①曲面化平面,如几何体的侧面展开,把曲线(折线)化为线段.②等积变换,如三棱锥转移顶点等.③复杂化简单,把不规则几何体通过分割,补体化为规则的几何体等.3.四个公理公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内. 公理2:过不在同一条直线上的三点,有且只有一个平面.公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.公理4:平行于同一条直线的两条直线互相平行.4.直线与直线的位置关系⎩⎨⎧共面直线⎩⎪⎨⎪⎧平行相交异面直线:不同在任何一个平面内,没有公共点5.平行的判定与性质(1)直线与平面平行的判定与性质判定性质定义定理图形条件a∩α=∅aα,b⊈α,a∥ba∥αa∥α,aβ,α∩β=b 结论a∥αb∥αa∩α=∅a∥b (2)面面平行的判定与性质判定性质定义定理图形条件α∩β=∅aβ,bβ,a∩b=P,a∥α,b∥αα∥β,α∩γ=a,β∩γ=bα∥β,aβ结论α∥βα∥βa∥b a∥α(3)空间中的平行关系的内在联系6.垂直的判定与性质(1)直线与平面垂直图形条件结论判定a⊥b,bα(b为α内的任意直线)a⊥αa⊥m,a⊥n,m,nα,m∩n=Oa⊥αa∥b,a⊥αb⊥α性质a⊥α,bαa⊥ba⊥α,b⊥αa∥b(2)平面与平面垂直的判定与性质定理文字语言图形语言符号语言判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直⎭⎬⎫lβl⊥α⇒α⊥β性质定理如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面⎭⎪⎬⎪⎫α⊥βα∩β=alβl⊥a⇒l⊥α(3)空间中的垂直关系的内在联系7.空间角(1)异面直线所成的角①定义:设a,b是两条异面直线,经过空间任一点O作直线a′∥a,b′∥b,把a′与b′所成的锐角(或直角)叫作异面直线a,b所成的角(或夹角).②范围:设两异面直线所成角为θ,则0°<θ≤90°.(2)二面角的有关概念①二面角:从一条直线出发的两个半平面所组成的图形叫作二面角.②二面角的平面角:以二面角的棱上任一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角叫作二面角的平面角.1.设m ,n 是两条不同的直线,α,β是两个不同的平面,若m ∥α,n ∥β,α∥β,则m ∥n .( × )2.已知a ,b 是两异面直线,a ⊥b ,点P ∉a 且P ∉b ,一定存在平面α,使P ∈α,a ∥α且b ∥α.( √ )3.平面α∥平面β,直线a ∥α,直线b ⊥β,那么直线a 与直线b 的位置关系一定是垂直.( √ )4.球的任意两个大圆的交点的连线是球的直径.( √ )5.若m ,n 在平面α内的射影依次是一个点和一条直线,且m ⊥n ,则n α或n ∥α.( √ )类型一 平行问题例1 如图所示,四边形ABCD 是平行四边形,PB ⊥平面ABCD ,MA ∥PB ,PB =2MA .在线段PB 上是否存在一点F ,使平面AFC ∥平面PMD ?若存在,请确定点F 的位置;若不存在,请说明理由.考点 线、面平行、垂直的综合应用 题点 平行与垂直的计算与探索性问题解 当点F 是PB 的中点时,平面AFC ∥平面PMD ,证明如下:如图连接AC 和BD 交于点O ,连接FO ,则PF =12PB .∵四边形ABCD 是平行四边形,∴O 是BD 的中点.∴OF ∥PD . 又OF ⊈平面PMD ,PD 平面PMD , ∴OF ∥平面PMD .又MA ∥PB ,MA =12PB ,∴PF ∥MA ,PF =MA .∴四边形AFPM 是平行四边形.∴AF ∥PM .又AF ⊈平面PMD ,PM 平面PMD . ∴AF ∥平面PMD .又AF ∩OF =F ,AF 平面AFC ,OF 平面AFC . ∴平面AFC ∥平面PMD .反思与感悟 (1)证明线线平行的依据①平面几何法(常用的有三角形中位线、平行四边形对边平行);②公理4;③线面平行的性质定理;④面面平行的性质定理;⑤线面垂直的性质定理. (2)证明线面平行的依据①定义;②线面平行的判定定理;③面面平行的性质. (3)证明面面平行的依据①定义;②面面平行的判定定理;③线面垂直的性质;④面面平行的传递性.跟踪训练 1 如图所示,四棱锥P -ABCD 的底面是边长为8的正方形,四条侧棱长均为217.点G ,E ,F ,H 分别是棱PB ,AB ,CD ,PC 上共面的四点,平面GEFH ⊥平面ABCD ,BC ∥平面GEFH .(1)证明:GH ∥EF ;(2)若EB =2,求四边形GEFH 的面积. 考点 线、面平行、垂直的综合应用 题点 平行与垂直的计算与探索性问题 (1)证明 因为BC ∥平面GEFH ,BC 平面PBC , 且平面PBC ∩平面GEFH =GH ,所以GH ∥BC . 同理可证EF ∥BC , 因此GH ∥EF .(2)解 连接AC ,BD 交于点O ,BD 交EF 于点K ,连接OP ,GK . 因为PA =PC ,O 是AC 的中点,所以PO ⊥AC ,同理可得PO ⊥BD .又BD ∩AC =O ,且AC ,BD 平面ABCD , 所以PO ⊥平面ABCD .又因为平面GEFH ⊥平面ABCD ,所以平面GEFH 必过平面ABCD 的一条垂线, 所以PO 平行于这条垂线,且PO ⊈平面GEFH ,所以PO ∥平面GEFH .又因为平面PBD ∩平面GEFH =GK ,PO 平面PBD , 所以PO ∥GK ,所以GK ⊥平面ABCD .又EF 平面ABCD ,所以GK ⊥EF ,所以GK 是梯形GEFH 的高. 由AB =8,EB =2,得EB ∶AB =KB ∶DB =1∶4, 从而KB =14BD =12OB ,即K 是OB 的中点.再由PO ∥GK 得GK =12PO ,所以G 是PB 的中点,且GH =12BC =4.由已知可得OB =42,PO =PB 2-OB 2=68-32=6, 所以GK =3,故四边形GEFH 的面积S =GH +EF2·GK =4+82×3=18.类型二 垂直问题例2 如图所示,在四棱锥P -ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC =60°,PA =AB =BC ,E 是PC 的中点.证明:(1)CD ⊥AE ; (2)PD ⊥平面ABE .考点 直线与平面垂直的判定题点直线与平面垂直的证明证明(1)在四棱锥P-ABCD中,∵PA⊥底面ABCD,CD平面ABCD,∴PA⊥CD.∵AC⊥CD,PA∩AC=A,PA,AC平面PAC,∴CD⊥平面PAC.而AE平面PAC,∴CD⊥AE.(2)由PA=AB=BC,∠ABC=60°,可得AC=PA.∵E是PC的中点,∴AE⊥PC.由(1)知,AE⊥CD,且PC∩CD=C,PC,CD平面PCD,∴AE⊥平面PCD.而PD平面PCD,∴AE⊥PD.∵PA⊥底面ABCD,AB底面ABCD,∴PA⊥AB.又∵AB⊥AD且PA∩AD=A,PA,AD平面PAD,∴AB⊥平面PAD,而PD平面PAD,∴AB⊥PD.又∵AB∩AE=A,AB,AE平面ABE,∴PD⊥平面ABE.反思与感悟(1)两条异面直线相互垂直的证明方法①定义;②线面垂直的性质.(2)直线和平面垂直的证明方法①线面垂直的判定定理;②面面垂直的性质定理.(3)平面和平面相互垂直的证明方法①定义;②面面垂直的判定定理.跟踪训练2 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面ABC上的射影恰好是BC的中点,且BC=CA=AA1.(1)求证:平面ACC1A1⊥平面B1C1CB;(2)求证:BC1⊥AB1.考点平面与平面垂直的判定题点利用判定定理证明两平面垂直证明(1)设BC的中点为M,∵点B1在底面ABC上的射影恰好是点M,∴B1M⊥平面ABC.∵AC平面ABC,∴B1M⊥AC.又∵BC⊥AC,B1M∩BC=M,B1M,BC平面B1C1CB,∴AC⊥平面B1C1CB.又∵AC平面ACC1A1,∴平面ACC1A1⊥平面B1C1CB.(2)连接B1C.∵AC⊥平面B1C1CB,∴AC⊥BC1.在斜三棱柱ABC-A1B1C1中,∵BC=CC1.∴四边形B1C1CB是菱形,∴B1C⊥BC1.又∵B1C∩AC=C,∴BC1⊥平面ACB1,∴BC1⊥AB1.类型三空间角问题例3 如图,在正方体ABCD-A1B1C1D1中,E,F,M,N分别是A1B1,BC,C1D1和B1C1的中点.(1)求证:平面MNF⊥平面ENF;(2)求二面角M-EF-N的正切值.考点平面与平面垂直的判定题点利用判定定理证明两平面垂直(1)证明连接MN,∵N,F均为所在棱的中点,∴NF ⊥平面A 1B1C 1D 1. 而MN 平面A 1B 1C 1D 1, ∴NF ⊥MN .又∵M ,E 均为所在棱的中点,∴△C 1MN 和△B 1NE 均为等腰直角三角形. ∴∠MNC 1=∠B 1NE =45°, ∴∠MNE =90°,∴MN ⊥NE ,又NE ∩NF =N , ∴MN ⊥平面NEF .而MN 平面MNF ,∴平面MNF ⊥平面ENF .(2)解 在平面NEF 中,过点N 作NG ⊥EF 于点G ,连接MG . 由(1)知MN ⊥平面NEF ,又EF 平面NEF ,∴MN ⊥EF .又MN ∩NG =N , ∴EF ⊥平面MNG ,∴EF ⊥MG .∴∠MGN 为二面角M -EF -N 的平面角. 设该正方体的棱长为2, 在Rt△NEF 中,NG =NE ·NF EF =233, ∴在Rt△MNG 中,tan∠MGN =MN NG =2233=62.∴二面角M -EF -N 的正切值为62. 反思与感悟 (1)面面垂直的证明要化归为线面垂直的证明,利用垂直关系的相互转化是证明的基本方法;(2)找二面角的平面角的方法有以下两种:①作棱的垂面;②过一个平面内一点作另一个平面的垂线,过垂足作棱的垂线.跟踪训练3 如图,在圆锥PO 中,已知PO ⊥底面⊙O ,PO =2,⊙O 的直径AB =2,C 是AB 的中点,D 为AC 的中点.(1)证明:平面POD⊥平面PAC;(2)求二面角B-PA-C的余弦值.考点平面与平面垂直的判定题点利用判定定理证明两平面垂直(1)证明连接OC.∵PO⊥底面⊙O,AC底面⊙O ,∴AC⊥PO.∵OA=OC,D是AC的中点,∴AC⊥OD.又∵OD∩PO=O,∴AC⊥平面POD.又∵AC平面PAC,∴平面POD⊥平面PAC.(2)解在平面POD内,过点O作OH⊥PD于点H. 由(1)知,平面POD⊥平面PAC,又平面POD∩平面PAC=PD,∴OH⊥平面PAC.又∵PA平面PAC,∴PA⊥OH.在平面PAO中,过点O作OG⊥PA于点G,连接HG,则有PA⊥平面OGH,∴PA⊥HG.故∠OGH为二面角B-PA-C的平面角.∵C是AB的中点,AB是直径,∴OC⊥AB.在Rt△ODA中,OD=OA·sin 45°=22.在Rt△POD中,OH=PO·ODPD=PO·ODPO2+OD2=2×222+12=105.在Rt△POA中,OG=PO·OAPA=PO·OAPO2+OA2=2×12+1=63.在Rt△OHG中,sin∠OGH=OHOG =10563=155.∴cos∠OGH=1-sin2∠OGH=1-1525=105.故二面角B-PA-C的余弦值为105.1.如图所示,观察四个几何体,其中判断正确的是( )A.①是棱台B.②是圆台C.③是棱锥D.④不是棱柱考点空间几何体题点空间几何体结构判断答案 C解析图①不是由棱锥截来的,所以①不是棱台;图②上、下两个面不平行,所以②不是圆台;图③是棱锥,图④前、后两个面平行,其他面是平行四边形,且每相邻两个四边形的公共边平行,所以④是棱柱,故选C.2.设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个说法:①若m⊥α,n ∥α,则m⊥n;②若α∥β,β∥γ,m∥α,则m∥γ;③若m∥α,n∥α,则m∥n;④若α⊥γ,β⊥γ,则α∥β.其中正确说法的序号是( )A.① B.②③ C.③④ D.①④考点线、面平行、垂直的综合应用题点平行与垂直的判定答案 A解析②如果mγ,则m不平行于γ;③若m∥α,n∥α,则m,n相交,平行或异面,④若α⊥γ,β⊥γ,则α,β相交或平行.3.正方体的8个顶点中,有4个为每个面都是等边三角形的正三棱锥的顶点,则这个三棱锥的表面积与正方体的表面积之比为( )A.1∶ 2 B.1∶ 3 C.2∶ 2 D.3∶ 6考点题点答案 B解析设正方体棱长为a,S正方体表面积=6a2,正三棱锥侧棱长为2a,则三棱锥表面积为S三棱锥表面积=4×34×2a2=23a2.∴S三棱锥表面积S正方体表面积=23a26a2=13.4.水平放置的△ABC的直观图如图所示,其中B′O′=C′O′=1,A′O′=32,那么原△ABC是一个( )A.等边三角形B.直角三角形C.三边中只有两边相等的等腰三角形D.三边互不相等的三角形考点平面图形的直观图题点由直观图还原平面图形答案 A解析由图形,知在原△ABC中,AO⊥BC.∵A′O′=32,∴AO= 3.∵B′O′=C′O′=1,∴BC=2,AB=AC=2,∴△ABC为等边三角形.故选A.5.如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;(2)求证:平面MOC⊥平面VAB.考点线、面平行、垂直的综合应用题点平行、垂直综合问题的证明证明(1)因为O,M分别为AB,VA的中点,所以OM∥VB.又因为VB⊈平面MOC,OM平面MOC,所以VB∥平面MOC.(2)因为AC=BC,O为AB的中点,所以OC⊥AB.又因为平面VAB⊥平面ABC,平面VAB∩平面ABC=AB,且OC平面ABC,所以OC⊥平面VAB.又因为OC平面MOC,所以平面MOC⊥平面VAB.1.转化思想是证明线面平行与垂直的主要思路,其关系为一、选择题1.给出下列说法中正确的是( )A.棱柱被平面分成的两部分可以都是棱柱B.底面是矩形的平行六面体是长方体C.棱柱的底面一定是平行四边形D.棱锥的底面一定是三角形考点多面体的结构特征题点多面体的结构特征答案 A解析平行于棱柱底面的平面可以把棱柱分成两个棱柱,故A正确;三棱柱的底面是三角形,故C错误;底面是矩形的平行六面体的侧面不一定是矩形,故它也不一定是长方体,故B错误;四棱锥的底面是四边形,故D错误.故选A.2.如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积为( )A.6 B.3 2C.6 2 D.12答案 D解析由斜二测画法规则可知,△OAB为直角三角形,且两直角边长分别为4和6,故面积为12.3.下列说法正确的是( )A.经过空间内的三个点有且只有一个平面B.如果直线l上有一个点不在平面α内,那么直线上所有点都不在平面α内C.四棱锥的四个侧面可能都是直角三角形D.用一个平面截棱锥,得到的几何体一定是一个棱锥和一个棱台考点线、面关系的综合问题题点线、面关系的其他综合问题答案 C解析在A中,经过空间内的不共线的三个点有且只有一个平面,故A错误;在B中,如果直线l上有一个点不在平面α内,那么直线与平面相交或平行,则直线上最多有一个点在平面α内,故B错误;在C中,如图的四棱锥,底面是矩形,一条侧棱垂直底面,那么它的四个侧面都是直角三角形,故C正确;在D中,用一个平行于底面的平面去截棱锥,得到两个几何体,一个是棱锥,一个是棱台,故D错误.故选C.4.设α-l-β是二面角,直线a在平面α内,直线b在平面β内,且a,b与l均不垂直,则( )A.a与b可能垂直也可能平行B.a与b可能垂直,但不可能平行C.a与b不可能垂直,但可能平行D.a与b不可能垂直,也不可能平行考点空间中直线与直线的位置关系题点空间中直线与直线的位置关系的判定答案 A解析 ∵α-l -β是二面角,直线a 在平面α内,直线b 在平面β内,且a ,b 与l 均不垂直,∴当a ∥l ,且b ∥l 时,由平行公理得a ∥b ,即a ,b 可能平行,故B 与D 不正确;当a ,b 垂直时,若二面角是直二面角,则a ⊥l 与已知矛盾,若二面角不是直二面角,则a ,b 可以垂直,且满足条件,故C 不正确;∴a 与b 有可能垂直,也有可能平行,故选A.5.在空间中,a ,b 是不重合的直线,α,β是不重合的平面,则下列条件中可推出a ∥b 的是( )A .a α,b β,α∥βB .a ∥α,b αC .a ⊥α,b ⊥αD .a ⊥α,b α考点 直线与平面垂直的性质题点 应用线面垂直的性质定理判定线线平行 答案 C解析 对于A ,若a α,b β,α∥β,则a 与b 没有公共点,即a 与b 平行或异面;对于B ,若a ∥α,b α,则a 与b 没有公共点,即a 与b 平行或异面;对于C ,若a ⊥α,b ⊥α,由线面垂直的性质定理,可得a ∥b ;对于D ,若a ⊥α,b α,则由线面垂直的定义可得a ⊥b ,故选C.6.《算数书》竹简于上世纪八十年代在湖北省张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“禾盖”的术:置如其周,令相乘也,又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L 与高h ,计算其体积V 的近似公式V ≈136L 2h .它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V ≈7264L 2h 相当于将圆锥体积公式中的圆周率π近似取为( ) A.15750 B.258 C.237 D.7考点 柱体、锥体、台体的体积 题点 锥体的体积 答案 D解析 设圆锥的底面半径为r ,则圆锥的底面周长L =2πr ,∴r =L2π,∴V =13πr 2h =L 2h 12π.令L 2h12π=7264L 2h ,得π=7,故选D. 7.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为( )A.26 B.36 C.23 D.22答案 A解析 由于三棱锥S -ABC 与三棱锥O -ABC 底面都是△ABC ,O 是SC 的中点,因此三棱锥S -ABC 的高是三棱锥O -ABC 高的2倍,所以三棱锥S -ABC 的体积也是三棱锥O -ABC 体积的2倍.在三棱锥O -ABC 中,其棱长都是1,如图所示,S △ABC =34×AB 2=34, 高OD =12-⎝⎛⎭⎪⎫332=63, ∴V S -ABC =2V O -ABC =2×13×34×63=26.8.在长方体ABCD -A 1B 1C 1D 1中,若AB =AD =23,CC 1=2,则二面角C 1-BD -C 的大小为( )A .30° B.45° C.60° D.90° 考点 二面角 题点 知题作角 答案 A解析 如图,连接AC 交BD 于点O ,连接OC 1.因为AB =AD =23,所以AC ⊥BD , 又易知BD ⊥平面ACC 1A 1, 所以BD ⊥OC 1,所以∠COC 1为二面角C 1-BD -C 的一个平面角. 因为在△COC 1中,OC =6,CC 1=2, 所以tan∠COC 1=33, 所以二面角C 1-BD -C 的大小为30°.二、填空题9.圆台的母线长为2a ,母线与轴的夹角为30°,一个底面圆的半径是另一个底面圆的半径的2倍,则两底面圆的半径分别为________. 考点 题点 答案 a ,2a解析 如图,画出圆台轴截面,由题设,得∠OPA =30°,AB =2a , 设O 1A =r ,PA =x ,则OB =2r ,x +2a =4r ,且x =2r , ∴a =r ,即两底面圆的半径分别为a ,2a .10.一个正四面体木块如图所示,点P 是棱VA 的中点,过点P 将木块锯开,使截面平行于棱VB 和AC ,若木块的棱长为a ,则截面面积为________.考点 直线与平面平行的性质 题点 与性质有关的计算问题 答案a 24解析 在平面VAC 内作直线PD ∥AC ,交VC 于D ,在平面VBA 内作直线PF ∥VB ,交AB 于F ,过点D 作直线DE ∥VB ,交BC 于E ,连接EF .∴PF ∥DE ,∴P ,D ,E ,F 四点共面,且面PDEF 与VB 和AC 都平行, 则四边形PDEF 为边长为12a 的正方形,故其面积为a 24.11.如图,若边长为4和3与边长为4和2的两个矩形所在平面互相垂直,则cos α∶cosβ=________.考点 平面与平面垂直的性质 题点 有关面面垂直性质的计算 答案5∶2解析 由题意,两个矩形的对角线长分别为5,25, 所以cos α=525+4=529, cos β=2529,所以cos α∶cos β=5∶2. 三、解答题12.如图所示,在正三棱柱ABC -A 1B 1C 1中,AB =3,AA 1=4,M 为AA 1的中点,P 是BC 上的一点,且由P 沿棱柱侧面经过棱CC 1到M 的最短路线为29.设这条最短路线与CC 1的交点为N ,求:(1)该三棱柱的侧面展开图的对角线的长; (2)PC 和NC 的长.考点 多面体表面上绕线最短距离问题 题点 棱柱体表面上绕线最短距离问题解 (1)该三棱柱的侧面展开图是宽为4,长为9的矩形, 所以对角线的长为42+92=97.(2)将该三棱柱的侧面沿棱BB 1展开,如图所示.设PC 的长为x , 则MP 2=MA 2+(AC +x )2.因为MP =29,MA =2,AC =3,所以x =2(负值舍去),即PC 的长为2. 又因为NC ∥AM ,所以PC PA =NC AM ,即25=NC 2,所以NC =45.13.如图所示,在几何体ABCDFE 中,△ABC ,△DFE 都是等边三角形,且所在平面平行,四边形BCED 是边长为2的正方形,且所在平面垂直于平面ABC .(1)求几何体ABCDFE 的体积; (2)证明:平面ADE ∥平面BCF . 考点 题点(1)解 取BC 的中点为O ,ED 的中点为G ,连接AO ,OF ,FG ,AG .∵AO ⊥BC ,AO 平面ABC ,平面BCED ⊥平面ABC , 平面BCED ∩平面ABC =BC , ∴AO ⊥平面BCED . 同理FG ⊥平面BCED . ∵AO =FG =3,∴V ABCDFE =13×4×3×2=833.(2)证明 由(1)知AO ∥FG ,AO =FG , ∴四边形AOFG 为平行四边形, ∴AG ∥OF .又∵DE ∥BC ,DE ∩AG =G ,DE平面ADE ,AG 平面ADE ,FO ∩BC =O ,FO 平面BCF ,BC平面BCF,∴平面ADE∥平面BCF.四、探究与拓展14.如图所示,在长方体ABCD-A1B1C1D1中,若AB=BC,E,F分别是AB1,BC1的中点,则下列结论中成立的是( )①EF与BB1垂直;②EF⊥平面BCC1B1;③EF与C1D所成的角为45°;④EF∥平面A1B1C1D1.A.②③ B.①④ C.③ D.①②④考点线面平行、垂直的综合应用题点平行与垂直的判定答案 B解析显然①④正确,②③错误.15.如图,在△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将△BAO沿AO折起,使B点与图中B′点重合.(1)求证:AO⊥平面B′OC;(2)当三棱锥B′-AOC的体积取最大时,求二面角A-B′C-O的余弦值;(3)在(2)的条件下,试问在线段B ′A 上是否存在一点P ,使CP 与平面B ′OA 所成的角的正弦值为53?证明你的结论,并求AP 的长. 考点 空间角问题题点 空间角的综合问题(1)证明 ∵AB =AC 且O 是BC 的中点,∴AO ⊥BC ,即AO ⊥OB ′,AO ⊥OC ,又∵OB ′∩OC =O ,OB ′平面B ′OC ,OC 平面B ′OC ,∴AO ⊥平面B ′OC .(2)解 在平面B ′OC 内,作B ′D ⊥OC 于点D ,则由(1)可知B ′D ⊥OA ,又OC ∩OA =O ,∴B ′D ⊥平面OAC ,即B ′D 是三棱锥B ′-AOC 的高,又B ′D ≤B ′O ,∴当D 与O 重合时,三棱锥B ′-AOC 的体积最大,过O 作OH ⊥B ′C 于点H ,连接AH ,如图.由(1)知AO ⊥平面B ′OC ,又B ′C 平面B ′OC ,∴B ′C ⊥AO ,∵AO ∩OH =O ,∴B ′C ⊥平面AOH ,∴B ′C ⊥AH ,∴∠AHO 即为二面角A -B ′C -O 的平面角.在Rt△AOH 中,AO =2,OH =22,∴AH =322, ∴cos∠AHO =OH AH =13, 故二面角A -B ′C -O 的余弦值为13. (3)解 如图,连接OP ,在(2)的条件下,易证OC ⊥平面B ′OA ,∴CP 与平面B ′OA 所成的角为∠CPO , ∴sin∠CPO =OC CP =53, ∴CP =35. 又在△ACB ′中,sin∠AB ′C =310=CP 2, ∴CP ⊥AB ′,∴B ′P =22-CP 2=55,∴AP =455.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2 直观图1.掌握斜二测画法的步骤.(重点)2.会用斜二测画法画出一些简单平面图形和立体图形的直观图.(重点、难点)3.通过观察直观图,了解空间几何体的表示形式,进一步认识几何体的结构特征.[基础·初探]教材整理1 斜二测画法的规则阅读教材P 7~P 8倒数第3行以上部分,完成下列问题.1.在已知图形中建立直角坐标系xOy .画直观图时,它们分别对应x ′轴和y ′轴,两轴交于点O ′,使∠x ′O ′y ′=45°,它们确定的平面表示水平平面.2.已知图形中平行于x 轴或y 轴的线段,在直观图中分别画成平行于x ′轴和y ′轴的线段.3.已知图形中平行于x 轴的线段,在直观图中保持原长度不变;平行于y 轴的线段,长度为原来的12.判断(正确的打“√”,错误的打“×”)(1)用斜二测画法画直观图时,在原图x 轴上长为4的线段,在直观图中的长度为4.( )(2)正方形的直观图仍是正方形.( ) (3)平行四边形的直观图仍是平行四边形.( )(4)用斜二测画法画直观图时,平行于y 轴的线段在直观图中长度减半.( ) 【答案】 (1)√ (2)× (3)√ (4)√ 教材整理2 立体图形的直观图的画法阅读教材P 8最后一段至P 12“练习”以上部分,完成下列问题. 立体图形直观图画法的“四步曲”在棱长为4 cm 的正方体ABCD A 1B 1C 1D 1中,作直观图时,棱AA 1在x 轴上,棱AD 在y 轴上,则在其直观图中,对应棱A ′D ′的长为________cm ,棱A ′A 1′的长为________cm.【解析】 在x 轴上的线段长度不变,故A ′A 1′=4 cm ,在y 轴上的线段变成原来的一半,故A ′D ′=2 cm.【答案】 2 4[小组合作型]图121【精彩点拨】 按照斜二测画法画水平放置的平面图形的画法步骤画直观图. 【自主解答】 (1)如图(1)所示,取AB 所在直线为x 轴,AB 中点O 为原点,建立直角坐标系,再建立如图(2)所示的坐标系x ′O ′y ′,使∠x ′O ′y ′=45°.(2)在图(2)中,以O ′为中点在x ′轴上取A ′B ′=AB .(3)在y ′轴上取O ′E ′=12OE ,以E ′为中点画C ′D ′∥x ′轴,并使C ′D ′=CD .(4)连接B ′C ′,D ′A ′,去掉辅助线,所得的四边形A ′B ′C ′D ′就是水平放置的等腰梯形ABCD 的直观图.如图(3)所示.1.画水平放置的平面多边形的直观图的关键是确定多边形顶点的位置.顶点位置可以分为两类:一类是在轴上或在与轴平行的线段上,这类顶点比较容易确定;另一类是不在轴上且不在与轴平行的线段上,这类顶点一般通过过此点作与轴平行的线段,将此点转到与轴平行的线段上来确定.2.要画好对应平面图形的直观图,首先应在原图形中确定直角坐标系,然后在此基础上画出水平放置的平面坐标系.[再练一题]1.用斜二测画法画如图122所示边长为4 cm 的水平放置的正三角形的直观图.【导学号:39292005】图122【解】 (1)如图①所示,以BC 边所在的直线为x 轴,以BC 边上的高线AO 所在的直线为y 轴.(2)画对应的x ′轴、y ′轴,如图②, 使∠x ′O ′y ′=45°.在x ′轴上截取O ′B ′=O ′C ′=OB =OC =2 cm ,在y ′轴上取O ′A ′=12OA ,连接A ′B ′,A ′C ′,去掉辅助线则三角形A ′B ′C ′即为正三角形ABC 的直观图,如图③所示.画出底面是正方形,侧棱均相等的四棱锥的直观图.【精彩点拨】 本题所要画的是四棱锥的直观图,是空间图形,所以要先画底面,先画水平放置的正方形的直观图.再画侧棱,最后成图.【自主解答】 画法:(1)画轴.画Ox 轴,Oy 轴,Oz 轴,∠xOy =45°(或135°),∠xOz =90°,如图.(2)画底面.以O 为中心在xOy 平面内,画出正方形的直观图ABCD . (3)画顶点.在Oz 轴上截取OP 使OP 的长度等于原四棱锥的高.(4)成图.顺次连接PA ,PB ,PC ,PD ,并擦去辅助线,将被遮住的部分改为虚线,得四棱锥的直观图.画空间几何体时,首先依照斜二测画法规则画出几何体的底面直观图,然后根据平行于z 轴的线段在直观图中保持长度不变,画出几何体的各侧面,所以画空间多面体的步骤可简单总结为:画轴→画底面→画侧棱→成图[再练一题]2.用斜二测画法画长、宽、高分别为4 cm,3 cm,2 cm 的长方体ABCD -A ′B ′C ′D ′的直观图.【解】 画法:(1)画轴.如图,画x 轴、y 轴、z 轴,三轴相交于点O ,使∠xOy =45°,∠xOz =90°.(2)画底面.以点O 为中点,在x 轴上取线段MN ,使MN =4 cm ;在y 轴上取线段PQ ,使PQ =32cm.分别过点M 和N 作y 轴的平行线,过点P 和Q 作x 轴的平行线,设它们的交点分别为A ,B ,C ,D ,四边形ABCD 就是长方体的底面ABCD .(3)画侧棱.过A ,B ,C ,D 各点分别作z 轴的平行线,并在这些平行线上分别截取2 cm 长的线段AA ′,BB ′,CC ′,DD ′.(4)成图.顺次连接A ′,B ′,C ′,D ′,并加以整理(去掉辅助线,将被遮挡的部分改为虚线),就得到长方体的直观图.[探究共研型]探究1 h ,图123根据直观图你知道原图形是什么吗?它有什么特点? 【提示】 原图形是一个直角梯形且高为2 h.探究2 已知△ABC 的直观图如图124所示,你能求出原△ABC 的面积吗?你发现直观图的画与原图形面积有何关系?图124【提示】 由题意,易知在△ABC 中,AC ⊥AB ,且AC =6,AB =3, ∴S △ABC =12×6×3=9.又S △A ′B ′C ′=12×3×(3sin 45°)=924,∴S △A ′B ′C ′=24S △ABC .如图125所示,一个水平放置的平面图形的斜二测画法的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,求原四边形的面积.图125【精彩点拨】 分别以A ′B ′,B ′C ′所在的直线为x ′轴,y ′轴,画出该直观图的对应图形,然后求面积.【自主解答】 如图(1)是四边形的直观图,取B ′C ′所在直线为x ′轴.因为∠A ′B ′C ′=45°,所以取B ′A ′所在直线为y ′轴.过D ′作D ′E ′∥A ′B ′,D ′E ′交B ′C ′于E ′,则B ′E ′=A ′D ′=1. 又因为梯形为等腰梯形,所以△E ′D ′C ′为等腰直角三角形,所以E ′C ′= 2.再建立一个直角坐标系xOy ,则O ,B 重合,如图(2)所示,在x 轴上截取线段BC =B ′C ′=1+2,在y 轴上截取线段BA =2B ′A ′=2.过A 作AD ∥BC ,截取AD =A ′D ′=1.连接CD ,则四边形ABCD 就是四边形A ′B ′C ′D ′的平面图形.四边形ABCD 为直角梯形,上底AD =1,下底BC =1+2,高AB =2,所以S 梯形ABCD =12AB ·(AD+BC )=12×2×(1+1+2)=2+ 2.将直观图还原为平面图的关键是找与x ′轴,y ′轴平行的直线或线段, 且平行于x ′轴的线段还原时长度不变,平行于y ′轴的线段被还原时放大为直观图中相应线段长的2倍,由此确定图形的各个顶点,顺次连接即可.由直观图中的已知量来计算原图形中的量,应依据线段的变化规律分别在两个图中计算.[再练一题]3.已知△ABC 的平面直观图△A ′B ′C ′是边长为a 的正三角形,那么原△ABC 的面积为( )A.32a 2B.34a 2 C.62a 2 D.6a 2【解析】 如图(1)为直观图,图(2)为实际图形.取B ′C ′所在直线为x ′轴,过B ′C ′中点O ′与O ′x ′成45°的直线为y ′轴,过A ′点作A ′N ′∥O ′x ′,交y ′轴于N ′点,过A ′点作A ′M ′∥O ′y ′,交x ′轴于M ′点.在直角三角形A ′O ′M ′中,∵O ′A ′=32a ,∠A ′M ′O ′=45°,∴A ′M ′=62a , 则AM =2A ′M ′=6a , ∴S △ABC =12×a ×6a =62a 2.【答案】 C1.用斜二测画法得到:①相等的线段和角在直观图中仍然相等; ②正方形的直观图是矩形;③等腰梯形的直观图仍然是等腰梯形; ④菱形的直观图仍然是菱形. 上述结论正确的个数是( ) A.0 B.1 C.2 D.3【解析】 根据斜二测画法通过举反例可知,上述结论全部错误. 【答案】 A2.如图126所示为一个平面图形的直观图,则原四边形ABCD 为( )图126A.平行四边形B.梯形C.菱形D.矩形【解析】 因为∠D ′A ′B ′=45°,由斜二测画法规则知∠DAB =90°,又因四边形A ′B ′C ′D ′为平行四边形,所以原四边形ABCD 为矩形.【答案】 D3.水平放置的△ABC 的斜二测直观图如图127所示,已知A ′C ′=3,B ′C ′=2,则AB 边上的中线的实际长度为________.图127【解析】 还原成原图是以3,4为直角边的直角三角形,而斜边上的中线等于斜边的一半.【答案】 2.54.如图128为△ABO 水平放置的直观图,其中O ′D ′=B ′D ′=2A ′D ′,且B ′D ′∥y ′轴由图判断原三角形中AB ,OB ,BD ,OD 由小到大的顺序是________.图128【解析】 将直观图还原为平面图形如下,由三角形的有关性质可知,OB >AB >BD >OD . 【答案】 OD <BD <AB <OB5.已知一等腰△ABC 底边AB =a ,高为32a ,求用斜二测画法得到的直观图的面积. 【导学号:39292006】【解】 如图(1)(2)所示的是实际图形和直观图, 由图可知,A ′B ′=AB =a ,O ′C ′=12OC =34a ,在图(2)中作C ′D ′⊥A ′B ′于D ′,则C ′D ′=22O ′C ′=68a , 所以S △A ′B ′C ′=12A ′B ′·C ′D ′=12×a ×68a =616a 2.。
