圆柱和圆锥的体积ppt
合集下载
六年级下册数学课件-2.4圆锥的体积苏教版共21张PPT

4.圆柱表面积的计算方法: 如果用S侧表示一个圆柱的侧面积,S底表示底面积,d表示底面直径, r表示底面半径,h表示高,那么这个圆柱的表面积为: S表=S侧+2S底 S表=πdh+2π(d÷2)² S表=2πrh+2πr²
5.圆柱表面积的计算方法的特殊应用: (1)圆柱的表面积只包括侧面积和一个底面积的,例如无盖水桶等圆 柱形物体。 (2)圆柱的表面积只包括侧面积的,例如烟囱、油管等圆柱形物体。 (3)圆柱的表面积包括侧面积和两个底面的,例如油桶等圆柱形物体。
3.圆锥的特征: (1)圆锥的底面是一个圆。 (2)圆锥的侧面是一个曲面。 (3)圆锥只有一条高。 (4)圆锥的侧面展开是一个扇形。
二、 圆柱的表面积 1.沿圆柱的高剪开,圆柱的侧面展开图是一个长方形(或正方形)。 (如果不是沿高剪开,有可能还会是平行四边形) 2.圆柱的侧面积=底面周长×高,用字母表示为: S侧=ch。 3.圆柱的侧面积公式的应用: (1)已知底面周长和高,求侧面积,可运用公式:S侧=ch; (2)已知底面直径和高,求侧面积,可运用公式:S侧=πdh; (3)已知底面半径和高,求侧面积,可运用公式:S侧=2πrh
第2单元 圆柱和圆锥
第4节 圆锥的体积
谈话引入
如果要知道这个容器 的容积,怎么办?
求体积
如果想知道这个容 器的容积,怎么办?
圆锥的体积
教学例5
这个圆柱和圆锥有什么相同的地方?
等底等高
估计一下,这个 圆锥的体积是这 个圆柱体积的几 分之几?
估计一下,这个圆锥的体积是这个圆柱体积的几分之几?
等底等高
求体积: 一个圆锥形谷堆, 底面直径为 6 m, 高 1.2 m。
(2) 如果每立方米稻谷的质量为 700 kg, 这堆稻谷的质量为多少千 克?
《简单几何体的表面积与体积》立体几何初步PPT课件(圆柱、圆锥、圆台、球的表面积与体积)

手 抄 报 : /shouchaobao/
PPT课 件 : /kejian/
语 文 课 件 : /kejian/yuwen/ 数 学 课 件 : /kejian/shuxue/
英 语 课 件 : /kejian/yingyu/ 美 术 课 件 : /kejian/meishu/
个 人 简 历 : /jianli/
试 卷 下 载 : /shiti/
教 案 下 载 : /jiaoan/
手 抄 报 : /shouchaobao/
PPT课 件 : /kejian/
知识点三 手抄报:/shouchaobao/
PPT课 件 : /kejian/
语 文 课 件 : /kejian/yuwen/ 数 学 课 件 : /kejian/shuxue/
英 语 课 件 : /kejian/yingyu/ 美 术 课 件 : /kejian/meishu/
科 学 课 件 : /kejian/kexue/ 物 理 课 件 : /kejian/wuli/
化 学 课 件 : /kejian/huaxue/ 生 物 课 件 : /kejian/shengwu/
地 理 课 件 : /kejian/dili/
历 史 课 件 : /kejian/lishi/
手 抄 报 : /shouchaobao/
PPT课 件 : /kejian/
语 文 课 件 : /kejian/yuwen/ 数 学 课 件 : /kejian/shuxue/
英 语 课 件 : /kejian/yingyu/ 美 术 课 件 : /kejian/meishu/
必修第二册·人教数学A版
知识点二 圆柱、圆锥、圆台的体积 知识梳理
人教版六年级下册数学《圆柱的体积》圆柱与圆锥说课教学复习课件

(1)帽子的侧面积:3.14×20×30=1884(平方厘米)
比计算结果
(2)帽顶的面积:3.14×(20÷2)2 =314(平方厘米)
以这类问题
(3)需要用的材料:1884+314=2198 ≈ 2200(平方厘米)
答:做这样一顶帽子至少需要用2200平方厘米的材料。
多一些,所
往往用“进
一法”取近
手抄报:课件/shouchaobao/
课件
课件 课件
课件 课件
课件
课件
课件 课件
课件
课件
UNDERSTANDING
课件
OF
CYLINDER
两个底面 ——圆
一个侧面 ——曲面
侧面展开是一个长方形。
你知道怎么计算
涂色的面积吗?
涂色面积就是圆柱的表面积。
圆柱表面积 = 侧面积 + 两个 2× 底面积
想一想:计算圆柱表面积需要知道哪些量?
也就是求前轮的侧面积。
前轮的侧面积:
3.14×1.2×2=7.536(m2)
答:压路的面积是7.536平方米。
2m
做一个无盖的圆柱形铁皮水桶,高是5分米。底面直径4分米,至少需要
多大面积的铁皮?
(1)水桶的侧面积:
求水桶的侧面积
和一个底面积。
4dm
5dm
3.14×4×5=62.8(平方分米)
(2)水桶的底面积:
面直径6cm的饮料
罐的长度。
箱子的宽是4个底
面直径6cm的饮料
罐的长度。
12c
m
圆柱的侧面积=底面周长×高
底面周长:C
高:h
半径:r
S侧 = Ch
圆柱的表面积=侧面积 + 两个底面的面积
8.3.2 圆柱、圆锥、圆台、球表面积和体积(课件)2022-2023学年高一下学期数学(人教A版2

解:当球内切于正方体时用料最省 此时棱长=直径=5cm
答:至少要用纸150cm2
练习
解析 设球 O 的半径为 r,则圆柱的底面半径为 r, 高为 2r,所以VV12=π43rπ2·r23r=32.
三、课堂小结:
1.圆柱、圆锥、圆台的表面积公式
1).圆柱 2).圆锥
S 2r 2 rl
S r 2 rl
如果圆台的上、下底面半径分别为r和R,母线长为l,你能计算它的
表面积吗?
r O’
RO
圆台的侧面展开图是扇环
x x
r 'O’
rO
xl r x r' l rr' x r'
xl 1 r 1 x r'
x r' l r r'
∵圆台侧面展开图是一个扇环
S侧面积
1 2
2 r( x
l)
1 2
2 r
'
x
r( x l ) r ' x rx rl r ' x
A
B
D
C
A1 D1
B1 C1
变式 球的内接长方体的长、宽、高分别为3、2、 3 ,求此球体的表面积 和体积。
分析:长方体内接于球,则由球和长方体都是中心对称图形可知,它们 中心重合,则长方体对角线与球的直径相等。
内切球问题
例题3 把直径为5cm钢球放入一个正方体的有盖纸盒中,至少要用多少纸? 分析:用料最省时,球与正方体有什么位置关系? 球内切于正方体
解:一个浮标的表面积为
2π×0.15×0.6 + 4π×0.152 =0.8478(m2) 所以给1000个这样的浮标涂防水漆约需涂料
0.8478×0.5×1000 =423.9(kg).
答:至少要用纸150cm2
练习
解析 设球 O 的半径为 r,则圆柱的底面半径为 r, 高为 2r,所以VV12=π43rπ2·r23r=32.
三、课堂小结:
1.圆柱、圆锥、圆台的表面积公式
1).圆柱 2).圆锥
S 2r 2 rl
S r 2 rl
如果圆台的上、下底面半径分别为r和R,母线长为l,你能计算它的
表面积吗?
r O’
RO
圆台的侧面展开图是扇环
x x
r 'O’
rO
xl r x r' l rr' x r'
xl 1 r 1 x r'
x r' l r r'
∵圆台侧面展开图是一个扇环
S侧面积
1 2
2 r( x
l)
1 2
2 r
'
x
r( x l ) r ' x rx rl r ' x
A
B
D
C
A1 D1
B1 C1
变式 球的内接长方体的长、宽、高分别为3、2、 3 ,求此球体的表面积 和体积。
分析:长方体内接于球,则由球和长方体都是中心对称图形可知,它们 中心重合,则长方体对角线与球的直径相等。
内切球问题
例题3 把直径为5cm钢球放入一个正方体的有盖纸盒中,至少要用多少纸? 分析:用料最省时,球与正方体有什么位置关系? 球内切于正方体
解:一个浮标的表面积为
2π×0.15×0.6 + 4π×0.152 =0.8478(m2) 所以给1000个这样的浮标涂防水漆约需涂料
0.8478×0.5×1000 =423.9(kg).
圆柱和圆锥的体积
长方体的底面积等于圆柱体的底面积 长方体的高等于圆柱体的高
长方体的体积=长×宽×高 圆柱的体积=底面积×高 V=Sh V=πr ² h
20厘米 25厘米
20)2=314(cm2) (1)水桶的底面积:3.14×( 2 3 (2)水桶的容积: 314×25=7850(cm )
4分米 10分米
把一个棱长是6厘米的正方体木 块,加工成一个最大的圆锥体, 圆锥的体积是多少立方厘米?
0.8米
求各圆柱的 体积。
0.5分米
求下面各圆柱的体积。
1、底面半径3cm,高5cm。 2、底面直径8m,高10m。 3、底面周长25.12dm,高2dm。
圆柱体积=底面积
高
圆柱体积=底面积
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积= 底面积
高
高
圆柱体积=底面积 圆锥体积= 底面积
高
高
1 3
圆柱与圆锥的体积之间有什么关系?
等底等高圆锥体积是圆柱体积的三分之一 等底底面周 长31.4米,高15米,这个玻璃罩的容积 是多少立方米?(玻璃厚度忽略不计)
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
高
圆柱体积=底面积 圆锥体积=
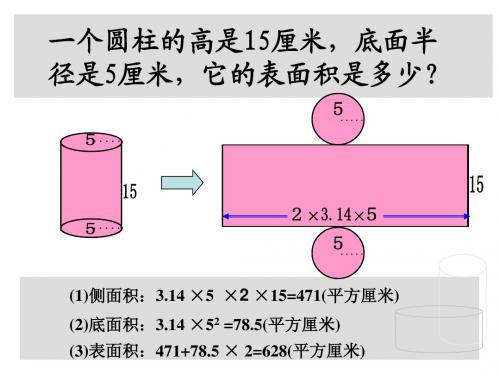
一个圆柱的高是15厘米,底面半 径是5厘米,它的表面积是多少?
【课件】圆柱、圆锥、圆台的表面积与体积+课件高一下学期数学人教A版(2019)必修第二册

设圆台的上底面面积为S',下底面面积为S
r O
1
1
2
2
2
2
V圆台 (r r r r )h ( S S S S )h
3
3
1
这和V棱台 ( S S S S )h是一致的。
3
1
因而得 V台体 = ( S S S S )h
3
【练习】 如图,在直角梯形 ABCD 中,BC∥AD,∠ABC=90°,AB=5,
1
V锥体 Sh
3
1 2
r h
3
1
V台体 = ( S SS S )h
3
1
= h(r 2 rr r 2 )
3
2
感谢聆听
S圆柱 =πr +πr +2πrl 2πr (r l )
2
2
(1)圆柱的表面积、体积
圆柱的侧面展开图是什么?如何计算它的表面积?
r O
l
2 r
O
圆柱的侧面展开图是一个矩形,
S圆柱表面积 2r 2rl 2r (r l ).
2
V圆柱 = πr h
2
例1 将一个边长分别为4π,8π的矩形卷成一个圆柱的侧面,则
圆台的表面积为(
A.81π
)
B.100π
C.168π
D.169π
解 圆台的轴截面如图所示,
设上底面半径为 r,下底面半径为 R,则它的母线长为
l= h2+R-r2= 4r2+3r2=5r=10,
所以 r=2,R=8。
故 S 侧=π(R+r)l=π(8+2)×10=100π,
S 表=S 侧+πr2+πR2=100π+4π+64π=168π。故选 C。
苏教版六年级下册数学《圆柱的体积》圆柱和圆锥PPT(第3课时)
教学新知
例二:计算圆柱的表面积。(单位:cm)(π取3.14)
S=2π×0.8+2π≈11.304 S=2π×0.5×3.5+2π×0.5²≈12.56
教学新知
例三:一个圆柱形油桶,底面直径是0.6米,高是1米。做这个油桶至少 需要铁皮多少平方米?(得数保留两位小数)
S=2π×0.3×1+2π×0.3²≈2.45(㎡)
能想到一些什么? (2)全部浸入,水面上升9厘米,你又能想到什么?怎样
计算出这个圆钢的体积? (3)这题还可以怎样思考?
教学新知
例一:一个圆柱形水桶的容积是80立方分米,里面装了2/5的水。 已知它的底面积是10平方分米,里面水的深度是多少?
【讲解】根据“水桶的容积是80立方分米”和“里 面装了 2/5的水”这两个条件,我们可以求出水桶 内水的体积,然后用水的体积除以水桶底面积得出 水桶内水的深度。 80× =32(立方分米)……水桶内水的体积 32÷10=3.2(分米)……水桶平均剖成两片,其中一片如图所示。(单位:厘米) (1)剖面面积是多少平方厘米? (2)这片木料的表面积和体积各是多少?
(1)S1=20×12=240(cm²) (2)S2=πrh+πr²+S1=3.14×6×20+3.14×6²+240=792.84(cm²)
V=1/2S3h=1/2×3.14×6²×20=1130.4(cm³)
课后习题
7.把一根长2.4米的圆柱形状的木料锯成4段,表面积增加了 0.18平方米。
这根木料原来的体积是多少立方米?
S=0.18÷6=0.03(m²)
V=sh=0.03×2.4=0.072(m³)
8.一个圆柱高4厘米,底面半径是2厘米。如果将它的底面平均分成若干份,
圆柱圆锥圆台体积和表面积.ppt
1
1
A.4
B.2
3 C. 6
3 D. 4
[答案] D
[解析]
三棱锥B1-ABC的高h=3,底面积S=S△ABC=
3 4
×12= 43,
则VB1-ABC=13Sh=13×
43×3=
3 4.
5.若一圆柱与圆锥的高相等,且轴截面面积也相等,那
么圆柱与圆锥的体积之比为( )
A.1
1 B.2
3
3
C. 2
D.4
例题解析
命题方向 多面体与旋转体的面积
【例1】圆台的上、下底面半径分别是10 cm和20 cm,它的侧 面展开图的扇环的圆心角是180°,那么圆台的表面积是多少?
命题方向 多面体的体积
[例 2] 长方体相邻三个面的面积分别为 2、3、6 求它的
体积.
[解析] 设长方体的长、宽、高分别为a、b、c则有
据条件得到
1 2
πl2=2π,解得母线长l=2,2πr=πl=2π,r=1所以
该圆锥的体积为:V圆锥=13Sh=13×
22-12π=
3 3 π.
[点评] 本题主要考查空间几何体的体积公式和侧面展开 图.审清题意,所求的为体积,不是其他的量,分清图形在 展开前后的变化;其次,对空间几何体的体积公式要记准记 牢,属于中低档题.
[解析]
三棱台ABC-A1B1C1的上、下底面积之比为4:9.连接 A1B、BC1和AC1,把棱台分为三个棱锥B-A1B1C1,C1- ABC,A1-ABC1.则这三个棱锥体积之比为________.
[答案] 4:9:6
[解析] 如图,设三棱锥B-A1B1C1,C1-ABC,A1- ABC1体积分别为V1、V2、V3,又设棱台的高为h,上、下底面 积分别为S1、S2.依题意,得
《圆柱的体积》圆柱和圆锥PPT教学课件下载
返回
圆柱和圆锥 圆柱的体积
课堂练习
1.求下列图形的体积。(单位:厘米)
3.14×32×10 = 282.6(cm³)
3.14×(8÷2)2×8
3.14×(4÷2)2×10
= 401.92(cm³)
= 125.6(cm³)
返回
圆柱和圆锥 圆柱的体积
2.哪根木料的体积大?
3.14×(0.4÷2)2×10 = 3.14×0.04×10 = 1.256(m3)
πr
S =πr×r=πr2 S =πr2
返回
圆柱和圆锥 圆柱的体积
是不是可以把圆柱转化成近似的长方体来推导圆柱 的体积公式呢?
?
返回
圆柱和圆锥 圆柱的体积
?
返回
圆柱和圆锥 圆柱的体积
……
圆柱等分的份数越多,拼成的图形越接近长方体。
返回
圆柱和圆锥 圆柱的体积
拼成后的长方体和圆柱体有什么关系呢? 长方体的体积和圆柱体的体积相等。
青圆岛柱版和五圆年锥制圆柱数的学体积五年级 下册
4 圆柱和圆锥
圆柱的体积
圆柱和圆锥 圆柱的体积
情境导入
从图中,你知道了哪些数学信息?
圆柱形包装盒的底面直径是12cm, 高是20cm。
圆柱形包装盒的体积是多少立方厘米?
返回
圆柱和圆锥 圆柱的体积
探究新知
圆柱形包装盒的体积是多少立方厘米? 求包装盒的体积就是求圆柱的体积。圆的面积公式是把圆转 化成近似的长方形推导出来的。
长方体的体积=底面积 × 高
圆柱的体积 = 底面积 × 高
V = Sh
返回
圆柱和圆锥 圆柱的体积
圆柱形包装盒的体积是多少立方厘米?
底面积: 3.14×(12÷2)2 = 3.14×36 = 113.04(平方厘米)
圆柱和圆锥 圆柱的体积
课堂练习
1.求下列图形的体积。(单位:厘米)
3.14×32×10 = 282.6(cm³)
3.14×(8÷2)2×8
3.14×(4÷2)2×10
= 401.92(cm³)
= 125.6(cm³)
返回
圆柱和圆锥 圆柱的体积
2.哪根木料的体积大?
3.14×(0.4÷2)2×10 = 3.14×0.04×10 = 1.256(m3)
πr
S =πr×r=πr2 S =πr2
返回
圆柱和圆锥 圆柱的体积
是不是可以把圆柱转化成近似的长方体来推导圆柱 的体积公式呢?
?
返回
圆柱和圆锥 圆柱的体积
?
返回
圆柱和圆锥 圆柱的体积
……
圆柱等分的份数越多,拼成的图形越接近长方体。
返回
圆柱和圆锥 圆柱的体积
拼成后的长方体和圆柱体有什么关系呢? 长方体的体积和圆柱体的体积相等。
青圆岛柱版和五圆年锥制圆柱数的学体积五年级 下册
4 圆柱和圆锥
圆柱的体积
圆柱和圆锥 圆柱的体积
情境导入
从图中,你知道了哪些数学信息?
圆柱形包装盒的底面直径是12cm, 高是20cm。
圆柱形包装盒的体积是多少立方厘米?
返回
圆柱和圆锥 圆柱的体积
探究新知
圆柱形包装盒的体积是多少立方厘米? 求包装盒的体积就是求圆柱的体积。圆的面积公式是把圆转 化成近似的长方形推导出来的。
长方体的体积=底面积 × 高
圆柱的体积 = 底面积 × 高
V = Sh
返回
圆柱和圆锥 圆柱的体积
圆柱形包装盒的体积是多少立方厘米?
底面积: 3.14×(12÷2)2 = 3.14×36 = 113.04(平方厘米)
8.3.2 圆柱、圆锥、圆台、球的表面积和体积课件(共57张PPT )
知识点一 圆柱、圆锥、圆台的表面积
圆柱 旋转体
圆锥
图形
表面积公式 底面积:S底=_2_π_r_2 侧面积:S侧=_2_π_r_l 表面积:S=_2_π_r_(r_+__l_)
底面积:S底=_π_r_2 侧面积:S侧=_π_r_l 表面积:S=_π_r(_r_+__l)_
旋转体 圆台
上底面面积:S上底=_π_r_′__2_ 下底面面积:S下底=_π_r_2_ 侧面积:S侧=_π_(_r′__l_+__r_l)_ 表面积:S=_π_(r_′__2_+__r_2+__r_′__l_ _+__r_l)_
D. 3∶2
解析 设圆锥底面半径为r,则高h=2r, ∴其母线长 l= 5r, ∴S 侧=πrl= 5πr2,S 底=πr2,S 底∶S 侧=1∶ 5.
(2)已知某圆台的一个底面周长是另一个底面周长的3倍,母线长为3,
圆台的侧面积为84π,则该圆台较小底面的半径为
√A.7
B.6
C.5
D.3
解析 设圆台较小底面的半径为r, 则另一底面的半径为3r. 由S侧=3π(r+3r)=84π,解得r=7.
∴r= πS, ∴底面周长为 2πr=2π πS,
又侧面展开图为一个正方形,∴侧面积是2π
πS2=4πS.
二、圆柱、圆锥、圆台的体积
例2 (1)(多选)圆柱的侧面展开图是长12 cm,宽8 cm的矩形,则这个
圆柱的体积可能是
√288 A. π
cm3
√192 B. π
cm3
C.288π cm3
D.192π cm3
反思 感悟
圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个 曲面展开为平面图形计算,而表面积是侧面积与底面圆的面 积之和.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱体积=底面积 高 圆锥体积=
圆柱体积=底面积 高 圆锥体积=
圆柱体积=底面积 高 圆锥体积=
圆柱体积=底面积 高 圆锥体积=
圆柱体积=底面积 高 圆锥体积=
圆柱体积=底面积 高 圆锥体积=
圆柱体积=底面积 高 圆锥体积=底面积 高
圆柱体积=底面积 高
圆锥体积=底面积
高
1 3
圆柱体积=底面积 高
圆锥体积=底面积
高
1 3
圆锥的体积= 1 ×底面积×高 3
本内容仅供参考,如需使用,请根据自己实际情况更改后使用!
放映结束 感谢各位批评指导!
谢 谢!
让我们共同进步
圆柱与圆锥的体积
长方体的体积=底面积 × 高 底面积
长方体的体积=底面积 ×高 底面积
长方体的体积=底面积 ×高 底面积
长方体的体积=底面积 ×高 底面积
长方体的体积=底面积 x 高 底面积
长方体的体积=底面积 x 高 底面积
长方体的体积=底面积 ×高 圆柱体的体积= 底面积 ×高
圆柱体积=底面积 高
圆柱体积=底面积 高
圆柱体积=底面积 高
圆柱体积=底面积 高 圆锥体积=
圆柱体积=底面积 高 圆锥体积=
圆柱体积=底面积 高 圆锥体积=
Байду номын сангаас
圆柱体积=底面积 高 圆锥体积=
圆柱体积=底面积 高 圆锥体积=
