2018年中考数学复习第2单元方程组与不等式组第9课时一元一次不等式组及其应用ppt课件(含答案)
湖南省2018年中考数学复习课件第9课时 一元一次不等式(组)及其应用

第9课时┃一元一次不等式(组)及其应用
[变式训练] 1.[2017·杭州]若x+5>0,则( D ) A.x+1<0 B.x-1<0 x C. <-1 D.-2x<12 5 1 2.[2015·广元]当 0<x<1 时,x, ,x2 的大小顺序是( C x 1 1 A. <x<x2 B.x<x2< x x 1 1 C.x2<x< D. <x2<x x x
对接中考
考点过关
突破重难
第9课时┃一元一次不等式(组)及其应用
(3)找出各解集的公共部分,并表示出不等式组的解集.
对接中考
考点过关
突破重难
第9课时┃一元一次不等式(组)及其应用
考|点|4 一元一次不等式(组)的应用
图 9- 3
对接中考
考点过关
突破重难
第9课时┃一元一次不等式(组)及其应用
突 破 重 难
第9课时
一元一次不等式(组)及 其应用
第9课时┃一元一次不等式(组)及其应用
对 接 中 考
命|题|点|1 不等式的基本性质 1.[2017· 株洲]已知实数a,b满足a+1>b+1,则下列选项错 误的是( D ) A.a>b B.a+2>b+2 C.-a<-b D.2a>3b
[解析] 由不等式的性质得 a>b,a+2>b+2,-a< -b.
突|破|点|1 不等式的基本概念与性质
例 1[2017· 常州 ] 若 3x >- 3y ,则下列不等式中一定成立的是 ( A ) A.x+y>0 B.x-y>0 C.x+y<0 D.x-y<0
[解析] 两边都除以 3,得 x>-y,两边都加 y,得 x+y>0.故 选 A.
对接中考
考点过关
突破重难
对接中考 考点过关 突破重难
中考复习数学:一元一次不等式组及应用.ppt

1-2x-1≤5 ① 【解答】(1)3x-2 2<x+12 ②
解不等式①,得 x≥-1.解不等式②,得 x<3. 在同一数轴上表示不等式①②的解集如下:
∴原不等式组的解集为-1≤x<3. (2)解不等式①,得 x>-2.解不等式②,得 x≤6. 在同一数轴上表示不等式①②的解集如下:
∴原不等式组的解集为-2<x≤6. ∴原不等式组的整数解为 x=-1,0,1,2,3,4,5,6.
x<1 条件,所以-a<1,解得 a>-1.
【解答】(1)A (2)A
1-2x-1≤5 (1)(2010·毕节)解不等式组3x-2 2<x+21
,并把解集在数轴上表示出来.
(2)(2010·芜湖)求满足不等式组23xx+ -58≤ >110①② 的整数解.
【点拨】求不等式组的特殊解时,首先应先求出每个不等式的解集,再确定出不等式组 的解集,然后再寻找出符合条件的特殊解.
(2010·莱芜)为打造“书香校园”,某学校计划用不超过 1 900 本科技类书籍和 1 620 本人文类书籍,组建中、小型两类图书角共 30 个.已知组建一个中型图书角需科技类书籍 80 本,人文类书籍 50 本;组建一个小型图书角需科技类书籍 30 本,人文类书籍 60 本.
(1)问符合题意的组建方案有几种?请你帮学校设计出来; (2)若组建一个中型图书角的费用是 860 元,组建一个小型图书角的费用是 570 元,试说 明在(1)中哪种方案费用最低?最低费用是多少元?
一、选择题(每小题 4 分,共 32 分)
1.(2010·广州)不等式组13x+1>0 的解集是(
)
2-x≥0
A.-13<x≤2 C.x≥2
中考数学总复习基础知识梳理第2单元方程组与不等式组2.4一元一次不等式组及其应用课件

有关一元一次不等式(组)的一些注意事项
1.“解与解集”的联系与区别 不等式的解是指使不等式成立的每一个数,而不等式的解集是指由 全体不等式的解组成的一个集合.因此,不等式的解可以是一个或 多个值,而不等式的解集应包含满足不等式的所有解. 不等式的解与不等式的解集的区别:解集是能使不等式成立的未知 数的取值范围,是所有解的集合,而不等式的解则是使不等式成立 的未知数的值,二者的关系是:解集包括解,所有的解组成了解 集.Biblioteka 2.4.4 一元一次不等式组
1.定义:含有相同未知数的若干个一元一次不等式组成的不等式组 叫作一元一次不等式组. 2.解不等式组一般先分别求出不等式组中各个不等式的解集并表示 在数轴上,再求出它们公共部分就得到不等式组的解集.
3.由两个一元一次不等式组成的不等式组的解集可划分为四种情况(假设a< b).
解:(1)设批发青菜x市斤,批发西兰花y市斤.则,
x y 200
x 100
2.8x 3.2 y 600
解得
y
. 100
即批发青菜100市斤,批发西兰花100市斤, ∴100×(4-2.8)+100×(4.5-3.2)=250(元). 答:当天售完后老王能盈利250元钱. (2)设给青菜定价为a元/市斤.根据题意可得:
第二单元 方程(组) 与不等式(组)
第9课时 一元一次不等式(组)及其应用
考纲考点
1.结合具体问题,了解不等式的意义,掌握不等式得基本性质. 2.会解一元一次不等式组,并会用数轴确定解集. 3.能够根据具体问题中的数量关系,列出一元一次不等式解决简单 的问题. 4.能根据具体问题的实际意义,检验结果是否合理. 一元一次不等式组的解法及在数轴上表示解集,江西近几年中考每 年都是考查一道题,预测未来一元一次不等式(组)的考查在江西 中考中仍会以这几种形式出现.
中考数学复习 一元一次不等式(组)及应用

“≠”连接而成的式子.
2.解集:一般地,一个含有未知数的不等式的所有
的解,组成这个不等式的解集.
如果a>b,那么a±c>b±c
3.性质如果a>b,c>0,那么ac>bc或ac>bc
如果a>b,c<0,那么ac
①_<_bc或ac
②_<_bc
第1部分 第二单元 方程(组)与不等式(组)
二、一元一次不等式 一元一次不等式
第二单元 方程(组)与不等式(组)
课时 8 一元一次不等式(组)及应用
CONTENTS
目 录
课前自测 知识梳理 知识过关
第1部分 第二单元 方程(组)与不等式(组)
课前自测
1.已知a>b,则下列不等式中不正确的是( C )
A.4a>4b
B.a+4>b+4
C.-4a>-4b
D.a-4>b-4
第1部分 第二单元 方程(组)与不等式(组)
第1部分 第二单元 方程(组)与不等式(组)
广东中考
1.(2013广东)已知实数a,b,若a>b,则下列结论 正确的是( D )
A.a-5<b-5 B.2+a<2+b C.a3<b3 D.3a>3b
第1部分 第二单元 方程(组)与不等式(组)
2.(2018广东)不等式3x-1≥x+3的解集是( D )
(1)求商场销售A,B两种型号计算器的销售价格分别 是多少元?(利润=销售价格-进货价格)
(2)商场准备用不多于2 500元的资金购进A,B两种 型号计算器共70台,问最少需要购进A型号的计算器多 少台?
第1部分 第二单元 方程(组)与不等式(组)
解:(1)设 A 种型号计算器的销售价格是 x 元,B 种
精选-中考数学总复习第二单元方程组与不等式组第09课时一元一次不等式组及其应用课件

如果 a>b,那么 a+c③ > b+c 或 a-c④ > b-c
如果 a>b,并且 c>0,那么 ac>bc 或 > ;如果 a>b,并且 c<0,那么 ac<bc 或 <
精选中小学课件
2
课前双基巩固 考点二 一元一次不等式及其解法
不等式组的解集的求法 ② 解集
不等式组的解集情况 (假设 a<b)
������ > , ������ >
������ < , ������ <
������ > , ������ <
������ < , ������ >
x>b x<a a<x<b 无解
同大取大 同小取小 大小小大中间找 大大小小解不了
最新
精选中小学课件
7
课前双基巩固
题组二 易错题
【失分点】不等式中的等号是否取到.
[答案] C
6. [2018·雅安]
不等式组
2������-1 3
-
5������ +1 2
≤
1,
的整数解的个数是
(
)
[解析] 解2���3���-1-5������2+1≤1 得 x≥-1;解
5������-1 < 3(������ + 1)
最新
精选中小学课件
3
课前双基巩固 考点三 一元一次不等式组的概念及其解集
一元一次不等式组的概念 不等式组的解集
把几个含有同一个未知数的一次不等式联立在一起,就组成了一个一元一次不等式组
人教版九年级数学第二单元《方程(组)与不等式(组)》中考知识点梳理
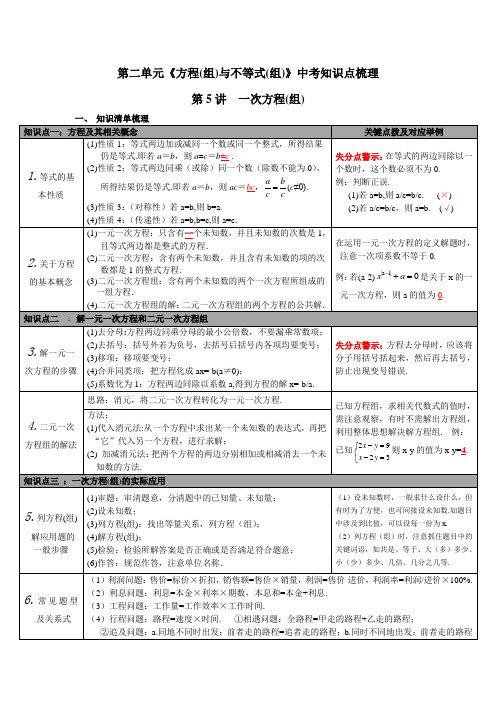
第二单元《方程(组)与不等式(组)》中考知识点梳理第5讲一次方程(组)第6讲一元二次方程第7讲分式方程三、知识清单梳理第8讲一元一次不等式(组)知识点一:不等式及其基本性质关键点拨及对应举例1.不等式的相关概念(1)不等式:用不等号(>,≥,<,≤或≠)表示不等关系的式子.(2)不等式的解:使不等式成立的未知数的值.(3)不等式的解集:使不等式成立的未知数的取值范围.例:“a与b的差不大于1”用不等式表示为a-b≤1.2.不等式的基本性质性质1:若a>b,则a±c>b±c;性质2:若a>b,c>0,则ac>bc,ac>bc;性质3:若a>b,c<0,则ac<bc,ac<bc.牢记不等式性质3,注意变号.如:在不等式-2x>4中,若将不等式两边同时除以-2,可得x<2.知识点二:一元一次不等式3.定义用不等号连接,含有一个未知数,并且含有未知数项的次数都是1的,左右两边为整式的式子叫做一元一次不等式. 例:若230mmx++>是关于x的一元一次不等式,则m的值为-1.4.解法(1)步骤:去分母;去括号;移项;合并同类项;系数化为1.失分点警示系数化为1时,注意系数的正负性,若系数是负数,则不等式改变方向.(2)解集在数轴上表示:x≥a x>a x≤a x<a知识点三:一元一次不等式组的定义及其解法5.定义由几个含有同一个未知数的一元一次不等式合在一起,就组成一个一元一次不等式组.(1)在表示解集时“≥”,“≤”表示含有,要用实心圆点表示;“<”,“>”表示不包含要用空心圆点表示.(2)已知不等式(组)的解集情况,求字母系数时,一般先视字母系数为常数,再逆用不等式(组)解集的定义,反推出含字母的方程,最后求出字母的值.如:已知不等式(a-1)x<1-a 的解集是x>-1,则a的取值范围是a<1.6.解法先分别求出各个不等式的解集,再求出各个解集的公共部分7.不等式组解集的类型假设a<b解集数轴表示口诀x ax b≥⎧⎨≥⎩x≥b大大取大x ax b≤⎧⎨≤⎩x≤a小小取小x ax b≥⎧⎨≤⎩a≤x≤b大小,小大中间找x ax b≤⎧⎨≥⎩无解大大,小小取不了知识点四:列不等式解决简单的实际问题8.列不等式解应用题(1)一般步骤:审题;设未知数;找出不等式关系;列不等式;解不等式;验检是否有意义.(2)应用不等式解决问题的情况:a.关键词:含有“至少(≥)”、“最多(≤)”、“不低于(≥)”、“不高于(≤)”、“不大(小)于”、“超过(>)”、“不足(<)”等;注意:列不等式解决实际问题中,设未知数时,不应带“至少”、“最多”等字眼,与方程中设未知数一致.。
中考数学总复习 第二章 方程(组)与不等式(组) 第9节 一元一次不等式(组)及应用课件
8.解一元一次不等式的步骤:去分母,___去__括__号____,移项,合并同类 项,___系__数__化__为__1___(注意不等号的方向是否改变). 9.解一元一次不等式组的步骤:①先求出各个不等式的__解__集____;② 再利用数轴找它们的_公__共__部__分___;③写出不等式组的解集.
解:1≤x<4,数轴上表示略
解一元一次不等式组,先解出不等式组中的各个不等式,再根据“同 大取大,同小取小,大小、小大中间找,大大、小小找不到”准确写 出不等式组的解集.
根据不等式组的解确定字母的取值范围
x<1, 【例 4】(2015·永州)若不等式组x>m-1恰有两个整数解,则 m 的取 值范围是( A ) A.-1≤m<0 B.-1<m≤0 C.-1≤m≤0 D.-1<m<0
一元一次不等式(组)的应用
12.列不等式(组)解应用题的基本步骤为:①审题;②设未知数;③列 不等式;④解不等式;⑤检验并写出答案. 13.列不等式(组)解应用题涉及的题型常与方案设计型问题相联系,如 最大利润、最优方案等. 14.审题时应紧紧抓住“至多”、“至少”、“不大于”、“不小于 ”、“不超过”、“大于”、“小于”等关键词,注意分析题中的不 等关系,列出不等式(组),然后根据不等式(组)的解法,结合题意求解 .
_____x_>_3_3_或___x_>_-___33______________;
(2)(2015·自贡)解不等式:4x- 3 1-x>1,并把解集表示在数轴上.
解:x>4,数轴上表示略
一元一次不等式组的解法
xБайду номын сангаас1≥0, 【例 3】(2015·玉林)解不等式组x-1<34x,并把解集在数轴上表示出来.
中考数学复习 第2单元 方程(组)与不等式(组)第9课时
第9课时 一元一次不等式(组)
不等式的概 念及其解集
知识体系图 概念(不等式、解集) 不等式的性质 解不等式
一元一次 不等式
一元一次不等式的概念 一元一次不等式的解法 一元一次不等式的应用
一元一次不等式(组)
一元一次 不等式组
不等式组的概念 不等式组的解法 不等式组的应用
解集在数轴上表示
求解规律
大大取较大 小小取较小 大小小大取中间
大大小小找不到 (无解)
1.不等式:用不等号连接表示不等关系的式子叫做不等式; 2.不等式的解:类似于方程,我们把那些使不等式成立的未知数的值叫做不等式 的解; 3.不等式的解集:一个含有未知数的不等式的解的全体,叫做不等式的解集; 4.解不等式:求不等式的解集的过程或证明不等式无解的过程,叫做解不等式.
故2不是不等式的解,所以选择D选项.
【例3】(2016年江西)将不等式3X-2<1的解集表示在数轴上正确的是(D)
【解析】此题考查了解一元一次不等式,并且将不等式的解集用数轴表示的方法.解不等 式得X<1,所以选择D选项.
【
例
4
】
(
2
0
1
6
年
达
州
)
不
等
式
组1x 3
30
x 2<x
1
的解集在数轴上表示为(A)
【解析】解该不等式组得
= 所以选择C选项,此不等式的解集为:
x 3
x>5 2Βιβλιοθήκη .-2.5<X≤3.
1.定义:含有相同未知数的若干个一元一次不等式组成的不等式组叫作一元一次 不等式组.
2.解不等式组一般先分别求出不等式组中各个不等式的解集并表示在数轴上,再 求出它们公共部分就得到不等式组的解集.
中考数学 第二章方程组与不等式组 第9讲 不等式及一元一次不等式精品课件(含11真题和12预测题)
A.a+c>b+c
B.c-a<c-b
ab C.c2>c2
D.a2>ab>b2
【解析】由于 a>b,则-a<-b,故 A、B、C 均正确;D
项中当 a=1,b=-2 时,a2<b2,故 D 不正确.
【答案】D
3.(2011中考预测题)若不等式(a+1)x>a+1的解集是x<1,则a必
须满足( )
A.a<0
4.一元一次不等式 只含有_一_个未知数,并且未知数的次数是_一__ 且系数不等于0___的不等式,叫一元一次不等式.其一般形式为ax_+__b_<__0__
或 ax+b>__0_(_a_≠_0_)___ _.
5.解不等式 求不等式 解集 的过程或证明不等式 无解 程,叫做解不等式.
的过
考点二 不等式的基本性质
(1)(2011·上海)如果 a>b,c<0,那么下列不等式成立的是( )
A.a+c>b+c
B.c-a>c-b
C.ac>bc
D.ca>cb
(2) 2010·河北 把不等式-2x<4 的解集表示在数轴上,正确的是
()
【解答】(1)A (2)A
方法总结: 1.在数轴上表示不等式的解集时,要确定边界和方向.边界:有等号 的用实心圆点,无等号的用空心圆圈.方向:大于向右,小于向左. 2.解不等式时,系数化为1时,必须明确系数的符号,当未知数的系 数为负数时,一定要改变不等号的方向.
B.a<1
C.a<-1
D.a>-1
【解析】原不等式中不等号的方向为“>”,而解集中不等号的方
向为“<”,说明系数a+1<0,解得a<-1.
【答案】C
4.(2010中考变式题)如图,a、b、c分别表示苹果、梨、桃子的质
「精品」中考数学第二单元方程(组)与不等式(组)第9课时一元一次不等式(组)及一元一次不等式的应用课
第9课时┃ 一元一次不等式(组)及一元一次不等式的应用
例 3 [2015·合肥庐阳区二模] 关于 x 的不等式 x- 3>3x+2 a的解集在数轴上表示如图 9-3 所示,则 a 的值是 (B )
图 9-3 A.-6 B.-12 C.6 D.12
考情分析
考题赏析
考点聚焦
考向探究
第9课时┃ 一元一次不等式(组)及一元一次不等式的应用
方法点析 解一元一次不等式的方法与解一元一次方程类似,一般 步骤为去分母、去括号、移项、合并同类项、系数化为1. 易错提示 1.去分母时,不要漏乘不含分母的项. 2.若分数线前有负号,去分母时,要注意符号的变化. 3.系数化为1时,若系数是负数,注意不等号要改变方 向.
考情分析
考题赏析
考点聚焦
考向探究
易错提示 运用不等式的性质时,应注意不等式的两边同时乘 以或除以同一个负数时,不等号的方向要改变.
考情分析
考题赏析
考点聚焦
考向探究
第9课时┃ 一元一次不等式(组)及一元一次不等式的应用
探究2 一元一次不等式的解法 命题角度: 1.已知一元一次不等式的解或解集,求字母系数的取值范 围; 2.解一元一次不等式. 例2 [2015·合肥蜀山区二模] 解不等式3(x+1)-6≤4x,并 把解集在图9 2中的数轴上表示出来.
图9-1
[解析] 解不等式x-3>0,得x>3;解不等式x+1≥0, 得x≥-1.两个解集的公共部分为x>3.在数轴上表示正确的 是D.
考情分析
考题赏析
考点聚焦
考向探究
第9课时┃ 一元一次不等式(组)及一元一次不等式的应用
2.[2010·安徽] _2_<__x_≤_4__.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
回归教材
考点聚焦
考向探究
第二单元┃ 方程(组)与不等式(组)
不等式 组(a <b)
x>a , (1) x>b x<a , (2) x<b x>a , (3) x<b x<a , (4) x>b
数轴表示
解
集
记忆口诀 同大取大 同小取小 大小小大 中间找 大大小小 解不了
回归教材
考点聚焦
考向探究
第二单元┃ 方程(组)与不等式(组)
|针对训练|
1.[2017·株洲]x的3 倍大于5,且x的一半与1的差小于或 5 <x≤6 . 等于2,则x的取值范围是________
3x>5, ① 5 [解析] 由题意得不等式组 x 由①得:x> ,由②得 3 -1≤2. ② 2 5 x≤6,故解集为: <x≤6. 3
回归教材 考点聚焦 考向探究
第二单元┃ 方程(组)与不等式(组)
防错提醒: 在步骤(5)中,不等式两边同时除以未知数的系数或乘未知数 系数的倒数时,要注意系数的符号,根据系数的符号确定是否 改变不等号的方向.
回归教材
考点聚焦
考向探究
第二单元┃ 方程(组)与不等式(组) 考点3 一元一次不等式组及其解法
x>b x<a a<x <b 无解
回归教材
考点聚焦
考向探究
第二单元┃ 方程(组)与不等式(组) 考点4 一元一次不等式的应用
1.列不等式解应用题的步骤:
(1)找出实际问题中的不等关系,设未知数,列出不等式; (2)解不等式; (3)从不等式的解集中找出符合题意的答案. 2.利用不等式解决日常生活中的实际问题
(2)【2017·安徽】不等式]不等式4-2x>0的解集是x<2,在数轴上表示为 ,故选D.
回归教材 考点聚焦 考向探究
第二单元┃ 方程(组)与不等式(组)
|针对训练| 【2017·株洲】已知实数a,b满足a+1>b+1 ,则下列 选项可能错误的是( D ) A.a >b B.a+2>b+2 C.- a<-b D.2a>3b
例 1(1)[2016·怀化] 不等式 3(x-1)≤5-x 的非负整 数解有( C ) A.1 个 B.2 个 C.3 个 D.4 个
回归教材
考点聚焦
考向探究
第二单元┃ 方程(组)与不等式(组)
3x-1 (2)[2016·苏州] 解不等式2x-1> ,并把它的解 2 集在数轴上表示出来. 图9-3
回归教材
考点聚焦
考向探究
第二单元┃ 方程(组)与不等式(组) |针对训练|
x>a , x<3
1.【2017·岳阳模拟】不等式组 个,则a的取值范围是( A ) A.-1≤a<0 B.-1<a≤0 C.-1≤a≤0 D.-1<a<0
[解析] ∵不等式组
x>a , x<3
的整数解有三
有整数解,∴不等式组
x>a , 的解集为a<x<3, x<3
由不等式组的整数解有三个,即x=0 ,1,2,得到-1 ≤a< 0,故选A.
回归教材 考点聚焦 考向探究
第二单元┃ 方程(组)与不等式(组)
x-2>3x, 2.[2017·怀化模拟]一元一次不等式组 的 x<a
2x-1≥5, 不等式组 的解集在数轴 8-4x<0
图9-5
回归教材 考点聚焦 考向探究
第二单元┃ 方程(组)与不等式(组)
(2)[2017·枣庄]x取哪些整数值时,不等式5x+2>3(x-1) 1 3 与 x≤2- x都成立? 2 2
5 解:解不等式5x+2>3(x-1),得:x>- ,解不等 2 1 3 式 x≤ 2- x,得:x ≤1, 2 2 5 所以它们的公共解为:- <x≤1,故满足条件的整 2 数有- 2、-1、0、 1.
<”“≤”向左画,其中“≥”“≤”要用实心圆点表示 ,“<”“>”要用空心圆圈表示.要注意区分方向与实 心圆点或空心圆圈.
回归教材 考点聚焦 考向探究
第二单元┃ 方程(组)与不等式(组) 探究3 一元一次不等式组及其解法
命题角度:
1.解一元一次不等式组; 2.求一元一次不等式组的整数解.
例3(1)[2016·长沙] 上表示为( C )
例1(1)若x>y,则下列不等式中不一定成立的是( D ) A.x+5>y+5 B.3x>3y x y C. > 3 3
回归教材
D.x2>y2
考点聚焦 考向探究
第二单元┃ 方程(组)与不等式(组)
[解析 ]根据不等式的性质1,不等式两边同时加上5,不等 号的方向不变,A正确;根据不等式的性质2,不等式两边 同时乘以正数3,不等号的方向不变, B正确;不等式两边 同时除以正数3,不等号的方向不变;当x=2,y=-3 2 2 时,x>y,但x <y ,所以D错误,故选择D.
回归教材 考点聚焦 考向探究
第二单元┃ 方程(组)与不等式(组)
考 点 聚 焦
考点1 不等式的相关概念及不等式的基本性质
不等号 表示不等关系的式子 用________ 把满足一个不等式的未知数的每一个值,称 为不等式的一个解 全体 称为这个不等 把一个不等式的解的________ 式的解集
不等式 不等式的解 不等式 的解集
回归教材 考点聚焦 考向探究
第二单元┃ 方程(组)与不等式(组)
解:错误的是①②⑤. 正确的解答过程如下: 去分母得3(1+x) -2(2x+1) ≤6, 去括号得3+3x-4x-2≤6, 移项得 3x-4x≤6 -3+2, 合并同类项得-x≤5 ,两边都除以- 1得x≥-5.
【方法模型】
在数轴上表示不等式的解集时,“>”“≥”向右画,“
回归教材
考点聚焦
考向探究
第二单元┃ 方程(组)与不等式(组)
2.[八上P138习题4.2第5(1)题] 由a>b得到ac2>bc2 ≠ 的条件是c________0. 3.[八上P143习题4.3第6题改编]关于x的不等式(a+ a<-1 . 1)x >a+1的解集是x<1,则a的取值范围是________
[解析] 根据不等式的性质即可得到a>b,a+2>b+2,-a <-b.可能错误的是D. 2x-a 2.若关于x的不等式 ≥-1的解集如图9-2所示,则 3 -1 a=________. 图9-2 a-3 [解析] 解不等式,得x≥ ,由图可知不等式的解集为 2 a-3 x≥-2,所以 =-2,解得a=-1. 2
【方法模型】
求不等式组的解集,通常采用“分开解”“集中判”的方法: (1)“分开解”就是分别求不等式组中各个不等式的解集; (2)“集中判”就是利用数轴求出各个不等式的解集的公共部 分
回归教材 考点聚焦 考向探究
第二单元┃ 方程(组)与不等式(组) 探究4 与不等式(组)的解集有关的求值问题
命题角度:
根据解的情况求相关字母的值(取值范围) .
例4【2017·黄石】已知关于x的不等式组 5x+1>3(x-1), 1 3 恰有两个整数解,求实数a的取值范 2x≤8-2x+2a 围.
回归教材
考点聚焦
考向探究
第二单元┃ 方程(组)与不等式(组)
5x+ 1>3(x-1), 解:由1 3 2 x≤8 -2x+2a x>- 2, 得 x≤a +4, ∴不等式组的解集为-2<x≤a+4, ∴不等式组的两个整数解为-1、0. ∴0≤ a+4<1, ∴实数 a的取值范围为-4≤a<-3.
回归教材
考点聚焦
考向探究
第二单元┃ 方程(组)与不等式(组)
性质 1:不等式的两边都加上(或减去)同一 个整式,不等号的方向不变,即:a>b⇒a > ±c____b±c; 性质 2:不等式的两边都乘以(或除以)同一 个正数,不等号的方向不变,即:a>b,c a b > > >0⇒ac________bc, ________ ; c c 性质 3:不等式的两边都乘以(或除以)同一 个负数,不等号的方向改变.即:a>b,c a < b < <0⇒ac________bc, ________ c c
2x≥-9-x, 2.[2017·长沙]解不等式组 并把它的解 5x-1>3(x+1)
3
集在数轴上表示出来. 图9 -6
回归教材 考点聚焦 考向探究
第二单元┃ 方程(组)与不等式(组)
2x≥-9-x, ① 解: 5x- 1>3(x+1) .
②
由①得x≥-3, 由②得x>2, ∴不等式组的解集为x>2. 解集在数轴上表示如下:
回归教材
考点聚焦
考向探究
第二单元┃ 方程(组)与不等式(组)
5x-1>3x-4, 4.[ 八上P150习题4.5第2题] 求不等式组 1 2 的 -3x≤3-x 整数解.
5x- 1>3x-4,① 解: 1 2 -3 x≤3-x,② 3 解不等式①,得x>- . 解不等式②,得x≤1. 2 3 ∴不等式组的解集为- < x≤1, 2 ∴不等式组的整数解为-1,0,1.
通过解不等式,求出某些变量的取值范围,以确定最佳方案
,最大收益,最省时间和可能的种类.
回归教材
考点聚焦
考向探究
第二单元┃ 方程(组)与不等式(组)
考 向 探 究
探究1 不等式的概念及性质 命题角度: (1)利用不等式的性质将不等式变形; (2)利用不等式的性质判断不等式变形是否正确.
(3)在数轴上表示不等式的解集.
解:去分母,得4x-2>3x-1,
移项,得4x-3x>2-1, 合并同类项,得x>1.
将不等式的解集表示在数轴上,如图所示:
