球赛积分表问题探究
《球赛积分表问题》教案

《球赛积分表问题》教案设计意图检验方程的解是否符合问题的实际意义,发展推理能力.由表中第一行数据可列方程10x+4×1=24.解得x=2.用表中其他行可以验证,得出结论:胜一场积2分,负一场积1分.问题3用代数式表示一支球队的总积分与胜、负场数之间的数量关系.若一支球队胜m场,则总积分为m+14.问题4 某队的胜场总积分能等于它的负场总积分吗?设一支球队胜了y场,则负了(14-y)场.若这支球队的胜场总积分能等于负场总积分,则得方程2y=14-y.解得y=143因为y(所胜的场数)的值必须是整数,所以y=143不符合实际,由此可以判定没有哪支球队的胜场总积分能等于负场总积分.总结:【对应训练】1.阳光体育季,赛场展风采.七年级组织迎新拔河比赛,每班代表队都需比赛10场,下表是此次比赛积分榜的部分信息:班次比赛场次胜场负场积分A班1010030B班108226C班1001010(1)结合表中信息可知:胜一场积_____分,负一场积_____分.(2)已知D班的积分是24分,求D班的胜场数.(3)某个班的胜场总积分能否是负场总积分的2倍?请说明理由.解:(2)设D班的胜场数为x,则负场数为10-x.由D班的积分是24分,得3x+1×(10-x)=24.解得x=7.因此,D班的胜场数为7.(3)能.理由:设这个班的胜场数为y,则负场数为10-y.若胜场总积分是负场总积分的2倍,则3y=2×1×(10-y).解得y=4.因此,当某个班的胜场数为4时,这个班的胜场总积分是负场总积分的2倍.2.教材P137练习第2题.教学建议【教学建议】问题4的分析过程中渗透了反证法的思想,即先假设某队的胜场总积分等于它的负场总积分,由此列出方程,解得获胜场次不是整数而是分数,这显然不合乎实际情况,由这种矛盾现象可知先前的假设不能成立,从而作出否定的判断.建议教学中不要提及反证法,只要引导学生注意这里方程的解应是整数,由此作出判断就够了.上面的问题说明,用方程解决实际问题时,不仅要注意解方程的过程是否正确,还要检验方程的解是否符合问题的实际意义.31教学步骤师生活动活动三:知识升华,巩固提升设计意图学会解决不同规则下的比赛积分问题.例在一次有12个队参加的足球循环赛中(每两队之间比赛一场),规定胜一场积3分,平一场积1分,负一场积0分,某队在这次循环赛中所胜场数比所负场数多2场,结果共积19分.求该队在这次循环赛中的平场数.解:设该队的负场数为x,则胜场数为x+2,平场数为11-x-(x+2).根据题意,得3(x+2)+1×[11-x-(x+2)]=19.解得x=4.所以11-x-(x+2)=1.答:该队在这次循环赛中的平场数为1.【对应训练】教材P137练习第1题.【教学建议】给学生说明:不同的比赛,规则各不相同.对于比赛结果,除了有胜、负外,可能还有平局.但一般来说,有以下相等关系(以有平局的情况为例):①比赛总场数=胜场数+平场数+负场数;②比赛总积分=胜场总积分+平场总积分+负场总积分.活动四:随堂训练,课堂总结【随堂训练】见《创优作业》“随堂小练”册子相应课时随堂训练.【课堂总结】师生一起回顾本节课所学主要内容,并请学生回答以下问题:1.我们是怎样根据表格中的信息,得出篮球联赛的胜、负积分规则的?2.在实际问题中,通过一元一次方程求出解后,还要注意什么问题?【作业布置】1.教材P140习题5.3第7,12,13题.2.《创优作业》主体本部分相应课时训练.板书设计第3课时球赛积分表问题1.从球赛积分表中读取信息2.用一元一次方程解决球赛积分问题教学反思球赛积分问题能较好地引起学生的学习兴趣.部分学生不能熟练地从表格中提炼自己需要的信息,今后要更注意对学生这方面能力的培养.另外,通过对方程解的实际意义的检验,学生更全面地理解了方程在实际问题中的应用.解题大招不同规则下的比赛问题不同的比赛,规则各不相同,如篮球比赛中,有2分球、3分球、罚球(罚中一次得1分);另外有些比赛,除了有得正分和零分的情况,还有得负分的情况.不管是哪种类型的比赛,按对应规则计算总分即可.例1为了增强学生的安全防范意识,某校九年级(3)班举行了一次安全知识抢答赛,抢答题一共30道,记分规则如下:每答对一道得5分,每答错或不答一道扣1分.张丹一共得84分,则张丹答对的道数为多少?解:设张丹答对的道数为x,则答错或不答的道数一共为30-x.由题意,得5x-(30-x)=84.解得x=19.答:张丹答对的道数为19.例2某篮球运动员在一次篮球比赛中20投16中(含罚球),得30分(罚球命中1次得1分),已知他投中了1个3分球,则他投中了几个2分球?解:设他投中了x个2分球,则罚球罚进的个数为16-x-1.由题意得2x+3×1+1×(16-x-1)=30.解得x=12.答:他投中了12个2分球课后·知能演练一、基础巩固1.某位同学连续答40道题,答对一题得5分,答错一题扣2分(不答同样算作答错),最终该同学获得144分.若所列的方程是x5+x-1442=40,则x表示的意义是()A.答对题的数目B.答错题的数目C.答对题目总得分D.答错题目总扣分2.某篮球联赛积分规则如表所示,某支球队一共打了20场比赛,共积25分.设该支球队胜了x 场,根据题意,可列方程()比赛结果胜负积分21A.2x+x=25B.2x+(20-x)=25C.2x+(15-x)=25D.2x+(25-x)=253.某县举行安全知识竞赛,共12所学校的代表参加.比赛采取双循环赛制,每所学校的代表队比赛22场(胜一场得2分,负一场得1分),最终甲学校以总分40分获得第一名,那么甲学校的胜场数为________.二、能力提升4.某中学举行“我爱祖国”知识竞答比赛,规定每名选手共要答20道题,每答对一题得5分,不答或答错一题扣2分.(1)设选手小丽答对x道题,则小丽不答或答错共________道题(用含x的代数式表示);(2)若小丽最终成绩为65分,结合(1),求小丽答对了多少道题.三、思维拓展5.“学习生活两不误,劳逸结合更健康”.某个周末,勤奋好学的小明和爸爸下棋,爸爸赢一盘记2分,输了不记分;小明赢一盘记6分,输了不记分.一共下了8盘,每盘都分出了胜负.(1)若两人得分相等,请应用方程求出两人各赢了多少盘;(2)比赛结束时,爸爸得分可能比小明多2分吗?为什么?【课后·知能演练】1.C2.B3.18解析:设甲学校胜了x场,根据每所学校的代表队比赛场数为22,则甲学校负(22-x)场,根据甲学校总分为40分,列得方程2x+(22-x)=40,解得x=18.即甲学校胜了18场.4.解:(1)20-x(2)根据小丽最终成绩为65分,列得方程5x-2(20-x)=65.解得x=15.答:小丽答对了15道题.5.解:(1)设小明赢了x盘,则爸爸赢了(8-x)盘,根据两人得分相等,列得方程6x=2(8-x),解得x=2.当x=2时,8-x=6.答:若两人得分相等,则小明赢了2盘,爸爸赢了6盘.(2)不可能,理由如下:设小明赢了n盘,假设爸爸的得分比小明多2分,列得方程6n+2=2(8-n), .解得n=74因为n为整数,所以比赛结束时爸爸的得分不可能比小明的得分多2分.。
8.球赛积分表问题

球赛积分表问题基础知识1.比赛总场数=胜场数+平场数+负场数比赛总积分=胜场积分+平场积分+负场积分2. 解决有关表格的问题时,首先要根据表格中给出的相关信息,找出数量间的关系,然后再运用数学知识解决问题.3.用方程解决实际问题时,要注意检验方程的解是否正确,且符合问题的实际意义.典型例题例某次篮球联赛共有十支队伍参赛,部分积分表如下:根据表格提供的信息,你能求出胜一场、负一场各积多少分吗?【提示:先观察C队的得分,可知胜场得分+负场得分=_____,然后再设未知数列方程求解】想一想:某队的胜场总积分能等于它的负场总积分吗?巩固练习一.选择题1. 某球队参加比赛,开局9场保持不败,积21分,比赛规则:胜一场得3分,平一场得1分,则该队共胜( )A. 4场B. 5场C. 6场D. 7场2.某中学利用课外活动时间进行班级篮球比赛,每场比赛都要决出胜负,每队胜一场得2分,负一场得1分.已知七年级一班在8场比赛中得到13分,则七年级一班胜了()A.7B.6场C.5场D.4场3.爸爸和儿子共下12盘棋(未出现和棋)后,得分相同,爸爸赢一盘记1分,儿子赢一盘记2分,则爸爸赢了()A.9盘B.8盘C.4盘D.3盘4.A,B,C,D四支足球队分在同一小组进行单循环足球比赛,争夺出线权.比赛规则规定:胜一场得3分,平一场得1分,负一场得0分,小组中积分最高的两个队(有且只有两个队)出线.小组赛结束后,如果A队没有全胜,那么A 队的积分至少要()分才能保证一定出线.【注:单循环比赛就是小组内的每一个队都要和其他队赛一场】A.7B.6C.4D.35.足球比赛积分规则为:胜一场记3分,平一场得1分,负一场得0分,一个队进行了13场比赛,其中负了4场共得19分,那么这个队胜了()场.A.3B.2C.41D.5一.填空题6.校园记者贝贝为了报道学校球队在市中学生运动会上的情况,她从领队老师那里得知校篮球队参赛16场得28分,按规则知胜一场得2分,平一场得1分,输一场记0分,老师说校球队创下了不败的纪录。
探究2:球赛积分表问题课件

辽宁盼盼
广东宏远 前卫奥神 江苏南钢 山东润洁 浙江万马 双星济军 沈部雄师
22
22 22 22 22 22 22 22
12
12 11 10 10 7 6 0
10
10 11 12 12 15 16 22
34
34 33 32 32 29 28 22
胜一场积2分,负一场积1分。
2000赛季全国男篮甲A联赛常规赛 拓展2: 最终积分榜 如果不看积分榜的最后一
队名 八一双鹿 上海东方 北京首钢 吉林恒和 辽宁盼盼 广东宏远 前卫奥神 比赛场次 22 22 22 22 22 22 22 胜场 18 18 14 14 12 12 11 负场 4 4 8 8 10 10 11 积分 40 40 36 36 34 34 33 可以从积分榜中积分不相同的两行数 据列方程求得,如:第二行和第三行 设胜一场积X分,则上海东方队胜场总 积分为18X, 负场总积分为40-18X, 他共负了4场, 所以负一场积分为(40-18X) ÷4, 同理从北京首钢队可知: 负一场积分为(36-14X)÷ 8, 负一场的积分一样, 列方程为(40-18X) ÷ 4= (36-14X) ÷8 解这个方程,得:x=2.
远大
卫星 钢铁
14
14 14
7
4 0
7
10 14
21
14
n 18 负场积分为_________,
总积分为:
2(14-n) +n=28-n
胜一场积2分,负一场积1分。
问题6:某队的胜场总积分数能等于负场总积分数吗?
(14-x) 解:设一个队胜了x场,则负 场,
如果这个队的胜场总积分等于负场总积分,则得方程
球赛积分表问题
2000赛季全国男篮甲A联赛常规赛最终积分榜 队名 八一双鹿 上海东方 北京首钢 吉林恒和 比赛场次 22 22 22 22 胜场 18 18 14 14 负场 4 4 8 8 积分 40 40 36 36
第4课时 球赛积分表问题
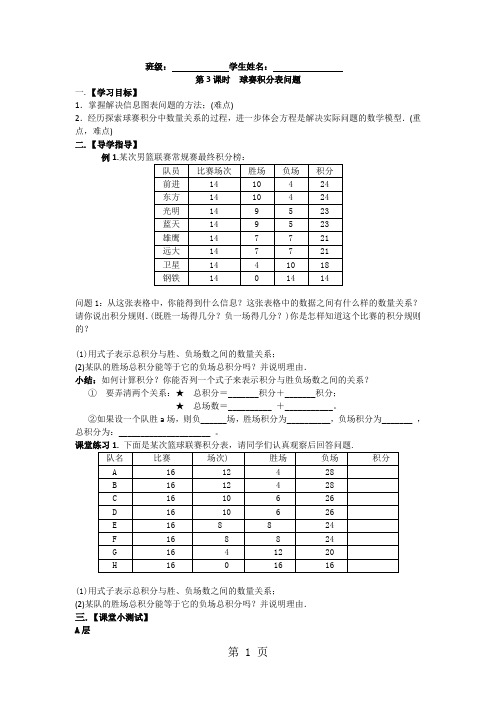
班级:学生姓名:第3课时球赛积分表问题一.【学习目标】1.掌握解决信息图表问题的方法;(难点)2.经历探索球赛积分中数量关系的过程,进一步体会方程是解决实际问题的数学模型.(重点,难点)二.【导学指导】例1.问题1:从这张表格中,你能得到什么信息?这张表格中的数据之间有什么样的数量关系?请你说出积分规则.(既胜一场得几分?负一场得几分?)你是怎样知道这个比赛的积分规则的?(1)用式子表示总积分与胜、负场数之间的数量关系;(2)某队的胜场总积分能等于它的负场总积分吗?并说明理由.小结:如何计算积分?你能否列一个式子来表示积分与胜负场数之间的关系?①要弄清两个关系:★总积分=_______积分+_______积分;★总场数=__________ +___________。
②如果设一个队胜a场,则负______场,胜场积分为__________,负场积分为_______ ,总积分为:_____________________ 。
(1)用式子表示总积分与胜、负场数之间的数量关系;(2)某队的胜场总积分能等于它的负场总积分吗?并说明理由.三.【课堂小测试】A层1.某次知识竞赛共20道题,每答对一题得8分,答错或不答要扣3分.某选手在这次竞赛中共得116分,那么他答对几道题?2.某班的一次数学小测验中,一共出了20道选择题,每题5分,总分为100分,现从中抽取5份试卷,进行分析,如下表:(1)某同学得了70分,问他答对了多少道题?(2)同学甲说他自己得了86分,同学乙说他自己得了72分,请你判断一下:谁说的是真话?为什么?B层1.有一批货物需要从A地运往B地,货主准备租用甲、乙两种货车,已知过去两次租用这两种货车运货情况如下表.现租用3辆甲种货车和5辆乙种货车,一次刚好运完这批货物,如果按每吨付502.例如:一户居民七月份用电420度,则需缴电费420×0.85=357(元).某户居民五、六月份共用电500度,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度.问该户居民五、六月份各用电多少度?。
34实际问题与一元一次方程探究2球赛积分表问题

胜负积 场场分
负一场积多少分吗?
前进
14
10 4 24
观察积分榜中的最后一 行,可以知道负一场得1分.
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
二、问题的初步探究
某次篮球联赛积分榜如下:
(1)如果一个学生得90分,那么他选对几道题?
(1)参加考试的同学中,有得83分的同学吗?为什么?
解: 设他答对了x道题,则他答错了_2_5_-_x__道题,
由题意可得方程. 4x-1×(25-x)=90
解得:x=23
4x-1×(25-x)=83
解得:x= 21 3 5
答:如果一个学生得90分,那么他选对23道题,x表示答对的 题数,它必须是整数.当x的值为分数时,不符合实际.由此可以判 断现有500名学生参加考试,没有得83分的同学.
你能得出什么结论?
上面问题说明,用方程解决实际问题时,不仅要注意解方程 的过程是否正确,还要检验方程的解是否符合问题的实际意义。
巩固应用
1.2000赛季篮球甲A联赛部分球队积分榜: 队名 比赛场次 胜场 负场 积分
八一双鹿 22 北京首钢 22 浙江万马 22 沈阳雄狮 22
18 4 40 14 8 36 7 15 29 0 22 22
(2)设x分时温度是34℃ . 则10+3x=34 解得x=8
答:8分时温度是34℃ .
课堂检测
1.一次足球赛11轮(即每队均需赛11场),胜一场 记2分,平一场记1分,负一场记0分,北京国安队所 负场数是所胜场数的二分之一,结果共得14分,求 国安队共平了多少场?
球赛积分问题PPT课件

光明 14 9 5 23 积分榜的最后一行,你
蓝天 14 9 5 23 还能求出胜一场的得分
雄鹰 14
7
7
21
或负一场的得分吗? (小组合作解决)
远大 14 7 7 21
卫星 14 4 10 18
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
畅所欲言
• 通过本节课的学习,你有哪 些收获?
10 4
10 4
9
5
9
5
7
7
7
7
4 10
0 14
积分
24 24 23 23 21 21 18 14
某次篮球联赛积分榜如下:
队名
比赛 场次
胜 场
负 场
积 分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
队名
比赛 场次
前进 14
东方 14
光明 14
蓝天 14
雄鹰 14
远大 14
卫星 14
钢铁 14
胜负积 场场分
10 4 24 10 4 24 9 5 23 9 5 23 7 7 21 7 7 21 4 10 18 0 14 14
问题3:若某队的总积分 为26分,你知道这个队的 胜场数和负场数吗?
队名
卫星 14 4 10 18
球赛积分表问题课件

的一元一次方程,有唯一解
问题4:有没有一个队的 胜场总积分等于负场总积分
呢?(请列式说明)
X表示什么量?它可以是分数吗?
注意:解决实际问题时,要考虑得到结果是不是符合实际。
根据题意,在假设结论成立
的条件下我们列方程,并正确 求解,但结果不符合实际,所
问题1、通过观察你能在这张表中获取到 什么信息?
我们要善于发现表
格的特殊之处所传达的
特殊的或重要的信息
某次男篮联赛常规赛最终积分榜
队名 前进 比赛场次 14 胜场 10 负场 4 积分 24
东方
光明 蓝天 雄鹰 远大 4 14 14
10
9 9 7 7 4 0
4
5 5 7 7 10 14
以我们只能否定假设
小结:
1.生活中数据信息的传递形式是多样的 2.解决有关表格问题,首先根据表格中给出的有 关信息,找出数量间的关系,再运用数学知识解 决有关问题. 3.利用方程不仅可以求得实际问题的具体数值,还 可以进行推理判断.
4.运用方程解决实际问题,要检验方程的解是否
符合实际意义.
应用1、下表是某校七——九年级某月课外兴趣小组 活动时间统计表,其中各年级同一兴趣小组每次活动 时间相同. 请将九年级课外兴趣小组活动次数填入下表。
参赛者
A B C D
答对题数
20 19 18 14
答错题数
0 1 2 6
得分
100 94 88 64
E
10
10
40
某次男篮联赛常规赛最终积分榜
队名 前进 比赛场次 14 胜场 10 负场 4 积分 24
东方
光明 蓝天 雄鹰 远大 卫星 钢铁
探究2球赛积分表问题

P107综合训练第8题
下表中记录了一次试验中时间和温度的数据:
(1)如果温度的变化是均匀的,21分的温度是多少? (2)什么时间的温度是34℃?
12
宇宙之大,粒子之微,火箭之速, 化工之巧,地球之变,生物之谜, 日用之繁,无处不用数学!
13
从表中其他任何一行可以列方程,求出x的值
例如:从第一行得方程
由此得
18x+1×4=40
x=2
结论: 胜一场积2分
18
4 40
18
4 40
14
8 36
14
8 36
12 10 34
12 10 34
11 11 33
10 12 32 10 12 32
7 15 29 6 16 28
0 22 22
5
结论:负一场积1分,胜一场积2分
如果这个队的胜场总积分等于负场总积分,
则得方程
2x - (22 -x)= 0
由此得
22
x=
3
7
x表示什么量?它可以是分数吗? x表示所胜的场数,必须是整数,
x = 232所以不符合实际,
由此你得出什么结论?
可以判定没有哪个队的胜场总积分等于负场总积分。
注意:解决实际问题时,要考虑得到的结果是不是符合实际。
40
18
4
40
14
8
36
14
8
36
12
10 34
12
10 34
11
11 33
10
12 32
10
12 32
7
15 29
6
16 28
0
22
22 4
球赛积分表问题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.4.3《球赛积分表问题探究》教案
教学目标
1.知识与技能
掌握应用方程解决实际问题的方法步骤,提高分析问题、解决问题的能力.
2.过程与方法
通过探索球赛积分表中数量关系的过程,进一步体会方程是解决实际问题的数学模型,并且明确用方程解决实际问题时,不仅要注意解方程的过程是否正确,还要检验方程的解是否符合问题的实际意义.
3.情感态度与价值观
鼓励学生自主探究,合作交流,养成自觉反思的良好习惯.
重、难点与关键
1.重点:把实际问题转化为数学问题,不仅会列方程求出问题的解,•还会进行推理判断.
2.难点:把实际问题转化为数学问题.
3.关键:从积分表中,找出等量关系.
学情分析:1:学生初学列方程解应用题时,往往弄不清解题步骤,不设未知数就直接进行列方程或在设未知数时,有单位却忘记写单位等。
2:学生在列方程解应用题时,可能存在三个方面的困难:
(1)抓不准相等关系;
(2)找出相等关系后不会列方程;
(3)习惯于用小学算术解法,得用代数方法分析应用题不适应,不知道要抓怎样的相等关系。
教具准备
投影仪.
教学过程
一、引入新课
教师操作投影仪,展示课本第106页中“某次篮球联赛积分榜”.
学生观察积分榜,并思考下列问题:
(1)用式子表示总积分与胜、负场数之间的数量关系;
(2)某队的胜场总积分能等于它的负场总积分吗?
在学生充分思考、合作交流后,教师引导学生分析.
要解决问题(1)必须求出胜一场积几分,负一场积几分,•你能从积分榜中得到负一场积几分吗?你选择其中哪一行最能说明负一场积几分?
通过观察积分榜,从最下面一行数据可以发现,负一场积1分,•那么胜一场积几分
呢?
学生可能会用算术方法,从积分榜中任意一行(除最后一行外),例如,从第一行244110
-⨯=2,即胜一场积2分. 你会用方程解吗?
设胜一场积x 分,从表中其他任何一行可以列方程,求出x 的值,例如从第三行得方程.
9x+5×1=23
解方程,得x=2
用表中其他行可以验证,得出结论,负一场积1分,胜一场积2分.
(1)如果一个队胜m 场,则负(14-m )场,胜场积分2m ,负场积分为14-m ,总积分为2m+(14-m )=m+14.
(2)问题(2),学生可能通过计算积分榜中各队的胜场总积分和负场总积分,说明某队的胜场总积分不能等于它的负场总积分.
你能用方程,说明上述结论吗?
如果设一个队胜了x 场,则负了(14-x )场,•如果这个队的胜场总积分等于负场总积分,那么列方程为
2x=14-x
由此,得 x=143
想一想,x 表示什么量?它可以是分数吗?由此你能得出什么结论? 这里x 表示一个队所胜的场数,它是一个整数,所以x=
143不符合实际意义.•由此可以判定没有哪个队的胜场总积分等于负场总积分.
这个问题说明:利用方程不仅能求出具体数值,而且还可以进行推理判断,是否存在某种数量关系.
另外,上面问题还说明,用方程解决实际问题时,不仅要注意方程的过程是否正确,还要检验方程的解是否符合问题的实际意义.
拓展延伸
如果删去积分榜的最后一行,你还能用式子表示总积分与胜、负场数之间的数量关系吗?
我们可以从积分榜中积分不相同的两行数据列方程求得胜、负一场各得几分,例如,从第一、三行.
设胜一场积x 分,则前进队胜场积分为10x ,负场积分为(24-10x )分,•他负了4场,所以负一场积分为
24104x -,同理从第三行得到负一场积分为2395
x -,从而列方程为 24104x -=2395x -
去分母,得5(24-10x)=4(23-9x)
去括号,得120-50x=92-36x
移项,得-50x+36x=92-120
合并同类项,得-14x=-28
x=2
当x=2时,2410
4
x
-
=
24102
4
+⨯
=1
仍然可得出结论:负一场积1分,胜一场积2分.
二、巩固练习
有一些分别标有5,10,15,20,25,…的卡片,后一张卡片上的数比前一张卡片上的数大5,小明拿到了相邻的3张卡片,且这些卡片上的数字之和为240.(1)小明拿到了哪3张卡片?
(2)你能拿到相邻的3张卡片,使得这些卡片上的数之和是63吗?
解:(1)设中间一个数为x,则前面一个数为x-5,后面一个数为x+5,根据这三个数之和为240,列方程(x-5)+x+(x+5)=240,解方程得x=80.
所以小明拿到卡片上的数分别是75,80,85.
(2)设中间一个数为x,则(x-5)+x+(x+5)=63,解方程得x=21.•因为卡片上的数都是5的倍数,所以x=21不符合题意,也就是说,卡片上的数之和是63的3张卡片不存在,所以不能拿到这样的3张卡片.
三、课堂小结
通过本节课的探究活动,使我们更加明白利用一元一次方程解决实际问题时,不仅要注意解方程的过程是否正确,还要检验方程的解是否符合问题的实际意义,同时,还可以利用方程对一些问题进行推理判断.
四、作业布置
1.课本第108页习题3.4第8、9题.
2.选用课时作业设计.
第三课时作业设计
解答题:
1.某城市按以下规定收取每月煤气费;用煤气如果不超过60立方米,按每立方米0.8元收费;如果超过60立方米,超过部分按每立方米1.2元收费,已知某用户10•月份的煤气费平均每立方米0.88元,求该用户10月份应交的煤气费是多少元?
2.某工程甲、乙合作6天完成,甲一人做需要5天完成,问乙一人做需几天完成?•这是小明给小华出的一道题,可小华说:“这道题有错,不能做”.你说呢?
3.甲每天制造零件3个,乙每天制造零件4个,甲已做4个零件,乙已知10个零件,•问几天以后,两人所做的零件个数相等?
4.观察每个月的日历,一个竖列上相邻的3个数之间有什么关系?
(1)如果设其中的一个数为x,那么其他两个数怎样表示?
(2)根据你所设的未知数x,列出方程,求出这3天分别是几号?
(3)如果小颖说出的和是60,小明能求出这3天分别是几号吗?为什么?(4)如果小颖说出的和是21,小明能求出这3天分别是几号吗?为什么?。
