高二数学异面直线PPT精品课件
合集下载
高二数学课件 异面直线课件
异面直线的距离公式：
d l 2 m2 n2 2mncos
练 习 已知正方体ABCD-A1B1C1D1 ,说出下列各对棱所在直
线的公垂线，并求它们之间的距离：
D'
C'
⑴A1B1与BC； ⑵AB与CB1 ；
⑶AC与D1B1； ⑷CD与B1C1； A'
B'
⑸A1B与CD;
这其中要注意公 式的变形及夹角。
D1
C1 (1)A到CD1的距离
A1
B1
D A
C B
正方体AC1的棱长为2,求下列距离问题
D1 A1
C1 B1
(1)A到CD1的距离 (2)A到BD1的距离
D A
C B
正方体AC1的棱长为2,求下列距离问题
D1 A1
C1 B1
(1)A到CD1的距离 (2)A到BD1的距离 (3)A到CE的距离
E
P
已知三棱锥P-ABC的
顶点P到底面三角形
ABC的三条边的距离
相等,试判断点P在底
A 面ABC的射影的位置？
B
O
内心
C
4、直线到平面的距离
一条直线和一个平面平行时，直线上任意一点 到这个平面的距离叫做直线到平面的距离
A lB
A1
B1
当直线与平面平行时，直线上不同点到平面的 距离有何关系？为什么？
Al B
O
（E为BB1的中点）
D
C
A
B
3、点到平面的距离
从平面外一点引这个平面的垂线 垂足叫做点在这个平面内的射影
这个点和垂足间的距离叫做
A
点到平面的距离
H
线面垂直
点的射影 点面距离
高二数学异面直线距离(PPT)4-3
练
习
已知正方体ABCD-A'B'C'D'的棱长为a，说出下列各对棱 所在直线的公垂线，并求它们之间的距离：
D'
⑴A'B'与BC； (1) BB' a
C'
⑵AB与CC'； (2) BC a A'
B'
⑶CD与B'C'； (3) CC’ a
⑷A'B与CD。 (4) BC a
⑸A'B与B'C' (5) OB'
O
D
C
要求：对于正方体、长方
体、正四面体中，已有的
A
B
公垂线段，能看出；简单
的公垂线段，能作出。
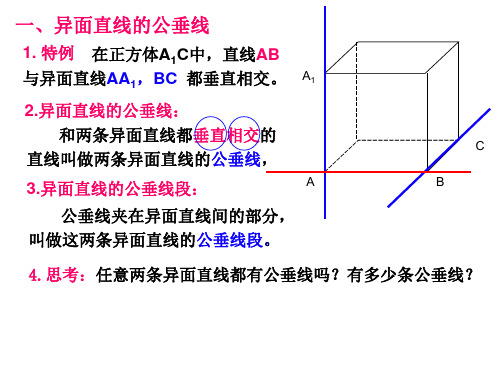
一、异面直线的公垂线
1. 特例 在正方体A1C中，直线AB 与异面直线AA1，BC 都垂直相交。 A1
2.异面直线的公垂线： 和两条异面直线都垂直相交的
直线叫做两条异面直线的公垂线，
3.异面直线的公垂线段：
A
公垂线夹在异面直线间的部分，
叫做这两条异面直线的公垂线段。
C B
4.思考：任意两条异面直线都有公垂线吗？有多少条公垂线？
经尿和粪排出。可通过胎盘屏障损及胎儿。元素砷基本无毒。但其氧化物及砷酸盐毒性较大，三价砷毒性较五价砷强。三氧化二砷的小鼠经口LD为4. mg/kg; 兔为mg/kg；猫吸入.4mg/L三氧化二砷、超过分钟即可发生急性中毒。砷可与细胞中含巯基的酶结合，抑制细胞氧化过程;还能麻痹血管运动中枢，使毛细血 管麻痹、扩张及通透性增高。急性砷化物中毒多见于砷化物污染食品或饮水，误服或自杀。临床表现以“急性胃肠炎型”较多见。重症可出现休克，肝脏损 害，甚至死于中毒性心肌损害。砷矿冶炼及三氧化二砷生产工人以及因大气、饮水长期受砷污染、或长期服用砷剂等，可发生慢性砷中毒。突出表现为皮肤
高二数学异面直线及其所成角PPT优秀课件
D ´
问题：正方体各面的对角线所
A ´
在的直线中与直线 BA´是异面
直线有哪些直线？
D
C ´ B ´
C
A
B
如图，已知两条异面直线 a、b ，经过空间任 一点O 作直线 a´∥a，b´∥ b, 我们把a´与b´所
成的锐角（或直角）叫做异面直线a与b所成 的角（或夹角）
若两异面直线所成的角为90o，我们就说这两直线垂直。
C ´
B ´
D
C
A
B
异面直线的判定方法：
连结平面内的一点与平面外一点的直线， 和这个 平面内不经过此点的直线是异面直线。
A.
.B
α
L
例1 ：如图，正方形ABCD-A´B´C´D´ 中
哪些棱所在直线与直线BA´是异面直线；
解：与直线BA´是异面直线的有
直线B´C´、AD、CC´、 DD´、
DC、D´C´。
记做a ⊥ b
b
a .o
´
α
a
.o a
´
b´
例2 ：如图，正方形ABCD-A´B´C´D´中
(1)哪些棱所在直线与直线AA´垂直； (2)求直线BA´和CC´的夹角的度数；
(3)求直线BA´和AD´的夹角的度数；D
´ A ´
C ´
B ´
D A
C B
例2 ：如图，正方形ABCD-A´B´C´D´中 E、 F分别是A´B´、BB´的中点， 1 求证BE 与C´F是异面直线
学习目标 1 熟练掌握异面直线及其所成角定义 2 掌握异面直线判定定理 3 掌握证明异面直线的常用方法
空间直线2
异面直线的概念： 把不同在任何一个平面内的两条
直线叫做异面直线
异面直线PPT课件
b'
b
a
a'
o
o a a'
平行移动法
.
7
思考：1、异面直线a、b所成角的范围？（0，90]
若异面直线a、b所成角是直角，则称 异面直线a、b互相垂直，记作a⊥b.
2、异面直线a、b所成的角的大小与点o的
位置是否有关？
异面直线a、b所成角的大小与点O的位置无 关,通常取在其中一条直线上或取特殊点.
.
1
复习回顾：
空间两直线的位置关系
位置关系
共面情况
公共点个数
相交
在同一个平面内 有且只有一个
平行 异面
在同一个平面内 不在同一个平面内
没有 没有
.
2
探究：
1、在下面长方体中，直线AB与A1C具有怎样的 位置关系？
2、在下面长方体中，还有哪些棱所在直线与A1C 异面？
3、在平面ABCD中，你还能找到哪些直线与A1C 异面？能否得到一般性结论？
这个平面内不经过该点的直线是异面直线。
符号表示:
若 l ,A ,B ,B l，A
则直线 AB与l是异面直. 线
B
l
.
5
常见异面直线的画法:
a
b
b
a
b
a
.
6
异面直线所成角:
设a、b是异面直线，过空间任一点O作
a//a， b//b，则 a，b所成的锐角(或直角)，
叫做异面直线a、b所成的角.
b
D1
C1
A
A1
D
A
B1 C
B
.
B
l
3
思考：
已l 知 ,A ： ,B ,B l
空间的异面直线ppt
4、正方体ABCD—A1B1C1D1的棱长为1，则BD1与所 CC1成角的正切值为_________ 2 5、M、N、P分别是正方体ABCD—A1B1C1D1的三个 面ABCD 、CC1DD1、BCC1B1的中心，则A1M与NP所 0 成角是___________ 90 6、已知在空间四边形ABCD中，M、N分别为AC、 BD的中点。试找出MN与AB、CD所成的角。
D B C D1 B1 C1
“垂 直”
=
“相交垂 直”
+
“异面垂 直”
习题： 1、异面直线是（ D ） A.空间不相交的两条直线 B.分别位于两个不同平面内的两条直线 C.平面内的一条直线与这个平面外的一条直线 D.既不平行又不相交的两条直线 2、下列命题正确的个数是（ A ） ①没有公共点的两条直线是平行线 ②互相垂直的两条 直线是相交线 ③与两条平行线中的一条异面的直线必 与另一条也异面 ④与两条相交线中的一条异面的直线 必与另一条也异面 A. 0 B. 1 C. 2 D. 3 3、若直线L与直线 a , b相交成等角，则a , b的位置关 系是（ D ） A. 相交 B. 平行 C.异面 D. 均有可能
异面直线定义：不同在任何一个平面 Ｄ＇ 内的两条直线叫异面直线。
Ａ＇ Ｃ＇ Ｂ＇
空间的两条直线的位置关系有：
相交、平行、异面
共 面
Ａ Ｂ
Ｄ Ｃ
不同在任何
一个平面内
异面直线所成的角的定义
直线a,b是异面直线，经过空间任意 一点o，分别作直线a1∥a, b1∥b, 我们 把直线a1和b1所成的锐角（或直角）叫做 异面直线a和b所成的角（或夹角）。
.
M
相交直线所成角的大 小，就是异面直线所成 角的大小 b
高中数学必修二2.1.2.异面直线课堂PPT.ppt
一.课题引入
问题1：在一个平面中有两条直线， 它们的位置关系有哪些？
m
n
相交，有一个公共点
m
n
平行，没有公共点
授课：XX
1
• 问题2：空间中没有公共点的直线一定平
•
行吗？
• 问题3：没有公共点的两直线一定在同一
•
平面内吗？
授课：XX
2
生活中的例子
地 铁 站
B A
授课：XX
C
D
3
螺母
a
授课：XX
a
授课：XX
10
概念辨析:两条异面直线指：
A、空间中不相交的两条直线； B、某平面内的一条直线和这平面外的直线； C、分别在不同平面内的两条直线； D、不在同一平面内的两条直线。 E、不同在任一平面内的两条直线； F、空间没有公共点的两条直线 G、既不相交，又不平行的两条直线
正确的说法是： E、G
A
H G(C)
D F(B)
AB,CD,EF,GH这四条线段所在 E 的直线是异面直线的有几对?
相交直线有几对? 平行直线有几对?
答：是异面直线的有3对， 分别为AB 与CD ；AB与GH； GH与EF
授课：XX
14
15
平行
异面
公共点个数
只有一个
没有 没有
授课：XX
是否共面
共面 共面 不共面
8
概念解析
思考题：分别在两个平面内的两条直线是否一定异面？ 答：不一定：它们可能异面，可能相交，也可能平行。
b a
M
ab
a与b是异面直线
a与b是相交直线
授课：XX
a
b
a与b是平行直线
问题1：在一个平面中有两条直线， 它们的位置关系有哪些？
m
n
相交，有一个公共点
m
n
平行，没有公共点
授课：XX
1
• 问题2：空间中没有公共点的直线一定平
•
行吗？
• 问题3：没有公共点的两直线一定在同一
•
平面内吗？
授课：XX
2
生活中的例子
地 铁 站
B A
授课：XX
C
D
3
螺母
a
授课：XX
a
授课：XX
10
概念辨析:两条异面直线指：
A、空间中不相交的两条直线； B、某平面内的一条直线和这平面外的直线； C、分别在不同平面内的两条直线； D、不在同一平面内的两条直线。 E、不同在任一平面内的两条直线； F、空间没有公共点的两条直线 G、既不相交，又不平行的两条直线
正确的说法是： E、G
A
H G(C)
D F(B)
AB,CD,EF,GH这四条线段所在 E 的直线是异面直线的有几对?
相交直线有几对? 平行直线有几对?
答：是异面直线的有3对， 分别为AB 与CD ；AB与GH； GH与EF
授课：XX
14
15
平行
异面
公共点个数
只有一个
没有 没有
授课：XX
是否共面
共面 共面 不共面
8
概念解析
思考题：分别在两个平面内的两条直线是否一定异面？ 答：不一定：它们可能异面，可能相交，也可能平行。
b a
M
ab
a与b是异面直线
a与b是相交直线
授课：XX
a
b
a与b是平行直线
高二数学最新课件-[整理]异面直线 精品
![高二数学最新课件-[整理]异面直线 精品](https://img.taocdn.com/s3/m/db745628f78a6529647d53b7.png)
如果两条异面直线所成的角是直角，就说这两 条异面直线互相垂直。 相交垂直（有垂足） 垂直 异面垂直（无垂足）
O α α O
因此，异面直线所成角的范围是 （00，900]
[例与练习1]
如图，正方体中，
A1
D1
C1
B1
1. A1B1与C1C所成的角
2. AD与B1B所成的角
D A B C
3. A1D与BC1所成的角
4. D1C与A1A所成的角 5. A1D与AC所成的角
答案: 900, 900, 900, 450, 600
b1
b
O
a 思考（1）AA1与BC、AA1与B1C1 （2）A1C1与BD、A1C1与 AD1 所成的角是几度？ A A1 D B D1 B1
两直线为异面直线 （2）从平面的性质 来讲，可分为： 两直线相交 ①在同一平面内 两直线平行
②不在同一平面内则两直线为异面线。
结论：不同在任何一个平面内的两条直线为异面直线
判定异面直线的方法： （1）根据异面直线的定义；应用反证法来证明。 （2）过平面内一点与平面外一点的直线，和这个平面内 不经过该点的直线是异面直线。（可作判断依据）
a1
C1
C
②如果两条异面直线所成的角是直角，那么我们说两条直线互 相垂直 例：图中：（1）哪些棱所在直线与 直线BA1是异面直线？ A1 （2）求直线BA1和CC1的夹角的度数 （3）哪些棱所在直线与直线AA1垂直？ D1 B1 C1
D 解：（1）由异面直线的判定方法可 C 知，与直线BA1成异面直线的有 A B 直线B1C1、AD、CC1、DD1、DC D1C1。 （2）由BB1∥CC1，可知∠B1BA等于异面直线BA1与 CC1的夹角，所以BA1与CC1的夹角为450
《异面直线的判断》课件
性质2
异面直线在任一平面上投影都不相 交。
性质3
异面直线之间的距离是固定的，可 以通过空间几何的方法来求解。
02
异面直线的判断方法
利用定义判断
总结词
直接应用定义
详细描述
根据异面直线的定义，两条直线不在同一平面上即为异面直线。因此，判断两 条直线是否为异面直线，可以直接观察它们是否在同一平面上。
利用空间几何的性质判断
《异面直线的判断》ppt课件
目录
• 异面直线的基本概念 • 异面直线的判断方法 • 异面直线的应用 • 异面直线的综合问题
01
异面直线的基本概念
异面直线的定义
01
02
03
异面直线定义
不在同一平面内且不相交 的直线。
异面直线判定
若两条直线分别与第三条 直线平行，且这两条直线 不在同一平面内，则这两 条直线为异面直线。
03
异面直线的应用
在几何问题中的应用
异面直线与平面
异面直线可以与一个平面 形成不同的角度，如垂直 、斜交等，这为解决几何 问题提供了重要的思路。
异面直线与点
通过给定的点，可以判断 该点是否在异面直线上， 或者通过异面直线找到与 该直线相关的点。
异面直线的性质
了解异面直线的性质，如 平行、相交等，有助于解 决与几何图形相关的问题 。
异面直线的性质
异面直线既不相交，也不 平行。
异面直线与平行直线、相交直线的关系
异面直线与平行直线
异面直线与平行直线没有交点，但平 行直线可能位于与异面直线相同的平 面内。
异面直线与相交直线
异面直线与相交直线没有交点，且它 们位于不同的平面内。
异面直线的性质
性质1
异面直线.ppt
两条互相垂直的异面直线 a，b，
记作 a b ．
例 如图所示的是正方体 ABCD－ABCD， (1) 哪些棱所在的直线与直线 BA 是异面直线？ (2) 求直线BA 与 CC 所成的角的度数； (3) 哪些棱所在的直线与直线 AA 垂直．
D 解： (3) 直线 AB，BC，CD， DA，AB，BC，CD，DA 都与直线 AA 垂直． D A B
如果没有特别说明，一般我们说两 条直线是指不重合的两条直线。
平面内两条直线的位置关系有哪几种？
平行和相交两种
观察正方体 ABCD－ABCD，
棱 AA 与 BC 所在的两条直线
D C
A
B
D
C
A
B
观察图片中两河流所在直线关系
• 图片：空中河流
图片的数学模型
一．异面直线的定义
我们把不同在任何一个平面内的两条直线
平面中角的概念
角是有公共端点的 两条射线组成的图 形
三．异面直线夹角．
我们把 a 和 b 所成的锐角(或直角)叫做直线 a，b 所成的角或夹角．
b
b' a O a'
b O a' a
为了简便，点 O 常取在两条异面直线中的一条上．
如果两条直线平行， 我们说它们所成的角或夹角为 0 ． 如果两条异面直线所成的角是直角， 我们就说两条异面直线互相垂直．
直线 AB 与 CD 所成的角＝ 2．直线 BC 与 CD 是 直线 BC 与 CD 所成的角＝
3．直线ห้องสมุดไป่ตู้AB 与 BC 是
直线 AB 与 BC 所成的角＝
直线，
．
D A
C
B
1．理解异面直线的定义，会判定两条直线的 位置关系是否是异面直线； 2．会求异面直线的夹角．
必修2《异面直线所成角》课件ppt(优秀课件)
所成的角是多少？
1. A1B与D1C1 2. A1B与C1C 3. A1B与CD
45° 45° 45°
D1
C 1 4. A1B与° B 1 6. B1B与AD 90°
D
C 7. A1B与B1C 60°
A
B
课件在线
14
练习2：如图，在正方体中，与A1B成 45 °角的棱有（ D ）条
呵护儿童健康成长
讲课人：优质老师
课件在线
1
课件在线
2
空间两条直线的位置关系
共面直线 异面直线
相交直线 平行直线
课件在线
3
如图所示：正方体的棱所在的 直线中，与直线BC1异面的直线 有哪些？
D
C 答案：
A
B A1B1、CD、AA1、
D1
C1 DD1、AD、A1D1
A1
B1
课件在线
4
练习:
1.垂直于同一条直线的两条直线的位
A、无数条 C、至多有两条
B、两条 D、一条
课件在线
17
练习5：在四面体ABCD中，AD=BC， 且AD⊥BC，EF分别为AB、CD的中 点，则EF与BC所成角为多少度？
A
45°
E B
D F C
课件在线
18
练习6：已知异面直线a，b所成角为 50°，P为空间一点，则过P点与a，b 所成角都是30 °直线有几条？
2条
课件在线
19
作业：课本51页第6、7、8题 B组1、2、3 课外作业:名家指路相关练习
课件在线
20
请看图: D
C
A D1
B
c1
看图得出:
A1
B1 ADC A1D1C1
高二数学异面直线成的角PPT优秀课件
问题：什么叫异面直线？
想一想：我们可以从哪些方面研究两条异面 直线的位置关系？
1.异面直线所成角
2.异面直线之间距离
▪ 看书第12页，思考下列问题： ▪ 1.什么叫异面直线所成角？ ▪ 2.异面直线所成角范围是什么？ ▪ 3.书中所谓“空间点O”的位置怎样？
直线a、b是异面直线，经过空间任意一点 O ,分别 引直线a′∥a , b′∥ b。我们把直线a′和b′所成的锐角 (或直角)叫做异面直线a和b所成的角.
例2.在四面体S-ABC中，异面直线SA与BC所成
角为90度, E, F分别为SC、AB 的中点，SA＝2，BC ＝4，求异面直线EF 与SA 所成的角.
S
E A
D
F
C
B
S
E
AGD C NhomakorabeaF B1.求异面直线所成角的基本思想是什么？
化“异面”为“共面”，通过解三角形求 角.体现了化归的数学思想。
2.求异面直线所成角的步骤有哪些？
）
2
▪ 2. 已知两条异面直线分别平行于一个150度角的两
边，那么这两条异面直线所成角为___3_0__0 ___
练习二
正 方 体ABCD- A1B1C1D1 中 , AC、BD 交 于 O, 则 OB1与A1C1所成的角的度数为 900
B1 A1
C1 D1
D O
A
C B
思考题： 长方体ABCD-A1B1C1D1，AB=AA1=2
异面直线所成角的范围是
（0，π2 ]
b′
b
O
a
a′
“空间点O”的位置 任意
例1.指出下面正方体中两条异面直线
所成角，说说理由。空间点选在哪？
（ 1） AB与 CC1 （ 2） A B与 D 1B1(3)AD1与 A1B
想一想：我们可以从哪些方面研究两条异面 直线的位置关系？
1.异面直线所成角
2.异面直线之间距离
▪ 看书第12页，思考下列问题： ▪ 1.什么叫异面直线所成角？ ▪ 2.异面直线所成角范围是什么？ ▪ 3.书中所谓“空间点O”的位置怎样？
直线a、b是异面直线，经过空间任意一点 O ,分别 引直线a′∥a , b′∥ b。我们把直线a′和b′所成的锐角 (或直角)叫做异面直线a和b所成的角.
例2.在四面体S-ABC中，异面直线SA与BC所成
角为90度, E, F分别为SC、AB 的中点，SA＝2，BC ＝4，求异面直线EF 与SA 所成的角.
S
E A
D
F
C
B
S
E
AGD C NhomakorabeaF B1.求异面直线所成角的基本思想是什么？
化“异面”为“共面”，通过解三角形求 角.体现了化归的数学思想。
2.求异面直线所成角的步骤有哪些？
）
2
▪ 2. 已知两条异面直线分别平行于一个150度角的两
边，那么这两条异面直线所成角为___3_0__0 ___
练习二
正 方 体ABCD- A1B1C1D1 中 , AC、BD 交 于 O, 则 OB1与A1C1所成的角的度数为 900
B1 A1
C1 D1
D O
A
C B
思考题： 长方体ABCD-A1B1C1D1，AB=AA1=2
异面直线所成角的范围是
（0，π2 ]
b′
b
O
a
a′
“空间点O”的位置 任意
例1.指出下面正方体中两条异面直线
所成角，说说理由。空间点选在哪？
（ 1） AB与 CC1 （ 2） A B与 D 1B1(3)AD1与 A1B
异面直线课件.ppt
(C )
(A) 1条
(B) 2条
(C) 3条
(D) 4条
例⒊如图，在长方体ABCD－A1B1C1D1的 所有棱所在的直线中，找出与棱AA1所在直 线成异面直线的所有直线。
答案
D1
与棱AA1所在直线 成异面直线的直线
A1
有：
D
C1
B1 C
BC、 CD、
A
B
B1C1、C1D1
思考：找出与AC1所在直线异面的直线。
α
aB
平面一定经过点B和直线a。
∵B ∈a，经过点B与直线a只能有一个平面α
∴直线AB与a应在平面α内。 ∴A∈α，这与已知A ∈α矛盾。
∴直线AB与a是异面直线。
例⒉选择题：
⒈异面直线是指（ D ） A、空间无公共点的两条直线 B、分别位于不同平面内的两条直线 C、某一平面内的一条直线与这平面外的
交；
④如果a和b共面，b和c共面，则a和c也共 面。
那么上述命题中，真命题的个数是（ E ） A、4 B、3 C、2 D、1 E、0
⒋如果两条直线a和b没有公共点，那么
a与b (A) 共面
( D) (B) 平行
(C) 是异面直线
(D) 可能平行，也可能是异面直线
⒌设直线a、b分别是长方体的相邻两个
面的对角线所在的直线，则a与b( D )
(A) 平行
(B) 相交
(C) 是异面直线
(D) 可能相交，也可能是异面直线
⒍如果OA∥O′A′，OB∥O′B′，那么
∠AOB和∠A′O′B′
( C)
(A) 相等
(B) 互补
(C) 可能相等，也可能互补
(D) 大小无关
⒎设AA1是长方体的一条棱，这个长方体
异面直线ppt课件
C
4、E、F分别是棱BC、DC
的中点，求异面直线AD1 与EF所成角的大小？
B
.
9
想一想:异面直线所成的角一般步骤是:
一作二证三计算
.
10
课堂小结：
1 一种思想：转化思想（空间问题平面化） 2 一个性质（异面直线判定定理） 3 一个方法：作异面直线所成的角
1
3、概念中所体现的立体几何的重要数学 思想方法是什么？
化空间问题为平面问.题的数学思想.
8
例1.已知ABCD-A1B1C1D1是棱长为a的正方体
D1
A1
D A
1、正方体的哪些棱所在直
C 1 线与直线BC1是异面直线？
2、求异面直线AA1与BC所 成的角？
B1
3、求异面直线BC1与AC所
成的角？
F
E
1.2.2空间两直线的位置关系
.
1
复习回顾：
空间两直线的位置关系
位置关系
共面情况
公共点个数
相交
在同一个平面内 有且只有一个
平行 异面
在同一个平面内 不在同一个平面内
没有 没有
.
2
探究：
1、在下面长方体中，直线AB与A1C具有怎样的 位置关系？
2、在下面长方体中，还有哪些棱所在直线与A1C 异面？
叫做异面直线a、b所成的角.
b
b'
b
a
a'
o
o a a'
平行移动法
.
7
思考：1、异面直线a、b所成角的范围？（0，90]
若异面直线a、b所成角是直角，则称 异面直线a、b互相垂直，记作a⊥b.
2、异面直线a、b所成的角的大小与点o的
高二数学异面直线距离实用PPT文档
定理一：任意两条异面直线有且只有一条公垂线。
找出或作出它们的公垂线段，再求出其长。
1
定理二：两条异面直线的公垂线段是分别连结两条异面直线上两点的线段中最短的一条。
定义：两条异面直线的公垂线段的长度，叫做两条异面直线的距离。
要求：对于正方体、长方体、正四面体中，已有的公垂线段，能看出；
将异面直线的距离转化为线面距离、点面距离。 方法1：找出或作出它们的公垂线段，再求出其长。 简单的公垂线段，能作出。
方法1：找出或作出它们的公垂线段， 再求出其长。 方法2；将异面直线的距离转化为线面 距离、点面距离等求解。
作业：、4。上面例3
C B
4.思考：任意两条异面直线都有公垂线吗？有多少条公垂线？
5.定理一：任意两条异面直线有且只有一条公垂线。
存在性： 直线AB就是异面直线a, b 的公垂线
唯一性： 假如还有直线A’B’也是a, b 的公垂线，则
β
A A’ a
Q
B
c a’
MP
α
B’ b
A’B’⊥a ，A’B’⊥b ，∵ a’//a ， ∴A’B’⊥a’
∴ A’B’⊥平面α 又∵AB ⊥平面α
∴AB//A’B’ ， 则 a, b共面， 得矛盾！
一个有用结论：
经过两条异面直线中的一条且与另一条平行的平
面有且只有一个。
6.定理二：两条异面直线的公垂线段 是分别连结两条异面直线上两点的线 段中最短的一条。
二、异面直线的距离
α
AC a
c
B
E
Db
1.定义：两条异面直线的公垂线段的长度，叫做两条异 面直线的距离。
(2)异面直线AD和BD1的距离。 A’B’⊥a ，A’B’⊥b ，∵ a’//a ， ∴A’B’⊥a’
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
汇报人：XXX
时间：20XX.XX.XX
2021/02/23
9
①异面直线a、b所成的角：过空间任一点O，分别引直线 a1∥a，b1∥b，则a1和b1所成的锐角（或直角）作为异 面直线a、b所成的角。（夹角）
b1
b
O
a1
a
思考（1）AA1与BC、AA1与B1C1
D1
（2）A1C1与BD、A1C1与
A1
AD1
所成的角是几度？
D
A
C1 B1
C B
②如果两条异面直线所成的角是直角，那么我们说两条直线互 相垂直
（3）直线AB、BC、CD、DA、A1B1、B1C1、C1D1、 D1A1都与直线AA1垂直。
巩固：①画两个相交平面，在这两个平面内各画一条直线，使 它们成为：⑴平行直线； ⑵相交直线； ⑶异面直线。
β
β
b α
a
b
a
α
β
b α
a
THANKS FOR WATCHING
谢谢大家观看
为了方便教学与学习使用，本文档内容可以在下载后随意修改，调整。欢迎下载！
异面直线的画法：
b
b
b
a
置关系：
d bc
a与b、c、d是怎样的
位置关系？a与b、c、
d的位置关系都一样
α
a
吗？
a与b、c、d都是异面直线 但a与b、c、d的位置关系都不一样，其差别在两方面，一 是倾斜程度不一样，如a、b间和a、c间倾斜程度不一样。 二是远近程度不一样，如a、d间和a、b间的远近就不一样。
新课引入： 在正方体A1B1C1D1-ABCD中，说出下列各对线段的位置关系
（1）AB和C1D1； （2）A1C1和AC； （3）A1C和D1B： （4）AB和CC1； （5）BD1和A1C1；
D1 A1
D A
C1 B1
C B
空间两直线的位置关系：
（1）从公共点的数目来看可分为： ①有且只有一个公共点则两直线相交 两平行直线
②没有公共点则 两直线为异面直线
（2）从平面的性质 来讲，可分为： 两直线相交
①在同一平面内 两直线平行
②不在同一平面内则两直线为异面直线。
结论：不同在任何一个平面内的两条直线为异面直线
判定异面直线的方法： （1）根据异面直线的定义；应用反证法来证明。
（2）连接平面内一点与平面外一点的直线，和这个平面不 经过此点的直线是异面直线。
例：图中：（1）哪些棱所在直线与
D1
直线BA1是异面直线？ （2）求直线BA1和CC1的夹角的度数
A1
（3）哪些棱所在直线与直线AA1垂直？
解：（1）由异面直线的判定方法可
D
C1 B1
C
知，与直线BA1成异面直线的有
直线B1C1、AD、CC1、DD1、DC A
B
D1C1。
（2）由BB1∥CC1，可知∠B1BA等于异面直线BA1与 CC1的夹角，所以BA1与CC1的夹角为450