2011-2015云南压轴题精选题之7、一次函数与几何图形综合题(含答案)
一次函数与几何压轴(十大题型)(解析版)—2024-2025学年八年级数学上册(浙教版)

一次函数与几何压轴(十大题型)【题型1 一函数中面积问题】【题型2 一次函数中等腰三角形的存在性问题】【题型3 次函数中直角三角形的存在性问题】【题型4 一次函数中等腰直角三角形的存在性问题】【题型5 一次函数中平行四边形存在性问题】【题型 6 一次函数中菱形的存在性问题】【题型7 一次函数中矩形的存在性问题】【题型8 一次函数中正方形的存在性问题】【题型9 一次函数与相等角/2倍角的问题】【题型10 一次函数中45°角问题】【技巧点睛1】铅锤法求三角形面积【技巧点睛2】处理与一次函数相关的面积问题,有三条主要的转化途径:①知底求高、转化线段;②图形割补、面积和差;③平行交轨、等积变换。
【技巧点睛3】处理线段问题(1)在平面直角坐标系中,若线段与y轴平行,线段的长度时端点纵坐标之差(上减下,不确定时相减后加绝对值),若线段与x轴平行,线段的长度时端点横坐标之差(右减左,不确定时相减后加绝对值);(2)线段相关计算注意使用”化斜为直”思想。
【技巧点睛4】角度问题(1)若有角度等量关系,不能直接用时,我们要学会角度转化,比如借助余角、补角、外角等相关角来表示,进行一些角度的和差和角度的代换等,直到转化为可用的角度关系。
(2)遇45°角要学会先构造等腰直角三角形,然后构造“三垂直”全等模型,一般情况下是以已知点作为等腰直角三角形的直角顶点【技巧点睛5】最值问题(1)求线段和最值,可以从“两点之间线段最短”“垂线段最短”“三角形两边之和大于第三边,两边之差小于第三边”的模型去考虑;(2)注意“转化思想”的运用,将不可用线段进行转化,变成我们熟悉的模型【技巧点睛6】特殊三角形存在问题等腰三角形存在性问题1、找点方法:①以AB 为半径,点A 为圆心做圆,此时,圆上的点(除 D 点外)与A、B构成以 A 为顶点的等腰三角形(原理:圆上半径相等)②以AB 为半径,点B 为圆心做圆,此时,圆上的点(除 E 点外)与A、B构成以 B 为顶点的等腰三角形(原理:圆上半径相等)③做AB 的垂直平分线,此时,直线上的点(除F 点外)与A、B 构成以C 为顶点的等腰三角形(原理:垂直平分线上的点到线段两端的距离相等)2、求点方法:二、直角三角形存在性问题若▲ABC是直角三角形,则分三种情况分类讨论:∠A=90°,∠B=90°,∠C=90°,然后利用勾股定理解题。
云南省中考数学总复习题型专项(七)一次函数与反比例函数的图象与性质试题

题型专项(七)一次函数与反比例函数的图象与性质一次函数与反比例函数的图象与性质的考查方式有两种:(1)对单类函数的考查:函数解析式的确定,函数图象上点的坐标,反比例函数中k的几何意义等;(2)综合考查一次函数与反比例函数:求解析式,根据其解析式解决面积、交点坐标、函数值的大小比较等相关问题.解决这些问题时,要认真观察图象,运用数形结合的思想方法,从题目和图象中挖掘隐含条件,进而解决问题.1.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是(D)A.y=2x+3 B.y=x-3C.y=2x-3 D.y=-x+32.(2016·昆明模拟)如图,A、B两点在双曲线y=错误!上,分别过A、B两点向x,y轴作垂线段,已知S阴影=1,则S1+S2=(D)A.3 B.4 C.5 D.63.(2016·云南考试说明)在同一平面直角坐标系中,函数y=-kx+k与y=错误!(k≠0)的图象大致是(C)4.(2015·陕西)如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=错误!的图象交于A、B两点,则四边形MAOB的面积为10.5.(2016·曲靖模拟)已知一次函数y=kx+3的图象经过点(1,4).(1)求这个一次函数的解析式;(2)求关于x的不等式kx+3≤6的解集.解:(1)∵一次函数y=kx+3的图象经过点(1,4),∴4=k+3.∴k=1。
∴这个一次函数的解析式是y=x+3.(2)∵k=1,∴x+3≤6。
∴x≤3,即关于x的不等式kx+3≤6的解集是x≤3。
6.(原创题)如图,一次函数的图象经过M点,与x轴交于A点,与y轴交于B点,根据图中信息求:(1)这个函数的解析式;(2)tan∠BAO的值.解:(1)设一次函数的解析式为y=kx+b。
∵函数的图象经过点M(-1,4),B(0,6),∴{-k+b=4解得错误!b=6∴这个函数的解析式为y=2x+6。
一次函数与几何综合(习题及答案)
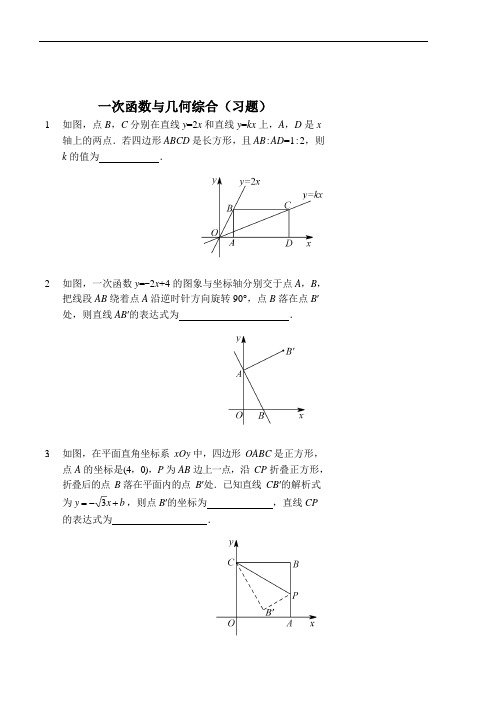
一次函数与几何综合(习题)1.如图,点B,C 分别在直线y=2x 和直线y=kx 上,A,D 是x轴上的两点.若四边形ABCD 是长方形,且AB:AD=1:2,则k 的值为.2.如图,一次函数y=-2x+4 的图象与坐标轴分别交于点A,B,把线段AB 绕着点A 沿逆时针方向旋转90°,点B 落在点B′ 处,则直线AB′的表达式为.3.如图,在平面直角坐标系xOy 中,四边形OABC 是正方形,点A 的坐标是(4,0),P 为AB 边上一点,沿CP 折叠正方形,折叠后的点B 落在平面内的点B′处.已知直线CB′的解析式为y =-3x +b ,则点B′的坐标为,直线CP 的表达式为.134.如图,点A 的坐标是( -,0),点B 的坐标是(6,0),点C在第一象限内,且△OBC 为等边三角形,直线BC 交y 轴于点D,过点A 作直线AE⊥BD,垂足为点E,交OC 于点F,则点C 的坐标为,直线AE 的表达式为.第4 题图第5 题图5.如图,一次函数的图象交x 轴于点B(-6,0),交正比例函数的图象于点A,且点A 的横坐标为-4,S△AOB =15,S△BOD=45,则一次函数的表达式为,正比例函数的表达式为.6.如图,在平面直角坐标系中,已知直线y =-3x + 3 与x 轴、y 4轴分别交于A,B 两点,点C(0,n)是y 轴上一点,把坐标平面沿直线AC 折叠,使点B 刚好落在x 轴上,则点C 的坐标是.7.如图,在平面直角坐标系中,函数y=-x 的图象l 是第二、四象限的角平分线.实验与探究:由图观察易知A(0,2)关于直线l 的对称点A′的坐标为(-2,0),请在图中分别标出B(-5,-3),C(-2,5)关于直线l 的对称点B′,C′的位置,并写出它们的坐标:B′,C′.归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第二、四象限的角平分线l 的对称点P′的坐标为.运用与拓广:已知两点D(0,-3),E(1,-4),试在直线l 上确定一点Q,使点Q 到D,E 两点的距离之和最小,并求出点Q 的坐标.8.如图,在平面直角坐标系中,直线y =x - 4 与x 轴、y 轴分别交于点A,B,P 为y 轴上B 点下方的一点,且PB=m(m>0),以点P 为直角顶点,AP 为腰在第四象限内作等腰Rt△APM.(1)用含m 的代数式表示点M 的坐标;(2)若直线MB 与x 轴交于点Q,求点Q 的坐标.5 5 【参考答案】➢ 巩固练习1. 252. y = 1 x + 423. (2, 4 - 2 ), y = -3 x +4 3 4. (3, 3 3 ), y =3 x + 13 5.y = x + 15 , y = - x 2 46. (0, 4 ),(0,-12)37. 实验与探究:(3,5),(-5,2) 归纳与发现:(-n ,-m )运用与拓广:点 Q 的坐标为(2,-2)8. (1)M (4+m ,-8-m )(2)Q (-4,0)3。
一次函数与几何综合练习(含答案)

一次函数与几何综合1.如图,在平面直角坐标系中,点A 的坐标为(2,0),以OA 为边在第四象限内作等边△ AOB,点 C 为 x 轴的正半轴上一动点( OC>2),连接 BC,以 BC 为边在第四象限内作等边△ CBD.(1)试问△ OBC 与△ ABD 全等吗?并证明你的结论;(2)直线 AD 与 y 轴交于点 E,在 C 点移动的过程中, E 点的位置是否发生变化?如果不变求出它的坐标;如果变化,请说明理由.yEA COxBD2.如图 1,在平面直角坐标系中,直线y=1 x m (m>0)与x轴,y轴分别交2于点 A,B,过点 A 作 x 轴的垂线交直线 y= x 于点 D, C 点坐标( m,0),连接CD.(1)求证: CD⊥ AB;(2)连接 BC 交 OD 于点 H(如图 2),求证: DH=3BC.2y y=x y y=x1D 1Dy= - x+m y=- x+m22B BHO CA x O CA x图1图23.如图,将边长为 4 的正方形置于平面直角坐标系第一象限, 使 AB 落在 x 轴正半轴上,直线 y 4 x 8经过点 C ,与 x 轴交于点 E .3 3( 1)求四边形 AECD 的面积;( 2)若直线 l 经过点 E ,且将正方形 ABCD 分成面积相等的两部分,求直线 l的解析式;( 3)若直线 l 1 经过点 F (- 3, 0)且与直线 y =3x 平行,将( 2)中直线 l 沿着2y 轴向上平移 1 个单位,交 x 轴于点 M ,交直线 l 1 于点 N ,求△ NMF 的面积.yDCO A E B x4.已知,如图,在平面直角坐标系内,点 A 的坐标为( 0,24),经过原点的直线 l1 与经过点 A 的直线 l2 相交于点 B ,点 B 坐标为( 18, 6).( 1)求直线 l 1,l 2的表达式;( 2)点 C 为线段 OB 上一动点(点 C 不与点 O ,B 重合),作 CD ∥y 轴交直线l 2 于点 D ,过点 C , D 分别向 y 轴作垂线,垂足分别为 F , E ,得到矩形 CDEF .①设点 C 的纵坐标为 a ,求点 D 的坐标(用含 a 的代数式表示);②若矩形 CDEF 的面积为 108,求出点 C 的坐标.y y l 2l 2AAE Dl 1l 1BBxFCxOO5.如图,四边形 ABCD 为矩形, C 点在 x 轴上, A 点在 y 轴上, D 点坐标是( 0,0),B 点坐标是( 3, 4),矩形 ABCD 沿直线 EF 折叠,点 A 落在 BC 边上的 G 处, E,F 分别在 AD, AB 上,且 F 点的坐标是( 2, 4).(1)求 G 点坐标;(2)求直线 EF 的解析式;(3)点 N 在 x 轴上,直线 EF 上是否存在点 M,使以 M、 N、 F、G 为顶点的四边形是平行四边形?若存在,请直接写出M 点的坐标;若不存在,请说明理由.yFA BGEO (D)C x1.解( 1)全等理由如下:∵△ AOB 和△ CBD 是等边三角形,∴OB= AB,∠ OBA=∠ CBD=60°, BC=BD∴∠ OBA+∠ ABC=∠ CBD+∠ ABC即∠ OBC=∠ ABD∴△ OBC≌△ ABD( 2)不变∵△ OBC≌△ ABD,△ AOB 是等边三角形∴∠ BAD=∠ BOC=60°∵∠ OAB= 60°∴∠ OAE= 180°- ∠OAB- ∠ BAD=60°∴Rt△OEA 中, AE= 2OA=4∴OE= 4222=2 3∴E(0, 2 3 )2.解:( 1)由题意知: A (2m , 0), B (0,m )∵ AD ⊥ x 轴,点 D 在直线 y =x 上 ∴ D (2m ,2m )∵ C (m , 0)∴ k CD= DA 2m =2CAm∵ k AB =12∴ k CD ·k AB = - 1∴ CD ⊥AB( 2)∵ B (0,m ), C ( m ,0)∴ OB = m ,OC =m∴ BC = 2m∵ k BC = - 1,k OD =1∴ k BC · k OD = - 1∴ BC ⊥ OD∴OH = 1BC2 m22∵ D (2m ,2m ) ∴ OD = 2 2m∴ DH = OD- OH =3 2m 2∴ DH = 3BC23.解:( 1)∵正方形 ABCD 的边长是 4,AB 在 x 轴上∴ C 点的纵坐标为 4代入 y 4 x 8得: C (5,4) 3 3∴ A (1,0),B (5,0),D (1,4)∵ y4x 8 与 x 轴交于点 E3 3 ∴ E (2,0)∴ AE =1,CD = 4, AD = 4∴ S 四边形 AECD = 1×( 1+ 4) ×4yDCPO A E B x( 2)如果直线 l 平分正方形的面积,则 l 一定过正方形的中心(即对角线的中点)如图, P 是对角线 AC 的中点∵ A (1,0), C (5,4)∴P (3,2)∴直线 l 经过点 E ( 2, 0),P (3,2)待定系数法可得直线解析式为: y =2x -4( 3)∵直线 l 1 经过点 F (- 3,0)且与直线 y =3x 平行,2设直线 l 1 的解析式为 y 1=kx +b ,则: k = 3 代入 F (- 3 , 0)得: b = 92 2∴ y 1 =3x + 92直线 l 沿着 y 轴向上平移 1 个单位,则所得的直线的解析式是:y =2x- 3,∴ M ( 3,0) 2y9联立即:3x2y2 x 315 x可得:2 y18即: N (-15,- 18)2S △NMF = 1 ×[ 3 - (- 3)] ×|- 18|=272 2 24.解:( 1)设直线 l 1 的表达式为 y=k 1x ∵点( 18,6)在直线 l 1 上∴ 6= 18k 1∴ k 1 = 13∴ y= 1x3设直线 l 2 的表达式为 y=k 2x +b∵点 A (0,24), B (18,6)在 l 2 上待定系数法可得直线 l 2 的解析式为: y=- x+24 ( 2)①∵点 C 在直线 l 1 上,且点 C 的纵坐标为 a ∴ x=3a ,∴点 C 的坐标为( 3a , a ) ∵ CD ∥ y 轴 ∴点 D 的横坐标为 3a ∵点 D 在直线 l 2 上,∴ y=- 3a+24∴ D (3a ,- 3a+24)②∵ C (3a , a ), D (3a ,- 3a+24) ∴ CF=3a , CD=- 3a+24- a=- 4a+24 ∵矩形 CDEF 的面积为 108∴ S 矩形 CDEF =CF?CD=3a ×(- 4a+24)=108,解得 a=3 当 a=3 时, 3a=9∴ C 点坐标为( 9,3)5.解:( 1)∵ F(2,4),B ( 3, 4),四边形 ABCD 是矩形∴ AF=2,OA=BC=4, AB=3在 Rt △BFG 中,由轴对称性质FG=AF=2∵ BF=AB- AF=1∴BG= 22 123∴ G (3,4- 3 )( 2)设 y=kx+b ∵在 Rt △ BFG 中,1BF=FG∴∠ BGF=30°∴∠ AFE=∠EFG=60°在 Rt△AEF 中, AF=2∴AE=2 3∴E(0,4- 2 3 )∴b=4- 2 3∵ |k|= | AE |=3|AF |∴y= 3 x+4- 2 3 (3) 存在.①M(94 3 , 3 )3yAFBMEO(D) N提示:如图,过 G 作 EF 的平行线交连接 MN, GN.GC xx轴于点 N,过 N 作 FG 的平行线交 EF 于点 M,则四边形 MNGF 为平行四边形.利用特殊角及平行四边形性质求点M 坐标即可.②M(34 3,- 3 )3yFA BG ENO(D)C x M提示:与①的方法类似.③M(3 4 3,8 3 )3y MFA BGEO (D) N C x提示:如图,过 G 作 EF 的平行线交 x 轴于点 N,连接 NF,过 G 作 NF 的平行线交直线EF 于点 M,连接 GM .则四边形 MFNG 是平行四边形.。
一次函数与几何图形综合题(含答案)

一次函数与几何图形综合题(含答案)近日,举行了一次关于一次函数与几何图形综合的专题讲座。
在思想方法方面,介绍了函数方法和数形结合法。
函数方法是通过观察运动和变化来分析数量关系,并将其抽象升华为函数模型,从而解决问题的方法。
数形结合法则是将数与形结合起来,分析研究并解决问题的一种思想方法,对于与函数有关的问题,使用数形结合法能够事半功倍。
在知识规律方面,讲座介绍了常数k和b对直线y=kx+b(k≠0)位置的影响。
当b大于0时,直线与y轴的正半轴相交;当b等于0时,直线经过原点;当b小于0时,直线与y轴的负半轴相交。
当k和b异号时,即b大于0时,直线与x轴正半轴相交;当k和b同号时,即k和b的乘积小于0时,直线与x轴负半轴相交。
当k大于0且b大于0时,图象经过第一、二、三象限;当k大于0且b等于0时,图象经过第一、三象限;当b大于0且b小于0时,图象经过第一、三、四象限;当k小于0且b大于0时,图象经过第一、二、四象限;当k小于0且b等于0时,图象经过第二、四象限;当b小于0且b小于0时,图象经过第二、三、四象限。
讲座还介绍了直线y=kx+b(k≠0)与直线y=kx(k≠0)的位置关系。
当b大于0时,将直线y=kx向上平移b个单位,即可得到直线y=kx+b;当b小于0时,将直线y=kx向下平移|b|个单位,即可得到直线y=kx+b。
另外,当k1不等于k2时,y1与y2相交;当k1等于k2且b1不等于b2时,y1与y2平行但不重合;当k1等于k2且b1等于b2时,y1与y2重合。
最后,讲座还通过一个例题对知识规律进行了精讲。
题目是直线y=-2x+2与x轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB。
要求求出AC的解析式。
的性质,需要灵活运用几何知识和代数知识。
在解答过程中,要注意清晰的逻辑思路和准确的计算,避免出现错误。
2) 在OA的延长线上任取一点P,作PQ⊥BP,交直线AC于Q。
我们来探究一下BP与PQ的数量关系,并证明结论。
(完整版)一次函数与几何图形综合题10及答案

专题训练:一次函数与几何图形综合1、直线y=-x+2与x 轴、y 轴交于A 、B 两点,C 在y 轴的负半轴上,且OC=OB(1) 求AC 的解析式;(2) 在OA 的延长线上任取一点P,作PQ ⊥BP,交直线AC 于Q,试探究BP 与PQ 的数量关系,并证明你的结论。
(3) 在(2)的前提下,作PM ⊥AC 于M,BP 交AC 于N,下面两个结论:①(MQ+AC)/PM 的值不变;②(MQ-AC)/PM 的值不变,期中只有一个正确结论,请选择并加以证明。
2.(本题满分12分)如图①所示,直线L :5y mx m =+与x 轴负半轴、y 轴正半轴分别交于A 、B 两点。
(1)当OA=OB 时,试确定直线L 的解析式;xyo BA CPQxyo BA CPQM第2题图①(2)在(1)的条件下,如图②所示,设Q 为AB 延长线上一点,作直线OQ ,过A 、B 两点分别作AM ⊥OQ 于M ,BN ⊥OQ 于N ,若AM=4,BN=3,求MN 的长。
(3)当m 取不同的值时,点B 在y 轴正半轴上运动,分别以OB 、AB 为边,点B 为直角顶点在第一、二象限内作等腰直角△OBF 和等腰直角△ABE ,连EF 交y 轴于P 点,如图③。
问:当点B 在 y 轴正半轴上运动时,试猜想PB 的长是否为定值,若是,请求出其值,若不是,说明理由。
3、如图,直线1l 与x 轴、y 轴分别交于A 、B 两点,直线2l 与直线1l 关于x 轴对称,已知直线1l 的解析式为3y x =+,(1)求直线2l 的解析式;(3分)第2题图②第2题图③CB Al 2l 1xy(2)过A 点在△ABC 的外部作一条直线3l ,过点B 作作CF ⊥3l 于F 分别,请画出图形并求证:BE +CF =(3)△ABC 沿y 轴向下平移,AB 边交x 轴于点P ,过P 点的直线与AC 边的延长线相交于点Q ,与y 轴相交与点M ,且BP =CQ ,在△ABC 平移的过程中,①OM 为定值;②MC 为定值。
一次函数与几何图形综合题(含答案)资料
一次函数与几何图形综合专题讲座思想方法小结 : (1)函数方法.函数方法就是用运动、变化的观点来分析题中的数量关系,抽象、升华为函数的模型,进而解决有关问题的方法.函数的实质是研究两个变量之间的对应关系,灵活运用函数方法可以解决许多数学问题.(2)数形结合法.数形结合法是指将数与形结合,分析、研究、解决问题的一种思想方法,数形结合法在解决与函数有关的问题时,能起到事半功倍的作用.知识规律小结 :(1)常数k ,b 对直线y =kx +b (k ≠0)位置的影响. ①当b >0时,直线与y 轴的正半轴相交; 当b =0时,直线经过原点;当b ﹤0时,直线与y 轴的负半轴相交. ②当k ,b 异号时,即-kb>0时,直线与x 轴正半轴相交; 当b =0时,即-k=0时,直线经过原点; 当k ,b 同号时,即-kb﹤0时,直线与x 轴负半轴相交.③当k >O ,b >O 时,图象经过第一、二、三象限; 当k >0,b =0时,图象经过第一、三象限; 当b >O ,b <O 时,图象经过第一、三、四象限; 当k ﹤O ,b >0时,图象经过第一、二、四象限; 当k ﹤O ,b =0时,图象经过第二、四象限; 当b <O ,b <O 时,图象经过第二、三、四象限. (2)直线y =kx +b (k ≠0)与直线y =kx (k ≠0)的位置关系. 直线y =kx +b (k ≠0)平行于直线y =kx (k ≠0)当b >0时,把直线y =kx 向上平移b 个单位,可得直线y =kx +b ; 当b ﹤O 时,把直线y =kx 向下平移|b |个单位,可得直线y =kx +b . (3)直线b 1=k 1x +b 1与直线y 2=k 2x +b 2(k 1≠0 ,k 2≠0)的位置关系.①k 1≠k 2⇔y 1与y 2相交; ②⎩⎨⎧=≠2121b b k k ⇔y 1与y 2相交于y 轴上同一点(0,b 1)或(0,b 2); ③⎩⎨⎧≠=2121,b b k k ⇔y 1与y 2平行;④⎩⎨⎧==2121,b b k k ⇔y 1与y 2重合.例题精讲:1、直线y =-2x +2与x 轴、y 轴交于A 、B 两点,C 在y 轴的负半轴上,且OC =OB(1) 求AC 的解析式;(2) 在OA 的延长线上任取一点P ,作PQ ⊥BP ,交直线AC 于Q ,试探究BP 与PQ 的数量关系,并证明你的结论。
部编数学八年级下册专题09一次函数与几何图形综合的七种考法(解析版)含答案
专题09 一次函数与几何图形综合的七种考法类型一、面积问题例.如图,直线AB 的表达式为364y x =-+,交x 轴,y 轴分别与B ,A 两点,点D 坐标为()4,0-点C 在线段AB 上,CD 交y 轴于点E .(1)求点A ,B 的坐标.(2)若CD CB =,求点C 的坐标.(3)若ACE △与DOE V 的面积相等,在直线AB 上有点P ,满足DOC △与DPC △的面积相等,求点P 坐标.∵CD CB =,∴DF BF =,∵点D 坐标为()4,0-,点B 的坐标为(∴12BD =,8OB =,∴6BF =,∴2OF =,∵DOC △与DPC △的面积相等,∴点O 和点P 到距离相等,此时OP ∥∴直线OP 的解析式为35y x =,联立得:36435y x y xì=-+ïïíï=ïî,解得:x y ì=ïïíï=ïî【变式训练1】如图,直线1:1l y kx =+与x 轴交于点D ,直线2:l y x b =-+与x 轴交于点A ,且经过定点(1,5)B -,直线1l 与2l 交于点(2,)C m .(1)填空:k =________;b =________;m =________;(2)在x 轴上是否存在一点E ,使BCE V 的周长最短?若存在,请求出点E 的坐标;若不存在,请说明理由;(3)若动点P 在射线DC 上从点D 开始以每秒1个单位的速度运动,连接AP ,设点P 的运动时间为t 秒.是否存在t 的值,使ACP △和ADP △的面积比为1:2?若存在,直接写出t 的值;若不存在,请说明理由.(3)∵点P 在射线DC 上从点∴(2,0)D -,∵(2,2)C ,∴22(22)225CD =++=,∵点P 的运动时间为t 秒.②点P 在线段DC 的延长线上,∵ACP △和ADP △的面积比为1:∴12CP DP =,∴22545DP =´=,综上:存在t 的值,使ACP △和【变式训练2】在平面直角坐标系中,O 为原点,点()4,0A ,()2,0B -,()3,2C -,点D 是y 轴正半轴上的动点,连接CD 交x 轴于点E .(1)如图①,若点D 的坐标为()0,2,求ACD V 的面积;(2)如图②,若12ABD ABC S S =V V ,求点D 的坐标.(3)如图③,若BDE ACE S S =△△,请直接写出点D 的坐标.【变式训练3】如图,平面直角坐标系中,直线AB :13y x b =-+交y 轴于点()0,1A ,交x 轴于点B .过点()1,0E 且垂直于x 轴的直线DE 交AB 于点D ,P 是直线DE 上一动点,且在点D 的上方,设()1,P n .(1)求直线AB 的解析式和点B 的坐标;(2)求ABP V 的面积(用含n 的代数式表示);(3)当ABP V 的面积为2时,以PB 为边在第一象限作等腰直角三角形BPC ,求出点C 的坐标.,则90PEB BP CGB Ð=Ð=Ð=°,PB BC =,∴90PBE BPE Ð+Ð=°,90BPE CPG Ð+Ð=°,∴BPE CPG Ð=Ð,∴()AAS BEP PGC ≌V V ,∴2BE PG ==,2PE CG ==,∴点()3,4C ;②以PB 为底时,如图,过点C 作CG PE ^于点G ,作CH x ^轴于点H ,则90PGC CGE CHB PEB PCB Ð=Ð=Ð=°=Ð=Ð,CP CB =,∴90GCH PCB Ð=°=Ð,∴PCG BCH Ð=Ð,∴∴()AAS BCH PCG ≌V V ,∴BH PG =,CH CG =,∴BE BH PE PG +=-,即22BH BH +=-,∴0BH PG ==,∴点()3,2C ;综上,符合题意的点C 坐标为()5,2或()3,4或()3,2.类型二、最值问题例.如图,在平面直角坐标系xOy 中,一次函数()0y kx b k =+¹的图像经过()4,0A 、()0,4B 两点.(1)k =______,b =______.(2)已知()1,0M -、()3,0N ,①在直线AB 上找一点P ,使PM PN =.用无刻度直尺和圆规作出点P (不写画法,保留作图痕迹);②点P 的坐标为______;③点Q 在y 轴上,那么PQ NQ +的最小值为______.【答案】(1)1-,4;(2)①见解析;②()1,3;③5【详解】(1)解:将()4,0A 、()0,4B 代入()0y kx b k =+¹中,得:044k b b =+ìí=î,解得;14k b =-ìí=î,故答案为:1-,4;(2)①如图,点P 即为所求;【变式训练1】在平面直角坐标系中,已知直线l经过1,32Aæöç÷èø和()3,2B-两点,且与x轴,y轴分别相交于C,D两点.(1)求直线l的表达式;V的面积等于2时,求点E的坐标;(2)若点E在直线AB上,当ODE-的值最小,则点P的坐标为______;(3)①在x轴上找一点P,使得PA PB-的值最大,则点Q的坐标为______.②在x轴上找一点Q,使得QA QB【变式训练2】如图,一次函数2y x =+的图象分别与x 轴和y 轴交于C ,A 两点,且与正比例函数y kx=的图象交于点()1,B m -.(1)求正比例函数的表达式;(2)点D 是一次函数图象上的一点,且OCD V 的面积是4,求点D 的坐标;(3)点P 是y 轴上一点,当BP CP +的值最小时,若存在,点P 的坐标是______.取点C 关于y 轴的对称点C ¢,则PC PC =CP BP C P BP C B ¢¢\+=+³,即点P 位于C B ¢与x 轴的交点时,BP +∵点(2,0)C - ,【变式训练3】如图,在平面直角坐标系内,()3,4A -,()3,2B ,点C 在x 轴上,AD x ^轴,垂足为D ,BE x ⊥轴,垂足为E ,线段AB 交y 轴于点F .若AC BC =,ACD CBE Ð=Ð.(1)求点C 的坐标;(2)如果经过点C 的直线y kx b =+与线段BF 相交,求k 的取值范围;(3)若点P 是y 轴上的一个动点,当PA PC -取得最大值时,求BP 的长.类型三、等腰三角形存在性问题例.如图,在平面直角坐标系中,一次函数21y x =--的图像分别交x 轴、y 轴于点A 和B .已知点C 的标为()3,0-,若点P 是x 轴上的一个动点.(1)A 的坐标是______,B 的坐标是______;(2)过点P 作y 轴的平行线交AB 于点M ,交BC 于点N ,当点P 恰好是MN 的中点时,求出P 点坐标.(3)若以点B 、P 、C 为顶点的BPC △为等腰三角形时、请求出所有符合条件的P 点坐标.【变式训练1】直线8y kx =-与x 轴、y 轴分别交于B C 、两点,且43OC OB =.(1)求OB 的长和k 的值:(2)若点A 是第一象限内直线8y kx =-上的一个动点,当它运动到什么位置时,AOB V 的面积是12?(3)在(2)成立的情况下,y 轴上是否存在点P ,使POA V 是等腰三角形?若存在,求出点P 的坐标;若不存在,请说明理由.(写过程)由题意得,12OB AD ´´=6OB =Q ,\解得,AD当21294OA OP =+==当397OA OP ==时,3P 当22AP OP =时,作2P H ^22AP OP =Q Q 2P 为线段OA 垂直平分线与【变式训练2】在平面直角坐标系中,直线MN 交x 轴正半轴于点M ,交y 轴负半轴于点()0,3N -,30Ð=°ONM ,作线段MN 的垂直平分线交x 轴于点A ,交y 轴于点B .(1)如图1,求直线MN 的解析式和A 点坐标;(2)如图2,过点M 作y 轴的平行线l ,P 是l 上一点,若ANP S =△P 坐标;(3)如图3,点Q 是y 轴的一个动点,连接QM 、AQ ,将MAQ V 沿AQ 翻折得到1M AQ △,当1M MN △是等腰三角形时,求点Q 的坐标.过T 作TS AM ^于S ,则AT ∴22333322AS æö=-=ç÷èø,同理2315Q P y x =--:,综上:()3,6P ,(3,P -(3)①如图,当MN MM =由轴对称的性质可得:AM ∵()223323AN =+=,∴()0,1Q .②当1NM NM =时,如图,由23AN NM AM ===,∴ANM V 为等边三角形,此时Q ,N 重合,∴()0,3Q -;③当11M M M N =时,1M 在直线∵30OAB Ð=°,【变式训练3】如图,一次函数()0y kx b k =+¹的图象与x 轴交于点C ,与y 轴交于点()0,5A ,与正比例函数12y x =的图象交于点B ,且点B 的横坐标为2,点P 为y 轴上的一个动点.(1)求B 点的坐标和k 、b 的值;(2)连接CP ,当ACP △与AOB V 的面积相等时,求点P 的坐标;(3)连接BP ,是否存在点P 使得PAB V 为等腰三角形?若存在,请求出点P 的坐标;若不存在,请说明理由.③当PA PB =时,如图2,设(0,P m 22(5)PA m =-,1PH m =-,所以PB 所以222(5)(1)2m m -=-+,解得m类型四、直角三角形存在性问题例.如图1,在平面直角坐标系xOy 中,点O 为坐标原点,直线AB :3y 4x b =+与直线AC :9y kx =+交于点(2,)A n ,与x 轴分别交于点0()6,B -和点C .点D 为线段BC 上一动点,将ABD △沿直线AD 翻折得到ADE V ,线段AE 交x 轴于点F .(1)直线AC 的函数表达式.(2)当点D 在线段BO 上,点E 落在y 轴上时,求点E 的坐标.(3)若DEF V 为直角三角形,求点D 的坐标.【变式训练1】综合与探究:如图,在平面直角坐标系中,直线2y x =+与x 轴,y 轴分别交于点A ,B ,与直线11433y x =-+交于点C .直线11433y x =-+与x 轴交于点D ,若点P 是线段AD 上的一个动点,点P 从点D 出发沿DA 方向,以每秒2个单位长度匀速运动到点A (到 A 停止运动).设点P 的运动时间为s t .(1)求点A 和点B 的坐标;△的面积为12时,求t的值;(2)当ACP△为直角三角形?若存在,请直接写出t的值;(3)试探究,在点P运动过程中,是否存在t的值,使ACP若不存在,请说明理由.【变式训练2】如图,平面直角坐标系中,直线AB 与x 轴交于点()30A -,与y 轴交于点()06B ,,点C 是直线AB 上的一点,它的坐标为()4m ,,经过点C 作直线CD x ∥轴交y 轴于点D .(1)求点C 的坐标;(2)已知点P 是直线CD 上的动点,①若POC △的面积为4,求点P 的坐标;②若POC △为直角三角形,请求出所有满足条件的点P 的坐标.②Q OCP Ð一定不是直角,当90OPC Ð=°时,点P 恰好在点D ,\()04P ,,当90POC Ð=°时,,由题可得221417OC =+=,2222416OP DP DP =+=+,()221CP DP =+,Q 222CP OC OP =+,\()2211716DP DP +=++,\16DP =,\()164P ,,综上所述,所有满足条件的点P 的坐标为()04,或()164P ,.【变式训练3】如图,已知函数1y x =+的图象与y 轴交于点A ,一次函数y kx b =+的图象经过点()0,1B -,与x 轴以及1y x =+的图象分别交于点C ,D ,且点D 的坐标为()1,n .(1)则k =______,b =______,n =______;(2)关于x ,y 的二元一次方程组y =x +1,y =kx +b的解为______;(3)求四边形AOCD 的面积;(4)在x 轴上是否存在点P ,使得以点P ,C ,D 为顶点的三角形是直角三角形,请求出点P 的坐标.①当P D DC ¢^时,22P C P D ¢¢=类型五、等腰直角三角形存在性问题例.模型建立:如图1,等腰直角三角形ABC 中,90ACB Ð=°,CB CA =,直线ED 经过点C ,过A 作AD ED ^于D ,过B 作BE ED ^于E .(1)求证:BEC CDA V V ≌.(2)模型应用:已知直线14:43l y x =+与y 轴交与A 点,将直线1l 绕着A 点顺时针旋转45°至2l ,如图2,求2l 的函数解析式.(3)如图3,矩形ABCO ,O 为坐标原点,B 的坐标为()8,6,A 、C 分别在坐标轴上,P 是线段BC 上动点,设PC m =,已知点D 在第一象限,且是直线26y x =-上的一点,若APD △是不以A 为直角顶点的等腰直角三角形,请直接写出点D 的坐标.∵45BAC Ð=°,∴ABC V 为等腰直角三角形,由(1)得:CBD BAO V V ≌∴BD AO =,CD OB =,∵直线4:4l y x =+,∴()626122AE x =--=-由(1)得:ADE DPF △△≌∴DF AE =,即1228x x -=-,解得:4x =;∴()4,2D ;∴266212BF x x =--=-;同(1)得,APB PDF △≌△∴8AB PF ==,PB DF ==∴()88BF PF PB x =-=--=∴21216x x -=-,解得:283x =;∴2838,33D æöç÷èø;【变式训练1】综合与探究:如图1,平面直角坐标系中,一次函数334y x =-+的图像分别与x 轴、y 轴交于点A ,B ,点C 是线段OA 的中点,点D 与点C 关于y 轴对称,作直线BD .(1)求A ,B 两点的坐标;(2)求直线BD 的函数表达式;(3)若点P 是直线BD 上的一个动点.请从A ,B 两题中任选一题作答.我选择______题.A .如图2,连接AP ,CP .直接写出ACP △为直角三角形时点P 的坐标.B .如图3,连接CP ,过点P 作PQ x ^轴于点Q .直接写出CPQ V 为等腰直角三角形时点P 的坐标.【变式训练2】如图,平面直角坐标系中,直线1:3AB y x b =-+交y 轴于点()0,1A ,交x 轴于点B .直线1x =交AB 于点D ,交x 轴于点E ,P 是直线1x =上一动点,且在点D 的上方,设()1,P n .(1)求直线AB 的解析式;(2)当2ABP S =△时,在第一象限内找一点C ,使BCP V 为等腰直角三角形,求点C 的坐标.∵1x =时,12133y x =-+=,P 在点∴23PD n =-,∴12PAB APD BPD S S S PD AM =+=×+V V V ∵2ABP S =△,3∵90,45CPB EPB Ð=°Ð=°,∴45NPC EPB Ð=Ð=°.又∵90,CNP PEB BP PC Ð=Ð=°=,∴CNP BEP ≌V V ,∴2PN =NC =EB =PE =,∴224NE NP+PE ==+=,∴()3,4C ;若90,PBC BP BC Ð=°=,如图,过点C 作CF x ^轴于点F .∵90,45PBC EBP Ð=°Ð=°,∴45CBF PBE Ð=Ð=°.又∵90,CFB PEB BC BP Ð=Ð=°=,∴CBF PBE ≌V V .∴2BF CF PE EB ====,∴325OF OB BF =+=+=,∴()5,2C ;若90,PCB CP EB Ð=°=,如图,∴45CPB EBP Ð=Ð=°,∵,,CP EB CPB EBP BP BP =Ð=Ð=,∴PCB PEB ≌V V ,∴2PC CB PE EB ====,∴()3,2C ;∴点C 的坐标是()3,4或()5,2或()3,2.【变式训练3】如图,在平面直角坐标系xOy 中,直线AP 交x 轴于点(),0P p ,与y 轴交于点()0,A a ,且a ,p ()230a +=.(1)求直线AP 的解析式;(2)如图1,直线2x =-与x 轴交于点N ,点M 在x 轴上方且在直线2x =-上,若MAP △的面积等于6,请求出点M 的坐标;(3)如图2,已知点()2,4C -,若点B 为射线AP 上一动点,连接BC ,在坐标轴上是否存在点Q ,使BCQ △是以BC 为底边,点Q 为直角顶点的等腰直角三角形,若存在,请直接写出点Q 坐标;若不存在,请说明理由.∵MD AP P ,MAP △的面积等于∴DAP V 的面积等于6,∴162A DP y ××=,即12DP ×∴4DP =,∴()3,0D -,y∴,33OE t BE t ==-,∵BCQ △是以BC 为底边的等腰直角三角形,∴BQ CQ =,90BQC Ð=∴90BQE NQC Ð=°-Ð=又∵BEQ QNC Ð=Ð,∴()AAS BEQ QNC V V ≌,∴BG t =,33OG t =-,∴BT t =,33OT t =-,同②可证CFQ QTB V V ≌∴QF BT t ==,QT CF =∴OQ OT QT OF =+=+∴52t =,∴513422OQ =+=,类型六、平行四边形存在性问题例.在平面直角坐标系xOy 中,直线36y x =+分别与x 、y 轴相交于A 、B 两点,将线段AB 绕点A 顺时针旋转90°得到线段AC .连接BC 交x 轴于点D .(1)求点C 的坐标;(2)P 为x 轴上的动点,连接PB ,PC ,当PB PC -的值最大时,求此时点P 的坐标.(3)点E 在直线AC 上,点F 在x 轴上,若以B 、D 、E 、F 为顶点的四边形是平行四边形,请直接写出点F 的坐标;【答案】(1)点C 的坐标为()4,2-(2)()6,0P (3)点F 的坐标为()17,0-或()13,0或()23,0【详解】(1)解:令0y =,则2x =-,()2,0A \-,令0x =,则6y =,()0,6B \,26OA BO \==,,过点C 作CH x ^轴于H ,9090CAD BAO BAO ABO ÐÐÐÐ+=°+=°Q ,,CAD ABO ÐÐ\=,90AHC BOA ÐÐ\==°,由旋转得AB AC =,()AAS ABO CAH \V V ≌,26CH OA AH BO \====,,4OH AH OA \=-=,\点C 的坐标为()4,2-;(2)作点C 关于x 轴的对称点C ¢,连接BC ¢延长交x 轴于点P ,则点P 就是所求的最大值点,\()4,2C ¢设直线BC ¢的解析式为y kx b =+,\642b k b =ìí+=î,解得16k b =-ìí=î,6y x \=-+,()6,0P \;(3)()()()2,04,20,6A C B --Q ,,,设直线AC 的解析式为y mx n =+,则2042m n m n -+=ìí+=-î【变式训练1】如图1,在平面直角坐标系中,直线AB 与x 轴交于点(),0A m ,与y 轴交于点()0,B n ,且m n ,满足:()260m n n ++-=.(1)求:AOB S V 的值;(2)D 为OA 延长线上一动点,以BD 为直角边作等腰直角BDE V ,连接EA ,求直线EA 与y 轴交点F 的坐标;(3)在(2)的条件下,当2AD =时,在坐标平面内是否存在一点P ,使以B E F Р、、、为顶点的四边形是平行四边形,如果存在,直接写出点Р的坐标,若不存在,说明理由.∵EDB △为等腰直角三角形,∴,90DE DB EDB =Ð=°,∴18090EDG ODB Ð+Ð=°-。
专题09 一次函数与几何图形的综合问题(解析版)
专题09 一次函数与几何图形的综合问题类型一、面积问题例.如图,一次函数1y ax b =+与反比例函数2k y x=的图象相交于A (2,8),B (8,n )两点,连接AO ,BO ,延长AO 交反比例函数图象于点C .(1)求一次函数1y 的表达式与反比例函数2y 的表达式:(2)当1y <2y 时,直接写出自变量x 的取值范围为_________;(3)点P 是x 轴上一点,当S △PAC =45S △AOB 时,求出点P 的坐标.【答案】(1)一次函数10,y x =-+ 反比例函数16y x =;(2)8x >或02x <<;(3)()3,0P 或()3,0P -【解析】(1)解:将A (2,8)代入k y x =得82k =,解得k =16,∴反比例函数的解析式为16y x =,把B (8,n )代入得,n =168=2,∴B (8,2),将A (2,8),B (8,2)代入y =ax +b 得2882a b a b ì+=ïí+=ïî,解得110a b =-ìí=î,∴一次函数为y =﹣x +10;(2)解:由图象可知,当y 1<y 2时,自变量x 的取值范围为:x >8或0<x <2,故答案为x >8或0<x <2;(3)解:由题意可知,A C 关于原点成中心对称,则OA =OC ,∴S △APC =2S △AOP ,如图,记AB 与x 轴的交点为D ,把y =0代入y 1=﹣x +10得,0=﹣x +10,解得x =10,∴D (10,0),∴111081023022AOB AOD BOD S S S =-=´´-´´=△△△,∵44302455PAC AOB S S ==´=△△,∴2S △AOP =24,∴12242A OP y ´´=,即128242OP ´´=,∴OP =3,∴P (3,0)或P (﹣3,0).【变式训练1】平面直角坐标系xOy 中,经过点(1,2)的直线y =kx +b ,与x 轴交于点A ,与y 轴交于点B .(1)当b =3时,求k 的值以及点A 的坐标;(2)若k =b ,p 是该直线上一点,当△OPA 的面积等于△OAB 面积的2倍时,求点P 的坐标.【答案】(1)1k =-,()3,0A ;(2)点P 的坐标为()1,2P 或()3,2--.【解析】(1)解:当3b =时,3y kx =+,将点()1,2代入可得:23k =+,解得:1k =-,∴一次函数解析式为:3y x =-+,当0y =时,3x =,∴()3,0A ;(2)解:∵k b =,∴y kx k =+,将点()1,2代入可得:2k k =+,解得:1k =,∴1y x =+,当0x =时,1y =,点()0,1B ,1BO =,当0y =时,1x =-,点()1,0A -,1OA =,∴11·22AOB S OA OB ==n ,设(),P x y ,且1y x =+,如图所示,连接OP ,21AOP AOB S S ==n n ,1·12OA y =,∴2y =,∴2y =±,当2y =时,21x =+,解得:1x =,∴()1,2P ;当2y =-时,21x -=+,解得:3x =-,∴()3,2P --;综上可得:点P 的坐标为()1,2P 或()3,2--.【变式训练2】如图,在平面直角坐标系中,直线m 经过点(﹣1,2),交x 轴于点A (﹣2,0),交y 轴于点B ,直线n 与直线m 交于点P ,与x 轴、y 轴分别交于点C 、D (0,﹣2),连接BC ,已知点P 的横坐标为﹣4.(1)求直线m 的函数表达式和点P 的坐标;(2)求证:△BOC 是等腰直角三角形;(3)直线m 上是否存在点E ,使得S △ACE =S △BOC ?若存在,求出所有符合条件的点E 的坐标,若不存在,请说明理由.【答案】(1)直线m 的解析式为24y x =+,点P 的坐标为(-4,-4)(2)见解析;(3)(23-,83)或(103-,83-)【解析】(1)解:设直线m 的解析式为y kx b =+,由题意得:220k b k b -+=ìí-+=î,解得24k b =ìí=î,∴直线m 的解析式为24y x =+,∵点P 在直线m 上,且点P 的横坐标为-4,∴点P 的纵坐标为4244-´+=-,∴点P 的坐标为(-4,-4);(2)解:设直线n 的解析式为11y k x b =+,∴111442k b b -+=-ìí=-î,解得11122k b ì=ïíï=-î,∴直线n 的解析式为122y x =-,∵B 是直线m 与y 轴的交点,C 是直线n 与x 轴的交点,∴点B 的坐标为(0,4),点C 的坐标为(4,0),∴OB =OC =4,又∵∠BOC =90°,∴△BOC 是等腰直角三角形;(3)解:设点E 的坐标为(m ,2m +4)∵A 点坐标为(-2,0),C 点坐标为(4,0),∴AC =6,∴1=3242ACE E S AC y m ×=+△,∵1==82ACE BOC S S OB OC =×△△,∴3248m +=,解得23m =-或103m =-,∴点E 的坐标为(23-,83)或(103-,83-).【变式训练3】如图,已知一次函数132y x =-+与x 轴交于点A ,与y 轴交于点B ,点C 与点A 关于y 轴对称.(1)求直线BC 的函数关系式;(2)若点M 在线段AC 上,过点M 作y 轴的平行线,交直线AB 于点P ,交直线BC 于点Q .①如图,当点M (a ,0)在线段OA 上时,△BPQ 的面积为S ,求S 与a之间的函数关系式;②连接BM ,若∠BMP =∠BAC ,求点P 的坐标.【答案】(1)直线BC 的函数解析式为132y x =+;(2)①2S a =()06a <<;②点P 的坐标为3(2-,9)4或3(2,154.【解析】(1)由132y x =-+,令0x =得:3y =,∴B (0,3).由0y =得:1302x -+=,解得6x =,\ A (6,0),Q 点C 与点A 关于y 轴对称.∴C (-6,0),设直线BC 的函数解析式为y kx b =+,\360b k b =ìí-+=î,解得123k b ì=ïíï=î,\直线BC 的函数解析式为132y x =+;(2)①Q 点(,0)M a ,则点1(,3)2P a a -+,点1(3)2Q a a ,+,过点B 作BD PQ ^与点D ,则(),3D a 则113(3)22PQ a a a =+--+=,||BD a =,\PQB D 的面积S 211·22PQ BD a ==,即2S a =()06a <<②如图,当点M 在y 轴的左侧时,Q 点C 与点A 关于y 轴对称,AB BC \=,BAC BCA \Ð=Ð,BMP BAC Ð=ÐQ ,90BMP BMA Ð+Ð=°Q ,90BMA BAC \Ð+Ð=°,180()90MBA BMA BAC \Ð=°-Ð+Ð=°,222BM BA MA \+=,设(0)M x ,,则1(3)2P x x +,,222223BM OM OB x =\=++,MA 2=(6-x )2,222226345BA OA OB =+=+=,22945(6)x x \++=-,解得32x =-,3(2P \-,94,当点M 在y 轴的右侧时,同理可得3(2P ,15)4,综上,点P 的坐标为3(2-,9)4或3(2,15)4.【变式训练4】如图,在平面直角坐标系中,函数212y x =+的图象分别交x 轴、y 轴于A 、B 两点.过点A 的直线交y 轴正半轴于点C ,且点C 为线段OB 的中点.(1)求直线AC 的表达式.(2)平面内是否存在点P ,使得四边形ACPB 是平行四边形?若存在,请求出点P 的坐标.(3)若点Q 为直线AC 上的一点,且满足ABQ △的面积为30,求点Q 的坐标.【答案】(1)6y x =+;(2)存在,()6,18P ;(3)()4,10或()16,10--【解析】(1)∵函数212y x =+的图象分别交x 轴、y 轴于A 、B 两点,令0x =,12y =,令0y =,6x =-,∴()6,0A -,()0,12B ,∵点C 为线段OB 的中点,∴()0,6C ,设直线AC 的表达式为y kx b =+,∴606k b b -+=ìí=î,解得:16k b =ìí=î,故直线AC 的表达式为6y x =+.(2)∵四边形ACPB 是平行四边形.∴PC AB =且PC AB ∥,PB AC =且PB AC ∥,如图1,过点P 作y 轴的垂线,垂足为Q ,∵AB PC ∥,∴ABO PCQ Ð=Ð,在OAB 和QPC 中,90AOB PQC ABO PCQ AB PC Ð=Ð=°ìïÐ=Ðíï=î,∴()OAB QPC AAS ≌△△,∴OA QP =,在Rt PQB △和Rt AOC 中,PQ AO PB AC=ìí=î,∴()Rt Rt PQB AOC HL ≌△△,∴6PQ AO ==,6BQ CO ==,∴18QO QB OB =+=,∴()6,18P .(3)如图所示,过点B 作BH AC ^于点H ,Q ()0,12B ,()6,0A -,()0,6C ,6,6BC AO \==,AC ==45BCH ACO \Ð=Ð=°,BCH \是等腰直角三角形,CH BH \===∵点Q 为直线AC 上一点且ABQ △的面积为30,∴1302ABQ S AQ BH =´=△,∴AQ =∵点Q 在直线AC :6y x =+上,∴设Q 点坐标为(),6t t +,∴()()()22226626200AQ t t t =+++=+=,∴()26100t +=,则14t =,216t =-,当4t =时,610t +=,则()4,10Q ,当16t =-时,610t +=-,则()16,10Q --,故Q 点坐标为()4,10或()16,10--类型二、几何图形存在问题例1.如图,在平面直角坐标系中,OA =OB =6,OD =1,点C 为线段AB 的中点.(1)直接写出点C 的坐标为 ;(2)点P 是x 轴上的动点,当PB +PC 的值最小时,求此时点P 的坐标;(3)在平面内是否存在点F ,使得以A 、C 、D 、F 为顶点的四边形为平行四边形?若存在,请求出点F 的坐标;若不存在,请说明理由.【答案】(1)(3,3);(2)P (2,0);(3)存在,(8,3),(4,-3)或(-2,3)【解析】(1)解:过点C 作CN OA ^于点N ,过点C 作CM OB ^于点N .∵CN OA ^∴//CN OB又∵点C 为线段AB 的中点,OA = 6∴132ON OA ==同理132OM OB ==∴C (3,3)(2)作点B 关于x 轴的对称点B ',连接CB '交x 轴于点P ,此时PB+PC 的值最小,由已知得,点B 的坐标为(0,6),∴点B 关于x 轴的对称点B'(0,﹣6),由(1)知,C (3,3),可设直线CB '的解析式为y =kx +b ,∴ 633b k b -=ìí=+î 解得36k b =ìí=-î∴ 直线CB '的解析式为y =3x ﹣6,令y =0,则3x ﹣6=0,解得: x =2,∴ P (2,0);(3)存在点F ,使以A 、C 、D 、F 为顶点的四边形为平行四边形,设点F 的坐标为(m ,n ).分三种情况考虑,如图所示:当AC 为对角线时,∵A (6,0),C (3,3),D (1,0),∴1632200322m n ++ì=ïïí++ï=ïî,解得:83m n =ìí=î, ∴点F 1的坐标为(8,3); ②当AD 为对角线时,∵A (6,0),C (3,3),D (1,0),∴3162230022m n ++ì=ïïí++ï=ïî,解得:43m n =ìí=-î,∴点F 2的坐标为(4,-3);③当CD 为对角线时,∵A (6,0),C (3,3),D (1,0),∴6312203022m n ++ì=ïïí++ï=ïî,解得:23m n =-ìí=î,∴点F 3的坐标为(-2,3).综上所述,点F 的坐标是(8,3),(4,-3)或(-2,3).例2.已知ABC 中,90BAC Ð=°,6AB AC ==,D 是AC 中点,作直线BD .分别以AC ,BC 所在直线为x 轴,y 轴建立直角坐标系(如图).(1)求直线BD的表达式.(2)在直线BD 上找出一点E ,使四边形ABCE 为平行四边形.(3)直线BD 上是否存在点F ,使AFC △为以AC 为腰的等腰三角形?若存在,直接写出点F 的坐标;若不存在,说明理由.【答案】(1)26y x =-+;(2)()6,6-;(3)存在,248,551æö-ç÷èø或()0,6或()6,6-或618,55æöç÷èø【解析】(1)∵6AB AC ==,由题可得,∴()0,6B ,()6,0C ,又∵点D 是AC 的中点,∴()3,0D ,∴设直线BD 的表达式为:y kx b =+代入B ,D 可得:306k b b +=ìí=î,解得:2k =-,6b =,∴直线BD 的表达式为:26y x =-+.(2)设点E 的坐标为(),26t t -+,∵四边形ABCE 是平行四边形,∴A C B E x x x x +=+,∴060t +=+,6t =,∴点E 的坐标为()6,6-.(3)∵点F 在BD 上,∴设点F 的坐标为(),26m m -+,∴()()222026AF m m =-+-+()2226m m =+-.()()222626CF m m =-+-+,∵AFC △是以AC 为腰的等腰三角形,∴当AC AF =时,则22AC AF =,∴()222626m m =+-,∴25240m m -=,解得:0m =或245=m .∴点F 的坐标为:2418,55æö-ç÷èø或()0,6,当AC FC =时,则22AC CF =,∴()()2226626m m =-+-+,2536360m m -+=,解得:6m =或65m =,∴点F 的坐标为()6,6-或618,55æöç÷èø.∴综上,点F 的坐标为2418,55æö-ç÷èø或()0,6或()6,6-或618,55æöç÷èø.例3.如图,正方形ABCD 的顶点()0,3A ,()10B ,,点P 在直线y x =上.(1)直接写出点C 和点D 的坐标:C ______,D ______.(2)Q 为坐标平面内一点,当以O 、B 、Q 、P 为顶点的四边形为菱形,直接写出点P 和对应的点Q 的坐标.【答案】(1)()4,1,()3,4(2)P 的坐标为:11,22æöç÷èø,,æççè,()1,1,Q 坐标为:11,22æö-ç÷èø,1æççè,1æççè,()0,1.【解析】(1)如图(1)所示,过C 作CE ⊥x 轴,∵正方形ABCD ,∴AB =BC ,∠ABC =90°,又∵∠AOB =90°,CE ⊥x 轴,∴∠AOB =∠BEC =90°,又∵∠ABO +∠CBE =180°-∠ABC =90°,∠ABO +∠BAO =180°-∠AOB =90°,∴∠BAO =∠CBE ,∴在△ABO 和△BCE 中,AOB BECBAO CBE AB BC Ð=ÐìïÐ=Ðíï=î,∴△ABO ≌△BCE (AAS ),∴OA =EB ,OB =EC ,又∵()0,3A ,()1,0B ,∴OA =EB =3,OB =EC =1,∴OE =OB +EB =1+3=4,∴点C 的坐标为:()4,1,又∵正方形ABCD ,∴A C B D A C B D x x x x y y y y +=+ìí+=+î,∴041310D D x y +=+ìí+=+î,解得:3D x =,4D y =,∴点D 的坐标为()3,4,故答案为:()4,1,()3,4.(2)∵点P 在直线y =x 上,∴设点P 的坐标为(),t t ,当点O ,B ,Q ,P 是以OB 为对角线的菱形时,O B Q PO B Q P x x x x y y y y PO PB +=+ìï+=+íï=î,∴代入可得:010Q x t ì+=+ï=∴解得:12t =,12Q x =,12Q y =-,∴点P 的坐标为11,22æöç÷èø,点Q 的坐标为11,22æö-ç÷èø,当点O ,B ,Q ,P 是以OQ 为对角线的菱形时,O Q B PO Q B P x x x x y y y y OB OP +=+ìï+=+íï=î,∴代入可得:01Q x tì+=+=∴解得:t=或t =,∴代入可得:点P的坐标为或æççè,点Q的坐标为1æ+ççè或1æççè,当点O ,B ,Q ,P 是以OP 为对角线的菱形时,O P Q BO P Q B x x x x y y y y BO BP +=+ìï+=+íï=î,∴代入可得01Q t x t ì+=+ï=t =1或t =0(舍去),∴点P 的坐标为()1,1,点Q 的坐标为()0,1,∴综上,符合条件的P,Q的坐标为:11,22æöç÷èø,11,22æö-ç÷èø或,1æççè或æççè,1æççè或()1,1,()0,1.【变式训练1】如图,直线AB交x轴于点B,交y轴于点A,过点A另一条的直线交x轴于点C,且AB BC=,线段OC、BC的长是方程2650x x-+=的两个根.(1)求A点坐标;(2)若过点()2,0D,()01E,的直线DE交直线AC于点F,求经过点F的正比例函数解析式;(3)在(2)的条件下,点P在直线AB上,点Q在直线AC上,使以D、E、P、Q为顶点的四边形是平行四边形,请直接写出点Q的坐标.【答案】(1)(0,3).(2)94y x=-(3)213()155-,或217(155,或141()155-,;【解析】(1)解:解方程2650x x-+=得,15=x,21x=,∴OC=1,BC=5,∴5AB BC==,OB=4,3OA==,A点坐标为(0,3).(2)解:设直线DE的解析式为y kx b=+,把()2,0D,()01E,代入得,201k bb+=ìí=î,解得,121kbì=-ïíï=î,直线DE的解析式为112y x=-+,同理,根据A(0,3),C(-1,0),求得AC的解析式为33y x=+,把两个函数解析式联立得,11233y xy xì=-+ïíï=+î,解得,4797xyì=-ïïíï=ïî,点F的坐标为49()77-,,设经过点F的正比例函数解析式为y ax=,代入49()77-,得,9477a=-,解得,94a=-,经过点F 的正比例函数解析式为94y x =-,(3)解:根据A (0,3),B (4,0),求得AB 的解析式为334y x =-+,设点P 坐标为3(3)4p p -+,,点Q 坐标为(33)q q +,,根据平行四边形对角线互相平分,()2,0D ,()01E ,,当PQ 为对角线时,2333314p q p q +=ìïí-+++=ïî,解得14154415q p ì=-ïïíï=ïî,点Q 坐标为141()155-,;当PD 为对角线时,2333314p q p q +=ìïí-+=++ïî,解得2152815q p ì=ïïíï=-ïî,点Q 坐标为217()155,;当PE 为对角线时,2331334p q p q =+ìïí-++=+ïî,解得2152815q p ì=-ïïíï=ïî,点Q 坐标为213(155-,;综上,点Q 坐标为213()155-,或217()155,或141()155-,.【变式训练2】如图,在平面直角坐标系中,直线1:5l y x =-+与y 轴交于点A ,直线2l 与x 轴、y 轴分别交于点(4,0)B -和点C ,且与直线1l 交于点(2,)D m .(1)求直线2l 的解析式;(2)若点E 为线段BC 上一个动点,过点E 作EF x ^轴,垂足为F ,且与直线1l 交于点G ,当6EG =时,求点G 的坐标;(3)若在平面上存在点H ,使得以点A ,C ,D ,H 为顶点的四边形是平行四边形,请直接写出点H 的坐标.【答案】(1)直线2l 的解析式为122y x =+;(2)(2,7)G -;(3)H 的坐标为:(2,0)或(2,6)或(2,4)-【解析】(1)解:Q 当2x =时,253y m =-+==,(2,3)D \.设直线2l 的解析式为y kx b =+,由题意得:2340k b k b +=ìí-+=î,解得:122k b ì=ïíï=î.\直线2l 的解析式为122y x =+.(2)解:EF x ^Q 轴,G \,E 的横坐标相同.设(),5G n n -+,则1,22E n n æö+ç÷èø.E Q 为线段BC 上一个动点,50n \-+>,1202n +>,5FG n \=-+,122FE n =+.3362EG FG FE n \=-=-+=.解得:2n =-.()2,7G \-.(3)如下图,当四边形AHCD 为平行四边形时,令0x =,则10222y =´+=,(0,2)C \.//CH AD Q ,\直线CH 的解析式为:2y x =-+.令0x =,则1055y =-´+=,(0,5)A \.//AH CD Q ,\直线AH 的解析式为:152y x =+.\2152y x y x =-+ìïí=+ïî.解得:24x y =-ìí=î.(2,4)H \-.如下图,当四边形AHDC 为平行四边形时,//DH AC Q ,\直线DH 的解析式为2x =,//AH DC Q ,\直线AH 的解析式为152y x =+,\当2x =时,12562y =´+=,()2,6H \.当四边形ADHC为平行四边形时,如下图,//DH AC Q ,\直线DH 的解析式为2x =,//CH AD Q ,\直线CH 的解析式为:2y x =-+,当2x =时,220y =-+=,(2,0)H \.综上,存在点H ,使得以点A ,C ,D ,H 为顶点的四边形是平行四边形,点H 的坐标为:(2,0)或(2,6)或(2,4)-.类型三、最值问题例.如图,在平面直角坐标系中,A (﹣1,4),B (﹣3,3),C (﹣2,1).(1)已知△A 1B 1C 1与△ABC 关于x 轴对称,画出△A 1B 1C 1;(2)在y 轴上找一点P ,使得△PBC 的周长最小,点P 的坐标为 .【答案】(1)见解析(2)(0,95)【解析】(1)解:如图所示,△A 1B 1C 1即为所求.(2)如图所示,点P 即为所求,点C 关于y 轴的对称点C ′(2,1),设BC ′所在直线解析式为y =kx +b ,则3321k b k b -+=ìí+=î,解得2595k b ì=-ïïíï=ïî,∴BC ′所在直线解析式为2955y x =-+,当x =0时,y =95,所以点P 坐标为(0,95).【变式训练1】在如图的网格中,只利用直尺作图:(1)将ABC 向左平移3个单位后的图形111A B C △;(2)作点P ,使P 到A 、B 的距离相等,且PB PC =;(3)点Q 在y 轴上,当QA QB +最小时,点Q 的坐标为______.【答案】(1)作图见解析(2)作图见解析(3)703æöç÷èø,【解析】(1)解:如图1;(2)解:如图2,作线段AB 、线段BC 的垂直平分线,交点即为点P ;(3)解:如图3,找A 关于y 轴的对称点A ¢,连接A B ¢,与y 轴的交点Q 即为QA QB +最小时的点Q ;∴()1,3A ¢-,()2,1B 设直线A B ¢的解析式为y kx b=+将()1,3A ¢-,()2,1B 代入y kx b =+得321k b k b -+=ìí+=î,解得2373k b ì=-ïïíï=ïî,∴直线A B ¢的解析式为2733y x =-+将0x =代入得73y =,∴70,3Q æöç÷èø,故答案为:70,3æöç÷èø.【变式训练2】如图,直线AB与反比例函数y=kx(x>0)的图象交于A,B两点,已知点A的坐标为(2,4),△AOB的面积为6.(1)反比例函数的表达式;(2)求直线AB的函数表达式;(3)若动点P在y轴上运动,当|PA﹣PB|最大时,求P点坐标.【答案】(1)y=8x;(2)y=﹣x+6;(3)P(0,6)【解析】(1)∵点A(2,4)在反比例函数y=kx(x>0),∴k=2×4=8,∴反比例函数的解析式为:y=8x;(2)设点B(m,8m),过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,∵直线AB与反比例函数y=kx(x>0)的图象交于A,B两点,∴k=OC×AC=OD×BD,∴S△AOC=S△BOD,∴S△AOB=S梯形ACDB,∴184(2)62mmæö´+´-=ç÷èø,∵m>0,解得m=4,∴B(4,2),设直线AB的解析式为:y=kx+b,4224k bk b=+ìí=+î解得16kb=-ìí=î,∴直线AB的解析式为:y=﹣x+6;(3)在△PAB中,根据两边之差小于第三边,即|PA﹣PB|≤AB,∴|PA﹣PB|的最大值为线段AB,∴此时P点为直线AB与y轴的交点,当x=0时,y=6,,∴P(0,6).课后训练1.如图,一次函数y=mx+1的图象与反比例函数y=kx的图象相交于A、B两点,点C在x轴正半轴上,点D(1,-2),连接OA、OD、DC、AC,四边形OACD为菱形.(1)求一次函数与反比例函数的解析式;(2)根据图象,直接写出反比例函数的值小于2时,x的取值范围;(3)设点P是直线AB上一动点,且S△OAP=12S菱形OACD,求点P的坐标.【答案】(1)一次函数的解析式为y=x+1;反比例函数的解析式为y=2x;(2)0x<或1x>;(3)P的坐标为(-3,-2)或(5,6)【解析】(1)解:如图,连接AD,∵四边形AODC是菱形,∴点A、D关于x轴对称,∵D(1,-2),∴A(1,2),将A (1,2)代入直线y =mx +1可得m +1=2,解得m =1,将A (1,2)代入反比例函数y =kx ,解得:k =2;∴一次函数的解析式为y =x +1;反比例函数的解析式为y =2x ;(2)解:∵当x =1时,反比例函数的值为2,∴当反比例函数图象在A 点下方时,对应的函数值小于2,此时x 的取值范围为:x <0或x >1;(3)解:∵OC =2OE =2,AD =2DE =4,∴11•24422OACD S OC AD ==´´=菱形,∵S △OAP =12S 菱形OACD ,∴S △OAP =2,设P 点坐标为(a ,a +1),在y =x +1中,令x =0,则y =1,故F (0,1),∴OF =1,11111222OAF A S OF x =×=´´= ,当P 在A 的左侧时,∵1=<22OFA S ,∴此时点P 在F 的左侧,a <0,()()1111=221222OAP OFP OFA S S S a OF a ×´=+-+=-+= ,解得a =-3,故a +1=-2,∴P (-3,-2),当P 在A 的右侧时,1111=222221OAP OFP OFA S S S a OF a ´-=-×-== ,解得a =5,故a +1=6,∴P (5,6),综上所述,点P 的坐标为(-3,-2)或(5,6).2.如图,在平面直角坐标系中,已知△ABC 的三个顶点A 、B 、C 的坐标分别为(﹣5,﹣1)、(﹣3,﹣4)、(﹣1,﹣3).(1)S △ABC = ;(2)画出△ABC 关于y 轴对称的△A 1B 1C 1;(3)已知点P 在x 轴上,且PA =PC ,则点P 的坐标是 .(4)若y 轴上存在点Q ,使△QAC 的周长最小,则点Q 的坐标是 .【答案】(1)4(2)见解析(3)(-2,0)(4)(0,83-)【解析】(1)解:111343221424222ABC S D =´-´´-´´-´´=,故答案为:4(2)解:如图所示,111A B C D 即为所求(3)解:如图,点P (-2,0),故答案为:(-2,0)(4)解:连接AC 1,交y 轴于Q ,设AC 1的函数关系式为y =kx +b ,51,3k b k b -+=-ì\í+=-î解得13,83k b ì=-ïïíï=-ïî8(0,),3Q \-故答案为:8(0,)3-3.如图,直线AB :y =-x +n 分别与x ,y 轴交于A (6,0)、B 两点,过点B 的直线交x 轴负半轴于C ,且OB :OC =3:1.(1)求点B 的坐标;(2)求直线BC 的函数表达式;(3)直线EF :()102y x k k =-¹交直线AB 于E ,交直线BC 于点F ,交x 轴于D ,是否存在这样的直线EF ,使得EBD FBD S S =△△?若存在,求出k 的值;若不存在,说明理由.【答案】(1)B (0,6)(2)直线BC 的解析式为36y x =+(3)37k =【解析】(1)∵y =-x +n 且过点A (6,0),∴-6+n =0,∴n =6,∴直线AB :y =-x +6,令x =6,则y =6,∴B (0,6);(2)解:∵B (0,6),∴OB =6,且OC :OB =1:3,∴OC =2,∴C (-2,0),设直线BC 的解析式为y =kx +6,把C (-2,0)代入得:-2k +6=0,解得k =3,∴直线BC 的解析式为y =3x +6;(3)解:存在.理由如下:如图中,∵S△BDF=S△BDE,∴只需DF=DE,即D为EF中点,∵E为直线AB与EF的交点,∴612y xy x k=-+ìïí=-ïî,可得E(23k+4 ,2−23k),∵F为直线BC与EF的交点,∴3612y xy x k=+ìïí=-ïî,可得F(−25k−125,−65k−65),令y=0,则0=12x−k,解得:x=2k,∴直线EF与x轴的交点D(2k,0),∵点D为EF的中点,∴利用中点公式可得(2−23k)+(−65k−65)=0,∴k=37,当k=37也满足2212435522k kk+--=,故存在.。
一次函数综合题(含详细解析)
一次函数综合题1.如图,平面直角坐标系中,直线:AB y x b =-+交y 轴于点(0,4)A ,交x 轴于点B . (1)求直线AB 的表达式和点B 的坐标;(2)直线l 垂直平分OB 交AB 于点D ,交x 轴于点E ,点P 是直线l 上一动点,且在点D 的上方,设点P 的纵坐标为n . ①用含n 的代数式表示ABP ∆的面积; ②当8ABP S ∆=时,求点P 的坐标;③在②的条件下,以PB 为斜边在第一象限作等腰直角PBC ∆,求点C 的坐标.2.如图在平面直角坐标系中,O 是坐标原点,长方形OACB 的顶点A ,B 分别在x ,y 轴上,已知3OA =,点D 为y 轴上一点,其坐标为(0,1),5CD =,点P 从点A 出发以每秒1个单位的速度沿线段A C B --的方向运动,当点P 与点B 重合时停止运动,运动时间为t 秒(1)求B ,C 两点坐标;(2)①求OPD ∆的面积S 关于t 的函数关系式;②当点D 关于OP 的对称点E 落在x 轴上时,求点E 的坐标; (3)在(2)②情况下,直线OP 上求一点F ,使FE FA +最小.3.如图,直线27y x =-+与x 轴、y 轴分别相交于点C 、B ,与直线32y x =相交于点A .(1)求A 点坐标;(2)如果在y 轴上存在一点P ,使OAP ∆是以OA 为底边的等腰三角形,则P 点坐标是 ;(3)在直线27y x =-+上是否存在点Q ,使OAQ ∆的面积等于6?若存在,请求出Q 点的坐标,若不存在,请说明理由.4.已知四边形OABC 是边长为4的正方形,分别以OA 、OC 所在的直线为x 轴、y 轴,建立如图1所示的平面直角坐标系,直线l 经过A 、C 两点. (1)写出点A 、点C 坐标并求直线l 的函数表达式;(2)若P 是直线l 上的一点,当OPA ∆的面积是5时,请求出点P 的坐标;(3)如图2,点(3,1)D -,E 是直线l 上的一个动点,求出使||BE DE -取得最大值时点E 的坐标和最大值(不需要证明).5.如图,在平面直角坐标系xOy 中,直线483y x =-+与x 轴,y 轴分别交于点A ,点B ,点D 在y 轴的负半轴上,若将DAB ∆沿直线AD 折叠,点B 恰好落在x 轴正半轴上的点C 处.(1)求AB 的长和点C 的坐标; (2)求直线CD 的解析式.6.如图,直线24y x =-+交x 轴和y 轴于点A 和点B ,点(0,2)C -在y 轴上,连接AC . (1)求点A 和点B 的坐标;(2)若点P 是直线AB 上一点,若BCP ∆的面积为3,求点P 的坐标;(3)过点B 的直线BE 交x 轴于点(E E 点在点A 右侧),当45ABE ∠=︒时,求直线BE 的表达式.7.如图,在平面直角坐标系中,过点(6,0)B的直线AB与直线OA相交于点(4,2)A,动点M在线段OA和射线AC上运动.(1)求直线AB的解析式.(2)求OAC∆的面积.(3)是否存在点M,使OMC∆的面积是OAC∆的面积的14?若存在求出此时点M的坐标;若不存在,说明理由.8.如图,在平面直角坐标系中,过点(0,6)A的直线AB与直线OC相交于点(2,4)C动点P 沿路线O C B→→运动.(1)求直线AB的解析式;(2)当OPB∆的面积是OBC∆的面积的14时,求出这时点P的坐标;(3)是否存在点P,使OBP∆是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.9.如图(1),在平面直角坐标系中,直线443y x =-+交坐标轴于A 、B 两点,过点(4,0)C -作CD 交AB 于D ,交y 轴于点E .且COE BOA ∆≅∆.(1)求B 点坐标为 ;线段OA 的长为 ; (2)确定直线CD 解析式,求出点D 坐标;(3)如图2,点M 是线段CE 上一动点(不与点C 、E 重合),ON OM ⊥交AB 于点N ,连接MN .①点M 移动过程中,线段OM 与ON 数量关系是否不变,并证明; ②当OMN ∆面积最小时,求点M 的坐标和OMN ∆面积.10.如图,在平面直角坐标系中,直线334y x =--交x 轴于点A ,交y 轴于点B ,交直线x a =于点C ,点D 与点B 关于x 轴对称,连接AD 交直线x a =于点E .(1)填空:ABD S ∆= . (2)求直线AD 的解析式;(3)在x 轴上存在一点P ,则PE PD +的和最小为 ;(直接填空即可)(4)当40a -<<时,点Q 为y 轴上的一个动点,使得QEC ∆为等腰直角三角形,求点Q 的坐标.11.如图,已知长方形OABC 的顶点A 在x 轴上,顶点C 在y 轴上,18OA =,12OC =,D 、E 分别为OA 、BC 上的两点,将长方形OABC 沿直线DE 折叠后,点A 刚好与点C 重合,点B 落在点F 处,再将其打开、展平.(1)点B 的坐标是 ; (2)求直线DE 的函数表达式;(3)设动点P 从点D 出发,以1个单位长度/秒的速度沿折线D A B C →→→向终点C 运动,运动时间为t 秒,求当2PDE OCD S S ∆∆=时t 的值.12.如图1,直线443y x =-+与坐标轴分别相交于A 、B 两点,在第一象限内,以线段AB 为边向外作正方形ABCD ,过A 、C 点作直线AC .(1)填空:点A 的坐标是 ,正方形ABCD 的边长等于 ; (2)求直线AC 的函数解析式;(3)如图2,有一动点M 从B 出发,以1个单位长度/秒的速度向终点C 运动,设运动的时间为t (秒),连接AM ,当t 为何值时,则AM 平分BAC ∠?请说明理由. 13.如图,在平面直角坐标系中,直线AB 交坐标轴于点A (0,6)、B (8,0),点C 为x 轴正半轴上一点,连接AC ,将ABC ∆沿AC 所在的直线折叠,点B 恰好与y 轴上的点D 重合.(1)求直线AB 的解析式; (2)求出点C 的坐标;(3)点P 为直线AB 上的点,请求出点P 的坐标使94COP S ∆=; (4)点Q 为直线AB 上一动点,连接DQ ,线段DQ 是否存在最小值?若存在,请求出DQ 的最小值,若不存在,请说明理由.14.如图,平面直角坐标系中,(0,2)A ,(1,0)B ,(2,3)C ,CD y ⊥轴于点D .(1)AOB CDA ∆≅∆;(2)连接BC ,判断ABC ∆的形状,并说明理由;(3)如图(2),已知(3,4)P ,(6,2)Q ,若PQM ∆是等腰直角三角形,且90QPM ∠=︒,则点M 坐标为 .15.如图,已知函数12y x b =-+的图象与x 轴、y 轴分别交于点A 、B ,与函数y x =图象交于点M ,点M 的横坐标为2,在x 轴上有点(,0)P a (其中2)a >,过点P 作x 轴的垂线,分别交函数12y x b =-+和y x =的图象于点C 、D .(1)求点A 的坐标; (2)若OB CD =,求a 的值;(3)在(2)条件下若以OD 线段为边,作正方形ODEF ,求直线EF 的表达式.16.如图,正方形ABOD的边长为2,OB在x轴上,OD在y轴上,且//AD OB,AB OD,点C为AB的中点,直线CD交x轴于点F.//(1)求直线CD的函数关系式;(2)过点C作CE DF∠=∠;⊥且交于点E,求证:ADC EDC(3)求点E坐标;(4)点P是直线CE上的一个动点,求PB PF+的最小值.17.已知长方形OABC的边长4AB=,E是OA的中点,分别以OA、OC所在的OA=,3直线为x轴、y轴,建立如图1所示的平面直角坐标系,直线l经过C、E两点.(1)求直线l的函数表达式;(2)如图2,在长方形OABC中,过点E作EG EC∆⊥交AB于点G,连接CG,将COE 沿直线l折叠后得到CEF=.∆,点F恰好落在CG上.证明:GF GA(3)在(2)的条件下求四边形AGFE的面积.18.如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上.90=,6OB=,∠=︒且OA ABOABOC=.点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线l与y轴5平行,直线l交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知4t=时,直线l恰好过点C.(1)求点A和点B的坐标;(2)当03<<时,求m关于t的函数关系式;t(3)当 3.5m=时,请直接写出点P的坐标.一次函数综合题参考答案与试题解析1.如图,平面直角坐标系中,直线:AB y x b =-+交y 轴于点(0,4)A ,交x 轴于点B .(1)求直线AB 的表达式和点B 的坐标;(2)直线l 垂直平分OB 交AB 于点D ,交x 轴于点E ,点P 是直线l 上一动点,且在点D 的上方,设点P 的纵坐标为n .①用含n 的代数式表示ABP ∆的面积;②当8ABP S ∆=时,求点P 的坐标;③在②的条件下,以PB 为斜边在第一象限作等腰直角PBC ∆,求点C 的坐标.【解答】解:(1)把(0,4)A 代入y x b =-+得4b =∴直线AB 的函数表达式为:4y x =-+.令0y =得:40x -+=,解得:4x =∴点B 的坐标为(4,0).(2)①l 垂直平分OB ,2OE BE ∴==.将2x =代入4y x =-+得:242y =-+=.∴点D 的坐标为(2,2).点P 的坐标为(2,)n ,2PD n ∴=-.APB APD BPD S S S ∆∆∆=+,1111(2)2(2)2242222ABP S PD OE PD BE n n n ∆∴=+=-⨯+-⨯=-. ②8ABP S ∆=,248n ∴-=,解得:6n =.∴点P 的坐标为(2,6).③如图1所示:过点C 作CM l ⊥,垂足为M ,再过点B 作BN CM ⊥于点N .设点(,)C p q .PBC ∆为等腰直角三角形,PB 为斜边,PC CB ∴=,90PCM MCB ∠+∠=︒.CM l ⊥,BN CM ⊥,90PMC BNC ∴∠=∠=︒,90MPC PCM ∠+∠=︒.MPC NCB ∴∠=∠.在PCM ∆和CBN ∆中,90PMC BNC MPC NCBPC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, PCM CBN ∴∆≅∆.CM BN ∴=,PM CN =.∴462p q q p -=-⎧⎨=-⎩,解得64p q =⎧⎨=⎩. ∴点C 的坐标为(6,4).如图2所示:过点C 作CM l ⊥,垂足为M ,再过点B 作BN CM ⊥于点N .设点(,)C p q .PBC ∆为等腰直角三角形,PB 为斜边,PC CB ∴=,90PCM MCB ∠+∠=︒.CM l ⊥,BN CM ⊥,90PMC BNC ∴∠=∠=︒,90MPC PCM ∠+∠=︒.MPC NCB ∴∠=∠.在PCM ∆和CBN ∆中,90PMC BNC MPC NCBPC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, PCM CBN ∴∆≅∆.CM BN ∴=,PM CN =.∴462p q q p -=-⎧⎨=-⎩,解得02p q =⎧⎨=⎩. ∴点C 的坐标为(0,2)舍去.综上所述点C 的坐标为(6,4).2.如图在平面直角坐标系中,O 是坐标原点,长方形OACB 的顶点A ,B 分别在x ,y 轴上,已知3OA =,点D 为y 轴上一点,其坐标为(0,1),5CD =,点P 从点A 出发以每秒1个单位的速度沿线段A C B --的方向运动,当点P 与点B 重合时停止运动,运动时间为t 秒(1)求B ,C 两点坐标;(2)①求OPD ∆的面积S 关于t 的函数关系式;②当点D 关于OP 的对称点E 落在x 轴上时,求点E 的坐标;(3)在(2)②情况下,直线OP 上求一点F ,使FE FA +最小.【解答】解(1)四边形OACB 是矩形,3BC OA ∴==,在Rt BCD ∆中,5CD =,3BC =,4BD ∴==,5OB ∴=,(0,5)B ∴,(3,5)C ;(2)①当点P 在AC 上时,1OD =,3BC =,32S ∴=, 当点在BC 上时,1OD =,538BP t t =+-=-,111(8)422S t t ∴=⨯⨯-=-+;(0)t ②当点D 关于OP 的对称点落在x 轴上时,点D 的对称点是(1,0), (1,0)E ∴;(3)如图2点D 、E 关于OP 对称,连接AD 交OP 于F , 则AD 的长度就是AF EF +的最小值,则点F 即为所求.3.如图,直线27y x =-+与x 轴、y 轴分别相交于点C 、B ,与直线32y x =相交于点A . (1)求A 点坐标;(2)如果在y 轴上存在一点P ,使OAP ∆是以OA 为底边的等腰三角形,则P 点坐标是 13(0,)6; (3)在直线27y x =-+上是否存在点Q ,使OAQ ∆的面积等于6?若存在,请求出Q 点的坐标,若不存在,请说明理由.【解答】解:(1)解方程组:2732y x y x =-+⎧⎪⎨=⎪⎩得:23x y =⎧⎨=⎩ A ∴点坐标是(2,3);(2)设P 点坐标是(0,)y ,OAP ∆是以OA 为底边的等腰三角形,OP PA ∴=,2222(3)y y ∴+-=, 解得136y =, P ∴点坐标是13(0,)6,故答案为13(0,)6; (3)存在;由直线27y x =-+可知(0,7)B ,7(2C ,0), 172136224AOC S ∆=⨯⨯=<,172762AOB S ∆=⨯⨯=>, Q ∴点有两个位置:Q 在线段AB 上和AC 的延长线上,设点Q 的坐标是(,)x y , 当Q 点在线段AB 上:作QD y ⊥轴于点D ,如图①,则QD x =, 761OBQ OAB OAQ S S S ∆∆∆∴=-=-=, ∴112OB QD =,即1712x ⨯=, 27x ∴=, 把27x =代入27y x =-+,得457y =, Q ∴的坐标是2(7,45)7, 当Q 点在AC 的延长线上时,作QD x ⊥轴于点D ,如图②则QD y =-, 213644OCQ OAQ OAC S S S ∆∆∆∴=-=-=, ∴1324OC QD =,即173()224y ⨯⨯-=, 37y ∴=-, 把37y =-代入27y x =-+,解得267x =, Q ∴的坐标是26(7,3)7-, 综上所述:点Q 是坐标是2(7,45)7或26(7,3)7-.4.已知四边形OABC 是边长为4的正方形,分别以OA 、OC 所在的直线为x 轴、y 轴,建立如图1所示的平面直角坐标系,直线l 经过A 、C 两点.(1)写出点A 、点C 坐标并求直线l 的函数表达式;(2)若P 是直线l 上的一点,当OPA ∆的面积是5时,请求出点P 的坐标;(3)如图2,点(3,1)D -,E 是直线l 上的一个动点,求出使||BE DE -取得最大值时点E 的坐标和最大值(不需要证明).【解答】解:(1)四边形OABC 是边长为4的正方形,(4,0)A ∴和(0,4)C ;设直线l 的函数表达式(0)y kx b k =+≠,经过(4,0)A 和(0,4)C 得044k b b =+⎧⎨=⎩, 解之得14k b =-⎧⎨=⎩, ∴直线l 的函数表达式4y x =-+;(2)设OPA ∆底边OA 上的高为h ,由题意等1452h ⨯⨯=, 52h ∴=, 5|4|2x ∴-+=,解得32x =或13213(2P ∴,5)2、213(2P ,5)2-; (3)O 与B 关于直线l 对称,∴连接OD 并延长交直线l 于点E ,则点E 为所求,此时||||BE DE OE DE OD -=-=,OD 即为最大值,如图2.设OD 所在直线为1y k x = 1(0)k ≠,经过点(3,1)D -,113k ∴-=,113k ∴=- ∴直线OD 为13y x =-, 解方程组:413y x y x =-+⎧⎪⎨=-⎪⎩,得62x y =⎧⎨=-⎩, ∴点E 的坐标为(6,2)-.又D 点的坐标为(3,1)-由勾股定理可得OD =.5.如图,在平面直角坐标系xOy 中,直线483y x =-+与x 轴,y 轴分别交于点A ,点B ,点D 在y 轴的负半轴上,若将DAB ∆沿直线AD 折叠,点B 恰好落在x 轴正半轴上的点C 处.(1)求AB 的长和点C 的坐标;(2)求直线CD 的解析式.【解答】解:(1)直线483y x =-+与x 轴,y 轴分别交于点A ,点B , (6,0)A ∴,(0,8)B ,在Rt OAB ∆中,90AOB ∠=︒,6OA =,8OB =,10AB ∴=,DAB ∆沿直线AD 折叠后的对应三角形为DAC ∆, 10AC AB ∴==.16OC OA AC OA AB ∴=+=+=. 点C 在x 轴的正半轴上,∴点C 的坐标为(16,0)C .(2)设点D 的坐标为(0D ,)(0)y y <, 由题意可知CD BD =,22CD BD =, 在Rt OCD ∆中,由勾股定理得22216(8)y y +=-, 解得12y =-.∴点D 的坐标为(0,12)D -,可设直线CD 的解析式为12(0)y kx k =-≠ 点(16,0)C 在直线12y kx =-上, 16120k ∴-=, 解得34k =, ∴直线CD 的解析式为3124y x =-. 6.如图,直线24y x =-+交x 轴和y 轴于点A 和点B ,点(0,2)C -在y 轴上,连接AC .(1)求点A 和点B 的坐标;(2)若点P是直线AB上一点,若BCP∆的面积为3,求点P的坐标;(3)过点B的直线BE交x轴于点(E E点在点A右侧),当45ABE∠=︒时,求直线BE的表达式.【解答】解:(1)24y x=-+交X轴和y轴于点A和点B,∴当0x=时,则4y=;当240y x=-+=时,解得2x=,(2,0)A∴,(0,4)B;(2)设点(,24)P a a-+,如图1,连接PC,则11(42)322BPCS BC a a∆==+=,解得1a=,当1a=时,242a-+=,故点(1,2)P;(3)当45ABE ∠=︒,如图,过点A 作AD AB ⊥交BE 于点D ,过点D 作DH x ⊥轴,45ABE ∠=︒,BAD ∴∆为等腰直角三角形, AB AD ∴=,90BAD ∠=︒,90BAO DAH ∴∠+∠=︒,90DAH ADH ∠+∠=︒, BAO ADH ∴∠=∠,在AOB ∆与DHA ∆中, 90BAO ADH AOB BAD AB AD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩, AOB DHA ∴∆≅∆()AAS , 2OA =,4OB =,246OH OA AH ∴=+=+=,2DH =,(6,2)D ∴, (0,4)B ,设直线BE 的表达式为y kx b =+,则264k b b =+⎧⎨=⎩,解得134k b ⎧=-⎪⎨⎪=⎩,故直线BE 的表达式为143y x =-+.7.如图,在平面直角坐标系中,过点(6,0)B 的直线AB 与直线OA 相交于点(4,2)A ,动点M 在线段OA 和射线AC 上运动.(1)求直线AB 的解析式.(2)求OAC ∆的面积.(3)是否存在点M ,使OMC ∆的面积是OAC ∆的面积的14?若存在求出此时点M 的坐标;若不存在,说明理由.【解答】解:(1)设直线AB 的解析式是y kx b =+, 根据题意得:4260k b k b +=⎧⎨+=⎩,解得:16k b =-⎧⎨=⎩,则直线的解析式是:6y x =-+;(2)在6y x =-+中,令0x =,解得:6y =, 164122OAC S ∆=⨯⨯=;(3)设OA 的解析式是y mx =,则42m =, 解得:12m =, 则直线的解析式是:12y x =,当OMC ∆的面积是OAC ∆的面积的14时, ∴当M 的横坐标是1414⨯=,在12y x =中,当1x =时,12y =,则M 的坐标是1(1,)2;在6y x =-+中,1x =则5y =,则M 的坐标是(1,5). 则M 的坐标是:11(1,)2M 或2(1,5)M .当M 的横坐标是:1-,在6y x =-+中,当1x =-时,7y =,则M 的坐标是(1,7)-; 综上所述:M 的坐标是:11(1,)2M 或2(1,5)M 或3(1,7)M -.8.如图,在平面直角坐标系中,过点(0,6)A 的直线AB 与直线OC 相交于点(2,4)C 动点P 沿路线O C B →→运动. (1)求直线AB 的解析式;(2)当OPB ∆的面积是OBC ∆的面积的14时,求出这时点P 的坐标; (3)是否存在点P ,使OBP ∆是直角三角形?若存在,直接写出点P 的坐标,若不存在,请说明理由.【解答】解:(1)点A 的坐标为(0,6), ∴设直线AB 的解析式为6y kx =+,点(2,4)C 在直线AB 上, 264k ∴+=, 1k ∴=-,∴直线AB 的解析式为6y x =-+;(2)由(1)知,直线AB 的解析式为6y x =-+, 令0y =, 60x ∴-+=, 6x ∴=,(6,0)B ∴,1122OBC C S OB y ∆∴==,OPB ∆的面积是OBC ∆的面积的14, 11234OPB S ∆∴=⨯=,设P 的纵坐标为m , 1332OPB S OB m m ∆∴===,1m ∴=,(2,4)C ,∴直线OC 的解析式为2y x =,当点P 在OC 上时,12x =, 1(2P ∴,1),当点P 在BC 上时,615x =-=, (5,1)P ∴,即:点1(2P ,1)或(5,1);(3)OBP ∆是直角三角形, 90OPB ∴∠=︒,当点P 在OC 上时,由(2)知,直线OC 的解析式为2y x =①, ∴直线BP 的解析式的比例系数为12-, (6,0)B ,∴直线BP 的解析式为132y x =-+②,联立①②,解得65125x y ⎧=⎪⎪⎨⎪=⎪⎩,6(5P ∴,12)5,当点P 在BC 上时,由(1)知,直线AB 的解析式为6y x =-+③,∴直线OP 的解析式为y x =④,联立③④解得,33x y =⎧⎨=⎩,(3,3)P ∴,即:点P 的坐标为6(5,12)5或(3,3).9.如图(1),在平面直角坐标系中,直线443y x =-+交坐标轴于A 、B 两点,过点(4,0)C -作CD 交AB 于D ,交y 轴于点E .且COE BOA ∆≅∆.(1)求B 点坐标为 (0,4) ;线段OA 的长为 ; (2)确定直线CD 解析式,求出点D 坐标;(3)如图2,点M 是线段CE 上一动点(不与点C 、E 重合),ON OM ⊥交AB 于点N ,连接MN .①点M 移动过程中,线段OM 与ON 数量关系是否不变,并证明; ②当OMN ∆面积最小时,求点M 的坐标和OMN ∆面积. 【解答】解:(1)直线443y x =-+交坐标轴于A 、B 两点,∴当0y =时,3x =,当0x =时,4y =, ∴点A 的坐标为(3,0),点B 的坐标为(0,4),3OA ∴=;故答案为:(0,4),3;(2)过点(4,0)C -作CD 交AB 于D ,交y 轴于点E .且COE BOA ∆≅∆, 4OC ∴=,OC OB =,OE OA =,点(3,0)A , 3OA ∴=,3OE ∴=,∴点E 的坐标为(0,3),设过点(4,0)C -,点(0,3)E 的直线解析式为y kx b =+, 403k b b -+=⎧⎨=⎩,得343k b ⎧=⎪⎨⎪=⎩, ∴直线CE 的解析式为334y x =+, 即直线CD 的解析式为334y x =+, 由334443y x y ⎧=+⎪⎪⎨⎪=-+⎪⎩,得12258425x y ⎧=⎪⎪⎨⎪=⎪⎩,即点D 的坐标为12(25,84)25; (3)①线段OM 与ON 数量关系是OM ON =保持不变, 证明:COE BOA ∆≅∆, OE OA ∴=,OEM OAN ∠=∠, 90BOA ∠=︒,ON OM ⊥, 90MON BOA ∴∠=∠=︒,MOE EON EON NOA ∴∠+∠=∠+∠, MOE NOA ∴∠=∠,在MOE ∆和NOA ∆中, MOE NOA OE OAOEM OAN ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()MOE NOA SAS ∴∆≅∆, OM ON ∴=,即线段OM 与ON 数量关系是OM ON =保持不变; ②由①知OM ON =, OM ON ⊥,OMN ∴∆面积是:222OM ON OM =, ∴当OM 取得最小值时,OMN ∆面积取得最小值,4OC =,3OE =,90COE ∠=︒, 5CE ∴=,当OM CE ⊥时,OM 取得最小值, ∴22OM CE OC OE=, ∴54322OM ⨯⨯=, 解得,125OM =, OMN ∴∆面积取得最小值是:212()725225=, 当OMN ∆取得最小值时,设此时点M 的坐标为3(,3)4a a +,∴222312(3)()45a a ++=,解得,3625a =-, ∴3483425a +=, ∴点M 的坐标为36(25-,48)25, 由上可得,当OMN ∆面积最小时,点M 的坐标是36(25-,48)25和OMN ∆面积是722510.如图,在平面直角坐标系中,直线334y x =--交x 轴于点A ,交y 轴于点B ,交直线x a =于点C ,点D 与点B 关于x 轴对称,连接AD 交直线x a =于点E .(1)填空:ABD S ∆= 12 . (2)求直线AD 的解析式;(3)在x 轴上存在一点P ,则PE PD +的和最小为 ;(直接填空即可)(4)当40a -<<时,点Q 为y 轴上的一个动点,使得QEC ∆为等腰直角三角形,求点Q 的坐标.【解答】解:(1)如图1,直线334y x =--交x 轴于点A ,交y 轴于点B ,令0x =,3y =-, (0,3)B ∴-,令0y =,3034x =--,4x ∴=-,(4,0)A ∴-,点D 与点B 关于x 轴对称, (0,3)D ∴, 11461222ABD S BD OA ∆∴=⨯=⨯⨯=, 故答案为:12;(2)如图1,设直线AD 的解析式为y kx b =+,由(1)知,(4,0)A -,(0,3)D , ∴403k b b -+=⎧⎨=⎩,∴343k b ⎧=⎪⎨⎪=⎩, ∴直线AD 的解析式为334y x =+; (3)解法一:如图2,点D 与点B 关于x 轴对称, ∴当BE AD ⊥时,BE 的值最小,即PD PE BE +=,4OA =,3OD =, 5AD ∴=,1122ABD S BD AO AD BE ∆∴==, 1164522BE ⨯⨯=⨯⨯, 245BE =; 则PE PD +的和最小为245; 解法二:如图2,由(2)知,直线AD 的解析式为334y x =+, 直线:CE x a =, 3(,3)4E a a ∴+,点D 与点B 关于x 轴对称,∴连接BE 交x 轴于P ,此时,PD PE +最小,最小值为BE ,BE ===BE ∴245=, 则PE PD +的和最小为245; 故答案为:245; (4)//EF OD ,AEF ADO ∴∆∆∽, ∴34EF OD AF AO ==, 设3EF x =,4AF x =,QEC ∆为等腰直角三角形时,存在以下三种情况:①当E 为直角顶点时,如图3,16EQ EC x ==, 则464x x +=,25x =, 635EF x ∴==, 16(0,)5Q ∴;②当C 为直角顶点时,如图3,同理得26(0,)5Q -;③当Q 为直角顶点时,如图4,此时Q 与O 重合,(0,0)Q综上,点Q的坐标为6(0,)5Q或6(0,)5或(0,0).11.如图,已知长方形OABC 的顶点A 在x 轴上,顶点C 在y 轴上,18OA =,12OC =,D 、E 分别为OA 、BC 上的两点,将长方形OABC 沿直线DE 折叠后,点A 刚好与点C 重合,点B 落在点F 处,再将其打开、展平.(1)点B 的坐标是 (18,12) ;(2)求直线DE 的函数表达式;(3)设动点P 从点D 出发,以1个单位长度/秒的速度沿折线D A B C →→→向终点C 运动,运动时间为t 秒,求当2PDE OCD S S ∆∆=时t 的值.【解答】解:(1)四边形ABCO 是矩形,AB OC ∴=,BC AO =,18OA =,12OC =,12AB ∴=,18BC =,∴点B 坐标(18,12)故答案为:(18,12)(2)折叠AD CD ∴=,ADE CDE ∠=∠,222OC OD CD +=,22144(18)OD OD ∴+=-,5OD ∴=,13CD ∴=,点D 坐标为(5,0),//BC AO ,CED EDA ∴∠=∠,且ADE CDE ∠=∠,CED CDE ∴∠=∠,13CE CD ∴==,∴点E 坐标为(13,12),设直线DE 的函数表达式为y kx b =+,∴051213k b k b =+⎧⎨=+⎩解得:32k =,152b =- ∴解析式31522y x =- (3)2PDE OCD S S ∆∆=,12125602PDE S OC OD ∆∴=⨯⨯⨯=⨯= 当点P 在AD 上时,112602PDE S PD ∆=⨯⨯=, 10PD ∴=10101t ∴==, 当点P 在AB 上时,()11108512136022PDE PBE APD ABED S S S S AP AP ∆∆∆=--=-⨯⨯--⨯⨯=梯形 92AP ∴= 91335212t +∴== 当点P 在BC 上时,112602PDE S PE ∆=⨯⨯= 10PE ∴=1051213401t +++∴==综上所述:当2PDE OCD S S ∆∆=时,t 的值为10,352,40. 12.如图1,直线443y x =-+与坐标轴分别相交于A 、B 两点,在第一象限内,以线段AB 为边向外作正方形ABCD ,过A 、C 点作直线AC .(1)填空:点A 的坐标是 (3,0) ,正方形ABCD 的边长等于 ;(2)求直线AC 的函数解析式;(3)如图2,有一动点M 从B 出发,以1个单位长度/秒的速度向终点C 运动,设运动的时间为t (秒),连接AM ,当t 为何值时,则AM 平分BAC ∠?请说明理由.【解答】解:(1)直线443y x =-+与坐标轴分别相交于A 、B 两点, 令0x =,则4y =,(0,4)B ∴,令0y =,则4043x =-+, 3x ∴=,(3,0)A ∴,5AB ∴=,故答案为:(3,0),5;(2)如图1,过点C 作CN OB ⊥于N ,90CBN BCN ∴∠+∠=︒,四边形ABCD 是正方形,AB BC ∴=,90ABC ∠=︒,90OBA CBN ∴∠+∠=︒,OBA BCN ∴∠=∠,在AOB ∆和BNC ∆中,90AOB BNC ABO BCNAB BC∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ()AOB BNC AAS ∴∆≅∆,4CN OB ∴==,3BN OA ==,7ON OB BN ∴=+=,(4,7)C ∴,设直线AC 的解析式为y kx b =+,(3,0)A ,∴4730k b k b +=⎧⎨+=⎩,∴721k b =⎧⎨=-⎩∴直线AC 的解析式为721y x =-;(3)如图2,过M 作MF AC ⊥当AM 为BAC ∠的角平分线时,MF AC ⊥,MB AB ⊥BM FM ∴=45MCF ∠=︒,MF CF ∴=设BM x =,则5CM x =-,则CM5x ∴-1)5x ∴=5x ∴==t ∴为5时,AM 平分BAC ∠.13.如图,在平面直角坐标系中,直线AB交坐标轴于点A(0,6)、B(8,0),点C为x轴正半轴上一点,连接AC,将ABC∆沿AC所在的直线折叠,点B恰好与y轴上的点D重合.(1)求直线AB的解析式;(2)求出点C的坐标;(3)点P为直线AB上的点,请求出点P的坐标使94COPS∆=;(4)点Q为直线AB上一动点,连接DQ,线段DQ是否存在最小值?若存在,请求出DQ的最小值,若不存在,请说明理由.【解答】解:(1)设直线AB的解析式为:y kx b=+,把A(0,6)、B(8,0)的坐标代入得:680bk b=⎧⎨+=⎩,解得:346k b ⎧=-⎪⎨⎪=⎩,AB ∴的解析式为:364y x =-+;(2)点A (0,6)、B (8,0),6OA ∴=,8OB =,10AB ∴===,由折叠的性质的10AD AB ==,设OC x =,则8BC CD x ==-,68OA OB ==,10AD AB ∴==,从而可知4OD =,∴在OCD ∆中由勾股定理得2224(8)x x +=-,解得3x =,(3,0)C ∴;(3)点P 为直线AB 上的点,∴设3(,6)4P m m -+, 1393|6|244COP S m ∆=⨯⨯-+=; 6m ∴=或10m =,3(6,)2P ∴或3(10,)2-; (4)DQ 存在最小值.理由如下:连接BD ,则ABD ∆为等腰三角形,由垂线段最短可知,DQ 的最小值即为ABD ∆腰上的高, DQ ∴的最小值8OB ==.14.如图,平面直角坐标系中,(0,2)A ,(1,0)B ,(2,3)C ,CD y ⊥轴于点D .(1)AOB CDA ∆≅∆;(2)连接BC ,判断ABC ∆的形状,并说明理由;(3)如图(2),已知(3,4)P ,(6,2)Q ,若PQM ∆是等腰直角三角形,且90QPM ∠=︒,则点M 坐标为 (1,1)或(5,7) .【解答】解:(1)(2,3)C ,3OD ∴=,2CD =,(0,2)A ,(1,0)B ,2OA ∴=,1OB =,1AD ∴=,AD OB ∴=,在AOB ∆和CDA ∆中,90OB AD AOB CDA AO CD =⎧⎪∠=∠=︒⎨⎪=⎩,()AOB CDA SAS ∴∆≅∆;(2)ABC ∆是等腰直角三角形,理由如下:AOB CDA ∆≅∆,ABO CAD ∴∠=∠,AC AB =,90ABO BAO ∠+∠=︒,90CAD BAO ∴∠+∠=︒,90BAC ∴∠=︒,又AC AB =,ABC ∴∆是等腰直角三角形;(3)如图2,过点P 作x 轴的平行线GH ,作MG GH ⊥于G ,QH GH ⊥于H , (3,4)P ,(6,2)Q ,3PH ∴=,2QH =,MPQ ∆为等腰直角三角形,90MPQ ∴∠=︒,PM PQ =,90MPG HPQ ∴∠+∠=︒,90MPG PMG ∠+∠=︒,GMP HPQ ∴∠=∠,在GMP ∆和HPQ ∆中,GMP HPQ PGM QHP PM PQ ∠=∠⎧⎪∠=∠⎨⎪=⎩,()GMP HPQ AAS ∴∆≅∆3GM PH ∴==,2GP HQ ==,∴点M 坐标为(1,1),过点P 作y 轴的平行线ST ,作M S ST '⊥于S ,QT ST ⊥于T , 同理可得,△M ST PTQ '≅∆,2M S PT ∴'==,3SP TQ ==,∴点M '坐标为(5,7),故答案为:(1,1)或(5,7).15.如图,已知函数12y x b =-+的图象与x 轴、y 轴分别交于点A 、B ,与函数y x =图象交于点M ,点M 的横坐标为2,在x 轴上有点(,0)P a (其中2)a >,过点P 作x 轴的垂线,分别交函数12y x b =-+和y x =的图象于点C 、D . (1)求点A 的坐标;(2)若OB CD =,求a 的值;(3)在(2)条件下若以OD 线段为边,作正方形ODEF ,求直线EF 的表达式.【解答】解:(1)点M 在直线y x =的图象上,且点M 的横坐标为2, ∴点M 的坐标为(2,2),把(2,2)M 代入12y x b =-+得12b -+=,解得3b =, ∴一次函数的解析式为132y x =-+, 把0y =代入132y x =-+得1302x -+=,解得6x =, A ∴点坐标为(6,0),(2)把0x =代入132y x =-+得3y =, B ∴点坐标为(0,3),CD OB =,3CD ∴=,PC x ⊥轴,C ∴点坐标为1(,3)2a a -+,D 点坐标为(,)a a , 1(3)32a a ∴--+=, 4a ∴=.(3)如图以OD 为边作正方形ODEF 有两种情况.(4,4)D ,当正方形为ODE F ''时,90DOF ∠'=︒,OD 与x 轴夹角为045,x ∴轴平分DOF ∠',∴正方形顶点1E 在x 轴上,由对称性知(8,0)E ∴',(4,4)F '-,∴直线E F ''的解析式为8y x =-,同理当正方形为ODEF 时,∴直线EF 的解析式为8y x =+.16.如图,正方形ABOD 的边长为2,OB 在x 轴上,OD 在y 轴上,且//AD OB ,//AB OD ,点C 为AB 的中点,直线CD 交x 轴于点F .(1)求直线CD 的函数关系式;(2)过点C 作CE DF ⊥且交于点E ,求证:ADC EDC ∠=∠;(3)求点E 坐标;(4)点P 是直线CE 上的一个动点,求PB PF +的最小值.【解答】解:(1)四边形ABOD 为正方形,2AB BO OD AD ∴====,(0,2)D ∴, C 为AB 的中点,1BC ∴=,(2,1)C ∴-,设直线CD 解析式为(0)y kx b k =+≠,∴212k b b -+=⎧⎨=⎩,解得122k b ⎧=⎪⎨⎪=⎩,∴直线CD 的函数关系式为122y x =+;(2)C 是AB 的中点,AC BC ∴=,四边形ABOD 是正方形,90A CBF ∴∠=∠=︒,在ACD ∆和BCF ∆中A CBFAC BC ACD BCF∠=∠⎧⎪=⎨⎪∠=∠⎩()ACD BCF ASA∴∆≅∆,CF CD∴=,CE DF⊥,CE∴垂直平分DF,DE FE∴=,EDC EFC∴∠=∠,//AD BF,EFC ADC∴∠=∠,ADC EDC∴∠=∠;(3)由(2)可2BF AD==,且1BC=,90CBF CBE FCE∠=∠=∠=︒,90 CFB FCB FCB ECB∴∠+∠=∠+∠=︒,CFB BCE∴∠=∠,BCF BEC∴∆∆∽,∴BF CBCB BE=,即211BE=,解得12BE=,13222OE OB BE∴=-=-=,E∴点坐标为3(2-,0);方法二:设DE EF x==,在Rt DEO∆中,利用勾股定理求出x即可.(4)如图,连接BD交直线CE于点P,由(2)可知点D与点F关于直线CE对称,PD PF∴=,PB PF PB PD BD∴+=+,(2,0)B -,(0,2)D ,BD ∴=,PB PF ∴+的最小值为17.已知长方形OABC 的边长4OA =,3AB =,E 是OA 的中点,分别以OA 、OC 所在的直线为x 轴、y 轴,建立如图1所示的平面直角坐标系,直线l 经过C 、E 两点.(1)求直线l 的函数表达式;(2)如图2,在长方形OABC 中,过点E 作EG EC ⊥交AB 于点G ,连接CG ,将COE ∆沿直线l 折叠后得到CEF ∆,点F 恰好落在CG 上.证明:GF GA =.(3)在(2)的条件下求四边形AGFE 的面积.【解答】(1)解:矩形OABC 的边长4OA =,3AB =,E 是OA 的中点, 3OC AB ∴==,2OE =,(2,0)E ∴,(0,3)C .设直线l 的解析式(0)y kx b k =+≠.将(2,0)E ,(0,3)C ,分别代入y kx b =+得203k b b +=⎧⎨=⎩解得323k b ⎧=-⎪⎨⎪=⎩,∴直线l 的解析式332y x =-+;(2)证明:四边形OABC 是矩形,90COA OAB ∴∠=∠=︒.又根据折叠的性质得到90COE CFE ∠=∠=︒,OE EF =,90EFG EAG ∴∠=∠=︒.又E 是OA 的中点,OE AE ∴=,EF EA ∴=,∴在Rt EFG ∆和Rt EAG ∆中,EF EA EG EG =⎧⎨=⎩, Rt EFG Rt EAG(HL)∴∆≅∆,GF GA ∴=;(3)解:由(2)知,GF GA =,根据折叠的性质知3OC CF ==.3BG AB AG AG =-=-,3CG CF GF GA =+=+,2AE =,∴在Rt CBG ∆中,由勾股定理得:222CG BC BG =+,即222(3)(3)4AG AG +=-+, 解得,43AG =. 由(2)知,Rt EFG Rt EAG ∆≅∆,Rt EFG Rt EAG S S ∆∆∴=,114822222233Rt EAG AGFE S S AE AG ∆∴==⨯⋅=⨯⨯⨯=四边形, 即四边形AGFE 的面积是83. 18.如图,在平面直角坐标系中,四边形OABC 的顶点O 是坐标原点,点A 在第一象限,点C 在第四象限,点B 在x 轴的正半轴上.90OAB ∠=︒且OA AB =,6OB =,5OC =.点P 是线段OB 上的一个动点(点P 不与点O ,B 重合),过点P 的直线l 与y 轴平行,直线l 交边OA 或边AB 于点Q ,交边OC 或边BC 于点R .设点P 的横坐标为t ,线段QR 的长度为m .已知4t =时,直线l 恰好过点C .(1)求点A 和点B 的坐标;(2)当03t <<时,求m 关于t 的函数关系式;(3)当 3.5m =时,请直接写出点P 的坐标.【解答】解:(1)如图:过点A 作AM OB ⊥于M ,90OAB ∠=︒,OA AB =,6OB =,AM OB ⊥,132AM OM MB OB ∴====, ∴点A 的坐标为(3,3),点B 的坐标为(6,0);(2)作CN x ⊥轴于N ,如图,4t =时,直线l 恰好过点C ,4ON ∴=,在Rt OCN ∆中,3CN =, C ∴点坐标为(4,3)-, 设直线OC 的解析式为y kx =,把(4,3)C -代入得43k =-,解得34k =-, ∴直线OC 的解析式为34y x =-, 设直线OA 的解析式为y ax =, 把(3,3)A 代入得33a =,解得1a =, ∴直线OA 的解析式为y x =, (P t ,0)(03)t <<,(,)Q t t ∴,3(,)4R t t -, 37()44QR t t t ∴=--=, 即7(03)4m t t =<<; (3)设直线AB 的解析式为y px q =+,把(3,3)A ,(6,0)B 代入得:3360p q p q +=⎧⎨+=⎩,解得16p q =-⎧⎨=⎩, ∴直线AB 的解析式为6y x =-+, 同理可得直线BC 的解析式为392y x =-, 当03t <<时,74m t =, 若 3.5m =,则73.54t =, 解得2t =,此时P 点坐标为(2,0);当34t <时,(,6)Q t t -+,3(,)4R t t -, ∴316()644m t t t =-+--=-+, 若 3.5m =,则13.564t =-+,解得10t =(不合题意舍去);当46t <时,(,6)Q t t -+,3(,9)2R t t -, ∴356(9)1522m t t t =-+--=-+, 若 3.5m =,则53.5152t =-+, 解得235t =,此时P 点坐标为23(5,0); 综上所述,满足条件的P 点坐标为(2,0)或23(5,0).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数与几何图形综合题云南省近3年真题展示:1、(2014·云南·T23)见2015《火线100天》(云南专版)P163 例备选变式题:1、(2011•曲靖·T24)如图:直线y=kx+3与x轴、y轴分别交于A、B两点,tan∠OAB=,点C(x,y)是直线y=kx+3上与A、B不重合的动点.(1)求直线y=kx+3的解析式;(2)当点C运动到什么位置时△AOC的面积是6;(3)过点C的另一直线CD与y轴相交于D点,是否存在点C使△BCD与△AOB全等?若存在,请求出点C的坐标;若不存在,请说明理由.解:(1)∵直线y=kx+3与y轴分别交于B点,∴B(0,3),∵tan∠OAB=,∴OA=4,∴A(4,0),∵直线y=kx+3过A(4,0),∴4k+3=0,∴k=﹣,∴直线的解析式为:y=﹣x+3;(2)∵A(4,0),∴AO=4,∵△AOC的面积是6,∴△AOC的高为3,∴C点的纵坐标为3,∵直线的解析式为:y=﹣x+3,∴3=﹣x+3,x=0,∴点C运动到B点时,△AOC的面积是6;(3)当过点C的另一直线CD与y轴相交于D点,且CD⊥y轴于点D时,BD=BO=3,△BCD与△AOB全等,∴C点纵坐标为6,∴6=﹣x+3,解得:x=﹣4,∴C点坐标为:(﹣4,6).83,边AB的垂直平分线CD分别2、(2011·玉溪·T23)如图,在Rt△OAB中,90A∠=°,30ABO∠=°,OB与AB、x轴、y轴交于点C、G、D.(1)求点G 的坐标;(2)求直线CD 的解析式;(3)在直线CD 上和平面内是否分别存在点Q 、P ,使得以O 、D 、P 、Q 为顶点的四边形是菱形?若存在,求出点Q 的坐标;若不存在,请说明理由.解:(1)∵DC 是AB 垂直平分线,OA 垂直AB ,∴G 点为OB 的中点. ∵OB,∴0). (2)过点C 作CH ⊥x 轴于点H.在Rt △ABO 中,∠ABO =30°,OB, ∴cos30°=8AB .即AB=4. 又∵CD 垂直平分AB ,∴BC =2. 在Rt △CBH 中,CH =12BC =1,BH∴OH-=,-1). ∵∠DGO =60°.∴OG=12OB ∴OD=4.∴D(0,4) . 设直线CD 的解析式为y=kx+b.则14b b⎧-=+⎪⎨⎪=⎩4k b ⎧=⎪⎨=⎪⎩ ∴y=4+.(3)存在点P 、Q ,使得点O 、D 、P 、Q 为顶点的四边形是菱形.①如图,当OD =DQ =QP =OP =4时,四边形DOPQ 为菱形. 设QP 交x 轴于点E ,在Rt △OEP 中,OP =4,∠OPE =30°,∴OE =2,PE=.∴Q(2,4-).②如图,当DQ =QP =PO =OD =4时,四边形DOPQ 为菱形. 延长QP 交x 轴于点F ,在Rt △POF 中,∵∠FPO =30°,OP =4.∴OF =2,PF=.∴QF=4+.∴Q(-2,4+. ③如图,当OP =PD =DQ =OQOPDQ 为菱形. 过Q 作MQ ⊥y 轴于点M ,在Rt △DQM 中,∵∠MDQ =30°,∴MQ=12DQ =.∴2). ④如图,当OD =DP =PQ =OQ =4时,四边形DOQP 为菱形.设PQ 交x 轴于点N ,此时∠OQD =∠ODQ =30°,∴∠GOQ =30°.在Rt △ONQ 中,NQ =12OQ =2.∴ON =.∴Q(,-2).综上所述,满足条件的点Q 共有四点:(2,4-),(-2,4+,,(,-2) .3、(2011·德宏·T23)如图,已知直线)0(≠+=a b ax y 与双曲线(0)ky k x=≠交于A 、B 两点,且点(2,1)A ,点B 的纵坐标为2.(1)求双曲线的解析式; (2)求直线的解析式; (3)求线段AB 的长度;(4)问在双曲线上是否存在点C ,使△ABC 的面积等于3?若存在,求出点C 的坐标;若不存在,说明理由(结果不需要分母有理化).解:(1)∵双曲线(0)ky k x=≠经过点(2,1)A , ∴ 21k=,解得2=k . ∴双曲线的解析式为xy 2=.(2)由(1)知,x22=,∴点B 坐标为),(21.∵直线)0(≠+=a b ax y 经过点(2,1)A ,B ),(21,∴⎩⎨⎧=+=+.2,12b a b a 解得⎩⎨⎧=-=.3,1b a∴直线的解析式为3+-=x y .(3)如图11-1,过点C 作x CD //轴,交直线AB 于点D ,过点B 作CD BF ⊥,垂足为点F ,过点A 作BF AG ⊥,垂足为点G ,则G 点坐标为),(11.图11-1在ABG Rt ∆中,1=AG ,1=BG , ∴222=+=BG AG AB .(4)存在.理由如下: 解法一:由(3)知,3=∆ABC S ,2=AB ,∴点C 到AB 边的距离为23.如图11-1,过点C 作AB CH ⊥,垂足为点H .即 23=CH .设点C 的坐标为),(x x 2,则点D 的坐标为),(x x 223-.∴x xCD --=23. 在CDH Rt ∆中,o45=∠CDB ,23=CH ,则6=CD .得方程 623=--x x. ①当623=--x x时,解得 11-=x ,22-=x . ∴点C 的坐标为),(21--或),(12--.②当623-=--x x 时,解得27391+=x ,27392-=x . ∴点C 的坐标为),(73942739++或),(73-94273-9. 因此,符合条件的点C 有4个,即:),(21--,),(12--,),(73942739++或),(73-94273-9. 解法二:①当点C 在第三象限时,如图11-1.设点C 的坐标为),(xx 2,则点D 的坐标为),(xx 223-. ∴x xCD --=23. 过点A 作CD AE ⊥,垂足为点E ,则E 、F 点的坐标分别为),(x22,),(x 21,x BF 22-=,xAE 21-=.1)23(212121⨯--=⋅-⋅=-=∆∆∆x xAE CD BF CD S S S ACDBCD ABC ∴31)23(21=⨯--x x.解方程得11-=x ,22-=x . ∴点C 的坐标为),(21--或),(12--.②当点C 在第一象限时,如图11-2.设点C 的坐标为),(x x 2,则点D 的坐标为),(x x 223-.∴32-+=xx CD .过点A 作CD AE ⊥,垂足为点E ,过点B 作CD BF ⊥,垂足为点F .图11-2则E ),(x 22、F ),(x21,22-=x BF ,12-=x AE . 1)32(212121⨯-+=⋅-⋅=-=∆∆∆xx BF CD AE CD S S S BCDACD ABC . ∴31)32(21=⨯-+x x .解方程得 27391+=x ,27392-=x . ∴点C 的坐标为),(73942739++或),(73-94273-9. 由①、②知,符合条件的点C 有4个,即:),(21--,),(12--,),(73942739++或),(73-94273-9. 4、(2014•齐齐哈尔·T28)如图,在平面直角坐标系中,已知R △AOB 的两直角边OA 、OB 分别在x 轴、y 轴的正半轴上(OA <OB ),且OA 、OB 的长分别是一元二次方程x 2﹣14x +48=0的两个根.线段AB 的垂直平分线CD 交AB 于点C ,交x 轴于点D ,点P 是直线CD 上一个动点,点Q 是直线AB 上一个动点. (1)求A 、B 两点的坐标; (2)求直线CD 的解析式;(3)在坐标平面内是否存在点M ,使以点C 、P 、Q 、M 为顶点的四边形是正方形,且该正方形的边长为AB 长?若存在,请直接写出点M 的坐标;若不存在,请说明理由.解:(1)∵214480-+=x x ,∴x 1=6,x 2=8.∵OA <OB ,∴OA =6,OB =8. ∴A (6,0),B (8,0).(2)根据勾股定理得AB =10.∵CD 是AB 的垂直平分线,∴AC =5,易求C (3,4) .由于△AOB ∽△ACD ,∴=AO AB OC AD,求得AD =253. ∴OD =AD -OA =73,∴D (73-,0) .由C 、D 坐标得y CD =34x +74.(3)存在,M 1 (2,-3),M 2 (10,3),M 3 (4,11),M 4(-4,5) .5、(2014•绥化·T27)如图,在平面直角坐标系中,已知矩形AOBC 的顶点C 的坐标是(2,4),动点P 从点A 出发,沿线段AO 向终点O 运动,同时动点Q 从点B 出发,沿线段BC 向终点C 运动.点P 、Q 的运动速度均为1个单位,运动时间为t 秒.过点P 作PE ⊥AO 交AB 于点E . (1)求直线AB 的解析式;(2)设△PEQ 的面积为S ,求S 与t 时间的函数关系,并指出自变量t 的取值范围;(3)在动点P 、Q 运动的过程中,点H 是矩形AOBC 内(包括边界)一点,且以B 、Q 、E 、H 为顶点的四边形是菱形,直接写出t 值和与其对应的点H 的坐标.解:(1)∵C (2,4),∴A (0,4),B (2,0), 设直线AB 的解析式为y =kx +b , ∴,解得∴直线AB的解析式为y=﹣2x+4.(2)如图2,过点Q作QF⊥y轴于F,∵PE∥OB,∴==∴有AP=BQ=t,PE=t,AF=CQ=4﹣t,当0<t<2时,PF=4﹣2t,∴S=PE•PF=×t(4﹣2t)=t﹣t2,即S=﹣t2+t(0<t<2),当2<t≤4时,PF=2t﹣4,∴S=PE•PF=×t(2t﹣4)=t2﹣t(2<t≤4).(3)t1=,H1(,),t2=20﹣8,H2(10﹣4,4).6、(2014•聊城·T25)如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(4,3),O(0,0),B(6,0).点M是OB边上异于O,B的一动点,过点M作MN∥AB,点P是AB边上的任意点,连接AM,PM,PN,BN.设点M(x,0),△PMN的面积为S.(1)求出OA所在直线的解析式,并求出点M的坐标为(1,0)时,点N的坐标;(2)求出S关于x的函数关系式,写出x的取值范围,并求出S的最大值;(3)若S:S△ANB=2:3时,求出此时N点的坐标.解:(1)设直线OA的解析式为y=k1x,∵A(4,3),∴3=4k1,解得k1=,∴OA所在的直线的解析式为:y=x,同理可求得直线AB的解析式为;y=﹣x+9,∵MN∥AB,∴设直线MN的解析式为y=﹣x+b,把M(1,0)代入得:b=,∴直线MN的解析式为y=﹣x+,解,得,∴N(,).(2)如图2,作NH⊥OB于H,AG⊥OB于G,则AG=3.∵MN∥AB,∴△MBN的面积=△PMN的面积=S,∴△OMN∽△OBA,∴NH:AG=OM:OB,∴NH:3=x:6,即NH=x,∴S=MB•NH=×(6﹣x)×x=﹣(x﹣3)2+(0<x<6),∴当x=3时,S有最大值,最大值为.(3)如图2,∵MN∥AB,∴△AMB的面积=△ANB的面积=S△ANB,△NMB的面积=△NMP的面积=S∵S:S△ANB=2:3,∴MB•NH:MB•AG=2:3,即NH;AG=2:3,∵AG⊥OB于G,NH⊥OB,∴NH∥AG,∴ON:OA=NH:AG=2:3,∵MN∥AB,∴OM:OB=ON:OA=2:3,∵OA=6,∴=,∴OM=4,∴M(4,0)∵直线AB的解析式为;y=﹣x+9,∴设直线MN的解析式y=﹣x+b∴代入得:0=﹣×4+b,解得b=6,∴直线MN的解析式为y=﹣x+6,解得,∴N(,2).7、(2014•新疆建设兵团·T23)如图,直线y=﹣x+8与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).(1)写出A,B两点的坐标;(2)设△AQP的面积为S,试求出S与t之间的函数关系式;并求出当t为何值时,△AQP的面积最大?(3)当t为何值时,以点A,P,Q为顶点的三角形与△ABO相似,并直接写出此时点Q的坐标.解:(1)令y=0,则﹣x+8=0,解得x=6,当x=0时,y=8,∴OA=6,OB=8,∴点A(6,0),B(0,8);(2)在Rt△AOB中,由勾股定理得,AB===10,∵点P的速度是每秒2个单位,点Q的速度是每秒1个单位,∴AP=2t,AQ=AB﹣BQ=10﹣t,∴点Q到AP的距离为AQ•sin∠OAB=(10﹣t)×=(10﹣t),∴△AQP的面积S=×2t×(10﹣t)=﹣(t2﹣10t)=﹣(t﹣5)2+20,∵﹣<0,0<t≤3,∴当t=3时,△AQP的面积最大,S最大=﹣(3﹣5)2+20=;(3)若∠APQ=90°,则cos∠OAB=,∴=,解得t=,若∠AQP=90°,则cos∠OAB=,∴=,解得t=,∵0<t≤3,∴t的值为,此时,OP=6﹣2×=,PQ=AP•tan∠OAB=(2×)×=,∴点Q的坐标为(,),综上所述,t=秒时,以点A,P,Q为顶点的三角形与△ABO相似,此时点Q的坐标为(,).8、(2014•黑龙江龙东·T28)如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB).(1)求点D的坐标.(2)求直线BC的解析式.(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.解:(1)x2﹣7x+12=0,解得x1=3,x2=4,∵OA>OB,∴OA=4,OB=3,过D作DE⊥y于点E,∵正方形ABCD,∴AD=AB,∠DAB=90°,∠DAE+∠OAB=90°,∠ABO+∠OAB=90°,∴∠ABO=∠DAE,∵DE⊥AE,∴∠AED=90°=∠AOB,在△DAE和△ABO中,,∴△DAE≌△ABO(AAS),∴DE=OA=4,AE=OB=3,∴OE=7,∴D(4,7);(2)过点C作CM⊥x轴于点M,同上可证得△BCM≌△ABO,∴CM=OB=3,BM=OA=4,∴OM=7,∴C(7,3),设直线BC的解析式为y=kx+b(k≠0,k、b为常数),代入B(3,0),C(7,3)得,,解得,∴y=x﹣;(3)存在.点P与点B重合时,P1(3,0),点P与点B关于点C对称时,P2(11,6).9、(2014•内江·T21)如图,一次函数y=kx+b的图象与反比例函数y=(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=B C.(1)求一次函数、反比例函数的解析式;(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.解:(1)∵AC=BC,CO⊥AB,A(﹣4,0),∴O为AB的中点,即OA=OB=4,∴P(4,2),B(4,0),将A(﹣4,0)与P(4,2)代入y=kx+b得:,解得:k=,b=1,∴一次函数解析式为y=x+1,将P(4,2)代入反比例解析式得:m=8,即反比例解析式为y=;(2)假设存在这样的D点,使四边形BCPD为菱形,如图所示,对于一次函数y=x+1,令x=0,得到y=1,即C(0,1),∴直线BC的斜率为=﹣,设过点P,且与BC平行的直线解析式为y﹣2=﹣(x﹣4),即y=,与反比例解析式联立得:,消去y得:=,整理得:x2﹣12x+32=0,即(x﹣4)(x﹣8)=0,解得:x=4(舍去)或x=8,当x =8时,y =1,∴D (8,1), 此时PD ==,BC ==,即PD =BC ,∵PD ∥BC ,∴四边形BCPD 为平行四边形, ∵PC ==,即PC =BC ,∴四边形BCPD 为菱形,满足题意,则反比例函数图象上存在点D ,使四边形BCPD 为菱形,此时D 坐标为(8,1).10、(2014·济南·T26)如图1,反比例函数)0(>=x xky 的图象经过点A (32,1),射线AB 与反比例函数图象交与另一点B (1,a ),射线AC 与y 轴交于点C ,y AD BAC ⊥=∠,75轴,垂足为D . (1)求k 的值;(2)求DAC ∠tan 的值及直线AC 的解析式;(3)如图2,M 是线段AC 上方反比例函数图象上一动点,过M 作直线x l ⊥轴,与AC 相交于N ,连接CM ,求CM N ∆面积的最大值.解:(1)由反比例函数)0(>=x xky 的图象经过点A (32,1),得32132=⨯=k ; (2)由反比例函数)0(32>=x xy 得点B 的坐标为(1,32),于是有 30,45=∠∴=∠DAC BAD ,33tan =∠DAC ,AD =32,则由33tan =∠DAC 可得CD =2,C 点纵坐标是-1,直线AC 的截距是-1,而且过点A (32,1),则直线解析式为133-=x y . (3)设点M 的坐标为)1)(,32(>m m m, 则点N 的坐标为)12,32(-mm ,于是CMN ∆面积为 )12(3221+-⨯⨯=∆m m m S CMN ])422(89[3)112(322--=++-⨯=m m m ,所以,当4=m 时,CMN ∆面积取得最大值839.。
