笛卡尔与蜘蛛网 平面直角坐标系
平面直角坐标系的历史发展过程

平面直角坐标系的历史发展过程
平面直角坐标系是现代几何学中的基础概念之一,它的历史发展可以追溯到17世纪。
以下是该坐标系的历史发展过程的概述:1.笛卡尔坐标系:平面直角坐标系的起源可以追溯到法国数学
家笛卡尔(RenéDescartes)的工作。
在1637年出版的《几何学》一书中,笛卡尔首次提出了直角坐标系的概念。
他将平面上的点表示为有序的数对(x, y),并通过横轴(x轴)和纵轴(y轴)的交叉点来确定点的位置。
2.点的坐标表示:笛卡尔的坐标系引入了将几何问题转化为代
数问题的方法。
通过使用坐标,点在平面上的位置可以用数值表示。
这使得几何问题可以更容易地进行计算和分析。
3.进一步发展:随着时间的推移,对直角坐标系的理解和使用
不断深入。
其他数学家如费马、欧拉、高斯等也为直角坐标系的发展做出了重要贡献。
4.应用拓展:直角坐标系的引入不仅在几何学领域产生了重要
影响,还被广泛应用于物理学、工程学、计算机科学等各个领域。
它成为了一种便捷且通用的坐标系统,使得各种数学和科学问题的描述、分析和解决更加方便和精确。
总结起来,平面直角坐标系的历史发展可以追溯到17世纪的笛卡尔,他的工作奠定了直角坐标系的基本原理和概念。
随后,直角坐标系的应用得到进一步发展,并成为现代数学和科学中不可或缺的工具。
笛卡尔与平面直角坐标系

笛卡尔与平面直角坐标系笛卡尔和他的平面直角坐标系,哎呀,这可是数学界的一颗璀璨明珠呀!大家可能听过他的名字,但到底有多厉害呢?我跟你说,笛卡尔不仅是个数学家,还是个哲学家,简直就是个全能选手。
想象一下,在17世纪的法国,那个时代的科技水平还停留在手工业的阶段,笛卡尔却在纸上画出了一种新的思维方式。
他说,嘿,咱们干脆把这个平面当成一个大画布,用两根线把它分成四个部分,搞得清清楚楚,多简单啊!所以,他的平面直角坐标系就这样诞生了,真是一个了不起的创意。
你想啊,笛卡尔的这个坐标系,就像是一个地图,告诉你在哪里能找到你想要的东西。
他用横轴和纵轴,把平面划分得一清二楚。
横轴上是X,纵轴上是Y。
哦,对了,X和Y可不是随便取的名字哦,X就像是个帅气的家伙,代表着“横”,而Y则像是个优雅的姑娘,代表着“竖”。
在这个坐标系里,任何一个点都可以用一对数字来表示,哎呀,这种感觉就像是给每个点都贴上了标签,方便得不得了。
比如说,假设你在寻找一块最爱的披萨,笛卡尔就会说:“好吧,给我一个点的坐标,我带你去!”如果你的披萨坐标是(3, 2),那么就意味着你要走3步横着,再走2步竖着,啪!就到了!这样的思维方式是不是让人觉得特别清晰呢?就像在找一个人,知道他在哪里,能轻松打电话找到他。
笛卡尔的坐标系让我们在几何和代数之间架起了一座桥,这可不是开玩笑的。
而且你知道吗,笛卡尔这个家伙还特别喜欢把抽象的东西具象化。
他觉得,数学不应该是高高在上的理论,而是要与生活紧密结合。
就像我们日常生活中的购物清单,咱们可以用坐标系来表示每个商品的价格和数量,清楚明了,不用再翻来翻去找。
笛卡尔就是这么个不走寻常路的 thinker,他让那些枯燥的数学变得有趣起来。
讲到这里,很多人可能会说:“好吧,那我怎么用这个坐标系呢?”别急,咱们一起来想想。
你得学会画坐标系。
拿一根铅笔和一张纸,先画一个大十字。
X轴在下面,Y 轴在旁边,嘿,这就成了你的舞台!给每个轴标上数字,从零开始,往两边画。
数学人教版七年级下册(阅读材料)笛卡儿与平面直角坐标系

(阅读材料)笛卡儿与平面直角坐标系一、笛卡儿简介二、笛卡儿与(笛卡儿坐标系)平面直角坐标系笛卡儿坐标系(Cartesian coordinates)就是直角坐标系和斜角坐标系的统称。
相交于原点的两条数轴,构成了平面仿射坐标系。
如两条数轴上的度量单位相等,则称此仿射坐标系为笛卡尔坐标系。
两条数轴互相垂直的笛卡尔坐标系,称为笛卡尔直角坐标系,否则称为笛卡尔斜角坐标系。
二维的直角坐标系是由两条相互垂直、0 点重合的数轴构成的。
在平面内,任何一点的坐标是根据数轴上对应的点的坐标设定的。
在平面内,任何一点与坐标的对应关系,类似于数轴上点与坐标的对应关系。
二维的直角坐标系通常由两个互相垂直的坐标轴设定,通常分别称为x-轴和y-轴;两个坐标轴的相交点,称为原点,通常标记为O ,既有“零”的意思,又是英语“Origin”的首字母。
每一个轴都指向一个特定的方向。
这两个不同线的坐标轴,决定了一个平面,称为xy-平面,又称为笛卡儿平面。
通常两个坐标轴只要互相垂直,其指向何方对于分析问题是没有影响的,但习惯性地(见右图),x-轴被水平摆放,称为横轴,通常指向右方;y-轴被竖直摆放而称为纵轴,通常指向上方。
两个坐标轴这样的位置关系,称为二维的右手坐标系。
任何一个点 P 在平面的位置,可以用直角坐标来独特表达。
只要从点 P 画一条垂直于 x-轴的直线。
从这条直线与 x-轴的相交点,可以找到点 P 的 x-坐标。
同样地,可以找到点 P 的 y-坐标。
这样,我们可以得到点 P 的直角坐标。
三、(笛卡儿坐标系)平面直角坐标系影响直角坐标系的创建,在代数和几何上架起了一座桥梁,它使几何概念用数来表示,几何图形也可以用代数形式来表示。
由此笛卡尔在创立直角坐标系的基础上,创造了用代数的方法来研究几何图形的数学分支——解析几何,他大胆设想:如果把几何图形看成是动点的运动轨迹,就可以把几何图形看成是由具有某种共同特征的点组成的。
举一个例子来说,我们可以把圆看作是动点到定点距离相等的点的轨迹,如果我们再把点看作是组成几何图形的基本元素,把数看作是组成方程的解,于是代数和几何就这样合为一家人了。
平面直角坐标系(

第一象限
O 1 2 3 4 5 6 x
1
-1 -2
第三象限
-3
-4 -5
第四象限
y
5 4
C(-4,1)
纵轴
3叫做点A的横坐标
C
·
-4 -3 -2
3 2
2叫做点A的纵坐标 B(2 ,3) A点在平面内的坐标为(3, 2) 记作:A(3,2)
·
1
0 -1 -1
· 方法:先横后纵
1 2 3 4 5
A(3,2)
3
,
2、已知点P到x轴和y轴的距离分别是2和5,求P点的 坐标。 P(5,2) 或P(5,-2) 或P(-5,2)或P(-5,-2) 3、点P的坐标为 (3,2),你知道点P到X轴的距离吗? 到Y轴的距离又是多少呢?在第二象限,到X轴的距 离为3,到Y轴的距离为2的点的坐标是多少呢?
y 4 3
1 0 1 -3 -2 -1-1 -2 P(3,2) 3 4x
(1). 若AB∥ x 轴, 则A( x , n ), B( x , n )
1 2
(2). 若AB∥ y轴, 则A( m, y ), B( m, y )
1 2
已知点A(10,5),B(50,5),则直线AB的位置特点是( ) A.与x轴平行 B.与y轴平行 C.与x轴相交,但不垂直 D.与y轴相交,但不垂直
-2
2、若点P(a,b)在第四象限,则 点Q(-a,b-4)在第 象限。
典例:
1、平行于x、y轴的点之间的距离。 2、点到x轴、y轴的距离。 3、点的位置确定坐标中字母的距离。 4、求图形的面积。
x
D(-3,-2)
B(3,-2)
笛卡尔坐标系的由来故事

笛卡尔坐标系的由来故事
咱来唠唠笛卡尔坐标系的由来,可有意思啦。
从前有个叫笛卡尔的哥们儿,这可是个超级聪明的家伙。
他整天就躺在床上想事儿,为啥呢?据说他在军队服役的时候,那地方可冷了,他就躲在暖和的被窝里思考人生和数学。
有一天啊,他看到天花板上有个蜘蛛在爬。
你想啊,一般人看到蜘蛛,可能就“啊”一声赶走了。
但笛卡尔不一样,他的小脑袋瓜就开始飞速运转。
他就想啊,怎么才能准确地说出这个蜘蛛的位置呢?
他就琢磨出来了一个超棒的办法。
他先在墙角那里想象出三条线,就像咱们现在说的坐标轴一样。
一条是横着的,一条是竖着的,还有一条是从墙里往外指的(当然啦,这是个大概的想象)。
然后呢,他发现只要知道蜘蛛到这三条线的距离,就能准确地说出蜘蛛在天花板这个平面上的位置啦。
这就是笛卡尔坐标系最初的灵感来源。
这个想法可不得了,一下子就把几何和代数联系起来了。
以前几何是研究图形的,代数是研究数字和方程的,就像两个不同星球的东西。
笛卡尔这么一搞,就像是建了一座超级大桥,让这两个星球能互通有无了。
后来啊,这个坐标系就不断发展,在数学、物理、工程学,甚至是游戏开发这些地方都超级有用。
咱们现在能玩那些超酷的3D游戏,里面人物的位置、物体的摆
放,都离不开笛卡尔坐标系这个超牛的发明呢。
所以说啊,有时候一个小小的想法,就像笛卡尔看到蜘蛛这个事儿,就能改变整个世界的面貌,是不是很神奇呢?。
为何说笛卡尔在蜘蛛结网中发现平面直角坐标系

为何说笛卡尔在蜘蛛结网中发现平面直角坐标系我们一起来看一则故事:笛卡尔与蜘蛛。
有一天,笛卡尔生病卧床,但他一直在反复思考一个问题:几何图形是直观的,而代数方程则比较抽象,能不能用几何图形来表示方程呢?同样几何图形可不可以通过代数形式来表达?这里,关键是如何把组成几何的图形的点和满足方程的每一组“数”挂上钩。
他就拼命琢磨。
通过什么样的办法、才能把“点”和“数”联系起来。
不经意间,他看见屋顶角上的一只蜘蛛,拉着丝垂了下来,一会儿,蜘蛛又顺着丝爬上去,在上边左右拉丝。
蜘蛛的“表演”,使笛卡尔思路豁然开朗。
他想,可以把蜘蛛看做一个点,它在屋子里可以上、下、左、右运动,能不能把蜘蛛的每个位置用一组数确定下来呢?他又想,屋子里相邻的两面墙与地面交出了三条线,如果把地面上的墙角作为起点,把交出来的三条线作为三根数轴,那么空间中任意一点的位置,不是都可以用这三根数轴上找到的有顺序的三个数来表示吗?反过来,任意给一组三个有顺序的数,例如3、2、1,也可以用空间中的一个点P来表示它们,如图1:同样,用一组数(a,b)可以表示平面上的一个点,平面上的一个点也可以用一组二个有顺序的数来表示,如图2:有人觉得在蜘蛛的启示下,笛卡尔创建了直角坐标系扯的有点远。
或许这则故事真实性有待查证,但笛卡尔确实创建坐标系。
直角坐标系的创建,在代数和几何上架起了一座桥梁。
它使几何概念得以用代数的方法来描述,几何图形可以通过代数形式来表达,这样便可将先进的代数方法应用于几何学的研究。
在参照系中,为确定空间一点的位置,按规定方法选取的有次序的一组数据,这就叫做“坐标”。
为了说明质点的位置、运动的快慢、方向等,必须选取其坐标系。
在某一问题中规定坐标的方法,就是该问题所用的坐标系。
坐标系的种类很多,常用的坐标系有:笛卡尔直角坐标系、平面极坐标系、柱面坐标系(或称柱坐标系)和球面坐标系(或称球坐标系)等。
在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称直角坐标系。
笛卡尔与蜘蛛网 平面直角坐标系

6.1.1 平面直角坐标系〇. 笛卡尔与蜘蛛网在蜘蛛网中,蜘蛛知道从中心向外第几圈,什么方向,就知道小虫位置. 怎样搜寻宇宙飞船安全着落的地点,GPS怎样搜索地理位置?一.位置的确定1. 地面上确定点的位置—经度、纬度、海拔高度在地图和地球仪上画有经线和纬线. 根据这些经纬线,可以准确地定出地面上任何一个地方的位置和方向. 如上海中心的位置是北纬31º14',东经121º29',如果确定一个人的位置,还要知道他所在位置的海拔高度.2. 生活中点的位置影剧院的票上的几排几座确定了唯一的座位. 围棋、国际象棋的棋子都用所在列与行(路)表示点的位置. 如下图围棋子A的位置记为:A(8,十二路).1.在如上图的围棋盘中,在点B(15,六路)上标出B;点C(6,十五路)是白子还是黑子:;点D(9,九路)呢:.2. 右上图是国际象棋的棋盘,当白棋在下方时,8条直线从白方左边到右边分别用字3. 如图,学校的示意图是全等的小正方形组成的,已知国旗杆在校门口正东100米处;实验楼在教学楼正南250处,那么教学楼在国旗杆处;从校门口先向走米,再向走米就到图书馆.4. 如图是八年级1班教室的座位平面图,已知同学A的座位是第2排第3列,用(2,3)表示,那么同学B的座位应该用表示.如果同学C的座位到A,B座位距离相等且最小,那么C的座位可以用表示.5. 如图是由5个半径分别为1,2,3,4,5的同心圆与6条夹角相等的直线构成的蜘蛛网.如果用(3,60º)表示A点,那么B点可以表示为,C点可以表示为.6. 在一次夏令营活动中,小芳从营地A 点出发,先沿北偏东70º方向走了600m 到达B 地,然后再沿北偏西20º方向走了2003m 达目的地C ,此时小芳在营地A 的 的方向上,距离A 点 m.7. 点 A 在B 北偏东60º距离2km 处,C 在A 北偏西60º距离4km 处,画出C 的位置并求B 与C 的距离(精确到0.1km).8. 一艺术团到各地巡回演出,第一天他们从出发地向东,第二天向北,第三天向西,第四天向南,第五天向东,第六天向北,第七天向西,第八天向南,第九天向东,…,如果他们第n 天行走22n km ,那么第40天结束时,他们离出发地的距离是 km.二. 平面直角坐标系平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系. 用来确定点的位置,观察有关数量的变化.特性 确定性,有序性,一一对应性.特殊点的坐标(1) 坐标轴上的点: (a,0)在x 轴上;(0,b)在y 轴上.(2) 分角线上的点: (a,a)在1、3象限分角线上;(b,-b)在2、4象限分角线上.(3) 对称点: P(a,b)有四个对称点(如图). 例 已知点A(a,-3)、B(4,b).若A在y轴上,B在第四象限分角线上,则a=,b=;若A、B关于x轴对称,则a=,b=;若AB平行于y轴,则a=,b.1. 有以下三个说法:①坐标的思想是法国数学家笛卡儿首先建立的;②除了平面直角坐标系外,我们也可以用方向和距离来确定物体的位置;③平面直角坐标系内的所有点都分别属于四个象限.其中错误的是().A.只有① B.只有② C.只有③ D.①②③2. 已知点P(a,2),点Q(3,b). 下列结论不正确的是().A. 若P,Q关于x轴对称,则a+b=1B. 若P,Q关于y轴对称,则a+b=-1C. 若P,Q关于原点对称,则a+b=-5D. 若P,Q关于直线y=x对称,则a+b=53. 在边长为1正方形网格中,△ABC如图所示. 在方格中建立坐标系,使点A为(1,4),点B为(-2,2),则C点坐标是;4. 如果ab<0,则P(a,b)在第象限;如果ab>0,a+b<0,那么P(a,b)在第象限. 如果点M(a,-b)在第二象限,那么点N(a+b,-ab)在第象限.5. 已知点A(6-5a,2a-1).若点A在第二象限,则a的取值范围是;点A 能否在第三象限,试说明理由:.6. 若P(a,b)关于x轴对称的点是Q,而Q点关于y轴对称的点是R(c,d),则a+b+c+d =.7. 根据条件求m的取值范围: (1) 若点P(m,2m-4)在第四象限,则. (2) 若P(3m-9,1-m)关于原点的对称点在第一象限,则.8. 根据下列条件求值:(1) 若点P(5-a,a-3)在第一、三象限角平分线上,则a的值是.(2) 已知两点A(-2,m),B(n,5). 若AB∥x轴,则m的值是,且n.(3) 已知点A(x,4-y)与点B(1-y,2x)关于y轴对称,则x,y的值分别是.三. 用坐标确定图形位置1. 建立平面直角坐标系建立的坐标系不同,得到的点的坐标也不同,要求简单.例已知等腰△ABC的底长BC=12,腰长10,适当建立坐标系,求A 、B ,C 的坐标.2. 确定图形位置的条件在平面直角坐标系中确定线段、角、三角形、四边形分别要2、3、3、4个点;确定正方形只要2个点(对称中心与一个顶点或对角线两个端点). 例 如图,正方形ABCD 对角线交点E 的坐标是(-2,1),顶点A 的坐标是(0,-2),则点B ,C ,D 的坐标依次是 .1. 如图,在平面直角坐标系中,点A 的坐标是(2,2),若点P 在x 轴上,且△APO 是等腰△,则点P 的坐标不可能是( ).A .(4,0)B .(1.0)C .(-22,0)D .(2,0)2. 等腰△OAB 在平面直角坐标系中,O 是坐标原点,点A 为(-1,1),点B 在x 轴上.则B 的横坐标可以是 .3. 等边△OAB 在平面直角坐标系中,O 是坐标原点,点A 为(-2,0),则点B 的坐标可以是 .4. 在平面直角坐标系中,矩形AOBC 的边AO 与x 轴构成120º,且AO =1,BO =3,则C 的坐标可以是 .5. 如图,所有正方形的中心均在坐标原点,且各边与x 轴或y 轴平行. 从内到外,它们的边长依次为2,4,6,8,…,顶点依次用 A 1,A 2,A 3,A 4,…表示,则顶点A 55的坐标是 .6. 已知正方形ABCD 在平面直角坐标系中,点A 坐标为(0,4),点B坐标为(-3,0),作图并求点C ,D 的坐标.7. 如图,已知A、C两点的坐标分别为(-2,0),C(0,-23),△ABC是底角为30º的等腰△,求出符合条件的点B的坐标.8. 在平面直角坐标系中,有一顶点在原点,长为4,宽为3的矩形OABC.当长边OA与x轴正方向构成30º角时(如图),求另三个顶点的坐标.。
笛卡尔曲线方程和图
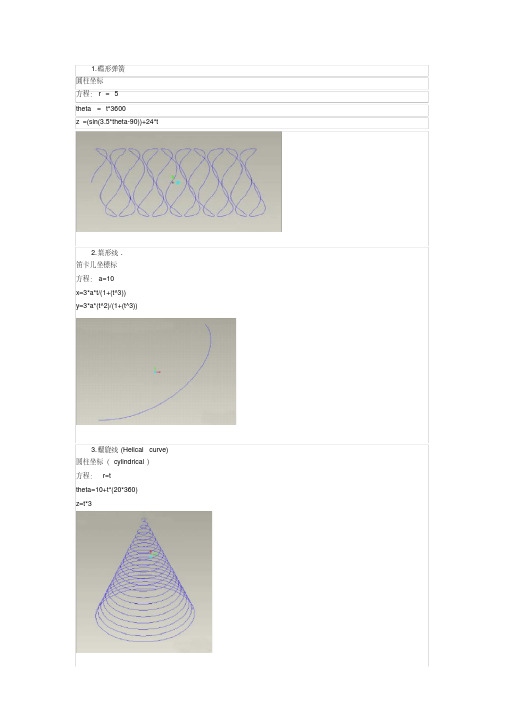
68. 篮子 圆柱坐标 r=5+0.3*sin(t*180)+t theta=t*360*30 z=t*5
45. 梅花曲线 柱坐标 theta = t*360 r=10+(3*sin(theta*2.5))^2
46. 另一个花曲线 theta = t*360 r=10-(3*sin(theta*3))^2 z=4*sin(theta*3)^2
47. 改一下就成为空间感更强的花曲线了 ;) theta = t*360 r=10-(3*sin(theta*3))^2 z=(r*sin(theta*3))^2
59. 环形二次曲线 笛卡儿方程:
x=50*cos(t*360) y=50*sin(t*360) z=10*cos(t*360*8)
60 蝶线 球坐标: rho=4*sin(t*360)+6*cos(t*360^2) theta=t*360 phi=log(1+t*360)*t*360
61. 正弦周弹簧 笛卡尔: ang1=t*360 ang2=t*360*20 x=ang1*2*pi/360 y=sin(ang1)*5+cos(ang2) z=sin(ang2)
11. 心脏线 圓柱坐标 方程: a=10 r=a*(1+cos(theta)) theta=t*360
12. 圆内螺旋线 采用柱座标系 方程: theta=t*360 r=10+10*sin(6*theta) z=2*sin(6*theta)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.1.1 平面直角坐标系
〇. 笛卡尔与蜘蛛网
在蜘蛛网中,蜘蛛知道从中心向外第几圈,什么方向,就知道小虫位置. 怎样搜寻宇宙飞船安全着落的地点,GPS怎样搜索地理位置?
一.位置的确定
1. 地面上确定点的位置—经度、纬度、海拔高度
在地图和地球仪上画有经线和纬线. 根据这些经纬线,可以准确地定出地面上任何一个地方的位置和方向. 如上海中心的位置是北纬31º14',东
经121º29',如果确定一个人的位置,还要知道他所在位置的海拔高度.
2. 生活中点的位置
影剧院的票上的几排几座确定了唯一的座位. 围棋、
国际象棋的棋子都用所在列与行(路)表示点的位置. 如
下图围棋子A的位置记为:A(8,十二路).
1.在如上图的围棋盘中,在点B(15,六路)上标出B;点C(6,十五路)是白子还是黑子:;点D(9,九路)呢:.
2. 右上图是国际象棋的棋盘,当白棋在下方时,8条直线从白方左边到右边分别用字
3. 如图,学校的示意图是全等的小正方形组成的,已知国旗杆在校
门口正东100米处;实验楼在教学楼正南250处,那么教学楼在国旗
杆处;从校门口先向走米,再向
走米就到图书馆.
4. 如图是八年级1班教室的座位平面图,已知同学A的座位是第
2排第3列,用(2,3)表示,那么同学B的座位应该用表示.
如果同学C的座位到A,B座位距离相等且最小,那么C的座位可
以用表示.
5. 如图是由5个半径分别为1,2,3,4,5的同心圆与6条夹角相
等的直线构成的蜘蛛网.如果用(3,60º)表示A点,那么B点可以表示
为,C点可以表示为.
6. 在一次夏令营活动中,小芳从营地A 点出发,先沿北偏东70º方
向走了600m 到达B 地,然后再沿北偏西20º方向走了2003m 达目的
地C ,此时小芳在营地A 的 的方向上,距离A 点 m.
7. 点 A 在B 北偏东60º距离2km 处,C 在A 北偏西60º距离4km 处,
画出C 的位置并求B 与C 的距离(精确到0.1km).
8. 一艺术团到各地巡回演出,第一天他们从出发地向东,第二天向
北,第三天向西,第四天向南,第五天向东,第六天向北,第七天向
西,第八天向南,第九天向东,…,如果他们第n 天行走2
2n km ,那么第40天结束时,他们离出发地的距离是 km.
二. 平面直角坐标系
平面上互相垂直且有公
共原点的两条数轴构成平
面直角坐标系. 用来确定
点的位置,观察有关数量的变化.
特性 确定性,有序性,一一对应性.
特殊点的坐标
(1) 坐标轴上的点: (a,0)在x 轴上;(0,b)在y 轴上.
(2) 分角线上的点: (a,a)在1、3象限分角线上;
(b,-b)在2、4象限分角线上.
(3) 对称点: P(a,b)有四个对称点(如图). 例 已知点A(a,-3)、B(4,b).
若A在y轴上,B在第四象限分角线上,则a=,b=;
若A、B关于x轴对称,则a=,b=;
若AB平行于y轴,则a=,b.
1. 有以下三个说法:①坐标的思想是法国数学家笛卡儿首先建立的;②除了平面直角坐标系外,我们也可以用方向和距离来确定物体的位置;③平面直角坐标系内的所有点都分别属于四个象限.其中错误的是().
A.只有① B.只有② C.只有③ D.①②③
2. 已知点P(a,2),点Q(3,b). 下列结论不正确的是().
A. 若P,Q关于x轴对称,则a+b=1
B. 若P,Q关于y轴对称,则a+b=-1
C. 若P,Q关于原点对称,则a+b=-5
D. 若P,Q关于直线y=x对称,则a+b=5
3. 在边长为1正方形网格中,△ABC如图所示. 在方格中建立坐标系,
使点A为(1,4),点B为(-2,2),则C点坐标是;
4. 如果ab<0,则P(a,b)在第象限;如果ab>0,a+b<0,那么P(a,b)在第
象限. 如果点M(a,-b)在第二象限,那么点N(a+b,-ab)在第象限.
5. 已知点A(6-5a,2a-1).若点A在第二象限,则a的取值范围是;点A 能否在第三象限,试说明理由:.
6. 若P(a,b)关于x轴对称的点是Q,而Q点关于y轴对称的点是R(c,d),则a+b+c+d =.
7. 根据条件求m的取值范围: (1) 若点P(m,2m-4)在第四象限,则. (2) 若P(3m-9,1-m)关于原点的对称点在第一象限,则.
8. 根据下列条件求值:
(1) 若点P(5-a,a-3)在第一、三象限角平分线上,则a的值是.
(2) 已知两点A(-2,m),B(n,5). 若AB∥x轴,则m的值是,且n.
(3) 已知点A(x,4-y)与点B(1-y,2x)关于y轴对称,则x,y的值分别是.
三. 用坐标确定图形位置
1. 建立平面直角坐标系
建立的坐标系不同,得到的点的坐标也不同,要求简单.
例已知等腰△ABC的底长BC=12,腰长10,适当建立
坐标系,求A 、B ,C 的坐标.
2. 确定图形位置的条件
在平面直角坐标系中确定线段、角、三角形、四边形分别要2、3、3、4个点;确定正方形只要2个点(对称中心与一个顶点或对角线两个端点).
例 如图,正方形ABCD 对角线交点E 的坐标是(-2,1),
顶点A 的坐标是(0,-2),则点B ,C ,D 的坐标依次
是 .
1. 如图,在平面直角坐标系中,点A 的坐标是(2,2),若点P 在x 轴上,
且△APO 是等腰△,则点P 的坐标不可能是( ).
A .(4,0)
B .(1.0)
C .(-22,0)
D .(2,0)
2. 等腰△OAB 在平面直角坐标系中,O 是坐标原点,点A 为(-1,1),点B 在x 轴上.则B 的横坐标可以是 .
3. 等边△OAB 在平面直角坐标系中,O 是坐标原点,点A 为(-2,0),则点B 的坐标可以是 .
4. 在平面直角坐标系中,矩形AOBC 的边AO 与x 轴构成120º,且AO =1,
BO =3,则C 的坐标可以是 .
5. 如图,所有正方形的中心均在坐标原点,且各边与x 轴或y 轴
平行. 从内到外,它们的边长依次为2,4,6,8,…,顶点依次用 A 1,
A 2,A 3,A 4,…表示,则顶点A 55的坐标是 .
6. 已知正方形ABCD 在平面直角坐标系中,点A 坐标为(0,4),点B
坐标为(-3,0),作图并求点C ,D 的坐标.
7. 如图,已知A、C两点的坐标分别为(-2,0),C(0,-23),△ABC
是底角为30º的等腰△,求出符合条件的点B的坐标.
8. 在平面直角坐标系中,有一顶点在原点,长为4,宽为3的矩
形OABC.当长边OA与x轴正方向构成30º角时(如图),求另三个
顶点的坐标.。
