人教版-数学-五年级上册-刘徽的“出入相补”原理 拓展资料
数学视野:经典算法割圆术

数学视野经典算法----割圆术根据刘徽的记载,在刘徽之前,人们求证圆面积公式时,是用圆内接正十二边形的面积来代替圆面积.应用出入相补原理,将圆内接正十二边形拼补成一个长方形,借用长方形的面积公式来论证《九章算术》的圆面积公式.刘徽指出,这个长方形是以圆内接正六边形周长的一半作为长,以圆半径作为高的长方形,它的面积是圆内接正十二边形的面积.这种论证“合径率一而弧周率三也”,即后来常说的“周三径一”,当然不严密.他认为,圆内接正多边形的面积与圆面积都有一个差,用有限次数的分割、拼补,是无法证明《九章算术》的圆面积公式的.因此刘徽大胆地将极限思想和无穷小分割引入了数学证明.他从圆内接正六边形开始割圆,“割之弥细,所失弥少,割之又割,以至不可割,则与圆周合体,而无所失矣.”也就是说将圆内接正多边形的边数不断加倍,则它们与圆面积的差就越来越小,而当边数不能再加的时候,圆内接正多边形的面积的极限就是圆面积.刘徽考察了内接多边形的面积,也就是它的“幂”,同时提出了“差幂”的概念.“差幂” 是后一次与前一次割圆的差值.刘徽指出,在用圆内接正多边形逼近圆面积的过程中,圆半径在正多边形与圆之间有一段余径.以余径乘正多边形的边长,即2倍的“差幂”,加到这个正多边形上,其面积则大于圆面积.这是圆面积的一个上界序列.刘徽认为,当圆内接正多边形与圆是合体的极限状态时,“则表无余径.表无余径,则幂不外出矣.”就是说,余径消失了,余径的长方形也就不存在了.因而,圆面积的这个上界序列的极限也是圆面积.于是内外两侧序列都趋向于同一数值,即,圆面积.利用圆内接或外切正多边形,求圆周率近似值的方法,其原理是当正多边形的边数增加时,它的边长和逐渐逼近圆周.早在公元前5世纪,古希腊学者安蒂丰为了研究化圆为方问题就设计一种方法:先作一个圆内接正四边形,以此为基础作一个圆内接正八边形,再逐次加倍其边数,得到正16边形、正32边形等等,直至正多边形的边长小到恰与它们各自所在的圆周部分重合,他认为就可以完成化圆为方问题.到公元前3世纪,古希腊科学家阿基米德在《论球和圆柱》一书中利用穷竭法建立起这样的命题:只要边数足够多,圆外切正多边形的面积与内接正多边形的面积之差可以任意小.阿基米德又在《圆的度量》一书中利用正多边形割圆的方法得到圆周率的值小于三又七分之一而大于三又七十分之十,还说圆面积与外切正方形面积之比为11:14,即取圆周率等于22/7.公元263年,中国数学家刘徽在《九章算术注》中提出“割圆”之说,他从圆内接正六边形开始,每次把边数加倍,直至圆内接正96边形,算得圆周率为3.14或157/50,后人称之为徽率.书中还记载了圆周率更精确的值3927/1250(等于3.1416).刘徽断言“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.其思想与古希腊穷竭法不谋而合.割圆术在圆周率计算史上曾长期使用.1610年德国数学家柯伦用2^62边形将圆周率计算到小数点后35位.1630年格林贝尔格利用改进的方法计算到小数点后39位,成为割圆术计算圆周率的最好结果.分析方法发明后逐渐取代了割圆术,但割圆术作为计算圆周率最早的科学方法一直为人们所称道.。
刘徽原理刘徽

刘徽原理刘徽刘徽(约公元225年—295年),汉族,山东邹平县人,魏晋期间伟大的数学家,中国古典数学理论的奠基者之一。
是中国数学史上一个非常伟大的数学家,他的杰作《九章算术注》和《海岛算经》,是中国最宝贵的数学遗产。
刘徽思想敏捷,方法灵活,既提倡推理又主张直观.他是中国最早明确主张用逻辑推理的方式来论证数学命题的人.刘徽的一生是为数学刻苦探求的一生.他虽然地位低下,但人格高尚.他不是沽名钓誉的庸人,而是学而不厌的伟人,他给我们中华民族留下了宝贵的财富。
刘徽是公元三世纪世界上最杰出的数学家,他在公元263年撰写的著作《九章算术注》以及后来的《海岛算经》,是我国最宝贵的数学遗产,从而奠定了他在中国数学史上的不朽地位。
刘徽的数学著作,留传后世的很少,所留均为久经辗转传抄之作。
他的主要著作有:《九章算术注》10卷;《重差》1卷,至唐代易名为《海岛算经》;《九章重差图》l卷。
可惜后两种都在宋代失传。
《九章算术》约成书于东汉之初,共有246个问题的解法。
在许多方面:如解联立方程,分数四则运算,正负数运算,几何图形的体积面积计算等,都属于世界先进之列。
但因解法比较原始,缺乏必要的证明,刘徽则对此均作了补充证明。
在这些证明中,显示了他在众多方面的创造性贡献。
他是世界上最早提出十进小数概念的人,并用十进小数来表示无理数的立方根。
在代数方面,他正确地提出了正负数的概念及其加减运算的法则,改进了线性方程组的解法。
在几何方面,提出了"割圆术",即将圆周用内接或外切正多边形穷竭的一种求圆面积和圆周长的方法。
他利用割圆术科学地求出了圆周率π=3.1416的结果。
他用割圆术,从直径为2尺的圆内接正六边形开始割圆,依次得正12边形、正24边形……,割得越细,正多边形面积和圆面积之差越小,用他的原话说是“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣。
”他计算了3072边形面积并验证了这个值。
刘徽的“出入相补”原理

刘徽的“出入相补”原理
在“九章算术注”中,刘徽发展了中国古代“率”的思想和“出入相补”原理。
用“率”统一证明“九章算术”的大部分算法和大多数题目,用“出入相补”原理证明了勾股定理以及一些求面积和求体积的公式。
刘徽的工作,不仅对中国古代数学发展产生了深远影响,而且在世界数学史上也确立了崇高的历史地位。
鉴于刘徽的巨大贡献,不少书上把他称作“中国数学史上的牛顿”。
所谓出入相补原理,简单地说,就是指:一个平面图形从一处移至他处,面积不变,假如把图形分割成若干块,那么各部分面积的和等于原来图形的面积,因而图形转移前后各部分面积的和、差有简单的相等关系。
立体的情形也是这样。
举几个简单的例子,如图:。
勾股定理的证明和出入相补原理(最全)word资料

勾股定理的证明和出入相补原理(最全)word资料勾股定理的证明和出入相补原理出入相补原理是我国著名数学家吴文俊先生提出的,他认为这个原理“就是指这样的明显事实:一个平面图形从一处移到他处,面积不变.又若把图形分割成若干块,那么各部分面积的和等于原来图形的面积,因而图形移置前后诸面积间的和、差有简单的相等关系.立体的情形也是如此”.我们教材中介绍的勾股定理的证明就用到了出入相补原理.下面我们再介绍刘徽的一种证明勾股定理的方法:如下图,正方形ABCD、BFGI的边长分别为b、a,在BF上取一点E,使AE=a连结DE、GE,将△ADE移至△CDH,将△EFG 移至△HIG,由此就可以证明勾股定理,你试一试吧!20中学数学教学2020 年第1期勾股定理证明的探讨与教学思考安徽省合肥市第四十五中学李光武孔云( :230001勾股定理的证明方法有很多种,目前教材给出的几种证明方法是面积法.如下图所示:①利用若干个全等的直角=三角形和一个小正方形,拼成一个大正方形(图1是邹元治的证明拼图法、图2是赵爽的证明拼图法;②利用两个全等的直角三角形和一个等腰直角三角形,拼成一个直角梯形(图3是1876年总统Garfield的证明拼图法.教材选用这几种证明方法,都是利用几个简单的直角三角形和一个正方形或等腰直角三角形,拼成一个学生比较熟悉,而且它们的面积也是很容易求解的一种几何图形.够珞图1图2图3然后,教材给出学生比较熟悉的证明方法——面积法,即先算出整个图形的面积,再算出各个部分的图形面积,利用图形分割前后的面积相等,构成一个等式,最后经过整式的化简、整理o,c9c’o'070?o_c'coc,t70’o’o’o’o,o’_。
,o’e'c.,e_,o’o’o’o,o’o_,070’o’o’o't,c'o,o,o’讳,,3,07.。
,亡oo,,—>7龇一5一[(学钿+(学2”] [(学2州+(学2州]一(学4州+[(学(学卜学+[(学(学卜学+(学4州一5一(1+√54计1+(1一√54井1. ————■歹r——~¨...L2,lL2什2一L2。
人教版小学五年级上册数学第6单元多边形的面积第3课时梯形的面积拓展资料刘徽的“出入相补”原理
刘徽的“出入相补”原理
在“九章算术注”中,刘徽发展了中国古代“率”的思想和“出入相补”原理。
用“率”统一证明“九章算术”的大部分算法和大多数题目,用“出入相补”原理证明了勾股定理以及一些求面积和求体积的公式。
刘徽的工作,不仅对中国古代数学发展产生了深远影响,而且在世界数学史上也确立了崇高的历史地位。
鉴于刘徽的巨大贡献,不少书上把他称作“中国数学史上的牛顿”。
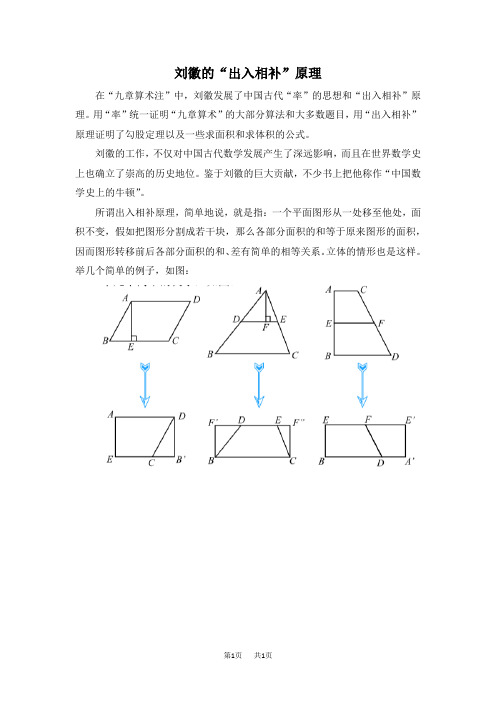
所谓出入相补原理,简单地说,就是指:一个平面图形从一处移至他处,面积不变,假如把图形分割成若干块,那么各部分面积的和等于原来图形的面积,因而图形转移前后各部分面积的和、差有简单的相等关系。
立体的情形也是这样。
举几个简单的例子,如图:
第1页共1页。
刘徽的“出入相补”原理

刘徽的“出入相补”原理
一、出入相补原理是刘徽提出来的
出入相补原理是刘徽提出来的从象棋思想,以及他在《新象棋考》中
阐述的一种战略思想,主要是针对当时局面解决问题的一种思维方法,也
可以说是他当时的棋术观念。
这里所说的出入相补,指的是出兵和撤军之
间的关系。
二、刘徽的出入相补原理是什么
刘徽的出入相补原理指的是,当一个军队出兵时,应该考虑同时准备
好计划撤军,而此时兵力应该整合,利用兵力调动的变化,将占领的地方
重新变得强大,从而使得整个军队能够通过撤军的方式实现赢得胜利的目的。
说白了,就是把原本在外面的兵力调动,重新调整到内部,反过来加
强内部的势力,从而让整个军队赢得胜利。
三、古代象棋思想
古代象棋思想是一种具有深厚文化内涵的游戏,它代表了当时的文化
价值观、政治观念和思想观念,是道家传统的文化和原则的体现。
在古代,以棋为代表的有节制的思想被大量传播,而其中讲究人文关怀的棋艺思想
是极富价值的。
四、刘徽的出入相补原理对象棋术的意义
刘徽的出入相补原理对象棋术的意义非常深远,它不仅融合了道家哲
学思想,而且具有非常高的价值取向,它将人性上的智慧、信念和勇气融
入到棋的实践和发展中去。
刘徽出入相补原理三角形面积公式的推导

刘徽出入相补原理三角形面积公式的推导刘徽是中国古代数学家,他在《九章算术》中提出了出色的相补原理,其中包括了三角形面积公式的推导。
以下是关于刘徽出入相补原理的推导的详细解释。
首先,让我们考虑一个任意的三角形ABC,三边分别为a、b和c。
我们将这个三角形分成三个小三角形-三角形ABC、三角形ADC和三角形BDC。
根据刘徽出入相补原理,我们可以得到以下公式:S_ABC=S_ADC+S_BDC其中,S_ABC表示大三角形ABC的面积,S_ADC表示三角形ADC的面积,S_BDC表示三角形BDC的面积。
根据几何知识,我们可以得到以下两个等式:S_ABC=(1/2)某a某h_aS_ADC=(1/2)某b某h_bS_BDC=(1/2)某c某h_c其中,h_a、h_b和h_c分别表示从顶点A、B和C到对边BC、AC和AB的高度。
现在,我们来看一下如何计算这些高度。
对于h_a,我们可以使用海伦公式来计算。
根据海伦公式,我们可以得到三角形ABC的半周长s为:s=(a+b+c)/2然后,根据海伦公式,我们可以计算三角形ABC的面积S_ABC:S_ABC=√(s某(s-a)某(s-b)某(s-c))接下来,我们来计算高度h_a。
根据几何知识,我们可以使用S_ABC 和对应边的长度计算高度h_a:h_a=(2某S_ABC)/a同样地,我们可以得到h_b和h_c:h_b=(2某S_ABC)/bh_c=(2某S_ABC)/c将以上结果代入到最初的公式中,我们可以得到:S_ADC=(1/2)某b某[(2某S_ABC)/a]S_BDC=(1/2)某c某[(2某S_ABC)/a]简化后可以得到:S_ADC=(S_ABC某b)/aS_BDC=(S_ABC某c)/a最后,将这两个公式代入到刘徽出入相补原理的公式中,我们可以得到:S_ABC=[(S_ABC某b)/a]+[(S_ABC某c)/a]S_ABC=S_ABC某(b+c)/a将S_ABC移到等式的左边,我们可以得到:S_ABC某(1-(b+c)/a)=0由于三角形ABC是一个实际存在的三角形,所以它的面积S_ABC不可能为0。
五年级数学上册拓展. 出入相补法-割补法求图形面积

平行四边形的面积= 底
×高=== Nhomakorabea梯形的面积(= 上底+下底) ×(高÷2)
=
=
=
长方形的面积= 长 × 宽
梯形的面积(= 上底+下底) ×(高÷2)
梯形的面积=(上底+下底)×高➗2
出入相补原理
出入相补原理就 是把一个图形分割、移 补,而面积保持不变, 来计算它的面积。
世界十大数学家之 一、被称作“中国 数学史上的牛顿” 的山东人刘徽
割补法 倍拼法 倍拼法
用割补法把三角形转化成长方形或平行四边形,试一试。
= =
=
= = =
长方形的面积 = 长 × 宽 平行四边形的面积 = 底 × 高
三角形的面积 = 底 ×(高÷2) 三角形的 面积 = 底 ×(高÷2)
倍拼法
割补法
三角形的面积=底×高÷2
三角形的面积=底×(高÷2)
三角形的面积=底×高÷2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学-数学-打印版
小学-数学-打印版 1 刘徽的“出入相补”原理
在“九章算术注”中,刘徽发展了中国古代“率”的思想和“出入相补”原理。
用“率”统一证明“九章算术”的大部分算法和大多数题目,用“出入相补”原理证明了勾股定理以及一些求面积和求体积的公式。
刘徽的工作,不仅对中国古代数学发展产生了深远影响,而且在世界数学史上也确立了崇高的历史地位。
鉴于刘徽的巨大贡献,不少书上把他称作“中国数学史上的牛顿”。
所谓出入相补原理,简单地说,就是指:一个平面图形从一处移至他处,面积不变,假如把图形分割成若干块,那么各部分面积的和等于原来图形的面积,因而图形转移前后各部分面积的和、差有简单的相等关系。
立体的情形也是这样。
举几个简单的例子,如图:。
