2012高考一轮复习——四川省各地市11年试题分类大汇编第5部分三角函数
2012年全国各省市高考题(三角函数)

2012高考试题分类汇编:三角函数1.【2012新课标文9】已知ω>0,πϕ<<0,直线4π=x 和45π=x 是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴,则φ=( )(A )π4 (B )π3 (C )π2 (D )3π42.【2012山东文8】函数2sin (09)63x y x ππ⎛⎫=-≤≤ ⎪⎝⎭的最大值与最小值之和为( )(A)2 (B)0 (C)-1(D)1-3.【2012浙江文6】把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是()4.【2012四川文5】如图,正方形ABCD 的边长为1,延长BA 至E ,使1AE =,连接EC 、ED 则sin CED ∠=( )A、B 、CD5.【2012辽宁文6】已知sin cos αα-=,α∈(0,π)则sin 2α=( )(A) -1 (B)(D) 17.【2012江西文9】已知2()sin ()4f x x π=+若a =f (lg5),1(lg )5b f =则( ) A.a+b=0 B.a-b=0 C.a+b=1 D.a-b=18.【2012湖北文8】△ABC 中,若三边的长为连续的三个正整数,且A >B >C ,3b=20acosA ,则sinA ∶sinB ∶sinC 为( )A.4∶3∶2B.5∶6∶7C.5∶4∶3D.6∶5∶49.【2012天津文科7】将函数f(x)=sin x ω(其中ω>0)的图像向右平移4π个单位长度,所得图像经过点(34π,0),则ω的最小值是( )(A )13(B )1 C )53(D )210.【2012陕西13】在三角形ABC 中,若a=2 ,B=6π,b= .11.【2012重庆13】△ABC 中,且1cos 4a b C ==1,=2,,则sin B =12.【2012江苏11】设α为锐角,若4cos 65απ⎛⎫+= ⎪⎝⎭,则)122sin(π+a 的值为 .13.【2012全国15】当函数sin (02)y x x x π=≤<取得最大值时,x =______14.【2012浙江18】在△ABC 中,。
2012年高考真题理科数学解析分类汇编5三角函数

2012年高考真题理科数学解析分类汇编5 三角函数 一、选择题1.【2012高考重庆理5】设tan ,tan αβ是方程2320x x -+=的两个根,则tan()αβ+的值为(A )-3 (B )-1 (C )1 (D )3 【答案】A【解析】因为βαt an ,t an 是方程2320x x -+=的两个根,所以3t an t an=+βα,2tan tan =βα,所以3213tan tan 1tan tan )tan(-=-=-+=+βαβαβα,选A.2.【2012高考浙江理4】把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是【答案】A【解析】把函数y =cos2x +1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)得:y 1=cos x +1,向左平移1个单位长度得:y 2=cos(x +1)+1,再向下平移1个单位长度得:y 3=cos(x+1).令x =0,得:y 3>0;x =12-π,得:y 3=0;观察即得答案. 3.【2012高考新课标理9】已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减.则ω的取值范围是( )()A 15[,]24 ()B 13[,]24()C 1(0,]2 ()D (0,2]【答案】A【解析】法1:函数)4sin()(πω+=x x f 的导数为)4cos()('πωω+=x x f ,要使函数)4sin()(πω+=x x f 在),2(ππ上单调递减,则有0)4cos()('≤+=πωωx x f 恒成立,则πππωππk x k 223422+≤+≤+,即ππωππk x k 24524+≤≤+,所以Z k k x k ∈+≤≤+,ωπωπωπωπ2424,当0=k 时,ωπωπ454≤≤x ,又ππ<<x 2,所以有πωππωπ≥≤45,24,解得45,21≤≥ωω,即4521≤≤ω,选A. 法2:选A592()[,]444x πππωω=⇒+∈ 不合题意 排除()D351()[,]444x πππωω=⇒+∈ 合题意 排除()()B C另:()22πωππω-≤⇔≤,3()[,][,]424422x ππππππωωπω+∈++⊂ 得:315,2424224πππππωπωω+≥+≤⇔≤≤ 4.【2012高考四川理4】如图,正方形ABCD 的边长为1,延长BA 至E ,使1AE =,连接EC 、ED 则sin CED ∠=( )A BC 、10 D 、15【答案】B【解析】2EB EA AB =+=,EC =3424EDC EDA ADC πππ∠=∠+∠=+=,由正弦定理得sinsin 5CED DC EDC CE ∠===∠,所以3sin sin sin 55410CED EDC π∠=∠==[点评]注意恒等式sin 2α+cos 2α=1的使用,需要用α的的范围决定其正余弦值的正负情况.5.【2012高考陕西理9】在ABC ∆中,角,,A B C 所对边长分别为,,a b c ,若2222a b c +=,则cos C 的最小值为( )A.B. 2C. 12D. 12-【答案】C.【解析】由余弦定理知214242)(212cos 222222222=≥+=+-+=-+=ab ab ab b a ab b a b a ab c b a C ,故选C.6.【2012高考山东理7】若42ππθ⎡⎤∈⎢⎥⎣⎦,,sin 2=8θ,则sin θ=(A )35 (B )45 (C(D )34 【答案】D【解析】法1:因为]2,4[ππθ∈,所以],2[2ππθ∈,02cos <θ,所以812sin 12cos 2-=--=θθ,又81s i n 212c o s 2-=-=θθ,所以169sin 2=θ,43sin =θ,选D.法2:由42ππθ⎡⎤∈⎢⎥⎣⎦,及sin 2θ可得434716776916761687312sin 1cos sin +=++=+=+=+=+θθθ, 而当42ππθ⎡⎤∈⎢⎥⎣⎦,时θθcos sin >,结合选项即可得47cos ,43sin ==θθ.答案应选D 。
三角函数讲义(适用于高三第一轮复习)

三角函数1.同角三角函数的基本关系式:1cos sin 22=+αα αααtan cos sin = 2.诱导公式 (奇变偶不变,符号看象限)ααπsin )sin(-=+ ααπcos )cos(-=+ ααπtan )tan(=+ ααπsin )sin(=- ααπcos )cos(-=- ααπtan )tan(-=-ααπcos )2sin(=+ ααπsin )2cos(-=+ ααπcos )2sin(=-ααπsin )2cos(=- ααsin )sin(-=- ααcos )cos(=- 3.两角和与差的公式βαβαβαsin cos cos sin )sin(+=+ βαβαβαsin cos cos sin )sin(-=- βαβαβαsin sin cos cos )cos(-=+ βαβαβαsin sin cos cos )cos(+=-βαβαβαtan tan 1tan tan )tan(-+=+ βαβαβαtan tan 1tan tan )tan(+-=-4.倍角公式 αααcos sin 22sin = 1cos 2sin 21sin cos 2cos 2222-=-=-=αααααααα2tan 1tan 22tan -=5.降幂公式 22cos 1sin 2αα-= 22cos 1cos 2αα+= ααα2sin 21cos sin =6.幅角公式 x b x a ωωcos sin +)sin(22ϕω++=x b a ,其中ab=ϕtan8.补充公式 ααααα2sin 1cos sin 21)cos (sin 2±=±=±, 2cos2sinsin 1ααα±=±知识点睛一.三角函数的图象与性质图象]1,1[-]1,1[-最值 当且仅当22ππ+=k x 时取到最大值1;当且仅当22ππ-=k x 时取到最小值1-当且仅当πk x 2=时取到最大值1;当且仅当ππ-=k x 2时取到最小值1-周期 最小正周期为π2最小正周期为π2奇偶性 奇函数偶函数单调性在]22,22[ππππ+-k k 上单调增; 在]232,22[ππππ++k k 上单调减在]2,2[πππk k -上单调增; 在]2,2[πππ+k k 上单调减 对称轴2ππ+=k x ;对称中心)0,(πk对称轴πk x =;对称中心)0,2(ππ+k说明:表格中的k 都是属于Z ,在选择“代表”的区间或点时,先尽量选择离坐标原点近的,再尽量选择正的。
2012年高考真题理科数学解析汇编:三角函数

2012年高考真题理科数学解析汇编:三角函数一、选择题1 .(2012年高考(天津理))在ABC ∆中,内角A ,B ,C 所对的边分别是,,a b c ,已知8=5b c ,=2C B ,则cos C =( )A .725B .725-C .725±D .24252 .(2012年高考(天津理))设R ϕ∈,则“=0ϕ”是“()=cos(+)f x x ϕ()x R ∈为偶函数”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件3 .(2012年高考(新课标理))已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减.则ω的取值范围是 ( )A .15[,]24B .13[,]24C .1(0,]2D .(0,2]4 .(2012年高考(浙江理))把函数y =cos2x +1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图像是5 .(2012年高考(重庆理))设tan ,tan αβ是方程2320x x -+=的两个根,则tan()αβ+的值为( )A .3-B .1-C .1D .36 .(2012年高考(上海理))在ABC ∆中,若C B A 222sin sin sin <+,则ABC ∆的形状是( )A .锐角三角形.B .直角三角形.C .钝角三角形.D .不能确定.7 .(2012年高考(陕西理))在ABC ∆中,角,,A B C 所对边长分别为,,a b c ,若2222a b c +=,则cos C 的最小值为( )A.2B.2C .12D .12-8 .(2012年高考(山东理))若42ππθ⎡⎤∈⎢⎥⎣⎦,,sin 2θ,则sin θ= ( )A .35B .45 CD .349 .(2012年高考(辽宁理))已知sin cos αα-=,α∈(0,π),则tan α=( )A .-1 B.2-C.2D .110.(2012年高考(江西理))若tan θ+1tan θ=4,则sin2θ= ( )A .15B .14C .13D .1211.(2012年高考(湖南理))函数f(x)=sinx-cos(x+6π)的值域为 ( )A .[ -2 ,2]B .C .[-1,1 ]D .[-2, 2] 12.(2012年高考(大纲理))已知α为第二象限角,sin cos 3αα+=,则cos 2α= ( )A.B.CD二、填空题13.(2012年高考(重庆理))设ABC ∆的内角,,A B C 的对边分别为,,a b c ,且35cos ,cos ,3,513A B b ===则c =______14.(2012年高考(上海春))函数()sin(2)4f x x π=+的最小正周期为_______.15.( 2012年高考(江苏))设α为锐角,若4cos 65απ⎛⎫+= ⎪⎝⎭,则)122sin(π+a 的值为____. 16.(2012年高考(湖南理))函数f(x)=sin (x ωϕ+)的导函数()y f x '=的部分图像如图4所示,其中,P 为图像与y轴的交点,A,C 为图像与x 轴的两个交点,B 为图像的最低点.(1)若6πϕ=,点P 的坐标为则ω=______ ; (2)若在曲线段 ABC 与x 轴所围成的区域内随机取一点,则该点在△ABC 内的概率为_______.17.(2012年高考(湖北理))设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c . 若()()a b c a b c ab +-++=,则角C =_________.18.(2012年高考(福建理))已知ABC ∆,则其最大角的余弦值为_________.19.(2012年高考(大纲理))当函数s i n c o s (02)y x x x π=≤<取得最大值时,x =_______________.20.(2012年高考(北京理))在△ABC 中,若2a =,7b c +=,1cos 4B =-,则b =___________. 21.(2012年高考(安徽理))设ABC ∆的内角,,A B C 所对的边为,,a b c ;则下列命题正确的是_____①若2ab c >;则3C π<②若2a b c +>;则3C π<③若333a b c +=;则2C π<④若()2a b c ab +<;则2C π>⑤若22222()2a b c a b +<;则3C π>三、解答题22.(2012年高考(天津理))已知函数2()=sin (2+)+sin(2)+2cos 133f x x x x ππ--,x R ∈.(Ⅰ)求函数()f x 的最小正周期; (Ⅱ)求函数()f x 在区间[,]44ππ-上的最大值和最小值.23.(2012年高考(浙江理))在∆ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A =23,sin B C .(Ⅰ)求tan C 的值;(Ⅱ)若a 求∆ABC 的面积.24.(2012年高考(重庆理))(本小题满分13分(Ⅰ)小问8分(Ⅱ)小问5分)设()4cos()sin cos(2)6f x x x x πωωωπ=--+,其中.0>ω(Ⅰ)求函数()y f x = 的值域 (Ⅱ)若()f x 在区间3,22ππ⎡⎤-⎢⎥⎣⎦上为增函数,求 ω的最大值.25.(2012年高考(四川理))函数2()6cos3(0)2xf x x ωωω=->在一个周期内的图象如图所示,A 为图象的最高点,B 、C 为图象与x 轴的交点,且ABC ∆为正三角形. (Ⅰ)求ω的值及函数()f x 的值域;(Ⅱ)若0()f x =,且0102(,)33x ∈-,求0(1)f x +的值.26.(2012年高考(上海理))海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为y 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰在失事船的正南方向12海里A 处,如图. 现假设:①失事船的移动路径可视为抛物线24912x y =;②定位后救援船即刻沿直线匀速前往救援;③救 援船出发t 小时后,失事船所在位置的横坐标为t 7.(1)当5.0=t 时,写出失事船所在位置P 的纵坐标. 若此时 两船恰好会合,求救援船速度的大小和方向;(2)问救援船的时速至少是多少海里才能追上失事船?27.(2012年高考(陕西理))函数()sin()16f x A x πω=-+(0,0A ω>>)的最大值为3, 其图像相邻两条对称轴之间的距离为2π, (1)求函数()f x 的解析式; (2)设(0,)2πα∈,则()22f α=,求α的值.28.(2012年高考(山东理))已知向量(sin ,1),cos ,cos 2)(0)3Am x n x x A ==> ,函数()f x m n =⋅的最大值为6.(Ⅰ)求A ;(Ⅱ)将函数()y f x =的图象向左平移12π个单位,再将所得图象上各点的横坐标缩短为原来的12倍,纵坐标不变,得到函数()y g x =的图象.求()g x 在5[0,]24π上的值域.29.(2012年高考(辽宁理))在ABC ∆中,角A 、B 、C 的对边分别为a ,b ,c .角A ,B ,C 成等差数列.(Ⅰ)求cos B 的值;(Ⅱ)边a ,b ,c 成等比数列,求sin sin A C 的值.30.(2012年高考(江西理))在△ABC 中,角A,B,C 的对边分别为a,b,c.已知,,sin()sin()444A b C cB a πππ=+-+=.(1)求证:2B C π-=(2)若,求△ABC 的面积.31.(2012年高考(江苏))在ABC ∆中,已知3AB AC BA BC =.(1)求证:tan 3tan B A =;(2)若cos C =求A 的值.32.(2012年高考(湖北理))已知向量(c o s s x x x ωωω=-a ,(cos sin ,)x x x ωωω=--b ,设函数()f x λ=⋅+a b ()x ∈R 的图象关于直线πx =对称,其中ω,λ为常数,且1(,1)2ω∈.(Ⅰ)求函数()f x 的最小正周期;(Ⅱ)若()y f x =的图象经过点π(,0)4,求函数()f x 在区间3π[0,]5上的取值范围.33.(2012年高考(广东理))(三角函数)已知函数()2cos 6f x x πω⎛⎫=+⎪⎝⎭(其中0ω>x ∈R )的最小正周期为10π. (Ⅰ)求ω的值;(Ⅱ)设α、0,2πβ⎡⎤∈⎢⎥⎣⎦,56535f απ⎛⎫+=- ⎪⎝⎭,5165617f βπ⎛⎫-= ⎪⎝⎭,求()cos αβ+的值.34.(2012年高考(福建理))某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.(1)2sin 13cos17sin13cos17︒+︒-︒︒ (2)2sin 15cos15sin15cos15︒+︒-︒︒ (3)2sin 18cos12sin18cos12︒+︒-︒︒ (4)2sin (18)cos48sin(18)cos48-︒+︒--︒︒ (5)2sin (25)cos55sin(25)cos55-︒+︒--︒︒Ⅰ 试从上述五个式子中选择一个,求出这个常数Ⅱ 根据(Ⅰ)的计算结果,将该同学的发现推广三角恒等式,并证明你的结论.35.(2012年高考(大纲理))(注意..:.在试卷上作答无效........) ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ,已知cos()cos 1,2A C B a c -+==,求C .36.(2012年高考(北京理))已知函数(sin cos )sin 2()sin x x xf x x-=.(1)求()f x 的定义域及最小正周期; (2)求()f x 的单调递增区间.37.(2012年高考(安徽理))设函数2())sin 24f x x x π=++ (I)求函数()f x 的最小正周期;(II)设函数()g x 对任意x R ∈,有()()2g x g x π+=,且当[0,]2x π∈时, 1()()2g x f x =-,求函数()g x 在[,0]π-上的解析式.2012年高考真题理科数学解析汇编:三角函数参考答案一、选择题 1. 【答案】A【命题意图】本试题主要考查了正弦定理、三角函数中的二倍角公式. 考查学生分析、转化与计算等能力. 【解析】∵8=5b c ,由正弦定理得8sin =5sin B C ,又∵=2C B ,∴8sin =5sin 2B B ,所以8sin =10sin cos B B B ,易知sin 0B ≠,∴4cos =5B ,2cos =cos 2=2cos 1C B B -=725.2. 【答案】A【命题意图】本试题主要考查了三角函数的奇偶性的判定以及充分条件与必要条件的判定.【解析】∵=0ϕ⇒()=cos(+)f x x ϕ()x R ∈为偶函数,反之不成立,∴“=0ϕ”是“()=cos(+)f x x ϕ()x R ∈为偶函数”的充分而不必要条件.3. 【解析】选A592()[,]444x πππωω=⇒+∈ 不合题意 排除()D351()[,]444x πππωω=⇒+∈ 合题意 排除()()B C另:()22πωππω-≤⇔≤,3()[,][,]424422x ππππππωωπω+∈++⊂ 得:315,2424224πππππωπωω+≥+≤⇔≤≤4. 【答案】A【解析】把函数y =cos2x +1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)得:y 1=cos x +1,向左平移1个单位长度得:y 2=cos(x +1)+1,再向下平移1个单位长度得:y 3=cos(x +1).令x =0,得:y 3>0;x =12π-,得:y 3=0;观察即得答案.5. 【答案】A【解析】tan tan 3tan tan 3,tan tan 2tan()31tan tan 12αβαβαβαβαβ++==⇒+===-+-【考点定位】此题考查学生灵活运用韦达定理及两角和的正切公式化简求值.6. [解析] 由条件结合正弦定理,得222c b a <+,再由余弦定理,得0cos 2222<=-+abc b a C ,所以C 是钝角,选C.7. 解析:由余弦定理得,222221cos 242a b c a b C ab ab +-+==≥当且仅当a b =时取“=”,选C.8. 【解析】因为]2,4[ππθ∈,所以],2[2ππθ∈,02cos <θ,所以812s i n 12c o s 2-=--=θθ,又81sin 212cos 2-=-=θθ,所以169sin 2=θ,43sin =θ,选D. 9. 【答案】A【解析一】sin cos )sin()144ππαααα-=-=-=3(0),,tan 14παπαα∈∴=∴=- ,,故选A 【解析二】2sin cos (sin cos )2,sin 21,ααααα--=∴=-33(0,),2(0,2),2,,tan 124ππαπαπααα∈∴∈∴=∴=∴=- ,故选A 【点评】本题主要考查三角函数中的和差公式、倍角公式、三角函数的性质以及转化思想和运算求解能力,难度适中.10. D 【解析】本题考查三角恒等变形式以及转化与化归的数学思想.因为221sin cos sin cos 1tan 41tan cos sin sin cos sin 22θθθθθθθθθθθ++=+===,所以.1sin 22θ=. 【点评】本题需求解正弦值,显然必须切化弦,因此需利用公式sin tan cos θθθ=转化;另外,22sin cos θθ+在转化过程中常与“1”互相代换,从而达到化简的目的;关于正弦、余弦的齐次分式,常将正弦、余弦转化为正切,即弦化切,达到求解正切值的目的. 体现考纲中要求理解三角函数的基本关系式,二倍角公式.来年需要注意二倍角公式的正用,逆用等.11.【答案】B【解析】f(x)=sinx-cos(x+6π)1sin sin )26x x x x π=+=-,[]sin()1,16xπ-∈- ,()f x ∴值域为【点评】利用三角恒等变换把()f x 化成sin()A x ωϕ+的形式,利用[]sin()1,1x ωϕ+∈-,求得()f x 的值域.12. 答案A【命题意图】本试题主要考查了三角函数中两角和差的公式以及二倍角公式的运用.首先利用平方法得到二倍角的正弦值,然后然后利用二倍角的余弦公式,将所求的转化为单角的正弦值和余弦值的问题.【解析】sin cos 3αα+=,两边平方可得121sin 2sin 233αα+=⇒=-α 是第二象限角,因此sin 0,cos 0αα><,所以cos sin αα-===22cos 2cos sin (cos sin )(cos sin )ααααααα∴=-=+-=法二:单位圆中函数线+估算,因为α是第二象限的角,又1sin cos 2αα+所以“正弦线”要比“余弦线”长一半多点,如图,故2cos α的“余弦线”应选A .二、填空题 13. 【答案】145c =【解析】由35412cos ,cos sin ,sin 513513A B A B ==⇒==,由正弦定理sin sin a b A B=得43sin 13512sin 513b A a B ⨯===,由余弦定理2222142cos 25905605a cb bc A c c c =+-⇒-+=⇒=【考点定位】利用同角三角函数间的基本关系求出sin B 的值是本题的突破点,然后利用正弦定理建立已知和未知之间的关系,同时要求学生牢记特殊角的三角函数值. 14. π15.【考点】同角三角函数,倍角三角函数,和角三角函数. 【解析】∵α为锐角,即02<<πα,∴2=66263<<πππππα++. ∵4cos 65απ⎛⎫+=⎪⎝⎭,∴3sin 65απ⎛⎫+=⎪⎝⎭.∴3424sin 22sin cos =2=3665525αααπππ⎛⎫⎛⎫⎛⎫+=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ .∴7cos 2325απ⎛⎫+= ⎪⎝⎭.∴sin(2)=sin(2)=sin 2cos cos 2sin 12343434a a a a πππππππ⎛⎫⎛⎫++-+-+ ⎪ ⎪⎝⎭⎝⎭247=2525- 16. 【答案】(1)3;(2)4π 【解析】(1)()y f x '=cos()x ωωϕ=+,当6πϕ=,点P 的坐标为时cos36πωω=∴=; (2)由图知222T AC ππωω===,122ABC S AC πω=⋅= ,设,A B 的横坐标分别为,a b .设曲线段ABC 与x 轴所围成的区域的面积为S则()()sin()sin()2bbaaS f x dx f x a b ωϕωϕ'===+-+=⎰,由几何概型知该点在△ABC内的概率为224ABC S P S ππ=== . 【点评】本题考查三角函数的图像与性质、几何概型等,(1)利用点P 在图像上求ω,(2)几何概型,求出三角形面积及曲边形面积,代入公式即得. 17.考点分析:考察余弦定理的运用.解析:由222()()a b c a b c ab a b c ab +-+-=⇒+-=-根据余弦定理可得22212cos 223a b c C C ab π+-==-⇒=18.【答案】4-【解析】设最小边为a ,,2a ,由余弦定理得,最大角的余弦值为222cos 4α==- 【考点定位】此题主要考查三角形中的三角函数,等比数列的概念、余弦定理,考查分析推理能力、运算求解能力.19.答案:56π 【命题意图】本试题主要考查了三角函数性质的运用,求解值域的问题.首先化为单一三角函数,然后利用定义域求解角的范围,从而结合三角函数图像得到最值点.【解析】由sin 2sin()3y x x x π=-=-由502333x x ππππ≤<⇔-≤-<可知22sin()23x π-≤-≤ 当且仅当332x ππ-=即116x π=时取得最小值,32x ππ-=时即56x π=取得最大值.20. 【答案】4【解析】在ABC ∆中,得用余弦定理22214()()47()cos 2444a c b c b c b c b B ac c c+-++-+-=⇒-==,化简得8740c b -+=,与题目条件7b c +=联立,可解得2,4,3a b c ===,答案为4.【考点定位】 本题考查的是解三角形,考查余弦定理的应用.利用题目所给的条件列出方程组求解.21. 【解析】正确的是①②③①222221cos 2223a b c ab ab ab c C C ab ab π+-->⇒=>=⇒< ②2222224()()12cos 2823a b c a b a b a b c C C ab ab π+-+-++>⇒=>≥⇒< ③当2C π≥时,22232233c a b c a c b c a b ≥+⇒≥+>+与333a b c +=矛盾④取2,1a b c ===满足()2a b c ab +<得:2C π<⑤取2,1a b c ===满足22222()2a b c a b +<得:3C π<三、解答题22. 【命题意图】本题考查两角和与差的正弦公式、二倍角的余弦公式,三角函数的最小周期,单调性等知识.()=sin 2coscos 2sin sin 2cos cos 2sin cos 23333f x x x x x x ππππ++-+sin 2cos 2)4x x x π=+=+所以,()f x 的最小正周期22T ππ==. (2)因为()f x 在区间[,]48ππ-上是增函数,在区间[,]84ππ上是减函数,又()14f π-=-,()()184f f ππ==,故函数()f x 在区间[,]44ππ-最小值为1-.【点评】该试题关键在于将已知的函数表达式化为=sin (+)y A x ωϕ的数学模型,再根据此三角模型的图像与性质进行解题即可.23. 【解析】本题主要考察三角恒等变换,正弦定理,余弦定理及三角形面积求法等知识点.(Ⅰ) ∵cos A =23>0,∴sin A,又C =sin B =sin(A +C )=sin A cos C +sin C cos Acos C +23sin C .整理得:tan C(Ⅱ)由图辅助三角形知:sin C又由正弦定理知:sin sin a cA C=,故c =对角A 运用余弦定理:cos A =222223b c a bc +-=. (2)解(1) (2)得:b =or b舍去). ∴∆ABC 的面积为:S. 【答案】(Ⅰ). 24. 【考点定位】本题以三角函数的化简求值为主线,三角函数的性质为考查目的的一道综合题,考查学生分析问题解决问题的能力,由正弦函数的单调性结合条件可列32424ππωππω⎧-≥-⎪⎪⎨⎪≤⎪⎩,从而解得ω的取值范围,即可得ω的最在值. 解:(1)()14sin sin cos 22f x x x x x ωωωω⎫=++⎪⎪⎝⎭222cos 2sin cos sin x x x x x ωωωωω=++-21x ω=+因1sin 21x ω-≤≤,所以函数()y f x =的值域为1⎡+⎣(2)因sin y x =在每个闭区间()2,222k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦上为增函数,故()21f x x ω=+()0ω>在每个闭区间(),44k k k Z ππππωωωω⎡⎤-+∈⎢⎥⎣⎦上为增函数.依题意知3,22ππ⎡⎤-⊆⎢⎥⎣⎦,44k k ππππωωωω⎡⎤-+⎢⎥⎣⎦对某个k Z ∈成立,此时必有0k =,于是 32424ππωππω⎧-≥-⎪⎪⎨⎪≤⎪⎩,解得16ω≤,故ω的最大值为16. 25. [解析](Ⅰ)由已知可得:2()6cos3(0)2xf x x ωωω=+->=3cos ωx+)3sin(32sin 3πωω+=x x又由于正三角形ABC 的高为23,则BC=4 所以,函数482824)(πωωπ===⨯=,得,即的周期T x f所以,函数]32,32[)(-的值域为x f(Ⅱ)因为,由538)(0=x f (Ⅰ)有 ,538)34(sin 32)(00=+=ππx x f 54)34(sin 0=+ππx 即 由x 0)2,2()34x (323100ππππ-∈+-∈),得,( 所以,53)54(1)34(cos 20=-=+ππx 即 故=+)1(0x f =++)344(sin 320πππx ]4)34(sin[320πππ++x)22532254(324sin)34cos(4cos)34([sin 320⨯+⨯=+++=ππππππx x567=[点评]本题主要考查三角函数的图像与性质同三角函数的关系、两角和的正(余)弦公式、二倍角公式等基础知识,考查运算能力,考查树形结合、转化等数学思想.26. [解](1)5.0=t 时,P 的横坐标x P =277=t,代入抛物线方程24912x y =中,得P 的纵坐标y P =3 由|AP |=2949,得救援船速度的大小为949海里/时由tan∠OAP =30712327=+,得∠OAP =arctan 307,故救援船速度的方向为北偏东arctan 307弧度(2)设救援船的时速为v 海里,经过t 小时追上失事船,此时位置为)12,7(2t t . 由222)1212()7(++=t t vt ,整理得337)(1442122++=tt v因为2212≥+t t ,当且仅当t =1时等号成立,所以22253372144=+⨯≥v ,即25≥v .因此,救援船的时速至少是25海里才能追上失事船27.解析:(1)∵函数()f x 的最大值为3,∴13,A +=即2A =∵函数图像的相邻两条对称轴之间的距离为2π,∴最小正周期为T π= ∴2ω=,故函数()f x 的解析式为sin(2)16y x π=-+(2)∵()2sin()1226f απα=-+=即1sin()62πα-=∵02πα<<,∴663πππα-<-<∴66ππα-=,故3πα=28.解析:(Ⅰ)⎪⎭⎫ ⎝⎛+=+=+=⋅=62sin 2cos 22sin 232cos 2sin cos 3)(πx A x A x A x A x x A n m x f ,则6=A ;(Ⅱ)函数y=f(x)的图象像左平移12π个单位得到函数]6)12(2sin[6ππ++=x y 的图象, 再将所得图象各点的横坐标缩短为原来的12倍,纵坐标不变,得到函数)34sin(6)(π+=x x g .当]245,0[π∈x 时,]1,21[)34sin(],67,3[34-∈+∈+ππππx x ,]6,3[)(-∈x g .故函数()g x 在5[0,]24π上的值域为]6,3[-. 另解:由)34sin(6)(π+=x x g 可得)34cos(24)(π+='x x g ,令0)(='x g ,则)(234Z k k x ∈+=+πππ,而]245,0[π∈x ,则24π=x ,于是367sin6)245(,62sin 6)24(,333sin 6)0(-======πππππg g g , 故6)(3≤≤-x g ,即函数()g x 在5[0,]24π上的值域为]6,3[-. 29. 【答案及解析】(1)由已知12=+,++=,=,cos =32B AC A B C B B ππ∴ (2)解法一:2=b ac ,由正弦定理得23sin sin =sin =4A CB 解法二:2=b ac ,222221+-+-=cos ==222a c b a c acB ac ac,由此得22+-=,a c ac ac 得=a c所以===3A B C π,3sin sin =4A C 【点评】本题主要考查三角形的正弦定理、余弦定理、三角形内角和定理及等差、等比数列的定义,考查转化思想和运算求解能力,属于容易题.第二小题既可以利用正弦定理把边的关系转化为角的关系,也可以利用余弦定理得到边之间的关系,再来求最后的结果.30. 【解析】解:(1)证明:由 sin()sin()44b Cc B a ππ+-+=及正弦定理得: sin sin()sin sin()sin 44B C C B A ππ+-+=,即sin )sin )B C C C B B -=整理得:sin cos cos sin 1B C B C -=,所以sin()1B C -=,又30,4B C π<< 所以2B C π-=(2) 由(1)及34B C π+=可得5,88B C ππ==,又,4A a π==所以sin 5sin 2sin ,2sin sin 8sin 8a B a Cbc A A ππ====, 所以三角形ABC的面积1521s n 2insi n288882b Aππππ=====【点评】本题考查解三角形,三角形的面积,三角恒等变换、三角和差公式以及正弦定理的应用.高考中,三角解答题一般有两种题型:一、解三角形:主要是运用正余弦定理来求解边长,角度,周长,面积等;二、三角函数的图像与性质:主要是运用和角公式,倍角公式,辅助角公式进行三角恒等变换,求解三角函数的最小正周期,单调区间,最值(值域)等.来年需要注意第二种题型的考查.31. 【答案】解:(1)∵3AB AC BA BC =,∴cos =3cos AB AC A BA BC B,即cos =3cos AC A BC B .由正弦定理,得=sin sin AC BCB A,∴sin cos =3sin cos B A A B . 又∵0<A B <π+,∴cos 0 cos 0A >B >,.∴sin sin =3cos cos B AB A即tan 3tan B A =.(2)∵ cos 0C <C <π=,∴sin C =.∴tan 2C =. ∴()tan 2A B π⎡-+⎤=⎣⎦,即()tan 2A B +=-.∴tan tan 21tan tan A BA B+=-- .由 (1) ,得24tan 213tan AA=--,解得1tan =1 tan =3A A -,. ∵cos 0A >,∴tan =1A .∴=4A π.【考点】平面微量的数量积,三角函数的基本关系式,两角和的正切公式,解三角形.【解析】(1)先将3AB AC BA BC =表示成数量积,再根据正弦定理和同角三角函数关系式证明.(2)由cos C =可求tan C ,由三角形三角关系,得到()tan A B π⎡-+⎤⎣⎦,从而根据两角和的正切公式和(1)的结论即可求得A 的值.32.考点分析:本题考察三角恒等变化,三角函数的图像与性质.解析:(Ⅰ)因为22()sin cos cos f x x x x x ωωωωλ=-+⋅+cos22x x ωωλ=-+π2sin(2)6x ωλ=-+.由直线πx =是()y f x =图象的一条对称轴,可得πsin(2π)16ω-=±,所以ππ2ππ()62k k ω-=+∈Z ,即1()23k k ω=+∈Z . 又1(,1)2ω∈,k ∈Z ,所以1k =,故56ω=.所以()f x 的最小正周期是6π5. (Ⅱ)由()y f x =的图象过点π(,0)4,得π()04f =,即5πππ2sin()2sin 6264λ=-⨯-=-=,即λ=故5π()2sin()36f x x =-由3π05x ≤≤,有π5π5π6366x -≤-≤,所以15πsin()1236x -≤-≤,得5π12sin()236x --故函数()f x 在3π[0,]5上的取值范围为[12-. 33.解析:(Ⅰ)210T ππω==,所以15ω=.(Ⅱ)515652cos 52cos 2sin 353625f ππαπαπαα⎡⎤⎛⎫⎛⎫⎛⎫+=++=+=-=-⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,所以3s i n5α=.5151652cos 52cos 656617f πβπβπβ⎡⎤⎛⎫⎛⎫-=-+== ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,所以8cos 17β=.因为α、0,2πβ⎡⎤∈⎢⎥⎣⎦,所以4c o s i n 5α=,15sin 17β=,所以()4831513c o s c o s c o s s i ns i n 51751785αβαβαβ+=-=⨯-⨯=-. 34. 【考点定位】本题主要考查同角函数关系、两角和与差的三角函数公式、二倍角公式、考查运算能力、特殊与一般思想、化归与转化思想.解:(1)选择(2)式计算如下213sin 15cos15sin15cos151sin 3024︒+︒-︒︒=-︒= (2)证明:22sincos (30)sin cos(30)αααα+︒--︒-22sin (cos30cos sin30sin )sin (cos30cos sin30sin )αααααα=+︒+︒-︒+︒2222311sin cos cos sin cos sin 442αααααααα=++-22333sin cos 444αα=+= 35. 【命题意图】本试题主要考查了解三角形的运用,给出两个公式,一个是边的关系,一个角的关系,而求解的为角,因此要找到角的关系式为好. 【解析】由()A B C B A C ππ++=⇔=-+, 由正弦定理及2a c =可得sin 2sin A C =所以cos()cos cos()cos(())cos()cos()A C B A C A C A C A C π-+=-+-+=--+cos cos sin sin cos cos sin sin 2sin sin A C A C A C A C A C =+-+=故由cos()cos 1A C B -+=与sin 2sin A C =可得22sin sin 14sin 1A C C =⇒= 而C 为三角形的内角且2a c c =>,故02C π<<,所以1sin 2C =,故6C π=. 【点评】该试题从整体来看保持了往年的解题风格,依然是通过边角的转换,结合了三角形的内角和定理的知识,以及正弦定理和余弦定理,求解三角形中的角的问题.试题整体上比较稳定,思路也比较容易想,先将三角函数关系式化简后,得到,A C 角关系,然后结合2a c =,得到两角的二元一次方程组,自然很容易得到角C 的值.36. 【考点定位】本题考醒三角函数知识,此类型题在平时练习时练得较多,考生应该觉得非常容易入手. 解:(sin cos )sin 2()sin x x x f x x -==(sin cos )2sin cos sin x x x xx-=2(sin cos )cos x x x -=sin 21cos 2x x --)14x π--,{|,}x x k k Z π≠∈(1) 原函数的定义域为{|,}x x k k Z π≠∈,最小正周期为π; (2)原函数的单调递增区间为[,)8k k k Z πππ-+∈,3(,]8k k k Z πππ+∈. 37. 【解析】2111())sin cos 2sin 2(1cos 2)24222f x x x x x x π=++=-+-11sin 222x =-(I)函数()f x 的最小正周期22T ππ== (2)当[0,]2x π∈时,11()()sin 222g x f x x =-=当[,0]2x π∈-时,()[0,]22x ππ+∈ 11()()sin 2()sin 22222g x g x x x ππ=+=+=- 当[,)2x ππ∈--时,()[0,)2x ππ+∈ 11()()sin 2()sin 222g x g x x x ππ=+=+=得:函数()g x 在[,0]π-上的解析式为1sin 2(0)22()1sin 2()22x x g x x x πππ⎧--≤≤⎪⎪=⎨⎪-≤<⎪⎩。
2013年、2012年、2011年高考题分类汇编之三角函数

第四章三角函数第一节三角函数的概念、同角三角函数的关系、诱导公式高考试题考点一三角函数的概念1.(2011年新课标全国卷,理5)已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则cos 2θ=()(A)-45(B)-35(C)35(D)45解析:①取x=1,则y=2,∴∴cos θcos 2θ=2cos2θ-1=-3 5 .②取x=-1,则y=-2,∴θ.cos 2θ=2cos2θ-1=-35.故选B.答案:B2.(2012年山东卷,理16)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,OP的坐标为.解析:如图所示,由题意知=OB=2,∵圆半径为1,∴∠BAP=2,故∠DAP=2-π2,∴DA=Apcos(2-π2)=sin 2, DP=APsin (2-π2)=-cos 2.∴OC=2-sin 2,PC=1-cos 2.∴OP =(2-sin 2,1-cos 2).答案:(2-sin 2,1-cos 2)考点二 同角三角函数的基本关系式1.(2013年浙江卷,理6)已知α∈R,sin α+2cos α则tan 2α等于() (A)43 (B)34 (C)-34 (D)-43解析:因为sin α+2cos α所以sin 2α+4sin α cos α+4cos 2α=52,所以3cos 2α+4sin α cos α=32, 所以2223cos 4sin cos sin cos ααααα++=32, 所以234tan 1tan αα++=32,即3tan 2α-8tan α-3=0,解得tan α=3或tan α=-13,所以tan 2α=22tan 1tan αα-=-34. 故选C.答案:C2.(2012年辽宁卷,理7)已知sin α-cos αα∈(0,π),则tan α=( )(A)-1(D)1解析:∵sin α-cos α∴(sin α-cos α)2=2,∴1-2sin αcos α=2,2sin αcos α=-1<0,∴α∈(π2,π),∴1+2sin αcos α=0,∴(sin α+cos α)2=0,sin α+cos α=0,由sin cos sin cos 0, αααα⎧-⎪⎨+=⎪⎩得sin α,cos α,tan α=sin cos αα=-1.故选A.答案:A3.(2012年江西卷,理4)若tan θ+1tan θ=4,则sin 2θ=() (A)15 (B)14 (C)13 (D)12解析:∵tan θ+1tan θ=sin cos θθ+cos sin θθ =1sin cos θθ =2sin 2θ=4,∴sin 2θ=12. 故选D.答案:D4.(2011年福建卷,理3)若tan α=3,则2sin 2cos αα的值等于( ) (A)2 (B)3 (C)4 (D)6解析: 2sin 2cos αα=22sin cos cos ααα=2tan α=6,故选D. 答案:D5.(2013年新课标全国卷Ⅱ,理15)设θ为第二象限角,若tan(θ+π4)=12,则sin θ+cos θ= . 解析:因为θ为第二象限角, 所以π2+2k π<θ<π+2k π,k ∈Z, 因此34π+2k π<θ+π4<54π+2k π,k ∈Z, 从而sin(θ+π4)<0. 又∵tan(θ+π4)=12, ∴sin(θ+π4, ∴sin θ+cos θθ+π4答案6.(2011年大纲全国卷,理14)已知α∈(π2,π),sin α,则tan 2α= . 解析:∵sin αα∈(π2,π), ∴cos α∴tan α=-12, ∴tan 2α=22tan 1tan αα-=1114--=-43.答案:-4 3考点三诱导公式及其应用(2010年大纲全国卷Ⅰ,理2)记cos (-80°)=k,那么tan 100°等于()解析:∵cos(-80°)=k,∴cos 80°=k,∴sin 80°,∴tan 100°=tan(180°-80°)=-tan 80°=-sin80 cos80.故选B.答案:B模拟试题考点一三角函数的概念1.(2011浙江杭州模拟)已知角α的终边经过点(3a-9,a+2),且cos α≤0,sin α>0,则实数a的取值范围是()(A)(-2,3] (B)(-2,3)(C)[-2,3) (D)[-2,3]解析:∵cos α≤0,sin α>0,∴390,20, aa-≤⎧⎨+>⎩∴-2<a≤3,故选A.答案:A2.(2013安徽省大江中学、开成中学高三联考)已知点P(sin 3π4,cos3π4)角θ的终边上,则tan(θ+π3)值为.解析:∵sin 3π4,cos3π4,∴点P的坐标为)∴tan θ=-1.则tan(θ+π3)=πtan tan3π1tan tan3θθ+-⋅=)212答案考点二同角三角函数基本关系式1.(2013山东师大附中高三月考)若α∈(π2,π),tan(α+π4)=17,则sin α等于()(A)35(B)45(C)-35(D)-45解析:∵tan(α+π4)=tan11tanαα+-=17,∴tan α=-34=sincosαα,∴cos α=-43sin α,又∵sin2α+cos2α=1,∴sin2α=9 25,又∵α∈(π2,π),∴sin α=3 5 .答案:A2.(2012山东潍坊模拟)已知α∈(0,π)且 sin α+cos α,则sin α-cos α=.解析:由sin α+cos α,两边平方得2sin αcos α=-1 2 ,∴(sin α-cos α)2=1-2sin αcos α=3 2 .又α∈(0,π),sin αcos α<0,∴sin α>0,cos α<0,∴sin α-cos α.答案考点三诱导公式1.(2013广东省深圳市高三第一次调研)化简sin 2013°的结果是()(A)sin 33°(B)cos 33°(C)-sin 33°(D)-cos 33°解析:sin 2013°=sin (5×360°+213°)=sin 213°=sin(180°+33°)=-sin 33°.故选C.答案:C2.(2012浙江丽水质检)设tan(π+α)=2,则()()()()sinπcosπsinπcosπ+αααα-+-+-等于()(A)3 (B)1 3(C)1 (D)-1解析:由tan(π+α)=2,得tan α=2,故()()()() sinπcosπsinπcosπ+αααα-+-+-=()sin cossin cosαααα-----=sin cos sin cosαααα+-=tan1 tan1αα+-=3.故选A.答案:A3.(2013浙江省建八高中月考)若α∈(0,π2),且cos2α+sin(π2+2α)=12,则tan α=.解析:cos2α+sin(π2+2α)=cos2α+cos 2α=3cos2α-1=1 2 ,∴cos2α=1 2 .∵α∈(0,π2 ),∴cos α,sin α,∴tan α=1.答案:1综合检测1.(2012江西八所重点高中模拟)在直角坐标平面内,已知函数f(x)=log a(x+2)+3(a>0且a≠1)的图象恒过定点P,若角θ的终边过点P,则cos2θ+sin 2θ的值等于()(A)-12(B)12(C)710(D)-710解析:因为函数y=log a x的图象恒过定点(1,0),所以f(x)的图象恒过定点P(-1,3),由三角函数的定义知sin θ,cos θ则cos 2θ+sin 2θ=cos 2θ+2sin θcos θ=110+2× =110-610=-12. 故选A.答案:A2.(2012安徽合肥一模)已知sin(π3-x)=35,则cos(5π6-x)= . 解析:cos(56π-x)=cos[π2+(π3-x)] =-sin(π3-x) =-35. 答案:-353.(2011江苏泰兴月考)已知sin(π-α)-cos(π+α(π2<α<π).求下列各式的值: (1)sin α-cos α;(2)sin 3(π2-α)+cos 3(π2+α).解:由sin(π-α)-cos(π+α,得sin α+cos α,(*) 将(*)式两边平方,得1+2sin α·cos α=29, 故2sin α·cos α=-79. 又π2<α<π, ∴sin α>0,cos α<0.(1)(sin α-cos α)2=1-2sin α·cos α=1-(-79) =169, ∴sin α-cos α=43. (2)sin 3(π2-α)+cos 3(π2+α) =cos 3α-sin 3α =(cos α-sin α)(cos 2α+cos α·sin α+sin 2α) =-43×(1-718) =-2227.第二节 三角函数的图象和性质高考试题考点一 三角函数的性质及应用1.(2012年湖南卷,理6)函数f(x)=sin x-cos(x+π6)的值域为( )(A)[-2,2] ](C)[-1,1] ] 解析:f(x)=sin x-cos(x+π6)cos x+12sin x=32cos xsin(x+π6),所以函数f(x)的值域为].故选B.答案:B2.(2012年新课标全国卷,理9)已知ω>0,函数f(x)=sin(ωx+π4)在(π2,π)上单调递减,则ω的取值范围是()(A)[12,54] (B)[12,34](C)(0,12] (D)(0,2]解析:∵ω>0,∴由2kπ+π2≤ωx+π4≤2kπ+3π2(k∈Z),得f(x)的单调减区间为[π2π+4kω,5π2π+4kω],k∈Z.又∵f(x)在(π2,π)上单调递减,∴π2ππ4, 25π2π4π,kkωω⎧+⎪≥⎪⎪⎨⎪+⎪≤⎪⎩即14,252,4kkωω⎧≥+⎪⎪⎨⎪≤+⎪⎩由ω>0及k∈Z知,只能k=0,即12≤ω≤54.答案:A3.(2011年山东卷,理6)若函数f(x)=sin ωx(ω>0)在区间[0,π3]上单调递增,在区间[π3,π2]上单调递减,则ω等于() (A)3 (B)2(C)32(D)23解析:据条件可知,f(x)=sin ωx在x=π3处取得最大值1,即sinπ3ω=1,∴π3ω=2kπ+π2(k∈Z).∴ω=6k+32,k∈Z,结合选项得ω=32.故选C.答案:C4.(2011年安徽卷,理9)已知函数f(x)=sin(2x+φ),其中φ为实数.若f(x)≤π6f⎛⎫⎪⎝⎭对x∈R恒成立,且f(π2)>f(π),则f(x)的单调递增区间是()(A)[kπ-π3,kπ+π6](k∈Z)(B)[kπ,kπ+π2](k∈Z)(C)[kπ+π6,kπ+2π3](k∈Z)(D)[kπ-π2,kπ](k∈Z)解析:由f(x)≤π6f⎛⎫⎪⎝⎭对x∈R恒成立知x=π6时,f(x)取得最值,故π3+φ=kπ+π2(k∈Z),φ=kπ+π6(k∈Z),又f(π2)>f(π),∴sin ϕ<0,∴ϕ=(2k+1)π+π6(k∈Z),∴f(x)=-sin(2x+π6 ),令2kπ+π2≤2x+π6≤2kπ+3π2(k∈Z),得kπ+π6≤x≤kπ+3π2,k∈Z.故选C.答案:C5.(2013年江西卷,理11)函数2x的最小正周期T为.解析(1-cos 2x)=2sin(2x-π3故函数的最小正周期T=2π2=π. 答案:π6.(2012年北京卷,理15)已知函数f(x)=()sin cos sin 2sin x x x x-.(1)求f(x)的定义域及最小正周期; (2)求f(x)的单调递增区间. 解:(1)∵sin x ≠0, ∴x ≠k π(k ∈Z),∴f(x)的定义域为{x ∈R|x ≠k π,k ∈Z}. 又∵f(x)=()sin cos sin 2sin x x x x-=2cos x(sin x-cos x) =sin 2x-cos 2x-1π4)-1. ∴f(x)的最小正周期T=2π2=π. (2)函数y=sin x 的单调递增区间为 [2k π-π2,2k π+π2](k ∈Z), 由2k π-π2≤2x-π4≤2k π+π2, 且x ≠k π(k ∈Z), 得k π-π8≤x ≤k π+3π8, 且x ≠k π(k ∈Z), ∴f(x)的单调递增区间为 [k π-π8,k π),(k π,k π+3π8] (k ∈Z). 考点二 三角函数的图象及变换1.(2013年湖北卷,理4)将函数∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是( )(A)π12(B)π6(C)π3(D)5π6解析:函数y=2(cos x+12sin x)=2cos(x-π6)的图象向左平移m个单位长度后,得图象的解析式为y=2cos(x-π6+m),由题意此函数为偶函数,故m-π6=kπ,k∈Z,即m=kπ+π6,k∈Z,m min=π6.故选B.答案:B2.(2013年山东卷,理5)将函数y=sin(2x+ϕ)的图象沿x轴向左平移π8个单位后,得到一个偶函数的图象,则φ的一个可能取值为()(A)3π4(B)π4(C)0 (D)-π4解析:由函数横向平移规律“左加右减”则y=sin(2x+ϕ)向左平移π8个单位得y=sin(2x+π4+ϕ).由y=sin(2x+π4+ϕ)为偶函数得π4+ϕ=π2+kπ,k∈Z,则ϕ=π4+kπ,k∈Z,则ϕ的一个可能值为π4 .故选B.答案:B3.(2012年浙江卷,理4)把函数y=cos 2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图象是()解析:y=cos 2x+1图象上所有点的横坐标伸长到原来的2倍得y1=cos x+1,再向左平移1个单位长度得y2=cos(x+1)+1,再向下平移1个单位长度得y3=cos(x+1),故相应的图象为选项A.答案:A4.(2011年大纲全国卷,理5)设函数f(x)=cos ωx(ω>0),将y=f(x)的图象向右平移π3个单位长度后,所得的图象与原图象重合,则ω的最小值等于( )(A)13(B)3 (C)6(D)9解析:由题意,得π3为函数f(x)=cos ωx 的最小正周期的正整数倍,∴π3=k ·2π (k ∈N *),∴ω=6k(k ∈N *),∴ω的最小值为6. 答案:C5.(2010年新课标全国卷,理4)如图,质点P 在半径为2的圆周上逆时针运动,其初始位置为P 0角速度为1,那么点P 到x 轴的距离d 关于时间t 的函数图象大致为( )解析:显然,当t=0时故排除选项A 、D.又因为质点是按逆时针方向转动,所以开始运动后,随时间t 的变化质点P 到x 轴的距离d 先减小,再排除选项B,即得选项C. 答案:C6.(2012年山东卷,理17)已知向量m=(sin Acos x,2Acos 2x)(A>0),函数f(x)=m ·n 的最大值为6. (1)求A;(2)将函数y=f(x)的图象向左平移π12个单位,再将所得图象上各点的横坐标缩短为原来的12倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)在[0,5π24]上的值域.解:(1)f(x)=m ·Asin xcos x+2Acos 2x12cos 2x)=Asin(2x+π6) 因为A>0,由题意知A=6. (2)由(1)得f(x)=6sin(2x+π6). 将函数y=f(x)的图象向左平移π12个单位后得到y=6sin[2(x+π12)+π6]=6sin(2x+π3)的图象; 再将得到的图象上各点横坐标缩短为原来的12,纵坐标不变,得到y=6sin(4x+π3)的图象. 因此g(x)=6sin(4x+π3). 因为x ∈[0,5π24], 所以4x+π3∈[π3,7π6], 故g(x)在[0,5π24]上的值域为[-3,6]. 考点三 由函数的图象求解析式1.(2013年四川卷,理5)函数f(x)=2sin(ωx+φ)(ω>0,-π2< <π2)的部分图象如图所示,则ω,φ的值分别是( )(A)2,-π3 (B)2,-π6 (C)4,-π63解析:因为34T =5π12-(-π3)=3π4,所以T=2πω=π,ω=2. 由2×5π12+ϕ=π2+2k π(k ∈Z),得ϕ=-π3+2k π(k ∈Z). 因为-π2<ϕ<π2,所以ϕ=-π3,故选A. 答案:A2.(2009年辽宁卷,理8)已知函数f(x)=Acos(ωx+φ)的图象如图所示,f (π2)=-23,则f(0)等于( )(A)-23(B)-12(C)23 (D) 12解析:由图象可得最小正周期为2π3, 于是f(0)=f (2π3),注意到2π3与π2关于7π12对称, 所以f (2π3)=-f(π2)=23. 答案:C3.(2011年江苏卷,9)函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,则f(0)的值是 .解析:由题图知 4T =7π12-π3=π4, ∴T=π,ω∴ω=2,∴ϕ),将点(7π12代入得,×7π12+ϕ)π6+ϕ), ∴sin(π6+ϕ)=1, ∴π6+ϕ=2k π+π2(k ∈Z), ∴ϕ=π3+2k π(k ∈Z),∴π3+2k ππ3),∴π3.答案 4.(2011年辽宁卷,理16)已知函数f(x)=Atan(ωx+ϕ)(ω>0,|ϕ|<π2),y=f(x)的部分图象如图,则f(π24)= .解析:由图象知f(x)周期为π2, ∴π2=πω,ω=2, 则f(x)=Atan(2x+φ), 又f(0)=Atan ϕ=1,f(3π8)=Atan(3π4+φ)=0, ∴tan(3π4+ϕ)=0,∴3π4+ϕ=k π,k ∈Z, 而|ϕ|<π2, ∴ϕ=π4,∴A=1, ∴f(x)=tan(2x+π4),故f(π24)=tan(π12+π4)=tan π3答案5.(2012年陕西卷,理16)函数f(x)=Asin(ωx-π6)+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为π2. (1)求函数f(x)的解析式; (2)设α∈(0,π2),f(2α)=2,求α的值.解:(1)由f(x)的最大值为3,得A+1=3,A=2, 由函数图象的相邻两条对称轴之间的距离为π2, 得2×π2=2πω,ω=2, ∴f(x)=2sin(2x-π6)+1. (2)∵f(2α)=2sin(α-π6)+1=2, ∴sin(α-π6)=12. ∵0<α<π2, ∴-π6<α-π6<π3, ∴α-π6=π6, 故α=π3. 模拟试题考点一 三角函数的性质及应用1.(2013安徽省望江四中高三月考)同时具有性质“周期为π,图象关于直线x=π3对称,在[-π6,π3]上是增函数”的函数是()(A)y=sin(2x-π6) (B)y=cos(2x+π3)(C)y=cos(2x-π6) (D)y=sin(2x+π6)解析:∵周期为π,∴ω=2,排除选项D.图象关于x=π3对称,即函数在x=π3处取得最值,排除选项C.又函数在[-π6,π3]上是增函数.故选A.答案:A2.(2013四川省成都市高新区月考)已知函数y=2sin(ωx+θ)(0<θ<π)为偶函数,其图象与直线y=2的交点的横坐标为x1,x2,若|x1-x2|的最小值为π,则()(A)ω=2,θ=π2(B)ω=12,θ=π2(C)ω=12,θ=π4(D)ω=2,θ=π4解析:由题意知,|x1-x2|的最小值即为三角函数的最小正周期.∴2π=π,∴ω=2.又∵y=2sin(2x+θ)(0<θ<π)为偶函数,即当x=0时,y取得最值.∴θ=π2 .故选A.答案:A3.(2012云南玉溪二模)当-π2≤x ≤π2时,函数f(x)=sin(x-2ππ-x)的值域为 .解析:f(x)=-sin(2ππ-x)=2sin(x+π3), 由-π2≤x ≤π2得-π6≤x+π3≤5π6. 则-12≤sin(x+π3)≤1, 故f(x)的值域为[-1,2].答案:[-1,2]考点二 三角函数的图象变换1.(2013广东省广州市综合测试)已知函数为了得到函数g(x)=sin 2x+cos 2x 的图象,只要将y=f(x)的图象( )(A)向右平移π4个单位长度 (B)向左平移π4个单位长度 (C)向右平移π8个单位长度 (D)向左平移π8个单位长度解析:g(x)=sin 2x+cos 2x=π4),若由得到π8)], 只要将f(x)的图象左移π8个单位长度即可. 故选D.答案:D2.(2012安徽合肥八中一模)将函数f(x)=2sin(2x+π4)的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的12倍,所得图象关于直线x=π4对称,则φ的最小正值为()(A)π8(B)3π8(C)3π4(D)π2解析:f(x)=2sin(2x+π4)y=2sin(2x-2ϕ+π4)y=2sin(4x-2ϕ+π4).因为直线x=π4为对称轴,所以4×π4-2φ+π4=kπ+π2(k∈Z),即ϕ=-12kπ+3π8(k∈Z).因为ϕ>0,则k=0时,φmin=3π8.故选B.答案:B考点三由函数的图象求解析式1.(2013浙江省重点中学六校联考)函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π2)的部分图象如图所示,则将y=f(x)的图象向右平移π6个单位后,得到的图象解析式为()(A)y=sin 2x (B)y=sin(2x-π6 )(C)y=sin(2x+2π3) (D)y=cos 2x解析:由图象知34T=11π12-π6=912π=34π,∴T=π=2πω,∴ω=2.∴2×π6+ϕ=π2,∴ϕ=π6,而A=1. ∴f(x)=sin(2x+π6), 右移π6个单位得g(x)=sin[2(x-π6)+π6] =sin(2x-π6). 故选B.答案:B2.(2013四川省乐山第二次调研)如果存在正整数ω和实数φ,使得函数f(x)=cos 2(ωx+ϕ)的部分图象如图所示,且图象经过点(1,0),那么ω的值为( )(A)4 (B)3(C)2 (D)1解析:f(x)=cos 2(ωx+φ) =()1cos 222x ωϕ++, 由图象知2T <1<34T,43<T<2, ∴43<πω<2, π2<ω<34π<3, 又ω∈N *, ∴ω=2.答案:C综合检测1.(2013安徽省屯溪一中高三第一次质检)设函数cos(2x+ϕ)+sin(2x+ϕ)(|ϕ|<π2),且其图象关于直线x=0对称,则( )(A)y=f(x)的最小正周期为π,且在(0,π2)上为增函数(B)y=f(x)的最小正周期为π,且在(0,π2)上为减函数(C)y=f(x)的最小正周期为π2,且在(0,π4)上为增函数(D)y=f(x)的最小正周期为π2,且在(0,π4)上为减函数解析:f(x)=2sin(2x+ϕ+π3 ),∴T=2π2=π.又图象关于x=0对称,∴ϕ+π3=π2+kπ,k∈Z,又∵|ϕ|<π2 ,∴ϕ=π6 .∴f(x)=2sin(2x+π2)=2cos 2x,∴在(0,π2)上为减函数.故选B.答案:B2.(2013重庆铁路中学高三考试)f(x)=sin ωx+cos(ωx+π6)的图象上相邻两条对称轴间的距离是2π3,则ω的一个值是()(A)23(B)43(C)32(D)34解析:f(x)=sin ωcos ωx-12sin ωx=sin(ωx+π3 ),T=2×2π3=4π3=2πω,所以ω=3 2 .答案:C第三节 三角恒等变换高考试题考点一 两角和与差的三角函数公式1.(2010年福建卷,理1)计算sin 43°cos 13°-cos 43°sin 13°的结果等于( )(A)12解析:原式=sin(43°-13°)=sin 30°=12.故选A.答案:A2.(2013年重庆卷,理9)4cos 50°-tan 40°等于( )解析:4cos 50°-tan 40°=4sin 40°-sin 40cos40 =4sin 40cos40sin 40cos40⋅- =2sin80sin 40cos40- =2sin10sin 40cos40-=()2cos10sin 3010cos40-+ =33cos10sin1022cos40-=)cos30cos10sin30sin10cos40-故选C.答案:C3.(2012年重庆卷,理5)设tan α,tan β是方程x 2-3x+2=0的两根,则tan(α+β)的值为( )(A)-3 (B)-1 (C)1 (D)3解析:易知tan α+tan β=3,tan αtan β=2,故tan (α+β)=tan tan 1tan tan αβαβ+-=312-=-3. 故选A.答案:A4.(2012年四川卷,理4)如图所示,正方形ABCD 的边长为1,延长BA 至E,使AE=1,连接EC,ED,则sin ∠CED 等于( )解析:∵四边形ABCD 是正方形,且AE=AD=1,∴∠AED=π4. 在Rt △EBC 中,EB=2,BC=1,∴.∴sin ∠∠. ∴sin ∠CED=sin(π4-∠BEC)cos ∠sin ∠BEC故选B.答案:B5.(2011年浙江卷,理6)若0<α<π2,-π2<β<0,cos(π4+α)= 13,cos(π4-2β则cos(α+2β) 等于( )解析:∵0<α<π2, ∴π4<α+π4<3π4. ∵cos (π4+α)=13,∴sin (π4+α) 又∵-π2<β<0, ∴π4<π4-2β<π2.∵cos (π4-2β),∴sin(π4-2β, ∴cos (α+2β)=cos[(α+π4)(π4-2β)] =cos (α+π4)cos(π4-2β)+ Sin(α+π4)sin(π4-2β)=13 故选C.答案:C 6.(2012年江苏卷,11)设α为锐角,若cos(α+π6)=45,则sin(2α+π12)的值为 . 解析:∵cos(α+π6)=45>0,且α为锐角, ∴α+π6∈(π6,π2), ∴sin(α+π6)=35, ∴sin(2α+π3)=2cos(α+π6)sin(α+π6) =2×35×45=2425,Cos(2α+π3)=2cos2(α+π6)-1=725,∴sin(2α+π12)=sin[(2α+π3)-π4]=sin(2α+π3)cosπ4-cos(2α+π3)sinπ4答案7.(2012年广东卷,理16)已知函数f(x)=2cos(ωx+π6)(其中ω>0,x∈R)的最小正周期为10π.(1)求ω的值;(2)设α,β∈[0,π2],f(5α+5π3)=-65,f(5β-5π6)=1617,求cos(α+β)的值.解:(1)∵T=10π=2π,∴ω=1 5 .(2)由(1)得f(x)=2cos(15x+π6),∵-65=f(5α+5π3)=2cos[15(5α+53π)+π6] =2cos(α+π2)=-2sin α,∴sin α=35,cos α=45.∵1617=f(5β-5π6)=2cos[15(5β-5π6)+π6] =2cos β,∴cos β=817,sin β=1517.∴cos(α+β)=cos αcos β-sin αsin β=45×817-35×1517=-1385.考点二 倍角公式与半角公式1.(2012年山东卷,理7)若θ∈[π4,π2],sin 2θ则sin θ等于( )(A)35 (B)45 (D)34解析:∵θ∈[π4,π2],∴2θ∈[π2,π],∴cos 2θ18,∴sin θ34.故选D.答案:D2.(2011年辽宁卷,理7)设sin(π4+θ)= 13,则sin 2θ等于( ) (A)-79 (B)-19 (C)19 (D)79解析:sin 2θ=-cos(2θ+π2)=2sin 2(θ+π4)-1=2×19-1 =-79.故选A.答案:A3.(2012年大纲全国卷,理7)已知α为第二象限角,sin α+cos α,则cos 2α等于()解析:sin α+cos α两边平方,∴1+2sin αcos α=13,∴sin 2α=-23.∴cos 2α=.又∵sin α+cos α>0,α是第二象限角, ∴2k π+π2<α<2k π+3π4(k ∈Z).∴4k π+π<2α<4k π+3π2 (k ∈Z),∴2α是第三象限角,∴cos 2α故选A.答案:A4.(2010年新课标全国卷,理9)若cos α=-45,α是第三象限的角,则1tan 21tan 2αα+-等于() (A)-12 (B)12 (C)2 (D)-2解析:∵cos α=-45,α是第三象限的角,∴2k π+π<α<2k π+54π,k ∈Z,∴k π+π2<2α<k π+58π,k ∈Z, ∴2α是第二、四象限角,∴tan 2α∴1tan 21tan 2αα+-=1313-+=-12.故选A.答案:A5.(2011年江苏卷,7)已知tan(x+π4)=2,则tan tan 2xx 的值为 .解析:由tan(x+π4)=2, 得πtan tan 4π1tan tan 4x x +-=2, 即tan 11tan x x +-=2,∴tan x=13,∴tan tan 2x x =2tan 2tan 1tan x x x-=21tan 2x -=21132⎛⎫- ⎪⎝⎭=49. 答案:496.(2013年四川卷,理13)设sin 2α=-sin α,α∈(π2,π),则tan 2α的值是 . 解析:法一 由sin 2α=-sin α得2sin αcos α=-sin α, 又 α∈(π2,π). 所以sin α≠0,所以cos α=-12, 所以sin αα. 则tan 2α=22tan 1tan αα-法二 由sin 2α=-sin α,得2sin α·cos α=-sin α,又α∈(π2,π),sin α≠0,所以cos α=-12,α=2π3,则tan 2α=tan 4π3=tan π3. 答案7.(2011年四川卷,理17)已知函数f(x)=sin(x+7π4)+cos(x-3π4),x ∈R.(1)求f(x)的最小正周期和最小值; (2)已知cos(β-α)= 45,cos(β+α)=-45,0<α<β≤π2.求证:[f(β)]2-2=0. (1)解:∵f(x)=sin(x+7π4)+cos(x-3π4)=sin xcos7π4+cos xsin 7π4+cos xcos 3π4+sin xsin 3π4cos x)=2sin(x-π4), ∴f(x)的最小正周期T=2π, 最小值为-2.(2)证明:∵0<α<β≤π2 ,∴0<β-α<π2,0<α+β<π.又cos(β-α)=45,cos(β+α)=-45,∴sin(β-α)=35,sin(β+α)=35,∴sin 2β=sin[(β-α)+(β+α)]=sin(β-α)cos(β+α)+cos(β-α)sin(β+α)=35×(-45)+45×35=0,∴[f(β)]2-2=[2sin(β-π4)]2-2=4×π1cos222β⎛⎫--⎪⎝⎭-2=2-2sin 2β-2=-2sin 2β=0,∴[f(β)]2-2=0.8.(2013年广东卷,理16)已知函数π12),x∈R.(1)求f(-π6)的值;(2)若cos θ=35,θ∈(3π2,2π),求f(2θ+π3).解:(1)f(-π6π6-π12π4)=π4=1.(2)f(2θ+π3θ+π3-π12θ+π4)=cos 2θ-sin 2θ.因为cos θ=35,θ∈(2π3,2π),所以sin θ=-45.所以sin 2θ=2sin θcos θ=-2425,cos 2θ=cos2θ-sin2θ=-725.所以f(2θ+π3)=cos 2θ-sin 2θ=-725-(-2425)=1725.模拟试题考点一两角和与差的三角函数公式应用1.(2012潍坊质检)已知α∈(0,π2),α+π3的终边上的一点的坐标为(-4,3),则sin α等于()解析:由α∈(0,π2)及三角函数的定义可知Sin(α+π3)=35,cos(α+π3)=-45,所以可得sin α=sin[(α+π3)-π3]=sin(α+π3)cosπ3-cos(α+π3)sinπ3故选A.答案:A2.(2012广东深圳一模)已知直线l:xtan α-y-3tan β=0的斜率为2,在y轴上的截距为1,则tan(α+β)等于()(A)-73(B)73(C)57(D)1解析:由题意,得tan α=2,tan β=-13,可得tan(α+β)=tan tan1tan tanαβαβ+-=1231123-+⨯=1.故选D.答案:D考点二倍角公式与半角公式1.(2011四川成都五校联考)已知锐角α满足cos 2α=cos(π4-α),则sin 2α等于()(A)12(B)-12解析:∵cos 2α=cos(π4-α),∴cos2α-sin2α(cos α+sin α),∴cos α-sin α.两边平方,得1-sin 2α=1 2 ,∴sin 2α=12. 故选A. 答案:A2.(2012江南五校联考)设函数f(x)=sin x+cos x,f ′(x)是f(x)的导数,若f(x)=2f ′(x),则22sin sin 2cos x xx -= .解析:f ′(x)=cos x-sin x,由f(x)=2f ′(x)得 sin x+cos x=2cos x-2sin x, ∴cos x=3sin x,于是22sin sin 2cos x x x -=22sin 2sin cos cos x x x x-=222sin 6sin 9sin x x x -=-59. 答案:-593.(2013广东湛江一中等“十校”高三联考)设f(x)=6cos 2sin 2x,(1)求f(x)的最小正周期、最大值及f(x)取最大值时x 的集合;(2)若锐角α满足f(α,求tan 45α的值.解:(1)f(x)=6×1cos22x+sin 2xcos 2x-12sin 2x)+3cos(2x+π6)+3.故f(x)的最大值为+3, 此时2x+π6=2k π,x=k π-π12,k ∈Z, 即x 的集合为ππ,12x x k k Z ⎧⎫=-∈⎨⎬⎩⎭,最小正周期T=2π2=π.(2)由f(αcos(2α+π6,故cos(2α+π6)=-1,又由0<α<π2得π6<2α+π6<7π6,故2α+π6=π,解得α=512π.从而tan 45α=tanπ3=.综合检测1.(2012东北三校联考)设α、β都是锐角,且cos αα+β)=35,则cos β等于()解析:cos β=cos[(α+β)-α]=cos(α+β)cos α+sin(α+β)sin α.又α、β都是锐角,当cos α,sin α又sin(α+β)=3 5 ,因此cos(α+β)=±4 5 ,又cos α<1 2 ,∴α>60°,∴α+β>60°,∴cos(α+β)<1 2 ,故cos(α+β)=-4 5 ,∴cos β故选A.答案:A2.(2013安徽大江中学、开成中学高三联考)在斜三角形ABC中,sin Bcos C,且tan B·tan C=1-则角A的值为()(A)π4 (B)π3 (C)π2(D)3π4解析即sin sin cos cos B CB C∵∴=cos Bcos C+sin A.∴cos Bcos C-sin Bsin C=-sin A, ∴cos(B+C)=-sin A, ∴-cos A=-sin A, ∴tan A=1, ∴A=π4. 故选A. 答案:A第四节 三角函数的最值与综合应用高考试题考点一 三角函数的最值1.(2012年大纲全国卷,理14)当函数≤x<2π)取得最大值时,x= .解析cos x=2sin(x-π3), ∵0≤x<2π, ∴x-π3∈[-π3,5π3), ∴当x-π3=π2时,y 取得最大值2, ∴x=56π. 答案:56π2.(2011年上海卷,理8)函数y=sin(π2+x)cos(π6-x)的最大值为 . 解析:y=cos x ·cos(π6-x)12sin x)cos 2x+12sin xcos x+sin 24x1412sin(2x+π3),答案3.(2009年全国卷Ⅰ,理16)若π4<x<π2,则函数y=tan 2xtan 3x 的最大值为 . 解析:∵π4<x<π2,∴tan x>1, 令tan 2x-1=t>0,则y=tan 2xtan 3x=422tan 1tan x x -=()221t t+-=-2(t+1t +2)≤-8,当且仅当t=1t ,t=1时取等号. 答案:-84.(2011年北京卷,理15)已知函数f(x)=4cos xsin (x+π6)-1. (1)求f(x)的最小正周期; (2)求f(x)在区间[-π6,π4]上的最大值和最小值. 解:(1)因为f(x)=4cos x ·sin(x+π6)-1sin x+12cos x)-12x-1=2sin(2x+π6), 所以f(x)的最小正周期为π.(2)因为-π6≤x≤π4,所以-π6≤2x+π6≤2π3.于是,当2x+π6=π2,即x=π6时,f(x)取得最大值2;当2x+π6=-π6,即x=-π6时,f(x)取得最小值-1.5.(2012年重庆卷,理18)设函数f(x)=4cos(ωx-π6)sin ωx-cos(2ωx+π),其中ω>0.(1)求函数y=f(x)的值域;(2)若f(x)在区间[-3π2,π2]上为增函数,求ω的最大值.解ωx+12sin ωx)sin ωx+cos 2ωxsin ωxcos ωx+2sin2ωx+cos2ωx-sin2ωxωx+1,因-1≤sin 2ωx≤1,所以函数y=f(x)的值域为].(2)因为y=sin x在每个闭区间[2kπ-π2,2kπ+π2](k∈Z)上为增函数,故sin 2ωx+1(ω>0)在每个闭区间[kπω-π4ω,kπω+π4ω](k∈Z)上为增函数.依题意知[-3π2,π2]⊆[kπω-π4ω,kπω+π4ω]对某个k∈Z成立,此时必有k=0,于是3ππ,24ππ,24ωω⎧-≥-⎪⎪⎨⎪≤⎪⎩解得ω≤1 6 ,故ω的最大值为1 6 .6.(2013年陕西卷,理16)已知向量a=(cos x,-12sin x,cos 2x),x∈R,设函数f(x)=a·b.(1)求f(x)的最小正周期.(2)求f(x)在[0,π2]上的最大值和最小值.解:f(x)=(cos x,-12)·sin x,cos 2x)12cos 2xsin 2x-12cos 2x=cosπ6sin 2x-sin π6cos 2x =sin (2x-π6). (1)f(x)的最小正周期为T=2πω=2π2=π, 即函数f(x)的最小正周期为π. (2)∵0≤x ≤π2, ∴-π6≤2x-π6≤5π6. 由正弦函数的性质,知当2x-π6=π2, 即x=π3时,f(x)取得最大值1. 当2x-π6=-π6, 即x=0时,f(x)取得最小值-12, 因此,f(x)在[0,π2]上的最大值是1,最小值是-12.7.(2013年辽宁卷,理17)设向量sin x,sin x),b=(cos x,sin x),x ∈[0,π2]. (1)若|a|=|b|,求x 的值;(2)设函数f(x)=a ·b,求f(x)的最大值.解:(1)由|a|=|b| 即4sin 2x=1.又因为sin 2x+cos 2x=1,x ∈[0,π2]. 所以sin x=12,x=π6.(2)f(x)=a ·sin xcos x+sin 2x,x ∈[0,π2].1cos22x sin 2x-12cos 2x+12=sin(2x-π6)+12.又2x-π6∈[-π6,5π6],f(x)∈[0,32]. 即f(x)最大值为32.8.(2012年湖北卷,理17)已知向量a=(cos ωx-sin ωx,sin ωx),b=(-cos ωx-sin ωcos ωx),设函数f(x)=a ·b+λ(x ∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(12,1). (1)求函数f(x)的最小正周期; (2)若y=f(x)的图象经过点(π4,0),求函数f(x)在区间[0,3π5]上的取值范围.解:(1)因为f(x)=sin 2ωx-cos 2ωωx ·cos ωx+λ=-cos 2ωsin 2ωx+λ =2sin(2ωx-π6)+λ. 由直线x=π是y=f(x)图象的一条对称轴, 可得sin(2ωπ-π6)=±1, 所以2ωπ-π6=k π+π2(k ∈Z), 即ω=2k +13(k ∈Z). 又ω∈(12,1),k ∈Z, 所以k=1,故ω=56. 所以f(x)的最小正周期是6π5. (2)由y=f(x)的图象过点(π4,0), 得f(π4)=0, 即λ=-2sin(56×π2-π6)=-2sinπ4故f(x)=2sin(53x-π6由0≤x≤3π5,有-π6≤53x-π6≤5π6,所以-12≤sin(53x-π6)≤1,得2sin(53x-π6故函数f(x)在[0,3π5]上的取值范围为考点二三角函数的综合应用1.(2011年陕西卷,理6)函数在[0,+∞)内()(A)没有零点 (B)有且仅有一个零点(C)有且仅有两个零点(D)有无穷多个零点解析的解,即y=cos x交点的横坐标.在同一直角坐标系中分别作出函数y=cos x的图象,如图所示,由于x>1时≤1,所以两图象只有一个交点,在[0,+∞)内只有一个根,所以在[0,+∞)内只有一个零点.故选B.答案:B2.(2010年浙江卷,理9)设函数f(x)=4sin(2x+1)-x,则在下列区间中函数f(x)不存在零点的是()(A)[-4,-2] (B)[-2,0](C)[0,2] (D)[2,4]解析:在同一坐标系中画出g(x)=4sin(2x+1)与h(x)=x的图象如图所示.由图可知g(x)=4sin(2x+1)与h(x)=x 的图象在区间[-4,-2]上无交点, 即函数f(x)=4sin(2x+1)-x 在区间[-4,-2]上没有零点.故选A. 答案:A3.(2009年江苏卷,15)设向量a=(4cos α,sin α),b=(sin β,4cos β),c=(cos β,-4sin β). (1)若a 与b-2c 垂直,求tan(α+β)的值; (2)求|b+c|的最大值;(3)若tan αtan β=16,求证:a ∥b. 解:(1)∵a 与b-2c 垂直, ∴a ·(b-2c)=a ·b-2a ·c=0,∵a ·b=4sin βcos α+4cos βsin α=4sin(α+β), a ·c=4cos αcos β-4sin αsin β=4cos(α+β). ∴4sin(α+β)-8cos(α+β)=0, ∴tan(α+β)=2.(2)|b+c|2=sin 2β+2sin βcos β+cos 2β+16cos 2β-32cos βsin β+16sin 2β=17-30sin βcos β =17-15sin 2β. ∴2max b c +=32.∴|b+c|max(3)证明:∵tan αtan β=16, ∴sin αsin β=16cos αcos β, 即4cos α·4cos β-sin αsin β=0. ∴a ∥b.4.(2013年福建卷,理20)已知函数f(x)=sin(ωx+ϕ)(ω>0,0<ϕ<π)的周期为π,图象的一个对称中心为(π4,0),将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得到的图象向右平移π2个单位长度后得到函数g(x)的图象. (1)求函数f(x)与g(x)的解析式; (2)是否存在x 0∈(π6,π4),使得f(x 0),g(x 0),f(x 0)g(x 0)按照某种顺序成等差数列?若存在,请确定x 0的个数,若不存在,说明理由;(3)求实数a与正整数n,使得F(x)=f(x)+ag(x)在(0,nπ)内恰有2013个零点解:法一(1)由函数f(x)=sin(ωx+ϕ)的周期为π,ω>0,得ω=2πT=2.又曲线y=f(x)的一个对称中心为(π4,0),ϕ∈(0,π),故f(π4)=sin(2×π4+ϕ)=0,得ϕ=π2,所以f(x)=cos 2x.将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得y=cos x的图象,再将y=cos x的图象向右平移π2个单位长度后得到函数g(x)=cos(x-π2)的图象,所以g(x)=sin x.(2)当x∈(π6,π4)时,12,0<cos 2x<12,所以sin x>cos 2x>sin xcos 2x.问题转化为方程2cos 2x=sin x+sin xcos 2x在x∈(π6,π4)内是否有解.设G(x)=sin x+sin xcos 2x-2cos 2x,x∈(π6,π4),则G′(x)=cos x+cos xcos 2x+2sin 2x(2-sin x).因为x∈(π6,π4),所以G′(x)>0,G(x)在(π6,π4)内单调递增.又G(π6)=-14<0,G(π4>0,且函数G(x)的图象连续不断,故可知函数G(x)在(π6,π4)内存在唯一零点x0,即存在唯一的x0∈(π6,π4)满足题意.(3)依题意,F(x)=asin x+cos 2x,令F(x)=asin x+cos 2x=0.当sin x=0,即x=kπ(k∈Z)时,cos 2x=1,从而x=kπ(k∈Z)不是方程F(x)=0的解,所以方程F(x)=0等价于关于x的方程a=-cos2sinxx,x≠kπ(k∈Z).现研究x∈(0,π)∪(π,2π)时方程a=-cos2sinxx的解的情况.。
2012年高考真题汇编——理科数学(解析版)5:三角函数
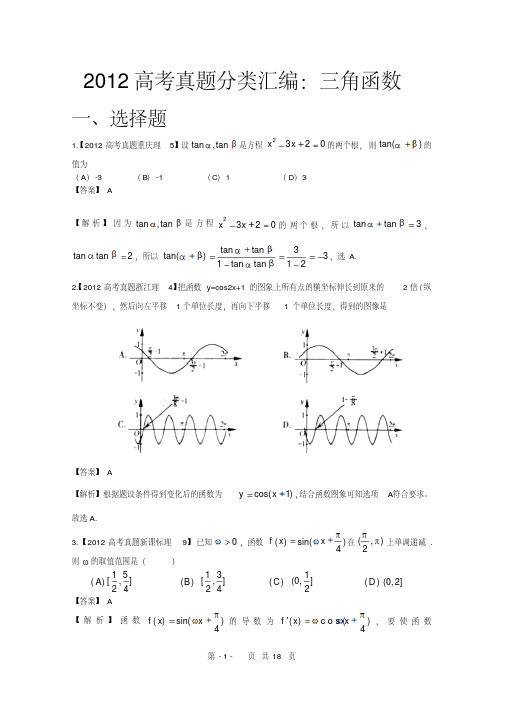
2 sin
cos
1 3 0, cos
, 所 以
2s i n c o s
2 3
0 , 因 为 已 知 α 为 第 二 象 限 角 , 所 以 sin 2 3 5 3 15 3 15 3
0 ,
sin
cos
1 2 sin
cos
1
,
所
以
c
2
c o
2
so s
2
(i s
sc n )
io s (
n )= s ic
a ,则另两边为 a
2
2 a,2 a .
2
所以最大角余弦
cos
2a 2a
2
4a 2a
2 4
3 5
,
19.【 2012 高考真题重庆理
13】 设
ABC 的内角 A , B , C 的对边分别为 a , b, c ,且 cos A
cos B
5 13
,b
3则 c
【答案】
14 5 3 5 5 13 4 5 12 13
2
, ) 上单调递减,则有 3 2k
, 即
f ' (x) 2k
cos( x x x
,选 A.
4 5 4
,又
)
0 恒成立, 2k x
, 所 以
2 2k
4 2k
2 ,k 1 2
4 0 时,
4 4 2 4 ,
4
,解得
Z ,当 k 5 4
,即
5 4
4. 【 2012 高考真题四川理
2 4 4 】 如图,正方形 ABCD 的边长为 1 ,延长 BA 至 E ,使 AE
(B) [
1 3 , ] 2 4
2012年高考数学分类汇编三角函数
2012年高考数学分类汇编三角函数一、选择题1 .(2012年高考(浙江文理))把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是???0)()?sin?xf(x个单位长度,(2012年高考(天津文))将函数的图像向右平移2 .4?3?,0)(的最小值是所得图像经过点 ,则()451 2 DC.. BA..1331?EAEABCDBA1连接,使,延长正方形3 .(2012年高考(四川文))如图,,的边长为至?CEDsin?ECED)则、(DC510510 CD.11110??x???(0?x?9)y?2sin)函数2012年高考(山东文)的最大值与最小4 .(??BEA36??值之和为()D.-1 B.0 C.A.3???231?????2??sincos2sin= ( ,5 .(2012 年高考(辽宁文))已知)(0,π),则22?? D... C.A11B22??5???xx??0=是函,直线和已标高.6 (2012年考(课文))知=>0,数44???)?x)?sin(xf(=,则()图像的两条相邻的对称轴πππ3πD. C.B.A .4234. ?)x?x)?sin(f(的图像的一条对称轴是( 7.(2012年高考(福建文))函数)4???????x?xxx??. BA...D C2244??x?????sin)f((x?)0,2??数纲文))若则函数,函高8.(2012年考(大是偶3)(????523 C. A.B.D.3322y?cos(2x?1)y?cos2x的图只要将函数的图象,年高考(安徽文)9.(2012)要得到函数象()B.向右平移1个单位 A.向左平移1个单位11个单位.向左平移个单位D.向右平移 C22?????)?,)xf()?sin((x0?.,已知函数在上单调递减10 .(2012年高考(新课标理))24?)则(的取值范围是15131](0,],[,][(0,2] C.BA...D 24224二、解答题11.(2012年高考(重庆文))(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)设函数????????x?0,sin(?x?)A?0,??(fx)?A处取得最大值2, )在其图(其中6?f(x)的解析式(I)求的轴象与的相邻两个交点距离为; (II)求函数242x??sin6cos1x?(x)g的值域.?)x?f(6???1?x?)f(x)?Asin(?0,0A?)的最大值为(3, 其(陕西文)2012.12(年高考)函数6?, 图像相邻两条对称轴之间的距离为2)xf(; 的解析式求函数(1)????2((0,?))?f. ,(2)求,则设的值22参考答案一、选择题A1. 【答案】,,具体考查了在x轴上的伸缩变换【命题意图】本题主要考查了三角函数中图像的性质.y轴上的平移变化,利用特殊点法判断图像的而变换在x轴、),2倍(纵坐标不变【解析】由题意,y=cos2x+1的图象上所有点的横坐标伸长到原来的为个单位平移一个单位为y=cos(x-1)+1,向下平移一向即解析式为y=cosx+1,左??????1,0,0?A. y=cos(x-1),利用特殊点变为,选????22????????????(x?))?sin?sin(x?)g(x)f(x?得到函数,【解析】函数向右平移2.4444???????333???(,?k0(?)0,)sin?(?)?因为此时函数过点,所以即,所以244444??Zk??2k,D.选的最小值为,所以2,]B答案3. [222?AD?AEAE?1,正方形的边长也为1?ED?[解析] 225?AB)?CBEC?(EA?1CD?222CD-ED?EC103???cos?CED10EC2ED?102??CED?CED?1?cossin1022的的范围决定其正余弦值的正负情α的使用,需要用sinα+cosα=1[点评]注意恒等式.况????7?x???9?x?0可知,可知4. 解析:由6363??3??x??],1)?[?sin(x?y?2sin??[?3,2],,则??36632??则最大值与最小值之和为,答案应选A. 32?5. 【答案】A2???????1sin2?cos,)?2,?sincos???2,(sin故选A【解析】【点评】本题主要考查三角函数中的倍角公式以及转化思想和运算求解能力,属于容易题.6. 【命题意图】本题主要考查三角函数的图像与性质,是中档题.?????5?????k?k?Z), 【解析】由题设知(=1,∴,,∴==?4424.??????Zk????0?k,∴=),∵故选=A. (,∴44C7. 【答案】???x??x?1?x)?f(.正确,答案代入后得到因而对称轴为【解析】把,C44. 代值逆推是主要解法【考点定位】此题主要考查三角函数的图像和性质,C答案8.,.????)f(x)?sin?20,()xf(y,【命题意图】本试题主要考查了偶函数的概念与三角函数图像性质??x【解析】由轴是函数为偶函数可知,图像的对称轴3故值时取得,函对称轴是在该数取得???????)(k?(0)f?sin???1???k3?k?Z0,2?0k?故,,而最而三角函数的????32323?3??C. 故选答案,时,21C1)?cos(2xy?cos2x?y?平移+1,9. 【解析】选左2A、【解析】选10???95??][?(,x?)??2)(D排除不合题意444???53??],x?)?[?1?()C(B)(排除合题意444???????3??????????]?[,])?2??([x?)?(?,:另 ,2242424?????531?????,??????:得4242422二、?577?([1,?),] 11. (Ⅰ)(Ⅱ)【答案】:44263112222[0,1]?cosx x????cosx1(cosx)cos因且,222.577(,)][1,)xg(的值域为故442A?23,A?1?f(x) 3,∴即的最大值为12. 解析:(1)∵函数???T ,∴最小正周期为∵函数图像的相邻两条对称轴之间的距离为2??1?x?)y?sin(22?)(xf的解析式为,∴故函数6???21?2sin()??f()? (2)∵62?1???sin()即26????????????0∵,∴3626????????∴故,366。
2012年高考真题汇编——理科数学(解析版)5:三角函数
2012高考真题分类汇编:三角函数一、选择题1.【2012高考真题重庆理5】设tan ,tan αβ是方程2320x x -+=的两个根,则tan()αβ+的值为(A )-3 (B )-1 (C )1 (D )3 【答案】A【解析】因为βαtan ,tan 是方程2320x x -+=的两个根,所以3tan tan =+βα,2tan tan =βα,所以3213tan tan 1tan tan )tan(-=-=-+=+βαβαβα,选A.2.【2012高考真题浙江理4】把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是【答案】A【解析】根据题设条件得到变化后的函数为)1cos(+=x y ,结合函数图象可知选项A 符合要求。
故选A.3.【2012高考真题新课标理9】已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减.则ω的取值范围是( )()A 15[,]24 ()B 13[,]24()C 1(0,]2 ()D (0,2]【答案】A【解析】函数)4sin()(πω+=x x f 的导数为)4c o s ()('πωω+=x x f ,要使函数)4sin()(πω+=x x f 在),2(ππ上单调递减,则有0)4cos()('≤+=πωωx x f 恒成立, 则πππωππk x k 223422+≤+≤+,即ππωππk x k 24524+≤≤+,所以Z k k x k ∈+≤≤+,ωπωπωπωπ2424,当0=k 时,ωπωπ454≤≤x ,又ππ<<x 2,所以有πωππωπ≥≤45,24,解得45,21≤≥ωω,即4521≤≤ω,选A. 4.【2012高考真题四川理4】如图,正方形ABCD 的边长为1,延长BA 至E ,使1AE =,连接EC 、ED 则sin CED ∠=( )A、10 B、10 C、10 D、15【答案】B【解析】2EB EA AB =+=,EC === 3424EDC EDA ADC πππ∠=∠+∠=+=,由正弦定理得sin sin 5CED DC EDC CE ∠===∠,所以3sin sin sin 4CED EDC π∠=∠==5.【2012高考真题陕西理9】在ABC ∆中,角,,A B C 所对边长分别为,,a b c ,若2222a b c +=,则cos C 的最小值为( )A.B. C. 12 D. 12- 【答案】C.【解析】由余弦定理知214242)(212cos 222222222=≥+=+-+=-+=ab ab ab b a ab b a b a ab c b a C ,故选C.6.【2012高考真题山东理7】若42ππθ⎡⎤∈⎢⎥⎣⎦,,sin 2=8θ,则sin θ=(A )35 (B )45 (C (D )34【答案】D【解析】因为]2,4[ππθ∈,所以],2[2ππθ∈,02cos <θ,所以812s i n 12c o s 2-=--=θθ,又81s i n 212c o s 2-=-=θθ,所以169sin 2=θ,43sin =θ,选D.7.【2012高考真题辽宁理7】已知sin cos αα-=α∈(0,π),则tan α=(A) -1 (B) 2- (C) 2(D) 1 【答案】A【解析一】sin cos )sin()144ππαααα-=-=∴-=3(0),,tan 14παπαα∈∴=∴=-,,故选A【解析二】2sin cos (sin cos )2,sin 21,ααααα-=-=∴=-33(0,),2(0,2),2,,tan 124ππαπαπααα∈∴∈∴=∴=∴=-,故选A 【点评】本题主要考查三角函数中的和差公式、倍角公式、三角函数的性质以及转化思想和运算求解能力,难度适中。
2012高考一轮复习——四川省各地市11年试题分类大汇编第3部分函数与导数
四川省各地市2011年高考数学最新联考试题分类大汇编第3部分:函数与导数 一、选择题:5.(四川省成都市外国语学校2011年3月高三考试理科)若函数()y f x =存在反函数1()y f x -=,且函数2()y x f x =-的图像过点(2,1),则函数1()2y f x x -=-的图象一定过点( D )A .(3,2)B .(2,3)-C .(4,3)-D .(3,4)-2. (四川省成都石室中学2011届髙三二诊模拟考试理科)当a 、b R 时,下列总能成立的是( B )(A) (B)(C) (D)5.(四川省成都石室中学2011届髙三二诊模拟考试理科)已知函数的反函数的图象的对称中心为(-1,5),则实数a 的是( D )(A) —3 (B) 1 (C) 5 (D) 710. (四川省成都石室中学2011届髙三二诊模拟考试理科)下图是的图象,则的值是( D )(A ) (B) (C) (D) 学科网ZXXK]11. (四川省成都石室中学2011届髙三二诊模拟考试理科)一给定函数的图象在下列图中,并且对任意,由关系式得到的数列满足,则该函数的图象是( A )2.(四川省成都市外国语学校2011年3月高三考试理科)命题p :若0a b ⋅<,则a 与b 的夹角为钝角。
命题q :定义域为R 的函数()f x 在(,0)-∞及(0,)+∞上都是增函数,则()f x 在(,)-∞+∞上是增函数。
下列说法正确的是( B )A .“p 或q ”是真命题B .“p 且q ”是假命题C .“p ⌝”为假命题D .“q ⌝”为假命题12.(四川省成都市外国语学校2011年3月高三考试理科)下列命题中:①函数()2()s i n (0,)s i n f x x x xπ=+∈的最小值是②在ABC ∆中,若sin2sin2A B =,则ABC ∆是等腰或直角三角形;③如果正实数,,a b c 满足a b c +>,则111a b c a b c +>+++;④如果()y f x =是可导函数,则0()0f x '=是函数()y f x =在0x x =处取到极值的必要不充分条件。
2012年高考真题理科数学解析分类汇编5三角函数
2012年高考真题理科数学解析分类汇编5 三角函数一、选择题1.【2012高考重庆理5】设tan ,tan αβ是方程2320x x -+=的两个根,则tan()αβ+的值为 (A )-3 (B )-1 (C )1 (D )3 【答案】A【解析】因为βαtan ,tan 是方程2320x x -+=的两个根,所以3tan tan =+βα,2tan tan =βα,所以3213tan tan 1tan tan )tan(-=-=-+=+βαβαβα,选A.2.【2012高考浙江理4】把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是【答案】A【解析】把函数y =cos2x +1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)得:y 1=cos x +1,向左平移1个单位长度得:y 2=cos(x +1)+1,再向下平移1个单位长度得:y 3=cos(x+1).令x =0,得:y 3>0;x =12-π,得:y 3=0;观察即得答案. 3.【2012高考新课标理9】已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减.则ω的取值范围是( )()A 15[,]24 ()B 13[,]24()C 1(0,]2 ()D (0,2]【答案】A【解析】法1:函数)4s i n()(πω+=x x f 的导数为)4c o s ()('πωω+=x x f ,要使函数)4s i n ()(πω+=x x f 在),2(ππ上单调递减,则有0)4cos()('≤+=πωωx x f 恒成立,则πππωππk x k 223422+≤+≤+,即ππωππk x k 24524+≤≤+,所以Z k k x k ∈+≤≤+,ωπωπωπωπ2424,当0=k 时,ωπωπ454≤≤x ,又ππ<<x 2,所以有πωππωπ≥≤45,24,解得45,21≤≥ωω,即4521≤≤ω,选A. 法2:选A592()[,]444x πππωω=⇒+∈ 不合题意 排除()D351()[,]444x πππωω=⇒+∈ 合题意 排除()()B C另:()22πωππω-≤⇔≤,3()[,][,]424422x ππππππωωπω+∈++⊂ 得:315,2424224πππππωπωω+≥+≤⇔≤≤ 4.【2012高考四川理4】如图,正方形ABCD 的边长为1,延长BA 至E ,使1AE =,连接EC 、ED 则sin CED ∠=( )A、10 B、10 C、10 D、15【答案】B【解析】2EB EA AB =+=,EC =3424EDC EDA ADC πππ∠=∠+∠=+=,由正弦定理得sin sin CED DC EDC CE ∠===∠,所以3sin sin sin 55410CED EDC π∠=∠==[点评]注意恒等式sin 2α+cos 2α=1的使用,需要用α的的范围决定其正余弦值的正负情况.5.【2012高考陕西理9】在ABC ∆中,角,,A B C 所对边长分别为,,a b c ,若2222a b c +=,则cos C 的最小值为( )A.B. C. 12 D. 12-【答案】C.【解析】由余弦定理知214242)(212cos 222222222=≥+=+-+=-+=ab ab ab b a ab b a b a ab c b a C ,故选C.6.【2012高考山东理7】若42ππθ⎡⎤∈⎢⎥⎣⎦,,sin 2θ,则sin θ=(A )35 (B )45 (C )4(D )34 【答案】D【解析】法1:因为]2,4[ππθ∈,所以],2[2ππθ∈,02cos <θ,所以812sin 12cos 2-=--=θθ,又81sin 212cos 2-=-=θθ,所以169sin 2=θ,43sin =θ,选D.法2:由42ππθ⎡⎤∈⎢⎥⎣⎦,及sin 2=8θ可得434716776916761687312sin 1cos sin +=++=+=+=+=+θθθ, 而当42ππθ⎡⎤∈⎢⎥⎣⎦,时θθcos sin >,结合选项即可得47cos ,43sin ==θθ.答案应选D ·7.【2012高考辽宁理7】已知sin cos αα-=α∈(0,π),则tan α=(A) -1 (B) (C) (D) 1 【答案】A【解析一】sin cos )sin()144ππαααα-=-=∴-=3(0),,tan 14παπαα∈∴=∴=-,,故选A【解析二】2sin cos (sin cos )2,sin 21,ααααα--=∴=-33(0,),2(0,2),2,,tan 124ππαπαπααα∈∴∈∴=∴=∴=-,故选A 【点评】本题主要考查三角函数中的和差公式、倍角公式、三角函数的性质以及转化思想和运算求解能力,难度适中·8.【2012高考江西理4】若tan θ+1tan θ=4,则sin2θ= A .15 B. 14 C. 13 D. 12【答案】D【命题立意】本题考查三角函数的倍角公式以及同角的三角函数的基本关系式·【解析】由4t an 1t an =+θθ得, 4cos sin cos sin sin cos cos sin 22=+=+θθθθθθθθ,即42s i n 211=θ,所以212s i n =θ,选D. 【点评】本题需求解正弦值,显然必须切化弦,因此需利用公式sin tan cos θθθ=转化;另外,22sin cos θθ+在转化过程中常与“1”互相代换,从而达到化简的目的;关于正弦、余弦的齐次分式,常将正弦、余弦转化为正切,即弦化切,达到求解正切值的目的. 体现考纲中要求理解三角函数的基本关系式,二倍角公式.来年需要注意二倍角公式的正用,逆用等. 9.【2012高考湖南理6】函数f (x )=sinx-cos(x+6π)的值域为A .2 , 2] 【答案】B【解析】f (x )=sinx-cos(x+6π)1sin sin )26x x x x π=+=-, []sin()1,16x π-∈-,()f x ∴值域为【点评】利用三角恒等变换把()f x 化成sin()A x ωϕ+的形式,利用[]sin()1,1x ωϕ+∈-,求得()f x 的值域.10.【2012高考上海理16】在ABC ∆中,若C B A 222sin sin sin <+,则ABC ∆的形状是( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .不能确定 【答案】C【解析】根据正弦定理可知由C B A 222sin sin sin <+,可知222c b a <+,在三角形中02c o s 222<-+=abc b a C ,所以C 为钝角,三角形为钝角三角形,选C.【点评】本题主要考查正弦定理及其推理、余弦定理的运用.主要抓住所给式子的结构来选择定理,如果出现了角度的正弦值就选择正弦定理,如果出现角度的余弦值就选择余弦定理.本题属于中档题. 11.【2012高考天津理2】设,R ∈ϕ则“0=ϕ”是“))(cos()(R x x x f ∈+=ϕ为偶函数”的 (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分与不必要条件 【答案】A【命题意图】本试题主要考查了三角函数的奇偶性的判定以及充分条件与必要条件的判定.【解析】函数)cos()(ϕ+=x x f 若为偶函数,则有Z k k ∈=,πϕ,所以“0=ϕ”是“)cos()(ϕ+=x x f 为偶函数”的充分不必要条件,选A.12.【2012高考天津理6】在ABC ∆中,内角A ,B ,C 所对的边分别是c b a ,,,已知8b=5c ,C=2B ,则cosC=(A )257 (B )257- (C )257± (D )2524【答案】A【命题意图】本试题主要考查了正弦定理、三角函数中的二倍角公式. 考查学生分析、转化与计算等能力.【解析】因为B C 2=,所以B B B C co s sin 2)2sin (sin ==,根据正弦定理有BbC c sin sin =,所以58sin sin ==B C b c ,所以545821s i n 2s i n c o s =⨯==B C B ·又1cos 2)2cos(cos 2-==B B C ,所以2571251621cos 2cos 2=-⨯=-=B C ,选A.13.【2012高考全国卷理7】已知α为第二象限角,33cos sin =+αα,则cos2α=(A) (B ) (C) 【答案】A【命题意图】本试题主要考查了三角函数中两角和差的公式以及二倍角公式的运用·首先利用平方法得到二倍角的正弦值,然后然后利用二倍角的余弦公式,将所求的转化为单角的正弦值和余弦值的问题· 【解析】因为33cos sin =+αα所以两边平方得31cos sin 21=+αα,所以032cos sin 2<-=αα,因为已知α为第二象限角,所以0c o s,0s i n <>αα,31535321cos sin 21cos sin ==+=-=-αααα,所以)s i n )(co s s i n (c o s s i n c o s 2c os 22ααααααα+-=-==3533315-=⨯-,选A.二、填空题14.【2012高考湖南理15】函数f (x )=sin (x ωϕ+)的导函数()y f x '=的部分图像如图4所示,其中,P 为图像与y 轴的交点,A,C 为图像与x 轴的两个交点,B 为图像的最低点.(1)若6πϕ=,点P 的坐标为(0,则ω= ; (2)若在曲线段ABC 与x 轴所围成的区域内随机取一点,则该点在△ABC 内的概率为 .【答案】(1)3;(2)4π【解析】(1)()y f x '=cos()x ωωϕ=+,当6πϕ=,点P 的坐标为(0)时cos36πωω=∴=; (2)由图知222T AC ππωω===,122ABCS AC πω=⋅=,设,A B 的横坐标分别为,a b . 设曲线段ABC与x 轴所围成的区域的面积为S则()()sin()sin()2bbaaS f x dx f x a b ωϕωϕ'===+-+=⎰,由几何概型知该点在△ABC 内的概率为224ABCSP Sππ===. 【点评】本题考查三角函数的图像与性质、几何概型等,(1)利用点P 在图像上求ω, (2)几何概型,求出三角形面积及曲边形面积,代入公式即得.15.【2012高考湖北理11】设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c . 若()()a b c a b c ab +-++=,则角C = . 【答案】32π 考点分析:考察余弦定理的运用.【解析】222222a =-a -ab 12cos =,2223a b c ba b c C C ab ab π+-+-==-∠=由(+b-c )(a+b-c)=ab,得到根据余弦定理故16.【2012高考北京理11】在△ABC 中,若a =2,b+c=7,cosB=41-,则b=_______· 【答案】4【解析】在△ABC 中,利用余弦定理cb c b c ac b c a B 4))((4412cos 222-++=-⇒-+= c b c 4)(74-+=,化简得:0478=+-b c ,与题目条件7=+c b 联立,可解得⎪⎩⎪⎨⎧===243a b c .17.【2012高考安徽理15】设ABC ∆的内角,,A B C 所对的边为,,a b c ;则下列命题正确的是_____①若2ab c >;则3C π<②若2a b c +>;则3C π<③若333a b c +=;则2C π<④若()2a b c ab +<;则2C π>⑤若22222()2a b c a b +<;则3C π>【答案】①②③【命题立意】本题解三角形的知识,主要涉及余弦定理与基本不等式的运算· 【解析】正确的是_____①222221cos 2223a b c ab ab ab c C C ab ab π+-->⇒=>=⇒< ②2222224()()12cos 2823a b c a b a b a b c C C ab ab π+-+-++>⇒=>≥⇒< ③当2C π≥时,22232233c a b c a c b c a b ≥+⇒≥+>+与333a b c +=矛盾④取2,1a b c ===满足()2a b c ab +<得:2C π<⑤取2,1a b c ===满足22222()2a b c a b +<得:3C π<18.【2012高考福建理13】已知△ABC_________. 【答案】42-. 【命题立意】本题考查了解三角形和等比数列的相关知识,难度适中. 【解析】设最小边长为a ,则另两边为a a 2,2.所以最大角余弦422242cos 222-=⋅-+=aa a a a α 19.【2012高考重庆理13】设ABC ∆的内角,,A B C 的对边分别为,,abc ,且53co s =A ,135cos =B ,3=b 则c =【答案】514 【解析】因为53cos =A ,135cos =B ,所以54s i n=A ,1312sin =B ,655653131213554)sin(sin =⨯+⨯=+=B A C ,根据正弦定理C c B b sin sin =得655613123c =,解得514=c . 20.【2012高考上海理4】若)1,2(-=是直线l 的一个法向量,则l 的倾斜角的大小 为 (结果用反三角函数值表示)· 【答案】2arctan【解析】设倾斜角为α,由题意可知,直线的一个方向向量为(1,2),则2tan =α, ∴α=2arctan ·【点评】本题主要考查直线的方向向量、直线的倾斜角与斜率的关系、反三角函数的表示.直线的倾斜角的取值情况一定要注意,属于低档题,难度较小. 21.【2012高考全国卷理14】当函数取得最大值时,x=___________.【答案】65π=x 【命题意图】本试题主要考查了三角函数性质的运用,求解值域的问题·首先化为单一三角函数,然后利用定义域求解角的范围,从而结合三角函数图像得到最值点· 【解析】函数为)3sin(2cos 3sin π-=-=x x x y ,当π20<≤x 时,3533πππ<-≤-x ,由三角函数图象可知,当23ππ=-x ,即65π=x 时取得最大值,所以65π=x . 22.【2012高考江苏11】(5分)设α为锐角,若4cos 65απ⎛⎫+= ⎪⎝⎭,则)122sin(π+a 的值为 ▲ .【考点】同角三角函数,倍角三角函数,和角三角函数· 【解析】∵α为锐角,即02<<πα,∴2=66263<<πππππα++·∵4cos 65απ⎛⎫+= ⎪⎝⎭,∴3sin 65απ⎛⎫+= ⎪⎝⎭·∴3424sin 22sin cos =2=3665525αααπππ⎛⎫⎛⎫⎛⎫+=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭·∴7cos 2325απ⎛⎫+= ⎪⎝⎭·∴sin(2)=sin(2)=sin 2cos cos 2sin 12343434a a a a πππππππ⎛⎫⎛⎫++-+-+ ⎪ ⎪⎝⎭⎝⎭ 2427217==2252550-三、解答题23.【2012高考新课标理17】(本小题满分12分)已知,,a bc 分别为ABC ∆三个内角,,A B C 的对边,cos sin 0a C C b c --= (1)求A (2)若2a =,ABC ∆的面积为3;求,b c .【答案】(1)由正弦定理得:cos sin 0sin cos sin sin sin a C C b c A C A C B C --=⇔=+sin cos sin sin()sin 1cos 1sin(30)2303060A C A C a C CA A A A A ︒︒︒︒⇔+=++⇔-=⇔-=⇔-=⇔=(2)1sin 42S bc A bc ==⇔= 2222cos 4a b c bc A b c =+-⇔+=24.【2012高考湖北理17】(本小题满分12分)已知向量(c os s in x x x ωωω=-a ,(cos sin ,)x x x ωωω=--b ,设函数()f x λ=⋅+a b ()x ∈R 的图象关于直线πx =对称,其中ω,λ为常数,且1(,1)2ω∈.(Ⅰ)求函数()f x 的最小正周期;(Ⅱ)若()y f x =的图象经过点π(,0)4,求函数()f x在区间3π[0,]5上的取值范围.【答案】(Ⅰ)因为22()sin cos cos f x x x x xωωωωλ=-+⋅+cos22x x ωωλ=-+π2sin(2)6x ωλ=-+.由直线πx =是()y f x =图象的一条对称轴,可得πsin(2π)16ω-=±,所以ππ2ππ()62k k ω-=+∈Z ,即1()23k k ω=+∈Z .又1(,1)2ω∈,k ∈Z ,所以1k =,故56ω=.所以()f x 的最小正周期是6π5.(Ⅱ)由()y f x =的图象过点π(,0)4,得π()04f =,即5πππ2sin()2sin 6264λ=-⨯-=-=,即λ=故5π()2sin()36f x x =-由3π05x ≤≤,有π5π5π6366x -≤-≤,所以15πsin()1236x -≤-≤,得5π12sin()236x --≤故函数()f x 在3π[0,]5上的取值范围为[12-.25.【2012高考安徽理16】)(本小题满分12分)设函数2())sin 4f x x x π=++· (I )求函数()f x 的最小正周期; (II )设函数()g x 对任意x R ∈,有()()2g x g x π+=,且当[0,]2x π∈时, 1()()2g x f x =-,求函数()g x 在[,0]π-上的解析式·【答案】本题考查两角和与差的三角函数公式、二倍角公式、三角函数的周期等性质、分段函数解析式等基础知识,考查分类讨论思想和运算求解能力·【解析】2111())sin cos 2sin 2(1cos 2)24222f x x x x x x π=++=-+- 11sin 222x =-, (I )函数()f x 的最小正周期22T ππ== (2)当[0,]2x π∈时,11()()sin 222g x f x x =-=当[,0]2x π∈-时,()[0,]22x ππ+∈ 11()()sin 2()sin 22222g x g x x x ππ=+=+=- 当[,)2x ππ∈--时,()[0,)2x ππ+∈ 11()()sin 2()sin 222g x g x x x ππ=+=+=得函数()g x 在[,0]π-上的解析式为1sin 2(0)22()1sin 2()22x x g x x x πππ⎧--≤≤⎪⎪=⎨⎪-≤<⎪⎩·26.【2012高考四川理18】(本小题满分12分)函数2()6cos3(0)2xf x x ωωω=+->在一个周期内的图象如图所示,A 为图象的最高点,B 、C 为图象与x 轴的交点,且ABC ∆为正三角形· (Ⅰ)求ω的值及函数()f x 的值域;(Ⅱ)若0()5f x =,且0102(,)33x ∈-,求0(1)f x +的值·【答案】本题主要考查三角函数的图像与性质、同角三角函数的关系、两角和差公式,倍角公式等基础知识,考查基本运算能力,以及数形结合思想,化归与转化思想. [解析](Ⅰ)由已知可得:2()6cos3(0)2xf x x ωωω=+->=3cosωx+)3sin(32sin 3πωω+=x x又由于正三角形ABC 的高为23,则BC=4 所以,函数482824)(πωωπ===⨯=,得,即的周期T x f所以,函数]32,32[)(-的值域为x f ·……………………6分 (Ⅱ)因为,由538)(0=x f (Ⅰ)有 ,538)34(sin 32)(00=+=ππx x f 54)34(s i n 0=+ππx 即 由x 0)2,2()34x (323100ππππ-∈+-∈),得,( 所以,53)54(1)34(cos 20=-=+ππx 即 故=+)1(0x f =++)344(sin 320πππx ]4)34(sin[320πππ++x)22532254(324sin)34cos(4cos )34([sin 3200⨯+⨯=+++=ππππππx x567=………………………………………………………12分 27.【2012高考陕西理16】(本小题满分12分) 函数()sin()16f x A x πω=-+(0,0A ω>>)的最大值为3, 其图像相邻两条对称轴之间的距离为2π, (1)求函数()f x 的解析式; (2)设(0,)2πα∈,则()22f α=,求α的值· 【解析】(Ⅰ)∵函数()f x 的最大值是3,∴13A +=,即2A =·∵函数图像的相邻两条对称轴之间的距离为2π,∴最小正周期T π=,∴2ω=· 故函数()f x 的解析式为()2sin(2)16f x x π=-+·(Ⅱ)∵()2f α2sin()126πα=-+=,即1sin()62πα-=, ∵02πα<<,∴663πππα-<-<,∴66ππα-=,故3πα=·28.【2012高考广东理16】(本小题满分12分) 已知函数)6cos(2)(πω+=x x f ,(其中ω>0,x ∈R )的最小正周期为10π.(1)求ω的值; (2)设]2,0[,πβα∈,56)355(-=+παf ,1716)655(=-πβf ,求cos (α+β)的值. 【答案】本题考查三角函数求值,三角恒等变换,利用诱导公式化简三角函数式与两角和的余弦公式求值,难度较低· 【解析】(1)21105T ππωω==⇔=(2)56334(5)cos()sin ,cos 352555f ππαααα+=-⇔+=-⇔== 516815(5)cos ,sin 6171717f πβββ-=⇔== 4831513cos()cos cos sin sin 51751785αβαβαβ+=-=⨯-⨯=-29.【2012高考山东理17】(本小题满分12分)已知向量(sin ,1),(3cos ,cos 2)(0)3Am x n A x x A ==>,函数()f x m n =⋅的最大值为6. (Ⅰ)求A ;(Ⅱ)将函数()y f x =的图象向左平移12π个单位,再将所得图象上各点的横坐标缩短为原来的12倍,纵坐标不变,得到函数()y g x =的图象.求()g x 在5[0,]24π上的值域. 解:(Ⅰ)()=⋅f x m nsin cos cos 2212cos 2)2sin(2)A x x xA x x A x π=+=+=+6因为 0A >,由题意知 6A =.(Ⅱ)由(I )()6sin(2)f x x π=+6将()y f x =的图象向左平移π12个单位后得到6sin[2()]6sin(2)y x x πππ=++=+1263的图象;再将得到图象上各点横坐标缩短为原来的12倍,纵坐标不变,得到6sin(4)y x π=+3的图象.因此()6sin(4)g x x π=+3,因为5[0,]x π∈24,所以74[,]x πππ+∈336,所以1sin(4)[,1]2x π+∈-3,所以()g x 在5[0,]π24上的值域为[3,6]-.30.【2012高考北京理15】(本小题共13分)已知函数xxx x x f sin 2sin )cos (sin )(-=·(1)求)(x f 的定义域及最小正周期; (2)求)(x f 的单调递减区间· 解(1):si n 0()x x k k Z π≠⇔≠∈得:函数()f x 的定义域为{,}x x k k Z π≠∈(sin cos )sin 2()(sin cos )2cos sin x x xf x x x x x-==-⨯sin 2(1cos 2))14x x x π=-+=--得:)(x f 的最小正周期为22T ππ==; (2)函数sin y x =的单调递增区间为[2,2]()22k k k Z ππππ-+∈ 则322224288k x k k x k πππππππππ-≤-≤+⇔-≤≤+得:)(x f 的单调递增区间为3[,),(,]()88k k k k k Z ππππππ-+∈ 31.【2012高考重庆理18】(本小题满分13分(Ⅰ)小问8分(Ⅱ)小问5分) 设)2cos(sin )6cos(4)(x x x x x f +--=ωωπω,其中.0>ω(Ⅰ)求函数)(x f y = 的值域 (Ⅱ)若)(x f y =在区间⎥⎦⎤⎢⎣⎡-2,23πx 上为增函数,求 ω的最大值.解:(1)()14sin sin cos 22f x x x x x ωωωω⎫=++⎪⎪⎝⎭222cos 2sin cos sin x x x x x ωωωωω=++-21x ω=+因1sin 21x ω-≤≤,所以函数()y f x =的值域为1⎡⎣(2)因s i n y x =在每个闭区间()2,222k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦上为增函数,故()21f x x ω=+()0ω>在每个闭区间(),44k k k Z ππππωωωω⎡⎤-+∈⎢⎥⎣⎦上为增函数· 依题意知3,22ππ⎡⎤-⊆⎢⎥⎣⎦,44k k ππππωωωω⎡⎤-+⎢⎥⎣⎦对某个k Z ∈成立,此时必有0k =,于是 32424ππωππω⎧-≥-⎪⎪⎨⎪≤⎪⎩,解得16ω≤,故ω的最大值为16· 32.【2012高考浙江理18】(本小题满分14分)在∆ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A =23,sin BC .(Ⅰ)求tan C 的值;(Ⅱ)若a∆ABC 的面积.【答案】本题主要考查三角恒等变换,正弦定理,余弦定理及三角形面积求法等知识点· (Ⅰ)∵cos A =23>0,∴sin A,C =sin B =sin(A +C )=sin A cos C +sin C cos Acos C +23sin C .整理得:tan C(Ⅱ)由图辅助三角形知:sin C又由正弦定理知:sin sin a cA C=,故c = (1)对角A 运用余弦定理:cos A =222223b c a bc +-=. (2)解(1) (2)得:b =or b 舍去).∴∆ABC 的面积为:S . 33.【2012高考辽宁理17】(本小题满分12分)在ABC ∆中,角A 、B 、C 的对边分别为a ,b ,c ·角A ,B ,C 成等差数列· (Ⅰ)求cos B 的值;(Ⅱ)边a ,b ,c 成等比数列,求sin sin A C 的值·【命题意图】本题主要考查等差数列、等比数列概念、正余弦定理应用,是容易题.【解析】(1)由已知12=+,++=,=,cos =32B AC A B C B B ππ∴ ……6分(2)解法一:2=b ac ,由正弦定理得23sin sin =sin =4A C B解法二:2=b ac ,222221+-+-=cos ==222a c b a c ac B ac ac ,由此得22+-=,a c ac ac 得=a c所以===3A B C π,3sin sin =4A C ……12分【点评】本题主要考查三角形的正弦定理、余弦定理、三角形内角和定理及等差、等比数列的定义,考查转化思想和运算求解能力,属于容易题·第二小题既可以利用正弦定理把边的关系转化为角的关系,也可以利用余弦定理得到边之间的关系,再来求最后的结果· 34.【2012高考江西理17】(本小题满分12分) 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ·已知,sin()sin()444A b C cB a πππ=+-+=(1)求证: 2B C π-=(2)若a =△ABC 的面积·解:(1)证明:由 sin()sin()44b Cc B a ππ+-+=及正弦定理得:sin sin()sin sin()sin 44B C C B A ππ+-+=,即sin (sin )sin ()22222B C C C B B +-+=整理得:sin cos cos sin 1B C B C -=,所以sin()1B C -=,又30,4B C π<< 所以2B C π-=(2)由(1)及34B C π+=可得5,88B C ππ==,又,4A a π== 所以sin 5sin 2sin ,2sin sin 8sin 8a B a Cbc A A ππ====,所以三角形ABC 的面积151sin sin cos 28888242bc A πππππ===== 【点评】本题考查解三角形,三角形的面积,三角恒等变换、三角和差公式以及正弦定理的应用.高考中,三角解答题一般有两种题型:一、解三角形:主要是运用正余弦定理来求解边长,角度,周长,面积等;二、三角函数的图像与性质:主要是运用和角公式,倍角公式,辅助角公式进行三角恒等变换,求解三角函数的最小正周期,单调区间,最值(值域)等.来年需要注意第二种题型的考查.35.【2012高考全国卷理17】(本小题满分10分)三角形ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,已知cos (A-C )+cosB=1,a=2c ,求c.【命题意图】本试题主要考查了解三角形的运用,给出两个公式,一个是边的关系,一个角的关系,而求解的为角,因此要找到角的关系式为好· 【解析】由()A B C B A C ππ++=⇔=-+, 由正弦定理及2a c =可得sin 2sin A C =所以cos()cos cos()cos(())cos()cos()A C B A C A C A C A C π-+=-+-+=--+cos cos sin sin cos cos sin sin 2sin sin A C A C A C A C A C =+-+=故由cos()cos 1A C B -+=与sin 2sin A C =可得22sin sin 14sin 1A C C =⇒= 而C 为三角形的内角且2a c c =>,故02C π<<,所以1sin 2C =,故6C π=· 【点评】该试题从整体来看保持了往年的解题风格,依然是通过边角的转换,结合了三角形的内角和定理的知识,以及正弦定理和余弦定理,求解三角形中的角的问题·试题整体上比较稳定,思路也比较容易想,先将三角函数关系式化简后,得到,A C 角关系,然后结合2a c =,得到两角的二元一次方程组,自然很容易得到角C 的值· 36.【2012高考天津理15】(本小题满分13分)已知函数.,1cos 2)32sin()32sin()(2R x x x x x f ∈-+-++=ππ(Ⅰ)求函数)(x f 的最小正周期; (Ⅱ)求函数)(x f 在区间]4,4[ππ-上的最大值和最小值.【解析】(1)2()=sin (2+)+sin(2)+2cos 133f x x x x ππ--2sin 2coscos 2)34x x x ππ=+=+ 函数()f x 的最小正周期为22T ππ==(2)32sin(2)11()444444x x x f x ππππππ-≤≤⇒-≤+≤⇒≤+≤⇔-≤≤当2()428x x πππ+==时,()max f x 2()444x x πππ+=-=-时,min ()1f x =-【点评】该试题关键在于将已知的函数表达式化为=sin (+)y A x ωϕ的数学模型,再根据此三角模型的图像与性质进行解题即可.37.【2012高考江苏15】(14分)在ABC ∆中,已知3AB AC BA BC =. (1)求证:tan 3tan B A =;(2)若cos C =求A 的值. 【答案】解:(1)∵3AB AC BA BC =,∴cos =3cos AB AC A BA BC B ,即cos =3cos AC A BC B ·由正弦定理,得=sin sin AC BCB A,∴sin cos =3sin cos B A A B · 又∵0<A B <π+,∴cos 0 cos 0A >B >,·∴sin sin =3cos cos B AB A即tan 3tan B A =·(2)∵ cos 0C <C <π=,∴sin C =·∴tan 2C =· ∴()tan 2A B π⎡-+⎤=⎣⎦,即()tan 2A B +=-·∴tan tan 21tan tan A BA B+=--·由 (1) ,得24tan 213tan AA=--,解得1tan =1 tan =3A A -,· ∵cos 0A >,∴tan =1A ·∴=4A π·【考点】平面微量的数量积,三角函数的基本关系式,两角和的正切公式,解三角形·【解析】(1)先将3AB AC BA BC =表示成数量积,再根据正弦定理和同角三角函数关系式证明·(2)由cos C =可求tan C ,由三角形三角关系,得到()tan A B π⎡-+⎤⎣⎦,从而根据两角和的正切公式和(1)的结论即可求得A 的值·。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四川省各地市2011年高考数学最新联考试题分类大汇编第5部分:三角函数 一、选择题:1.(四川省成都市外国语学校2011年3月高三考试理科)函数sin (3sin 4cos ) ()y x x x x R =+∈的最大值为M ,最小正周期为T ,则有序数对(,)M T 为( B )A .(5,)πB .(4,)πC .(1,2)π-D .(4,2)π1.(四川省成都市外国语学校2011年3月高三考试文科)函数sin (3sin 4cos ) ()y x x x x R =+∈的最大值为M ,最小正周期为T ,则有序数对(,)M T 为( B )A .(5,)πB .(4,)πC .(1,2)π-D .(4,2)π5.(四川省资阳市资阳中学2011年高三第一次高考模拟文科)若tan 2α=,则2sin cos sin 2cos αααα-+的值为(B )(A )12 (B )34 (C )1 (D )542.(四川省资阳市资阳中学2011年高三第一次高考模拟文科) “cos 0θ<且tan 0θ>”是“θ为第三象限角”的( A )(A )充要条件 (B )必要不充分条件(C )充分不必要条件(D )既不充分也不必要条件12.(四川省成都市外国语学校2011年3月高三考试理科)下列命题中:①函数()2()sin (0,)sin f x x x xπ=+∈的最小值是22②在ABC ∆中,若sin2sin2A B =,则ABC ∆是等腰或直角三角形;③如果正实数,,a b c满足a b c +>,则111a b c a b c +>+++;④如果()y f x =是可导函数,则0()0f x '=是函数()y f x =在0x x =处取到极值的必要不充分条件。
其中正确的命题是( C )A .①②③④B .①④C .②③④D .②③5、(四川省泸州高中2011届高三一模适应性考试理科)设ω>0,函数y=sin(ωx+3π)+2的图像向右平移34π个单位后与原图像重合,则ω的最小值是( C ) A 23 B 43 C 32 D 34. (四川省泸州高中2011届高三一模适应性考试文科)已知x x x x f cos sin sin )(2+=,则)(x f 的最小正周期和一个单调增区间分别为 ( C )A.π,[0,π]B. 2π,[-4π,43π]C.π, [-8π,83π]D. 2π,[-4π,4π]7. (四川省泸州高中2011届高三一模适应性考试文科)在⊿ABC 中,若sin2A=sin2B,则⊿ABC 的形状是( C )A .等腰三角形B .直角三角形C .等腰三角形或直角三角形D .等腰直角三角形[来源:] 1.(四川省南充市2011届高三第一次高考适应性考试理科)若以集合(a,b,c 均为正数)中三个元素为边长构成一个三角形,则该三角形一 定不可能是( D ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.等腰三角形6.(四川省攀枝花市七中2011届高三下学期开学考试文科)为了得到函数sin(2)6y x π=+的图象,只需把函数x y 2sin =的图象 ( D )A .向左平移6π个长度单位B .向右平移6π个长度单位C .向右平移3π个长度单位D .向左平移12π个长度单位2.(四川省2011届普通高考考生知识能力水平摸底测试一理科)为了得到函数3sin(2),5y x x Rπ=+∈的图象,只需把函数3sin(),5y x x Rπ=+∈的图象上所有的点的( B )A .横坐标伸长到原来的2倍,纵坐标不变B .横坐标缩短到原来的12倍,纵坐标不变C .纵坐标伸长到原来的2倍,横坐标不变D .纵坐标缩短到原来的12倍,横坐标不变4.(四川省2011届普通高考考生知识能力水平摸底测试一文科)下列函数中最小正周期是π的函数是 (D )[来源:] A .sin cos y x x =+ B .sin cos y x x =-C .|sin ||cos |y x x =+D .|sin cos |t x x =+二、填空题:13.(四川省成都市外国语学校2011年3月高三考试理科)已知a 、b 、c 分别是ABC ∆的三个内角A 、B 、C 所对的边,若cos cos 2B bC a c =-+,则B = 。
23π[来源:学科网]15.(四川省资阳市资阳中学2011年高三第一次高考模拟文科)在ABC ∆中,3A π∠=,3BC =,6AB =则C ∠=________.4π16.(四川省成都市外国语学校2011年3月高三考试理科)下面给出的四个命题中:①对任意的*n N ∈,点(,)n n P n a 都在直线21y x =+上是数列{}n a 为等差数列的充分不必要条件; ②“2m =-”是直线(2)10m x my +++=与“直线(2)(2)30m x m y -++-=相互垂直”的必要不充分条件;③设圆22220(40)x y Dx Ey F D E F ++++=+->与坐标轴有4个交点1(,0)A x ,2(,0)B x ,1(0,)C y ,2(0,)D y ,则有12120x x y y -=;④将函数cos2y x =的图象向右平移3π个单位,得到函数sin(2)6y x π=-的图象。
[来源:学|科|网Z|X|X|K]其中是真命题的有 (将你认为正确的序号都填上)。
①③④[来源:学#科#网] 13.(四川省成都市外国语学校2011年3月高三考试文科)已知a 、b 、c 分别是ABC ∆的三个内角A 、B 、C 所对的边,若cos cos 2B bC a c =-+,则B = 。
23π14、(四川省泸州高中2011届高三一模适应性考试理科)在锐角三角形ABC ,A 、B 、C 的对边分别为a 、b 、c ,6cos b a C a b +=,则tan tan tan tan C CA B +=___2_ 。
三、解答题:18.(四川省成都市外国语学校2011年3月高三考试理科)(本小题满分12分)在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA )的变化情况来决定买入或卖出股票。
股民老王在研究股票的走势图时,发现一只股票的MA 均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy ,则股价y (元)和时间x 的关系在ABC 段可近似地用解析式sin()(0)y a x b ωϕϕπ=++<<来描述,从C 点走到今天的D 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D 点和C 点正好关于直线:34l x =对称。
老王预计这只股票未来的走势如图中虚线所示,这里DE 段与ABC 段关于直线l 对称,EF 段是股价延续DE 段的趋势(规律)走到这波上升行情的最高点F 。
现在老王决定取点 (0,22)A ,点 (12,19)B ,点 (44,16)D 来确定解析式中的常数,,,a b ωϕ,并且已经求得72πω=。
(1)请你帮老王算出,,a b ϕ,并回答股价什么时候见顶(即求F 点的横坐标);(2)老王如能在今天以D 点处的价格买入该股票5000股,到见顶处F 点的价格全部卖出,不计其它费用,这次操作他能赚多少元?18.解:(1),C D 关于直线l 对称C ∴点坐标为(23444, 16)⨯-,即(24, 16),把A 、B 、C 的坐标代入解析式,得18.(四川省成都市外国语学校2011年3月高三考试文科)(本小题满分12分)在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线(记作MA )的变化情况来决定买入或卖出股票。
股民老王在研究股票的走势图时,发现一只股票的MA 均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xoy ,则股价y (元)和时间x 的关系在ABC 段可近似地用解析式sin()(0)y a x b ωϕϕπ=++<<来描述,从C 点走到今天的D 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D 点和C 点正好关于直线:34l x =对称。
老王预计这只股票未来的走势如图中虚线所示,这里DE 段与ABC 段关于直线l 对称,EF 段是股价延续DE 段的趋势(规律)走到这波上升行情的最高点F 。
现在老王决定取点 (0,22)A ,点 (12,19)B ,点 (44,16)D 来确定解析式中的常数,,,a b ωϕ,并且已经求得72πω=。
(1)请你帮老王算出,,a b ϕ,并回答股价什么时候见顶(即求F 点的横坐标);(2)老王如能在今天以D 点处的价格买入该股票5000股,到见顶处F 点的价格全部卖出,不计其它费用,这次操作他能赚多少元?18.解:(1),C D 关于直线l 对称C ∴点坐标为(23444, 16)⨯-,即(24, 16),把A 、B 、C 的坐标代入解析式,得22sin 19sin()616sin()3a b a ba b ϕπϕπϕ⎧⎪=+⎪⎪=++⎨⎪⎪=++⎪⎩①②③ 。
②-①得[sin()sin ]36a πϕϕ+-=-,③-①得[sin()sin ]63a πϕϕ+-=-,2sin()2sin sin()sin 63ππϕϕϕϕ∴+-=+-33cos 3in sin 2s ϕϕϕϕ∴+=+。
333(1(3)sin 3(1)sin 2ϕϕϕ∴-==-,3tan ϕ∴=0ϕπ<< 566ππϕπ∴=-=, 代入②得19b =,再由①得6a =。
6,19a b ∴==,56πϕ=。
于是,ABC 段的解析式为56sin()19726y x ππ=++,由对称性得,DEF 段的解析式为56sin[(68)]19726y x ππ=-++。
5(68)7262F x πππ∴-+=,解得92F x =。
∴当92x =时,股价见顶。
(2)由(1)可知,61925F y =+= ,故这次操作老王能赚5000(2516)45 000⨯-=元。
18.(四川省资阳市资阳中学2011年高三第一次高考模拟文科)(本小题满分12分)已知函数()sin()f x A x ωϕ=+(0A >,0ω>,0ϕπ<<)在6x π=取得最大值2,方程()0f x =的两个根为1x 、2x ,且12||x x -的最小值为π. (Ⅰ)求()f x ;(Ⅱ)将函数()y f x =图象上各点的横坐标压缩到原来的12,纵坐标不变,得到函数()y g x =的图象,求函数()g x 在[,]44ππ-上的值域.[来源:]17、(四川省泸州高中2011届高三一模适应性考试理科)(本小题满分12分)设函数()22cos 2cos ,32x f x x x Rπ⎛⎫=++∈ ⎪⎝⎭。
