著名的数学公式总结
小升初数学的常用计算公式总结

小升初数学的常用计算公式总结
小升初数学的常用计算公式总结
常用计算公式表
1.长方形面积=长×宽,计算公式S=ab
2.正方形面积=边长×边长,计算公式S=a×a=a2
3.长方形周长=(长+宽)×2,计算公式C=(a+b)×2
4.正方形周长=边长×4,计算公式C=4a
5.平行四边形面积=底×高,计算公式S=ah
6.三角形面积=底×高÷2,计算公式S=a×h÷2
7.梯形面积=(上底+下底)×高÷2,计算公式S=(a+b)×h÷2
8.长方体体积=长×宽×高,计算公式V=abh
9.圆的面积=圆周率×半径平方,计算公式V=πr2
10.正方体体积=棱长×棱长×棱长,计算公式V=a3
11.长方体和正方体的体积都可以写成底面积×高,计算公式V=sh
12.圆柱的体积=底面积×高,计算公式V=sh
下载全文。
数学史上神奇的公式

数学史上神奇的公式
1. 欧拉公式:e^(i*pi)+1=0。
欧拉公式将自然对数e、圆周率π、虚数单位i和实数1联系在了一起,形成一条神奇的等式,其美学上的意义远超实际应用。
2.黄金分割数公式:(1+√5)/2。
黄金分割数公式是一种极具美感的比例关系,广泛存在于自然界、美术和建筑设计等领域,同时也是一些数学难题的核心。
3. 柯西-斯瓦舍定理:f(a)=1/2πi∮C(f(z)/(z-a)dz)。
柯西-斯瓦舍定理是复分析中最重要的定理之一,它描述了复变函数在复平面内的积分和函数值之间的关系,为解决多种复分析问题提供了有效的工具。
4.美哉分数连分式:φ=1+1/(1+1/(1+1/(1+……)))。
美哉分数连分式是一个可以无限展开的分数,它可以近似表示黄金分割,同时在求某些不可约分数的时候也有实用价值。
5.费马大定理:a^n+b^n=c^n(当n≥3时无整数解)。
费马大定理是数论中最著名的问题之一,经过几百年的研究,最终在20世纪被证明,同时也催生出了许多重要的数学工具和方法。
实用的初中数学公式总结归纳

实用的初中数学公式总结归纳虽说,数学的学习,不讲求死记硬背,但是最起码的公式是必须要掌握的,任何一门学科基础总是最重要的。
下面是小编为大家整理的关于实用的初中数学公式,希望对您有所帮助!初中三角函数知识点提纲一锐角三角函数定义锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),余割(csc)都叫做角A的锐角三角函数。
正弦(sin):对边比斜边,即sinA=a/c余弦(cos):邻边比斜边,即cosA=b/c正切(tan):对边比邻边,即tanA=a/b余切(cot):邻边比对边,即cotA=b/a正割(sec):斜边比邻边,即secA=c/b余割(csc):斜边比对边,即cscA=c/a二特殊角三角函数值三三角函数关系互余角的关系sin(90°-α)=cosα, cos(90°-α)=sinα,tan(90°-α)=cotα, cot(90°-α)=tanα.平方关系sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)积的关系sinα=tanα·cosαcosα=cotα·sinαtanα=sinα·secαcotα=cosα·cscαsecα=tanα·cscαcscα=secα·cotα倒数关系tanα·cotα=1sinα·cscα=1cosα·secα=1四锐角三角函数公式两角和差公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB)tan(A-B) = (tanA-tanB)/(1+tanAtanB)cot(A+B) = (cotAcotB-1)/(cotB+cotA)cot(A-B) = (cotAcotB+1)/(cotB-cotA)三角和的公式sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)倍角公式tan2A = 2tanA/(1-tan? A)Sin2A=2SinA?CosACos2A = Cos^2 A--Sin? A =2Cos? A-1 =1-2sin^2 A三倍角公式sin3A = 3sinA-4(sinA)?;cos3A = 4(cosA)? -3cosAtan3a = tan a ? tan(π/3+a)? tan(π/3-a)半角公式sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα积化和差公式sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]和差化积公式sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]万能公式sin(a) = [2tan(a/2)] / {1+[tan(a/2)]?}cos(a) = {1-[tan(a/2)]^2} / {1+[tan(a/2)]?}tan(a) = [2tan(a/2)]/{1-[tan(a/2)]^2}推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=(sinα/2+cosα/2)^2初中数学几何公式1 同角或等角的余角相等2 过一点有且只有一条直线和已知直线垂直3 过两点有且只有一条直线4 两点之间线段最短5 同角或等角的补角相等6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180°18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22边角边公理有两边和它们的夹角对应相等的两个三角形全等23 角边角公理有两角和它们的夹边对应相等的两个三角形全等24 推论有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理有三边对应相等的两个三角形全等26 斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合30 等腰三角形的性质定理等腰三角形的两个底角相等31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于60°34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35 推论1 三个角都相等的三角形是等边三角形36 推论 2 有一个角等于60°的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a+b=c47勾股定理的逆定理如果三角形的三边长a、b、c有关系a+b=c,那么这个三角形是直角三角形48定理四边形的内角和等于360°49四边形的外角和等于360°50多边形内角和定理 n边形的内角的和等于(n-2)×180°51推论任意多边的外角和等于360°52平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(a×b)÷267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78 平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81 三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82 梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=(a+b)÷2 S=L×h83 (1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d84 (2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85 (3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b86 平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87 推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88 定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90 定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA)92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93 判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)94 判定定理3 三边对应成比例,两三角形相似(SSS)95 定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96 性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97 性质定理2 相似三角形周长的比等于相似比98 性质定理3 相似三角形面积的比等于相似比的平方99 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107到已知角的两边距离相等的点的轨迹,是这个角的平分线108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三个点确定一条直线110垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧111推论1①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧②弦的垂直平分线经过圆心,并且平分弦所对的两条弧③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧112推论2 圆的两条平行弦所夹的弧相等113圆是以圆心为对称中心的中心对称图形114定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等115推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等116定理一条弧所对的圆周角等于它所对的圆心角的一半117推论1 同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等118推论2 半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径119推论3 如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形120定理圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角121①直线L和⊙O相交 d﹤r②直线L和⊙O相切 d=r③直线L和⊙O相离 d﹥r122切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线123切线的性质定理圆的切线垂直于经过切点的半径124推论1 经过圆心且垂直于切线的直线必经过切点125推论2 经过切点且垂直于切线的直线必经过圆心126切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角127圆的外切四边形的两组对边的和相等128弦切角定理弦切角等于它所夹的弧对的圆周角129推论如果两个弦切角所夹的弧相等,那么这两个弦切角也相等130相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等初中数学公式及公式定理乘法与因式分a2-b2=(a+b)(a-b)a3+b3=(a+b)(a2-ab+b2)a3-b3=(a-b(a2+ab+b2)三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a-b-√(b2-4ac)/2a根与系数的关系X1+X2=-b/a X1__X2=c/a注:韦达定理判别式b2-4ac=0注:方程有两个相等的实根b2-4>0注:方程有两个不等的实根b2-4ac<0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c__h斜棱柱侧面积S=c'__h正棱锥侧面积S=1/2c__h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi__r2圆柱侧面积S=c__h=2pi__h圆锥侧面积S=1/2__c__l=pi__r__l 弧长公式l=a__r a是圆心角的弧度数r>0扇形面积公式s=1/2__l__r锥体体积公式V=1/3__S__H圆锥体体积公式V=1/3__pi__r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s__h圆柱体V=pi__r2h常见的初中数学公式1过两点有且只有一条直线2两点之间线段最短3同角或等角的补角相等4同角或等角的余角相等5过一点有且只有一条直线和已知直线垂直6直线外一点与直线上各点连接的所有线段中,垂线段最短7平行公理经过直线外一点,有且只有一条直线与这条直线平行8如果两条直线都和第三条直线平行,这两条直线也互相平行9同位角相等,两直线平行10内错角相等,两直线平行11同旁内角互补,两直线平行12两直线平行,同位角相等13两直线平行,内错角相等14两直线平行,同旁内角互补15定理三角形两边的和大于第三边16推论三角形两边的差小于第三边17三角形内角和定理三角形三个内角的和等于180°实用的初中数学公式。
初中数学实用的公式总结(优秀6篇)

初中数学实用的公式总结(优秀6篇)(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如计划报告、合同协议、心得体会、演讲致辞、条据文书、策划方案、规章制度、教学资料、作文大全、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays, such as plan reports, contract agreements, insights, speeches, policy documents, planning plans, rules and regulations, teaching materials, complete essays, and other sample essays. If you would like to learn about different sample formats and writing methods, please stay tuned!初中数学实用的公式总结(优秀6篇)总结是事后对某一时期、某一项目或某些工作进行回顾和分析,从而做出带有规律性的结论,它是增长才干的一种好办法,让我们好好写一份总结吧。
解方程公式法的公式

解方程公式法的公式解方程是数学中常见的问题之一,公式法是其中一种常用的解题方法。
这种方法是基于一些已经发现的数学规律和性质,通过将方程中的未知数用一个或多个变量表示,然后根据一系列的等式和不等式关系进行一系列的代数变换,最终得出方程的解。
在解方程的过程中,可以使用一些常见的公式,下面将详细介绍其中一些常用的公式。
1.一元二次方程的求根公式:对于形如ax^2+bx+c=0的方程,其中a、b、c为已知常数,x为未知数,可以使用求根公式来解方程。
x = (-b ± √(b^2-4ac))/(2a)2.一元一次方程的解法:对于形如ax+b=0的一元一次方程,可以直接通过变形得到解。
x=-b/a3.二元一次方程组的解法:对于形如a1x+b1y=c1a2x+b2y=c2的二元一次方程组,可以利用克拉默法则来求解。
x=(c1b2-c2b1)/(a1b2-a2b1)y=(a1c2-a2c1)/(a1b2-a2b1)4.三元一次方程组的解法:对于形如a1x+b1y+c1z=d1a2x+b2y+c2z=d2a3x+b3y+c3z=d3的三元一次方程组,可以使用克拉默法则或矩阵法来求解。
5.二次三项式完全平方式:对于形如(a+b)^2的二次三项式,可以利用平方式来展开,得到如下公式:(a+b)^2 = a^2 + 2ab + b^26.二次三项式差平方式:对于形如(a-b)^2的二次三项式,可以利用差平方式来展开,得到如下公式:(a-b)^2 = a^2 - 2ab + b^27.二次三项式完全立方方式:对于形如(a+b)^3的二次三项式,可以利用完全立方方式来展开,得到如下公式:(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^38.二次三项式差立方方式:对于形如(a-b)^3的二次三项式,可以利用差立方方式来展开,得到如下公式:(a-b)^3 = a^3 - 3a^2b + 3ab^2 - b^39.欧拉公式:欧拉公式是数学中著名的公式之一,表示了数学中的常见数学常数e 与虚数单位i和三角函数之间的关系。
最出名的数学公式

最出名的数学公式数学的世界就像一个神秘的大花园,里面长满了各种各样奇妙的公式。
而在这众多的公式当中,有那么几个可谓是大名鼎鼎,家喻户晓。
要说最出名的数学公式,那勾股定理肯定能占一席之地。
勾股定理说的是直角三角形两条直角边的平方和等于斜边的平方。
也就是我们常说的“a² + b² = c²”。
这公式看似简单,却有着无比强大的力量。
我记得有一次去朋友家做客,他家的小孩正在为一道数学题抓耳挠腮。
题目是这样的:一个直角三角形的两条直角边分别是 3 和 4,求斜边的长度。
我一看,这不是正好可以用勾股定理嘛!于是我就跟小朋友说:“别着急,咱们用勾股定理来试试。
”小朋友一脸迷茫地看着我。
我就耐心地给他解释:“你看啊,两条直角边分别是 3 和 4,那咱们就先算出 3 的平方是 9,4 的平方是 16,然后把它们加起来,9 + 16 = 25,这个 25 就是斜边的平方啦。
那斜边是多少呢?就是 25 的平方根 5 呀。
”小朋友听了之后,眼睛一下子亮了起来,兴奋地说:“原来是这样,太神奇啦!”看到他那开心的样子,我也感到特别有成就感。
还有一个不得不提的著名公式,那就是爱因斯坦的质能方程 E=mc²。
这个公式揭示了质量和能量之间的等价关系,简直是物理学中的一颗璀璨明珠。
曾经有一次在物理课堂上,老师给我们讲了这个公式背后的故事。
他说爱因斯坦当年提出这个公式的时候,可是引起了轩然大波。
大家都觉得这太不可思议了,怎么质量和能量能相互转换呢?但是随着科学的不断发展,这个公式被一次次地验证,成为了现代物理学的重要基石。
再来说说圆的周长公式C = 2πr 。
想象一下,你去买一个甜甜圈,老板告诉你这个甜甜圈的半径是多少,你马上就能算出它的周长,是不是感觉很厉害?我有一次去面包店买面包,看到展示柜里有一个特别漂亮的圆形蛋糕。
我就好奇地问老板这个蛋糕的半径,老板告诉我是 10 厘米。
我心里马上就开始计算,2×3.14×10 = 62.8 厘米,我就跟老板说:“这个蛋糕的周长大概是 62.8 厘米呢。
你觉得最经典的数学公式是什么?
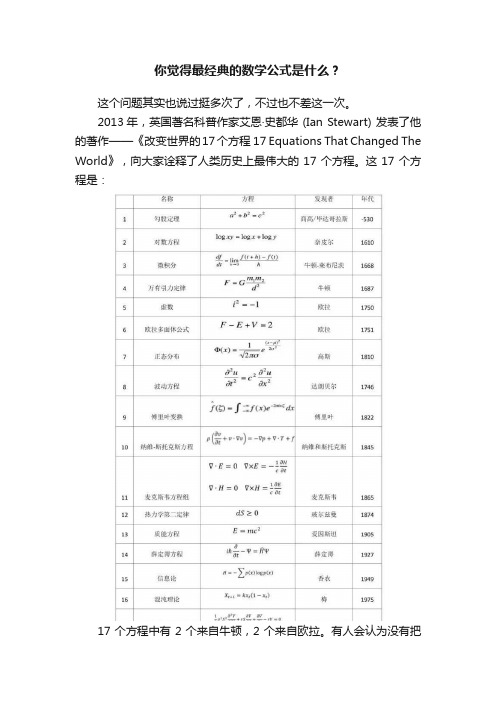
你觉得最经典的数学公式是什么?这个问题其实也说过挺多次了,不过也不差这一次。
2013年,英国著名科普作家艾恩·史都华 (Ian Stewart) 发表了他的著作——《改变世界的17个方程 17 Equations That Changed The World》,向大家诠释了人类历史上最伟大的17个方程。
这17个方程是:17个方程中有2个来自牛顿,2个来自欧拉。
有人会认为没有把欧拉恒等式e^iπ+ 1 = 0 纳入是一大疏忽,欧拉把数学中最基本的5个常数——0、1、圆周率π、自然对数的底e和虚数单位i,以及数学中最基本的两个符号,等号和加号,通过一个简单的恒等式联系在了一起,实在是让人叹服,欧拉恒等式被誉为世界上最美丽的公式。
史都华选中了i^2= -1,可能在《改变世界》和《美》之间他更注重前者。
如果把《改变世界》和《美》折中一下,并且只选择100年前的数学方程,同时抛开在物理、信息论等方面应用的话,可以得到以下10个方程或等式:人类花了千万年来从数量转向数字,数字概念的诞生是一个漫长的思维抽象的过程。
至少3万年以前,人类就已经会计数了,这是人之所以为人的重要转折点,是人类与动物的根本区别之一。
公元前8千年左右,算术诞生了,人类渐渐走上了科学之路,虽然路漫漫其修远兮,但上下求索,一发不可收拾。
1+ 1 = 2 对世界的改变是巨大的,故把它选入放于首位。
至于《爱情曲线》,它源于一个传说:法国数学家笛卡尔在1649年欧洲大陆爆发黑死病时流浪到瑞典,在斯德哥尔摩的街头,52岁的笛卡尔邂逅了18岁的瑞典公主克里斯汀。
几天后,他意外的接到通知,国王聘请他做小公主的数学老师。
跟随前来通知的侍卫一起来到皇宫,他见到了在街头偶遇的女孩子。
从此,他当上了小公主的数学老师。
小公主的数学在笛卡尔的悉心指导下突飞猛进,笛卡尔向她介绍了自己研究的新领域——直角坐标系。
每天形影不离的相处使他们彼此产生爱慕之心,公主的父亲国王知道了后勃然大怒,下令将笛卡尔处死,小公主克里斯汀苦苦哀求后,国王将其流放回法国,克里斯汀公主也被父亲软禁起来。
高等数学极限的公式总结

高等数学极限的公式总结在高等数学中,极限的公式是非常重要的概念,这些公式能够帮助我们理解函数的极限,并进行极限的运算。
以下是一些常见的高等数学极限的公式总结:1. 极限的四则运算性质:lim(a+b) = lim a + lim blim(a-b) = lim a - lim blim(ab) = lim a lim b (假设lim a 和 lim b都存在)lim(a/b) = lim a / lim b (假设lim b 不等于0)2. 极限的常数性质:lim a = a (当a是一个常数)3. 极限的单调性:lim(f(x0+delta x) - f(x0)) / delta x = f'(x0) (当delta x -> 0)4. 连续函数的性质:如果f(x)在x0处连续,那么lim f(x) = f(x0) 当 x -> x05. 无穷小量与无穷大量:当x -> 0时,x是无穷小量,1/x是无穷大量。
6. 洛必达法则:如果lim (f'(x)/g'(x))存在,那么lim (f(x)/g(x)) = lim (f'(x)/g'(x)) (当x->a时)。
7. 泰勒公式:对于任何n阶可导函数f(x),存在一个多项式Pn(x),使得对于所有-∞ < x < ∞,有f(x) = Pn(x) + o(x^n),其中o(x^n)是高阶无穷小。
8. 夹逼准则:如果存在一个区间或闭区间[a, b],满足f(a) <= g(a), f(b) >= g(b),并且lim f(x) = lim g(x),则lim g(x)存在,并且lim g(x) = lim f(x)。
9. 无穷大与无穷小的关系:lim x -> ∞ f(x) = lim x -> ∞ f(x) (如果存在的话)lim x -> ∞ f(x) = 0 (如果lim x -> ∞ f(x)存在的话)10. 极限的唯一性:对于任意给定的正数ε,总存在一个正数δ,使得当x - x0 < δ时,有f(x) - A < ε。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
同时主验证验证此公式,可透过因式分解,首先运用环的原理,设以下公式:然后代入:透过因式分解,可得:这样便可验证:和立方验证透过和立方可验证立方和的原理:那即是只要减去及便可得到立方和,可设:右边的方程运用因式分解的方法:这样便可验证出:几何验证图象化透过绘立体的图像,也可验证立方和。
根据右图,设两个立方,总和为:把两个立方体对角贴在一起,根据虚线,可间接得到:要得到,可使用的空白位置。
该空白位置可分割为3个部分:∙∙∙把三个部分加在一起,便得:之后,把减去它,便得:上公式发现两个数项皆有一个公因子,把它抽出,并得:可透过这样便可证明反验证透过也可反验证立方和。
以上计算方法亦可简化为一个表格:这样便可证明1. 把因式分解∙把两个数项都转为立方:∙运用立方和可得:2. 把因式分解∙把两个数项都转为立方:∙运用立方和便可得:∙但这个并非答案,因为答案仍可被因式分解:∙亦可使用另一个方法来减省步骤。
首先把公因子抽出:∙直接使用立方和,并得:立方差立方差也可以使用立方和来验证,例如:运用负正得负,可得:然后运用立方和,可得:这个方法更可验证到立方差的公式是平方差及的排列并不重要,可随意排放。
来验证。
先设及。
那即是,同时运用了若上列公式是的话,就得到以下公式:以上运用了,也即是两方是相等,就得到:注:塞尔伯格迹公式空间的函数空间上某类算子的,其中而设为紧致、负常曲率曲面,这类曲面可以表为上半平面对的某离散子群的商。
考虑上的拉普拉斯算子由于为紧曲面,该算子有离散谱;换言之,下式定义的值至多可数事实上,更可将其由小至大排列:对应的特征函数,并满足以下周期条件:行变元代换于是特征值可依排列。
塞尔伯格迹公式写作和式中的取遍所有双曲共轭类。
所取函数须满足下述性质:∙在带状区域上为解析函数,在此为某常数。
∙偶性:。
∙满足估计:,在此为某常数。
函数是的。
后续发展的尖点问题提供了纯粹的代数框架。
最后,为紧的情形可藉处理,然而,一旦取泰勒公式称为指数函数在0处的n阶泰勒展开公式。
这个公式只对0附近的x有用,x离0越远,这个公式就越不准确。
实际函数值和多项式的偏差称为泰勒公式的余项。
对于一般的函数,泰勒公式的系数的选择依赖于函数在一点的各阶导数值。
这个想法的原由可以由微分的定义开始。
微分是函数在一点附近的最佳线性近似:,其中也就是说,或。
注意到和在a处的零阶导数和一阶导数都相同。
对足够光滑的函数,如果一个多项式在a处的前n次导数值都与函数在a处的前n次导数值重合,那么这个多项式应该能很好地近似描述函数在a附近的情况。
以下定理说明这是正确的:定理:设n是一个正整数。
如果函数f是区间[a, b] 上的n阶连续可微函数,并且在区间[a, b) 上n+1 次可导,那么对于[a, b) 上的任意x,都有:[2]其中的多项式称为函数在a处的泰勒展开式,剩余的是泰勒公式的余项,是的高阶无穷小。
的表达形式有若干种,分别以不同的数学家命名。
带有皮亚诺型余项的泰勒公式说明了多项式和函数的接近程度:也就是说,当x无限趋近a时,余项将会是的高阶无穷小,或者说多项式和函数的误差将远小于[3]。
这个结论可以由下面更强的结论推出。
带有拉格朗日型余项的泰勒公式可以视为拉格朗日微分中值定理的推广:即,其中[4]。
带有积分型余项的泰勒公式可以看做微积分基本定理的推广[5]:余项估计拉格朗日型余项或积分型余项可以帮助估计泰勒展开式和函数在一定区间之内的误差。
设函数在区间[a−r, a + r]上n次连续可微并且在区间(a−r, a + r) 上n + 1 次可导。
如果存在正实数M n使得区间(a−r, a + r) 里的任意x都有,那么:其中。
这个上界估计对区间(a−r, a + r) 里的任意x都成立,是一个一致估计。
如果当n趋向于无穷大时,还有,那么可以推出,f是区间(a−r, a + r) 上解析函数。
f在区间(a−r, a + r) 上任一点的值都等于在这一点的泰勒展开式的极限。
对所有,其中的α 是多重指标。
其中的余项也满足不等式:对所有满足|α| = n + 1 的α,π的莱布尼茨公式证明初等证明考虑如下分解对于|x| < 1,右侧的分式是余下的几何级数的和。
然而,上面的方程并没有包含无穷级数,并且对任何实数x成立。
上式两端从0到1积分可得:当时,除积分项以外的项收敛到莱布尼茨级数。
同时,积分项收敛到0:当这便证明了莱布尼茨公式。
乘法公式:。
:。
:。
:。
:。
:。
:。
:。
9.10. 。
二倍角公式二倍角公式是数学三角函数中常用的一组公式,通过角的三角函数值的一些变换关系来表示其二倍角的三角函数值,二倍角公式包括正弦二倍角公式、余弦二倍角公式以及正切二倍角公式。
二倍角公式均可通过和角公式推出。
此式就是正弦二倍角公式:余弦二倍角公式余弦二倍角公式有三组表示形式,三组形式等价:正切二倍角公式此式就是正切二倍角公式:全概率公式又因为条件概率的期望值在离散情况下,上述公式等于下面这个公式。
但后者在连续情况下仍然成立:此处N是任意随机变量。
这个公式还可以表达为:全期望公式1.验证验证方法与两数和平方差不多,可透过多项式乘法验证:透过几何验证也同样,根据右图将所有部分加在一起:因式分解因式分解,在数学中一般理解为把一个多项式分解为两个或多个的因式的过程。
在这个过后会得出一堆较原式简单的多项式的积。
两个平方之和或两个平方之差(请参见平方差)根据以上两条恒等式,如原式符合以上条件,即可运用代用法直接分解。
两个n次方数之和与差两个立方数之和可分解为两个立方数之差可分解为两个n次方数之差两个奇数次方数之和一次因式检验法一个整系数的一元多项式,假如它有整系数因式,且p,q互质,则以下两条必成立:(逆叙述并不真)∙∙不过反过来说,即使当和都成立时,整系数多项式也不一定是整系数多项式的因式另外一个看法是:一个整系数的n次多项式,若是f(x)之因式,且p,q互质,则:(逆叙述并不真)∙∙因式定理指出,一个多项式有一个因式当且仅当。
因式定理普遍应用于找到一个多项式的因式或多项式方程的根的两类问题。
从定理的推论结果,这些问题基本上是等价的。
若多项式已知一个或数个零点,因式定理也可以移除多项式中已知零点的部份,变成一个阶数较低的多项式,其零点即为原多项式中剩下的零点,以简化多项式求根的过程。
方法如下:1. 先设法找出多项式的一个零点。
2. 利用因式定理确认是多项式的因式。
3. 利用长除法计算多项式。
4. 中,所有满足条件的根都是方程式的根。
因为的多项式阶数较要小。
因此要找出多项式的零点可能会比较简单。
另外欲使A=BQ+R成立,就令除式BQ=0,则被除式A=R,能使此方程式成立,被除式=(商式)(除式)+余式or被除式/除式=商式+余式/除式外尔特征标公式外尔特征标公式(Weyl's character formula) 描述紧李群不可约表示的特征标。
其名来自证明者赫尔曼·外尔。
定义:群G的表示r的特征标为一函数,,其中Tr为线性算子之迹。
(由彼得-外尔定理可知紧李群的任何不可约表示都是有限维的;故迹之定义为线性代数中之定义。
)特征标χ 记住了表示r本身的重要讯息。
外尔特征标公式用群G的其他资料来表达χ 。
本文考虑复表示,不失一般亦设其为酉表示,因而―不可约‖亦等价于―不可分解‖(即非二子表示之直和)。
其中在1 维表示的特例中,特征标为1, 而外尔特征标公式简化成外尔分母公式:。
外尔维度公式若只考虑单位元1之迹,则外尔特征标公式特殊化成外尔维数公式,其中∙VΛ为有限维表示,其最高权为Λ;∙ρ为外尔向量,∙α 遍历所有正根。
由于式中分子与分母俱为高阶零,故必须取G中之元素渐近单位元1时之极限。
;其中∙Λ 为一最高权,∙λ 为另一权,∙dim Vλ为权λ 之重数,∙ρ 为外尔向量,∙外和中之α 历遍所有正根。
外尔-Kac 特征标公式其中S为一修正项:所有与最高权正交、且互相正交之有限子。
Peterson 发现了(广义)可对称化[3]卡茨-穆迪代数之根重数mult(β)递归公式。
此公式等价于外尔-卡茨分母公式,但更便于计算:,其中γ 与δ 遍历所有正根,而。
婆罗摩笈多公式婆罗摩笈多公式的最简单易记的形式,是圆内接四边形面积计算。
若圆内接四边形的四边长为a, b, c, d,则其面积为:证明圆内接四边形的面积= 的面积+ 的面积但由于是圆内接四边形,因此。
故。
所以:对和利用余弦定理,我们有:代入(这是由于和是互补角),并整理,得:把这个等式代入面积的公式中,得:它是的形式,因此可以写成的形式:引入,两边开平方,得:证毕。
更特殊情况若圆O的圆内接四边形的四边长为a, b, c, d,且外切于圆C,则其面积为:证明由于四边形内接于圆O,所以:其中p为半周长:又因为四边形外切圆C,所以:则:同理:,,综上:证毕。
对一般四边形的面积,扩展的婆罗摩笈多公式用到了四边形的对角和:其中是四边形一对角和的一半。
(选取另一对角也不会影响答案,因其和的一半是。
而,所以。
)因为圆内接四边形的对角和为,,而,所以项为零,给出公式的基本形式。
差分到概念。
差分的定义差分的定义分为前向差分和逆向差分两种。
前向差分函数的前向差分通常简称为函数的差分。
对于函数,如果:,则称为的一阶前向差分。
在微积分学中的有限差分(的解法相似。
当是逆向差分对于函数,如果:则称为的一阶逆向差分。
称为的阶差分,即前向阶差分,如果根据数学归纳法,有其中,为二项式系数。
特别的,有∙线性:如果和为常数,则有∙乘法定则:∙除法定则:或∙级数:牛顿数列牛顿数列(级数),也称作牛顿前向差分方程是一个以数学与物理学家牛顿命名的函数关系。
具体为:为的阶差立方主验证差立方可直接计算验证:以上计算方式便可证明:布巴克尔多项式有时也会使用另一种定义,可以通过递归的方式进行定义。
首先,规定前三个布巴克尔多项式为:生成解布巴克尔多项式的通解为 :微分操作代表布巴克尔多项式亦可记为 :布雷特施奈德公式在公式当中, a, b, c, d均是四边形的边长, s则是半周界,亦即是a+ b+c+ d再除以2, 而 and 则是其中两个对角。
半周界一个四边形在几何学当中, 布雷特施奈德公式是一条任意四边形的面积公式:设四边形的面积为A。
由此得到因此这亦可改写为接着在中代入这亦可改写为刚才半周界的公式因此上式成为得证。
弗莱纳公式在向量微积分中,弗莱纳公式(Frenet–Serret 公式)用来描述欧几里得空间R3中的粒子在连续可微曲线上的运动。
更具体的说,弗莱纳公式描述了曲线的切向,法向,副法方向之间的关系。
单位切向量T,单位法向量N,单位副法向量B,被称作弗莱纳标架,他们的具体定义如下:弗莱纳公式如下:由于假设r′ ≠ 0,因此可以将t表示为s的函数,因此可将曲线表示为弧长s的函数r(s) = r(t(s))。
