某地典型风电功率数据
各地区风能_微_畜力发电情况(1)
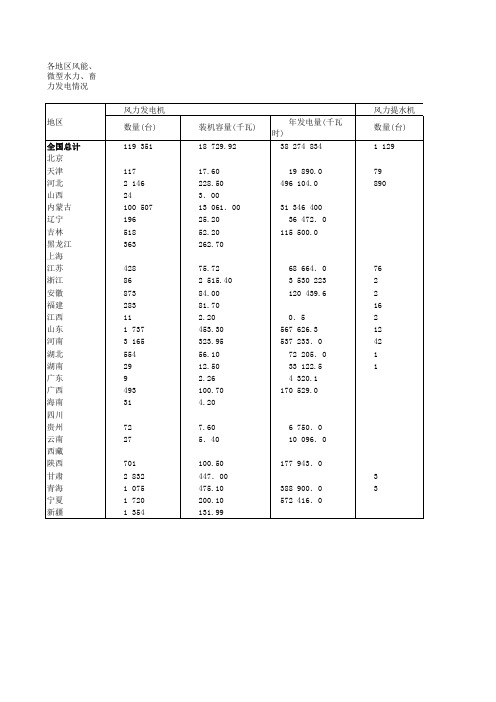
(续) 微型水力发电 灌溉面积(公 顷) 1 525.99 813.20 332.50 数量(台) 76 535 24 99 6 2 11 13 装机容量(千瓦) 191 985.33 16 329.00 70.30 701.10 1.20 100.80 14 247.00 地区 全国总计 北京 天津 河北 山西 内蒙古 辽宁 吉林 黑龙江 上海 江苏 浙江 安徽 福建 江西 山东 河南 湖北 湖南 广东 广西 海南 四川 贵州 云南 西藏 陕西 甘肃 青海 宁夏 新疆
80.35 2.00 2.00 4.80 125.70 29.24 33.30 100.30
615 326 315 10 799 53 83 604 12 482 1 949 34 503 2 448 2 809 7 331 1 887 107 69
4 343.70 987.80 581.90 14 045.50 3 552.50 276.45 2 052.20 19 471.80 13 604.36 71 763.60 4 150.22 6 216.00 10 053.70 8 267.80 1 124.00 44.40
73.00 52.15 148.00 1 204.00 161.00 18.00 365.00 3 960.00 5 763.83 6 088.00 37.04 716.00 1 648.00 22.00 347.00 19.50
1 781 1 343 2 520 32 021 18 000 4 661 8 817 103 058 178 562 108 493 53 282 66 842 49 608 24 186 378
68 664.0 3 530 223 120 439.6 0.5 567 626.3 537 233.0 72 205.0 33 122.5 4 320.1 170 529.0
南通电网典型地区风电与光伏出力统计特性分析

南通电网典型地区风电与光伏出力统计特性分析
南通电网典型地区风电与光伏出力统计特性分析
冯士睿,王莹,牛涛
(中国能源建设集团江苏省电力设计院有限公司,江苏 南京 211102)
摘 要:为更好地了解地区大规模风电与光伏接入对于电网稳定的影响,以江苏省南通市典型地区 为研究对象,全面分析了风电场及光伏电站的出力特性,以历史实测出力数据为基础定性或定量归纳了 其出力特征,包括波动性、持续出力特性、季节特性、风光相关性以及同时性。分析结果可以为江苏乃 至华东沿海地区的风电、光伏发电等新能源的消纳、新能源接入系统设计以及新能源发展规划提供理论 与数据基础。
FENG Shi-rui, WANG Ying, NIU Tao (China Energy Engineering Group Jiangsu Power Design Institute Co., Ltd, Nanjing 211102, China) Abstract: In order to know the impacts of regional large-scale wind power and photovoltaic access on power grid stability, taking the type area of Nantong in Jiangsu province as the research object, this paper comprehensively analyzed the output characteristic of wind farm and photovoltaic power station. The output characteristics were qualitatively and quantitatively concluded on the basis of historical measured output data, including volatility, continuous output characteristics, seasonal characteristics, correlation and simultaneity of wind and light. The analysis results can provide theoretical and data basis for the design of new energy access system and the planning of new energy development. Key words: output characteristic; correlation; wind power; photovoltaic
基于风功率数据的风电机组性能预测与健康状态评估

基于风功率数据的风电机组性能预测与健康状态评估马然;栗文义;齐咏生【摘要】为及时准确地预测风电机组整机性能,文章基于风功率数据提出了一种考虑工况波动的相似性度量算法,结合概率和模糊理论评估机组健康状态.该方法基于聚类思想对风功率数据进行数据预处理和工况划分,针对工况子空间的正常样本与测试样本,基于主成分分析法以第二主成分方向上投影变量的标准差作为样本相似性度量指标,依据概率不确定性融合得到综合健康状态指标,量化机组性能的退化程度.结合机组性能实际退化过程,依据模糊理论确定健康状态隶属度,基于隶属度最大原则和信度准则判断机组健康状态等级.将该方法应用于某具有小样本数据的实例中,可提前两周获知风电机组发生异常,对机组健康状态的过渡过程作出了准确评估,验证了所提方法的可行性.【期刊名称】《可再生能源》【年(卷),期】2019(037)008【总页数】8页(P1252-1259)【关键词】风电机组;风功率数据;聚类;主成分分析;模糊理论;性能预测;健康状态评估【作者】马然;栗文义;齐咏生【作者单位】内蒙古工业大学能源与动力工程学院, 内蒙古呼和浩特 010050;内蒙古工业大学能源与动力工程学院, 内蒙古呼和浩特 010050;内蒙古工业大学电力学院, 内蒙古呼和浩特 010080;内蒙古工业大学电力学院, 内蒙古呼和浩特010080【正文语种】中文【中图分类】TK830 引言目前,风电机组的故障预测与健康管理(PHM,prognostic and health management)受到了国内外学者的广泛关注,即借助各种算法和智能模型预测机组性能和剩余寿命、评估健康状态,实现视情维护。
其中,整机性能分析与运行状态评估是实现PHM 的关键,国际电工委员会就风力发电系统整机性能测量出台了相关标准,即IEC 61400-12-1 Ed.2[1]。
因风电机组属于复杂装置,机理建模困难,基于风电场 SCADA(supervisory control and data acquisition)系统的数据驱动法成为主要研究方法之一[2]。
基于实测数据分析的大型风电场风电功率预测

基于实测数据分析的大型风电场风电功率预测严干贵1,刘 玉1,刘吉刚1,孟磊1,陈宝生2(1.东北电力大学 电气工程学院,吉林 312012 2.吴忠市利通区友谊路吴忠供电局保护自动化所 751100)摘要:风力发电具有波动性、间歇性的特点,大容量的风力发电接入电网,对电力系统的安全、经济运行带来严重挑战。
为了减小这种不利影响,便于电网合理调度,需对风功率进行预报。
本文在风电场实测数据详细的分析基础上,应用混沌时间相空间理论建立了超短期风电功率预测一阶局域模型,对某风电场未来5min、15min、30min内的风电功率进行预测,最后对预测结果进行了评价,验证了该方法的可行性。
关键词:风电场;风电功率;功率预测;混沌0.引言风力发电是可再生能源发电技术中发展最快和最为成熟的一种,其正逐步走向规模化和产业化[1]。
我国风资源丰富的地方大都位于电网末端,由于风电场的输出功率具有间歇性和波动性,风电接入电网后会对区域系统运行的经济性及稳定性带来严重影响。
随着风电场数量的装机容量的不断增加,这种影响变得越来越明显[2]。
为了减小这种不利影响,对风速和风功率进行预报,将有助于电网调度部门提前了解即将入网的风电功率,便于电网合理、经济调度[3]。
风电功率的预测以时间尺度的不同可以分为三种:一种是超短期预测(几分钟到几十分钟),这种时间尺度内的预测主要针对风电机组控制;另一种为短期预测(几十分钟到几个小时),这一时间尺度内的预测主要针对风电并网、调度;最后一种是中长期风电功率预测(几周到几个月),这个时间尺度内的风电功率预测主要应用于风电场安排机组检修计划有关。
现阶段国内外常用的风电功率预测方法主要可以分为两类:1:根据数值天气预报预测的风速,利用风电场等效风电功率特性曲线,将预测来的风速换算成风电场输出功率。
根据大气实际情况,在一定初值和边界条件下,通过数值计算求解描写天气演变过程的流体力学和热力学方程组来预报未来天气的方法。
风速及平均风功率密度 - 贵州气象在线

风速及平均风功率密度
各详查区观测年度风能参数表
黔南详查区
六盘水详查区
毕节详查区
各详查区70m高度风速和风功率密度年变化曲线图
黔南详查区
六盘水详查区
毕节详查区
各详查区70m风速和风功率密度日变化曲线图
各等级风速及其风能频率分布
各详查区测风塔观测年度各风速等级小时数(h)
黔南详查区
六盘水详查区
毕节详查区
各详查区观测年度风速和风能频率分布直方图风向和风能密度分布
各详查区测风塔观测年度各高度各风向频率(%)
黔南详查区
六盘水详查区
毕节详查区
各详查区测风塔全年各高度风向及风能玫瑰图风速垂直切变
各详查区测风塔观测年度风切变指数
黔南详查区
六盘水详查区
毕节详查区
各详查区观测年度平均风速廓线
湍流强度
各详查区测风塔各高度全风速段和风速15m/s的大气湍流强度
黔南详查区
六盘水详查区
毕节详查区
图6.8 各详查区各测风塔湍流强度年变化曲线
黔南详查区
六盘水详查区
毕节详查区
各详查区各测风塔湍流强度日变化曲线
风频曲线及威布尔分布参数
各详查区测风塔70m高度风速威布尔分布参数
黔南详查区
六盘水详查区
毕节详查区
各详查区测风塔70m高度风速威布尔分布曲线图。
2019年山西风电电力交易及消纳情况

山西省风电电力交易及消纳情况一、2018年山西风电场运行情况2018年山西省内直接交易电量644亿千瓦时,省间交易314.2 亿千瓦时,合同转让交易241.96 亿千瓦时,全年市场化交易电量1200.16亿千瓦时。
2018年山西省新能源全年交易电量38.31亿千瓦时,与北京、冀北开展省间发电权交易0.25亿千瓦时,煤改电交易4.18亿千瓦时。
现根据山西能监局公布的2018年山西双细则考核公告,虽然山西风场平均利用小时达到了2196小时,但各风场发电情况还是差距较大,具体各电场运行情况如下表:(具体数据参考附件一)表1:2018年山西省各风电场运行情况按2018年山西省电力交易公布数据,2018年山西省完成新能源电力交易38.31亿千瓦时(光伏:风电3:7的交易比列),按国家能源局公布的2018年山西发电量为212亿千瓦时,利用小时数2196,得出2018年山西计算风电容量为9653MW (综合考虑2018年新增风电场)。
交易电量占比为12.6%。
所以按照2018年平均风电利用小时数2196计算,交易电量小时数为276小时,保障利用小时数为1920小时左右。
满足国家能源局保障利用小时数最低要求。
现将2018年山西省12个月纳入电网结算的电量整理后发现,年通过电网公司结算的风电发电量为196亿千瓦时(推测196亿内含特高压交易电量,由电网公司代理交易,按当地燃煤标杆电价0.332元/千瓦时结算,对应利用小时数2030),与山西212亿千瓦时风电发电量相差约16亿千瓦时,即这16亿千瓦时电量是通过煤改电交易、发电权交易、弃风交易等方式进行的,即不按照山西燃煤标杆电价(0.332元/千瓦时)与电网公司结算,对应利用小时数约166小时。
综上所述,2018年山西各风电场与电网公司结算电量对应利用小时数为2030小时(按燃煤标杆电价结算),市场化交易构成利用小时166小时(市场化电价结算),合计就是国家能源局公布的利用小时数2196小时。
基于风力发电机组功率特性的数据分析
基于风力发电机组功率特性的数据分析【摘要】功率曲线是风电机组的重要运行性能的表现形式,本文简要的叙述了针对2.0MW风电机组,通过获取反映机组运行性能的实测风速、空气密度、扫风面积、功率等数据,计算得到了风电机组的实际运行功率曲线、风能利用曲线及其标准差值进行可视化分析,从而对功率曲线进行性能评估。
【关键词】风电机组;数据处理;性能评估;功率曲线;风能利用系数0 引言功率曲线是由风速作为自变量(X),有功功率作为因变量(Y),建立坐标系。
用一条拟合曲线拟合风速与有功功率的散点图,最终得到能够反映风速与有功功率相关性的曲线。
功率特性是风电机组的重要运行性能的表现形式之一,通过得到的功率特性曲线评估风电机组的发电量与发电效率。
验证功率特性曲线精度,提高了风功率预测的准确性和预测精度,进而衡量风电机组的风能转换实际能力。
1 功率曲线计算方法通过利用机组SCADA数据,准确计算出机组的功率曲线、风能利用系数Cp曲线,可以用来衡量风机性能参数是否满足风场当地外的风资源特点,为风机参数调整提供强有力的依据,从而最终提高功率曲线特性及风电场发电量。
1.1风电机组的发电功率:其中:1.1.1空气密度:P为气压Pa;T为绝对热力学温度,R为空气的气体常数,对于干燥空气而言,R=287.05J/(kg·K)。
在计算功率曲线时,由于环境数据获取难度较大,一般直接采用风机合同中“项目风电场空气密度”。
1.1.2扫风面积:D为风轮直径,一般直接采用风机合同中“叶轮直径”。
1.1.3实时风速:一般采用SCADA系统中导出的机舱外实时风速。
1.2风能利用系数根据功率曲线能够计算风电机组在不同风速段下的风能利用系数。
表示了风力发电机将风能转化为电能的转换效率,一般用Cp表示,是衡量风电机组从风中摄取的能量的百分率。
根据贝兹理论,风力发电机最大风能利用系数为0.593;行业内,双馈机组测量得到的max普遍为0.4-0.45左右。
风力发电场生产统计指标解释
风力发电场生产统计指标解释风力发电场的生产统计指标包括装机容量、发电量、利用小时数、等效满负荷小时数、弃风率、装机利用率等。
这些指标对于评估风力发电场的生产性能、运行情况以及经济效益起着至关重要的作用。
下面对这些指标逐一进行解释。
首先,装机容量是指风力发电场安装的风力发电机组的总功率,通常以千瓦(kW)或兆瓦(MW)为单位。
装机容量是评估风力发电场规模和潜在发电能力的重要指标,一般情况下,装机容量越大,风力发电场的发电能力就越强大。
第二,发电量是指风力发电场在一定时间内实际发电的总电量,通常以千瓦时(kWh)或兆瓦时(MWh)为单位。
发电量是用来衡量风力发电场实际生成的电能,可以用来计算收入和碳减排等重要指标。
第三,利用小时数是指风力发电场在一定时间内实际运行的小时数,通常以小时(h)为单位。
利用小时数反映了风力发电场的运行时间,较高的利用小时数意味着风力发电机组充分享受到了风能资源,并能持续稳定地发电。
第四,等效满负荷小时数是指风力发电场实际发电量与装机容量的比值,通常以小时(h)为单位。
等效满负荷小时数是衡量风力发电场利用率的重要指标,它表明在风力发电场所在地的特定条件下,每年的平均发电量与额定功率的比值,数值越大表示风力发电场的利用率越高。
第五,弃风率是指风力发电场因各种原因而未能将可利用的风能转化为电能的百分比。
弃风率是一个反映风力发电场损失程度的重要指标,数值越小表示风力发电场的系统效率越高。
最后,装机利用率是指风力发电场实际发电量与装机容量的比值,通常以百分比(%)表示。
装机利用率是评价风力发电场运行效率和经济效益的重要指标,它反映了风力发电场的实际输出与其潜在能力之间的差异。
综上所述,风力发电场生产统计指标是评估风力发电场性能和经济效益的重要依据,这些指标能够直观地反映风力发电的发电能力、运行时间、利用率等关键信息,帮助评估风电项目的盈利能力和可行性,对于风力发电行业的发展以及可持续能源的推广具有重要意义。
贵州高原山区空气密度对风电功率影响研究
贵州高原山区空气密度对风电功率影响研究文贤馗,肖永,林呈辉,徐梅梅【摘要】贵州大部分风电场处于海拔高、空气湿度大的山区,通过对计及海拔、湿度的空气密度进行推导、计算,发现这2个因素都与空气密度成反比,且目前风电场在计算中通常将山区空气按照干空气进行计算,未考虑湿度的影响。
同一型风机在相同风速的情况下,其输出功率与空气密度等比例降低,因此,在机组选型、发电量估算,风功率预测等方面应加以考虑。
【期刊名称】中国电力【年(卷),期】2014(047)007【总页数】3【关键词】高原山区,海拔,湿度,空气密度,风电功率0 引言近年来,随着人们的环保意识的增强,可再生能源的利用日益引起人们的关注。
特别是风力资源发电的开发利用,在中国能源发展战略上已起到越来越重要的作用[1-6],2012年,中国(不包括台湾地区)新增安装风电机组7872台,装机容量12960MW;累计安装风电机组53764台,装机容量75324.2MW,同比增长20.8%[7]。
贵州作为南方重要的能源基地,近年来风力发电得到了迅速发展,截至2012年年底,已有507.1MW风力发电机组投入运行,占贵州电网容量的1.7%。
贵州特有的高原山区气象性能决定了风能有着海拔高、湿度大等特点,明显区别于我国其他区域的平原、海上风电。
1 贵州省风能资源情况贵州位于青藏高原东南侧,从地形来看,贵州是一个山峦重叠、丘陵起伏的高原地区,从地势上看,贵州东西有3个阶梯,西高东低。
由于贵州特殊的地理位置及地形地势,从各个方向来的气流进入贵州后都将受到不同程度的阻隔削弱及地面摩擦削弱,但在海拔较高,地形相对开阔的地方,这种削弱并不明显。
西部、中部及西南部部分地区、南部部分地区具有较为丰富的风能资源储量,风能资源可开发利用区主要集中在上述区域海拔较高的高地平台[8]。
根据贵州省设立的气象站数据显示[9]:大部分台站年平均风功率密度在5.0 W/m2以下,约占全省总面积的80%左右,贵州省的东部、南部、北部及西南部的大部分地区年平均风功率密度在2.5 W/m2以下。
基于实测数据分析的风电功率预测
基于实测数据分析的风电功率预测胡渊;谭宗柒;朱华玲;张涛【摘要】由于风力发电所利用的近地风能具有波动性、间歇性、低能量密度等特点,对风电场的发电功率进行尽可能准确的预测是风电发展的关键.本文根据某风场的实测数据,采用了时间序列中的自回归移动平均模型(ARMA),对风电功率进行了实时预测;为进一步提高风电功率实时预测的精确性,本文提出了一种基于BP神经网络和ARMA组合模型的预测方法,并对上述实测数据采用该方法进行了实时预测,预测结果表明:组合模型的预测结果与单独的自回归移动平均模型相比,风电功率的实时预测的均方根误差和百分比误差分别减少了4.01%和3.25%,工程中可以采用该组合模型对风电功率进行预测,%Close wind of what wind power generation used features volatility, intermittence and low energy density etc. So it is key to the development of wind power that the accurately predicting the wind power generation power. According to measured data of a wind field, this paper uses time series auto-regression moving average(ARMA) model for wind power real-time prediction. To further enhance the accuracy of realtime prediction of wind power, this paper puts forward a predicting method based on the BP neutal network and ARM A model portfolios; and with this method the measured data are used for the real-time prediction. The prediction results show that: compared the results of combination model with ARMA model, wind power real-time prediction of the RMS error and percentage error are reduced to 4. 01% and 3. 25% respectively; This combination predicting model of wind power can be used to predict the wind power.【期刊名称】《三峡大学学报(自然科学版)》【年(卷),期】2012(034)005【总页数】4页(P48-51)【关键词】风电功率预测;ARMA模型;组合预测【作者】胡渊;谭宗柒;朱华玲;张涛【作者单位】三峡大学机械与材料学院,湖北宜昌 443002;北碚供电局,重庆北碚400700;三峡大学机械与材料学院,湖北宜昌 443002;三峡大学机械与材料学院,湖北宜昌 443002;三峡大学机械与材料学院,湖北宜昌 443002【正文语种】中文【中图分类】TM715风力发电主要利用的是近地风能,近地风具有波动性、间歇性等特点,因而风电功率也是波动的.当大规模的风电场接入电网运行时,大幅度的风电功率波动会对电网的功率平衡和频率调节带来不利影响.如果可以对风电场的发电功率进行实时预测,电力调度部门就能够根据预测的风电发电功率预先安排调度计划,保证电网的功率平衡和运行安全[1-5].经过多年的积累,欧洲和美国已经有多款商业化的风电功率预测软件,如丹麦的 WPPT和Prediktor、西班牙的SIPREOLICO等.由于我国对于风能的研究主要集中在风力发电机组的变频控制、对电力系统的影响等方面,而关于风电场功率预测的研究才刚刚起步,要得到较精确的风电功率预测结果难度很大[6].目前风电功率预测的模型主要有:①时间序列方法,主要包括自回归移动平均模型、自回归条件异方差模型、人工神经网络方法等,采用时间序列方法可对风速做时间序列分析,然后将其转换成风电场输出功率,也可直接对风电场输出功率做时间序列分析;②基于数值天气预报的预测模型,即利用气象部门提供的数值气象预报模型,对风电场或附近某个点的天气情况进行预测,建立预测模型,并结合其他输入,将数值气象预报模型的预测值转换成风电场的功率输出[7-8].由于时间序列同时蕴含着数据顺序和数据大小,表现出客观世界的某一动态过程,能反映出客观世界及其变化的信息,又由于风电场功率数据具有按时间排序和离散性[9]的特征,故本文提出采用时间序列分析方法对风电场功率进行预测,并根据时间序列分析方法来寻求一种更好的预测方法,以提高预测精度.1 自回归移动平均模型预测1.1 模型建立采用时间序列分析方法对风电场的发电功率进行预测.对风电机组输出功率数据建立自回归移动平均模型 ARMA(n,m)如下[9-11]:式中,φi(i=1,2,…,n)为自回归参数;θj(j=1,2,…,n)为移动平均参数;{αt}是均值为零、方差为σ2a的正态白噪声过程.为保证计算精度、减小舍入误差、避免溢出,对风电机组原始输出功率序列进行标准化处理.记{x(0)t}为原始输出功率序列,对{x(0)t}中各数据进行如下标准化处理:式中,μx 与σ2x 分别为的均值与方差的估值,它们的算法如下:以上两式中,N为功率序列的个数.对由式(2)所得的时序{xt}按式(1)进行功率建模,得到预测功率序列{SWt}如下:1.2 模型求解在选定模型后,需进行模型的定阶和模型参数的估计,模型定阶和模型参数估计是应用时间序列分析法进行建模时很重要的过程,该过程的适当与否直接影响到模型预测的精度.在ARMA(n,m)模型的阶数确定时,采用的是AIC准则函数定阶,使得AIC准则函数极小时的n和m值即为该模型的最佳阶数[12];在估计自回归移动平均模型ARMA(n,m)的参数φi,θj 和σ2a 时,采用了先后估计法[13],即先根据 Yule-Walker法估计φi,后采用近似极大似然法估计θj.原始数据由某风电场58台风电机组给出,每台机组的额定输出功率为850kW.给出了2006年5月10日至2006年6月6日时间段内该风电场中指定的4台风电机组(A、B、C、D)输出功率数据(分别记为PA,PB,PC,PD;另设该4台机组总输出功率为P4)及全场58台机组总输出功率数据(记为P58).该模型把5月31日P58的总输出功率作为已知历史序列,对6月1日的总输出功率进行预测.图1为5月31日P58的总输出功率序列的自相关函数和偏相关函数图,从图中可以看出,此处应用ARMA(n,m)模型进行预测合理;图2为采用ARMA (n,m)模型预测的6月1日P58总输出功率与实测值的对比图[14].2 基于ARMA和BP神经网络的组合模型预测2.1 模型建立为了提高风电功率实时预测的准确程度,改善风电联网运行的性能,重新构建了实时预测模型.首先分析了影响风电功率的各影响因素,主要有风速和风向,空气密度等因素,再结合给出的数据信息,从数据中可以得到风速和风向信息,即邻近时间段的发电功率序列[xt,xt-1,…,xt-m1];也可以挖掘到空气密度信息,因为空气密度与温度和气压有关,而邻近几天中同一时刻的温度和气压很接近,即邻近几天中同一时刻的发电功率序列[yt,yt-1,…,yt-m1].分别利用这两个发电功率序列,采用自回归移动平均模型(ARMA)方法进行预测,为了充分提取两组预测结果信息,使得预测准确性得到提高,文中考虑再把这两个预测的风电功率结果作为BP神经网络模型的输入,神经网络最后的输出即为最后的预测结果[15-18].组合模型的原理示意图如图3所示.图3 原理示意图2.2 模型求解该模型中把5月10日至5月31日P58的总输出功率作为已知历史序列,对6月1日的总输出功率进行预测.功率序列[xt,xt+1,…,xt+m]为5月31日P58的总输出功率,功率序列[yt,yt+1,…,yt+m]为5月10日至5月31日每日相同时点P58的总输出功率(96个时点,共96组功率序列),分别通过ARMA 模型预测出6月1日的总输出功率的初始结果;再把这两个预测结果输入到经过训练的BP神经网络,最后输出即为最终预测结果,求解过程如图4所示.图4 组合模型求解过程图5为采用组合模型预测的6月1日P58总输出功率与实测值的对比图.3 结果分析从图2和图5可以很直观地看出,单独采用自回归移动平均模型(ARMA)进行预测与实测值的变化趋势较为一致,而采用ARMA和BP神经网络的组合模型进行预测与实测值吻合得较好.图5 P58总输出功率实测值与预测值根据均方根误差公式(6)和百分比误差公式(7),分别计算了上述自回归移动平均模型(ARMA)和组合预测模型两种方法的均方根误差和百分比误差.计算结果见表1.式中,Cap为风电场开机容量.表1 模型预测的准确率及合格率预测方法均方根误差/% 百分比误差/%ARMA 12.52 10.1组合模型8.51 6.85从表1的数据可以看出,ARMA模型预测的均方根误差和百分比误差分别为12.52%和10.1%,组合模型预测的均方根误差和百分比误差分别为8.51%和6.85%.对P58总输出功率采用组合模型预测方法后均方根误差和百分比误差分别减少了4.01%和3.25%,组合模型更能充分利用各自模型所包含的信息,具有更高的预测精度.4 结论风电功率预测对电力系统的安全、稳定、经济运行以及提高运行效益具有重要意义.自回归移动平均模型适合数据波动性大且没有规律的预测,其预测的均方根误差和百分比误差较小,故使用ARMA模型对风电功率进行实时预测可以达到理想的效果.并由此推导出组合预测模型的方法,有效地提高了预测精度.在根据已有历史数据的基础上,为风电功率的预测提供了一种行之有效的方法,并且为今后对风电功率预测的研究提供了一定的理论依据.参考文献:[1]谷兴凯,范高峰,王晓蓉,等.风电功率预测技术综述[J].电网技术,2007,31(2):335-338.[2]廖明夫,Gasch R,Twele J.风力发电技术[M].西安:西北工业大学出版社,2009.[3]张希良.风能开发技术[M].北京:化学工业出版社,2005.[4]王素霞.国内外风力发电的情况及发展趋势[J].电力技术经济,2007,19(1):29-31.[5]时庆花,高山,陈昊.2种风电功率预测模型的比较[J].能源技术经济,2011,23(6):31-35.[6]杨桂兴,常喜强,王维庆,等.对风电功率预测系统中预测精度的讨论[J].电网与清洁能源,2011,27(1):67-71.[7]徐曼,乔颖,鲁宗相.短期风电功率预测误差综合评价方法[J].电力系统自动化,2011,35(12):20-26.[8]刘玉.基于实测数据分析的大型风电场风电功率预测研究[J].黑龙江电力,2011,33(1):11-15.[9]丁明,张立军,吴义纯.基于时间序列的风电场风速预测模型[J].电力自动化设备,2005,25(8):32-34.[10]高俊芳,吴清.时间序列ARMA模型及其应用[J].上海工程技术大学学报,1996,10(4):68-73.[11]李建康.时间序列建模应用[J].江苏工学院学报,1994,15(2):72-77. [12]许国辉,余春林.时间序列分析方法的研究[J].广州大学学报:自然科学版,2003,2(6):556-559.[13]杨位钦,顾岚.时间序列分析与动态数据建模[M].北京:北京工业学院出版社,1986.[14]韩爽,杨勇平,刘永前.三种方法在风速预测中的研究应用[J].华北电力学报,2008,35(3):57-61.[15]李蔚,盛德仁,陈坚红,等.双重BP神经网络组合模型在实时数据预测中的应用[J].中国机电工程学报,2007,27(17):94-97.[16]范高峰,王伟胜,刘纯.基于人工神经网络的风电功率短期预测系统[J].电网技术,2008,32(22):72-76.[17]蔡凯,谭伦农,李春林,等.时间序列与神经网络法相结合的短期风速预测[J].电网技术,2008,32(8):82-86.[18]杨叔子,吴雅,王治藩,等.时间序列分析的工程应用[M].武汉:华中科技大学出版社,1991.。
