水平荷载作用下横观各向同性地基的力学分析及应用
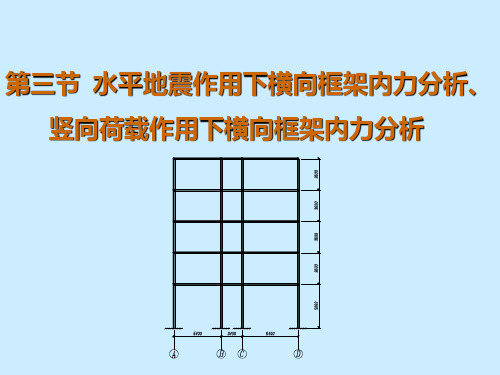
第三节 水平地震作用下横向框架内力分析、竖向荷载作用下横向框架内力分析
走道板传给横梁的自重
1、楼（屋）盖荷载传递形式
八、竖向荷载作用下横向框架内力分析
中纵梁自重
边纵梁自重
中纵梁上墙、门窗自重（顶层无）
P2
边纵梁上墙、窗自重（顶层无）
P1
板传给中纵梁自重
次梁自重
板传给边纵梁自重
次梁自重
次梁传来的荷载
次梁上墙重
（顶层无）
次梁传来的荷载
次梁上墙重
（顶层无）
板传给次梁自重
板传给次梁自重
边柱集中力矩
C
D
q
' 2
走道板传给横梁的活载
板传给中纵梁活载
P2 板传给次梁活载
M 2 P2e2
中柱集中力矩
1、楼（屋）盖荷载传递形式
八、竖向荷载作用下横向框架内力分析
竖向荷载计算
恒载
楼面活荷载 （屋面取活荷载）
楼面活荷载 （屋面取雪荷载）
2、竖向荷载计算
八、竖向荷载作用下横向框架内力分析 举例说明：
恒荷载作用下弯矩二次分配
3、竖向荷载作用下的内力计算
八、竖向荷载作用下横向框架内力分析
上柱
0.340
3.80 2.87 -1.27 5.41 0.340
3.80 1.90 -0.94 4.76 0.340
3.80 1.90 -0.79 4.91 0.299
2.94 1.90 -0.37 4.47
下柱 0.514 3.41 5.75 1.90 -0.24 7.41 0.340 3.41 3.80 1.90 -1.27 4.43 0.340 3.41 3.80 1.90 -0.94 4.76 0.340 3.41 3.80 1.47 -0.79 4.48 0.419 4.77 4.11 0.00 -0.51 3.60
横观各向同性层状场地的动力分析及应用
同济大学博士学位论文横观各向同性层状场地的动力分析及应用姓名：陈镕申请学位级别：博士专业：岩土工程指导教师：陈竹昌19991001摘要本文回顾了桩一土一结构动力相互作用课题国内外研究的现状，选定了“横观各向同性层状场地的动力分析及应用”这一桩～士一结构动力相互作用中的基本问题作为本文的研究内容。
、√根据研究的内容本文分为两部分。
、第一部分：主要研究横观各向同性层状场地对平面入射波的响应及应用。
在这部分中，本文主要作了如下的工作：１、根据矗角坐标系中的基本方程，推导横观各向同性土层在平面入射ＳＨ波、Ｐ—ｓＶ波时的动力刚度矩阵：２、给出横观各向同性层状场地对平面入射ＳＩ－Ｉ波、Ｐ—ＳＶ波的求解方法，并以平面入射ＳＨ波为例说明如何应用这种方法求解场地的响应；３、通过参数的分析，说明场地的横观各向同性性质对场地的自振特性、场地的地震响应等的影响。
其中场地的共振频率随场地横观各向同性性质的变化规律系首先被发现：第二部分：主要研究横观各向同性层状场地对外加荷载的响应及应用。
在这一部分本文主要作了如Ｆ的工作：Ｉ、推导了横观各向同性层状场地底部阻尼边界条件及半空闾边界条件，并给出它们进入离散化后的Ｒａｙｌｅｉｇｈ波与Ｌｏｖｅ波代数特征方程的方法：２、利用状态空间法求出上述代数特征方程的特征值及规格化特征向量，并给出了相应的正交关系，利用求得的特征值与特征向量给出了各种荷载作用下位移的表达式，即格林函数公式：３、对不同的边界条件下位移响应进行比较，指出它们的适用范围；４、指出求得的位移公式应用于桩一土动力相互作用的方法，并举例说明了它们的具体应用以及场地横观各向性质等参数对横观各向同性场地中桩一土动力相互作用的影、响：５、通过与试验结果的对比，检验了本文方法的有效性。
善，为今后在桩一通过上述二部分的研究，土一结构动力相互作用分析中关ｔ词ｚ桩一土一结构动力相互作用，横观各向同性层状场地，平面入射波，响应上、动力分析，边界条件，特征值鸟特征向量，格林函数｛ＡＢＳＴＲＡＣＴＲｅｖｉｅｗｉｎｇｔｈｅｐｒｅｓｅｎｔｓｉｔｕａｔｉｏｎｏｆｓｏｉｌ・ｐｉｌｅ—ｓｔｒｕｃｔｕｒｅｉｎｔｅｒａｃｔｉｏｎｒｅｓｅａｒｃｈ，ｔｈｅｄｙｎａｍｉｃａｎａｌｙｓｉｓｏｆｔｒａｎｓｖｅｒｓｅｌｙｉｓｏｔｒｏｐｉｃｌａｙｅｒｅｄｓｔｒａｔｕｍａｎｄｉｔｓａｐｐｌｉｃａｔｉｏｎｓａｒｅｃｈｏｓｅｎａｓｔｈｅｔｏｐｉｃｏｆｔｈｉｓｔｈｅｓｉｓ，ｗｈｉｃｈａｒｅｔｈｅｆｕｎｄａｍｅｎｔａｌｐｒｏｂｌｅｍｓｉｎｄｙｎａｍｉｃｓｏｉｌ－ｐｉｌｅ－ｓｔｒｕｃｔｕｒｅｉｎｔｅｒａｃｔｉｏｎａｎａｌｙｓｉｓ．Ｔｈｅｔｈｅｓｉｓｉｓｄｉｖｉｄｅｄｉｎｔｏ懈ｏｐａｒｔｓ．Ｉｎｔｈｅｆｉｒｓｔｐａｒｔ，ｔｈｅｒｅｓｐｏｎｓｅｓｏｆｔｒａｎｓｖｅｒｓｅｌｙｉｓｏｔｒｏｐｉｃｌａｙｅｒｅｄｓｔｒａｔｕｍｔｏｉｎｃｉｄｅｎｔｐｌａｎｅｗａｖｅｓａｎｄｔｈｅｉｒａｐｐｌｉｃａｔｉｏｎｓａｒｅｄｉｓｃｕｓｓｅｄ．ＴｂｅｍａｉｎＣｏｎｔｅｎｔｓａｒｅａｓｆｏｌｌｏｗｉｎｇ：１．ＴｈｅｄｙｎａｍｉｃｓｔｉｆｆｎｅｓｓｍａｔｒｉｃｅｓｏｆｔｒａｎｓｖｅｒｓｅｌｙｉｓｏｔｒｏｐｉｃｓｏｉｌｌａｙｅｒｔｏｉｎｃｉｄｅｎｔｐｌａｎｅＳＨａｎｄＰ－ＳＶｗａｖｅｓａｒｅｄｅｒｉｖｅｄ，ｗｈｉｃｈａｒｅｉｎｔｈｅＣａｒｔｅｓｉａｎｃｏｏｒｄｉｎａｔｅｓ；２．ＴｈｅｅｖａｌｕａｔｉｏｎｍｅｔｈｏｄｓｏｆｔｒａｎｓｖｅｒｓｅｌｙｉｓｏｔｒｏｐｉｃｌａｙｅｒｅｄｓｔｒａｔｕｍｒｅｓｐｏｎｓｅｓｔｏｉｎｃｉｄｅｎｔｐｌａｎｅＳＨａｎｄＰ・ＳＶｗａｖｅｓａｒｅｐｒｅｓｅｎｔｅｄ．ａｎｄｔｈｅｉｎｃｉｄｅｎｔｐｌａｎｅＳＨｗａｖｅｉｓｔａｋｅｎ∞ｔｈｅｅｘａｍｐｌｅｔｏｉｌｌｕｓｔｒａｔｅｈｏｗｔｏＨｕｅｔｈｅｓｅｍｅｔｈｏｄｓｔｏｅｖａｌｕａｔｅｔｈｅｒｅｓｐｏｎｓｅｓｏｆｔｈｅｓｔｒａｔｕｍ；ｆｕｎｄａｍｅｎｔａｌｆｒｅｑｕｅｎｃｙ，３．ＴｈｅｅｆｆｅｃｔｓｏｆｔｒａｎｓｖｅｒｓｅｌｙｉｓｏｔｒｏｐｉｃｐｒｏｐｅｒｔｙｏｆｓｏｉｌｏｎｔｈｅｅａｒｔｈｑｕａｋｅｒｅｓｐｏｎｓｅｓｅＩｃ．Ｏｆｔｈｅｌａｙｅｒｅｄｓｔｒａｔｕｍａｒｅｃａｌｃｕｌａｔｅｄ，ｉｎｗｈｉｃｈｔｈｅｒｕｌｅｏｆｆｕｎｄａｍｅｎｔａｌｆ『ｅｑｕｅｎｃｙｖａｒｙｉｎｇｗｉｔｈｔｈｅｔｒａｎｓｖｅｒｓｅｌｙｉｓｏｔｒｏｐｉｃｐｒｏｐｅｒｔｙｏｆｔｈｅｓｔｒａｔｕｍｉｓｆｏｕｎｄｆｏｒｔｈｅｆｉｒｓｔｔｉｍｅ．／ｎｔｈｅｓｅｃｏｎｄｐａｎ，ｔｈｅｒｅｓｐｏｎｓｅｓｏｆＵａｎｓｖａｒｓｅｌｙｉｓｏｔｒｏｐｉｃｌａｙｅｒｅｄｓｔｒａｔｕｍｔｏｅｘｔｅｒｎａｌｌｏａｄｓａｎｄｔｈｅｉｒａｐｐｌｉｃａｔｉｏｎｓａｒｅｓｔｕｄｉｅｄ．Ｔｈｅｍａｉｎｃｏｎｔｒｉｂｕｔｉｏｎｓａｒｅａｓｆｏｌｌｏｗｉｎｇ：１Ｔｈｅｄａｍｐｉｎｇａｎｄｈａｌｆｓｐａｃｅｂｏｕｎｄａｒｙｃｏｎｄｉｔｉｏｎｓａｔｔｈｅｂｏｔｔｏｍｏｆｔｒａｎｓｖｅｒｓｅｌｙｉｓｏｔｒｏｐｉｃｌａｙｅｒｅｄｓｔｒａｔｕｍａｒｅｆｏｒｍｕｌａｔｅｄ，ａｎｄｔｈｅｍｅｔｈｏｄｓ，ｃｏｍｂｉｎｉｎｇｔｈｅｍｉｎｔｏｔｈｅａｌｇｅｂｒａｉｃｅｉｇｅｎｖａｌｕｅｅｑｕａｔｉｏｎｓｏｆｇｅｎｅｒａｌｉｚｅｄＲａｙｌｅｉｇｈａｎｄＬｏｖｅｗａｖｅｓ，ａｒｅａｌｓｏｐｒｅｓｅｎｔｅｄ；２．Ｔｈｅｅｉｇｅｎｖａｌｕｅｓａｎｄｎｏｒｍａｌｉｚｅｄｅｉｇｅｎｖｅｃｔｏｒｓｆｕｒａｂｏｖｅｅｑｕａｔｉｏｎｓａｒｅｅｖａｌｕａｔｅｄｂｙｕｓｉｎｇｔｈｅｓｔａｔｅｓｐａｃｅｍｅｔｈｏｄ．ａｎｄｔｈｅｃｏｒｒｅｓｐｏｎｄｉｎｇｏｒｔｈｏｇｏｎａｌｉｔｙｒｅｌａｔｉｏｎｓａｒｅａｌｓｏｇｉｖｅｎ．１１１ｅｄｉｓｐｌａｃｅｍｅｎｔｆｏｒｍｕｌ∞ｔｏｄｉｆｆｅｒｅｎｔｅｘｔｅｒｎａｌｌｏａｄｓ，ｉｎｏｔｈｅｒＷＯｒｄｓ，ｔｈｅＧｒｅｅｎ’Ｓｆｕｎｃｔｉｏｎｓ，ａｎｄｅｉｇｅｎｖｅｃｔｏｍ；ａｌｅｅｘｐｒｅｓｓｅｄｂｙｕｓｉｎｇｔｈｅｓｅｅｉｇｅｎｖａｌｕｅｓ３．Ｔｈｅｄｉｓｐｌａｃｅｍｅｎｔｒｅｓｐｏｎｓｅｓｃｏｒｒｅｓｐｏｎｄｉｎｇｔｏｄｉｆｆｅｒｅｎｔｂｏｕｎｄａｒｙｃｏｎｄｉｔｉｏｎｓ，ａｒｅｃｏｍｐａｒｅｄｗｉｔｈｅａｃｈｏｔｈｅｒ，ａｎｄｔｈｅａｐｐｌｉｃａｂｌｅｒａｎｇｅｓｏｆｔｈｅｓｅｂｏｕｎｄａｒｙｃｏｎｄｉｔｉｏｎｓａｒｅｓｕｇｇｅｓｔｅｄ；４．Ｔｈｅａｐｐｌｉｃａｔｉｏｎｍｅｔｈｏｄｓｏｆａｂｏｖｅｄｉｓｐｌａｃｅｍｅｎｔｆｏｒｍｕｌａｅｉｎｄｙｎａｍｉｃｓｏｉｌ－ｐｉｌｅｉｎｔｅｒａｃｔｉｏｎｉｎｔｒｏｄｕｃｅｄｔｈｒｏｕｌｇｈｓｏｍｅｅｘａｍｐｌｅｓ，ｅｎｄｔｈｅｅｆｆｅｃｔｓｏｆｓｏｉｌｔｒａｎｓｖｅｍｅｌｙａｎａｌｙｓｉｓａｒｅｄｙｎａｍｉｃｓｏｉｌ’ｐｉｌｅｉｎｔｅｒａｃｔｉｏｎａｒｅｒｅｖｅａｌｅｄ；ｉｓｏｔｒｏｐｉｅｐｒｏｐｅｒｔｙｅｔｃ．ｏｎｔｈｅ５．Ｔｈｅｅｆｆｅｃｔｉｖｅｎｅｓｓｏｆｔｈｅｍｅｔｈｏｄｓｉｎｔｈｉｓｔｈｅｓｉｓｉｓｅｘａｍｉｎｅｄｔｈｒｏｕｇｈｔｈｅｃｏｍｐａｒｉｓｏｎｗｉｔｈｔｅｓｔｉｎｇｒｅｓｕｌｔｓ，Ｔｈｒｏｕｇｈｔｈｅｓｔｕｄｙｉｎｔｒｏｄｕｃｅｄａｂｏｖｅ，ｔｈｅｍｏｄｅｌｏｆｔｒａｎｓｖｅｒｓｅｌｙｉｓｏｔｒｏｐｉｃｌａｙｅｒｅｄｓｔｒａｔｕｍｉｓｍａｄｅｍｏｒｅｃｏｍｐｌｅｔｅｔｈａｎｅｖｅｒｂｅｆｏｒｅ，ｗｈｉｃｈｗｉｌｌｐｒｏｍｏｔｅｔｈｅｗｉｄｅａｐｐｌｉｃａｔｉｏｎｏｆｔｈｉｓｍｏｄｅｌｉｎｔｈｅｄｙｎａｍｉｃａｎａｌｙｓｉｓｏｆｓｏｉｌ－ｐｉｌｅ－ｓｔｒｕｃｔｕｒｅｉｎｔｅｒａｃｔｉｏｎ．Ｋｅｙｗｏｒｄｓ：ｄｙｎａｍｉｃｓｏｉｌ－ｐｉｌｅ－ｓｔｒｕｃｔｕｒｅｉｎｔｅｒａｃｔｉｏｎ，ｔｒａｎｓｖｅｒｓｅｌｙｉｓｏｔｒｏｐｉｃｌａｙｅｒｅｄｓｔｒａｔｕｍｉｎｃｉｄｅｎｔｐｌａｎｅｗａｖｅｓ，ｒｅｓｐｏｎｓｅ，ｄｙｎａｍｉｃａｎａｌｙｓｉｓ，ｂｏｕｎｄａｒｙｃｏｎｄｉｔｉｏｎ，ａｎｄｅｉｇｅｎｖｅｃｔｏｒｓ，Ｇｒｅｅｎ’Ｓｆｕｎｃｔｉｏｎ・ｅｉｇｅｎｖａｔｕｅｓ簟论绪论桩基础是土建结构中广泛采用的基础形式，许多重要的工程往往都采用桩基础，如高层及超高层建筑，核电站主厂房结构，海洋平台结构，桥梁的桥墩．悬索桥斜拉桥主塔结构，高耸结构（如电视塔、高压电线塔架等等）以及大型工业厂房、大型动力设备基础等等。
横观各向同性地基模型的理论分析及其应用
横观各向同性地基模型的理论分析及其应用
乔世范;顿志林;刘宝琛
【期刊名称】《岩土工程技术》
【年(卷),期】2003(000)004
【摘要】根据横观各向同性体各向同性面水平时本构方程推导出了横观各向同性面倾斜时的本构方程并得出了横观各向同性地基在上述两种情况下的自重应力计算公式.运用本论文的理论,从自重应力角度能很好的解释水平应力大于竖直应力和水平应力的各向异性这些重要的实测现象.
【总页数】7页(P213-219)
【作者】乔世范;顿志林;刘宝琛
【作者单位】中南大学士建学院,长沙,410075;焦作工学院土建系,焦作,454000;中南大学士建学院,长沙,410075
【正文语种】中文
【中图分类】TU47
【相关文献】
1.基于横观各向同性超弹性理论的短纤维增强橡胶本构模型的建立与应用 [J], 董金平;张志强
2.倾斜横观各向同性单层地基模型的研究 [J], 尹久仁;吴文虎;常瑞鼎;徐勣辉;谢威
3.横观各向同性在抗滑桩加固边坡中的应用 [J], 胡聪;张永攀
4.应用横观各向同性材料模型的钢缆接触分析 [J], 段立志;高超
5.惯性熵理论在横观各向同性圆柱壳中的应用 [J], 王蔚;赵社戌
因版权原因，仅展示原文概要，查看原文内容请购买。
横观各向同性
横观各向同性
横观各向同性现象在地质材料中比较常见，各向异性性状对岩体的应力一应变分析以及破坏力学行为有很重要的影响，国内外学者做了很多的研究工作。
各向同性指物体的物理、化学等方面的性质不会因方向的不同而有所变化的特性，即某一物体在不同的方向所测得的性能数值完全相同，亦称均质性。
横观各向同性体是各向异性体的特殊情况。
在岩石某一平面内的各方向弹性性质相同，这个面称为各向同性面，而垂直此面方向的力学性质是不同的，具有这种性质的物体称为横观各向同性体。
横观各向同性体的特点是在平行于各向同性面（横向）都具有相同的弹性。
物理性质不随量度方向变化的特性。
即沿物体不同方向所测得的性能，显示出同样的数值。
如所有的气体、液体（液晶除外）以及非晶质物体都显示各向同性。
例如：金属和岩石虽然没有规则的几何外形，各方向的物理性质也都相同，但因为它们是由许多晶粒构成的，实质上它们是晶体，也具有一定的熔点。
由于晶粒在空间方位上排列是无规则的，所以金属的整体表现出各向同性。
体力学中，如果弹性体的沿个方向的性质均相同，或者说材料关于任意平面对称，这时的弹性体称为各向同性材料。
均布荷载下横观各向同性沥青路面力学行为分析
均布荷载下横观各向同性沥青路面力学行为分析李群;游凌云;颜可珍;庾付磊【期刊名称】《合肥工业大学学报（自然科学版）》【年(卷),期】2017(040)005【摘要】文章采用广义Maxwell模型描述沥青混合料面层的黏弹性,考虑碎石基层和土基的横观各向同性特征对路面结构力学行为的影响.在弹性假设条件下引入材料水平模量与竖直模量比值为变量,运用有限元方法建立路面结构三维有限元模型;通过模拟计算,对比分析均布荷载作用下碎石基层和土基各向同性与横观各向同性对各结构层应力和应变及路表弯沉值的影响,并对沥青路面服务寿命进行预估分析.分析结果表明:均布荷载作用下碎石基层的横观各向同性特征对路表弯沉影响较小,而土基横观各向同性特征对路表弯沉影响较大;路基顶部压应变受碎石基层及土基横观各向同性特征影响较大,而面层层底拉应变和基层底拉应力仅受碎石基层横观各向同性特征影响较大;沥青路面服务寿命受碎石基层横观各向同性特征影响较大,且在碎石基层各向同性时服务寿命最长.因此,在路面结构设计中应适当考虑基层和路基材料的横观各向同性特征.【总页数】6页(P679-684)【作者】李群;游凌云;颜可珍;庾付磊【作者单位】湖南大学土木工程学院,湖南长沙 410082;湖南大学土木工程学院,湖南长沙 410082;湖南大学土木工程学院,湖南长沙 410082;郑州市政工程勘测设计研究院,河南郑州 450052【正文语种】中文【中图分类】U416.217【相关文献】1.基于横观各向同性的沥青路面加铺层力学分析 [J], 刘能源;颜可珍;胡迎斌;游凌云2.圆面积均布荷载下横观各向同性地基位移和应力计算 [J], 顿志林;高雪冰;李婕3.考虑层间状态的横观各向同性沥青路面力学分析 [J], 朱向平;颜可珍;张虎;游凌云4.水平条形均布荷载下横观各向同性弹性地基的位移分析 [J], 金耀华;孙炎;钱玉林5.条形均布荷载下横观各向同性弹性地基中附加应力的分布规律 [J], 陈越因版权原因，仅展示原文概要，查看原文内容请购买。
横观各向同性地基各向异性对应力场影响研究
横观各向同性地基各向异性对应力场影响研究王炳军;肖洪天;党彦;孙凌志【期刊名称】《四川大学学报（工程科学版）》【年(卷),期】2015(047)006【摘要】在重力的作用下,岩层和土层往往呈现横观各向同性.基于横观各向同性双材料基本解,发展了横观各向同性地基弹性场的分析方法,并编写了相应的Fortran 程序.该方法能分析加载域为任意形状和荷载为非均匀分布的半无限地基问题,并且能获得很高的计算精度.采用建议方法分析了法向或切向均布力作用下平行与垂直层面方向的弹性模量、剪切模量和泊松比的各向异性对矩形基底中心点与角点下附加应力的影响.结果表明:弹性模量的各向异性仅对法向均布力时中心点与角点下的附加应力有明显影响;剪切模量的各向异性除对角点下平行层面的附加应力基本无影响外,其他均影响明显;泊松比的各向异性基本无影响.【总页数】9页(P40-48)【作者】王炳军;肖洪天;党彦;孙凌志【作者单位】山东科技大学土木工程与建筑学院山东省土木工程防灾减灾重点实验室,山东青岛266590;山东科技大学土木工程与建筑学院山东省土木工程防灾减灾重点实验室,山东青岛266590;青岛滨海学院建筑工程学院,山东青岛266555;山东科技大学土木工程与建筑学院山东省土木工程防灾减灾重点实验室,山东青岛266590【正文语种】中文【中图分类】TU431【相关文献】1.板面为各向异性面的横观各向同性拉伸板的精化理论 [J], 李荣荣;赵宝生2.板面为各向异性面的横观各向同性弯曲板的精化理论 [J], 李荣荣;赵宝生3.自由面压力作用下横观各向同性地基多裂纹分析 [J], 王炳军;肖洪天;党彦;岑达4.横观各向同性双参数地基上矩形薄板的弯曲 [J], 何芳社;悦峰5.基于FLAC3D横观各向同性模型的煤矿井田初始地应力场反演方法 [J], 余大军;杨张杰;郭运华;杨永刚;王波因版权原因，仅展示原文概要，查看原文内容请购买。
各向同性和横观各向同性材料的统一点力解Ξ
将式 ( 15) 代入式 ( 18) , 就有
4Π
∑ΗA
i i= 1
i
- P = 0
( 19)
求解由式 ( 17) 和 ( 19) 所构成的方程组, 可定出系数 A i ( i = 1, 2)
A
1
= - A2=
4Π( Η Η 1 2)
P
=
( c13 + c44 ) P 2 2 4Π c33 c44 ( s2 - s1 )
u= P
Κ+ Λ P x z Λ( Κ+ 2Λ) 8ΠR 3 Κ+ Λ P y z v = Λ( Κ+ 2Λ) 8ΠR 3 Κ+ Λ P z 2 Κ+ 3Λ P 1 + Λ( Κ+ 2Λ) 8ΠR 3 Λ( Κ+ 2Λ) 8Π R
( 22)
w =
式 ( 22) 与 Soko ln ikoff〔9〕 书上所列的结果一致。
+ 2
2x 2
3
R 0R 0
3
∑D
i= 1
1
R iR i
3 2
2x 2
R iR i
3 3
x 3 R iR i
2
2 2 2 2
( 29)
z z
2
Σx z = Ξ0 Σy z = Ξ0
2
2
( 16)
∑A
i= 1
i
= 0
( 17)
同时, 考虑在原点两侧, 由平面 z = ± h 所割出的一个弹性层的力平衡条件, 可以得到另 一个关系式:
+ ∞+ ∞
[ Ρ (x , y , h ) ∫ ∫
z
Ρz ( x , y , - h ) ]d x d y + P = 0
横观各向同性饱和地基单桩有限元分析
２１ 第５ ０卷 月 １ 期 第６ 年５
中国科技论文在线
Ｓ Ｅ ＣＩＮＣＥ ＡＰ Ｒ ＯＮ Ｉ Ｐ Ｅ ＬＮＥ
ＶＩ Ｎ ． ｏ６ Ｏ ． ５
Ｍ ａ ．０１ ｙ２ １
横观各 向同性饱和地基单桩有 限元分析
艾 智 勇 ，董 洲
（ 同济大学地 下建 筑－ ｂ工程 系，岩土及地下工程教 育部重点实验 室，上 海 ２ ０ ９ ） － ０ ０ ２
ＦＥＭ ｎ ｌ ｓｓｏ ｎ ｌ ｉ ｍ ｂ ｄ ｅ ｒ ｎ ｖ ｒ ｅｙｉｏ ｒ ｐ ｃｓ ｔ ｒ ｔｄ ｓ ｉ ａ ａｙ ｉ ｆ ｉ ｇｅｐ ｌ ｅ ｅ ｄ ｄｉ ｔａ ｓ ｅ ｓｌ ｔｏ ｉ ａ ｕ ａ ｅ ｏ ｓ ｅ ｎ ｓ ｌ
Ａｉ ｙｎ Ｚｈｉｏ ｇ， Ｄ ｏ ｏ ｎｇＺｈ ｕ
问题 ；Ｎ ｕ ｒ ｉ ｉ ａｔ ｍｐ ｄ
研究了半空间饱和土体 中轴向
非常复杂。自 １６ 年开始对桩土相互作用问题进行研 ９０ 究 ，并 日益受到重视 ，取得了许多研究成果 ，但大多 数的研究都将土体视为单相介质 ，较少考虑饱和地 基中孔隙水与土骨架之间的耦合作用。事实上 ，饱和 地 基在外荷载作用下会 由于孔隙水压力的消散而 引起 固结变形 ，因此 ，在分析饱和地基与桩之间的相互作 用问题时 ，应考虑地基随时间变化的特性 。应用积分 方程法【，Ａ ｉ ｔ ｏａｉ ｊ ｐｒ ｈ ｒ ｊ等 分析了半空 间饱和土体 Ｊ ａｖ ｋ
横观各向同性土强度与破坏准则的研究_姚仰平
收稿日期：2010-11-28基金项目：国家自然科学基金项目（10872016；11072016；50879001）作者简介：姚仰平（1960-），男，陕西西安人，博士，教授，主要从事土的基本特性和本构模型研究。
E-mail ：ypyao@ 水利学报SHUILI XUEBAO 2012年1月第43卷第1期文章编号：0559-9350（2012）01-0043-08横观各向同性土强度与破坏准则的研究姚仰平，孔玉侠（北京航空航天大学交通科学与工程学院，北京100191）摘要：建立横观各向同性土的破坏准则必须考虑其应力水平和材料横观各向同性的综合影响。
本文通过分析横观各向同性土的试验规律，基于横观各向同性土的强度随SMP 面（空间滑动面）和沉积面的夹角减小而变小这一假设，建立横观各向同性土的峰值强度表达式。
提出了一个关于横观各向同性土的峰值强度和应力张量函数的各向异性变换应力张量。
在各向异性变换应力空间，横观各向同性土体被认为是各向同性材料。
将变换应力与SMP 准则结合，建立了横观各向同性土的三维破坏准则。
分别采用具有横观各向同性的Santa Monica 海滩砂土和San Francisco 海湾黏土真三轴试验数据验证了该破坏准则的合理性。
预测结果与试验结果的对比表明，本文提出的横观各向同性破坏准则能够合理地描述横观各向同性对土体强度特性的影响。
关键词：横观各向同性；强度；破坏准则；砂土；黏土中图分类号：TV411.2文献标识码：A1研究背景在边坡、大坝以及地基稳定性分析等岩土工程设计计算中应考虑土体变形和强度的各向异性［1-2］。
土的力学特性与其沉积过程密切相关，由于土体在天然沉积过程中受到重力的影响，土颗粒倾向于沿水平方向优势排列，从而使土体呈现出横观各向同性，即平行于沉积面的各个方向的力学特性大致相同，在垂直于沉积面的方向则具有轴对称性。
各向异性对土体力学特性的重要影响一直以来备受各国研究人员的关注［3-4］，试验结果表明具有横观各向同性的土体在竖向的压缩性小于在横向的压缩性，并且在受力过程中土颗粒的优势排列变化很小。
横观各向同性砂岩储层水平井井壁应力分析
中 图分 类 号 ： Ｔ Ｅ ２ １ 文献标识码 ： Ａ
Ｔｈｅ ａ ｎａ ｌ ｙ ｓ ｉ ｓ ｏ ｆ ｈｏ ｒ ｉ ｚ ｏ ｎｔ ａ ｌ ｗｅ ｌ ｌ ｂｏ ｒ ｅ ｓ ｔ ｒ ｅ ｓ ｓ ｉ ｎ ｔ ｒ ａ ｎｓ ｖｅ ｒ ｓ ｅ ｌ ｙ ｉ ｓ ｏ ｔ ｒ ｏ ｐｉ ｃ ｓ ａ ｎｄｓ ｔ ｏ ｎｅ ｒ ｅ ｓ ｅ ｒ ｖ ｏ ｉ ｒ
向异性度较小 时， 周 向拉 应力会 出现 四个 最值点 ， 当拉应力超过 岩石抗张 强度 时 ， 水 力裂缝在这 四个 最值 点 同时起裂 ， 从
而解释 了水力压裂过程 中出现 的近 井筒效应。岩石弹性模量各 向异 性度 对井壁周 向应力分布有较大 影响， 而泊松 比各 向
横观各向同性砂岩储层水平井井壁应力分析
横观各向同性砂岩储层水平井井壁应力分析李小刚;易良平;苏建政;张汝生;刘长印;杨兆中【摘要】在经典的井壁应力场计算模型中,将地层岩石力学性质视为各向同性,而对于砂岩这类层理性地层,垂直于层理面和平行于层理面的岩石力学性质存在明显差异,即砂岩为横观各向同性体,因此,基于各向异性材料力学理论,建立了正交各向异性地层中井壁应力场计算新模型.新模型表明,与力学性质各向同性相比,力学性质正交各向异性条件下井壁径向应力和剪应力没有发生改变,而周向应力发生了变化,周向应力是岩石力学性质、地应力、井筒压力的函数.并运用此模型分析了横观各向同性砂岩储层水平井井壁应力分布特征,分析表明,在弹性模量各向异性度较大时,或者地应力各向异性度较小时,周向拉应力会出现四个最值点,当拉应力超过岩石抗张强度时,水力裂缝在这四个最值点同时起裂,从而解释了水力压裂过程中出现的近井筒效应.岩石弹性模量各向异性度对井壁周向应力分布有较大影响,而泊松比各向异性度对井壁周向应力分布影响很小.【期刊名称】《油气藏评价与开发》【年(卷),期】2016(006)006【总页数】6页(P45-50)【关键词】正交各向异性;横观各向同性;水平井;水力压裂;裸眼井【作者】李小刚;易良平;苏建政;张汝生;刘长印;杨兆中【作者单位】西南石油大学油气藏地质及开发工程国家重点实验室,四川成都610500;西南石油大学油气藏地质及开发工程国家重点实验室,四川成都 610500;中国石化页岩油气富集机理与有效开发国家重点实验室,北京 100083;中国石化页岩油气富集机理与有效开发国家重点实验室,北京 100083;中国石化页岩油气富集机理与有效开发国家重点实验室,北京 100083;西南石油大学油气藏地质及开发工程国家重点实验室,四川成都 610500【正文语种】中文【中图分类】TE21致密砂岩气是非常规天然气的主要类型，是指覆压渗透率小于0.1×10-3μm2的致密砂岩经过增产改造而产出的天然气，也是目前国际上开发规模最大的非常规天然气[1-5]。
横观各向同性双参数地基上矩形薄板的弯曲
横观各向同性双参数地基上矩形薄板的弯曲何芳社;悦峰【摘要】弹性地基板是建筑工程中常见的构件,对其进行分析具有重要意义.对于工程中的大量由沉积作用形成的天然地基和分层碾压填筑而成的人工地基,采用横观各向同性地基模型更接近工程实际地基.本文将地基—板作为一个整体系统,利用最小势能原理,经过变分运算,推导建立了横观各向同性双参数弹性地基上矩形薄板弯曲的控制方程及其相应的边界条件.然后选取合理的挠度试函数,采用里兹法,对受横向荷载作用的四边自由矩形薄板进行了数值分析.计算表明:通过与其他文献的结果对比,两者吻合良好.所用理论在研究地基板的相互作用中具有普适性,为横观各向同性双参数弹性地基的应用奠定了基础.【期刊名称】《西安建筑科技大学学报（自然科学版）》【年(卷),期】2018(050)005【总页数】6页(P755-760)【关键词】横观各向同性;双参数地基;最小势能原理;矩形薄板;里兹法【作者】何芳社;悦峰【作者单位】西安建筑科技大学理学院,陕西西安710055;西安建筑科技大学理学院,陕西西安710055【正文语种】中文【中图分类】TU348研究结构物基础与支撑土介质间的相互作用对结构工程和岩土工程均具有重要意义.随着建设项目的不断增多，出现了许多梁状、板状和壳型的结构物，相应地对于基础与地基提出更高的标准和要求.特别是基础工程具有隐蔽性，对于结构的安全和经济方面会有重大的影响；工程中质量事故有一部分出现在基础与地基中，不但损失巨大，而且难以采取合适的措施来加固.学术界和工程界致力于如何将这些工程实例合理地简化为相应的弹性地基上的梁、板、壳的问题，并进行更加准确且简便的计算.针对弹性地基上梁、板、壳的模型，国内外专家学者都进行了许多富有成果的工作.比如 Vallabhan C V G等对双参数地基上板、梁的能量和参数及内力、边界条件进行了求解说明[1].Yang用有限元法分析双参数地基时指出还没有方法可以计算参数值[2].Jones和Xenophontos推导出了双参数地基中参数和表面变形的联系[3].Nogami和Lam分析了地基板的双参数模型，然而此方法仅限于平面应变[4].Celep Z分析研究了无拉力情形下弹性地基上矩形板的弯曲[5].国内方面，王克林、黄义[6]和张福范、黄晓梅[7]用叠加法分析探讨了地基上矩形板体的弯曲；陈叔陶等根据变分原理通过Ritz法分析求解了弹性地基上板体的弯曲[8]；阎红梅、崔维成等引入新挠度函数，通过伽辽金法对弹性地基上矩形板进行了研究[9].前人对地基板经典问题的研究存在有待深入探讨的方面.比如现有的弹性地基理论体系认为介质是连续、线弹性、均匀和各向同性的，且服从小变形假设.对应的弹性地基模型可总结为：文克尔模型、双参数模型和弹性半空间模型[10].但试验表明许多地基的性质更接近于横观各向同性.鉴于目前对横观各向同性地基上矩形板的研究并不充分，本文考虑地基横观各向同性，研究双参数地基上矩形板的弯曲问题，对地基与矩形薄板的相互作用进行系统的分析.首先利用最小势能原理，经过变分运算，建立了横观各向同性弹性地基上板的控制微分方程和边界条件，该结果可退化到经典的双参数弹性地基板理论.综上所述，本文的创新之处在于：从能量角度出发，考虑实际土体的横观各向同性的属性，改进和丰富了符拉索夫双参数弹性地基模型，具有一定的学术与应用价值.为验证理论正确性，最后利用里兹法进行了数值计算，效果较好.1 系统形变势能将地基—板作为一个整体，该系统的总势能泛函[11-12]为U=UP+US+Uq(1)式中，各物理量依次为总势能，板的形变势能，地基的形变势能和外力势能.根据弹性薄板理论[13]，得板的形变势能(2)其中：是板的弯曲刚度；E和μ是板的弹性模量和泊松比；w是板的挠度；Ω是矩形薄板区域，即x∈[0,a],y∈[0,b].根据弹性理论中弹性体的形变势能，有∭(σxεx+σyεy+σzεz+τxyγxy+τyzγyz+τzxγzx)dxdydz(3)假定地基的水平位移分量us=0,vs=0，竖直位移分量ws(x,y,z)=w(x,y)φ(z)，φ(z)为衰减函数，且满足条件φ(0)=1,φ(H)=0.令E1,μ1为各向同性面内变形模量和泊松比，E2,μ2为各向同性面法线方向变形模量和泊松比，G为与各向同性面垂直的平面内剪切模量.则横观各向同性弹性地基的本构关系和几何关系[14][15]为(4)其中的Cij是地基土的物性常数，与工程常用的材料弹性常数有如下关系(5b)(6a)(6b)将上面(4)和(6)式代入(3)式，得地基的形变势能(7)其中：VS为地基体积区域；ΩS为地基表面区域.(8)外力势能为(9)2 控制方程和边界条件由最小势能原理，经过变分，可得板控制方程D4w=q-kw+Gp2w(10)及板外地基控制方程-kws+Gp2ws=0(11)图1 弹性地基板示意图Fig.1 Element of plate and foundation现将地基ΩS区域划分为为板下区域和板外区域进一步将板外地基范围分为四个边域(Ⅰ、Ⅱ、Ⅲ、Ⅳ)和四个角域(A,B,C,D)，如上图1所示.假设ws(x,y)按指数规律衰减，子域地基表面位移形式如表1所示，其中的α由(11)式及位移连续性可确定为α2=k/Gp (12)表1 地基挠度的表达式Tab.1 Deflection expression of foundation子域地基挠度表达式Ⅰws=w(a,y)e-α(x-a)Ⅱws=w(x,b)e-α(y-b)Ⅲws=w(0,y)eαxⅣws=w(x,0)eαyAws=w(a,b)e-α(x-a)e-α(y-b)Bws=w(0,b)eαxe-α(y-b)Cws=w(0,0)eαxeαyDws=w(a,0)e-α(x-a)eαyΩws=w(x,y)经过计算，并注意到变分项的任意性，可得关于x=a边和(a,b)角点的边界条件如下若边界为固定边，则挠度与转角为零，即(13)若边界为简支边，则挠度与弯矩为零，即(14)若边界情况为自由边，得(15)Mx|x=a=0(16)当(a,b)为自由角点时，则δw为零，得(18)矩形薄板其它边界和角点的条件与上类似.令物性常数E1=E2=Es,μ1=μ2=μs,C44=Gs，可将横观各向同性地基退化为各向同性地基，得到那么式(10)—式(18)退化后与传统的各向同性双参数地基上矩形板的控制方程和边界条件保持一致[16-17]，即方程表达形式没有变化，但其中地基土的双参数发生变化.表明土体的各向同性属性是横观各向同性属性的一种特殊情况，而横观各向同性则更具有普遍的意义.3 算例采用里兹法对弹性地基上矩形薄板进行计算.对于四边自由的边界条件而言，可以选取如下的挠曲试函数(19)其中：而w0,θx,θy,Amn,Bm,Cn是待定系数.具体分析如下：w0+xθx+yθy为整个板的刚体位移，中间的为板任意位置上的二维挠度，最后两项表示板在对应方向上的挠曲.由下列各式20)(21)分别整理后可以得到如下系列方程组，即[kab+2Gpα(a+b)+3Gp]w0+(23)(24)…[1-(-1)n]Bm+[1-(-1)m]Cn=(m,n=1,2,3,···)(25)(m,n=1,2,3,…)(26)(m,n=1,2,3,…)(27)可见未知数的数目和方程的个数相等，问题可解.以下算例中均取m=50,n=50. 例1 取板的弹性模量E=1.96×104 MPa，泊松比为μ=0.167，地基的弹性模量为Es=39.2 MPa，泊松比为μs=0.4，深度为H=0.6 m，地基参数γ=1.55，板宽a=1 m，板厚h=0.04 m，集中力P=98 kN，均布荷载q=9.8 kN/m2.图2是依据本法绘制的双参数地基上矩形薄板的挠度图，图3是弯矩图，宏观定性看出图形的趋势走向及数值大小与实际符合.表2中第一行是双参数地基矩形薄板的精确解[18-19]，第二行是本文由横观各向同性弹性地基退化为各向同性弹性地基的计算结果.微观定量进行比较，两者结果吻合良好，百分误差都在可接受的较小范围之内，证明了分析结果的可靠性.图2 矩形板的挠度分布Fig.2 Deflection distribution of rectangular plate图3 矩形板的弯矩分布Fig.3 Bending moment of rectangular plate表2 例1中板的挠度值/mTab.2 Deflection of rectangle plate in Example1x/my/m0.5000.6250.7500.8750.5000.002 70.002 00.001 10.000 40.002690.001 970.001 130.000 520.6250.002 00.001 60.000 90.000 30.001970.001 600.000 960.000 460.7500.001 10.000 90.000 50.000 20.001130.000 960.000 630.000 310.8750.000 40.000 30.000 2-0.000 1 0.000 520.000 460.000 310.000 14例2 矩形薄板的物理和几何参数，荷载情况同例1，横观各向同性地基参数选取如下，Es1=39.2 MPa,Es2=29.4 MPa,μ1=0.4,μ2=0.4,G=14 MPa,计算结果见文后的表3.由于现有文献中没有关于横观各向同性双参数地基上矩形薄板受横向荷载作用的弯曲挠度，所以本算例只与退化后的各向同性双参数地基上矩形薄板的结果相比较. 首先，经过编程运算，横观各向同性双参数地基上受横向荷载作用的矩形薄板的变形图与图2相似，也就是图形的趋势走向及数值大小与实际吻合.其次，定量地分析，表3中第一行是本文各向同性双参数地基板的挠度，第二行是本文横观各向同性双参数地基板的计算结果.经过比较，同性地基情况解略大于横观各向同性地基情况的解.定性分析原因在于地基土体假设为横观各向同性体，相比于各向同性体而言，土体的本构关系有所不同；也就是在对横观各向同性地基假定弹性常数时，弹性模量比各向同性地基土的较小，从而导致横观各同性双参数的地基参数k变大，所以板与地基的变形局部变小.最后，值得一提的是，关于结果符合工程实际的讨论中，本文只在理论上给出证明，即采用更接近工程实际情况的横观各向同性地基来推导计算，核心在于其本构关系不同于经典的各向同性双参数地基；缺少通过原位试验来测量矩形薄板受载后的变形结果，或者利用有限元软件来模拟计算，这将是之后科研的方向和目标.另外，参考文献[18-19]中采用了一些旧的单位制，为了既可方便地与已有结果进行对比，同时又遵循国标单位制，现给出基本的单位换算关系1 t=103 kg,1Pa=1 N/m2,g=9.8 m/s2表3 例2中板的挠度值(m)Tab.3 Deflection of rectangle plate in Example2x/my/m0.5000.6250.7500.8750.5000.002 690.001 970.001 130.000520.002 500.001 800.001 000.000 450.6250.001 970.001 600.000 960.000 460.001 800.001 440.000 850.000 390.7500.001 130.000 960.000 630.000 310.001 000.000 850.000 550.000 260.8750.000 520.000 460.000 310.000 140.000 450.000 390.000 260.000 124 结论分析了横观各向同性双参数弹性地基上矩形薄板的弯曲问题，主要工作为：考虑地基土体的横观各向同性，推导出地基—板系统的形变势能，利用最小势能原理，通过变分运算，建立了弹性地基上矩形薄板弯曲的控制方程和边界条件；然后选取挠度试函数，采用里兹法求解四边自由矩形板受横向荷载的弯曲挠度.得到如下几点结论：(1)从能量方面出发，利用最小势能原理推导出横观各向同性双参数地基上矩形薄板弯曲的控制方程和边界及角点条件.考虑实际地基土体的横观各向同性，改进和丰富了符拉索夫双参数弹性地基模型，可促进其更加广泛地应用.(2)横观各向同性双参数弹性地基模型，与Vlasov双参数弹性地基模型一样，用两个独立参数表示抗压和抗剪性能.主要区别在于考虑地基土体横观各向同性时，由土体本构关系不同而导致的双参数具体计算表达形式不同.(3)选取合适的挠度函数，将地基上板受横向荷载作用的控制微分方程问题转化为代数方程组的求解问题.算例分为退化成各向同性双参数和横观各向同性双参数地基两种.模型退化过程中，通过与其他文献的计算结果对比，两者吻合良好，证明了本文理论推导和计算结果的正确性.(4)结果表明，考虑地基土体的横观各向同性属性时，矩形板和地基的变形会与各向同性弹性地基的情况不同，即地基模型的假设简化会对板的弯曲产生一定的影响，所受影响的大小由选取的横观各向同性地基土体的物性常数来决定.总之，本文对于横观各向同性双参数地基上四边自由矩形薄板的弯曲问题进行了相关研究.修正的模型和方法具有一定的创新性，相关成果和结论具有重要的理论意义，同时对于实际工程问题的解决和设计仿真软件的开发等方面均具有指导价值和参考作用.参考文献 References【相关文献】[1] VALLABHAN C V G,DAS Y C.Modified Vlasov model for beams on elastic foundations[J].Journal of Geotechnical Geoenvironmental Engineering,1991,117(6):956-966.[2] YANG T Y.A finite element analysis of plates on a two-parameter foundationmodel[J].Comput.Struct.,1972,(2):593-614.[3] JONES R,XENOPHONTOS J.The Vlasov foundation model[J].International Journal of Mechanical Sciences,1977,19(6):317-323.[4] NOGAMI T,LAM Y C.Two-parameter layer model for analysis of slab on elastic foundation[J].J.Engrg.Mech.,1987,113(9):1279-1291.[5] CELEP Z.Rectangular plates resting on tensionless elastic foundation[J].Journal of Engineering Mechanics,1988,114(12):2083-2092.[6] 王克林,黄义.弹性地基上四边自由矩形板[J].计算结构力学及其应用,1985,2(2)47-58.WANG Kelin,HUANG Yi.Rectangular plates with four free edges on elasticfoundations[J].Computational Structural Mechanics and Applications,1985,2(2):47-58. [7] 张福范,黄晓梅.弹性地基上的自由矩形板[J].应用数学和力学,1984,5(3):345-353.ZHANG Fufan,HUANG Xiaomei.A free rectangular plate on the elasticfoundation[J].Applied Mathematics and Mechanics,1984,5(3):345-353.[8] 陈叔陶.弹性地基上的自由边矩形板[J].力学学报,1960,4(1):23-35.CHEN Shutao.Rectangular plates with free edges on elasticfoundations[J].Acta.Mechanican Sinica,1960,4(1):23-35.[9] 阎红梅,崔维成,刘应中.弹性地基上四边自由矩形板问题的一种新型挠度函数[J].船舶力学,2003,7(2):61-63.YAN Hongmei,CUI Weicheng,LIU Yingzhong.A new deflction fuction for the problem of a rectangular plate on elastic foundation with four free edges[J].Journal of Ship Mechanics,2003,7(2):61-63.[10] VLASOV V Z,LEONTIEV N N.Beams,plates and shells on elasticfoundations[M].Jerusalem,Israel：Israel Program for Scientific Translations,1966.[11] VALLABHAN C V G,DAS Y C.Refined model for analysis of plates on elastic foundations[J].J.Engrg.Mech.,ASCE,1991,117(12):2830-2843.[12] VALLABHAN C V G,DAS Y C.Parametric study of beams on elasticfoundations[J].Journal Eng.Mech.,1988,114:2072-2082.[13] 张福范.弹性薄板[M].北京：科学出版社,1984.ZHANG Fufan.Elastic thin plate[M].Beijing:Science Press,1984.[14] 乔世范,顿志林,刘宝琛.横观各向同性地基模型的理论分析及其应用[J].岩土工程技术,2003,(4):213-219.QIAO Shifan,DUN Zhilin,LIU Baochen.The study on constitutive equations of a transversely isotropic foundation and its application[J].Geotechnical EngineeringTechnique,2003,(4):213-219.[15] 李婕,张学民,顿志林,等.横观各向同性地基空间问题的位移函数解法[J].岩土工程学报,2007,29(1):137-142.LI Jie,ZHANG Xuemin,DUN Zhilin,et al.Displacement function method of space problems for transversely isotropic foundation[J].Chinese Journal of Geotechnical Engineering,2007,29(1):137-142.[16] 何芳社,黄义,郭雅云.双参数弹性地基板的动力问题[J].西安建筑科技大学学报(自然科学版),2006,38(1):130-134.HE Fangshe,HUANG Yi,GUO Yayun.The dynamic problem of plates on the bi-parameter elastic foundations[J].J.Xi′an Univ.of Arch.&Tech.(Natural Science Edition),2006,38(1):130-134.[17] SELVADURAI A P S.Elastic analysis of soil-foundation interaction[M].London: Elsevier Scientific Publishing Co.,1979.[18] 生跃,黄义.双参数弹性地基上自由矩形板[J].应用数学和力学,1987,8(4):317-329.SHENG Yao,HUANG Yi.A free rectangular plate on the two-parameter elastic foundation [J].Applied Mathematics and Mechanics,1987,8(4):317-329.[19] 黄义,何芳社.弹性地基上的梁、板、壳[M].北京:科学出版社,2005.HUANG Yi,HE Fangshe.Beams,plates,and shells on elastic foundations[M].Beijing: Science Press,2005.。
横观各向同性土的三维强度准则
横观各向同性土的三维强度准则各向同性土是指土壤在各个方向上的性质和行为相同，也就是说，土壤在任何方向上都具有相同的强度特性。
在土工工程中，为了描述土壤的强度特征，常采用三维强度准则来进行分析和计算。
一、对土壤的应力、应变和强度特征的描述在三维强度准则中，需要了解土壤的应力和应变特征。
应力是指单位面积上的力，通常用应力张量来表示。
应变是指物体在受到力作用下产生的变形量，通常用应变张量来表示。
而土壤的强度特征通常是由一组参数来描述的，包括弹性模量、剪切模量和泊松比等。
二、Mohr-Coulomb准则Mohr-Coulomb准则是最常用的三维强度准则之一，也是最早提出的强度准则之一、该准则基于理想平面内剪切的实验事实，认为土壤的强度与剪切应力和正应力之间存在一个线性关系。
该准则可用如下的方程表示：τ = c + σn tanφ其中，τ为剪切应力，c为内聚力，σn为法向正应力，φ为内摩擦角。
该准则适用于各种土壤类型，并且容易应用于实际工程中。
三、Drucker-Prager准则Drucker-Prager准则是一种改进的Mohr-Coulomb准则，考虑了土壤的体积效应。
该准则认为，当土壤受到的应力达到一定程度时，会发生体积塑性变形。
因此，在计算土壤的强度时，需要考虑剪切应力和正应力之间的非线性关系。
该准则可用如下的方程表示：f=α+β(P-q)其中，f为土壤的强度准则，α为黏聚力，β为剪切强度参数，P为平均应力，q为孔隙水压力。
该准则适用于压实土和粘土，在模拟土壤的体积塑性变形方面具有较好的效果。
四、Cam-Clay准则Cam-Clay准则是一种用来描述细粒土特性的三维强度准则。
该准则基于气泡模型并考虑了土壤颗粒之间的排列方式。
该准则假设细粒土中的颗粒间隙通过应力增大而变小，从而影响土壤的强度特性。
该准则可用如下的方程表示：I1n = ln(I1 + α)其中，I1n为体积不变应变，I1为一次应力不变量，α为一个参数。
横观各向同性地基轴对称问题的应力和沉降分析
横观各向同性地基轴对称问题的应力和沉降分析
顿志林;刘干斌;乔世范;任良
【期刊名称】《河南理工大学学报（自然科学版）》
【年(卷),期】2002(021)001
【摘要】通过实验发现岩土地基中普遍存在各向异性现象,而目前按照各向同性地基模型计算势必会引起较大误差,为了提高地基中应力和沉降计算的精确度,本文将各向同性轴对称问题下的拉甫位移函数推广到横观各向同性地基轴对称问题,得到了位移分量与横观各向同性下拉甫位移函数的关系式,并通过积分变换得到了横观各向同性地基应力和沉降的通解.
【总页数】5页(P64-68)
【作者】顿志林;刘干斌;乔世范;任良
【作者单位】焦作工学院土木建筑工程系,河南,焦作,454000;焦作工学院土木建筑工程系,河南,焦作,454000;中南大学,湖南长沙,410083;焦作工学院土木建筑工程系,河南,焦作,454000
【正文语种】中文
【中图分类】TB12
【相关文献】
1.横观各向同性多层地基中单桩的弹性沉降分析 [J], 施金坤;陈志祥;徐满清
2.横观各向同性地基上的碾压混凝土重力坝应力应变研究 [J], 苏超;董安雨;刘崇巍;何志亮;徐汇
3.横观各向同性轴对称问题的非协调元和杂交应力元计算 [J], 万力;郭乙木
4.层状横观各向同性地基轴对称问题的位移解法 [J], 顿志林;刘干斌;苌向阳
5.几种常见荷载作用下横观各向同性地基轴对称问题的解析解 [J], 顿志林;刘干斌因版权原因，仅展示原文概要，查看原文内容请购买。
圆面积上作用垂直荷载下横观各向同性地基的统一解
圆面积上作用垂直荷载下横观各向同性地基的统一解高雪冰;顿志林【摘要】A general three-dimensional analysis of transversely isotropic axial symmetrical foundation in the image domain is made by the displacement function method and the Love's displacement function is modified. The rationale of displacement function method, Hankel integration transform, Hankel integration contrary transform and Bessel function theory are employed in the solution. The uniform solution to displacement and stress of transversely isotropic foundation under rigid load in circular area is obtained when the characteristic root is equal.%从横观各向同性弹性体轴对称问题的基本方程出发，对各向同性下的Love位移函数进行了重新修正，采用位移解法的基本原理，利用Hankel积分变换和其反演变换以及Bessel函数理论，得到了当材料特征值s1=s2=s时，圆面积上作用垂直荷载下的横观各向同性地基问题的统一解，为求解圆面积上作用任意垂直轴对称荷载下的横观各向同性地基问题的解析解提供理论依据。
【期刊名称】《黄山学院学报》【年(卷),期】2012(040)005【总页数】4页(P37-40)【关键词】横观各向同性;轴对称;位移法;Hankel变换【作者】高雪冰;顿志林【作者单位】黄山学院建筑工程学院,安徽黄山245041;河南理工大学土木工程学院,河南焦作454000【正文语种】中文【中图分类】TU40 引言目前，在地基基础工程设计中，应用最广泛的是Winkler模型和弹性半空间地基模型，但实际地基并不是均质各向同性、理想的半无限体。
圆面积均布荷载下横观各向同性地基位移和应力计算
本文 通过对 各 向同性下 的 Ｌ ｖ 位 移 函数重新 修 正 ， ｏｅ 采用 位移法 ， 同时利 用 Ｈａ ｋｌ 分变 换和 Ｂ ｓｅ ｎ ｅ积 ｅｓｌ函
数理论［ 讨论 材料特 征值 ｓ＝： ， ８ １ ， １ｓ时 圆面积上 作用 均布 垂直荷 载 的横 观各 向同性 地基 的位移与 应力解 析解 ．
维普资讯
—
—
９ ８— ３ —
河
南 科
学
第２ 卷 第 ６ ５ 期
献 ［］ Ｌ ｖ 位 移 函数 重新修 正后 的位 移 函数为 ： ９ 对 ｏｅ 一 ■ （一一 ｒｚ ，）
ｗ ＝
Ｈ ＋ 卦 。 軎
（） ４
由 （） （） （） １ ， ２ ，３ 式可求 得与 工程 弹性 常数有 关 的常数 ａ， ｂ 及横 观各 向同性轴 对称 问题 的３Ａ（ ２， 酯 Ｇ ， ｄ３ ｎ＆ １ ＝ ． ２ ，３ １ ）ｄ ＝ ２ ＝
丽
・
Ｅ ， — —横 观各 向 同性 面 （ｏ 面） 。 ｘｙ平 内的弹性 模 量和 泊 松 比； ： ， Ｅ ， —— 垂 直横 观 各 向 同性 面 （ 轴 方 ｚ
圆面积 均布荷 载下横观 各 向同性地基位移 和应 力计算
顿志林 ， 高雪冰 ， 李
（ 南 理工 大 学 土 木工 程 学 院，河 南 焦 作 河 摘
婕
４４０） ５０ ０
要 ：从 横 观 各 向 同性 弹 性 体 轴对 称 问题 的基 本 方程 出发 ， 过对 各 向 同性 下 的 Ｌｖ 移 函 数 重 新 修 正 ， 用 通 ｏｅ位 采
程 中一般都 具有 固有 的横 观 各 向同性 ，ｉ ｏ ｓＫ ｎ 、ｅｖｄ ｒｉ ３ Ｓｍ ｎ 、 ｉｇ Ｓ ｌ ｕａ １ 多学 者认 为成 层 均匀 的横观 各 向同性 ａ ｔ 等许 弹性 半空 间可 以表 示 范 围广 泛 的地基 ．其 中弹 性体轴 对称 应力 分析 问题 在工 程 中有重要 意义 ， ｅｈ ｉｋｉ Ｌ ｋ ｎｔ ｉ］ ｓ １ ４
圆面积上作用垂直荷载下横观各向同性地基的统一解
对 上 式进 行 零 阶 Ｈａｋ ｌ 分 变换 ，其变 换 式 ｎ ｅ积
） ＝
Ｊ ） ｒ ．
④ 和 代入 （０ 式 ， 可得 到横 观 各 向 ＝ １） 即
， ．、 即 可 得 到 （ ） 中 的 ４ Ｇ， ｒ ｅ ２式
（） ｏ （）（ ｒ＝ 。 ∈ｕ ） ， Ｙ ，， ｚ 。 ｚ ０
ｆ‘ ７
运 用 Ｂ ｓ ｌ 数 的性 质 和 其 导 函 数 的 Ｈａｋ ｌ ｅ ｅ函 ｓ ｎｅ
变换 ， 将 （，） ｒｚ 导 ， 将 其 代 入 （ ） （ ） ｒｚ 对 ，求 再 ３ ， ６ 式 ， 可得 到 横观 各 向 同性 轴对 称 问题 的位 移 和 应 即
｛ 一 ） ＋ ＋ ＋ｚ０ ） ｒ 【 （ ｆ （ ） ． ） ｌ 哦 ２ 】 ２∈ ， Ｄ 。 ８ ｄ １ｆＢ 。｛ ）＋ ）（ ∈｝） 。 一ｚｏ ）一 ＋１∈ ｏ （ ｚ ＇ ＋ Ｄ ， 。 ｄ （ ＋ ３∈ ０ ］ｚ（ｓＤ ｌ （ ｌ 一ｚ 一 ｅ ＋ ＋ｚ０ｃ啦 ∈ ） － 【 ∈ ＋ ｏ ｒ ８ Ｓ ３ ） ） ￣ ＝ ∈【 ）一 ］ｚ【 ）＋ ｏｚ（ ｌ ｃ ｛２ ∈ ｏ ｅ ＋ ＋ｚ口Ｃｓ ） ０ 一 一ｚ 哦 － （ ∈ ］） （ Ｂ Ｓ ２ Ｄ ｅＪ ￣ ￣
＋ ＋
ｒ ｚ－ －－ － － － ￣
０ｒ
１
ｚ
ｒ
Ｊ
将 几 何 方 程 代 入 横 观 各 向 同性 轴 对 称 问题 的
１４ ９ ０年 给 出 了横观 各 向同性 体 轴 对称 问题 的通 解 ， Ｅ ｂ ｎ ｓ Ｓｅ ｅｇ １ ｕ ａｋ 和 ｔ ｂ ｒ ５ 位 移 表 示 的平 衡 方 程 出 ｒ ］从
（ ． 山学 院 建 筑 工 程 学 院 ， 徽 黄 山 ２ ５ ４ ； ． 南理 工 大 学 土 木 工 程 学 院 ， 南 焦 作 ４ ４ ０ ） １黄 安 ４ ０ １２河 河 ５ ００
在体积力作用下横观各向同性弹性体的平衡问题
在体积力作用下橫觀各向同性弹性体的平衡问题近年来，各向同性弹性体的平衡问题受到越来越多的关注。
这是因为各向同性弹性体在体积力作用下的平衡问题是一个具有挑战性的研究领域，也是当今社会发展和科学研究进步的重要组成部分。
本文将探讨各向同性弹性体在体积力作用下的平衡问题，以期为后续研究和应用提供参考。
首先，让我们了解一下各向同性弹性体的基本概念。
弹性体是指任何在承受外力作用时具有可逆力学性质的物体结构，而各向同性弹性体则是指任何在任何方向上具有相同弹性变形特性的弹性体，其扩张系数和拉伸系数相等。
各向同性弹性体存在于大多数机械和航空构件中，是结构力学中重要的一类物体。
其次，让我们来研究各向同性弹性体在体积力作用下的平衡问题。
体积力是通过外界外力或材料内部的变形力等造成的某种力的作用，其中可能包括快速运动或静止时的惯性力、湿度变化和温度变化等，都会影响各向同性弹性体的平衡。
通常情况下，当各向同性弹性体的体积受到影响时，物体的平衡会发生变化，而各向同性弹性体在体积力作用下的平衡也随之而变化。
第三，我们将讨论各向同性弹性体在体积力作用下的平衡问题的测量方法。
常见的测量方法有动态测量和静态测量，其中动态测量主要通过对弹性体的振动来探测它的体积变形情况，而静态测量则是通过体积变形LED灯来检测它的体积变形情况。
此外，能够准确测量弹性体体积变形的还有一种新技术，即电容测量技术。
最后，我们将讨论各向同性弹性体在体积力作用下的平衡问题的应用。
由于各向同性弹性体在体积力作用下的平衡问题，其广泛应用于社会发展和科学研究，特别是在航空航天、石油天然气处理、矿物加工、汽车制造、核能发电等行业中，都能看到其广泛而重要的应用，这些应用的成功完全依赖于对各向同性弹性体在体积力作用下的平衡问题的精确掌握和理解。
综上所述，各向同性弹性体在体积力作用下的平衡问题是当今社会发展和科学研究进步的重要组成部分，本文讨论并总结了各向同性弹性体在体积力作用下的平衡问题，相关技术和应用，为后续研究和应用提供了参考。
基桩在水平和竖向荷载作用下的受力分析
建 立 关于 节 点 2 %52 的 ， 在 轴、 横 向 荷 载 作 用
下的地 基柔度 矩阵［ δ］ 和刚 度矩 阵［!6］7 ［δ］82。 由 桩土 连 结 节 点处 位 移 的连 续 性 有 ：
[ K s ] {U } = { R}
1-3
式 中 ： ［ ! 6］ 和 ｛# ｝ 为 阶 数 扩 充 矩 阵 和 向
2 IF G I D ? G 2F 84G4E 2F E FE 4@ FF?I
有 限元 2 IF GF I ?E 84G4:
2F E FE 2D FF??
从 表 - 和图 #、& 可见 ， 本 文 方 法计 算 结 果 与 幂 级 数 和 有 限 元 法 所 得 结 果 基 本 一 致 。 由 于 !(Δ 效应，桩身弯矩和位移值 提高较大 ，当计入 轴力 时 ， 其 桩 顶 位 移 增 大 %-./0， 地 面 处 桩 身 位 移 增 大 )&./0 ， 弯 矩 增 大 %$.,0 ， 桩 身 最 大 弯 矩 增 大 %$0。 如 果 轴 向 荷 载 再 增 加 ， 桩 身 的 内 力 和 位 移 将增加 得更快 ，并呈 非线 性关 系增 加。 因此 ，当 基 桩 的 自 由 长 度 及 轴 向 荷 载 较 大 时 ，!(Δ 效 应是 不 可忽 视 的 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1
+ de
∋| & |z
2
( 9) ( 10) = - i& d ∃( & , z) dz
对式 ( 5) 中的边界条件取傅氏变换, 可得象域里的边界条件为 ( 这里先求 P = 1 时的基本解 ) 。 = 0,
zx
= p
当体力为零时, 式( 5) 的傅氏变换为
x
=
d ∃( & , z) 2 , dz i , |& |& (∋ 1- ∋ 2)
王春河
( 中铁十四局集团有限公司 , 山东 济南 250002)
摘
要 : 根据横观各向同性体的基本方程 , 运用数 学力学方法得出了横观各向同性地基的 平面塞露蒂 ( Cerruti) 问题
的基本解 , 然后利用积分的方法分别得出了横观各向同性地基在条形面积上作用有水平 均布荷载 、 水 平三角形 分布荷载 及水平梯形分布荷载的应力计算公式 , 并利用测出的一组弹性参数 , 将横观各向同性地基 中的附加应 力与现有 的计算理 论给出的各向同性地基中的附加应力通过图形作分析比较 , 得出了一些有利于工程安全 设计的结论 , 供岩土工 程设计人 员参考 。 关键词 : 横观各向同性地基 ; 本构方程 ; 应力解 ; 傅氏变换 中图分类号 :TU431 文献标识码 : A 文章编号 : 1671- 0231( 2003) 04- 0085- 06
4 2 E1 ∀ 2 d ∃ (& , z) 2 1 2 d ∃( & , z) 4 1 2 1 ( 1- ∀1 ) - & ( 1+ ∀ 1) ∀ 2 + & ( 1) ∃( & , z) = 0 4 2 G2 E2 E2 E2 E2 dz dz 2
( 7)
式( 7) 为四阶常系数微分方程, 其通解为: ∃( & , z ) = ae 1 + be 2 + ce 1 + de 2 ( 8) 式中 a 、 b、 c、 d 均为傅氏变换参数 & 的函数, 可根据边界条件确定。 a 1 、 a 2 为关于 ∋ 的四次代数方程 的两个正实数根 : 1 2 4 ( 1- ∀1 ) ∋ E1 E1 ∀ 1 - 2 ( 1+ ∀ ) ∀ 2 1 2 1 2 ∋+ ( 1)= 0 G2 E 2 E2 E2
pA 2 x- a x+ a a tan ∋ z - a tan ∋ z ( 2 2
图2 在条形面积上作用水平均布 作用水平三角形分布荷载的附加应力解
对于条形基础受倾斜荷载、 风荷载的情况 , 若其水平分量沿条形基础的宽度方向变化率相同 , 且在 y
横观各向同性现象在地质材料中比较常见。如在沉积过程中形成的层状结构粘土层、 页岩等 , 不同薄 层内的矿物成份及物理力学性质是不同的, 在水平方向可以近似地看成各向同性, 但在垂直方向其性态的 差异就比较大。所以类似这样沉积形成的天然地基, 其应力、 应变关系就可以采用横观各向同性地基模型 来描述。象公路、 铁路的路基也属于这种情况。前人对横观各向同性地基模型已做了一些研究
3
z = -
2xz 2 2 2 ; (( x + z )
2
= -
2x z 2 2 2 , 这与在水平集中力作用下的各向同性半无限体的附加应力的解析解相吻合, 这也证 ( (x + z )
明了笔者所推导出的式( 14) 的正确性。
2
横观各向同性地基在条形面积上作用水平均布荷载的附加应力解
一般情况下 , 公路、 铁路以及条形基础受倾斜荷载作用时, 可将倾斜荷载分解为垂直荷载与水平荷载
轴上为零时, 如图 3 所示( 垂直线表示该处所受荷载的大小) , 则地基中任一点的附加应力可利用平面塞露 蒂基本解式( 14) 在区间 [ 0, b ] 上积分求解在 xoz 平面内附加应力解析解。其计算结果如下:
x
x ( x - b) + ∋ 1z x- b x p ln + b+ ∋ - a tan ) 1 2 2 2 1 z ( atan = 6( A 1 ∋ 2 ∋ 1z ∋1 z x + ∋ 1z
将式 ( 13) 作傅氏逆变换可得应力分量为
x
= =
A1 ∋ 1 -
z
A 1 G( x , ∋ A2 G ( x, ∋ 1 z) 2z ) + p ∋1 x ∋ 2 x G(x , ∋ 1z ) G( x , ∋ 2 z) - A2 p (∋ 1 z) ( ∋2 z ) G( x, ∋ iz ) = 1 2 2 ln[ x + ( ∋ iz ) ] ; 2( G( x , ∋ iz ) = - 1 2 x 2 , ( i = 1, 2) 。 x (x + ( ∋ iz )
2 - ∋| & |z - ∋| & |z ∋| & |z ∋ |& |z
1. 2. 2 横观各向同性体平面问题的两种求解思路 a) 第一种求解思路 ∃( & , z)
经傅氏逆变换
∃( x , z )
代入边界条件
x
,
z
,
zx
, u, w
b) 第二种求解思路
86
边界条件
经傅氏变换
∃( & , z)
[ 8, 9]
同性地基中的解由塞露蒂给出, 而在横观各向同性地基中的解析解, 经典的弹性力学并没有给出。这里也沿 用这个名词, 称之为横观各向同性地基的平面塞露蒂问题。如 图 1 所示的坐标系, 以水平线分布集中力的作用点 o 为坐标原 点, 以横向平面 ( 水平面 ) 内的两个相互垂直方向为 x 、 y 轴, 以 纵向( 垂直于层面的铅直方向) 为 z 轴。其基本方程为: ( 1) 平衡方程
zx
= P# ( x)
, x= 0 0, x 0 1. 2 横观各向同性体平面问题的解法 1. 2. 1 横观各向同性体平面问题的应力函数及其傅氏变换 由几何方程式( 2) , 将 x 对 z 的二阶导数和 z 对 x 的二阶导数相加, 可得变形协调方程 : ! zx + = ( 4) x z z x 若体力为常量, 把横观各向同性体平面问题的应力分量也表示为 2 2 2 ∃ ∃ ∃ x= 2 - f x ( x) , z= 2 - f z ( z) , zx = ( 5) x z z x 式中 ∃= ∃( x , z ) 仍称为艾瑞( G. B. Airy) 应力函数。 应力函数 ∃( x , z ) 自动满足平衡方程式( 1) 。将横观各向同性体平面应变问题的物理方程式 ( 3) 代入 变形协调方程式 ( 4) , 然后再将式 ( 5) 代入, 即得到用应力函数表示的相容方程
2 2 2
x= -
zx
= A1
式中
Ai=
∋ i ; ∋ 1- ∋ 2
G( x, ∋ ∋ iz ) iz = - 1 2 2; (∋ z ) ( i x + (∋ iz ) 若令 E 1 = E 2 = E , ∀ 1= ∀ 2 = ∀, G =
2 x
E , 则式 ( 14) 变为 2( 1+ ∀)
2x 2 2 2 ; (( x + z )
在象空间求解
x
经傅氏逆变换
,
z
,
zx
, u,w
x
,
z
,
zx
, u, w
按照第一种求解思路涉及到积分方程组, 积分和求导均很繁, 而按第二种思路求解相对简单些。因 此, 笔者将按第二种思路求解 1. 3 。 横观各向同性地基平面塞露蒂问题的解答 对于正轴坐标系中的横观各向同性体平面塞露蒂问题来说, 只需考虑 Z ! 0 的下半平面 , 所以对应力 函数的象 ∃( & , z ) 只能取式 ( 8) 的后半部分, 即 ∃( & , z ) = ce 当 z = 0 时,
85
( 2) 几何方程 u w u w , , ! + z= zx = x z z x 式中 u 、 w 分别为沿 x 、 z 轴的位移。 ( 3) 物理方程 ( 本构方程 ) 由于本问题是平面应变问题, y = ! xy = ! yz = 0 , 这时横观各向同性体物理方程式为
x
=
( 2)
x
2 = 1 ( 1- ∀1 ) E1
x
x
zx
+ +
xz
z
z
+ fx = 0 ( 1) + fz = 0
x
z
式中 , f x 、 f z 分别为沿 x 、 z 轴的体积力;
x
、 y 分别为沿 x 、 z 轴的正应力 ; 为沿 x 方向的剪应力。
图 1 横观各向同性地基的平面塞露蒂问题
zx
收稿日期 : 2003- 09- 18 作者简介 : 王春河 ( 1972- ) , 男 , 山东冠县人 , 工程师 , 研究方向 : 岩土工程理论及工程施工技术与管理 .
2 2 2 x 2 x 2
E 1 ∀2 1 ) 2 ( 1% E 2
2
4 x
∃ 4 +
1 2 2 G 2 - E 2 ( 1+ ∀1 ) ∀
∃ 1 2 ∃ ( 1- ∀1 ) 4 = 0 2+ E1 x z z
4 2 4
( 6)
由此可知, 当体力为常量时, 横观各向同性体平面问题的求解归结为寻求满足方程式 ( 7) 及边界条件 的应力函数 ∃( x , z ) 。将式( 6) 对 x 作傅氏变换可得 :
x
= =
2 ∋| & |z 2 ∋ |& |z i& 2 1 (∋ - ∋ ) 2e 1 e |& |( ∋ 2- ∋ 1)