人教版2019届九年级中考复习数学课件:第26课时 全等三角形 (共19张PPT)
合集下载
三角形全等判定复习ppt课件
N 明方法与前题基本相同,只
须证明⊿ABN≌⊿BCM
A
C
B
变式4:如图,⊿ABD,⊿ACE都是正三角形, 求证CD=BE
D
A
E
B
C
分析:此题实质上是把题目中的条件B,A,C三点改为 不共线,证明方法与前题基本相同.
变式6:如图,分别以⊿ABC的边AB,AC为一边 画正方形AEDB和正方形ACFG,连结CE,BG.
求证BG=CE
E
分析:此题是把两个三
角形改成两个正方形而
D
A
G 以,证法类同
FBBiblioteka C小结:1.证明两个三角形全等,要结合题目的条件 和结论,选择恰当的判定方法
2.全等三角形,是证明两条线段或两个角相 等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三 角形中。
②分析要证两个三角形全等,已有什么条件,还缺 什么条件。
AB=CB
A
AD=CD
BD=BD
_
=
P
∴ △ABD≌△CBD(SSS)
B
D
∴∠ABD=∠CBD
_
=
在△ABP和△CBP中
C
AB=BC
∠ABP=∠CBP
BP=BP
∴ △ABP ≌ △CBP(SAS)
∴PA=PC
例4。已知:如图AB=AE,∠B=∠E,BC=ED AF⊥CD 求证:点F是CD的中点
分析:要证CF=DF可以考虑CF 、 DF所在的两个三角形全等,为此可 添加辅助线构建三角形全等 ,如何 添加辅助线呢?
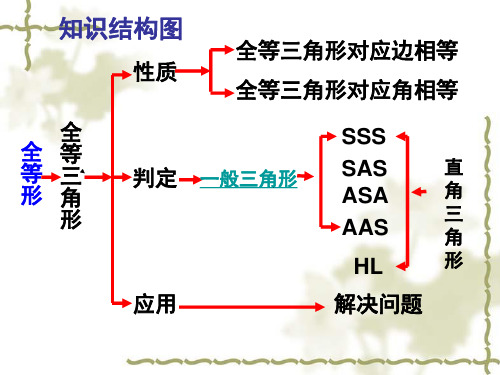
知识结构图
性质
全等三角形对应边相等 全等三角形对应角相等
全 全等 等三 形角
形
人教版九年级数学中考总复习《全等三角形》 (共23张PPT)

等三角形的判定方法SAS即可得解. 证明:∵∠1=∠2,
∴∠1+∠FBE=∠2+∠FBE,即∠ABE=∠CBF.
∴△ABE≌△CBF(SAS).
考题再现 1. (2014深圳)如图1-4-3-7,△ABC和△DEF中,AB=DE,∠B= ∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( C )
∴△AED≌△AEF(SAS).
考点点拨: 本考点的题型一般为解答题,难度中等. 解答本考点的有关题目,关键在于掌握全等三角形的判定方法 与思路. 注意以下要点: 判定两个三角形全等的一般方法有SSS、SAS、ASA、AAS、HL (相关要点详见“知识梳理”部分),同时要结合其他知识点 如平行线、平行四边形的性质等来证明三角形全等. 另外,注 意AAA、SSA不能判定两个三角形全等,判定两个三角形全等时, 必须有边的参与,且若有两边一角对应相等时,角必须是两边 的夹角.
3. 全等三角形的判定 (1)边边边:三边对应相等的两个三角形全等(可简写成 “SSS”). (2)边角边:两边和它们的夹角对应相等的两个三角形全等 (可简写成“SAS”). (3)角边角:两角和它们的夹边对应相等的两个三角形全等 (可简写成“ASA”). (4)角角边:两角和其中一角的对边对应相等的两个三角形 全等(可简写成“AAS”). (5)斜边直角边:斜边和一条直角边对应相等的两个直角三 角形全等(可简写成“HL”).
方法规律
中考考点精讲精练
考点1 全等三角形的概念和性质
考点精讲
【例1】(2016厦门)如图1-4-3-1,点
E,F在线段BC上,△ABF与△DCE全等,
点A与点D,点B与点C是对应顶点,AF与
DE交于点M,则∠DCE=
()
∴∠1+∠FBE=∠2+∠FBE,即∠ABE=∠CBF.
∴△ABE≌△CBF(SAS).
考题再现 1. (2014深圳)如图1-4-3-7,△ABC和△DEF中,AB=DE,∠B= ∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( C )
∴△AED≌△AEF(SAS).
考点点拨: 本考点的题型一般为解答题,难度中等. 解答本考点的有关题目,关键在于掌握全等三角形的判定方法 与思路. 注意以下要点: 判定两个三角形全等的一般方法有SSS、SAS、ASA、AAS、HL (相关要点详见“知识梳理”部分),同时要结合其他知识点 如平行线、平行四边形的性质等来证明三角形全等. 另外,注 意AAA、SSA不能判定两个三角形全等,判定两个三角形全等时, 必须有边的参与,且若有两边一角对应相等时,角必须是两边 的夹角.
3. 全等三角形的判定 (1)边边边:三边对应相等的两个三角形全等(可简写成 “SSS”). (2)边角边:两边和它们的夹角对应相等的两个三角形全等 (可简写成“SAS”). (3)角边角:两角和它们的夹边对应相等的两个三角形全等 (可简写成“ASA”). (4)角角边:两角和其中一角的对边对应相等的两个三角形 全等(可简写成“AAS”). (5)斜边直角边:斜边和一条直角边对应相等的两个直角三 角形全等(可简写成“HL”).
方法规律
中考考点精讲精练
考点1 全等三角形的概念和性质
考点精讲
【例1】(2016厦门)如图1-4-3-1,点
E,F在线段BC上,△ABF与△DCE全等,
点A与点D,点B与点C是对应顶点,AF与
DE交于点M,则∠DCE=
()
人教版《三角形全等的判定》PPT全文课件

知识回顾
问题探究
课堂小结
随堂检测
活动2
0
探究一:探索三角形全等的条件
建立模型,探索发现
只给定一条边相等:
只给定一个角相等:
3cm
3cm
3cm
30°
30°
30°
满足一个条件相等时,两个三角形不一定全等.
知识回顾
问题探究
课堂小结
随堂检测
活动3
0
探究一:探索三角形全等的条件
问题:两个三角形满足六个条件中的两个条件,两个三角形全等吗?两个条件有几种情况?
证明:连接AC,
【解题过程】
如图, 在四边形ABCD中, AB=AD, CB=CD, 求证:∠B=∠D.
∴∠B=∠D.(全等三角形对应角相等)
【思路点拨】先连接AC, 由于AB=AD, CB=CD, AC=AC, 利用SSS可证△ABC≌△ADC, 于是∠B=∠D. 要求学生从“形”思维到“质”的思维飞跃, 实现将“文字语言”, “图形语言”转化为“符号语言”.
∥
∵BC=DE, ∴BC+CD=DE+CD. 即BD=CE.
【数学思想】 数形结合思想,分类讨论思想.
∴ ∠ADB=∠FEC,AD=EF (全等三角形对应角相等) ∴AD∥EF(同位角相等,两直线平行)
在△ABD和△FCE中
∴△ABD≌△FCE (SSS).
知识回顾
问题探究
课堂小结
随堂检测
例4
0
探究三:利用三角形全等的判定“SSS”解决问题
△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,请问AD⊥BC吗?请说明理由.
在△ABD和△ADC中,
∴△ABD≌△ACD (SSS).
问题探究
课堂小结
随堂检测
活动2
0
探究一:探索三角形全等的条件
建立模型,探索发现
只给定一条边相等:
只给定一个角相等:
3cm
3cm
3cm
30°
30°
30°
满足一个条件相等时,两个三角形不一定全等.
知识回顾
问题探究
课堂小结
随堂检测
活动3
0
探究一:探索三角形全等的条件
问题:两个三角形满足六个条件中的两个条件,两个三角形全等吗?两个条件有几种情况?
证明:连接AC,
【解题过程】
如图, 在四边形ABCD中, AB=AD, CB=CD, 求证:∠B=∠D.
∴∠B=∠D.(全等三角形对应角相等)
【思路点拨】先连接AC, 由于AB=AD, CB=CD, AC=AC, 利用SSS可证△ABC≌△ADC, 于是∠B=∠D. 要求学生从“形”思维到“质”的思维飞跃, 实现将“文字语言”, “图形语言”转化为“符号语言”.
∥
∵BC=DE, ∴BC+CD=DE+CD. 即BD=CE.
【数学思想】 数形结合思想,分类讨论思想.
∴ ∠ADB=∠FEC,AD=EF (全等三角形对应角相等) ∴AD∥EF(同位角相等,两直线平行)
在△ABD和△FCE中
∴△ABD≌△FCE (SSS).
知识回顾
问题探究
课堂小结
随堂检测
例4
0
探究三:利用三角形全等的判定“SSS”解决问题
△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,请问AD⊥BC吗?请说明理由.
在△ABD和△ADC中,
∴△ABD≌△ACD (SSS).
2019年中考数学第一阶段复习课件:全等三角形 (共19张PPT)

【例4】(2017·衡阳)如图,已知线段 AC,BD 相交于
点 E,AE=DE,BE=CE. (1)求证:△ABE≌△DCE; (2)当 AB=5 时,求 CD 的长.
考点梳理
考点二 全等三角形的性质
全等三角形的对应边相等,对应角相等.全等三角形的对应 线段(高、中线、角平分线)、周长、面积分别相等。
C
3.(2018·菏泽)如图, AB∥CD ,AB=CD, CE=BF,请写出DF与AE的数量关系,并证明你的结 论.
核心素养题
1.如图,有一张三角形纸片,已知,按下列方案 用剪刀沿着箭头方向剪开,可能得不到全等三角形 纸片的是( )
A.
B.
C.
D.
2.以四边形ABCD的边AB、AD为边分别向外侧作等边三 角形ABF和ADE,连接EB、FD,交点为G. (1)当四边形ABCD为正方形时(如图1),EB和FD的数量关 系是____________; (2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的 数量关系?请加以证明; (3)四边形ABCD由正方形到矩形到一般平行四边形的变化 过程中,∠EGD是否发生变化?如果改变,请说明理由; 如果不变,请在图3中求出∠EGD的度数。
2019年中考数学第一阶段复习 ---全等三角形
命题趋势:
考点 命题角度 备考方略
近几年中考试题对于 这一部分的考查主要 以全等三角形的性质 与判定为主预计2019 年将会延续往年的考 查形式全等三角形往 往与四边形或圆相结 合 全等三角形 掌握判定三角形全等所需要的 条件 的判定 全等三角形 能够判定两个三角形全等,并 的性质 能利用全等三角形的性质解决 相关题目
于点F,请添加一个条件,使得△ADC≌△BEC(不添加其他字 母及辅助线),你添加的条件是 ____________________ .
全等三角形-中考数学总复习精品课件

三角形全等的条件
如何找边相等、 角相等
1.找“角”相等的途径主要有:对顶角相等;两直线平行,同位角、 内错角相等;余角等角代换;角平分线;平行四边形对角相等等.
2.找“边”相等主要借助中点、平行四边形对边相等来证明.
三角形全等的证明
如何找边相等、 角相等
3.判定两个三角形全等的三个条件中,“边”是必不可少的.
垂足分别是点 D,E,AD=3,BE=1,则 DE 的长是( B )
3 A.2
B.2
C.2 2
D. 10
61.2如0° 图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=________.
7.如图,已知∠ABC=∠DCB,添加下列条件中的一个:①∠A=∠D,②AC=DB, ③AB=DC,其中不能确定△ABC≌△DCB的是_②_____(只填序号).
A.∠A=∠D B.AC=DF C.AB=ED D.BF=EC
平移加翻折型
2.如图,在△ABC和△DEF中,AB=DE,AC=DF,BE=CF,且 BC=5,∠A=70°,∠B=75°,EC=2,则下列结论中错误的是
( C)
A.BE=3 B.∠F=35° C.DF=5 D.AB∥DE
平移型
3.如图,小强利用全等三角形的知识测量池塘两端M,N的距离,如果
对称型
解:(1)在△ABC 和△ADC 中,AABC= =AADC,,∴△ABC≌△ADC(SSS), BC=DC,
∴∠BAC=∠DAC,即 AC 平分∠BAD (2) 由 (1) 得 ∠BAE = ∠ DAE , 在 △BAE 和 △DAE 中 ,
BA=DA, ∠BAE=∠DAE,∴△BAE≌△DAE(SAS),∴BE=DE AE=AE,
《全等三角形》PPT课件_人教版1

B
C
(等量减等量差相等)
即BD=CE.
课堂小结
1.这节课你有什么收获? ①知识方面 ②师友互助方面
2.班长点评、评选最佳学师、学友。
要求:独立思考,学友展示,学师给予点评、补充。
4. 如图,两个三角形全等,则锐角
的度数是________
a 50° c
58° 72°
b
a
c
指出下列全等三角形的对应边和对应角:
即∠1=∠2.
要求:①所有同学完成后,师友交流答案。②完成后请学友口答问 题,学师点评、完善。③其他师友倾听、补充。
4.如图,在△ ABC中,D是BC边上一点,
且△ABD ≌△ACD.求证AD BC.
证明: ∵ ΔABD≌ΔACD
A
∴ ∠ADB=∠ADC
(全等三角形的对应角相等)
又因为∵ ∠ADB+∠ADC=180°B D
1.在图中,将ABC平移至DEF , 则 ABC △DEF.指出对应顶点、对应边和对应角。
要求:①所有同学完成后,师友交流答案。②完成后请学友口答问 题,学师点评、完善。③其他师友倾听、补充。
2.在图中,将ABC沿AC翻折至则ADC, 则ABC △ACD.指出对应顶点、对应边和对应角。
要求:①所有同学完成后,师友交流答案。②完成后请学友口答问 题,学师点评、完善。③其他师友倾听、补充。
《全等三角形》优秀课件人教版1-精 品课件p pt(实 用版)
典型例题
例4:如图,已知ΔABC≌ΔFED, 求证:AB∥EF
证明: ∵ΔABC≌ΔFED (已知)
∴∠ A=∠ F, ( 全等三角形的对应角相等 ) ∴A D AB∥EF
B
E F
C
人教版《全等三角形》PPT精品课件

练一练
一、挖掘“隐含条件”判全等
AD
1.如图(1),AB=CD,AC=BD,
则△ABC≌△DCB吗? 说说理由.
B 图(1) C
2.如图(2),点D在AB上,点E在AC B
D
上,CD与BE相交于点O,且
O
A
AD=AE,AB=AC.∠B=20°,CD=5cm,则 C ∠C= 20°,BE= 5c.m说说理由.
全等三角形的性质: 全等三角形的对应边、对应角相等.
全等三角形的判定 SAS、ASA、AAS、SSS、HL
角平分线的性质、判定:
三个角对应相等的两个三角形全等吗?
三个角对应相等的两个三角形不一定全等
两边和其中一边的对角对应相等的两个三 角形全等吗?
\
==
两边和其中一边的对角对应相等的两个三
角形不一定全等
3、全等三角形的性质?
例1: 如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是
.
要使△ABD≌△ACD,
两边和其中一边的对角对应相等的两个三角形全等吗?
证明题的方法①要证什么
B
添加条件判定全等
A
D
2. 如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
C
根据“SAS”需要添加条件AB=AC ;
12 A
EB
典例分析: 基本图形变式探究 例3:已知如图,AB⊥DC于B,且BD=BA,
BE=BC. 问:AC与DE有什么关系呢?
F
变式练习: 基本图形变式探究 变式1.将上题中的△DBE沿DC方向平移
A EE
DD
BF C
变式练习: 基本图形变式探究
人教版《全等三角形》优秀课件

(1)
记两个三角形全等时, 通常把表示对应顶点 的字母写在对应的位 置上.
△ABC和△DEF全等,记做△ABC≌△DEF. 符号“≌”表示全等,读作“全等于”.
练习
同学们再试着在图(2)(3)中,找到对应顶点、对应边
和对应角,并写成△***≌△***的形式.
A
B
C
E A
D
B
CD
(2)
(3)
△ABC≌△DBC
对应边为:EF与MN,EG与NH
方法3 从图形的生成过程出发,动态思考一个三角形是怎样与另一个三角形重合的.
(全等三角形的对应边相等)
E 符号“≌”表示全等,读作“全等于”. 1.1 H 生活中存在丰富的全等形,从哪种全等形开始研究呢?
M
的,是它们之间的一种特2.殊1 的关系,即全等关系.
在图(1)中,把△ABC 在图(2)中,把△ABC
利用全等三角形 ∴ AB=DE, BC=EF, CA=FD,
图(1)中,△ABC≌△DEF,对应边有什么关系?对应角呢?
54°
a
c
b1 c
的性质求解 ∠B与∠D.
对应角: ∠BAC与∠DCA,∠BCA与∠DAC,
60°
△ABC和△DEF全等,记做△ABC≌△DEF. ∵△ABC≌△DEF, 对应角: ∠BAC与∠DCA,∠BCA与∠DAC, 例 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1等于多少度?
字母排列的位置对应寻找;
方法2 如果题目中没有明确的符号表示,可以 B
D
从边的长短、角的大小出发.只有长度相同的边才 C
有可能成为对应边,大小相等的角,才有可能成为对应角;
方法3 从图形的生成过程出发,动态思考一个三角形是怎样
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点悟:判断两个三角形全等,先挖掘题目中隐含的条件 (如公共边、公共角、对顶角等),再根据具体条 件选择判定方法.
考点3:角的平分线的性质及判定
性质 判定
角的平分线上的点到角的两边的 距离 的点在
相等
. 上.
角的内部到角的两边的距离相等
角的平分线
[八上 P50 练习第 2 题]如图,△ABC 的 ABC 的外角的平 分线 BD 与∠C 的外角的平分线 CE 相交于点 P. 求证:点 P 到三边 AB、BC、CA 所在直线的距离相等.
证明:在 Rt△ ACB 和 Rt△ BDA 中
A
B
O AB BA D C BC AD ∴ Rt△ ACB ≌ Rt△BDA ( HL )
(2)若 ABC 35o ,求 CAO 的度数.
解:∵ C 90 , ABC 35
o o
A
B
∴ BAC 90o ABC 55o
a
66
o
.
54o
b
c
b
1
c
60o
[2016 厦门]如图,点 E,F 在线段 BC 上, △ ABF 与 △ DCE 全等,点 A 与点 D,点 B 与点 C 是对应 顶点,AF 与 DE 交于点 M,则 DCE ( A ) A. B C. EMF
A B M E
F
B. A D. AFB
一条直角边
分别相等的两个直角
三角形全等(“斜边、直角边”或“ HL ”).
[八上 P44 习题第 11 题]如图,点 B,F,C,E 在一 条直线上, FB CE ,AB∥ED,AC∥FD. A 求证: AB DE , AC DF .
证明:∵AB∥ED,AC∥FD B F ∴∠B =∠E,∠ACB =∠DFE
第26课时 全等三角形
考点1:全等三角形的概念及性质
全等 图形 能够 的两个图形叫做全等形, 大小 全等图形的形状和 都相同. 的两个三角形叫做全等 完全重合
全等三 能够 完全重合 角形 三角形.
性质
(1)全等三角形的 (2)全等三角形的
对应边 对应角
相等; 相等.
[八上 P33 习题第 3 题]如图是两个全等三角形,图中 的字母表示三角形的边长,则 1
B
C
∴ △ABD ≌ △ACD ( AAS )
∴ AB AC .
3.如图,在 △ ABC 中, AB AC ,点 D 在边 AC 上. (1)作图:连接 BD 并延长,在 BD 的延长线上取 点 E,使 AE AB ,连接 AE,作 EAC 的平分 线 AF,AF 交 DE 于点 F (用尺规作图,保留作图痕迹,不写作法);
相等
夹角 夹边
的两个三角形全等 对应相等的两个三角 对应相等的两个三角 分别相等的两个
(“边边边”或“ SSS ”). 两边和它们的 一般三 角形 两角和它们的 形全等(“边角边”或“ SAS ”). 形全等(“角边角”或“ ASA ”). 两角和其中一个角的 对边 直角三 角形 斜边和 三角形全等(“角角边”或 AAS ”).
AB AD BC DC AC AC
A
B
D
C
∴ △ ABC ≌ △ ADC ( SSS )
∴ BAC DAC .
2.[2016 镇江]如图,AD,BC 相交于点 O, AD BC ,
C D 90o .
(1)求: △ ACB ≌ △ BDA ;
C
D
E
∵FB =CE ∴ FB FC CE FC 即BC=EF ∴△ABC≌△DEF( ASA ) ∴AB =DE,AC =DF.
1.[2016 福州]一个平分角的仪器如图所示,其中
AB AD , BC DC .求证: BAC DAC .
证明:在 △ ABC 和 △ ADC 中
A B
D
C
2.如图所示,已知 1 2 ,请你添加一个条件, 证明: AB AC . (1)你添加的条件是 (2)请写出证明过程.
解:(1)添加的条件是 B C (答案不唯一)
;
A
12
D
(2)证明:在 △ABD 和 △ACD 中
B C 1 2 AD AD
D
C
如图,在 △ ABC 和 △ EDB 中, C EBD 90o , 点 E 在 AB 上,若 △ ABC ≌ △ EDB , AC 4 ,
BC 3 ,则 AE 的长为
1
D
.
B A E
C
点悟:掌握全等三角形的对应边相等,对应角相等是解 题的关键.
考点 2:三角形全等的判定
三边分别
解:过点D作DE⊥AB,垂足为E
D P
由题意得 AP 是 CAB 的平分线, C 90o
解:(1)如图所示;
A
D
E F
A
D
B
B
C
C
(2)在(1)条件下,连接 CF,求证: E ACF .
(2)证明:∵ AB AC , AB AE
E A D B
C
∴ AE AC ∵AF 平分 EAC
F
∴ EAF CAF 又∵ AF AF
∴ △ AEF ≌ △ ACF ∴ E ACF .
证明:过点P分别作PM⊥AB, PN⊥BC, PQ⊥AC,垂足分别为M、N、Q. ∵BD是∠ABC的外角的平分线,
Q
C
D P
N
A B M
E
PM⊥AB,PN⊥BC
∴PM =PN ∴PM =PN =PQ
即点P到三边AB、BC、CA所在直线的距离相等.
[2016 淮安]如图,在 Rt△ ABC 中, C 90o .以顶点 A 为圆心,适当长为半径画弧,分别交 AC,AB 于点 M,N, 再分别以点 M,N 为圆心,大于 1 MN 的长为半径画弧, 2 两弧交于点 P,作射线 AP 交边 BC 于点 D,若 CD 4 , AB 15 ,求 △ ABD 的面积. C
∵ Rt△ ACB ≌ Rt△BDA
∴ BAD ABC 35o
C
O
D
∴ CAO BAC BAD
55o 35o 20o .
1. 如图 , 已知 AB AD , 添加下列一个条件后 , 仍无法判定 △ ABC ≌ △ ADC 的是( C ) A. CB CD B. BAC DAC C. BCA DCA D. B D 90o
