11化学动力学(一)习题PPT优秀课件
合集下载
化学动力学-快速反应的实验方法PPT课件

化学松弛法
当一个快速对峙反应在一定的外界条件下达成 平衡,然后突然改变一个条件,给体系一个扰动, 偏离原平衡,在新的条件下再达成平衡。
对平衡体系施加扰动信号的方法可以是脉冲 式、阶跃式或周期式。改变反应的条件可以是温 度跃变、压力跃变、浓度跃变、电场跃变和超声 吸收等多种形式。
例:采用化学松弛法研究某二级对峙反应,以测定对峙反 应的速率常数。反应和速率方程如下:
快速反应的实验方法
化学反应动力学研究的实质是测量体系组成随时间 的变化,对于快速反应,检测方法必须足够灵敏以 反映组成的变化。常用方法:压力测量,核磁共振, 紫外和可见光谱,气相色谱等等,选择原则是分析 时间快于反应时间。
测量技术的反应时间范围
例:电子自旋共振谱(探 测含未成对电子的物质) 中,谱的吸收峰宽度代表 了自由基的平均寿命,由 量子力学测不准关系式, 峰越宽,寿命越短。
将X代入速率方程,得:
dcB dt
k1cA2
k1cB2
dX dt
k1(cAe
X )2 k1(cBe
X )2
X2 X dX dt
k1cA2 e k1cB2e (2k1cAe 2k1cBe ) X
dX k1cA2 e k1cB2e dt
(2k1cAe 2k1cBe ) X
近似一级反应
dX dt
(2k1cAe 2k1cBe )X
ln
X 初始 X
=(2k1cAe 2k1cBe )t
通过实验测定反应的弛豫时间t,t的定义为当cBe 如果B均由A转化来t 1 =2k1(cA0 cBe ) 2k1cBe
由于温度变化范围很小,所以速率系数的变化也很小,可 以近似认为不变,从而可通过测定一系列平衡浓度下的弛
化学动力学

返回
2021/1/23
3.基元反应的速率方程——质量作用定律
➢ 反应分子数
在元反应中反而反应物分子个数之和
AP A+BP 2A + B P
单分子反应 双分子反应(多数) 三分子反应
➢ 质量作用定律
对于基元反应 aA + bB + … 产物
dcB dt
kcAa cBb ...
反应速率与反应物浓度的幂乘积成正比。 幂指数是基元反应中各反应物的系数。
dpA/dt =kp pAn
可知: k=kp (RT)n-1
上一内容 下一内容 回主目录
返回
2021/1/23
§11.2 速率方程的积分形式
➢ 零级反应 ➢ 一级反应 ➢ 二级反应 ➢ n 级反应
上一内容 下一内容 回主目录
返回
2021/1/23
1.零级反应
➢ 定义:
A → 产物
反应速率与反应物A浓度的零次方成正比 即:反应速率与反应物浓度无关
返回
2021/1/23
3.二级反应
b) 当a b,但cB,0/b= cA,0/a,则任一时刻cB/b = cA/a 所以:
dcA dt
kAcAcB
b a
kAcA2
kA cA2
积分形式:
1 cA
1 cA,0
kA t
kA
b a
k
上一内容 下一内容 回主目录
返回
2021/1/23
3.二级反应
c) 当a b,但cB,0 cA,0,则任一时刻cB cA
返回
2021/1/23
4.化学速率方程的一般形式,反应级数
例如:
r k0
r k[A]
《化学动力学习题》PPT课件
1 a n 1
kn的单位:
moldm3 1n s -1
8
化学动力学习题课
三.复杂反应 (1)对峙反应
A k1 B
特征
k1
k 1
B(y)
(2)平行反应
C(z)
A
k 2
k 1 K k
1
yk 1
zk 2 9
化学动力学习题课
(3)连串反应
A k B k C 对B可以获得最大产率及所需要的时间
1
2
K
ln( 2 )
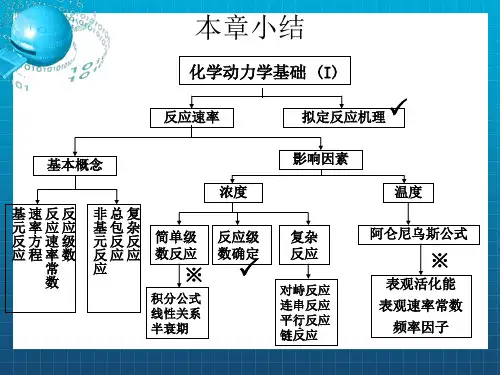
本章小结
化学动力学基础 (I)
反应速率
拟定反应机理
基本概念
基速反反 元率应应 反方速级 应程率数
常 数
浓度
非总复 基包杂 元反反 反应应 应
简单级 数反应
※
反应级 数确定
积分公式 线性关系 半衰期
影响因素
复杂 反应
对峙反应 连串反应 平行1 反应 链反应
温度
阿仑尼乌斯公式
※
表观活化能 表观速率常数
3.KM和rm的确定
ห้องสมุดไป่ตู้
r k2 [E0 ][S] KM [S] 14 rm k2 [E0 ]
1 KM 1 1 r rm [S] rm
化学动力学习题课
八.反应机理的确定
1.假设反应机理,利用质量作用定律,写
出基元反应的速率方程。
2.依据稳态近似法、平衡态假设法或速决步确定反应的速率方程。
K
t 最大、B K
1
K
2
101
化学动力学习题课
四. Arrhenius方程
ln k Ea B RT
e k A
Ea RT
11化学动力学(一)习题ppt课件

(A) 提高反应温度 (B) 延长反应时间 (C) 加入适当催化剂 (D) 降低反应温度
8
C
某具有简单级数反应的速率常数的单位是 mol·dm-3·s-1,该化学反应的级数为: () (A) 2 级 (B) 1 级 (C) 0 级 (D) 3 级
9
B
. 基元反应的分子数( ) (A) 可以是0,1,2,3 (B)只能是 1,2,3 这三个正整数 (C) 可以是小于1的数 (D)正数,负数和零都可以
Ea ,2
1 2
Ea,1 2Ea,4
B、Ea Ea,2 Ea,1 Ea,4 1/2
C、Ea
Ea ,2
1 2
Ea,1 Ea,4
D、Ea
Ea
,2
(
Ea ,1 2Ea,4
)
1 2
12
Ea
k Ae RT
ln k ln A Ea
1
RT
k
k2
k1 2k4
2
1 ln k ln k2 2 (ln k1 ln k4 ln
A2
Ea,2 RT
1 2
ln
A1
Ea,1 RT
ln
A4
Ea,4 RT
ln 2
[ln
A2
1 2
ln
A1
ln
A4
ln
2]
[
Ea,2
1 2
( Ea,1 RT
Ea,4
) ]
13
、由动力学实验测得某反应的若干组cAt数 据, 然后以lncA对t作图得一直线, 已知该直 线的截距为100, 斜率为2.0102 s1, 则该
10
C
. 反应2A+2B→C,其速率方程式v=k[A][B]2, 则对A而言,反应级数为( )。 (A)4; (B)3; (C)1; (D)2
8
C
某具有简单级数反应的速率常数的单位是 mol·dm-3·s-1,该化学反应的级数为: () (A) 2 级 (B) 1 级 (C) 0 级 (D) 3 级
9
B
. 基元反应的分子数( ) (A) 可以是0,1,2,3 (B)只能是 1,2,3 这三个正整数 (C) 可以是小于1的数 (D)正数,负数和零都可以
Ea ,2
1 2
Ea,1 2Ea,4
B、Ea Ea,2 Ea,1 Ea,4 1/2
C、Ea
Ea ,2
1 2
Ea,1 Ea,4
D、Ea
Ea
,2
(
Ea ,1 2Ea,4
)
1 2
12
Ea
k Ae RT
ln k ln A Ea
1
RT
k
k2
k1 2k4
2
1 ln k ln k2 2 (ln k1 ln k4 ln
A2
Ea,2 RT
1 2
ln
A1
Ea,1 RT
ln
A4
Ea,4 RT
ln 2
[ln
A2
1 2
ln
A1
ln
A4
ln
2]
[
Ea,2
1 2
( Ea,1 RT
Ea,4
) ]
13
、由动力学实验测得某反应的若干组cAt数 据, 然后以lncA对t作图得一直线, 已知该直 线的截距为100, 斜率为2.0102 s1, 则该
10
C
. 反应2A+2B→C,其速率方程式v=k[A][B]2, 则对A而言,反应级数为( )。 (A)4; (B)3; (C)1; (D)2
化学动力学-反应速率方程PPT课件

k[Cl2 ]1Fra bibliotek 2[H2 ]
Br2 H2 2HBr
v 1 d[HBr] k[Br2]1/2[H2] 2 dt 1 k[HBr] / [Br2]
反应速率方程
Reaction Rate Equations
反应速率方程 (动力学方程) ——在其它因素固定不变的条件下,定量描
述各种物质的浓度对反应速率影响的数学方程。
v f (cA ,cB , )
反应速率方程由反应本性决定,与反应器的型式 和大小无关。 严格的反应速率方程难以获得,一般用经验半经 验方法得到近似的速率方程。
(mol m3 )1n s1
k kA kP
A P
非幂函数型速率方程
(non-power function type)
v
1
kcAa cBb kcAa cBb
反应机理决定速率方程形式。
I2 H2 2HI Cl2 H2 2HCl
v
1 2
d[HI] dt
k[I2
][H2
]
v
1 2
d[HCl] dt
基元反应
反应分子数
AP
单分子反应
AB P
双分子反应
2A B P
三分子反应
基元反应(elementary reactions) :
基元反应的反应速率正比于该反应的反应物 浓度之积——质量作用定律(mass action law)
单分子反应 A P
v kcA
双分子反应 2A P
AB P
v kcA2 v kcAcB
复合反应(complex reactions):
幂函数型速率方程
(power function type)
Br2 H2 2HBr
v 1 d[HBr] k[Br2]1/2[H2] 2 dt 1 k[HBr] / [Br2]
反应速率方程
Reaction Rate Equations
反应速率方程 (动力学方程) ——在其它因素固定不变的条件下,定量描
述各种物质的浓度对反应速率影响的数学方程。
v f (cA ,cB , )
反应速率方程由反应本性决定,与反应器的型式 和大小无关。 严格的反应速率方程难以获得,一般用经验半经 验方法得到近似的速率方程。
(mol m3 )1n s1
k kA kP
A P
非幂函数型速率方程
(non-power function type)
v
1
kcAa cBb kcAa cBb
反应机理决定速率方程形式。
I2 H2 2HI Cl2 H2 2HCl
v
1 2
d[HI] dt
k[I2
][H2
]
v
1 2
d[HCl] dt
基元反应
反应分子数
AP
单分子反应
AB P
双分子反应
2A B P
三分子反应
基元反应(elementary reactions) :
基元反应的反应速率正比于该反应的反应物 浓度之积——质量作用定律(mass action law)
单分子反应 A P
v kcA
双分子反应 2A P
AB P
v kcA2 v kcAcB
复合反应(complex reactions):
幂函数型速率方程
(power function type)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
、实验测得化学反应S2O82 + 2I →I2 + 2SO4 2的
速率方程为
dcs2O82 dt
kc c S2O82 I
D
根据上述条件可以认为:
A 反应分子数为3
B 反应分子数为2
C 反应级数为3
D 反应级数为2
1
、反应2O3 →3O2其反应速率方程式为
dcO3 dt
kO3cO23cO12
或者
dcO2 dt
[lnA212lnA1lnA4ln2][Ea,212(RETa,1Ea,4)]
13
、由动力学实验测得某反应的若干组cAt数 据, 然后以lncA对t作图得一直线, 已知该直 线的截距为100, 斜率为2.0102 s1, 则该
反应的半衰期 为 s。 34.7s
. ln(a x) 与 时间 t 呈线性关系,为一级反
A 二级反应
D
B 基元反应
C 双分子反应
D 以上都无法确定
4
、某反应,当反应物反应掉5/9所需时间是它反 应掉1/3所需时间的2倍,则该反应是:
A.一级反应 B.零级反应 A
C.二级反应 D.3/2级反应
ln
1 1
y
k1t
5
、反应A+B→P为二级 反应, 反应物的起始 浓度相等,则其半衰期 与反应物起始浓度( ) A.无关 B.成正比 C.成反比 D.无法 判断
17
应
ln
a
a
x
k1t
lna-ln(ax)k1t
ln(ax)lna-k1t
斜率为-k1
t1/ 2
ln 2
k1
14
、由基元反应构成的复杂反应A 物质G的浓度变化为dcG/dt=
①③
k1 k2
G k3
H
②
。
k1cAk2cGk3cG
15
已知2NO + O2 = 2NO2 的反应机理拟定为: 2NO ⇄ N2O2 (快平衡,平衡常数为 K1)
10
C
. 反应2A+2B→C,其速率方程式v=k[A][B]2, 则对A而言,反应级数为( )。 (A)4; (B)3; (C)1; (D)2
11
某复杂反应的表观速率常数k与各基元反应速率
常数之间的关系式:
1
k
k2
k1 2k4
2
C
则表观活化能Ea与各基元反应活化能之间的关
系为:
A 、 EaEa,21 2Ea,12Ea,4 B 、 E aE a,2E a,1E a,41/2
(A) 提高反应温度 (B) 延长反应时间 (C) 加入适当催化剂 (D) 降低反应温度
8
C
某具有简单级数反应的速率常数的单位是 mol·dm-3·s-1,该化学反应的级数为: () (A) 2 级 (B) 1 级 (C) 0 级 (D) 3 级
9
B
. 基元反应的分子数( ) (A) 可以是0,1,2,3 (B)只能是 1,2,3 这三个正整数 (C) 可以是小于1的数 (D)正数,负数和零都可以
C 、 EaEa,21 2Ea,1Ea,4
D、Ea
Ea,2(2EEaa,1,4
1
)2
12
Ea
k Ae RT
lnk ln A Ea
RT
k
k2
k1 2k4
2
1 lnklnk22(lnk1lnk4ln2)
lnAR ETa lnA2E RaT,2 12lnA1E RaT,1lnA4E RaT,4ln2
N2O2+ O2 →2NO2 (慢反应,速率常数为 k2) 请推导证明总包反应对 O2是一级;对 NO 是二 级反应。(总反应速率可近似等于决速步速率)
16
rr2k2 [N 2 O 2]O [2]
根据平衡假设法:
[N2O2 ] [ NO ]2
K1
[N2O2]K1[N]O 2
rk2[N 2O 2]O [2] k2K1[N]O 2[O 2]
C
1 t1/2 k 2 a
6
B
.某反应的速率常数k=4.62×10-2min-1,又初始 浓度为0.1mol·dm-3,则该反应的半衰期为:
(A)10min (B)15min (C)30min (D)20min
7
.反应 A
B
(I) B
D
(II)
已知反应 I 的活化能 E1大于反应 II 的活化能 E2, 以下措施中哪一种不能改变获得 B 和 D 的比例?
kO2cO23cO12
则速率常数kO3和kO2的关系是
A 2kO3=3kO2
B kO3=kO2
C
C 3kO3=2kO2
D -3kO3=2kO2
2
r1dcO3 1dcO2 2 dt 3 dt
1 2kO3cO 23cO 12 1 3kO2cO 23cO 12
3kO3=2kO2
3
、某化学反应的方程式为2A→P,则在动力学研究中 中表明该反应为
速率方程为
dcs2O82 dt
kc c S2O82 I
D
根据上述条件可以认为:
A 反应分子数为3
B 反应分子数为2
C 反应级数为3
D 反应级数为2
1
、反应2O3 →3O2其反应速率方程式为
dcO3 dt
kO3cO23cO12
或者
dcO2 dt
[lnA212lnA1lnA4ln2][Ea,212(RETa,1Ea,4)]
13
、由动力学实验测得某反应的若干组cAt数 据, 然后以lncA对t作图得一直线, 已知该直 线的截距为100, 斜率为2.0102 s1, 则该
反应的半衰期 为 s。 34.7s
. ln(a x) 与 时间 t 呈线性关系,为一级反
A 二级反应
D
B 基元反应
C 双分子反应
D 以上都无法确定
4
、某反应,当反应物反应掉5/9所需时间是它反 应掉1/3所需时间的2倍,则该反应是:
A.一级反应 B.零级反应 A
C.二级反应 D.3/2级反应
ln
1 1
y
k1t
5
、反应A+B→P为二级 反应, 反应物的起始 浓度相等,则其半衰期 与反应物起始浓度( ) A.无关 B.成正比 C.成反比 D.无法 判断
17
应
ln
a
a
x
k1t
lna-ln(ax)k1t
ln(ax)lna-k1t
斜率为-k1
t1/ 2
ln 2
k1
14
、由基元反应构成的复杂反应A 物质G的浓度变化为dcG/dt=
①③
k1 k2
G k3
H
②
。
k1cAk2cGk3cG
15
已知2NO + O2 = 2NO2 的反应机理拟定为: 2NO ⇄ N2O2 (快平衡,平衡常数为 K1)
10
C
. 反应2A+2B→C,其速率方程式v=k[A][B]2, 则对A而言,反应级数为( )。 (A)4; (B)3; (C)1; (D)2
11
某复杂反应的表观速率常数k与各基元反应速率
常数之间的关系式:
1
k
k2
k1 2k4
2
C
则表观活化能Ea与各基元反应活化能之间的关
系为:
A 、 EaEa,21 2Ea,12Ea,4 B 、 E aE a,2E a,1E a,41/2
(A) 提高反应温度 (B) 延长反应时间 (C) 加入适当催化剂 (D) 降低反应温度
8
C
某具有简单级数反应的速率常数的单位是 mol·dm-3·s-1,该化学反应的级数为: () (A) 2 级 (B) 1 级 (C) 0 级 (D) 3 级
9
B
. 基元反应的分子数( ) (A) 可以是0,1,2,3 (B)只能是 1,2,3 这三个正整数 (C) 可以是小于1的数 (D)正数,负数和零都可以
C 、 EaEa,21 2Ea,1Ea,4
D、Ea
Ea,2(2EEaa,1,4
1
)2
12
Ea
k Ae RT
lnk ln A Ea
RT
k
k2
k1 2k4
2
1 lnklnk22(lnk1lnk4ln2)
lnAR ETa lnA2E RaT,2 12lnA1E RaT,1lnA4E RaT,4ln2
N2O2+ O2 →2NO2 (慢反应,速率常数为 k2) 请推导证明总包反应对 O2是一级;对 NO 是二 级反应。(总反应速率可近似等于决速步速率)
16
rr2k2 [N 2 O 2]O [2]
根据平衡假设法:
[N2O2 ] [ NO ]2
K1
[N2O2]K1[N]O 2
rk2[N 2O 2]O [2] k2K1[N]O 2[O 2]
C
1 t1/2 k 2 a
6
B
.某反应的速率常数k=4.62×10-2min-1,又初始 浓度为0.1mol·dm-3,则该反应的半衰期为:
(A)10min (B)15min (C)30min (D)20min
7
.反应 A
B
(I) B
D
(II)
已知反应 I 的活化能 E1大于反应 II 的活化能 E2, 以下措施中哪一种不能改变获得 B 和 D 的比例?
kO2cO23cO12
则速率常数kO3和kO2的关系是
A 2kO3=3kO2
B kO3=kO2
C
C 3kO3=2kO2
D -3kO3=2kO2
2
r1dcO3 1dcO2 2 dt 3 dt
1 2kO3cO 23cO 12 1 3kO2cO 23cO 12
3kO3=2kO2
3
、某化学反应的方程式为2A→P,则在动力学研究中 中表明该反应为
